Introduction

The demand for lightweight, high-performance materials that can sustain mechanical integrity at ultralow temperatures is increasing due to advancements in hydrogen storage, aerospace applications and quantum computing1,2. Liquid hydrogen storage systems operate at 20 K, and structural components for spacecraft and satellite systems encounter severe cryogenic conditions during space missions3,4. Furthermore, next-generation quantum computing devices require extreme cold (4–20 K) to maintain the coherence of qubits1,5. One of the most significant challenges is to develop lightweight, strong, and ductile materials that can sustain deformation without failure at cryogenic temperatures below 20 K. While face-centered cubic (fcc) alloys, such as high-entropy alloys and austenitic steels, exhibit excellent strength-ductility synergy at cryogenic temperatures, their high cost and limited printability pose challenges. In contrast, additively manufactured (AM) aluminum-based alloys provide a scalable and cost-effective alternative. However, their mechanical behavior at extreme cryogenic temperatures remains largely unexplored.

Laser powder bed fusion (LPBF), a leading AM process, has revolutionized the production of high-performance alloys, including aluminum-based alloys like Al10SiMg6,7. The ability of LPBF to create intricate, lightweight structures with tailored properties has enabled advances in aerospace, automotive, and defense applications8,9,10. However, most studies on LPBF alloys have focused on their mechanical performance at ambient temperatures7,11,12,13,14,15,16. Despite its critical importance, the deformation behavior of LPBF alloys at cryogenic temperatures remains underexplored. This knowledge gap must be addressed to support the development of next-generation cryogenic systems for hydrogen energy storage, aerospace, and quantum computing.

This study investigates the deformation of LPBF-fabricated and hot isostatic pressed (HIPed) Al10SiMg at 15 K, providing one of the first detailed analyses of its mechanical response at ultralow temperatures. Using in-situ neutron diffraction, we tracked real-time stress evolution and lattice strain development in both the α-Al matrix and the Si precipitates, enabling unique insights into stress partitioning, phase-specific deformation, and grain refinement mechanisms. While in-situ neutron diffraction provides valuable insights into phase-specific stress partitioning and strain evolution, it assumes homogeneous stress distribution within each phase. This limitation may introduce slight discrepancies in absolute stress values. Additionally, neutron diffraction provides an averaged response from a large material volume, which could overlook localized strain gradients at phase boundaries. Despite these limitations, neutron diffraction remains a powerful technique for real-time deformation analysis at extreme temperatures. The findings presented here establish LPBF Al10SiMg as a viable candidate material for lightweight cryogenic applications due to its improved performance at 15 K.

Results

Mechanical properties comparison at room temperature

The tensile stress–strain curves of four LPBF-fabricated and HIPed Al10SiMg alloys, produced under four different scanning and laser power conditions (Table S1 and Fig. S1), are shown in Fig. 1. The mechanical properties, such as yield strength, ultimate tensile strength, total elongation, and elastic modulus are listed in Table 1. The samples with scanning speeds of 0.6, 0.8 and 1.1 m/s (laser power between 200 and 400 W) showed good mechanical properties for industrial applications. However, the sample with the highest scanning speed (1.4 m/s) and the lowest laser power (85 W) was weak and brittle. As it has been reported for similar processing parameters by LPBF17, the weak bonding could be related to insufficient melting caused by the low energy transferred to the powder. As a result, the sample had just 24 MPa yield strength and <1.5% elongation. All the other samples had yield strength between 63 and 91 MPa, the ultimate tensile strength of 164 and 179 MPa, and an average total elongation of ~19.5%. Among all these alloys, the one with 1.1 m/s scanning speed and 275 W laser power showed the best strength–ductility combination. Hence, this alloy was selected for microstructural and in-situ neutron diffraction deformation investigations at room temperature (RT) and cryogenic deformation at 15 K.

Fig. 1: Tensile stress-strain curves at room temperature.
figure 1

Stress-strain curves of Al10SiMg alloys produced by laser powder bed fusion and hot isostatic pressing, using four different processing parameters, i.e., laser power (in W) and scanning speed (in m/s).

Full size image
Table 1 Mechanical properties of four LPBF+HIPed Al10SiMg alloys tested at room temperature: yield strength (σYS), ultimate tensile strength (σUTS), total elongation (εt), and elastic modulus (E) comparison of alloy with different process parameters
Full size table

Microstructure of as-built and HIPed samples

Optical and scanning electron microscopy (SEM) images of the selected as-built sample (scanning speed of 1.1 m/s and laser power of 275 W) are given in Fig. 2. The arch-shaped molten pool boundaries can be observed perpendicular to the build direction as a result from the layer-by-layer LPBF processing (Fig. 2a). The microstructure consists of eutectic microconstituent (α + Si phase) surrounding the grains of α-Al matrix as seen in Fig. 2b, c. Figure 2d shows SEM-EDS chemical analysis for the present phases (α-Al matrix and eutectic phase) in the Al10SiMg alloy.

Fig. 2: Microstructure of as-built alloy (laser power: 275 W and scanning speed: 1.1 m/s).
figure 2

a Optical micrograph showing general view and melt pool boundary with a cellular structure. b, c SEM images displaying coarse and fine cells consisting of α-Al matrix and eutectic phase. d EDS elemental analyses of the constituent phases.

Full size image

SEM microstructure shows a transition from a fine cellular-dendritic structure to a coarser dendritic structure from center towards the melt pool border (Fig. 2b). In other words, it consists of coarser zones at the heat affected zone regions or melt pool boundaries. Upon closer inspection, Fig. 2c reveals the dendritic and inter-dendritic structure, showcasing the significant impact of heat flux during layer-wise manufacturing on the microstructure of LPBF material. As a result, heterogeneous microstructural features are prevalent.

The microstructure of the selected sample after HIPing treatment is presented in Fig. 3. It is clear that melt pool structure through eutectic network began to disappear, and slightly coarsened Si particles are observed after HIPing process. Basically, the HIPing treatment enhances densification by reducing porosity, resulting in a more compact bulk structure. At the applied temperature, it promotes the partial dissolution of pre-existing Mg2Si and Al-Si eutectic phases, leading to a Si-enriched matrix. Subsequent cooling facilitates the precipitation of fine Si-enriched precipitates18,19,20.

Fig. 3: Representative microstructure after hot isostatic pressing.
figure 3

a Optical micrograph, and (b) SEM-BSE image.

Full size image

Figure 4 shows electron backscatter diffraction (EBSD) orientation map and pole figures of HIPed sample. It also shows representative EBSD inverse pole figure (IPF) maps along the build direction (BD), transverse direction (TD) and the normal direction (ND). IPF maps show a preferred orientation of crystals towards <001> and <101> relative to BD, which can be expected in LPBF-fabricated alloys21. A stronger orientation of grains towards <111> and <001> can be observed relative to TD and ND. IPF maps are congruent with the pole figures of the Al matrix, which show a strong intensity of {001}, {101}, and {111} planes. This preferred orientation is compatible with the cube texture commonly reported in annealed fcc metals22, being possibly associated to the HIPing post-treatment. Different melt pools can be distinguished because the elongated grains grow towards the center of the melt pool and epitaxial growth occurs due to heterogeneous heat flow23. At the centerline of the melt pool, grains grow epitaxially, whereas away from the centerline, smaller nucleated grains can be observed. Similar observations have been reported in Al10SiMg alloy produced by LPBF previously23.

Fig. 4: Orientation map and pole figures of hot isostatic pressed sample before deformation.
figure 4

EBSD orientation map showing the crystallographic texture and grain structure, accompanied by pole figures that indicate the preferred crystal orientations.

Full size image

In-situ mechanical properties at 293 and 15 K

Figure. 5 shows engineering and true stress-strain curves along with the strain-hardening rate curves of Al10SiMg alloy (LPBF at 275 W and 1.1 m/s, followed by HIPing) at room temperature (RT) and ultralow temperature (ULT) of 15 K. The alloy at 15 K showed the yield strength of 124 MPa and delayed necking (Fig. 5a), being an indication of an effective defect-driven dislocation blocking capability as well as high dislocation accumulation capability. While dislocation blocking results in strengthening, the capability for dislocation density increment resulted in the high strain-hardening in Fig. 5c. As expected from the high strain-hardening of the alloy tested at 15 K, the difference between yield (124 MPa) and ultimate (395 MPa) strength is significantly large, i.e., ~3.2-fold. In contrast, the alloy tested at RT has just a 2-fold increment from the yield (80 MPa) to the ultimate (160 MPa) strength, which is explained by its lower strain-hardening rate compared to the ULT-deformed sample. The difference in strain-hardening rate between the samples, which is the capability to provide further work-hardening, also explains the higher ductility for the ULT-tested sample. Thus, the uniform elongation (εu) of the ULT-tested sample was ~25% while the RT-sample only reached to ~15%. From Fig. 5 and Table 2, εu of ULT-sample is quite close to its total elongation (εt), being another result of the high strain-hardening that delayed the necking instability. Both curves from Fig. 5c show a decreasing trend typical of alloys with a single strengthening mechanism. Dislocation slip and accumulation is expected to be the dominant mechanism based on the high stacking fault energy (SFE) of the Al10SiMg alloy.

Fig. 5: Mechanical behavior comparison during in-situ tensile testing at room temperature and 15 K.
figure 5

(a) Engineering stress-strain curves, (b) true stress–strain curves, and (c) strain-hardening rate curves.

Full size image
Table 2 Mechanical properties of in-situ deformed samples at RT and 15 K, including yield strength (\({\sigma }_{{YS}}\)), ultimate tensile strength (σUTS), uniform elongation (εu), total elongation (εt), extent of strain-hardening (∆σ=σUTS−σYS), and elastic modulus (E)
Full size table

Deformation-induced structure evolution

Figure. 6 shows representative neutron diffractograms along the loading direction during deformation at RT and 15 K. The alloy consists of two phases, i.e., Al phase (fcc, space group 225) and Si phase (diamond cubic, space group 227). The reflections for both phases are distinctively marked in Fig. 6. As expected, Al is the dominant phase and showed strong peaks. There are no apparent changes in the phases during deformation at RT and 15 K, except for peak shifting, change in intensity and peak broadening due to deformation.

Fig. 6: Neutron diffraction patterns during in-situ tensile deformation at room temperature and 15 K.
figure 6

Selected diffraction patterns along the loading direction at (a) room temperature and (b) 15 K. The deformation strain is indicated for each pattern on the right side of panel. The crystallographic reflections for Al and Si phases are also marked.

Full size image

The EBSD maps of deformed samples (after fracture) at both temperatures are shown in Fig. 7. EBSD analyses were performed on the section parallel to the loading axis which corresponds to normal direction (ND) in Fig. S1a. As is evident from Fig. 4, LPBF is often characterized by elongated grains pointing towards the centerline of melt pools which displays some degree of random texture24,25,26 (visible in Fig. 7 as well). Meanwhile, the elongated grains preferentially oriented along [001] indicating a strong texture confirmed by the high intensity of crystallographic planes oriented towards specific orientations as shown in the pole figures (right sides of Fig. 7a, b). The formation of complex texture components as a result of the deformation is evident in the appearance of locally intense signals in positions that differ from those shown by the cube texture of the as-HIPed sample (Fig. 4). This is a clear indication of crystal rotation due to deformation.

Fig. 7: Orientation maps and pole figures after deformation.
figure 7

EBSD grain orientation maps and pole figures near the fracture zones of tensile samples after deformation at (a) 293 K and (b) 15 K.

Full size image

The EBSD also revealed a non-uniform grain size distribution (see Fig. 7), which is a typical characteristic of the heterogeneous heat flow during LPBF. As a result of the intense deformation, the alloy deformed at 15 K demonstrates a more pronounced elongated grain size distribution. Grain boundary analysis at the zones displayed in Fig. 7, reveals a substantial presence of low-angle grain boundaries (LAGBs) within zone delimited by high-angle grain boundaries (HAGBs). This phenomenon is attributed to dislocation accumulation and rearranging into low-energy configurations, i.e., LAGBs, during deformation. Therefore, a substantial number of LAGBs are distributed at the boundary of the molten pool, with LAGBs accounting for 69% in the Al10MgSi alloy after deformation at RT and 74% after deformation at 15 K.

EBSD maps and IPFs of the tensile tested samples at higher magnifications are shown in Fig. 8. They show the presence of large columnar grains with preferred <001> texture along the build direction and <111> texture along the normal direction, which is stronger at 15 K. The columnar grains are accompanied by some semi-equiaxed grains with no evident preferred orientation. The development of elongated grains can also be observed at the top of the melt pool. There is also a small amount of equiaxed grains as a result of the so-called columnar to equiaxed transition27,28,29,30. As a result of the overlap between neighboring tracks and deformed regions, the partial remelting of previous layers can be observed, and therefore only very small part of the equiaxed grains formed by columnar to equiaxed transition.

Fig. 8: High-magnification orientation maps after deformation.
figure 8

EBSD grain orientation maps of tensile samples deformed at (a) 293 K and (b) 15 K.

Full size image

Both RT and 15 K conditions were constituted of α-Al matrix surrounded by a network of Si but the grain size distribution showed accelerated grain refinement at 15 K as shown in Fig. 9. 82% to 85% of grains in the as-HIPed and RT-deformed samples showed areas smaller than 100 μm2 but this percentage increased to 95% after deformation at 15 K. Moreover, the grain area of the sample deformed at 15 K range from 1.7 to 550 μm2 while those of the as-HIPed and RT-deformed samples reach up to 910 and 860 μm2, respectively. This phenomenon may be related to the lower atomic diffusion at cryogenic temperatures that suppresses dynamic recovery, enhances dislocation density, and limits grain boundary migration.

Fig. 9: Grain area distribution before and after deformation.
figure 9

Comparison of grain area distribution for undeformed (as-HIP) and deformed samples at room temperature (RT) and ultralow temperature (ULT, 15 K).

Full size image

The enhancement of dislocation density during deformation at 15 K can be observed in the kernel average misorientation (KAM), geometrically necessary dislocations (GNDs), and grain boundary maps of Fig. 10. The highest GND density was observed in the sample deformed at 15 K (Fig. 10c), which agrees with its smallest grain size encouraged by more effective dislocation accumulation. High GND densities are commonly found in AM-produced alloys because they accommodate strain gradients given by microstructural heterogeneities, e.g., grain size, caused by thermal cycles and rapid solidification31. For this reason, GNDs are mostly found near interfaces between zones with mechanical mismatches. The green to red zones showing medium to high GND density in Fig. 10 can be mostly found near grain boundaries. Based on the high SFE of the Al10SiMg alloy, dislocations are expected to accumulate, form dislocation tangles, arranging in dislocation cells and blocks, before forming new grain boundaries.

Fig. 10: Geometrically necessary dislocation maps before and after deformation.
figure 10

Comparison of dislocation density maps for (a) undeformed (as-HIP), and deformed samples at (b) RT and (c) 15 K.

Full size image

Lattice strain and texture development during deformation

The evolution of lattice strain during deformation for different orientations is presented in Fig. 11 for both phases, i.e., Al and Si, at RT and 15 K. From Fig. 11, while the Al phase presents a nearly linear increasing behavior as a function of the applied true stress, the Si phase shows the higher lattice strain during the elastic region while relatively small increase in the plastic region. It should be recalled from Table 2 that the Si phase has ~1.6 times higher yield strength compared to the Al phase (124 vs 79 MPa). The lattice strain of Si and Al at RT reached up to 0.33 and 0.24%, respectively. However, the lattice strain of Si and Al phases at 15 K reached almost twice of the RT but almost to similar values for both phases. Though, the lattice strain initially developed faster for Si phase and then it saturated while it developed linearly for the Al phase until fracture. This behavior at 15 K (Fig. 11d) is drastically different than that at RT (Fig. 11b). Similar to RT, Si phase at 15 K has a higher yield strength compared to Al, and it develops higher lattice strain in the elastic region. At 15 K, the yield strength of Si phase is ~3 times higher than that of Al phase (272 vs 90 MPa). However, towards the end, the lack of any increase in lattice strain for Si points towards its permanent yielding and hence it can’t increase anymore. Table 3 shows the elastic moduli for different hkl planes (\({E}_{{hkl}}\)) for Al and Si phases at RT and 15 K. The table also lists the overall elastic moduli for Al and Si phases (\({E}_{{Al}}\) and \({E}_{{Si}}\)) as well as their lattice parameters. The \({E}_{{hkl}}\), \({E}_{{Al}}\) and \({E}_{{Si}}\) all increase with a decrease in temperature.

Fig. 11: Lattice strain development during deformation.
figure 11

Lattice strain development along the loading direction for Al (left panels) and Si (right panels) phases at (a, b) RT and (c, d) 15 K. The yield strengths of Al and Si are indicated with a vertical dashed line at both temperatures.

Full size image
Table 3 Elastic properties of Al and Si phases at RT and 15 K
Full size table

The texture evolution (in the form of normalized integrated peak intensities) of the matrix, i.e., Al phase, is shown in Fig. 12a, c. More grain rotations occurred due to the dominant dislocation slip at 15 K than at RT. Preferred crystallographic orientation towards the {111} and decrease for the {220} were observed at both temperatures but with a stronger effect at 15 K. Moreover, the preferred orientation mainly increases for the {111}, a slight increase for the {100}, almost no change for {311}, and decrement for the {110} during uniaxial testing is anticipated32,33,34. However, for the Si phase, the grain rotation was extremely small as shown in Fig. 12b, d.

Fig. 12: Texture evolution during deformation.
figure 12

Evolution of texture along the loading direction for Al (left panels) and Si (right panels) at (a, b) RT and (c, d) 15 K. The yield strength of each phase is indicated as well.

Full size image

Phase stresses

The development of phase stresses for both Si and Al, as a result of stress partioning, is shown in Fig. 13. The Si phase, being stronger, yields at higher stress and shows further increase after yielding. The phase stresses for Si become massive while the trend for Al is almost linear with the applied stress (Fig. 13a, b). The phase stress for Si at RT is almost twice that of the Al phase. Similarly, at 15 K, the Si phase stress reaches around ~600 MPa, which is again significantly higher than Al phase as well as the ultimate strength of the alloy. A similar stress-partitioning behavior has been reported in the past for Al10SiMg alloy deformed at RT15,16,35. It is worth noting that both phases, i.e., Al matrix and Si precipitates, at RT in Fig. 13c have similar hardening behavior (slope) after initial deformation. However, at 15 K, the trend in Fig. 13d shows that the higher strain hardening of the bulk alloy follows that of Al phase. This shows that Al is the dominant phase, despite being softer, work hardens significantly due to it being fcc and having the capability to accumulate higher dislocation density.

Fig. 13: Stress partitioning between Al and Si phases during deformation.
figure 13

Stress partioning with applied true stress (top panels) and applied true strain (bottom panels) at (a, c) RT and (b, d) 15 K. The yield strength of each phase is marked in (a, b), while the stress-strain curves of the bulk alloy are included in (c, d).

Full size image

Discussion

The Al10SiMg alloy showed an improved strength–ductility combination at 15 K. This enhancement seems to be linked to strengthening provided by grain refinement together with high GND density and strain hardening because of the capability of GND accumulation. From the EBSD results in Figs. 7 and 8, no twins were formed during the deformation at 15 K. Moreover, no phase transformation (Fig. 6) was observed during deformation at RT or 15 K. Lack of twinning and phase transformation is consistent with the high SFE of the Al matrix36, which restricts the formation of partial dislocations, necessary for twinning, stacking faults, and displacive phase transformation37. Therefore, Al10SiMg alloy did not have any strengthening or strain-hardening contribution from transformation-induced plasticity (TRIP) or twinning-induced plasticity (TWIP) effects. Among the other possible strengthening mechanisms is the second-phase dispersion, which happens to be the case due to Si particles formation after the HIPing treatment (Fig. 3). However, a similar area under diffraction peaks (Fig. 6) indicates a comparable amount of Si particles before and after deformation at RT and 15 K. Thus, the presence of second-phase particles cannot be considered a major contributor to the simultaneous improvement of strength and ductility at 15 K compared to RT.

Therefore, grain refinement (Fig. 9) encouraging Hall-Petch strengthening38 and GND density (Fig. 10) promoting hetero-deformation induced (HDI) strengthening39, which were higher at 15 K than RT, are apparently responsible for the improved mechanical behavior at 15 K. Limited atomic diffusion and defects mobility, such as at 15 K, may have promoted higher dislocation accumulation, and consequently, dislocation cells and blocks that typically result in sub-grains and the formation of new grains, i.e., grain refinement in high-SFE alloys40. Reduced dynamic recovery kinetics during 15 K deformation, i.e., slowing down annihilation or rearranging of dislocations, can be deduced from the higher GND density in the alloy deformed at 15 K compared to RT (Fig. 10), contributing to more effective grain refinement.

On the other hand, HDI strengthening and HDI strain hardening may have been promoted by the mechanical disparity between the fcc-Al matrix and diamond-like Si particles, as well as between different grain sizes. This mechanical disparity can be observed in the higher elastic moduli of Si particles (87.7 and 107.7 GPa) compared to the Al matrix (74.6 and 85.5 GPa) from RT to 15 K (Table 3). As a result of the higher stiffness of the Si particles, they carry a larger portion of the load, leading to higher phase stress (Fig. 13), and a negligible crystal orientation rotation (Fig. 12) during deformation at both temperatures. This is also evident from the lattice strain in Fig. 11, where Al yielded earlier at both temperatures and the lattice strain did not develop so much after yielding of the stiffer Si phase to maintain strain compatibility with the more compliant α-Al matrix. It should be noted that the Si phase undergone permanent yielding at 15 K (Fig. 11d) which does not seem to be the case at RT (Fig. 11b).

The heterogeneous grain size and morphology in the as-HIPed condition (Fig. 4) consisted of elongated grains produced by epitaxial growth surrounded by smaller semi-equiaxed grains, which may have provided another reason for heterogeneous deformation. These zones differ significantly in flow stress from the smaller and semi-equiaxed grains, creating a heterogeneous response to applied strain41. Soft zones (indicated in green color in Fig. 10), typically coarse-grained (micro-metric sized), undergo larger deformations, while hard zones (indicated in blue color in Fig. 10), often nano- or ultrafine-grained, act as barriers to dislocation movement, enhancing global material strength and strain hardening42. Interfaces between these zones, also known as zone boundaries, are crucial to accommodate strain mismatches by generating GNDs39.

Interfaces with high mechanical disparity promote the formation of GNDs to accommodate the strain gradient near the boundaries between the mutually constraining Al matrix and the Si particles, as well as between heterogeneous grain sizes and morphologies39. As explained before, the reduced defect mobility at 15 K may have encouraged higher GND density than at RT. The stress exerted by GND pileups against the interface results in back stress in the softer Al matrix, and consequent forward stress in the harder Si phase43. Long-range back stress in soft zones and long-range forward stress in hard zones, provide simultaneous extra strengthening and strain-hardening, respectively44. Together, back stress and forward stress form HDI stress39. A significant contribution of HDI strengthening and HDI strain hardening has been reported in Al and Al-alloys constituted by zones or phases with mechanical disparity between them45,46, such as the present Al10SiMg alloy.

Other fcc alloys, including Al-alloys, Cu-alloys, high-entropy alloys, and austenitic steels have shown similar strength–ductility improvement at cryogenic temperatures by deformation mechanisms that activate according to their SFE47,48,49,50. The strengthening of fcc materials typically increases when temperature decreases due to the lowering of SFE, which facilitates the activation of multiple deformation mechanisms, such as deformation twinning, phase transformation, higher dislocation density, and reduced dynamic recovery. However, the high SFE of Al may have limited the activation of twinning and phase transformation, allowing only the increment of the activation energy for cross slip of screw dislocations48. This resulted in increased dislocation density and reduced dynamic recovery, i.e., reduced cross slip51.

Conclusions

The findings of this study provide valuable insights into optimizing LPBF Al10SiMg for ultralow temperature applications by highlighting its enhanced mechanical stability, strain-hardening behavior, and stress partitioning between the Al matrix and Si phase at 15 K. In hydrogen storage systems, the alloy’s high specific strength and refined microstructure suggest its potential for lightweight cryogenic tanks and pipelines, where fracture resistance and stress redistribution are critical. For aerospace applications, the observed strain-hardening response indicates its suitability for cryogenic fuel tanks and structural components subjected to extreme thermal cycling, with potential benefits from further process optimization and thermal expansion control. In quantum computing, the alloy’s mechanical integrity at cryogenic temperatures makes it a promising candidate for support structures and cryogenic shielding, where dimensional stability is essential. Additionally, the observed grain refinement at 15 K suggests that cryogenic deformation processing could be explored as a method to further strengthen LPBF alloys. These insights contribute to the broader adoption of additively manufactured Al-Si alloys in cryogenic technologies, where process standardization and long-term durability at ultralow temperatures remain key considerations for future industry applications.

Methods

Processing of samples

Four batches of test specimens with different LPBF parameters were prepared. The fabrication of these specimens was carried out by using the CONCEPT LASER M2 laser cusing system. This system was equipped with a 400 W maximum power Yb-fiber laser, ensuring high-precision laser melting. The printing environment within the build chamber was controlled by filling with argon to keep the oxygen level below 0.4%, thereby minimizing any potential oxidation of the material. The gas atomized Al10SiMg powder was supplied by CONCEPT LASER and the chemical composition is given in Table S2.

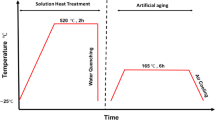
The LPBF process parameters used in this study were optimized based on previous simulations52. The selected laser power, scanning speed, and hatch spacing were iteratively refined through experimental validation. The specific details of the process parameters are outlined in Table S1, while the laser spot size and the layer thickness were kept constant at 140 µm and 25 µm, respectively. These parameters were applied to produce specimens using a continuous scanning strategy with a hatch spacing of 112 μm. The samples were fabricated in a horizontal orientation (Fig. S1a), forming bar-shaped structures consisting of four hundred layers. As-built bars were subjected to hot isostatic pressing (HIPing) using the Quintus QIH-21 hot isostatic press in a full metal Moly basket. The HIPing was conducted in argon atmosphere at 520 °C for 2 h under the pressure of 100 MPa, followed by cooling at 30 °C/min.

Microstructural characterization

Optical microscopy (Olympus BX53M) and field emission scanning electron microscopy (FE-SEM, Hitachi SU7000) were performed to investigate the microstructure of the mechanically polished samples etched using Keller’s reagent (95 ml H2O + 2.5 ml HNO3 + 1.5 ml HCl + 1 ml HF). Electron backscatter diffraction (EBSD) was employed with a step size of 0.45 and 0.97 μm to analyze the crystallographic texture after tensile tests using the FE-SEM system for samples treated by the vibrometer via colloidal silica polishing process and then ion milled at 80° angle, 20 min and 3 kV (Hitachi IM4000Plus). Grain size was quantified using AZtecCrystal software, which only included indexed points and applied a 10° misorientation threshold. The estimation of geometrically necessary dislocations (GNDs) was performed using the kernel average misorientation method, which involves calculating the misorientation around a measurement point relative to its nearest neighbors utilizing AZtecCrystal software and a threshold misorientation angle of 15° to highlight the most heavily deformed regions.

Ex-situ tensile experiments

The HIPed samples were cut into flat dog-bone shaped tensile specimens using electric discharge machining. These specimens had gauge dimensions of 25 mm length, 4 mm width, and 3 mm thickness (Fig. S1b). Subsequently, ex-situ tensile experiments were conducted on all four types of samples produced using different LPBF process parameters (Table S1). These experiments were carried out using an Instron 3382 Universal Testing Machine at a constant strain rate of 1 × 10−3 s−1. The strain was measured with extensometer mounted on the sample. Afterward, alloy with the best strength–ductility combination was selected for further real-time deformation experiments with neutron diffraction at room temperature (293 K, RT) as well as at an ultralow temperature (ULT) of 15 K.

In-situ neutron diffraction deformation experiments

The in-situ deformation measurements with neutron diffraction were carried out at the TAKUMI Engineering Materials Diffractometer (BL19) of the Materials and Life Science Experimental Facility at the Japan Proton Accelerator Research Complex (J-PARC Center). The sample loading axis was aligned 45° to the incident neutron beam. The two sets of detector banks, installed at ‒90° and +90° to the incident neutron beam, collected diffracted neutrons with scattering vector parallel (Q∥) and normal (Q⊥) to the sample’s loading axis, respectively. This setup allowed to simultaneously collect time-resolved data in both the loading and the transverse direction during deformation. Neutron diffraction measurements were conducted with an incident slit of 5 mm in width and 5 mm in height. The radial collimators of 5 mm in width for both detector banks were employed. For cryogenic experiments, the cooling was carried out with a Gifford-McMahon (GM) cooler mounted in a cryogenic load cell chamber53. Cernox® thin film resistance sensors were attached to both sides of sample grips, to monitor the sample temperature. The cryogenic loading experiments were carried out in vacuum ( < 10–4 Pa). Before starting the loading, the samples were cooled and held for about 2 h at the low temperature of 15 K. The step-loading was used for the elastic region with ten equal step and holding time of 300 s at each step, to ensure good statistics. In the plastic region, continuous loading was employed at a displacement speed of 0.04 mm/min, corresponding to a strain rate of ~2.67 × 10–5 s–1. Neutron data were continuously collected throughout the entire deformation process. Images of the deforming specimen were also captured every 5 s using a charge-coupled device camera. The specimen’s elongation was precisely determined from these images using a digital image correlation (DIC) method.

The neutron diffraction data were reduced using the EMAKi program54. To ensure statistical reliability, data binning was performed at 300-second intervals which can lead to minor deviations in stress-strain behavior. Multiple peak fitting of the neutron diffraction data was carried out using the Z-Rietveld software55,56. The lattice strain for individual orientations \({\varepsilon }_{{hkl}}\) was obtained by Eq. (1):

$${\varepsilon }_{{hkl}}=\frac{{d}_{{hkl}}-{d}_{{hkl}}^{\circ }}{{d}_{{hkl}}^{\circ }}$$
(1)

where dhkl is the measured lattice spacing of hkl plane during loading, while \({d}_{{hkl}}^{\circ }\) is the lattice spacing of same plane before loading. Similarly, the average lattice strain of individual phases (\({\varepsilon }_{{phase}}\)) were obtained by Eq. (2):

$${\varepsilon }_{{phase}}=\frac{{a}_{{phase}}-\,{a}_{{phase}}^{\circ }}{{a}_{{phase}}^{\circ }}$$
(2)

where \({a}_{{phase}}\) and \({a}_{{phase}}^{\circ }\) represents the lattice parameters of each phase (i.e., Al and Si) before and during deformation, respectively.

By applying linear fitting to the elastic region of the \({\varepsilon }_{{hkl}}\) and \({\varepsilon }_{{phase}}\) curves, the orientation-dependent elastic moduli (\({E}_{{hkl}}\)) and the bulk elastic moduli of each phase (\({E}_{{phase}}\)) were determined, respectively. It should be noted that the diffraction data along the loading direction during deformation is considered here.

The phase stress (\({\sigma }_{{phase}}\)) for Al and Si was determined from the phase lattice strain evolution using Hooke’s law:

$${\sigma }_{{phase}}={E}_{{phase}}{\varepsilon }_{{phase}}$$
(3)

where \({E}_{{phase}}\) values for Al and Si are provided in Table 3.

The yield strength of the constituent phases (\({\sigma }_{{YS},{Al}}\) and \({\sigma }_{{YS},{Si}}\)) was determined using the 0.2% offset method. In this approach, a parallel line with a slope equivalent to the phase’s elastic modulus is drawn from 0.2% strain, and its intersection with the phase stress vs. engineering strain curve is taken as the yield strength for each phase.