Introduction

The outstanding developments in quantum computation and quantum information science in a wide and diverse range of fields during the last few years led to a remarkable number of solutions for many arising challenges in fields such as quantum security1, quantum machine learning2 and quantum optimization3. The number of potential qubit platforms has significantly expanded, now encompassing systems as trapped ions4,5,6, superconducting circuits7,8 or photonic systems9,10. Additionally, the losses and transmission rates of quantum links have been optimized substantially, allowing for longer distances to be covered11,12,13,14. Despite these advancements, no single experimental platform proves ideal for all aspects of quantum technologies in quantum information science. Consequently, it is unavoidable to combine different platforms to achieve optimal performance in quantum technologies. Hybrid quantum devices that, e.g., can convert quantum information from a matter-based system to a photonic system, and vice versa, are therefore a key component for realizing such optimized approaches15. One hybrid system able to facilitate this conversion are exciton-polaritons, from now on referred to as polaritons, which arise from the strong coupling between excitons and confined cavity photons. Furthermore, due to their bosonic nature, these quasi particles show a wide range of nonlinear effects such as polariton lasing16, superfluidity17 and Bose-Einstein like condensation18. Polariton condensates may carry quantum superpositions in the Fock basis, which can either be directly exploited as a resource or transferred into quantum entanglement or other nonclassical correlations19,20. This opens the path to a multitude of applications in quantum information science including quantum thermodynamics, quantum algorithms, quantum metrology or quantum phase transitions21. Therefore, optimizing the amount of quantum superpositions in polariton condensates proves essential for applications in hybrid quantum technologies22,23,24,25,26,27.

Here, we create a polariton condensate by optically trapping nonresonantly excited, long-living polaritons within an annular-shaped laser beam to optimize the amount of quantum superpositions. We spatially separate the polariton condensate from the surrounding incoherent carrier reservoir, minimizing the interaction between them. In terms of g(1), it has already been demonstrated that this method improves the condensate’s spatial28 and temporal29,30 coherence. To quantify the amount of quantum superpositions, we use the quantum coherence C, given by the squared Hilbert-Schmidt norm of the distance between the state’s density matrix \(\hat{\rho }\) and its closest incoherent counterpart \({\hat{\rho }}_{inc}\)21,31,32,33:

$$C(\hat{\rho })=| | \hat{\rho }-{\hat{\rho }}_{{{{\rm{inc}}}}}| {| }_{HS}^{2}=\sum\limits_{m,n,m\ne n}| {\rho }_{m,n}{| }^{2}.$$
(1)

Quantum coherence consequently takes only the nondiagonal elements of the state’s density matrix into account, making it complementary to the well-known photon correlation functions. Assuming the condensate can be described by a displaced thermal state, a superposition of both, coherent and thermal contributions, we demonstrate that the spatial separation between the condensate and the reservoir enhances the achievable quantum coherence of the system.

Results and discussion

Characterisation of the condensation process

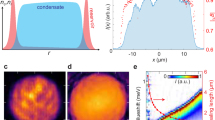
To ensure that the polariton condensate forms separately from the reservoir of carriers consisting of electrons, holes and also excitons, we create an optical trap using a spatial light modulator (SLM) to generate an annular-shaped continuous-wave laser beam with a diameter of 9.6 μm when focused on the sample. This configuration allows us to minimize the decoherence effects arising from carrier-polariton interactions. Figure 1 shows the momentum and real space distributions of the resulting polaritons. Three different excitation densities are considered: (I) below the condensation threshold, (II) at the condensation threshold, and (III) above the threshold. Below the threshold, the real space distribution displays polaritons remaining in the vicinity of the excitation laser, thus also exhibiting an annular-shaped emission pattern. Under these conditions, the ground state energy of the lower polariton branch (LPB) amounts to 1.603 eV. As the pump power reaches the condensation threshold, the system becomes unstable and begins to switch between an emission either dominated by noncondensed polaritons or the condensate. Meanwhile, the momentum-resolved emission reveals a strongly blueshifted photoluminescence (PL) at 1.608 eV, emerging from the condensate formed in the center of the optical trap. Although the polariton system is not yet stable, the first signatures of condensation start to appear. Therefore, we define this pump power as the power threshold for condensation (Pth). Once the system is above the onset for condensation (see panels III) the PL blueshift continues to increase with the excitation power. Throughout this process, the condensate remains at the center of the ring. Since its intensity shows a highly nonlinear increase, the emission from residual uncondensed polaritons vanishes in comparison.

Fig. 1: Spectroscopic analysis of the power dependent polariton emission.
figure 1

Polariton PL in momentum (a) and real space (b), at three different pump powers: 0.57 Pth (I), 1.00 Pth (II), and 1.35 Pth (III). The images for case II are a superposition of consecutive images acquired under identical external conditions. In that case, the system shows critical mode competition over time, switching between polariton emission within the circular barrier and strong spontaneous condensate emission.

Full size image

To investigate the formation of the condensate in more detail, the intensity of the emission, i.e, the polariton occupation, its linewidth and blueshift are displayed in Fig. 2a, b. All parameters are extracted by analyzing a region of interest in momentum space with a width of 1 μm−1 and centered at k = 0. As seen in panel (a), the intensity experiences a strong nonlinear increase by a factor of 108 at the condensation threshold, while simultaneously the linewidth drops by a factor of six. Furthermore, when the system is excited at 1.35 Pth, the blueshift increases up to 5.4 meV. All analyzed parameters exhibit clear signatures of Bose-Einstein condensation, confirming our observations in Fig. 1.

Fig. 2: Polariton condensation signatures.
figure 2

a PL intensity (black circles) and linewith (red diamonds) as a function of P/Pth. b Corresponding blueshift extracted from the momentum-resolved emissions at k = 0. LPB denotes spectra where the polariton system only occupies the ground state of the lower polariton branch. BEC denotes spectra where the system displays a polariton condensate state.

Full size image

It is worth noting that the blueshift experienced by the condensate is rather large compared to that reported in previous works on similar GaAs-based samples34,35,36. This raises the question of the interactions at play and their respective contributions to the blueshift. In our case, the optical trap spatially separates the condensate from the reservoir of free carriers and bright excitons. However, as demonstrated in ref. 37, long-lived dark excitons with k-vectors beyond the light cone, are able to move distances larger than 30 μm. One must therefore assume that a non-negligible number of dark excitons accumulates inside the center of the ring and interacts with the condensate38. More importantly, the long lifetime of these dark excitons allows them to thermalize more effectively, resulting in a stable contribution to the local potential landscape. As a result, a large blueshift is observed in our system, but it is the fluctuations in the potential, rather than its absolute value, that might affect the coherence of the system. Consequently, the system’s quantum state must reveal the impact of these interactions on the condensate’s coherence39,40.

Long timescale evolution of the polariton condensate subject to external noise

In the last section we have demonstrated that the condensate is indeed separated from most of the carrier reservoir. To further understand the dynamics of the system, we next examine the temporal evolution of the emission photon number N and the second-order correlation function g(2)(0), calculated from single channel homodyne detection measurements. The time resolution is achieved by calculating N and g(2)(0) based on data subsets of 30,000 quadratures each, corresponding to around 40 μs. Furthermore, a moving average with a step size of 10,000 quadratures is used to smooth the results. The temporal dynamics of these two parameters are shown for the powers 1.05 Pth, 1.10 Pth and 1.35 Pth in Fig. 3. At the lowest power of 1.05 Pth, immediately after the threshold, the system is still strongly affected by external noise. In consequence, the system switches repeatedly between an uncondensed and a condensed state. The transitions between both states are rapid, revealing the pronounced nonlinearities in the threshold region, which exhibit a high sensitivity to minor changes in the excitation. Whenever the system condenses, g(2)(0) drops immediately to around 1.04, although it is still subject to significant low-frequency noise. During the time intervals where no condensate emission is detected, the measured signal is equivalent to vacuum. This is expected due to the absence of signal intensity in the optical mode of interest defined by the properties of the local oscillator. The local oscillator is on purpose set to the condensate mode and not overlapping with the uncondensed lower polariton branch. For clarity, the intervals where only vacuum is present are shown as greyed out for the photon number and omitted for g(2)(0).

Fig. 3: Long scale time-resolved emission properties.
figure 3

Long scale time resolved (a) second order correlation function g(2)(0) and (b) photon number of the polariton emission for the powers 1.05 Pth, 1.10 Pth and 1.35 Pth. In the case of 1.05, Pth the system shows switching between an uncondensed state and a polariton condensate. For clarity, the uncondensed state photon number is greyed out and its g(2)(0)-values are omitted.

Full size image

As the excitation power increases to 1.10 Pth, the system stabilizes and stays continuously in a condensed state, exhibiting a slightly higher photon number in the condensed state compared to 1.05 Pth. Although we do not observe any more jumps in the photon number for this pump power, g(2)(0) does not decrease yet, probably due to the fact that condensed polaritons still exhibit some thermal characteristics, as the power is not sufficiently far away from the threshold. Finally, at the maximal measured power of 1.35 Pth, the photon number rises to values between 4.5 and 6. At the same time, g(2)(0) decreases to a significantly lower value of 1.02, with its uncertainty also decreasing significantly in magnitude.

In addition, the data in Fig. 3b exhibit oscillations over time, originated from unavoidable experimental mechanical noise. Vibrations of the sample along the z-axis, with frequency contributions at 24 Hz and 424 Hz, perturb the effective diameter of the excitation potential, modulating the signal out-coupling efficiency. Near the condensation threshold, even small amounts of noise can disturb the condensate emission; however, as the condensate stabilizes, the influence of this external noise becomes less pronounced. It is important to note that these oscillations appear only in the photon number and not in g(2)(0). The reason for this is that we evaluate g(2)(0) on timescales that are fast compared to the typical timescales of the external noise, so this extrinsic noise does not distort our measurements41.

Estimation of the condensate quantum coherence

Finally, for a comprehensive understanding of the quantum state of our system, we discuss its coherence properties taking into account g(2)(0) and the initially introduced quantum coherence. By examining these properties, we gain deeper insights into the underlying mechanisms that govern the formation and stability of the polariton condensate.

The value of g(2)(0) is determined by the density matrix’s diagonal elements while the quantum coherence can be accessed by its nondiagonal elements. Experimentally, the density matrix can be reconstructed using quantum state tomography. However, this requires a temporally stable phase between the local oscillator (LO) and the signal, a condition not satisfied in polariton condensates. We circumvent this obstacle by assuming that the polariton condensate is in a single mode Gaussian state in the absence of squeezing, and can thereby, be described as a displaced thermal state with both coherent and thermal components. In this case, the formulas for g(2)(0) and C are defined as

$${g}^{(2)}(0)=2-{\left(\frac{| {\alpha }_{0}{| }^{2}}{| {\alpha }_{0}{| }^{2}+\bar{n}}\right)}^{2}$$
(2)

and

$$C(\hat{\rho })=\frac{1-\exp \left(-\left\{2| {\alpha }_{0}{| }^{2}/\left(2\bar{n}+1\right)\right\}\right){{\mbox{I}}}_{0}\left(2| {\alpha }_{0}{| }^{2}/\left(2\bar{n}+1\right)\right)}{2\bar{n}+1}\,{\mbox{,}}\,$$
(3)

which depend only on the state’s thermal and coherent photon numbers \(\bar{n}\) and ∣α0∣2. Both photon numbers are accessible from the state’s photon statistics and, therefore, do not rely on the phase information. In principle, the photon statistics can be measured using single photon detectors. However, this method requires first that the condensate consists of a single mode, and second, that is susceptible to noise for states near the vacuum.

Therefore, instead of measuring the photon statistics directly, we measure the phase averaged Husimi-Q distribution in phase space, which provides equivalent information. The Husimi-Q distribution is well-defined for states near the vacuum, and its positivity and smoothness allow it to be accessed experimentally. The Husimi-Q distribution is then generated by the 2D probability distribution of orthogonal quadrature pairs (q,p), which are recorded using homodyne detection. This also simplifies the mode selection in case of multiple modes, as only the mode overlapping with the LO is amplified. A more detailed description of the used setup is given in the methods section. The generated Husimi-Q distribution takes then the form of a ring, whose squared radius corresponds to ∣α∣2 and width to \(\bar{n}\). Both quantities are then accessible using the formula

$${Q}_{{{{\rm{inc}}}}}(\alpha )=\frac{\exp \left[-\left(| \alpha {| }^{2}+| {\alpha }_{0}{| }^{2}\right)/\left(\bar{n}+1\right)\right]}{\pi \left(\bar{n}+1\right)}{I}_{0}\left(\frac{2| \alpha | | {\alpha }_{0}| }{\bar{n}+1}\right),$$
(4)

which depends on the coherent amplitude ∣α∣. The phase spaces spanned by (q,p) and the complex α are in this occasion connected by the relation

$${\alpha }_{{{{\rm{j}}}}}(q,p)=\frac{1}{\sqrt{2}}\left({q}_{{{{\rm{j}}}}}+{\mbox{i}}{p}_{{{{\rm{j}}}}}\right).$$
(5)

For a more detailed derivation of the formulas showed in this section see ref. 42.

The resulting 2D Husimi distributions are exemplified in Fig. 4a–d for different powers. Note that in this case, the distributions are not time dependent.

Fig. 4: Evolution of the polariton state in phase space.
figure 4

a–d Phase averaged Husimi distributions for excitation powers of 0.77 Pth, 1.05 Pth, 1.15 Pth and 1.35 Pth, displaying the transition from a vacuum state, characterized by a Gaussian probability distribution, to a displaced thermal state with a ring-like distribution. In case (b), the main figure only shows the condensate state distribution, the distribution of the whole recorded data set is given in the corresponding inset. e Coherent (black circles) and thermal (red diamonds) photon numbers extracted from the Husimi representations at different excitation powers. f Corresponding g(2)(0) as a function of the excitation power. g Calculated quantum coherence in dependence of the excitation power.

Full size image

For excitation powers around the threshold area, where the time-dependent emission shows contributions from both condensed and uncondensed polaritons, as already highlighted in Fig. 3, only the subset of data where a condensate is actually present is taken into account. This approach is necessary because the LO mode does not overlap with the uncondensed polaritons, resulting in a quadrature distribution that corresponds to the vacuum state, characterized by a Gaussian Husimi-Q distribution. When the polariton system is stable in a condensed state, all recorded quadratures are used to form the Husimi-Q function. This is well illustrated in Fig. 4b, which shows the subset of data when only the condensate is present, while the inset shows the distribution of the full recorded data set, including both condensed and uncondensed polaritons.

At 0.77 Pth, panel (a), the Husimi distribution exhibits a 2D Gaussian profile, indicating a vacuum state with no signs of condensation. When the system is driven above the threshold, the distribution evolves into a ring whose radius increases with power, indicating a system with increasing coherence. In this context, the entire polariton system can be seen as a superposition of both coherent condensed and thermal uncondensed polariton populations43,44,45.

The coherent and thermal photon numbers as well as the calculated g(2)(0) and C are presented in Fig. 4e–g as a function of the excitation power. In panel (e) one can directly see that the coherent photon number immediately increases with power after the condensation threshold is exceeded. Meanwhile, the thermal photon number remains constant at a value close to zero. These results are attributed to the spatial separation between the condensate and polaritons at the excitation barrier, which is formed by thermal emission. This trend can then also be observed in the values of g(2)(0). Below the condensation threshold, our estimated g(2)(0) consistently exhibits a value of 2. We want to emphasize that our fitting method provides this value for a vacuum state and the uncondensed lower polariton branch does not overlap with the local oscillator. Nevertheless, previous works have exhaustively demonstrated that polaritons below the condensation threshold are generally characterized by a thermal state with g(2)(0) = 243,44,45. As the condensation threshold is reached, g(2)(0) drops immediately to 1.2, and with increasing power, further converges nonlinearly towards 1. Conversely, as one focuses on the estimated quantum coherence displayed in panel (g), an abrupt jump from 0 to about 0.5 is observed. As power continues to rise, C further increases, fluctuating between a value of 0.6 and 0.7. These fluctuations are mainly caused by minor variations in the thermal photon number, to which the quantum coherence is highly sensitive, unlike g(2)(0).

Finally, we compare our estimated quantum coherence with previous measurements conducted by Lüders et al., who used the same quantifier. In their case, shorter living polaritons in a lower Q-factor microcavity were excited by a Gaussian excitation spot of a diameter of 70 μm33. In comparison, we achieve a quantum coherence three times higher than the previously observed maximum of C = 0.21. At first, this result may seem surprising. Although the polariton lifetime is much longer in our study which allows the condensate to thermalize more properly, also the condensate blueshift we observe is significantly larger compared to that earlier study. However, it should be noted that in our case the blueshift arises most likely from interactions between the condensate and a residual reservoir of long-lived dark excitons, which also have sufficient time to thermalize. Therefore, it seems reasonable to assume that it is not the bare presence of a reservoir that reduces the coherence of a condensate, but rather its fluctuations. We conclude that increasing the polariton lifetime to bring the polariton condensate closer to a thermalized equilibrium state is significantly more beneficial to its quantum coherence properties than just separating it from incoherent reservoirs. It seems to be sufficient to separate the condensate from strongly fluctuating reservoirs as is the case for, e.g., reservoirs of free electrons and holes.

Conclusions

In summary, our investigation reveals a significant enhancement in the amount of quantum coherence observed in polariton condensates compared to earlier studies. We ascribe this improvement to the long polariton lifetimes we are able to achieve, which in turn result in significantly better thermalization46. Near the threshold, time-resolved measurements reveal an initially unstable polariton condensate, susceptible to external noise sources. Nonetheless, full stability is achieved already at 1.35 Pth, evidenced by g(2)(0) approaching unity. The extensive analysis of the system’s coherence has demonstrated an effective increase of the coherent population resulting from first, the ability of long-living polaritons to overcome macroscopic distances and thermalize while maintaining their coherence, and second, minimizing the interactions with strongly fluctuating incoherent reservoirs. As a result, our measurements indicate a build up of quantum coherence significantly stronger compared to previous observations with Gaussian excitation profiles in moderate-lifetime samples33. Taking these results into account, the influence of the residual excitonic reservoir could be further mitigated by increasing the excitation power and the size of the annular trap. However, most importantly our results show that the presence of incoherent reservoirs is not detrimental per se, which may open up the possibility to tailor them to even enhance the performance of polariton condensates in quantum technology tasks. Such insights hold promise for the integration of polariton condensates as low-threshold sources of resourceful quantum states for future hybrid quantum devices.

Methods

Sample

The sample used in this experiment is a high Q-factor 3λ/2 optical microcavity containing 12 GaAs quantum wells (each 7 nm thick), embedded between two DBR mirrors. The QWs are arranged into three sets of four, with each set located at one of the three antinodes of the cavity. The DBRs consisting of 32(top) and 40(bottom) layers of AlAs/Al0.2Ga0.8As ensure a long polariton lifetime of  ~200 ps47. The measurements have been performed in a region of the sample with a cavity-exciton detuning of δ ≈ 0 meV.

Experimental Setup

To create polaritons, the sample was cooled down to 10 K in a cold-finger flow cryostat. We excited the sample nonresonantly at its first Bragg minimum, 1.746 eV, with a continuous-wave laser manufactured by M Squared. The intensity distribution of the laser was reshaped into a ring using an SLM to modulate its phase front by imposing an axicon phase map. The diameter of the resulting ring-shaped optical trap was fixed at 9.6 μm during the experiments. A microscope objective with a numerical aperture of 0.26 was used for both, exciting the sample and collecting its photoluminescence. The PL was then filtered to allow only the polarization component parallel to the main axis of the cavity, which also corresponds to the polarization direction of the polariton condensate generated at high pump powers.

For the analysis of the emission, two distinct techniques were used. First, the PL was focused on the entrance slit of a spectrometer and a charge-coupled device (CCD) to measure the spatial distribution and far-field angular distribution of the emission. Second, to investigate the quantum properties of the polariton emission, a two-channel homodyne detection setup was used to reconstruct the phase-space representation of the system’s quantum state. To this end, the polariton PL was overlapped with a local oscillator, generated with a fs pulsed-laser beam, allowing a quadrature sampling rate of 75.4 MHz, while maintaining a quadrature time resolution of around 1 ps. To ensure a stable orthogonality between the quadrature pairs (q,p) in both channels, the LO was delayed in one of the channels by adding an additional λ/4 plate. The full configuration of the setup is illustrated in Fig. 5. For the detection, two high-speed balanced photoreceivers with integrated Si pin diodes and a bandwidth of 100 MHz were used. For a more detailed description of the used homodyne setup see refs. 42,48,49.

Fig. 5: Scheme of the experimental setup.
figure 5

The sample is nonresonantly excited in reflection geometry by a cw laser, spatially reshaped to an annular trap. The emission is then either analyzed using a combination of spectrometer and CCD or a two-channel homodyne detection setup. (SLM: spatial light modulator; PBS: polarized beam splitter; MO: microscope objective; FM: flip mirror; λ/2: half waveplate; λ/4: quarter waveplate).

Full size image

Reconstruction and analysis of the quantum states

The calculation of the field quadratures, the Husimi-Q distribution states, as well as the followed analysis based on the model of a displaced thermal state, were calculated following the method described by Lüders et al.33. Our measurements around the condensation threshold showed uncondensed and condensed polariton populations still coexisting in the system. Therefore, to proceed with the analysis, a minimum photon number of 0.6 was selected to assume the system was indeed a polariton condensate. A further separation of the states is not considered since the calculated g(2)(0, t) shows no correlation with the observed temporal fluctuations in the photon number, as shown in Fig. 3. It is important to remark that the quantum coherence of the uncondensed polaritons could not be determined because (I) the intensity of the emission was too low to be detected, therefore comparable to vacuum, and (II) the strong blueshift of the emission prevents the energy of the LO from overlapping simultaneously with the condensed and uncondensed polaritons. Thus, only the condensate state was taken into account for the analysis of the system’s usability in future hybrid quantum devices.