Introduction

Thermoelectric (TE) power generation and refrigeration are enabling technologies for climate change abatement, providing means to convert otherwise wasted heat into useful electrical energy and greenhouse-gas-free cooling and refrigeration1,2,3,4. So far, extensive thermoelectric research has been focusing on the longitudinal effect, i.e., Seebeck effect, in which the generated potential gradient is parallel to the applied heat flux. TE modules based on this effect are piles made from multiple thermocouples, each made of separate materials with different polarities of charge carriers. This construction is necessary to build up useful voltages1, but it requires multiple metal/semiconductor electrical connections, each with an unavoidable electrical and thermal contact resistance leading to the loss of efficiency. In contrast, transverse TEs utilizing Nernst effect, in which the created voltage is perpendicular to the applied temperature gradient, may vastly simplify the module fabrication2. They require only one material, can be optimized by changing the geometry only, and make it possible to set up electrical contacts only at one end, preferably the one near room temperature. These advantages circumvent the need of longitudinal devices to have contacts at the hot side of thermoelectric generators (TEGs), where they degrade. In TE coolers, single-stage longitudinal (Peltier) coolers can reach only a limited temperature difference, so that large temperature drops require complex and delicate multi-stage devices. Transverse (Nernst-Ettingshausen) TE coolers bypass this limitation as well. In the present work, we demonstrate how harnessing the anomalous Nernst effect (ANE) in a magnetic Weyl semimetal (WSM) contributes to a record transverse thermopower.

In recent years, more and more efforts have been dedicated to the exploration of ANE5,6,7,8,9,10,11,12,13,14,15,16,17,18, aiming at considerable transverse thermoelectric performance. While nonmagnetic semimetals with high mobility and low carrier concentration can produce a large Nernst effect in a strong applied magnetic field (e.g., refs. 19,20), the ANE offers the promise of a strong Nernst response without requiring a strong applied field, since the time reversal symmetry breaking required for a transverse response is already intrinsic to the material. ANE has been commonly observed in ferromagnets (FMs)5,8,9,10,11,13,15,16,21. Co2MnGa8,9,22, Co3Sn2S210,11, and Fe3Ga13 exhibited ANE coefficients (SANE) ranging from 3 to 8 μV K−1. In addition, UCo0.8Ru0.2Al15 was found to possess an SANE of 23 μV K−1, a record at that time. FMs can break time-reversal symmetry (TRS) and give rise to a non-zero Berry curvature, which is the intrinsic origin of ANE7,8,13,23, but the disadvantages of FMs in thermoelectric applications are also obvious: 1. they usually exhibit high electrical resistivity resulting from heavy band mass; 2. they are prone to create magnetic disruption owing to the high magnetization and strong inherent stray field17.

Given the difficulties described above, searching for other materials retaining the advantages of FMs while overcoming their drawbacks has been a pressing challenge. In 2022, Pan et al. reported that YbMnBi2, an antiferromagnetic (AFM) WSM with spins canted in the [110] direction providing broken TRS24, has low resistivity arising from the light effective band mass, weak magnetization, a substantial ANE thermopower SANE of up to 6 μV K−1 and ANE conductivity αANE of up to 10 A m−1 K−1 in the configuration of H // [100], jQ // [010], V // [001] and H // [100], jQ // [001], V // [010], respectively17. These responses were claimed to transcend all the previously reported large SANE and αANE values in AFMs6,12,14,25, making YbMnBi2 an encouraging candidate for Nernst devices (the properties of those samples are summarized in Supplementary Table 1). The Nernst thermopower Syx is the ratio of the transverse electric field to the longitudinal temperature gradient, whereas the Nernst conductivity αyx is the ratio of the transverse current flow to the longitudinal temperature gradient; both are related as will be shown later.

Because the results depend critically on the position of the chemical potential vis-à-vis the Weyl points, and because this potential depends on unintentional doping of the material, those early transport experiments on this material were not yet comprehensive enough to unveil the potential of YbMnBi2. In this report, we examine two YbMnBi2 samples (sample 1 and sample 2) with lower Hall densities (2.22 × 1019 cm−3 at T = 8 K for sample 1) and higher Hall mobilities (1.05 × 105 cm2 V−1 s−1 at T = 8 K for sample 1) than the samples in ref. 17, bringing the chemical potential μ closer to the Weyl points. We show here how this change in μ drastically changes the physical origin of SANE. In ref. 17 with heavier-doped material, the Nernst response is dominated by αANE with significant contributions from some indefinite extrinsic sources. Here, in contrast, the record value of SANE is due to the synergistic effect between a topological anomalous Hall conductivity, a Nernst conductivity that is non-topological in origin, and the strong anisotropy of the dispersion of the Weyl bands near the Weyl points. Supplementary Table 1 compares the properties of samples 1 and 2 used here and those in ref. 17; Supplementary Fig. 3 gives the temperature dependence of our Hall density and mobility. We caution that the interpretation of the Hall density and its temperature dependence are complicated by the coexistence of multiple bands at the Fermi level. We discuss this issue in detail in the Supplementary Information.

Another key difference with the previous work of Pan et al. is that in their study the external magnetic field, applied temperature gradient, and measured voltage signal were along the three primitive axes. Here, we performed transport property measurements with field applied along the spin canting direction [110] (Fig. 1c–f). We report that sample 1 in this study has a Nernst thermopower that sets a significantly enhanced record in magnetic materials, now reaching maximum Syx ~110 μV K-1 in the configuration of H // [110], jQ // [\(1\bar{1}0\)], and V // [001], likely ANE-dominated (see Supplementary Table 1), and a considerable thermal Hall effect (THE) angle 0.02 <∇yT/∇xT (−9 T) <0.06. In the Supplementary, we present results on sample 2, which has a higher Hall density and lower Hall mobility than sample 1, implying its chemical potential is farther from the Weyl points. Qualitatively, the results of this study are notably reproducible, although the Nernst coefficient (maximum Syx ~38 μV K−1) is smaller in sample 2 than in sample 1.

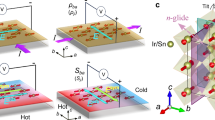
Fig. 1: Crystal structure of YbMnBi2, schematic Fermi surface, and experimental setups.
figure 1

a The spins of Mn atoms in single crystal YbMnBi2 are antiparallel within the ab plane, slightly canted along the [110] direction, and ferromagnetically stacked along the c axis. b Schematic depiction of the Fermi surface near the Weyl points. The Fermi surface is extremely elongated along the c direction, while the Fermi velocity (indicated by the color) is much larger in the ab plane. Note that this image is broadened in the \({{{{\boldsymbol{k}}}}}_{{{{\boldsymbol{x}}}}}\)-\({{{{\boldsymbol{k}}}}}_{{{{\boldsymbol{z}}}}}\) plane for visual clarity; the actual aspect ratio of the Fermi surface is closer to 200:1. c A schematic drawing of the experimental configuration of the Nernst effect measurement, in which magnetic field H was applied along the spin canting direction [110], heat flux jQ was along \([1 \bar{1} 0]\), and recorded transverse voltage V was along [001]. d A schematic drawing of the experimental configuration of the thermal Hall measurement, in which magnetic field H was applied along the spin canting direction [110], heat flux jQ was along \([1\bar{1}0]\), and the transverse temperature difference ∆yT was obtained through the subtraction of the readouts of the two transverse thermometers, which is T3 – T2 in this setup. e A schematic drawing of the experimental setup of the electrical Hall experiment, in which external magnetic field H was along the spin canting direction [110], applied current flow I was along \([1 \bar{1} 0]\), and measured transverse voltage V was along [001]. f A schematic drawing of the experimental setup of a separate electrical transport experiment, in which external magnetic field H was along the spin canting direction [110], applied current flow I was along [001], and measured voltage V was also along [001].

Full size image

To the best of our knowledge, these lower-doped YbMnBi2 samples have the highest anomalous Nernst thermopower of any magnetic materials (see Table 1). Below we present evidence that the synergism between the topological nature of the Weyl bands, classical effects in filled bands, and anisotropy plays a pivotal role in producing this large Nernst thermopower. Together our results provide robust evidence for a large topological contribution to the Nernst effect that is driven by a spin canting transition, and in this way point toward a new pathway for designing efficient transverse thermoelectrics by exploiting band topology arising from field-tunable magnetic order.

Table 1 Comparison of ANE thermopower SANE of this study with some of the largest reported SANE values in AFMs and FMs
Full size table

Results and discussion

As shown by Fig. 1a, the crystal structure of YbMnBi2 falls into a tetragonal system, whose space group is P4/nmm. There are two types of Bi atoms: type I forms nearest-neighbors of Mn atoms while type II constitutes an interlayer. The Néel temperature TN is reported to be around 290 K and the antiferromagnetic ordering of Mn atoms with spins aligned along c axis within about 3° is confirmed26. The spin canting direction is [110]. Pan et al. published that the spin canting temperature (i.e., below which the spin canting shows up) is ~250 K with a small canting angle17. Although the magnitude of spin canting is minor, it induces the formation of Weyl points which act as sources of Berry curvature, as we describe below, and these Weyl points allow for an anomalous Hall response.

YbMnBi2 contains topological bands arising primarily from px/y orbitals on the interlayer Bi atoms17,24; as is obvious from the nearly two-dimensional arrangement of these Bi atoms, these bands are extremely anisotropic, an important attribute for the observations reported here. If one uses a description that assumes simple antiferromagnetic ordering of the Mn spins and neglects spin-orbit coupling, then the topological bands form a nodal line slightly below the Fermi level. When spin-orbit effects are included, the nodal line becomes gapped everywhere except at four Dirac points. The effect of spin canting is to split each of these four Dirac points into two Weyl points with opposite chirality, leaving 8 Weyl points in total17,24. The splitting of the Dirac points into Weyl point pairs allows for the possibility of an anomalous Hall conductivity that is proportional to the separation in momentum space of the two opposite-chirality Weyl points within a pair27,28.

The resulting linear dispersion near the Weyl points has a very large Fermi velocity ( ≈ 1 × 106 m/s) within the ab plane, and a much smaller Fermi velocity ( ≈ 6 × 103 m/s) in the c (layering) direction24,29. Thus, the Fermi surface in the vicinity of the Weyl points has a highly elongated cigar shape, stretched in the c direction (as depicted in Fig. 1b). Coexisting with the Weyl bands is a heavy, trivial hole band associated primarily with Mn d orbitals17.

Giant anomalous Nernst effect thermopower

Figure 2a shows the behavior of the Nernst coefficient Syx with respect to magnetic field at a variety of temperatures for sample 1 (the data on sample 2 are in Supplementary Fig. 4a). Consistent with each other, Syx of both sample 1 and sample 2 first increases and then decreases with temperature when 5 T ≤ |μ0H | ≤ 9 T, achieving a maximum around 250 K. This nonmonotonic dependence of the Nernst effect on temperature is characteristic of nodal semimetals with low Fermi energy, for which thermally excited holes in the valence band cause the Hall conductivity to drop when kBT becomes comparable to or larger than EF30,31.

Fig. 2: Transverse transport properties of sample 1.
figure 2

a Field dependence of Nernst thermopower Syx at various temperatures. The similarity of the results of this sample with those on sample 2 (see Supplementary Fig. 4a) confirms that the observation of the enormous Nernst thermopower is reproducible. b–e, Field dependence of (b) electrical Hall resistivity ρyx, (c) electrical Hall conductivity σyx, (d) Nernst conductivity αyx obtained from measured properties outlined by Eq. (1), and (e) theoretical curves for the Nernst conductivity αyx, at various temperatures.

Full size image

Both samples exhibit a characteristic combination of ONE (ordinary Nernst effect) and ANE. We caution that it is difficult in general to separate the contributions of ONE and ANE to the total Nernst effect. The usual method used in literature is to assume that the ONE is linear in magnetic field and to subtract this linear dependence from the total Syx in order to estimate the ANE. However, the higher the carrier mobility, the narrower the linear regime of the field dependence of ONE, and when the ONE is beyond the linear region the superimposition of ONE and ANE has complicated features, and this linear subtraction becomes questionable. In the Supplementary Fig. 4b, SANE of sample 2 is tentatively derived from the data by assuming the ONE contribution is linear and then subtracting it out following the procedures outlined in ref. 17. The resulting estimated maximum value in sample 2 is SANE ~30 μV K−1 when 5 T ≤ |μ0H | ≤ 9 T and 200 K < T < 260 K. Apparently, ANE dominates Syx of sample 2, and this is a record-high ANE thermopower as well, exceeded only by sample 1. Regarding sample 1, at T = 254 K, Syx goes up to ~110 μV K−1 when 5 T ≤ |μ0H | ≤ 9 T and stays almost constant there, also presumably with SANE dominant.

Figures 2 and 3 give the transverse and longitudinal electronic transport properties respectively for sample 1 (Supplementary Figs. 4 and 6 for sample 2). The Hall resistivity ρyx of sample 1 is given in Fig. 2b. The in-plane and cross-plane resistivities ρxx and ρyy are shown in Figs. 3a, d, respectively. ρyy increases as temperature rises and its values are surprisingly large. The anisotropy ratio of the longitudinal resistivity ρyy/ρxx observed here is at the level of thousands, much larger than that in the prior study (which saw ρyy/ρxx up to 30 (ref. 17)). This large anisotropy is accounted for by the anisotropic nature of the Fermi surface, which is highly dispersive in the xz plane but has little dispersion along y axis32. Our measured values of ρyy are dozens of times higher than the values reported in ref. 17, while the in-plane resistivity is smaller. Both observations are attributed to the fact that the chemical potential in the present samples is closer to the Weyl points. What’s more, ρyy of sample 2 (Supplementary Fig. 6d) unexpectedly showcases a negative magnetoresistance (NMR) of up to ~25% at low temperatures, which persists through the whole range of measured temperatures (47 K ~ 307 K), indicating a temperature-robust NMR, while only a slight positive magnetoresistance is observed in ρyy of sample 1 (Fig. 3d).

Fig. 3: Longitudinal transport properties of sample 1.
figure 3

Field dependence of (a) electrical resistivity ρxx, (b) Seebeck coefficient Sxx, (c) thermal conductivity κxx, and (d) electrical resistivity ρyy, at various temperatures.

Full size image

From these data, the Hall conductivity σyx = -ρyx/(ρxxρyy + ρyx2) can be derived (see Supplementary Information) and is given in Fig. 2c for sample 1 (Supplementary Fig. 4d for sample 2). σyx exhibits a jump as a function of magnetic field H near H = 0, and this jump becomes increasingly sharp as the temperature is lowered. Such a jump is consistent with an anomalous Hall effect (AHE) arising from the filled Weyl band, with the sign of the Berry curvature at the Weyl points becoming inverted when the magnetic field direction is inverted and switches the direction of spin canting. The in-plane thermopower Sxx and thermal conductivity κxx are given in Fig. 3b, c, respectively.

This behavior of σyx can be contrasted with the behavior of the Nernst conductivity, which is given by (see Supplementary Information):

$${\alpha }_{{yx}}\,=\,\frac{{-\rho }_{{yx}}{S}_{{xx}}\,+\,{\rho }_{{xx}}{S}_{{yx}}}{{\rho }_{{xx}}{\rho }_{{yy}}+\,{{\rho }_{{yx}}}^{2}}$$
(1)

where Sxx and Syx are the Seebeck and Nernst coefficients, respectively. The experimental value of αyx is plotted in Fig. 2d for sample 1 (Supplementary Fig. 4e for sample 2) as a function of magnetic field at various temperatures. The anomalous Nernst conductivity αANE for sample 2 (Supplementary Fig. 4g) can be estimated following the same method as for estimating SANE. An explicit and quantitative explanation for αANE was attempted in ref. 17, but this explanation did not explain the temperature dependence well even in highly doped samples, which made the authors invoke the possibility that extrinsic mechanisms contributing to the ANE might also be present, such as skew scattering33,34 and side jump scattering35,36. Interestingly, while ref. 17 showed trends of T-dependence of αANE that were opposite from theoretical predictions, in this study we find an αANE with a T-dependence that is generally consistent with the first-principle calculations presented in ref. 17, as shown in Supplementary Fig. 4h. This consistency allows us to explain our data with a relatively simple analytical model based on Weyl/Dirac semimetal physics (see Supplementary Information for a detailed discussion); the calculated αyx is given in Fig. 2e for sample 1 (Supplementary Fig. 4f for sample 2) and describes the data quite well. Unlike σyx, which has a constant contribution from the filled bands, αyx is proportional to \(\frac{d{\sigma }_{{yx}}}{{dE}}{|}_{E={E}_{{{{\rm{F}}}}}}\) (ref. 37, see Supplementary Information for a detailed discussion), so that the filled bands do not contribute. Consequently, in our samples αyx is smaller in magnitude than that in ref. 17, does not exhibit a sharp jump around H = 0, and is consistent with a theoretical description that does not invoke Berry curvature. Our theoretical description of αyx contains two parameters which depend on the Fermi energy and mobility. The fitted values of these parameters are consistent with sample 1 having a lower Fermi energy and higher mobility than sample 2, as we describe in detail in the Supplementary Information.

Why, if the Nernst conductivity αyx is smaller than that in ref. 17, is the Nernst thermopower that much larger? As mentioned above, the main difference between the samples in this study and in ref. 17 are the much lower Hall densities and much higher Hall mobilities, due to changes in the unintentional doping levels. This brings the chemical potential closer to the Weyl points, as evidenced by two observations: (i) the Hall density increases with temperature (T > 80 K) (shown in Supplementary Fig. 3) and (ii) the polarity of high-field dρyx/dH flips as temperature changes (shown in Fig. 2b). Both behaviors are characteristic of intrinsic semiconductors or semimetals with small or zero band overlap: they imply the dominance of thermally excited intrinsic charge carriers. (We discuss the behavior of the Hall resistivity in more detail in the Supplementary Information.)

Rewriting Eq. (1), it now is possible to back-calculate Syx from:

$${S}_{{yx}}=\frac{{\alpha }_{{yx}}-{\sigma }_{{yx}}{S}_{{xx}}}{{\sigma }_{{yy}}}$$
(2)

The derivation of Eq. (2) is in the Supplementary Information. The back-calculated values of Syx, which fit the data very well, are given in Supplementary Fig. 5. Equation (2) gives insight into the origin of the record Syx. Observing that αyx and the product σyxSxx have opposite signs, the large numerator of this equation is a result of the fact that the absolute values of the two quantities add up, producing a sum of the absolute values of a topological term (σyx) and a classical one (αyx). The Nernst thermopower is then further boosted by the large anisotropy of the resistivity, producing a small denominator. It can thus be concluded that the record Syx results from the synergy of anisotropy, classical and topological transport.

Appreciable thermal Hall effect angle

The thermal Hall effect (THE) is another transport property that is strongly influenced by the Berry curvature of the carriers. Figure 4a shows the field dependence of the thermal Hall resistivity wxy of sample 1 at varying temperatures, which is relatively large, up to ~3.3 × 10−3 W−1 m K. The data for sample 2 (Supplementary Fig. 7a) exhibit excellent consistency. In YbMnBi2, wxy behaves approximately linearly with field at low temperatures (T < 100 K for samples 1 and 2), displays a plateau-like, field-independent character in the intermediate range (100 K < T < 250 K for samples 1 and 2), and then tends to be linear in field again as temperature further increases. The THE is of electronic origin and thus largely reflects the electrical Hall effect, which has a substantial contribution from the Berry curvature of the Weyl bands. While a similarly large or even larger THE signal can appear in trivial materials if the mobility is high and the carrier density and lattice thermal conductivity are sufficiently low38,39,40, the sharp step in wxy near B = 0 is qualitatively different from what appears in that context and suggests that there is a large anomalous contribution to the THE in addition to the trivial contribution.

Fig. 4: Appreciable thermal Hall effect signal (sample 1).
figure 4

Field dependence of (a) thermal Hall resistivity wxy, (b) thermal resistivity wxx, and (c) the tangent of thermal Hall angle ∇yT/∇xT, at various temperatures.

Full size image

In THE measurements, the transverse temperature difference is measured for a given applied heat flux, meaning that the actually measured variable is one of the thermal Hall resistivity terms in the thermal resistivity matrix. The commonly used representative for THE is the so-called thermal Hall conductivity κxy calculated through the inversion of the thermal resistivity matrix. Here, the corresponding formula can be written as κxy = -wxy/(wxxwyy + wxy2), where wxx and wyy are thermal resistivities along x and y direction, respectively. In general, wxxwyy » wxy2, so κxy approximates -wxy/wxxwyy. If either wxx or wyy depends strongly on magnetic field, the longitudinal thermal magnetoresistance will heavily contaminate the dependence of thermal Hall signal on magnetic field. Considering this weakness, to get a clear picture of THE in YbMnBi2, the tangent of thermal Hall angle tan(θ) ≡ ∇yT/∇xT = wxy/wxx is reported in Fig. 4c for sample 1 and Supplementary Fig. 7c for sample 2: it simply equals the ratio of the transverse and longitudinal components of the temperature gradient, does not require matrix operation, and incorporates the magnetoresistance in the longitudinal thermal transport. The field dependence and temperature dependence of ∇yT/∇xT is analogous to those of wxy. The absolute values of ∇yT/∇xT at individual magnetic fields do not change rapidly with temperature, supported by the observation that 0.02 <∇yT/∇xT (−9 T) < 0.06 while T changes between 40 K and 310 K.

In summary, we report in the magnetic Weyl semimetal YbMnBi2 the largest anomalous Nernst thermopower observed in a magnetic solid and attribute it to the synergism of a Berry-curvature-induced Hall conductivity, a classical Nernst conductivity, and a highly anisotropic resistivity. This synergy works only if the carrier density is low and the chemical potential is close to the Weyl points. The samples also have a sizable thermal Hall effect, benefiting from the significant topological contributions of the Weyl bands. These results open up the possibility of furthering the leading edge of research on transverse (Nernst) thermoelectrics and provide a powerful pathway to do so, by means of Fermi level tuning in materials with exotic band topology and structures.

Methods

Sample preparation

The single crystals of YbMnBi2 measured in this research were synthesized at Max Plank Institute for Chemical Physics of Solids (CPfS) using the self-flux method with an element molar ratio of Yb:Mn:Bi = 1:1:10. Yb of purity 99.99%, Mn of purity 99.98%, and Bi of purity 99.999% were pruned into small pieces, mixed up, and then placed in an alumina crucible. The mixture was sealed in a quartz tube under a partial argon pressure. The temperature of the sealed tube was increased to 1273 K with a rate of 50 K/h, held there for 20 hours, and then cooled down slowly to 673 K at a rate of 3 K/h. Finally, single crystals of YbMnBi2 were obtained by removing the Bi flux through centrifugation at 673 K. Given that YbMnBi2 is a relative new material system and a ternary compound, control over its defect chemistry is not yet well developed. Unintentional doping occurs. A study of the dependence of the transport properties on μ is therefore carried out by selecting and characterizing different crystals from the melt rather than by deliberate extrinsic doping, as can be done for heritage semiconductors and semimetals. Two pieces of single crystals, labeled as Sample 1 and Sample 2, respectively, were used throughout this work to examine the role of μ and compare the results to those of the previous work17.

Transport property and magnetization measurements

Both thermal transport and electrical transport properties were measured in a Quantum Design PPMS® (Physical Property Measurement System; serial number: PPMS149) with a breakout box via a standard four-probe steady-state method41. National Instruments™ LabVIEW was utilized to build the customized test protocols and control the associated instruments. The magnetization measurements were conducted in a SQUID (Superconducting Quantum Interference Device) magnetometer, which specifically is Quantum Design MPMS®3.

Sample characterization

Laue X-ray diffraction was employed to determine the single-crystallinity and orientation of the as-grown crystals. Energy-dispersive X-ray spectroscopy (Quantax, Bruker) was utilized to examine the composition. Combining these two methods, with the benefit of the non-destructive nature of the instrumental approach, the phase purity of the as-grown samples can be confidently verified. X-ray diffraction (XRD) test on an after-measurement mounted sample was conducted by using Bruker D2 PHASER.