Picosecond anisotropic phase separation governing photoinduced phase stability in submicron Ti₃O₅ crystals

Abstract

Recently developed ceramic material Ti₃O₅ exhibits fascinating application properties, from ultrafast switching between metallic and insulating phases to light-to-heat conversion and storage. While the states conferring such properties are not spatially homogeneous, the origin of phase separation and the link between the phase coexistence and dynamics, key for stability of such states, is still little known. In this work, we use time-resolved X-ray diffraction and numerical simulations to establish rules by which the dynamics of heat-driven transition in laser excited Ti₃O₅ crystallites occur in space and time. The studies are conducted on submicron Ti₃O₅ crystallites and span a broad timescale allowing separation of phase change regimes. Our results reveal the influence of nanoscopic morphology on the mechanism of macroscopic transformation triggered by laser excitation.

Introduction

Ultrafast light-matter interactions give rise to the fascinating phenomenon of photo-induced phase transitions^1,2. Such a concept stems from the nonequilibrium states of matter^3,4. Recent advancements in ultrafast and intense laser technologies have opened up unprecedented opportunities to manipulate the macroscopic properties of various materials, further expanding the potential of this field^5,6. The dominant states are often not spatially homogeneous, yet the origin of phase separation and the link between the phase coexistence and non-equilibrium dynamics is key for understanding the stability of such states^7,8,9,10. In addition, while sample morphology can be a critical factor that determines the dynamical response of a material^11,12 ferroelastic nano-texturing was also shown to be the origin of complex dynamics on the mesoscopic scale¹³. The thermodynamic definition of phase transition implies divergence of fluctuation length scale, which becomes intrinsically limited in the case of nanocrystals¹⁴. From such perspective, finite size effects offer new properties or enhanced performance compared to bulk materials. This is the case for trititanium pentoxide Ti₃O₅ which already exhibits fascinating application properties: bistability between metallic and insulating phases at nanoscale (optical re-writability for high-density data storage)¹⁵, large latent heat in the reversible transition under small pressure (for long-term heat storage)¹⁶, solar steam generation (for seawater desalination)¹⁷. β-Ti₃O₅ undergoes phase transition from this semiconductor phase to metallic λ-phase, with significant structural changes. One Ti-Ti dimer in the β-phase dissociates upon transition to the λ-phase¹⁸ leading to a change of the monoclinic angle from 91.5° to 91.2° in the (a, c) lattice plane (Fig. 1a,b). This rearrangement in the dimer causes a notable expansion of the c lattice parameter by 6.4% whereas the b parameter remains essentially unaffected, resulting in a highly anisotropic distortion. In the λ-phase, the monoclinic angle decreases with temperature until it locks to 90° when a second-order phase transition towards a high-symmetry metallic phase (α) occurs (around 500 K).

Fig. 1: β and λ-phase Ti₃O₅.

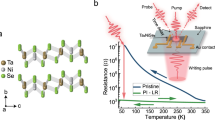
a, b Schematic crystal structure representation of Ti₃O₅ in the λ and β phases in (a, c) plane (left) and (b, c) plane (right). Titanium atoms are represented in orange for the λ-phase and in blue for the β-phase. The oxygen atoms are grey dots. The horizontal arrows show the direction of the lattice expansion (parallel to c) when going from β to λ-phase. Rotation axis for the Ti-Ti dimers is also depicted in the two crystallographic planes. c Evolution of the β-phase fraction (∆X_β) with the variation of pressure (logarithmic scale) for the three different morphological forms of the polycrystalline Ti₃O₅ powder: the flake type, stripe type and block type. d Temperature evolution of ∆X_β for the three types. The pressure and temperature values at 50% conversion are extracted from a sigmoidal fitting of the data (dashed lines). The temperature and pressure plots are adapted from references^15,16, and ²¹ for the flake type, stripe type and block type respectively.

In bulk single crystals, the β to λ transition occurring at a temperature T_SM of 450 K, is first order with a very narrow hysteresis¹⁹. However, in submicron crystals, the hysteresis broadens and the metallic phase is stabilized at room temperature and below^15,20. Here we focus on three morphologically different types of Ti₃O₅ crystals with submicron size crystallites namely flake type, stripe type and block type, previously described and obtained by different synthesis methods (see^15,16, and²¹, respectively). For the flake type, the crystallite size was found to be smaller than 100 nm on average and broadly distributed, by independent measurements with Transmission Electron Microscopy (TEM) and X-ray diffraction (XRD)^15,22. For the stripe type, TEM images show nanorod-shaped crystallites with a long dimension of 200 nm in majority¹⁶. For the block type, TEM images show crystals with cubic shapes of sub-micron size, and on average bigger than the two other forms (∼500 nm)²¹. In the bistability region of such submicron crystals, the transition between the high-volume metallic λ-phase and the low-volume semiconducting β-phase can be induced by applying moderate pressures¹⁶. Interestingly, transition pressure strongly depends on sample morphology as seen in Fig. 1c. Pressure needed at ambient temperature for 50% conversion to the β-phase are 320 MPa, 62 MPa and 10 MPa in the flake type, stripe type and block type respectively^21,23,24. However, the temperatures required for 50% conversion, at ambient pressure, is found to be very similar (487 ± 4 K) for the three morphological types of Ti₃O₅ as seen in Fig. 1d. Interestingly, the latent heat involved in the phase transition, as previously estimated from Differential Scanning Calorimetry measurements, is also very similar in the three types^15,16,21.

The non-equilibrium transition in Ti₃O₅ has been investigated with different pump-probe techniques, and even though a clear consensus has not yet been reached, all results reveal multiscale dynamics. References^25,26,27 hinted at the driving role of thermodynamics on nanosecond to microsecond time scales. Asahara et. al.²⁵ proposed an empirical nucleation model for a sample treated as continuum, neglecting thermodynamics at nanoscale. Nor were considered the initial conditions for the thermal switching after laser impact. It was recently demonstrated²² that about 30% of the photoexcited crystallites below the surface undergo a phase change on the picosecond timescale driven by strainwaves propagating through the nano-crystallites, followed by a complete phase transformation driven thermally at ns time scale. Partial transformation was explained by the fact that only the crystallites oriented favourably with respect to the incident pulse laser were initially transformed. This hypothesis was reinforced with optical spectroscopy measurements showing orientation-dependent photoinduced response²⁸. However, recent observation on single crystals^29,30 might indicate that partial transformation occurs even within a single object. Domain transformation was also supported by two recent computational studies^31,32.

In this paper, we explore the multiscale dynamics of the photoinduced phase transition in polycrystalline Ti₃O₅, using laser pump and X-ray diffraction probe. We show that the phase transition dynamics is strongly dependent on the morphology of the crystallites and that the ultrafast phase separation inherited from the strain wave propagation determines the stabilization of the photoinduced state at the ns time scale.

Results

Time-resolved XRD

The evolution of the structural changes during the photoinduced phase transition from the semiconducting β-phase to the metallic λ-phase in the polycrystalline Ti₃O₅ has been studied using time-resolved X-ray diffraction measurements performed at the ID09 beamline at ESRF. Ti₃O₅ pellets were prepared using three different types of polycrystalline powders namely, flake type¹⁵, stripe type¹⁶ and block type²¹, described in the Introduction. The pellets are cylinders with flat surface, 8 mm in diameter and 1–2 mm in width. The preparation procedure is further described in the Methods section. The pellets were photoexcited with laser pulses at normal incidence with the pellet surface. The structural changes were monitored using 12 keV X-ray pulses with a pulse duration of 100 ps. We used an X-ray incidence angle of 0.4°. At this incidence, the estimated X-ray penetration depth is about 800 nm, taking into account the surface roughness measured by Atomic Force Microscopy (Supplementary Fig. 1). It means that even with the biggest crystallites of the block type pellet, the X-rays probe beyond the first crystallite layer in depth and several times beyond the laser penetration depth (estimated as 70 nm (Supplementary Fig. 4a)). A comprehensive description of the measurement procedure is presented in the Methods section. The 1D diffraction patterns obtained from the azimuthally unfolded 2D diffraction images (Fig. 2a) for the three types of Ti₃O₅ pellets are shown in Fig. 2b, c, d respectively. The widths of the Bragg peaks are dominated by the X-ray energy bandwidth (∆E/E ∼1.5%) and the large footprint of X-rays on the sample due to the small incidence angle. Despite limited q resolution, Rietveld refinement with constrained atomic positions could be applied to extract the relative β/λ-phase fractions. The initial λ-phase fractions before photo-excitation were found to be 30%, 8% and 2% for the flake type, stripe type and block type pellets, respectively.

Fig. 2: X-ray diffraction patterns measured at ID09 beamline, ESRF.

a The 2D azimuthal unfolded pattern of the diffraction image on the stripe type Ti₃O₅ pellet. b–d Results of Rietveld refinement of the 1D pattern for the block, stripe and flake type Ti₃O₅ respectively. Measured powder pattern is plotted in gray dashed line, calculated patterns are in red b (block type), yellow c (stripe type) and green d (flake type). Orange and blue curves are the contribution of the λ and β-phase respectively. Labels are shown only for the most intense peaks and not when too many overlap. The residual curve is shown as a grey dotted line. e 1D diffraction patterns measured for the photoexcited stripe type Ti₃O₅ pellet at different time delays. The shift in the peak (110) is shown in the inset. The arrows indicate the increase or decrease in the peak intensity with delays. f The differential diffraction patterns for the same delays to follow the photoinduced structural changes. The blue and orange dashed vertical lines in subfigure e and f mark the positions of the β and λ-phase peaks respectively. Only selected intense peak labels are indicated in the plot.

The out-of-equilibrium absolute and differential patterns are shown in Fig. 2e and 2f, respectively, for different time delays after photo-excitation with a laser pulse at 800 nm. The differential patterns are obtained by subtracting the laser-off (unpumped) patterns from the laser-on (pumped) patterns, thereby highlighting the photoinduced structural changes. These patterns are obtained by averaging over several repetitions as described in the Methods section. We observe that upon photo-excitation, the β peaks (201), (003) and (004) decrease in intensity (shown by the blue arrows), whereas the λ peaks (200), (20-3)/(203) increase in intensity (shown by the orange arrows) with the increase in delays. In a crude, yet often satisfactory approximation, we can attribute the apparent peak dynamics to a strained crystal (peak shift) and a phase transition (peak shifts and intensity redistribution). The shift of Bragg peak (110) (inset of Fig. 2e) has a maximum at a time delay (<100 ps) beyond the resolution of the experiment. This is consistent with the time needed to dilate a single crystallite following a strain-wave travelling at the speed of sound of 6500 m s^−1 22. A late dynamics is observed for the peaks which are more sensitive to the phase transition. For example, (20-3)/(203) shows a significant intensity redistribution due to the change of both the c parameter and the monoclinic angle, whereas for (201)/(002) intensity, respectively decreases/ increases at the transition from β to λ-phase. For these peaks, the maximum change is observed around 100 ns. This time scale matches thermal diffusion over 150 nm based on thermal diffusivity of 230 nm² ns⁻¹ in Ti₃O₅¹⁶. Such kinetics would thus be associated with thermal equilibrium in the sample, leading to a late transition towards hot metallic phase. Our experimental resolution does not allow us to discriminate between the two metallic phases (λ or α), and so the photo-induced metallic phase will be referred to as λ in the following.

In a previous study²², the strain-driven early dynamics was observed within the first 20 ps. According to that study, for the block-type crystallites, the propagation of volumic strain and the phase transition would be completed within 80 ps after laser excitation. In the present study carried out at ID09, those early dynamics are too fast to be resolved. However, the time resolution of the current experiment (∼100 ps) allows us to follow and quantify accurately the slower increase of the λ-phase upon heat diffusion. The time evolution of the weight percentage of the λ-phase (∆X_λ) is plotted in Fig. 3a. In this figure, ∆X_λ is normalized to its value at a delay of 0.1 ns when the strain-wave propagation has been completed in all types of Ti₃O₅ pellets. The evolution of ∆X_λ, as determined from Rietveld refinement, is shown in Supplementary Fig. 3. The most striking observation is that both the amplitude and time evolution of this thermally driven phase transformation are strongly dependent on the crystallite type. The maximum is reached at 180 ns for the smallest crystallites (flake type), 60 ns for the intermediate size (stripe type) and 40 ns for the biggest crystallites (block type) and this trend has been plotted in Fig. 3b. So the phase transition develops longer in pellets containing smaller crystallites. The same trend is observed for all laser fluences, from a transition threshold of ∼ 0.1 mJ mm⁻² up to the damage point found at 0.8 mJ mm⁻² (see Fig. 3c and d, and Supplementary Fig. 5). Besides, the weight percentage of the λ-phase at 100 ns time delay shows a non-linear increase with increasing fluence in contrast to the linear behaviour at 200 ps time delay. This is true for both flake-type and block-type crystallites as shown in Fig. 3c and d, respectively. Such fluence dependence emphasizes the different mechanisms at play in the early time (<100 ps) and nanosecond time scale. In order to study the effect of the laser penetration, block-type and flake-type pellets were also photoexcited with different laser wavelengths, namely 800 nm and 1550 nm (see Supplementary Fig. 4). The laser penetration depth of 1550 nm is estimated to be twice that of the 800 nm wavelength. Seemingly, varying penetration does not affect the dynamics of the phase transformation due to heat diffusion.

Fig. 3: Photoinduced transient structural changes as a function of delays and laser fluence.

a Evolution of the λ-phase fraction (∆X_λ) as extracted from Rietveld refinement of the TR-powder patterns for the three types of powder pellets with different crystallite size, the block type, stripe type and flake type Ti₃O₅. The ∆X_λ has been normalised to its value at 0.1 ns and the time delays are represented in logarithmic scale. The error bars in ∆X_λ have been extracted from the Rietveld refinement and do not consider experimental drifts. The dashed lines are plotted using a spline interpolation of zeroth-order and indicate guides for the eyes. b The delays at which the λ-phase fraction reaches maximum are plotted as a function of crystallite sizes in the different types of pellets. The dashed line represents a power law fit. c The variation of ∆X_λ in the flake type pellet and d in the block type pellet as a function of laser fluence for few time delays, 200 ps, 100 ns and 1 µs after the photo-excitation. The curve at 200 ps is fitted with a linear function while the curves at 100 ns and 1 µs are fitted with a power law, as indicated by the dashed lines.

Heat-diffusion model

To understand the nanosecond dynamics of phase transition in photoexcited Ti₃O₅ and provide the rationale for the observed size-dependent build-up of the high temperature phase, we developed a heat-flow model based on finite difference method^33,34. Similar methods have been used previously to simulate the heat conduction in composite materials with specific boundary conditions³⁵ and to study the out-of-equilibrium dynamics in spin crossover complexes by coupling with elastic interactions^12,36. In this model, the compound has been represented by a 2-dimensional grid of ’nodes’ as shown in Fig. 4a–c. The nodes correspond to the center of mass of elementary building blocks. They are scaled to the real crystallite size, hence the distance between consecutive nodes is 10 nm. This size justifies assigning thermodynamic parameters to the nodes. Several such building blocks form a crystallite. We have assumed the quadratic and symmetric shape of the crystallites for computational simplicity. This allows us to isolate the effect of the crystallite size without introducing additional shape-related variations in the system. The whole system consists of many crystallites separated by grain boundaries. To avoid the multi-parameter problem in the simulations, only temperature has been used to distinguish the two phases. A node with 300 K < T < 470 K is tagged as β-phase and that with T > 470 K is tagged as λ-phase. The system evolves over time by solving the heat conduction equation between each node and its four nearest neighbours. Different effective exchange coefficients are considered, depending on the phase (λ or β) and crystallite indices (i, j) of the nodes (see Fig. 4c). This allows us to take into account the heat exchange between the nodes within a grain (c_i,i), across the grain boundaries (c_i,j) and the heat loss through the surface of the pellet or within the bulk (c_i,air and c_i,bulk, respectively). The values of these heat exchange coefficients are estimated based on physical parameters as discussed in the Methods section. The values used for the simulation displayed in Fig. 5 are summarized in Table 1. However, direct comparisons of the 2D model with a real system should be done with care.

Fig. 4: Heat diffusion model.

a–c Schematic description of the 2-dimensional model system. a Experimental geometry showing the laser pump pulse incident normally on the Ti₃O₅ pellet and X-ray probe at a grazing incidence. b A section of the Ti₃O₅ pellet is represented with a simulation box of 500 × 500 nodes of which 400 nodes below the surface are photoexcited. In this scale, the X-ray probed depth is about 80 nodes and laser penetration depth is 10 nodes. c A zoomed image on the photoexcited region of the system shows the 2-dimensional grid of ”nodes”. Several nodes together form crystallite/grain (for example, the ith and jth grains) and are separated by grain boundaries. Three different thermal exchange coefficients between the nodes are represented by the green, orange and purple arrows for respectively the intragrain coefficient(c_i,i), intergrain coefficient(c_i,j) and the heat exchange coefficient(c_i,air) with the surrounding air across the sample surface. d, e The initial spatial distribution of the λ-phase domains within the X-ray probed regime for d S = 100 × 100 nm² and e S = 500 ×  500 nm² crystallite sizes. The grain boundaries are denoted with the dashed lines. Random number of assymetric λ-phase domains are distributed within each grain.

Fig. 5: Simulations of the heat driven transformation.

a, b Spatial distribution of λ and β-phase domains for a S = 100 × 100 nm² grain size and b S = 500 × 500 nm² grain size at the time delay at which the λ-phase fraction reaches maximum (dynamics in c). The initial states of these are in Fig. 4d, e. c (top) Exponentially decreasing temperature profile on the λ-phase filaments at the initial state of the simulation for two different grainsizes: S = 100 × 100 nm² and different filament lengths for S = 500 × 500 nm². (bottom) Evolution of the λ-phase fraction (∆X_λ) as a function of delays for the 100 nm grain (in green) and 500 nm grain (in shades of red). The dynamics for different domain depths have been plotted for the bigger grain (S = 500 × 500 nm²). The time axis is represented in logarithmic scale.

Table 1 Parameters for the heat-diffusion model

To simulate the geometry of the experiment, where only a small localised part of the pellet surface is photo-excited, we have chosen to apply initial transformation only within a limited region along the simulation sample surface. This region is 4 µm broad in the center of the surface (over 5 µm total surface width equivalent to 500 nodes). To represent the state of the system after propagation of strain wave, a part of the crystallites within this 4 µm broad region is initially switched to λ-phase. For the flake type crystallites, the amount of transformation within the first layer of 100 nm in depth (about one crystallite layer in this case) after the strain wave propagation was previously estimated to be 30% for a pump fluence of 0.5 mJ  mm⁻²²². To replicate this observation, 1200 nodes are switched within a region of 4000 nodes (400 nodes in width equivalent to 4 µm and 10 nodes in depth equivalent to 100 nm) below photoexcited surface. Those 1200 nodes represent the photoexcited region for the small crystallites. The total number of switched nodes scale with absorbed laser energy, hence kept the same for the system with bigger crystallites, even when the initial state is set up with transformation beyond photoexcited region. The initial temperature of the photoexcited nodes is defined as exponentially decaying with depth, with maximum at the surface, as shown in Fig. 5c (top). The surface temperature is estimated based on the incoming laser energy used in the experiment and the known index of refraction (Supplementary Information in ref. ²²).

Different initial states of the system with patterns of λ-phase nodes have been tested in the simulations. The corresponding time evolution of λ-phase fraction and the state of the systems for two different grain sizes are shown in Fig. 5 and Supplementary Figs. 6, 7 and 8. Based on the previous hypothesis that the probability of transition depends on crystal orientation, we first assumed an initial state with a certain number of fully transformed single crystallites (Supplementary Figs. 6, and 7). The phase transition dynamics indicate that the maximum transformation is achieved faster in the smaller crystallites than in the larger ones. This result is in contradiction with experimental observation. We then assumed crystallites fully transformed along the photoexcited surface with transformation limited in depth by the laser penetration (i.e., λ-phase domains extending 100 nm in depth, see Supplementary Fig. 8). Again, maximum phase transformation occurs faster in smaller crystallite, in contrast with experimental observation.

A model based on fully transformed crystallites failed to reproduce our experimental results, prompted us to consider an alternative scenario - phase coexistence within individual crystallites. Such a scenario is indeed supported by recent molecular dynamics study which demonstrate that the β to λ-phase transformation initiates with the formation of two-dimensional nuclei and then progresses layer by layer³². To explore this, we considered some asymetric λ-phase domains at the initial state: only tens of nanometers wide (about 10 to 40 nm wide) at the photoexcited surface and 100 nm in depth for both the crystallite sizes S = 100 × 100 nm² and S = 500 × 500 nm². We then conducted a systematic study by gradually increasing the domain depth (from 100 nm to 500 nm) in the bigger crystallites to study how the size of the domains influences the transformation. One such initial state with the domains extending 400 nm in depth in the bigger crystallite S = 500 × 500 nm² is shown in Fig. 4e. The simulations shown in Fig. 4d, e were carried out with the thermal exchange parameters in Table 1.

In this case, as shown in Fig. 5c (bottom), we observed that the maximum transformation occurs earlier in the bigger crystallites, even when the initial domain size and distribution are identical in both the small and big crystallites. As the domain depth is increased in the bigger crystallite, the peak position shifts towards shorter time delays, thereby making the peak shift more pronounced. Besides, the amount of transformation also decreases with the increased depth at the outset of the simulation. By comparing the amplitude of transformation for small and big crystallites, the best match with the experimental observations shown in Fig. 3a is obtained for domains of 500 nm in depth. This clearly indicates that the phase coexistence scenario is in better agreement with experimental results than a scenario based on fully transformed crystallites.

Discussion

In this section, we will discuss the observed dynamics of phase transformation, how they scale with varying size of the excited system, and investigate by means of numerical simulations how different patterns of excitation are reflected in the dynamics.

First and foremost, the flake type sample was previously studied on the ultrafast (femto to picoseconds) and slower (nanoseconds) timescale, following excitation with 800 nm²². That study demonstrated picosecond switching in nanocrystals by strain waves triggered with laser excitation and several decades later thermal switching governed by heat diffusion. However, it was impossible to determine the limits defining the spatial distribution of transformation, since the laser penetration, the average crystallite size and the phase front limit were very similar, around 100 nm. In this study, the experiments are set up in order to discriminate between those purportedly critical parameters. Figure 3a shows the temporal evolution of the λ-phase fraction, normalised to the initial fraction transformed by strain, for the three samples of different crystallite sizes, namely the block type, stripe type and flake type Ti₃O₅. All three reveal a thermal transformation peak in 10−100 nanosecond timescale followed by a relaxation in microsecond time. The first step is convoluted with X-ray pulse duration, but its origin and dynamics are known as mentioned above. The two mechanisms, one following the strain propagation and the other following heat diffusion, not only unfold on very different timescales but also the dependency on the excitation density points to different physical underpinnings (Fig. 3c, d). It is noteworthy that the phase conversion by strain waves, estimated at 200 ps, scales linearly with the laser excitation, unlike the nonlinear response at 100 ns or 1 µs. The most striking observation from the experimental results (Fig. 3a, b) is that the smaller the crystallite size, the longer it takes to reach the maximum transformation to the λ-phase following heat diffusion. Yet, the percentage gain in the final phase transition is highest in the smaller crystallites. To assess whether light scattering affects the observed differences, the reflectance of the pellets was measured as a function of wavelength (Supplementary Fig. 2). The results show only few percent variation in total integrated reflectance across the different pellets, indicating that the effective absorbed fluence is comparable. This suggests that the observed difference in transformation dynamics is independent of the amount of laser light scatter on each morphological type.

We were able to replicate such seemingly non-intuitive temporal behavior with a relatively simple heat diffusion model. The outcome of the simulation strongly depends on the initial conditions, hence several were tested to replicate the experimental observations. The simulations that best reproduced the observed trends in Fig. 5c were obtained with initial transformation patterns resembling thin finite size domains of λ-phase that propagate deep, beyond 100 nm, in the bigger crystallites (Fig. 4d, e). The assumption of thus shaped domains in the 2D model, which correspond to layered or elongated domains in the real 3D crystallites, is reasonable considering the strong anisotropy of the structure. It is also consistent with the already mentioned computational studies^31,32. Also, because of random orientation of crystallites and the acoustic impedance at the grain boundaries, it is fair to assume that the phase boundary for strain wave mechanism will be that of individual grain, unlike a situation where the phase front stops randomly within a grain. Hence, in the simulation the initial λ-phase domains do not spill onto neighbouring grains. Importantly, the temperature of the macroscopic photo-switched domains does not equilibrate on the picosecond timescale, so the temperature gradient is assumed to retain the initial laser excitation. Thus, separated λ/β phases within crystallite set up the initial conditions for heat diffusion, and T_SM determines whether transition occurs, as described in the previous section.

The numerical steps of simulation, for instance at the maximum transformation in Fig. 5a,b, allow mapping the spatial distribution of the zones above and below T_SM, λ- and β-phase, respectively. It is now intuitively conceivable that the fastest thermal conversions on a given length scale will occur within the same grain, where no thermal boundaries slow down the diffusion process. Amplitude-wise, the bigger the crystallite surface, the quicker the exchange with bath. Considering the above, the phase transition is fastest in the block type, slower in the stripe type and slowest in flake type λ-Ti₃O₅.

The absolute timescales of the simulated phase change coincides with the experimental timescales for the lower fluence of 0.25 mJ mm⁻² (Supplementary Fig. 5) better than for the higher fluence of 0.5 mJ mm⁻². Importantly, the relative shift (about one order in magnitude in time) between the small and large crystallites is in excellent agreement with the experimental observations. The slight mismatch in absolute timescales may arise from underestimation of the temperature distribution in the initial states and/or the number of initially transformed λ-phase nodes. Additionally, the non-transformed β-phase nodes could be at a higher temperature than T_SM which our simple model does not fully account for. The model does allow examining the influence of latent heat. Simulations using different latent heat values (Supplementary Fig. 9) show that the delay to reach the maximum λ-phase conversion remains largely unaffected, the relaxation dynamics following the peak is influenced. Larger values of latent heat only slow down the relaxation back to the β-phase, whereas for lower values, the dynamics is indistinguishable from the curves with no latent heat.

Apart from the grain size, we also tested the laser penetration as a factor likely to determine the phase boundary limit. The block type and flake type samples were excited with two different laser wavelengths (see Supplementary Fig. 4). Despite a factor of two in the penetration depths, both excitations lead to indiscernible temporal evolution also evident from the simulations with the same domain depth of 100 nm (Fig. 5c). We would like to point out that the consideration based on the wavelength dependency study is not as strong as that drawing from comparison between different crystallites at fixed wavelength and fluence. The essential finding of this work is that the dynamics depend on the crystal size under given excitation conditions.

Conclusion

With time-resolved XRD experiments and numerical simulations of heat diffusion, we established the set of rules by which the dynamics of heat-driven transition in laser-excited Ti₃O₅ nanocrystallites are likely to occur in space and time. Our investigations highlight the role of causality for determining the spatio-temporal patterns of phase separation in non-equilibrium conditions. Even though the dynamics evolving on very different timescales obey different regimes, we show that the outcome of the fast-driven transition predetermines that of the slower thermal transition. The results expose how nanoscopic morphology of a material impacts the mechanism of macroscopic transformation triggered by laser excitation. The work provides insights for developing capabilities to control materials with multiscale approach, from microscopic to material scale and on timescales native to new technologies. From a broader perspective, metastable phase formation has been a vividly pursued problem in the field of photoinduced phase transitions. Our conclusions should have important experimental implications and also encourage theoretical work on feedback mechanisms operating in nonequilibrium between elastic deformations and electronic band structure.

Methods

Sample preparation

The metastable phase of λ-Ti₃O₅ was obtained in three different morphological forms using different synthesis methods. The flake form of λ-Ti₃O₅ was obtained by calcinating the anatase form of TiO₂ nanoparticles of 7 nm under hydrogen flow at 1473 K¹⁵. The crystallite size was estimated to be 100 ± 40 nm by performing static powder X-ray diffraction in transmission geometry²². Sintering rutile TiO₂ particles in a hydrogen atmosphere at 1390 K gave the stripe-type Ti₃O₅. The nanocrystals were in the shape of rectangular nanorods with dimensions 200 × 30 nm¹⁶. Sintering the same polymorph of TiO₂ particles in a hydrogen atmosphere at 1573 K for 2 h yielded a block-type Ti₃O₅ with sub-micrometer dimensions²¹. The polycrystalline powders obtained from the aforementioned processes were ground into finer powders and compacted in an enclosed cavity of defined geometry called a pellet die. A pressure of 50 MPa is applied on the pellet die in an uniaxial direction using a manual hydraulic press. The pellets were 8 mm in diameter and a few millimeters thick. The pellets contained a mixture of pressure-induced β and λ-phase crystallites, the proportion of which depends on the form and effective pressure applied for pelleting. The phase fractions in the three types of pellets were extracted from Rietveld refinement of the diffraction patterns. Surface roughness of the pellets was characterized using Atomic Force Microscopy (AFM). AFM images were recorded in tapping mode using a Veeco diInnova microscope with a silicon probe (force constant 42 N m⁻¹, resonance frequency 285 kHz, radius of curvature typically <10 nm). Across all pellets, a surface roughness of 350 nm ± 50 nm was measured with no significant variation between samples (height distribution is shown in Supplementary Fig. 1).

Time-resolved XRD

X-ray diffraction experiment was performed at ESRF, ID09 beamline during hybrid mode (7/8th continuous filling+1 isolated electron bunch). The isolated electron bunch was used in the experiment. The ID09 setup was discussed in detail previously^37,38. Briefly, fast rotating choppers were used to isolate X-ray single pulses (each 100 ps long) at a 40 Hz repetition rate. The X-ray energy was centered at 12 keV (λ = 1.0332 Å) with ∼1.5% bandwidth. The FWHM of the X-ray beam at sample position was 23 (horizontal) × 14 (vertical) µm² leading to a footprint of 23 µm × 1.9 mm at 0.4° incidence angle. In this geometry, the calculated X-ray penetration (at 1/e) is 450 nm for a perfect surface and measured sample density of 3.2 g cm⁻³. However, considering the measured surface roughness of 350 nm (see Supplementary Fig. 1), the effective penetration is estimated to 800 nm. Diffracted X-rays were integrated on a Rayonix MX170-HS CCD detector with pixel size of 44.25 µm. Measurements are taken in stroboscopic mode and each image was recorded with 400 shots exposure (i.e., 10 s exposure at 40 Hz). A synchronized laser 800 nm with 1–2 ps pulse duration was used to excite the sample. Laser excitation with quasi-normal incidence lead to measured beam size on sample of 0.13 × 4.2 mm². Laser fluences between 0.1 mJ mm⁻² and 0.8 mJ mm⁻² were typically used and this refers to the incident laser fluence on the sample. The effective absorbed fluence is about 85% and is similar across the flake, stripe and block type pellets (Supplementary Fig. 2). XRD images are measured at different time delays before (“negative” delays) and after (“positive” delays) photo-excitation. The delay sequence is repeated several times to correct for drift effects and increase the measurement statistics. Reference patterns with no laser excitation are interleaved in the sequence to track X-ray beam/ sample drifts and permanent or long-lived effects.

Powder XRD analysis

Each diffraction image was azimuthally integrated using the pyFAI library³⁹ in order to obtain the 1-dimensional diffraction patterns. Rietveld refinement of the whole powder patterns was performed using the TOPAS⁴⁰ software. The experimental profile was described with X-ray beam energy of 12 keV and a Gaussian profile with FWHM of 17 mÅ. The X-ray beam height and the incidence angle were fixed to the values measured during experiment. The sample-to-detector distance was fixed at 151 mm, after refining for the “laser off” pattern. The refinement was performed within a q range from 1.06 Å⁻¹ to 4.06 Å⁻¹. The background was described by the Chebyshev polynomials with 7 coefficients. The peak width and sample displacement were refined on the reference patterns without photo-excitation. These parameters were then fixed for the refinements of the patterns at negative and positive delays. The atomic positions could not be refined due to lack of sensitivity and were therefore fixed to published values. Typical R_wp values were 5 ± 1%. After refinement, the weight percentages of the interleaved reference patterns were used to correct for drifts. The interpolated value between two interleaved references was used as the reference and subtracted to extract the change in weight percentage for each measurement at positive/negative delays. The values were then averaged over multiple repetitions of the time sequence.

Heat diffusion model

A portion of the Ti₃O₅ pellet is depicted using a mesh of 500 × 500 nodes as illustrated in Fig. 4b. 400 nodes below the systems’s surface are considered to be photoexcited. The system is assumed to consist of crystallites with dimensions of S = 10 × 10 nodes and S = 50 × 50 nodes for the smaller 100 nm and bigger 500 nm crystallites, respectively. Scaled to the estimated sizes of flake type and block type Ti₃O₅, respectively, it corresponds to a distance between node of 10 nm.

The heat flow from node (m-p, n-q) to node (m, n) for this 2D system is given by:

$${q}_{\left(m-p,n-q\right)\to \left(m,n\right)}={k}_{\left(m-p,n-q\right)\to \left(m,n\right)}A\frac{{T}_{m-p,n-q}-{T}_{m,n}}{\varDelta {x}_{\left(m-p,n-q\right)\to \left(m,n\right)}}$$

(1)

with (p, q) = (1, 0), (0, 1), (−1, 0), (0, −1) respectively for each of the 4 nearest neighbours. The heat flow q is in W, k is the heat conductivity in W m⁻¹ K⁻¹, ${T}_{m,n}$ is the temperature of the node in K and A is the exchange area in m². In this square and regular lattice, the exchange area A and the distance $\varDelta {x}_{\left(m-p,n-q\right)\to \left(m,n\right)}$ between node ($m-p,n-q$) and node ($m,n$) are constant.

The temperature change of each node is calculated from the heat flux q:

$$\varDelta {T}_{m,n}={\sum }_{\left(p,q\right)}{q}_{\left(m-p,n-q\right)\to \left(m,n\right)}/{C}_{p}^{(m,n)}$$

(2)

with (p, q) = (1, 0), (0, 1), (−1, 0), (0, −1) for the 4 nearest neighbours and heat capacity ${C}_{p}^{(m,n)}$ is either ${C}_{p}^{\beta }$ for the β-phase nodes or ${C}_{p}^{\lambda }$ for the λ-phase nodes and is in units of J K⁻¹ mol⁻¹.

We define an effective heat exchange coefficient c to compare the heat flow between different pairs of nodes:

$${c}_{\left(m-p,n-q\right)\to \left(m,n\right)}=\frac{{q}_{\left(m-p,n-q\right)\to \left(m,n\right)}}{{T}_{m-p,n-q}-{T}_{m,n}}=\frac{1}{{R}_{\left(m-p,n-q\right)\to \left(m,n\right)}}$$

(3)

where ${R}_{\left(m-p,n-q\right)\to \left(m,n\right)}$ is the effective thermal resistance between the nodes.

The heat exchange coefficients within a single crystallite i are estimated based on the reported thermal conductivity values for β and λ-phase.

Secondly, the heat exchange between two nodes in neighboring crystallites i and j takes into account a thin polymer layer of few nodes in thickness between the crystallites.

In order to estimate the effective heat exchange coefficient, we use the following expression for the thermal resistance between two nodes (m, n) and (m-p, n-q) belonging to two different crystallites separated by a grain boundary (B) layer (shown by the black line in Fig. 4c):

$${R}_{\left(m,n\right)\to \left(m-p,n-q\right)}=\frac{\varDelta x/2}{{k}_{\left(m,n\right)}A}+\frac{\varDelta {x}_{B}}{{k}_{B}A}+\frac{\varDelta x/2}{{k}_{\left(m-p,n-q\right)}A}$$

(4)

where ${k}_{\left(m,n\right)}$ and ${k}_{\left(m-p,n-q\right)}$ are the thermal conductivities of nodes (m, n) and (m-p, n-q) respectively. $\varDelta x$ is the distance between the consecutive nodes within a crystallite and A is the area over which heat exchange takes place. $\varDelta {x}_{B}$ is the thickness of the boundary layer.

The heat loss at the surface of the pellets (between a crystallite i and the environment) assumes a thick air layer acting as a thermal bath. On the three other edges, the heat is lost through a thick (non-excited) layer of Ti₃O₅ also acting as a thermal bath.

A time step is concluded when the heat exchange is done between the nodes and the phase of each node is checked for phase transition based on its final temperature. A node with T increasing above 470 K is converted to the λ-phase and a node with T decreasing below 470 K is converted to β-phase. At the end of each time step, the λ-phase fraction is calculated as the ratio of the number of λ nodes to the total number of nodes in the probed region. The full relaxation is considered to be achieved when all the nodes are switched back to the low-temperature β-phase.

For the study of the effect of latent heat on the dynamics of the phase transition (Supplementary Fig. 9), we have included it during the phase transition of the nodes at each time step. When a λ-node transforms to the β-phase, latent heat (δH_L) is released and distributed equally to neighboring nodes (the temperature of the nodes increases). Whereas when a β-node transforms to λ-phase, the required latent heat is extracted equally from the neighbouring nodes (temperature of the nodes decreases). The temperature of the transforming node itself remains unchanged during the phase transition. The amount of latent heat on each neighbouring node (δH_L/4) is then converted to temperature change depending on the phase and hence specific heat capacity of these nodes.