Introduction

Waveguide Quantum Electrodynamics (wQED) studies how matter interacts with photons propagating along a transmission guide1,2,3. Recent experimental realizations of wQED span the optical to microwave regimes, incorporating real or artificial atoms and various material supports for the waveguides4,5,6,7,8,9,10,11,12,13,14,15,16,17,18. These experiments reveal collective effects in the emission of quantum emitters and help harnessing photon-induced correlations with potential applications for quantum technologies.

So far, in wQED the focus has been mainly on otherwise quasi-independent emitters, where all interactions are mediated by the photons. Besides, the excitation spectra of systems showing long-range order, e.g. layered magnetic materials19, have also been measured using microwave transmission lines. In the latter case, spin excitations are collective states, but correlations are dominated by interactions that are inherent to the material. Exploring situations in which the two effects compete remains virtually uncharted. Yet, there are compelling reasons to consider them. Firstly, because the close packing of emitters unavoidably generates interactions among them20,21,22. And secondly, because their different signs and ranges can introduce ways to tune the order and thus create novel states23,24,25.

In this work, we study the competition between light-mediated and intrinsic spin-spin interactions in a magnetic material coupled to microwave photons propagating via a superconducting transmission line (Fig. 1a). We focus on a particular model system, an organic free radical, in which spin- spin correlations grow along 1D chains26 and can, therefore, be gradually controlled by either changing temperature or magnetic field. The broadband nature of the waveguide helps overcoming the limitations associated with narrow band in cavity QED26,27,28,29, albeit at the price of a weaker spin-photon coupling. In particular, it allows studying within a single experiment the coupling to spin excitations at different energy scales. Here, we exploit this characteristic to study how the photon transmission reflects changes in the nature and properties of such excitations. The results show the possibility of attaining a very high collective spin- photon coupling in the paramagnetic regime, at sufficiently high T, which then competes with intrinsic spin-spin correlations as T decreases. When the latter take over, the microwave transmission bears evidence for a change in the statistics governing the elemental spin excitations, from single spin flips to bosonic magnons.

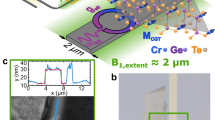
Fig. 1: Experimental setup and characterization of DPPH as a model 1D spin system.
figure 1

a Sketch of the setup used in transmission experiments and image of the two molecular subspecies, A and B, present in the DPPH crystal structure31. b Product of the magnetic susceptibility χ times temperature, measured on a powdered DPPH sample from 0.3 K up to 100 K and for B = 0.1 T. The blue (gray) solid line is a fit with a model that considers the formation of antiferromagnetic dimers within sublattice A and then of spin chains (dimers) within sublattice B, as T decreases. The inset shows the correlation function between nearest neighbor spins estimated as \(\langle {S}_{i}^{x}{S}_{i+1}^{x}\rangle \simeq -| 1-\chi T/{C}_{{{\rm{B}}}}|\)44,45, where CB = 0.1536 emu K/mol Oe is the Curie constant of the B-type DPPH molecules. c Specific heat of DPPH measured from 0.3 K to 100 K at B = 0. The blue (gray) solid line are results calculated with the chain45 (dimer31) model for the magnetic contribution of spins in sub-lattice B.

Full size image

Results and discussion

DPPH as a 1D spin system

All experiments described below used the 2, 2−diphenyl−1−picrylhydrazyl (hereafter DPPH) organic free radical30,31 in powder form, as purchased from Sigma Aldrich (see methods). X-ray diffraction experiments, shown in Supplementary Fig. 1, suggest that this material exhibits the DPPH-III crystal structure31 (Fig. 1a) that contains two inequivalent DPPH sites, referred to as A and B sublattices. Each DPPH radical hosts a spin S = 1/2 with a nearly isotropic gS ≃ 2.004 factor. At either high temperatures or in a sufficiently diluted form, it behaves as an ensemble of quasi-identical paramagnetic moments, which has made this material a widely used standard in Electron Paramagnetic Resonance (EPR)32. On the other hand, in dense materials and for sufficiently low temperatures, interactions between neighbor radicals become relevant26,31,33,34.

The magnetic response of DPPH has been studied via a combination of magnetic susceptibility and specific heat experiments performed in a broad temperature range 0.3 K ≤ T ≤ 100 K. The results are outlined in Fig. 1 and shown in detail in Supplementary Note 1 and Supplementary Figs. 4–7. The main conclusions are: i) a fraction, ~15%, of DPPH molecules are oxidized, thus have S = 0; ii) molecules belonging to the A crystal sublattice form antiferromagnetic (AF) dimers, also with an S = 0 ground state, at relatively high temperatures ≲ 50 K, and iii) DPPH spins in sublattice B form 1D chains along which AF correlations grow continuously as temperature decreases (see the inset of Fig. 1b). Below 10 K, only B-type molecules can therefore couple to microwave photons.

Broadband microwave transmission in the paramagnetic regime

Microwave transmission experiments were performed with on-chip superconducting coplanar waveguides using two different 3He-4He dilution refrigerators (see methods and Supplementary Fig. 2 for details). Magnetic fields up to 0.5 T were oriented along the y axis of the device. A 1-mm wide polycrystalline DPPH pellet containing  ~1017 molecules, half of them belonging to sublattice B, was fixed on the 400-μm wide central line by means of apiezon N grease. The complex transmission \({S}_{21}=| {S}_{21}| {{{\rm{e}}}}^{{{\rm{i}}}{\varphi }_{21}}\) and reflection \({S}_{11}=| {S}_{11}| {{{\rm{e}}}}^{{{\rm{i}}}{\varphi }_{11}}\) were measured in the frequency range 10 MHz ≤ ω/2π ≤ 14 GHz. Since the sample size is smaller than the shortest photon wavelengths (λ ≥ 4.4 mm) we can disregard the dependence of the electromagnetic modes along the y axis of the device (cf Fig. 1a). In order to extract the changes in transmission and reflection that arise from the coupling to spins and to compensate for the decay of S21 with increasing ω, both quantities were normalized using data measured at two different magnetic fields35,36, as shown in Supplementary Note 2 and Supplementary Figs. 8–11.

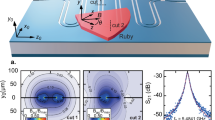
We first examine the transmission measured at T = 2 K. Normalized ∣S21∣ data are shown as a function of frequency and magnetic field in Fig. 2a, which also includes examples of complex transmission and reflection normalized data taken at 150 mT. Transmission minima are observed for magnetic fields and frequencies fulfilling the condition ω = Ω ≡ gSμBB/ℏ, indicating the resonant absorption of photons by paramagnetic spins. Note that the normalization of the data induces an additional line of ∣S21∣ maxima to the right of the resonance curve in Fig. 2a, as shown in Supplementary Fig. 8. Besides, the data show also contributions from spurious modes, caused by unavoidable imperfections at the chip boundaries or contact bonds, which manifest themselves as horizontal lines in Fig. 2a. The resonances are accompanied by maxima in reflection. The fact that ∣S11∣ ≃ ∣S21∣ − 1 (see Fig. 2 and Supplementary Fig. 11) shows that the spin-photon interaction process preserves the photon coherence that characterizes wQED.

Fig. 2: Microwave transmission in the paramagnetic regime.
figure 2

a Two- dimensional plot of the normalized microwave transmission ∣S21∣ of a superconducting wave guide coupled to a DPPH polycrystalline pellet, measured at T = 2 K. The insets show the shape of both the absorption (reflection) amplitude ∣S21∣ (∣S11∣) and its phase φ21 (φ11) with their corresponding fits based on Eq. (1), from which we determine the collective spin-photon coupling G and the decay rate Γ. b Values for G and Γ obtained from these fits as a function of magnetic field. The lines are least-square fits based on Eq. (2), for G, and on a constant function Γ/2π ≃ 14 MHz. The inset shows the maximum transmission visibility η as a function of magnetic field (open dots) and the prediction derived from Eq. (1) (solid line).

Full size image

These results are analyzed through the light-matter Hamiltonian \({{\mathcal{H}}}={{{\mathcal{H}}}}_{{{\rm{M}}}}+{{{\mathcal{H}}}}_{{{\rm{WG}}}}+{{{\mathcal{H}}}}_{{{\rm{I}}}}\), which encompasses the spin system \({{{\mathcal{H}}}}_{{{\rm{M}}}}\), the waveguide \({{{\mathcal{H}}}}_{{{\rm{WG}}}}\), and their interaction \({{{\mathcal{H}}}}_{{{\rm{I}}}}\)37,38,39. In the paramagnetic regime, spins are considered as non-interacting and \({{{\mathcal{H}}}}_{{{\rm{M}}}}\approx -{g}_{S}{\mu }_{{{\rm{B}}}}{\sum}_{j}{{\bf{B}}}{{{\bf{S}}}}_{{{\bf{j}}}}\). The changes in S21 and S11 associated with the spin resonance can be fitted with the following expression, derived from \({{\mathcal{H}}}\) using input-output theory as described in the methods (see also refs. 9,40,41,42),

$$\begin{array}{rcl}{S}_{21}&=&1-\frac{G}{G+\Gamma +{{\rm{i}}}(\Omega -\omega )}\\ {S}_{11}&=&-\frac{G}{G+\Gamma +{{\rm{i}}}(\Omega -\omega )}\end{array}$$
(1)

to obtain the collective spin-photon coupling G and the decay rate Γ, which parametrizes the losses. Illustrative fits are shown as insets in Fig. 2a, while the field-dependent parameters extracted at T = 2 K are shown in Fig. 2b.

We find a nearly constant Γ/2π ≈ 14 MHz. This value is larger than the spin dephasing rate γϕ/2π = 1/2πT2 ≅ 4.8 MHz (T2 = 33 ns) obtained from time-resolved electron paramagnetic resonance experiments (Supplementary Fig. 7), thus showing that the resonance width has contributions from inhomogeneous broadening. The spin-photon coupling G increases with B, reaching remarkably high values G/2π ≃ 12 MHz for B ≃ 0.5 T. Oscillations in G likely originate from deviations of the transmission line spectral density from its ideal behavior, caused by its spurious modes. The maximum change in ∣S21∣, denoted as η (inset of Fig. 2b), characterizes the collective spin resonance visibility, i.e. the efficiency of the spins in affecting photon propagation3. At the highest fields and frequencies reached in these experiments, it becomes higher than 1/2, which agrees with \(\eta =\frac{G}{G+\Gamma }\) for ω = Ω (Eq. (1)) and with the fact that the collective spin-photon couplings are then comparable to the single spin decay rates.

For N quasi-independent spin emitters, G is given by (see ref. 3 and Supplementary Note 3)

$$G=2\pi {\lambda }_{\Omega }^{2}\,{N}_{{{\rm{eff}}}}$$
(2)

where \({\lambda }_{\Omega }^{2}=\alpha \Omega\) is the spin-photon coupling spectral density for a one-dimensional waveguide and \({N}_{{{\rm{eff}}}}=N\tanh (\hslash \Omega /2{k}_{{{\rm{B}}}}T)\) is the effective spin number at the given temperature, proportional to the spin polarization along B. Figure 2b and Supplementary Fig. 12 show that Eq. (2) accounts well for the enhancement of G with increasing Neff that is observed above 1.2 K, with α as the sole free parameter.

Detecting this remarkable enhancement in spin-photon coupling and its visibility has been made possible by the broadband nature of these transmission experiments. It reflects the increase in the photon-induced decay rate from superradiant collective states. In the single-photon limit and at zero temperature, this serves as a signature of the formation of Dicke states. In our case, these are thermal collective states that emit in a superradiant manner, G ∝ Neff, while the emission to other channels is determined by the single-spin decay rates Γ. The experimental data confirm that, at this temperature, DPPH molecules mainly act as non-interacting S = 1/2 emitters and that it is possible to reach a regime in which collective spin-photon couplings become dominant over the individual spin decay rates.

Microwave transmission at the onset of 1D spin correlations: interactions competition

Lowering temperature allows exploring how AF correlations along spin chains43,44,45 modify the interaction with microwave photons. Figure 3 shows transmission data measured at a fixed B = 125 mT as a function of ω and (decreasing) T. The spin resonance first gets enhanced on cooling below 2 K, as a result of the higher spin polarization, but then, for T ≲ 0.8 K, its visibility decreases (Fig. 4a and Supplementary Fig. 10). Moreover, the effective spin-photon coupling G also decreases and its dependence with temperature and magnetic field deviate from what is expected for a paramagnetic system (Supplementary Fig. 13). The data therefore point to a crossover to a different regime in the spin-photon interaction. The access to a wide frequency window allows observing that this is accompanied by a significant broadening, by a factor ten between 1.5 K to 10 mK and, as Fig. 3c shows, by a 7% upwards shift of the resonance center frequency. This qualitative behavior persists for magnetic fields up to 300 mT (see Supplementary Figs. 13–15), although its magnitude, as gauged by the resonance broadening and by the drop in its visibility, seems to get somewhat reduced by increasing B.

Fig. 3: Microwave transmission at the onset of spin-spin interactions.
figure 3

Experimental (a) and simulated (b) changes in transmission associated with the coupling to DPPH spins measured at B = 125 mT as a function of frequency and temperature. The weak thin line near 3.38 GHz in (a) arises from a spurious mode in the transmission line (horizontal lines in Fig. 2a) that has not been fully eliminated by the data normalization. c Dependence of the spin resonance frequency Ω on the angle ψ that the magnetic field forms with the anisotropy axis of the spin-spin interactions, derived from Eq. (3). The line thickness is proportional to the contribution to the spin resonance, which increases for molecules forming larger angles and therefore, for larger frequencies. The central Ω obtained from the experiments in (a) and from the simulations in (b) is given by the gray open symbols and the solid black line, respectively.

Full size image
Fig. 4: Spin transmission visibility and elementary spin excitations.
figure 4

a Transmission visibility of the spin resonance obtained from the experimental results shown in Fig. 3a (red points) and from theoretical simulations based on describing the spin excitations with either a classical mean-field model (dashed light-red line) or as bosonic magnons (solid red line). b Experimental (open blue symbols) and theoretical (lines) spin resonance width. The different lines progressively add different contributions to the line width: the dashed-pointed gray line represents the paramagnetic inhomogeneous broadening, the dashed light-blue line includes the additional damping arising from the emergence of antiferromagnetic spin-spin correlations and, finally, the solid darker blue line, obtained from the results in Fig. 3b, adds also the broadening caused by the spin-spin interaction anisotropy that makes chains with different orientations interact differently with the microwave field. The inset illustrates the nature of the excitations that couple to propagating photons: single spin excitations in the paramagnetic regime and bosonic spin waves in the low-T region.

Full size image

Experiments performed for different input microwave powers, shown in Supplementary Note 5 and Supplementary Fig. 16, lead to the same results. Therefore, the broadening is not associated with any spin saturation effect. It is also much larger than the line width arising from the weak anisotropy, less than 0.1 %, between the principal gS-factors of DPPH31. A possible origin is the combined effect of growing spin correlations and of a weak anisotropy in the spin-spin exchange interactions, which is not unusual with free-radical molecules46. As a result, each DPPH crystallite in the powder would acquire a different Ω(ψ), depending on its orientation ψ with respect to B. The ensuing additional inhomogeneous broadening makes DPPH molecules located in different powder grains ‘distinguishable’ and therefore tends to suppress the collective emission from superradiant states. By contrast, increasing B brings the spins closer to the paramagnetic state, as shown by field-dependent heat capacity experiments (Supplementary Fig. 5), and would then reduce such effects, as it is indeed observed (see Supplementary Note 4 and Supplementary Fig. 15).

In order to provide a firmer basis to this interpretation, we model the light-matter Hamiltonian incorporating intrinsic interactions into the spin Hamiltonian \({{{\mathcal{H}}}}_{{{\rm{M}}}}\). We treat the spin chains in DPPH by a mean field (MF) approximation (see ref. 47, Supplementary Note 6 and Supplementary Figs. 17–20 for details):

$${{{\mathcal{H}}}}_{{{\rm{M}}}}=-{g}_{S}{\mu }_{{{\rm{B}}}}{{\bf{B}}}({{{\bf{M}}}}_{{{\bf{1}}}}+{{{\bf{M}}}}_{{{\bf{2}}}})+{{{\bf{M}}}}_{{{\bf{1}}}}\hat{J}{{{\bf{M}}}}_{{{\bf{2}}}}$$
(3)

where M1 and M2 are the macro-spin vectors of the two magnetic sublattices within each chain and the exchange interaction tensor \(\hat{J}={{\rm{diag}}}\left(J,J(1+\epsilon \sin \psi ),J(1+\epsilon \cos \psi )\right)\) introduces an uniaxial anisotropy in the spin-spin interactions. The exchange constant J has been determined comparing the Weiss temperature θ = −0.7 K, which determines the paramagnetic susceptibility measured between 1 K and 10 K (Fig. 1b and Supplementary Note 1), with the MF prediction θ = − J/kB. Then, Ω and its distribution can be obtained by solving the Landau-Lifshitz-Gilbert equation in the linear regime and considering that the powder sample has a random distribution of anisotropy axes48. The comparison with experimental data allows to determine both ∣ϵ∣, from the resonance broadening, and its sign, from the observed shift in the resonance center frequency (gray dots in Fig. 3c). In particular, a negative ϵ leads to higher frequencies for angles closer to π/2, which then dominate the average in a random distribution. We then find ϵ = − 0.086, which accounts well for the experimental results in Fig. 3. Note that the solid black curve in Fig. 3c emerges naturally from the resonance curves shown in Fig. 3b. Therefore, it is not an additional fit.

Again, the transmission can be computed using input-output theory49, as shown by Eqs. (5)–(12) in the Methods. However, it is essential to consider two limitations of the MF theory. First, MF overestimates the sharpness of changes occurring when T approaches ∣θ∣ ≡ TN, as it predicts a transition towards an AF phase that does not occur in 1D systems. Additionally, the MF low-energy excitations involve tilting the relative orientations of M1 and M2. In reality, bosonic spin-wave excitations occur. Our theory incorporates these modes by assuming that, below TN, excitations are magnons with Ω(ψ) calculated by MF. Consequently, the classical Hamiltonian (3) is replaced by the spin-wave one \({{{\mathcal{H}}}}_{{{\rm{M}}}}=\hslash \Omega (\psi )({b}^{{\dagger} }b+1/2)\), where b and b† are magnon annihilation and creation operators that fulfill the condition [b, b†] = 1. Note that, since the excitations are bosonic, the system then behaves exactly as an harmonic oscillator and its coupling to the waveguide loses its dependence with temperature. Then, S21 can be calculated as follows (see Methods):

$${S}_{21}=\frac{1}{1+\int\,d\psi \sin \psi \frac{2\pi {\lambda }_{\Omega }^{2}{N}_{{{\rm{eff}}}}({T}_{{{\rm{N}}}})}{\Gamma +{{\rm{i}}}\left(\Omega (\psi )-\omega \right)}}\,.$$
(4)

This formula gives the transmission shown in Fig. 3b, which, apart from the discussed sharpness, accounts well for the experimental results in the whole temperature region.

It is worth taking a closer look at the temperature dependence of the visibility shown in Fig. 4a. The dashed red curve shows η calculated with the classical MF Hamiltonian, considering the usual thermal dependence of the coupling between the single spin excitations and the photons. In this case, η increases as T decreases. The solid red line follows instead from freezing this thermal dependence, accounting for the spin-wave character of the excitations. Clearly, only the latter agrees with the experimental data. The nearly constant η observed below 700 mK therefore provides direct evidence for a change in the statistics of the elementary spin excitations that couple to the microwave photons.

This conclusion is further supported by the line width Γ of the transmission resonances, whose temperature dependence is shown in Fig. 4b. It has been both observed and proven50,51,52 that the line width in antiferromagnetic resonance is broader than its ferromagnetic or paramagnetic counterparts. The origin of this effect is linked to the intrinsic nature of magnon excitations in antiferromagnetic chains: the magnon resonance frequency Ω(ψ) acquires an imaginary component that adds to the paramagnetic Γ in Eq. (4). This broadening emerges naturally from MF calculations (see Supplementary Eqs. (24) and (25) in Supplementary Note 6) without further fitting and it is represented by the dashed blue curve in Fig. 4b. However, as can be seen in this plot, the sources of broadening present in isotropic antiferromagnetic chains are not sufficient to account for the experimentally observed Γ. Only when we include in the model an anisotropic exchange (i.e. we take ϵ ≠ 0) with randomly oriented anisotropy axes does it account for Γ measured at very low temperatures. The theoretical ΓvsT curve labeled as “distinguishable spin chains”, which includes all these effects, is directly extracted from the theoretical transmission curves in Fig. 3b. Thus, the increase in Γ has two sources: the onset of antiferromagnetic correlations and the anisotropic nature of this interaction in randomly oriented chains.

Conclusions

In summary, we have observed a crossover from quasi identical spins interacting collectively with microwave photons to a regime governed by 1D magnetic correlations. In the former, paramagnetic region, spin-photon couplings comparable to the decay rates have been achieved, which lead to a coupling efficiency  >0.5. When T decreases and spin-spin interactions gain prominence, they tend to suppress the collective emission from superradiant modes because different molecules are no longer equivalent to each other. Transmission data allow detecting, and estimating, the anisotropy in the spin-spin interaction along each chain. Besides, we find that its temperature dependence reflects the change in the spin excitation statistics. As it is illustrated in Fig. 4, when the material is paramagnetic these are single spin flips, while antiferromagnetic interactions stabilize bosonic magnon excitations. These results illustrate a regime in waveguide Quantum Electrodynamics that arises from the delicate interplay between light-mediated and intrinsic matter interactions. Besides, they provide a method to characterize in detail the strength and nature of spin- spin interactions in low-dimensional systems.

Methods

Sample preparation and structural characterization

DPPH (2, 2−diphenyl−1−picrylhydrazyl) is an organic free radical molecule hosting a spin S = 1/2 with a nearly isotropic gS = 2.004 factor, very close to that of a free electron30,31. DPPH samples used throughout this work were purchased, in powder form, from Sigma Aldrich (reference D9132). Even though solvent-free DPPH has been known for a long time30, a full structural determination was not performed until quite recently31. The results of powder X- ray diffraction experiments performed on our sample are shown in Supplementary Fig. 1. They suggest that it corresponds to the DPPH-III structure31, shown in Fig. 1a, which contains two inequivalent DPPH sites, referred to as A and B sublattices.

Magnetic measurements

The dc magnetic susceptibility and magnetic isotherms were measured above 2 K in a Magnetic Properties Measurement System (MPMS) by Quantum Design, a commercial magnetometer based on a dc-SQUID, operated by the Servicio de Apoyo a la Investigación (SAI) of the University of Zaragoza. In addition, magnetic measurements were also performed, for 0.3 K ≤ T ≤ 10 K, with a homemade micro-Hall magnetometer53 mounted in the insert of a Physical Properties Measurement System (PPMS), also by Quantum Design and operated by the SAI. The magnetometer (Supplementary Fig. 3) consists of two semiconducting layers of GaAs and Al1−αGaαAs, shaped in the form of a double cross, with a two-dimensional electron gas confined at the interface between the two materials. A current Iac is introduced through the main arm and a magnetic field B is applied parallel to it. The DPPH sample was placed on the edge of one of the two Hall crosses of the device and fixed/thermalized with Apiezon N grease. Its magnetization M generates an additional magnetic field BM, perpendicular to the plane of the device, which induces a Hall voltage VHall proportional to ∣M∣. In order to reduce noise and detect this signal, the current was modulated at a frequency of 107 Hz, with an Iac = 10 μA amplitude, and the reference voltage Vref in the bare cross was subtracted from VHall by means of a differential lock-in amplifier.

Heat capacity measurements

Heat capacity experiments were also carried out in a PPMS. The calorimeter consists of a sapphire disc on which the sample is placed. This holder integrates a heater and a thermometer, and it is connected to a thermal reservoir by thin gold wires. Sample and holder are mutually thermalized with apiezon N grease. The constant-pressure heat capacity is measured using a relaxation technique54. A heat power is applied for a short time and then removed. The time constant of the exponential increase and decrease in temperature during this process is proportional to the heat capacity of the combined sample-calorimeter system. The contributions from the empty calorimeter and the grease are known from previous calibration experiments, and then subtracted from the measurement in order to get the sample specific heat.

Electron paramagnetic resonance

Electron Paramagnetic Resonance (EPR) experiments were performed in a commercial Elexsys E-580 by Bruker operating in the X-band (~9.8 GHz). The spectrometer consists of a resonant cavity, in which the paramagnetic sample is placed, located at the center of a 0−1.3 T electromagnet. Temperatures between 7 K and 300 K can be accessed by means of a Helium flow cryostat. In continuous wave EPR (cw-EPR) experiments, the cavity is continuously irradiated while the DC magnetic field is swept slowly. The absorption signal is obtained with a field-modulation detection. Time-domain EPR experiments measure the signal emitted by the spin system after sending a series of microwave pulses to the cavity. When homogeneous broadening is dominant, as it is the case with DPPH, the phase memory time Tm of the spin system is obtained as the characteristic time constant of the free induction decay, which is the signal that the spin system induces in the cavity after a microwave pulse generates a coherence between the two spin states of a given transition.

On-chip microwave transmission and reflection measurements

Microwave transmission experiments were performed with on-chip superconducting coplanar waveguides fabricated by optical lithography on a 100 nm Nb thin film deposited onto crystalline sapphire wafers. A 100-μm thick DPPH pellet was fixed on the 400-μm-wide central line by means of apiezon N grease, matching roughly the width of the central line plus the separation to both ground planes, see Supplementary Fig. 2a. Based on this, we estimate a sample area and volume of the order of 1 mm2 and 0.1 mm3, respectively. DPPH-III has a molecular density of 1.06 × 1027 molecules/m3, with two independent DPPH molecules (A and B) per unit cell55. Only type B DPPH molecules couple to the waveguide at low temperatures, thus the number of spins that effectively interact with the propagating photons is N ~ 5 × 1016. The superconducting chips were integrated into two different 3He-4He dilution cryostats. The first one, sketched in Supplementary Fig. 2, gives access to temperatures between 7 and 800 mK. A cold finger (Supplementary Fig. 2b) places the chip at the center of an axial superconducting magnet (Supplementary Fig. 2c), which applies magnetic fields up to 1 T along the \(\hat{y}\) axis of the laboratory reference frame, which is parallel to the waveguide. The complex transmission \({S}_{21}=| {S}_{21}| {{{\rm{e}}}}^{{{\rm{i}}}{\varphi }_{21}}\) through the device was measured in the frequency range 10 MHz ≤ ω/2π≤ 14 GHz with a vector network analyzer. The input signal was attenuated by  −50 dB before reaching the chip, while the transmitted signal was amplified by 30 dB at 4 K with a low-noise cryogenic amplifier. This setup is tailored to measure only the transmission, with the reflection S11 doubly attenuated instead of amplified. For this reason, microwave transmission and reflection experiments were also performed, for 130 mK ≤ T ≤ 4.2 K, in a different setup with less attenuation in the lines inside the cryostat and without an output cryogenic amplifier. This 3He-4He cryostat is equipped with a 9T/1T/1T superconducting vector magnet.

Waveguide QED theory

The Brms field lies in the xz plane, that is, perpendicular to the applied dc magnetic field B. Therefore, the photons from the guide will essentially induce spin-flips in the DPPH sample. Thus, the Hamiltonian for our calculations will be \({{\mathcal{H}}}={{{\mathcal{H}}}}_{{{\rm{WG}}}}+{{{\mathcal{H}}}}_{{{\rm{I}}}}+{{{\mathcal{H}}}}_{{{\rm{M}}}}\), where

$${{{\mathcal{H}}}}_{{{\rm{WG}}}}=\int\,{{\rm{d}}}\omega \,\omega \,({r}_{\omega }^{{\dagger} }{r}_{\omega }+{l}_{\omega }^{{\dagger} }{l}_{\omega })\,,$$
(5)

with \({r}_{\omega }^{{\dagger} }\) (\({l}_{\omega }^{{\dagger} }\)) bosonic operators that create right (left) moving photons, and

$${{{\mathcal{H}}}}_{{{\rm{I}}}}={\sum}_{j,n}\int_{{\Omega }_{-}}^{{\Omega }_{+}}d\omega \,{\lambda }_{\omega }({{{\bf{r}}}}_{{{\bf{j}}},{{\bf{n}}}})\,{\sigma }_{j,n}^{x}\,X(\omega ).$$
(6)

In Eq. (6), X(ω) = (rω + lω) + h.c. and \({\sigma }_{j,n}^{x}={\sigma }_{j,n}^{+}+{\sigma }_{j,n}^{-}\) with \({\sigma }_{j,n}^{\pm }\) the Pauli spin-raising and lowering operators for the j-th DPPH molecule from the n-th chain. The coupling between spins and photons is determined by the spectral function λω(rj,n), which essentially depends on the magnetic field generated by the waveguide at the position rj,n of the molecule. Given that the sample size is much smaller than the wavelength of the photons, we neglect distance effects and assume λω(rj,n) ≃ λω.

For computing the transmission, S21, and reflection, S11, we use input-output theory49. We need to compute the input/output right/left fields such that \({S}_{21}=\frac{\langle {r}_{{{\rm{out}}}}\rangle }{\langle {r}_{{{\rm{in}}}}\rangle }\) and \({S}_{11}=\frac{\langle {l}_{{{\rm{out}}}}\rangle }{\langle {r}_{{{\rm{in}}}}\rangle }\). First, let’s focus on the single spin scenario. For a coherent driving on our system \({{{\mathcal{H}}}}_{{\rm{drive}}}=\sqrt{2\pi }{\lambda }_{\Omega }{\alpha }_{{{\rm{in}}}}{e}^{-{{\rm{i}}}\omega t}{\sigma }_{x}\), with Ω = gSμBB/ℏ, we can express

$$\langle {r}_{{{\rm{out}}}}\rangle (t)=\langle {r}_{{{\rm{in}}}}\rangle (t)-2\pi {\lambda }_{\omega }^{2}{\chi }_{{\sigma }_{x}}(\omega )\langle {r}_{{{\rm{in}}}}\rangle (t)\,,$$
(7)
$$\langle {l}_{{{\rm{out}}}}\rangle (t)=\langle {l}_{{{\rm{in}}}}\rangle (t)-2\pi {\lambda }_{\omega }^{2}{\chi }_{{\sigma }_{x}}(\omega )\langle {r}_{{{\rm{in}}}}\rangle (t)\,.$$
(8)

The spectral density λω is considered to be a smooth function so that for frequencies ω close to the frequency of the spin system λω ≈ λΩ. In order to obtain \({\chi }_{{\sigma }_{x}}\) we compute the time dependence of 〈σ±〉 from the quantum master equation, which leads to

$$\frac{d}{dt}\langle {\sigma }_{\pm }\rangle =\pm {{\rm{i}}}\Omega \langle {\sigma }_{\pm }\rangle -\Gamma \langle {\sigma }_{\pm }\rangle \pm {{\rm{i}}}\sqrt{2\pi }{\lambda }_{\Omega }{\langle {\sigma }_{z}\rangle }_{\beta }{\alpha }_{{{\rm{in}}}}{e}^{-{{\rm{i}}}\omega t}\,,$$
(9)

where \({\langle {\sigma }_{z}\rangle }_{\beta }=\tanh (\hslash \Omega /2{k}_{{{\rm{B}}}}T)\) is the thermal population of the spin and \(\Gamma ={\gamma }_{\phi }+[2\bar{n}(\Omega ,T)+1]\cdot 2\pi {\lambda }_{\Omega }^{2}\) includes the contributions of dissipation channels that are either intrinsic to the spin sample (γϕ) or related to its coupling to the transmission line through the bosonic occupation number for thermal photons (\(\bar{n}\)). Typically, the single spin-photon coupling \(2\pi {\lambda }_{\Omega }^{2}\ll {\gamma }_{\phi }^{-1}\), thus Γ ≈ γϕ. Solving Eq. (9) in the stationary limit and applying the previous relations we get

$${S}_{21}^{(1)}(\omega )=1-\frac{2\pi {\lambda }_{\Omega }^{2}{\langle {\sigma }_{z}\rangle }_{\beta }}{{{\rm{i}}}(\Omega -\omega )+\Gamma }\,,$$
(10)
$${S}_{11}^{(1)}(\omega )=-\frac{2\pi {\lambda }_{\Omega }^{2}{\langle {\sigma }_{z}\rangle }_{\beta }}{{{\rm{i}}}(\Omega -\omega )+\Gamma }\,.$$
(11)

The superscript indicates that these relations account for a system with a single spin. In order to extend these relations to the case of an spin ensemble we use the transfer matrix formalism, where the output field of one spin becomes the input field for the next one. Defining \({\theta }_{j}(\omega )={S}_{11}^{(1)}(\omega )/{S}_{21}^{(1)}(\omega )\) and using that S21 = 1 + S11, the transmission and reflection read

$${S}_{21}(\omega )=\frac{1}{1-{\sum}_{j}{\theta }_{j}};\;{S}_{11}(\omega )=\frac{{\sum}_{j}{\theta }_{j}}{1-{\sum}_{j}{\theta }_{j}}.$$
(12)

In the paramagnetic regime, Ωj ≈ Ω and defining \(G=2\pi {\lambda }_{\Omega }^{2}N{\langle {\sigma }_{z}\rangle }_{\beta }\) we get the relations given in Eq. (1). When the AFM correlations grow below TN, the resonant frequency Ωj of each DPPH chain depends on its orientation ψ with respect to the magnetic field. Then, we replace the sum for an integral over solid angle (since our sample is a powder pellet, all orientations are present), which leads to Eq. (4). Moreover, since spin excitations are then of a bosonic nature, the temperature dependence is lost and 〈σz〉(T) ≈ 〈σz〉(TN) for T ≤ TN.