Introduction

Ruthenium dioxide (RuO2) with rutile structure has long been considered as a Pauli paramagnetic metal1,2,3, and has been used in catalysis, microelectronics, and supercapacitors4,5,6 due to its high catalytic activity and chemical stability. However, the neutron diffraction and resonant x-ray scattering experiment seem to show that RuO2 is an antiferromagnet with a high Néel temperature (>300K) and a small magnetic moment of  ~0.05 μB/Ru7,8. Subsequently, RuO2 was considered as an altermagnet, a third fundamental magnetic phase beyond traditional ferromagnetism (FM) and antiferromagnetism (AFM) in crystals with collinear magnetic order9,10,11,12,13,14,15,16,17,18, which has sparked much interest in its magnetism and transport properties.

At first, it was predicted theoretically that the rutile RuO2 would have the largest alermagnetic spin splitting, up to 1.4 eV14,15, indicating its potential for various spintronics applications by proving a storage signal. However, very recently, the angle-resolved photoemission spectroscopy (ARPES) and spin-resolved ARPES performed on the thin film and single-crystal rutile RuO2 did not detect the band splitting expected from altermagnetism19, indicating that RuO2 is highly unlikely to be an altermagnet. Broadband infrared spectroscopy measurements revealed that RuO2’s optical conductivity was best described by a nonmagnetic model20. Second, as a model material of the collinear antiferromagnet, RuO2 was expected to exhibit the spontaneous Hall effect due to its crystal symmetry breaking, so-called the crystal Hall effect (CHE), in which the crystal chirality can be used to control the sign of the Hall effect21. However, both the muon spin rotation (μSR)22 and the nuclear magnetic resonance (NMR)23 measurements demonstrate the absence of long-range magnetic order, and the density-functional theory (DFT) + U calculation by A. Smolyanyuk et al.24 suggest stoichiometric RuO2 is non-magnetic, while Ru vacancies can promote the formation of a magnetic state. In order to check whether the CHE emerges in RuO2, a careful investigation of its transport properties is needed using high-quality single crystals. To confirm the presence of CHE in RuO2 by the transport property measurements becomes a direct evidence for its altermagnetism.

In this paper, we report on our work with high-quality RuO2 single crystals, characterized by a residual resistivity ratio (RRR = 152). We meticulously measured their magnetization, longitudinal resistivity (ρxx), and Hall resistivity (ρyx), and calculated their electronic band and Fermi surface (FS) using DFT. Additionally, we conducted numerical simulations for their transport properties. We found that no magnetic transition occurs below 400 K, indicating that our RuO2 single crystals are paramagnetic, rather than collinear antiferromagnets. We also observed that the magnetoresistance (MR), ρyx(B), and Hall conductivity σxy(B), as well as the anisotropy of ρxx, are consistent with the results from numerical simulations, suggesting that the calculated bands can accurately describe all the transport properties of our RuO2 crystals. Notably, no CHE was observed in our crystals. These findings further suggest that RuO2 is unlikely to be an altermagnet.

Results and discussion

Topological electronic structure

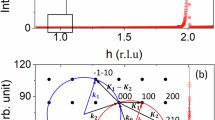
Figure 1a shows the powder XRD pattern, confirming that RuO2 crystallizes in the rutile structure with nonsymmorphic space-group symmetry P42/mnm (No. 136). The lattice parameters a = b = 4.501(2) Å, and c = 3.114(3) Å were determined using Rietveld refinement of the powder XRD data, yielding a weighted profile factor Rwp of 6.2% and a goodness of fit χ2 of 1.1. The primitive cell consists of two RuO2 molecules, with two Ru atoms occupying the Wyckoff 2(a) sites, and four O atoms occupying the 4(f) sites, as illustrated in the inset of Fig. 1a. Each Ru atom is surrounded by a distorted octahedron of six O atoms. Proper rotation of the surrounding oxygen octahedra renders the two Ru positions at the center and the corner equivalent, indicating the coexistence of inversion symmetry (\({{{\mathcal{P}}}}\)), time-reversal symmetry (\({{{\mathcal{T}}}}\)), and nonsymmorphic symmetries in RuO2. These symmetries impose strict constraints that hinder the stabilization of AFM ordering. \({{{\mathcal{P}}}}\) ensures the cancellation of magnetic moments, while \({{{\mathcal{T}}}}\) mandates invariance under time reversal, incompatible with a unique AFM state. Nonsymmorphic symmetries further complicate the formation of long-range AFM order. Based on the structure and lattice parameters detailed above, we perform DFT calculations of the band structure and FS. Figure 1c–e show the band structure and FS with spin-orbit coupling (SOC) considered; for more details about the band and FS without SOC, see Fig. S1 of Supplementary Information. The band structure exhibits multiple bands crossing the Fermi level, indicating metallic behavior, and significant splitting due to SOC, especially near high-symmetry points like Γ and X, but this does not lead to the characteristic band splitting observed in altermagnets. It has been suggested that potential Dirac points near high-symmetry points in the Brillouin zone, particularly around the X and M points, indicate the presence of topological nodal lines protected by crystal symmetries25,26. The FS, shown from both top and side views, displays a complex, multi-sheeted structure with both electron and hole pockets; the electron pockets are prominently located near the Γ point, while the hole pockets are distributed around the M and A points. The three-dimensional dispersion of these pockets shows significant kz dependence, typical in topological semimetals. The intricate FS topology supports the possibility of Dirac points, as evidenced by potential band intersections near the Fermi level, indicating regions of high Berry curvature. Notably, our electronic structure calculations, conducted within the framework of DFT, converge to a nonmagnetic solution without requiring additional adjustments.

Fig. 1: Structure and electronic band.
figure 1

a Polycrystalline x-ray diffraction (XRD) pattern with refinement profile at room temperature and crystal structure of RuO2 (inset). b Single-crystal XRD pattern and photograph of RuO2 crystal (inset). c Band structures with spin-orbit coupling (SOC). d, e Top and side views of FS calculated with SOC.

Full size image

No magnetic transition

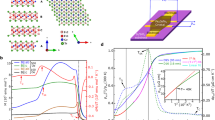
Figure 2a shows the temperature dependence of susceptibility measured at magnetic field B = 1 T applied perpendicular to the (110) plane with a zero-field cooling (ZFC) process. The susceptibility decreases slightly with decreasing temperature, reaches a minimum around 25 K, and then increases. No magnetic transition was observed in the entire temperature range (2–400 K), which is consistent with the recent observation by μSR and neutron diffraction studies22,27. The slight increase in susceptibility at low temperatures is attributed to the contribution of impurities containing Ru3+ (s = \(\frac{5}{2}\)) due to the presence of oxygen vacancies. As shown in the left inset of Fig. 2a, the molar fraction of impurities was estimated to be 0.21% by fitting the χ(T) data below 5 K using the modified Curie–Weiss law \(\chi ={\chi }_{0}+\frac{C}{T-\theta }\). The linear dependence of magnetization (M) on magnetic field (H) [see the right inset of Fig. 2a] and the χ(T) behavior described above demonstrate that our RuO2 crystal is paramagnetic with trace magnetic impurities. As shown in Fig. S2a of Supplementary Information, the susceptibility along [001] is very similar to that along the [110] direction across the full temperature range of 2–400 K. The susceptibility remains nearly temperature-independent and shows no indication of magnetic ordering. To our knowledge, the controversy over the magnetic ground state of RuO2 has persisted for a long time. Very early magnetic measurement indicated that it is a Pauli paramagnetic metal1,2,3. Early resonant x-ray scattering measurements of thin films and bulk crystals suggested antiferromagnetic ground state with the Néel temperature higher than 300 K8, and neutron diffraction experiments exhibited a small magnetic moment of  ~0.05 μB/Ru7. While recent μSR measurement which are highly sensitive to local magnetic moments revealed vanishingly small ordered moments (~1.4 × 10−4μB/Ru in single crystals and  ~7.4 × 10−4μB/Ru in thin films)22,27. Latest experiment in Cr-doped RuO2 exhibits anomalous Hall effect (AHE) due to altermagnetism with the assumption of antiferromagnetism in RuO228, while DFT calculations performed by Smolyanyuk and Šmejkal et al. revealed that AHE stems from Cr impurity, and RuO2 remain nonmagnetic29. From the various experimental results above, it is evident that RuO2 does not exhibit any magnetism.

Fig. 2: Susceptibility and longitudinal resistivity.
figure 2

a Temperature dependence of susceptibility (χ) measured at B = 1 T perpendicular to the (110) plane with zero-field cooling (ZFC) processes. The left inset shows the temperature dependence of magnetic susceptibility below 20K, and the right inset displays magnetization (M) as a function of magnetic field (H) measured at temperatures T = 2 K and 300K. b Temperature dependence of resistivity ρxx at various magnetic fields. The left inset shows the fitting results, and the right inset shows an enlarged view at low temperatures.

Full size image

Figure 2b presents the temperature dependence of the longitudinal resistivity ρxx(T) for a RuO2 single crystal (sample 1, S1). The current was applied in the (110) plane [see the inset of Fig. 1b, the cleavage surface], with both zero field and a 7 T magnetic field applied perpendicular to the (110) plane. The ρxx measured at zero field decreases monotonically with decreasing temperature, with ρxx(300 K) = 28.87 μΩ cm and ρxx(6 K) = 0.19 μΩ cm. The residual resistivity ratio (RRR) = [ρxx(300 K)/ρxx(6 K)] = 152, indicating that our RuO2 crystals are of high quality, surpassing those reported in previous studies (RRR = 80)30. To elucidate the scattering mechanisms in RuO2 crystals, we fitted the ρxx(T) data using the Bloch-Grüneisen model31, as described by the equation:

$$\rho (T)={\rho }_{0}+C{(\frac{T}{{\Theta }_{D}})}^{n}\int_{0}^{{\Theta }_{D}/T}\frac{{x}^{n}}{({e}^{x}-1)(1-{e}^{-x})}dx$$
(1)

where the residual resistivity ρ0 = 0.19μΩ cm, the Debye temperature ΘD = 900K (consistent with the results reportted in ref. 32), and the constant C = 241.35μΩ cm were obtained from the fitting, as shown in the inset of Fig. 2b. The power exponent n = 2.73 (close to 3) obtained from the best fit suggests that the scattering is influenced by phonon-assisted s − d interband scattering31,33,34. Compared with ρxx(T) measured at zero field, the ρxx(T) at 7 T exhibits a similar behavior except for the enhancement of resistivity at low temperatures. As shown in the lower-right inset of Fig. 2(b), a field-induced upturn in resistivity, saturating to a field-independent constant, is observed, i.e., extreme large magnetoresistance (XMR) emerging at low temperatures, similar to those observed in many topological trivial/non-trivial semimetals35,36,37,38.

Scaling behavior of MR and Hall resistivity

Next, we analyze the MR, Hall resistivity (ρyx), and Hall conductivity (σxy) experimental data using the scaling law, specifically the extended Kohler’s law, and perform simulations based on Boltzmann transport theory and first-principles calculations, as done in CrSb39. Considering the relaxation time approximation, the conductivity tensor σij can be calculated in the presence of a magnetic field by solving the Boltzmann equation, as described in refs. 40,41,42,43,44,45 and implemented in WannierTools46.

$${\sigma }_{ij}^{(n)}({{{\boldsymbol{B}}}})=\frac{{e}^{2}}{\alpha {\pi }^{3}}\int{d}^{3}{{{\boldsymbol{k}}}}{\tau }_{n}{v}_{n}^{i}({{{\boldsymbol{k}}}}){\bar{v}}_{n}^{j}({{{\boldsymbol{k}}}}){(-\frac{\partial f}{\partial \varepsilon })}_{\varepsilon = {\varepsilon }_{n}({{{\boldsymbol{k}}}})}$$
(2)

where e is the charge of electron, n is the band index, α = 4 (or 8) when SOC is within (or without) in the Hamiltonian, τn is the relaxation time of nth band, which is independent on the wave vector k, f is the Fermi-Dirac distribution, \({v}_{n}^{i}({{{\boldsymbol{k}}}})\) is the ith component of group velocities, and \({\bar{v}}_{n}({{{\boldsymbol{k}}}})\) is the weighted average of velocity over the past history of the charge carrier41. It’s easy to derive that the conductivity tensor σ divide by τ, i.e., σ/τ is a function of Bτn

$${\sigma }_{ij}^{(n)}({{{\boldsymbol{B}}}})/{\tau }_{n}=f(B{\tau }_{n})$$
(3)

Assuming all bands have the same relaxation time τn = τ0, the total conductivity σ(B) = Σσ n(B) follows a scaling law:

$$\sigma (B)/{\tau }_{0}=g(B{\tau }_{0})$$
(4)

According to the Drude model σ0 = ne2τ0/m, and ρ = σ−1, where n is the carrier density and m is the effective mass, we derive the Kohler’s law47,48:

$$\Delta \rho /{\rho }_{0}=h(B/{\rho }_{0})$$
(5)

or the extended Kohler’s law in its general form49:

$$\frac{\Delta \rho }{n{\rho }_{0}/m}=h\left(\frac{B}{n{\rho }_{0}/m}\right)$$
(6)

The Hall resistivity could also exhibits scaling behavior50:

$$\frac{{\rho }_{yx}}{n{\rho }_{0}/m}=h\left(\frac{B}{n{\rho }_{0}/m}\right)$$
(7)

Figure 3a shows MR as a function of magnetic field B at various temperatures, defined by the standard equation: MR = \(\frac{\Delta \rho }{\rho (0)}=\left[\frac{\rho (B,T)-{\rho }_{0}(T)}{{\rho }_{0}(T)}\right]\times 100 \%\), where ρ(B, T) and ρ0(T) are the resistivities measured at field B and zero field, respectively. The measured MR is extremely large at low temperatures, reaching 380% at 6 K and 7 T, which is nearly twice as large as that reported recently for RuO2 single crystals at 2 K in 9 T30, and it does not show any signs of saturation at the highest field of our measurement. To examine the MR behavior under high magnetic fields, measurements were performed with a water-cooled magnet up to 35 T. The inset of Fig. 3a shows the MR as a function of field up to 35 T at 1.6K, where the MR reaches 1500% and also shows no saturation. Figure 3e presents the numerical simulation results of MR as a function of B, based on FS calculations using first-principles, and experimental ρ0(T), which capture most of the essential features of the experimental MR curves, exhibiting a similar increase with field and a decrease with increasing temperature. The consistency between experimental and theoretical results demonstrates the validity of our first-principles approach in capturing the essential physics of MR in RuO2. As discussed above, MR can be described by Kohler’s scaling law48:

$${{{\rm{MR}}}}=\frac{\Delta {\rho }_{xx}(T,H)}{{\rho }_{0}(T)}=\alpha {\left[B/{\rho }_{0}(T)\right]}^{m}$$
(8)

As shown in the inset in Fig. 3d, all MR data from T = 6 K to 100 K collapse onto a single line when plotted as MR  ~ B/ρ0 curve, with α = 0.01 \({(\mu \Omega {{{\rm{cm}}}}{{{{\rm{T}}}}}^{-1})}^{1.66}\) and m = 1.66 obtained by fitting. The power field dependence of MR observed in RuO2 is attributed to the FS structure without AFM order discussed above. The MR data obtained from other sample (S2) measured up to 14 T exhibit a similar behavior (see Figs. S2b, c in the Supplementary Information).

Fig. 3: MR and Hall resistivity.
figure 3

a Measured magnetoresistance (MR) of RuO2 at various temperatures, with an inset showing MR measured with a water-cooled magnet with fields up to 35 T at 1.6 K. b Field dependence of Hall resistivity at various temperatures; the upper inset shows the Hall resistivity at 1.6 K up to 35 T, while the lower inset shows the Hall resistivity at 6 K and 7 T. c Hall conductivity at various temperatures with a fitting line using a two-band model. d Kohler scaling analysis on MR with m = 1.66. e–g Calculated MR, Hall resistivity, and Hall conductivity from first-principles calculations at different temperatures. h Scaling analysis of Hall resistivity at various temperatures.

Full size image

As one of altermagnetic candidates, RuO2 would exhibit CHE due to its conventional time-reversal symmetry breaking in the electronic structure. We rechecked the possibility of CHE emerging in RuO2 crystals through both experiments and theoretical analysis. Figure 3b shows the Hall resistivity (ρyx) as a function of magnetic field (B) measured at various temperatures. As shown in the lower inset of Fig. 3b, at 6 K, ρyx starts as a positive value, increases to a maximum, and then decreases to negative with increasing magnetic field. We also measured ρyx at lower temperatures down to 1.6 K and higher fields up to 35 T, as shown in the upper inset of Fig. 3b, exhibiting a similar behavior in the lower field region (B < 7 T). Below 70 K, all the ρyx exhibit the same behavior with that at 6K. At higher temperatures (90, 150, 200K), ρyx exhibits a linear behavior with a positive slop, indicating that hole carriers dominate. Then, we performed numerical simulations for the ρyx(B). Similar to the MR data discussed above, based on the band structure and Boltzmann transport equation, as shown in Fig. 3f, the simulations capture the essential behaviors of the measured ρyx(B), especially the ρyx(B) sign reversal behavior at lower temperatures. As shown in Fig. 3h, it is found that all ρyx(B) data measured at different temperatures (6 - 100K), normalized by the ρ0 at each temperature, collapse onto a single curve, indicating that a scaling law can describe the ρyx(B) behavior.

Meanwhile, we calculated the Hall conductivity based on a two-band model using the ρxx(B) and ρyx(B) data measured at various temperatures by the equation51:

$${\sigma }_{xy}=\frac{{\rho }_{yx}}{{\rho }_{xx}^{2}+{\rho }_{yx}^{2}}=eB\left[\frac{{n}_{h}{\mu }_{h}^{2}}{1+{\mu }_{h}^{2}{B}^{2}}-\frac{{n}_{e}{\mu }_{e}^{2}}{1+{\mu }_{e}^{2}{B}^{2}}\right]$$
(9)

where ne (nh) is the charge density of electrons (holes), μe (μh) is the mobility of electrons (holes), and e is the charge of electron. The calculated σxy [see Fig. 3g] from the simulations can also capture the main behaviors of σxy(B) measured at various temperatures. The ne, nh and μe, μh values at different temperatures were obtained by the simultaneously fitting to the experimental σxy(B) [see Fig. 3c] and σxx(B) data [see Fig. S3a in Supplementary Information], the results are shown in Fig. S3b, at 6 K, the obtained ne = 9.27  × 1021 cm−3, nh = 8.47 × 1021 cm−3, which are close but not completely compensated, similar to the case discussed by Zhang et al.50.

For comparison, we also performed DFT + U calculations for band structure and magneto-transport simulations with various Hubbard U to check the influence of AFM/altermangetic order on the MR and Hall resistivity. It was assumed that the magnetic moments were aligned along the easy magnetization c-axis, with various U applied to the d-orbits of Ru atoms to account for on-site Coulomb interactions. As an example, Fig. 4 presents the band structure, the simulation results of the MR, ρyx and σxy as a function of magnetic fields, with SOC for U = 2.0 eV, μ = 1.095 μB/Ru. It is clear that the resulting band structure [Fig. 4a] exhibits significant differences with that of non-magnetic configurations [Fig. 1c], particularly along high-symmetry lines associated with the Γ-point. As shown in Fig. 4b, within a 7 T magnetic field range, the MR reaches a maximum value of 3500%, substantially exceeding the magnitude (380%) observed experimentally. The Hall resistivity, ρyx, maintains the same sign and linear characteristics at different temperatures, while the Hall conductivity, σxy(B), manifests only a single kink, inconsistent with the two kinks observed experimentally, as seen in Fig. 3b, c. The band structures and the simulation results of magneto-transports for others U = 1.1, 1.2, 1.25, 1.3, and 1.5 eV are represented in Fig. S4. Even for U = 1.1 eV with a small magnetic moment μ = 0.05 μB/Ru7,8, the calculated maximum MR reaches 1500%, significantly larger than that observed experimentally, the first peak at low magnetic field in σxy(B) is obviously suppressed. It is due to the splitting of bands (tens meV) driven by the Coulomb interaction (U), which results in the changes of FS shape and size, thus influences the magneto-transport behavior. We also found that, with increasing U, the magnetic moment increases monotonously, the splitting of bands becomes bigger and bigger, the FS is driven to reform obviously. The first peak in the calculated σxy(B) is gradually suppressed, then disappears with increasing magnetic moment, however, all the calculated maximum MR values are over 1000%. It is worthy mentioning that to calculate the magneto-transport behavior is feasible by modifying the Hubbard U discussed above, for the magnetism resulting from other mechanisms (such as Oxygen vacancies, magnetic impurities, the interface effect in th films). These pronounced discrepancies between the simulation results with considering AFM/altermagnetic order and experimental observations strongly suggest that the RuO2 does not adopt the previously proposed altermagnetic structure. Our findings are consistent with recent results of torque magnetometry and magnetization measurements on RuO2 single crystals52.

Fig. 4: Calculation results with considering AFM order.
figure 4

a Band structure with SOC for U = 2.0 eV. b–d Calculated MR, ρyx, σxy, as a function of magnetic fields at various temperatures, respectively.

Full size image

Anisotropy of longitudinal resistivity

At the same time, we measured the angular dependence of longitudinal resistivity ρxx [see Fig. 5a], and MR [see Fig. 5b] in the ab plane (with the applied current along the c-axis), and performed numerical calculations for them, as shown in Fig. 5c, d, respectively. Notably, ρxx(B) exhibits inversion symmetry, i.e., ρxx(θ) = ρxx(θ + π), although its anisotropy is not significant, with a minimum at θ = 0∘ when B is applied in the [110] direction and a maximum at θ = 45∘, corresponding to when θ aligns with the a/b-axis. This behavior is consistent with the crystal structure of RuO2 and the symmetry of the FS projected onto the ab plane, as illustrated in Fig. 1a, d, e. A similar power-law field dependence of MR at 6 K, characterized as ∝ Bm (with m ranging from 1.66 to 1.72 for different θ values), was confirmed by both measurements and numerical simulations, as shown in Fig. 5b, d, respectively. Meanwhile, we also measured the resistivity ρxx at 6 K with various field orientations relative to the applied current I, (see the inset of Fig. S5 in the Supplementary Information), further confirming that the MR is determined by the Lorentz force on the carriers, consistent with recent report53.

Fig. 5: Anisotropy of resistivity ρxx.
figure 5

a, c Measured and calculated anisotropy of resistivity ρxx for field rotated in a-b plane. b, d Measured and calculated MR as a function of field for the various directions, inset of (b) Schematic diagram of resistivity measurements: current align c axis, θ is the angle between field and z axis.

Full size image

Conclusion

In summary, we successfully grew RuO2 single crystals with rutile structure and performed the measurements of magnetization, longitudinal resistivity, and Hall resistivity. The numerical simulations for its transport properties were conducted based on Boltzmann transport theory and first-principles calculations. It was found that no magnetic transition occurs below 400K, and all the transport properties can be described by the intrinsic electric structure and dominated by the Lorentz force, consistent with numerical simulations results. Notably, no CHE was observed in our crystals. These results further demonstrate that RuO2 is a typical semimetal, rather than an altermagnet.

Methods

Sample growth

RuO2 single crystals were grown using a chemical vapor transport (CVT) method. Polycrystalline RuO2 (99.9%, Alfa Aesar) was sealed in an evacuated quartz tube with 10 mg cm−3 TeCl4 as a transport agent and then heated for two weeks at 1100 ∘C in a tube furnace with a gradient 100 ∘C. Polyhedral crystals with typical dimensions of 2 × 0.5 × 0.5 mm3 [see the inset of Fig. 1b] were found in the cold end of the quartz tube.

Measurements

The composition of the crystals, confirmed as Ru: O = 1 : 2, was verified using the energy-dispersive x-ray (EDX) spectrometer. The crystal structure was determined using a powder x-ray diffractometer (XRD, PANalytical, Rigaku Gemini A Ultra) with the sample produced by grinding pieces of crystals. Electrical resistivity (ρxx), Hall resistivity (ρyx) were conducted using a Quantum Design physical property measurement system (PPMS-9 T) and a water-cooled magnet with the highest magnetic field up to 35 T, and magnetization measured on a Quantum Design magnetic property measurement system (MPMS-7 T).

Calculations

Meanwhile, the numerical simulations were carried out based on the Boltzmann transport theory and first-principles calculations, for comparing with the experimental results of ρxx and ρyx. DFT calculations were performed using the Vienna ab initio simulation package (VASP)54,55 with the generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE) for the exchange-correlation potential56. A cutoff energy of 520 eV and a 7 × 7 × 11 k-point mesh were used to perform the bulk calculations. The Fermi surface (FS), magnetoresistance (MR) and Hall resistivity calculations were performed using the open-source software WannierTools46, which is based on the Wannier tight-binding model (WTBM)57,58,59 constructed using Wannier9060.