Introduction

Magnetic topological materials, particularly those hosting Weyl fermions—massless chiral quasiparticles in momentum space—have emerged as a fascinating class of systems exhibiting unique transport phenomena1,2,3,4,5. Among several Weyl systems, magnetic Weyl semimetals like Co3Sn2S2 present a unique opportunity to explore the interplay between topology and magnetism1,6,7,8. Furthermore, they host unique transport phenomena, including the anomalous Hall effect (AHE), anomalous Nernst effect, ultra-high mobility, and exceptionally large positive transverse magnetoresistance (MR). While nonmagnetic Weyl semimetals such as TaAs, Cd3As2, NbP, ZrTe5, and WTe2 have demonstrated large MR values exceeding 105 % at low temperatures, the contribution of magnetic Weyl semimetals to this field remains comparatively underexplored9,10,11,12,13,14,15.

The study of magnetic Weyl semimetals is particularly compelling due to their ability to combine topological electronic properties with magnetism, offering new opportunities for spintronics and quantum transport. Despite these advantages, the reported MR in magnetic topological materials such as Co3Sn2S2, Fe3Sn2, and Co2MnGa has been relatively modest, with values around 20–30%, and moderate for MnBi, around 250% at 2 K under 9 T1,2,4,5. These results, while larger than those found in conventional ferromagnetic metals, are still significantly lower than the MR observed in their nonmagnetic counterparts. This relatively lower value arises primarily due to enhanced electron and spin scattering, which limits the mobility of charge carriers to below 103 cm² V−¹ s−¹ in most ferromagnetic materials. Achieving high mobility is crucial for meeting the condition μB > 1 (where B is the applied magnetic field and μ is mobility), which is a prerequisite for observing intrinsic topological and quantum effects, including a large linear non-saturating MR16.

Thus, both theoretical interest and practical applications drive the quest for topological magnetic materials with a large MR and large carrier mobility17,18. Placing the Fermi level near the Weyl nodes reduces scattering effects, leading to enhanced carrier mobility and a significant increase in magnetoresistance. Indeed, in non-magnetic Weyl semimetals with broken inversion symmetry (IS), the proximity of Weyl points to the Fermi level results in enhanced MR and mobility, as the linear band crossing and associated Berry curvature effects dominate the electrical transport. However, in magnetic Weyl semimetals, where time-reversal symmetry (TRS) is broken by magnetism, the Fermi level tuning has been unsuccessful, thereby complicating the realization of Weyl fermions’ ideal transport properties. This difficulty arises from the degradation of structure and magnetism by the conventional doping methods. For example, the Curie temperature (Tc) of Co3Sn2−xInxS2 has been systematically decreased with x, probably due to a significant structural change of the Kagome layer19. Most conventional doping strategies degrade magnetic properties or disrupt the Kagome lattice structure, preventing effective Fermi level tuning.

To overcome the limitations of conventional doping, we adopt an alternative strategy: controlled anti-site defect engineering. Co3Sn2S2 crystallizes in a layered shandite-type structure20. The crystal is built up from layers in which cobalt (Co) atoms form a distinctive two-dimensional Kagome lattice. It is ferromagnetic with a Tc of around 174 K. One remarkable feature is its half-metallic nature, and the states at the Fermi level are mainly derived from the Co 3d orbitals8. We investigate electron doping via the Co3+xSn2−xS2 route because it uses a substitution on a site (the Sn site) that is less critical for maintaining the key structural motifs of the material. A chemical environment similar to pristine and relatively favorable hybridization between excess Co and its neighboring constituents’ orbital allows the lattice to accept the extra Co without significant distortion. This results in an effective adjustment of the electron count (and consequently the Fermi level) while preserving the overall crystal structure, in stark contrast to other dopants that might disrupt the Kagome network or introduce considerable lattice strain.

In this study, we investigate the transport properties of ferromagnetic Weyl semi-metallic single-crystal Co3+xSn2−xS2 (0 ≤ x ≤ 0.3). Our findings reveal, for x = 0.27 at 2 K and under 9 T, a large, non-saturating MR, 1150 %, and one of the highest carrier mobilities, 18,000 cm2 V−1 s−1 reported in ferromagnetic materials. These remarkable transport properties can be directly attributed to the optimized electronic structure achieved through anti-site-defect engineering. The large MR and ultra-high mobility in x = 0.27 position it as a unique candidate among topological ferromagnetic materials and hold promise for future spintronic applications, where efficient charge transport, robust topological protection, and high-speed operation are crucial. Our findings suggest that Co3+xSn2−xS2 is a promising material for both fundamental studies and next-generation quantum technologies.

Results

Basic characterization of a series of Co3 + xSn2−xS2 (0 ≤ x ≤ 0.3) single crystals grown

A series of Co3+xSn2−xS2 (0 ≤ x ≤ 0.3) single crystals were successfully grown using the self-flux method, as described in the method section. Within the context of non-stoichiometry, it is crucial to evaluate the formation energy of various types of defects to understand their stability and impact on material properties. Using density functional theory (DFT) calculations21,22,23,24, the formation energies of different disorder configurations—such as in-plane Co/Sn anti-site (excess Co atom at in-plane Sn vacancy), out-of-plane Co/Sn anti-site (excess Co atom at out-of-plane Sn vacancy), interstitial Co+in-plane Sn vacancy, interstitial Co+out-of-plane Sn vacancies, in-plane Sn vacancy, and out-of-plane Sn vacancy—have been systematically investigated. Among these, the in-plane and out-of-plane Co/Sn anti-site defect exhibits the lowest formation energy, likely making them the most thermodynamically stable configurations, as shown in Supplementary Table 1. This stability may arise from the minimized lattice distortion and favorable bonding environment associated with the anti-site disorder. Thus, Co/Sn anti-site defects are the most likely to occur under realistic synthesis conditions. The relaxed crystal structure for all defects is shown in Supplementary Fig 1(a–f).

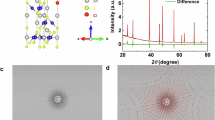
The crystal structure of Co3Sn2S2 and its doped derivatives were investigated to confirm the structural integrity and stoichiometry of the samples. The x-ray diffraction (XRD) patterns for all compositions, shown in Supplementary Fig 2(b), confirm that the samples are single-phase without any detectable secondary phases, indicating high structural purity. The obtained lattice parameters “a” and “c” are shown in Supplementary Fig 2(d). Both parameters exhibit a gradual decrease, slightly more in “a” in comparison to “c”, with increasing Co substitution, indicating that the unit cell volume contracts as the relatively larger Sn atoms are substituted by smaller Co atoms. However, the overall shrinkage remains mild, suggesting that the structural integrity of the material is largely preserved. To further elucidate the extra Co occupancy, we have performed the synchrotron high-resolution powder X-ray diffraction (SPXRD) for x = 0 and 0.2 at room temperature. The observed SPXRD patterns were refined via the Rietveld refinement method using the FullProf program, for x = 0.2 shown in Fig. 1(a) and that for x = 0 in Supplementary Fig 2(c) [for more details, see the “Method” section]. The result for x = 0.2 was tabulated in Table 1, which is in line with the DFT calculation [for x = 0, see Supplementary Table 2].

Fig. 1: Synchrotron high-resolution powder X-ray diffraction (SPXRD) and X-ray Photoelectron Spectroscopy (XPS) measurement.
figure 1

(a) Rietveld refinement of synchrotron high-resolution powder X-ray diffraction pattern of x = 0.2 measured at room temperature. XPS measurement is conducted for x = 0, 0.2, and 0.3 to determine whether the non-stoichiometry introduces electron or hole doping into the synthesized compound. (b) and (c) Co 2p and Sn 3 d scan XPS spectra, respectively. Compared to the characteristic Co 2p and Sn 3 d peaks in the pristine sample (indicated by the red dashed lines), the corresponding peaks in the doped samples exhibit a clear shift toward lower binding energies (BE), indicating an increase in local electron density and consistent with electron doping.

Full size image
Table 1 Rietveld refinement result of the Co3+xSn2-xS2 (x = 0.2)
Full size table

X-ray Photoelectron Spectroscopy (XPS) and energy-dispersive X-ray spectroscopy (EDX) measurements

To determine whether the non-stoichiometry in Co3+xSn2−xS2 introduced electron or hole doping, we have performed X-ray Photoelectron Spectroscopy (XPS) for some representative samples (x = 0, 0.2, and 0.3). The XPS data for the Co-2p and Sn-3d scans are shown in Fig. 1(b, c), while that of the S-2p scan is shown in Supplementary Fig 2(e). XPS analysis of the Co3+xSn2−xS2 system elegantly reveals an electron doping (n-type) mechanism through the systematic shifts in core-level binding energies. For the undoped compound (x = 0), the Co 2p spectrum exhibits peak at 776.88 eV (Co 2p3/2) and 791.82 eV (Co 2p1/2), alongside satellite structures at 780.05 eV (for Co 2p3/2) and 795.65 eV (for Co 2p1/2) [Fig. 1(b)], aligning closely with previously reported values25. These satellite peaks, positioned approximately 3.17 eV and 3.83 eV higher in binding energy than their respective main peaks, suggest the presence of shake-up processes, which are often associated with specific electronic configurations and bonding environments, providing a characteristic signature of the oxidation state (Co+2). Upon doping, a remarkable transformation occurs in the Co 2p spectrum. The main peaks systematically shift towards lower binding energies, reaching 776.76 eV (Co 2p3/2) and 791.70 eV (Co 2p1/2) for x = 0.2, and further decreasing to 776.60 eV (Co 2p3/2) and 791.62 eV (Co 2p1/2) for x = 0.3. This consistent reduction in binding energy signifies an increase in the electron density around the cobalt ions, which is characteristic of electron doping25,26,27.

Even more striking is the evolution of satellite structures. The satellite peak associated with the Co 2p1/2 state, clearly present in the undoped sample, completely vanishes upon doping (x = 0.2 and x = 0.3). Simultaneously, the satellite peak corresponding to the Co 2p3/2 state, while present in x = 0, undergoes a significant diminution in intensity with increasing x. The disappearance and weakening of these satellite features suggest a change in the electronic relaxation processes, likely due to the increased electron screening, consistently indicating an enhanced local electron density around the cobalt atoms25,26,27.

Simultaneously, the Sn 3d spectrum for x = 0 shows peaks at 485.47 eV (Sn+4 3d5/2), 493.86 eV (Sn+4 3d3/2), 484.18 eV (Sn+2 3d5/2), and 492.60 eV (Sn+2 3 d3/2) [Fig. 1(c)], revealing a mixed tin oxidation state as previously reported25. With increasing doping, these Sn 3d peaks shift towards lower binding energies, accompanied by a predominance of Sn+2 over Sn+4 at x = 0.2, culminating in the complete disappearance of Sn+4 at x = 0.3. This synchronous reduction in binding energies for both Co and Sn, coupled with the evolution of Sn’s oxidation state, compellingly supports the scenario of electron doping, where excess cobalt contributes electrons to the system, thereby increasing the electronic screening and lowering the energy required to eject core electrons from both metallic centers. This evolution of the main peak positions of Co and Sn, along with the satellite structures of Co, provides a compelling picture of the electronic modifications and the effective electron doping within the Co3+xSn2−xS2 system25,26,27.

Furthermore, energy-dispersive X-ray spectroscopy (EDX) results for the pristine sample, presented in Supplementary Fig 2(a), validate the elemental composition of the undoped material. The nominal and experimentally determined stoichiometries of all samples, summarized in Supplementary Table 3 of the Supplementary information, reveal that the actual compositions are in close agreement with the nominal values, confirming the successful synthesis of Co3+xSn2-xS2 with minimal deviations. These results provide a robust foundation for investigating electronic and transport properties as a function of doping.

Electrical transport and magnetization measurements

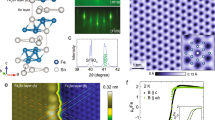
Figure 2(a) illustrates the longitudinal resistivity (ρxx) as a function of temperature, spanning from 300 K to 2 K. A noticeable kink in the resistivity curve corresponds to the Tc of approximately 170–178 K. Intriguingly, the derivative dρxx/dT vs T, shown in Fig. 2(b), reveals that Tc for the doped samples appears at slightly higher temperatures than that of the pristine sample. This observation is further supported by magnetization measurement as a function of temperature (M–T) in zero field cooling (ZFC) mode [Fig. 2(d)]. The dM/dT vs T, shown in Fig. 2(e), indicates the clear ferromagnetic transition corresponding to the Tc of approximately 170–178 K, consistence with Fig. 2(b). This behavior deviates from the common trend observed in many doping studies on Co3Sn2S2, where Tc typically decreases with the addition of dopants19,28,29,30. Furthermore, the rate of resistivity reduction at lower temperatures is steeper for the doped samples compared to the pristine sample, indicating an increase in the mean free path of charge carriers, also reflected in lower residual resistivity (RR) values. The residual resistivity ratio (RRR) and RR as a function of nominal doping x are depicted in Fig. 2(c). Notably, the RRR for the doped samples exceeds that of the pristine sample, especially for x = 0.27, which has the largest RRR among all, implying an improved crystalline quality [the RRR of some topological ferromagnetic materials along with x = 0.27 are shown in Fig. 2(f)1,2,3,5,31,32]. This result is unexpected, as introducing non-stoichiometry generally may lead to a deterioration in crystalline quality. These findings suggest that the controlled non-stoichiometry not only preserves but may enhance the crystalline order, enabling the observation of remarkable transport properties in the doped samples.

Fig. 2: Resistivity-temperature (ρ-T) and magnetization-temperature (M-T) measurements.
figure 2

(a) The resistivity measurements are performed over 300 K to 2 K for all samples, revealing metallic behavior across the entire span. A distinct kink is observed in the resistivity curves around 171–180 K, indicating a characteristic phase transition. To further analyze this transition, the derivative of resistivity with respect to temperature (dρxx/dT) is plotted against T (b), clearly identifying the Curie temperature (Tc) of each sample. The results indicate a slight improvement in Tc for the doped samples compared to the pristine ones, suggesting that doping subtly influences the magnetic interactions while preserving the metallic nature of the material. c The residual resistance ratio (RRR) and residual resistivity, RR, (ρ0) are plotted as a function of nominal doping (x) for all samples. The observed trend shows that RRR increases while ρ0 decreases with increasing doping concentration. This behavior suggests an enhancement in crystalline quality with doping, likely due to a reduction in structural defects and scattering centers. d The magnetization measurements are performed in zero field cooling (ZFC) mode, where data are taken by applying a magnetic field of 0.5 T while warming from 2 K to 300 K (the data are presented after subtracting the linear background above Tc). A clear paramagnetic to ferromagnetic transition can be seen around 171–180 K for all samples. The dM/dT vs T, (e) indicates a slight improvement in Tc for the doped samples compared to the pristine, as observed in ρ–T. f The comparison of the RRR of some topological ferromagnetic materials with that of x = 0.27 indicates good crystalline quality among them.

Full size image

To explore the electronic properties of the samples, we performed MR and Hall measurements using the six-probe method. In these experiments, a magnetic field was applied along the c-axis (B//c) while the current was directed within the ab-plane (I//ab). This setup, schematic shown in Fig. 3(a), allowed simultaneous measurements of the transverse MR and Hall resistivity (ρxy) by recording the longitudinal and transverse voltages. The MR of representative samples, x = 0, 0.1, 0.27, and 0.3, at different temperatures is shown in Fig. 3(b–e), respectively [For remaining samples, see Supplementary Fig. 4], illustrating the evolution of large and unsaturated positive MR with doping. Importantly, the doped samples exhibit significantly higher positive MR values with no signature of saturation even up to 9 T at lower temperatures [Fig. 4(a) for all samples at 2 K and Fig. 4(b) for MR at 2 K and 9 T, showing systematic enhancement of MR with doping]. Notably, the x = 0.27 sample achieves an extraordinary MR of 1150% at 2 K under a 9 T magnetic field—nearly 50 times greater than that of the pristine sample.

Fig. 3: Schematics of the experimental setup and evolution of transverse magnetoresistance (MR) with doping.
figure 3

(a) The schematics of the experimental setup for transverse MR and Hall measurements, where a magnetic field was applied along the c-axis (B//c) while the current was directed within the ab-plane (I//ab). b–e The large MR without any sign of saturation up to 9 T at low temperatures is depicted for some representative samples x = 0,0.1, 0.27, and 0.3, respectively. The MR is increased with increasing doping and achieves as large as 1150 % for the x = 0.27 sample.

Full size image
Fig. 4: MR and Hall measurement.
figure 4

(a) MR for all samples at 2 K up to magnetic field 9 T (b) MR for all samples at 9 T and 2 K, indicating enhancement of MR with non-stoichiometric doping, x. c, d Hall resistivity as a function of magnetic field (B) for x = 0 and 0.27 below Curie Temperature (Tc), respectively. Well-defined anomalous Hall effect for doped samples, like in the pristine sample below Tc, suggests the ferromagnetic ordering and intrinsic behavior is largely preserved upon doping.

Full size image

The Hall effect plays a crucial role in understanding the electrical transport properties of materials, particularly in systems like Co3Sn2S2, where the interplay between magnetic and topological properties is key to their behavior8,33,34. The Hall effect measures the transverse voltage that develops across a sample when a current is passed through it while subjected to a magnetic field. As shown in Fig. 4(c, d) for x = 0 and 0.27 [for x = 0.025, see Supplementary Fig. 3(a)] and across all investigated samples, a qualitatively consistent Hall behavior is observed, distinguished by a characteristic hysteresis jump. This specific feature is a typical signature of ferromagnetic materials when examined below their Tc. However, for the multicarrier system, generally at low temperature, where more than one carrier type contributes to the transport, the Hall effect is governed by the type and density of charge carriers (electrons or holes) and the material’s carrier mobility. The measured Hall resistivity (ρxy(B)) for all samples at 2 K is presented in Fig. 5(a). The pristine sample still preserves a well-defined hysteresis loop, which is characteristic of the anomalous Hall effect. However, with the introduction of doping, the hysteresis behavior undergoes a dramatic transformation. For lower doping concentrations (x < 0.15), the hysteresis loop is preserved but significantly reduced in magnitude. As the doping level increases beyond x > 0.15, the hysteresis mostly disappears, as shown in Fig. 5(b). Therefore, rather than the anomalous Hall plateau, the notable nonlinear magnetic field dependence of ρxy(B) suggests the involvement of more than one type of charge carrier in ρxy(B) at 2 K across all samples. Interestingly, a clear evolution in the nonlinearity of ρxy(B) with doping is observed, transitioning from hole-dominated conduction to electron-dominated conduction. To further explore the charge carrier dynamics and their mobilities, we analyzed the ρxy(B) data for all samples at 2 K using a two-band model described by the formula14,35:

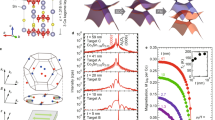
$${\rho }_{xy}(B)=\frac{B}{q}\frac{({n}_{h}{\mu }_{h}^{2}-{n}_{e}{\mu }_{e}^{2})+({n}_{h}-{n}_{e}){\mu }_{h}^{2}{\mu }_{e}^{2}{B}^{2}}{{({n}_{h}{\mu }_{h}+{n}_{e}{\mu }_{e})}^{2}+{({n}_{h}-{n}_{e})}^{2}{\mu }_{h}^{2}{\mu }_{e}^{2}{B}^{2}},$$

where nh and ne are the hole and electron carrier concentrations, and µh and µe are their respective mobilities. In a multiband material, extracting carrier concentrations and mobilities is not straightforward and can only be done with highly simplified assumptions. Even then, as a result of the number of fitting parameters, the parameters obtained from such fitting might not be unique. In our case, the two-band model of ρxy(B) fitted well to the experimental data for all samples (Supplementary Fig. 3(c) for that of x = 0.025). The fitting parameters obtained from the two-band fit of the Hall resistivity show remarkable consistency when applied to calculate the longitudinal resistivity (ρxx) using the corresponding two-band model values [Supplementary Fig. 3(d)], with small deviation (possibly due to deviation from quadratic B dependence [Supplementary Fig. 3(b)]), supporting the reliability of the extracted parameters and confirming internal consistency between the Hall and longitudinal components. The fitting parameters obtained from this model, including the carrier concentrations and mobilities for both holes and electrons, are plotted as a function of nominal doping (x) in Fig. 5d, e. A distinct crossover in the dominant charge carriers is observed in the doping range around x = 0.23 to 0.27, where the system transitions from hole-dominated to electron-dominated conduction. The pronounced non-monotonic evolution of the ρxy(B) across x = 0.23–0.30 originates from the carrier-type crossover induced by electron doping. As Co substitutes Sn, the hole carrier density decreases while electron density increases, resulting in a transition from hole- to electron-dominated transport around x = 0.23–0.27. In this critical regime, the low-field Hall effect becomes highly sensitive to the delicate balance between hole and electron contributions, leading to strong non-linearity and apparent anomalies in the Hall data. In contrast, the carrier mobility exhibits a more continuous and gradual change due to the gradual reduction in available phase space for scattering as the Fermi level smoothly shifts toward the nodal points with increasing doping. This behavior is consistent with two-band transport in the presence of Fermi-level tuning and supports our interpretation that electronic structure evolution is central to the observed transport phenomena.

Fig. 5: Analysis of Hall resistivity (ρxy(B)) data.
figure 5

(a) Hall resistivity for all samples at 2 K. A systematic evolution of non-linearity can be seen as doping increases, indicating the fine-tuning of the Fermi level. b The zoomed figure of (a) for a small field range shows the evolution of Hall hysteresis (anomalous Hall effect) with doping at 2 K. c The schematic of Fermi level tuning due to electron doping. The solid line is the Fermi level for the pristine, and the dashed line is after the electron doping. The red shaded part is the hole band, and the blue shaded part is the electron band after doping. We have used a two-band model to fit these Hall resistivities to get carrier concentrations and mobility for holes and electrons as fitting parameters [for more details, see Supplementary Fig 3]. d Carrier concentrations for holes and electrons as a function of doping (x). With doping, the hole carriers are suppressed, and the crossover of holes and electrons occurs around x = 0.23– 0.27. e Hole and electron mobilities as a function of x. Both the mobilities increase with doping, where electron mobilities dominate over the hole mobilities and reach as high as 18,000 cm2 V−1 s−1 for x = 0.27. f Comparison of MR and mobility at 2 K under 9 T among different magnetic (orange oval) and non-magnetic (violet oval) topological materials. Our sample shows the highest MR and mobility values ever observed among magnetic topological materials.

Full size image

Figure 5(c) shows the schematic of the band structure after SOC, Fermi level of Co3Sn2S2 and its tuning towards the band crossing with doping. In the absence of SOC, a nodal line occurs and is gapped upon SOC, except a pair of Weyl nodes. Since Weyl points above Ef are more sensitive to electron doping36, proximity to these nodes minimizes backscattering, a hallmark of topologically protected states, and significantly enhances the material’s transport properties like MR and mobility. The electron mobility dominates over hole mobility, reaching an impressive value of ~18,000 cm2 V−1 s−1 for x = 0.27 sample [Fig. 5(e)]. These values have profound implications for the electronic and transport properties of Co3+xSn2−xS2. The ability to achieve such exceptional mobility through Fermi-level tuning underscores the suitability of our approach, making Co3+xSn2−xS2 a promising platform for exploring topological quantum phenomena and their integration into advanced technological applications.

Comparison of MR and mobility of x = 0.27 with broader class of Weyl and Dirac semimetals

We extend our findings of large MR and ultra-high mobility to a broader class of Weyl and Dirac semimetals. To place our results in context, we compiled data in terms of the MR and mobility values from various compounds reported in the literature1,5,10,15,37,38,39,40,41,42,43,44 at ~2 K and 9 T and included our x = 0.27 sample for comparison, as illustrated in Fig. 5(e). To enhance clarity, we categorized the data by highlighting magnetic topological materials in orange and non-magnetic topological materials in violet. Notably, the results for our x = 0.27 sample represent the first-ever observation of such remarkable MR and mobility among the magnetic topological materials to the best of our knowledge. This finding is of profound significance as it establishes a new benchmark for magnetic topological semimetals, which are inherently more complex due to the interplay of magnetism and topology. The ultra-high mobility and giant magnetoresistance in this system highlight its potential for applications requiring high-speed charge transport, such as next-generation spintronic devices, high-speed electric components, and quantum computing parts. Furthermore, our results open up exciting opportunities for studying the unique interplay between electronic, magnetic, and topological properties, offering a promising platform for both fundamental research and technological applications.

Discussion

Our XRD analysis confirms that the doped samples retain the same fundamental crystal structure as pristine Co3Sn2S2. This structural consistency suggests that the overall electronic band structure, which is intrinsically linked to the crystal lattice, is largely preserved upon substitution. Concurrently, our XPS results indicate that Co substitution for Sn effectively donates electrons to the system. Therefore, the principal electronic consequence of this doping mechanism is an increase in electron concentration, leading to an upward shift of the Fermi level within the relatively stable band framework of the host material. The observed changes in the XPS spectra in the Co3+xSn2−xS2 system can be understood as a direct consequence of electron doping driven by excess Co substitution for Sn within the lattice. Electron doping in Co3+xSn2−xS2 is simply the result of substituting a 4-valence-electron Sn atom with a 9-valence-electron Co atom; the five extra electrons per substitution occupy Kagome-derived conduction bands and raise the Fermi level, as confirmed by the Hall measurements. The XPS data further corroborates this mechanism, as the increasing cobalt content (x) leads to a pronounced shift of both Co 2p and Sn 3d core levels towards lower binding energies, indicative of enhanced electron screening. The evolution of the Co 2p satellite features, their disappearance, and weakening intensity with doping suggest a change in the electronic relaxation processes, likely due to the increased electron screening, consistently indicating an enhanced local electron density around the cobalt atoms. These shift in oxidation states and screening behavior is a strong indicator that the non-stoichiometry induces a redistribution of charge within the lattice, enhancing metallicity and altering the electronic environment around Co and Sn.

The prior band structure analysis of Co3Sn2S2 reveals that the density of states (DOS) at the Fermi level is predominantly governed by Co 3d electrons, which play a crucial role in determining the compound’s electronic and magnetic properties. Previous studies on electron doping, such as Sb and Ni substitution for Sn and Co28,29, respectively, have shown a reduction in the Tc without significant improvements in transport properties like MR or carrier mobility, raising questions about the effective tuning of the Fermi level due to electron doping. However, non-stoichiometric electron doping, such as Co3+xSn2−xS2, remains unexplored and presents a promising avenue. This approach not only introduces additional electrons into the system but could also directly modulate the Co 3 d orbital contributions, potentially enhancing electrical transport and magnetization properties. By altering the Co-Sn ratio, this strategy may provide deeper insights into the interplay between electronic structure and material performance, offering a pathway to optimize functional properties for spintronic applications.

Furthermore, the surprising increase in Tc with non-stoichiometric doping as seen from ρ–T and M–T measurements contradicts the typical trend of Tc with substitutional doping like In-, Fe-, Ni-, or Sb-doped Co3Sn2S2, where substitutional disorder weakened ferromagnetism19,28,29,30. Moreover, in the Co3+xSn2−xS2 system, the ρxx at Tc displays a non-monotonic trend with increasing substitution levels, while the Tc itself exhibits an initial elevation upon a small substitution (from x = 0 to 0.025) and remains unchanged with increasing substitution. The exact origin of the non-monotonic behavior of ρxx at Tc with increasing substitution, despite Tc itself exhibiting an initial sharp rise (from x = 0 to 0.025) followed by saturation, remains elusive. This intriguing trend likely reflects a complex interplay between doping-induced changes in carrier concentration, scattering mechanisms, and magnetic exchange interactions, which may not scale linearly with substitution. Therefore, further detailed theoretical modeling and advanced spectroscopic or microscopic studies are essential to unravel the underlying mechanisms governing this behavior.

The systematic tuning of the Fermi level in Co3+xSn2−xS2 (0 ≤ x ≤ 0.3), particularly for the doped sample with x = 0.27 is evident from the observed change in charge carrier type from hole-dominated to electron-dominated transport. The prior angle-resolved photoemission spectroscopy (ARPES) and band structure calculations predicted that the Weyl points lie around 60 meV above and below the Fermi level, whereas the Weyl points above the Fermi level are more sensitive to electron doping36. Tuning the Fermi level in Co3+xSn2−xS2 not only suppresses the backscattering but also increases the topological protection, ensuring longer carrier lifetimes, leading to large carrier mobility and enhancing MR, giving rise to linear, non-saturating behavior. The observed lower residual resistivity (RR) and higher residual resistance ratio (RRR) across the doped samples also indicate increased mobility values. This enhancement is caused by the fine-tuning of the Fermi level in our doped system. These changes significantly influence the transport properties, leading to enhanced carrier dynamics and quantum transport phenomena.

Topological materials like NbP and WTe2, which exhibit ultra-high MR, typically rely on topological protection, perfect electron-hole compensation, and ultra-high mobility to achieve their remarkably high MR values11,15. In such systems, MR generally displays a quadratic dependence on the magnetic field due to the balanced contributions of electrons and holes. In contrast, materials like YSb attribute their MR to a significant disparity between electron and hole mobilities combined with moderate carrier compensation, showcasing an alternative mechanism for achieving enhanced MR45. However, in our case, the observed large MR can be attributed to the high carrier mobility, which is a direct consequence of the gradual tuning of the Fermi level achieved by systematic non-stoichiometric doping. When the Fermi level is tuned through doping, it can shift closer to the upper Weyl nodes. This results in a significant reduction in carrier scattering and an enhancement in mobility. The enhanced mobility resulting from Fermi-level tuning may provide optimal conditions for achieving significant MR. While it is true that topologically trivial pockets with ultra-high mobility can also contribute to transport phenomena, several key observations in our study support the role of Fermi level tuning responsible for the observed phenomenon. The anomalous Hall effect, which arises because of the system’s non-trivial band topology, is qualitatively similar in both pristine and non-stoichiometric samples below Tc. It’s systematic evolution at 2 K, together with the systematic changes in carrier mobility and MR upon doping, indicates that electron doping shifts the Fermi level closer to the upper Weyl nodes. This Fermi-level tuning suppresses the backscattering and enhances topological protection, ensuring longer carrier lifetimes, leading to high carrier mobility and large MR, a hallmark of topological transport. Therefore, we believe that the observed phenomena are predominantly governed by the non-trivial topological protection resulting from the tuning of the Fermi level rather than arising from trivial high-mobility carriers.

Conclusion

In conclusion, we have demonstrated that non-stoichiometric doping in Co3+xSn2−xS2 enables precise Fermi level tuning without disrupting magnetic order, resulting in large MR and ultra-high mobility. The doped sample with x = 0.27 exhibited ultra-high mobility, large MR, and remarkable crystalline quality. These results not only establish Co3+xSn2-xS2 (0 ≤ x ≤ 0.3), as a promising candidate for next-generation quantum devices but also pave the way for further exploration of its unique properties. Future theoretical and experimental investigations are essential to gain deeper insights into the band structure and topological characteristics as well as to unravel the interplay between electronic, magnetic, and structural properties. Such comprehensive studies will enhance our understanding of Co3+xSn2-xS2 (0 ≤ x ≤ 0.3), and its potential applications in spintronics, quantum computing, and other advanced technologies.

Methods

Sample synthesis and characterization

The Co3+2Sn2-xS2 (0 ≤ x ≤ 0.3) single crystals used in this study were grown by the self-flux method. High-purity elements Co, Sn, and S with a molar ratio of 3+x:2−x:2, where x = 0.025, 0.05, 0.075, 0.1, 0.15, 0.2, 0.23, 0.27, 0.3 were put into an alumina crucible and then sealed in a quartz tube under high vacuum. The quartz tube was slowly heated to 673 K within 12 h and maintained for one day. Afterward, the tube was heated to 1323 K within 12 h and maintained at this temperature for two days for better homogeneity. It is then slowly cooled down to 873 K within 120 h before switching off the furnace. Shining small crystals can be obtained by cleaving large crystals.

These samples were characterized by measuring X-ray photoemission spectroscopy (XPS), energy-dispersive X-ray (EDX) analysis, and powder X-ray diffraction, confirming the electron doping, close stoichiometric ratio, and single phase of as-grown single crystals Co3+2Sn2−xS2 (0 ≤ x ≤ 0.3).

To further probe the extra Co occupancy, we have performed the Synchrotron high-resolution powder X-ray diffraction (PXRD) for x = 0 and 0.2 samples. The PXRD data were collected at the 9B-HRPD beamline of the PLS-II (Pohang Light Source) in Pohang, Republic of Korea. The incident X-rays were monochromated to a wavelength of 1.5460 Å via a double-crystal Si(111) monochromator. The synchrotron PXRD data were obtained using a six multi-detector system with Ge (111) analyzer crystals, covering 2θ = 16 − 137° with a step size of 0.005°, neighboring detectors overlapped by 1.0°. Each powder sample was spun continuously during acquisition to increase the number of crystallites statistics and to minimize the preferred orientation effects. The sample surface was sealed with imid tape to prevent powder loss from the holder during rotation. The observed PXRD patterns were refined via the Rietveld refinement method using the FullProf program46 and the Thompson−Cox−Hastings pseudo-Voigt profile function47 was used to fit the observed PXRD patterns. Refined variables included the scale factor, lattice parameters, peak-width parameters (X, Y, GauSiz), asymmetry parameters, an atomic coordinate for S, Sn and Co occupancies, and preferred orientation. Since the Biso values consistently converged to negative numbers, the Biso parameters for all atoms were fixed at 0.05 and the occupancies of Co1 site (0.5, 0.5, 0.5) and S atom were also fixed throughout the refinement. Preferred orientation was described with a modified March−Dollase function.

DFT calculation

Density functional theory (DFT) simulations were performed by the Vienna ab initio Simulation Package (VASP 5.4.4). The Perdew-Burke-Ernzerhof (PBE) approximation was utilized for the exchange-correlation functional, and the frozen-core all-electron projector augmented wave (PAW) method was employed to describe the electron-ion interaction. The generalized gradient approximation (GGA) with Hubbard Ueff = 4.0 eV and Ueff = 0 eV on Co have been tested. Our results show that the magnetic moments of Co without the Hubbard correction align more closely with experimental values. The cutoff energy for the plane wave expansion was set to 500 eV. The atoms were relaxed until the energy and force were converged to 10−6 eV and 0.01 eV/Å, respectively. A Γ-center k-mesh of 12 × 12 × 4 was used for the hexagonal Co3Sn2S2 unit cell (a total of 21 atoms). A 2 × 2 × 1 supercell of hexagonal Co3Sn2S2 (a total of 84 atoms) was used to study the effects of doping with different defects.

Electrical transport and Magnetization

The electrical transport measurements of these flux-grown single crystals were performed in a cryogen-free magnet system (Cryogenic, Inc.) from 1.7 to 300 K and B = ± 9 T using the six-probe method. We conducted direct voltage measurements (Vxx and Vxy) using a current source (Keithley 220) and a nanovoltmeter (Agilent 34470 A). The magnetization measurements are performed by using the vibrating sample magnetometer (VSM) in the cryogen-free magnet system.