Introduction

Aerosol impacts on climate constitute one of the challenges in estimating current and future climate changes1. An important error source arises from absorbing natural aerosols, such as desert dust1,2,3, because they can both absorb and scatter radiation at short and long wavelengths, giving rise to a complicated relationship with the resulting net (shortwave plus longwave) direct radiative effect (DRE)2,3. The absorption capability relative to the scattering by dust aerosols dictates whether they foster or suppress precipitation locally and whether they warm or cool the planet4,5,6,7. These climatic impacts are still subject to large uncertainty, primarily due to poorly known attributes of dust aerosols, such as their optical properties8,9. To limit computational cost, most global climate models consider dust particles as a globally homogenous mixture of minerals, despite the strong regional variation of mineralogical composition10,11,12 and, thus, the optical properties of dust aerosols9,13. In contrast, recent studies3,11,14,15,16,17,18,19,20,21 have speciated dust into multiple mineral components, enabling the representation of regional variations of dust composition and resulting complex refractive index (CRI)14.

Modeling studies3,16,20 and observations13,22 have identified two types of iron oxides, specifically hematite and goethite, as key mineral components to estimate dust DRE because of their strong absorption at ultraviolet and visible wavelengths13,14,19,23, particularly when they are internally mixed with other minerals that are less absorbing14. Other light-absorbing oxide types, including manganese-oxides and titanium-oxides24,25,26, along with iron oxide minerals in addition to hematite and goethite, coexist in dust aerosols. However, measurements consistently indicate that hematite and goethite are the most common types of light-absorbing oxides and predominate in mass over the other types in major dust source regions11,12,27,28. Consequently, despite the potential comparability of some other light-absorbing oxide types in terms of the imaginary part of the CRI (referred to as imaginary CRI for brevity), a fundamental parameter linked to the aerosol absorption ability, their overall quantities are typically insufficient to exceed the importance of hematite and goethite for dust absorption within the shortwave spectral range. The imaginary hematite CRI, however, shows over two orders of magnitude difference in the literature (Supplementary Fig. 1)19, exhibiting strong29, moderate30, to weak31 absorption at visible wavelengths (referred to as STRONG, MODERATE, and WEAK index, respectively). In contrast to this diversity, there is only one set of imaginary goethite CRI32 available for use, whose accuracy has been questioned33.

Furthermore, the calculation of optical properties for dust aerosols, which are typically composed of a mixture of minerals, necessitates the application of a mixing rule to combine the CRI of each individual mineral. Two commonly employed mixing rules are the volume averaging method and the Maxwell Garnett approximation. The volume averaging method calculates the effective CRI of component aerosols by averaging the CRIs of individual components weighted by their volume fractions. In comparison, the Maxwell Garnett approximation estimates the effective CRI of a mixture by considering the impact of inclusions within the host medium. The appropriate use of the mixing rule depends generally upon the geometric arrangement of minerals within aerosols. Scanning and transmission electron microscopy reveal distinct forms of iron oxides in relation to other minerals13,34,35,36,37,38, typically categorized as internal and/or external mixing states. The mixing state, along with the amount and imaginary CRI of iron oxides, predominantly governs dust absorption and, consequently, DRE in models, particularly within the shortwave spectral range. The uncertainty in these factors poses a challenge in modeling dust optical properties. Especially in climate models, it remains unclear which imaginary hematite CRI and mixing rule provide more accurate descriptions of the optical properties of dust aerosol particles.

This work aims at constraining the imaginary hematite CRI as a function of the mixing rule used to calculate the CRI of dust aerosols and its sensitivity to iron oxides (hematite plus goethite)3,14,15,16,19,39,40,41. Addressing these aspects is fundamental for representing the dust DRE in modeling studies.

To achieve our purpose, we utilize existing laboratory measurements of dust mineralogical composition and its spectrally resolved optical properties19,22,42, and compare these laboratory optical properties with those we calculated for dust aerosols. These laboratory datasets include retrieved CRI and measured single scattering albedo (SSA, the ratio of scattered radiation to total extinction), mineralogical composition, and size distribution for dust aerosols with representative sizes akin to medium-range transported aerosols22,42. These aerosols were generated within a chamber that mimicked dust emission processes, using nineteen soil samples taken from worldwide dust sources (Fig. 1b). Due to the soil-to-aerosol conversion process, the size distribution and mineralogical composition of the dust aerosols analyzed here may differ slightly from those of the soil samples. The imaginary CRI and SSA are two key parameters widely used to characterize dust absorption and absorption relative to scattering, respectively. Both parameters vary substantially across dust source regions, contributing to large uncertainty in the estimate of dust DRE.

Fig. 1: Mineralogy of dust aerosols.
figure 1

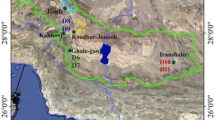
Existing soil atlases inadequately represent laboratory dust mineralogy, whereas data from the Earth’s surface Mineral dust source InvesTigation (EMIT) project enhance spatial accuracy for iron oxides. a Laboratory data at selected 19 sites. Black dash lines represent volume fractions of 0.25, 0.50, and 1.0, respectively. b Locations of the 19 sites grouped by seven geographical zones where the laboratory soil samples were taken to generate dust aerosols42. c Similar to (a) but for simulated mineral fractions at each of the 19 sites with one of the existing soil atlases (C1999)10 for comparison with the laboratory data. Mass fractions of the minerals rereported in the literature were converted to volume fractions (a and c) using their densities: illite-2750 kg m−3, kaolinite-2600 kg m−3, smectite-2350 kg m−3, hematite-5260 kg m−3, goethite-3860 kg m−3, quartz-2660 kg m−3, calcite-2710 kg m−3, feldspar-2560 kg m−3, gypsum-2300 kg m−3, chlorite-2950 kg m−3, and dolomite-2840 kg m−3. Iron oxides consist of both hematite and goethite (a, c), which is not distinguished in C1999. The laboratory mineralogy data were used with the assumption that regards all clays as kaolinite for sites where the partitioning between illite and kaolinite is unavailable42. Sensitivity tests on this and some other assumptions, e.g., all as illite or smectite, suggest minor impacts on the comparison here and on the conclusion of this study. d The comparison of iron oxides (mass fractions) for dust aerosols converted from soil atlases that were created based on high-bound3 iron oxides identified by existing global soil atlases (C199910 and J201411: royal blue and light sea green, respectively) and from EMIT (dark orange) retrievals (vertical bars: standard deviation over pixels around the sampling sites; see Methods for the data processing) against those from laboratory (the black solid line is the 1:1 line. Black and gray dash lines represent a factor of 2 and 4 differences, respectively). Metrics used to measure the model performance on reproducing the volume or mass fractions of the in-common minerals include the Pearson correlation coefficient (“*” denotes significance at the 95% confidence level) and root mean square error (RMSE).

Full size image

Similar to previous studies13,14,37, we focus on how to represent the absorption of dust aerosols due to iron oxides at the visible wavelengths where the dust absorption is enhanced43, and incoming radiative fluxes at the tropopause typically reach their peak (Supplementary Fig. 2). We do not extend the analysis to include long wavelengths due additionally to (1) the reduced importance of iron oxides: they show diminished importance compared to other factors, such as particle size and absorption by quartz and clays3,20, particularly when contrasted with the relevance of iron oxides to the shortwave dust DRE and (2) the lower variation of imaginary hematite CRI in the longwave spectral range, compared to the visible band, with the exception of the far infrared19.

The laboratory data explicitly measure the abundance of hematite and goethite, while excluding the other types of light-absorbing oxides. Consequently, our results, derived through various methods based upon the laboratory chamber data, can only be attributed to the combination of hematite and goethite.

Specifically, we (1) calculate the CRI of dust aerosols, which comprise multiple mineral components, by applying two mixing rules: the volume averaging or Maxwell Garnett approximation (results shown in Supplementary Information), along with the three sets of imaginary hematite CRIs19 (Supplementary Fig. 1), using laboratory dust mineralogical composition42 (Fig. 1a); (2) perform Mie simulations to compute the dust SSA with necessary inputs (See Methods; uncertainty provided in Supplementary Table 1); and (3) compare our calculations with the laboratory data22.

In the absence of quantitative information on the mixing state of laboratory minerals, this study adopts an internal mixing assumption when employing both mixing rules, while disregarding the other forms of iron oxides in relation to other minerals (see Discussion). Specifically, when using the volume averaging method, we consider dust particles to be a uniform blend of different components. When applying the Maxwell Garnett approximation, we consider iron oxides to be inherently embedded in the mineral lattice of illite plus smectite, forming a homogeneous matrix, and all non-matrix minerals are spherical, as described in Methods and Supplementary Information.

The internal mixing assumption and the use of the Mie Theory are necessary here to maintain consistency with the laboratory study, which also employed such assumptions when retrieving the CRI of dust aerosols in the chamber. Noting that the imaginary hematite CRI can differ from any of the three sets considered in this study, we further utilize optimal estimation techniques to retrieve a CRI that best matches the laboratory data. Given the sensitivity of dust DRE within the shortwave spectral range to the quantity of iron oxides in dust aerosols3,14,20, our constraint also lies in determining the most suitable mixing rule and set of imaginary hematite CRIs to accurately represent the relationship between the imaginary dust CRI and the volume (or mass) fraction of iron oxides in dust aerosols observed in laboratory settings.

Furthermore, we incorporate the Maxwell Garnett approximation into a global model to calculate the optical properties of dust aerosols (see Methods and Supplementary Notes). Currently, the volume averaging method serves as the default for this calculation in the model. With the addition of the new mixing rule, we assess which combination of imaginary hematite CRI and mixing rule most closely aligns with laboratory measurements of dust CRI, SSA, DRE efficiency (defined as the ratio of the dust DRE under clear-sky conditions to dust optical depth, DOD; unit: W m−2 DOD−1) in dust-dominated regions, and absorbing DOD (calculated as the product of 1-SSA and DOD) in the current climate (see Methods).

The primary results obtained from the volume averaging method are presented in the main text, while additional information, such as results derived from the Maxwell Garnett approximation and sensitivity tests conducted with different assumptions than those employed here, are included in Supplementary Information.

Overall, the extensive experiments in this study, complemented by laboratory measurements of dust quantities including composition, absorption, and scattering, markedly narrowed the range of plausible imaginary CRIs for hematite, despite the challenge of independently constraining the mixing rule and imaginary CRI. By incorporating a set of imaginary hematite CRI (MODERATE index) indicative of moderate radiation absorption in the visible spectrum along with the volume averaging method, the global climate model accurately simulated the optical properties of dust aerosols and their sensitivity to variations in iron oxide amounts within the particles. This constrained solar absorption of hematite, combined with precise descriptions of surface soil mineralogy, will enhance our understanding of the role desert dust plays in the Earth system based on its mineralogical composition.

Results

Constraints using laboratory measurements

We first consider the most likely combination of imaginary hematite CRI and mixing rule to accurately reproduce laboratory measurements of the imaginary CRI of dust aerosols. Comparison of the results using different combinations suggests that using the MODERATE index, representing moderate hematite absorption30 compared to the other two sets of imaginary hematite CRIs, and employing the volume averaging method (Fig. 2a) is competent for accurately reproducing the laboratory data at 0.52 µm. This combination yields a statistically significant correlation (Pearson correlation R = 0.86) at the 95% confidence level and a root mean square error (RMSE) not significantly different from the laboratory data at the 95% confidence level (Supplementary Table 2). In contrast, the other hematite indices either significantly overestimate (STRONG) or underestimate (WEAK) the observations at the 99% confidence level (Supplementary Table 2), with the RMSEs ranging between 0.0031–0.010 and 0.0018–0.0021, respectively, which are larger than that obtained using the OPTIMAL index (0.00034–0.0014). These results generally hold true with the Maxwell Garnett approximation (Supplementary Fig. 3a), although the errors could be higher, and the MODERATE and STRONG indices yield statistically indistinguishable RMSEs at the 95% confidence level for imaginary dust CRI.

Fig. 2: Predicted dust optical properties against laboratory data.
figure 2

The index representing moderate hematite absorption is superior to other indices for predicting the complex refractive index (CRI) and single scattering albedo (SSA) of dust aerosols, as confirmed by optimal estimation techniques. a Comparison of the calculated imaginary part (y-axis) of the CRIs to laboratory data (x-axis) at the wavelength of 0.52 µm for the 19 sites (Fig. 1b). The black solid line is the 1:1 line. Black and gray dash lines represent a factor of 2 and 4 differences, respectively. The calculated dust imaginary CRIs were obtained using the volume averaging method, utilizing laboratory mineral fractions (Fig. 1a), distinguishing between hematite and goethite (CRI taken from a previous publication3), and considering various hematite CRIs (STRONG: violet, MODERATE: red, and WEAK: forest green). Also included are constant dust CRIs (CONSTANT: gray) with no spatial and temporal variation79, and dust CRIs calculated based on the optimal hematite index (OPTIMAL: deep sky blue; derived using the optimal estimation techniques). For the calculated imaginary CRI of dust aerosols, the vertical standard-error bars denote uncertainty due to various error sources (see Methods). b Similar to (a) but for SSA (black dash lines represent a factor of 1.1 differences). The SSA was calculated based on the Mie Theory with the inputs of the calculated/constant dust CRI, as shown in (a), and the other inputs taken from the laboratory data42. The vertical standard-error bars represent uncertainty arising from error sources in the input to the Mie simulations, including those propagated from calculations for the imaginary CRI of dust aerosols (see Methods). The horizontal standard-error bars in both (a, b) indicate uncertainty in the laboratory data22. Metrics used to measure the distance between the calculations and measurements include the Pearson correlation coefficient (R; “*” denotes significance at the 95% confidence level) and root mean square error (RMSE). The RMSE obtained using a bootstrap procedure (see Methods) for imaginary dust CRI ranges between [0.0031, 0.010], [0.00034, 0.0014], [0.0018, 0.0021], and [0.00066, 0.00074] for the STRONG, MODERATE, WEAK, and OPTIMAL index cases, respectively. For dust SSA, it ranges between [0.069, 0.15], [0.022, 0.050], [0.064, 0.072], and [0.032, 0.034]. No RMSE range was estimated for the CONSTANT index case, since the resulting imaginary dust CRI and SSA show poor spatial variability.

Full size image

Next, we investigate how the different imaginary CRIs (and mixing rules) reproduce the laboratory SSA of dust aerosols. To achieve this purpose, we calculate the dust SSA using the Mie Theory with inputs including the imaginary dust CRI (Fig. 2a and Supplementary Fig. 3a), as well as parameters for five log-normal mode number distributions of dust aerosols observed in the laboratory, which vary from one site to another22. We then compare the results to observations. We find that employing the MODERATE index and volume averaging method allows to replicate the laboratory SSA of dust aerosols with a correlation coefficient of 0.68 (significant at the 95% confidence level; Fig. 2b). In comparison, the other indices working with the volume averaging method statistically either undershoot (STRONG) or overshoot (WEAK) the laboratory SSA of dust aerosols at the 95% confidence level (Supplementary Table 2). As a result, they cannot accurately reproduce the overall dust absorption relative to scattering (Fig. 2b). When employing the Maxwell Garnett approximation, the STRONG index, however, works better than the other two indices (Supplementary Fig. 3b). This combination yields a SSA of dust aerosols even superior to that achieved by the combination of the MODERATE index and volume averaging method. The relatively lower correlation between the laboratory data and calculations in the SSA compared to the imaginary CRI between the laboratory data and calculations is as expected, as the errors accumulate from the point where we calculated the imaginary CRI of dust aerosols.

Furthermore, we assess the sensitivity of imaginary dust CRI and SSA to the volume fraction of iron oxides. Compared to estimates based on the laboratory data, the MODERATE index working with the volume averaging method more accurately reproduces the sensitivity of the imaginary dust CRI to the volume fraction of iron oxides than the other indices: the calculated regression slope with the MODERATE index is approximately 0.12, which falls within the laboratory range of 0.11–0.19 (Fig. 3a). This result, however, contrasts with the performance of the Maxwell Garnett approximation, which shows better performance with the STRONG index compared to the other two indices (Supplementary Fig. 4a). Combining the STRONG index and the Maxwell Garnett approximation yields a statistically indistinguishable sensitivity at the 95% confidence level when compared to the combination of the MODERATE index and the volume averaging method.

Fig. 3: Predicted relationship between dust optical properties and iron oxides compared to laboratory data.
figure 3

The index representing moderate hematite absorption outperforms other indices in predicting the sensitivity of the complex refractive index (CRI) and single scattering albedo (SSA) of dust aerosols to variations in iron oxides, as confirmed by optimal estimation techniques. a Imaginary part of the CRI of dust aerosols as a function of volume fractions of iron oxides. The imaginary CRIs were obtained using the volume averaging method, utilizing laboratory mineral fractions (Fig. 1a) and various imaginary hematite CRIs (STRONG: violet, MODERATE: red, WEAK: forest green, and OPTIMAL: deep sky blue) at the wavelength of 0.52 µm. Additionally, the results include calculations based on laboratory data (OBSERVATION: gray). b Similar to (a) but for SSA, calculated based on the Mie Theory (see Methods). Note that results obtained using the MODERATE and OPTIMAL imaginary hematite CRIs greatly overlap. Metrics used to measure the relationship between the imaginary CRI and SSA of dust aerosols and the volume fractions of iron oxides include the Pearson correlation coefficient (R; “*” denotes significance at the 95% confidence level) and slope from the linear least squares regression. The slope of calculated imaginary dust CRI or SSA to the volume fraction of iron oxides, obtained using a bootstrap procedure (see Methods), ranges between [0.20, 1.0], [0.058, 0.26], [0.00084, 0.039], and [0.11, 0.12] for imaginary CRI, contrasted with [0.11, 0.19] in the observations, and ranges between [−14, −3.9], [−6.5, −1.6], [−1.1, −0.056], and [−3.3, −2.9] for SSA, contrasted with [−5.0, −1.3] in the observations, for the STRONG, MODERATE, WEAK, and OPTIMAL index cases, respectively.

Full size image

Consistently, the MODERATE index tends to better reproduce the sensitivity of dust SSA to the volume fraction of iron oxides than the other indices when used with the volume averaging method (Fig. 3b). In comparison, the STRONG index shows improved performance when used with the Maxwell Garnett approximation (Supplementary Fig. 4b).

In addition to evaluating existing reported CRIs, we prescribe a mixing rule to obtain an optimal CRI (imaginary part referred to as the OPTIMAL index; Supplementary Fig. 1: dodger blue or dark orange) through an inverse calculation that matches the laboratory data (see Methods). This new index indeed helps statistically reproduce the laboratory measurements at a 99% confidence level (Supplementary Table 2), as expected (Fig. 2 and Supplementary Fig. 3). It also aids in reproducing the relationships between iron oxides and dust CRI (imaginary part: Fig. 3a and Supplementary Fig. 4a) and SSA (Fig. 3b and Supplementary Fig. 4b). The OPTIMAL index gets close to the MODERATE index, regardless of the mixing rule used for the inverse calculation. However, there is a considerable difference between the two OPTIMAL indices inversed using different mixing rules, particularly at shorter wavelengths (e.g., 0.37 µm) compared to that at 0.52 µm (Supplementary Fig. 1a), suggesting that the imaginary hematite CRI and mixing rule cannot be constrained separately.

Evidence from global climate model simulations

To corroborate the laboratory-based findings, we compare climate model results at the visible band centered at approximately 0.53 µm using different imaginary hematite CRIs and mixing rules to dust-filtered SSA and absorbing DOD retrievals at the wavelength of 0.55 µm from sun photometers at 21 dust-dominated stations of the AErosol RObotic NETwork (AERONET) (see Methods). To simplify the representations of minerals in the model, we consider all iron oxides as hematite when using the volume averaging method, while maintaining the total volume fractions of iron oxides and other minerals unchanged. This treatment on the partitioning between hematite and goethite does not substantially alter the relative comparison between the imaginary CRIs of dust aerosols calculated using different imaginary hematite CRIs (Fig. 2a versus Supplementary Fig. 5a). For example, the superiority of the MODERATE index over the STRONG index with the volume averaging method remains consistent.

We find that, when employing the volume averaging method, reducing the amplitude of imaginary hematite CRI by switching from the previously3,16 used STRONG index to the MODERATE/OPTIMAL index, as constrained/derived here, substantially reduces the model error in reproducing the AERONET SSA of dust aerosols (Fig. 4b). These results are statistically significant at the 95% confidence level, indicating a robust finding.

Fig. 4: A snapshot of implications of the hematite index constraint.
figure 4

The constrained hematite index improves the modeling of dust optical properties, with important implications for accurately estimating the shortwave (SW) direct radiative effect (DRE). a Simulated annual single scattering albedo (SSA) of dust aerosols at the visible band centered at approximately 0.53 µm with the soil atlas of C199910, using the combination of the MODERATE index for hematite and the volume averaging method. Overlaid dots represent AErosol RObotic NETwork (AERONET) retrievals at the wavelength of 0.55 µm (see Methods). b Comparison between the simulated dust SSA using the volume averaging method with different hematite indices (STRONG: violet, MODERATE: red, and OPTIMAL: deep sky blue) and AERONET-based retrievals. R and RMSE denote the Pearson correlation coefficient (R; “*” denotes significance at the 95% confidence level) and root mean squared error, respectively, calculated based on annual dust SSA “The black solid line is the 1:1 line”. Black dash lines represent a factor of 1.05 differences. Horizontal error bars indicate uncertainty in the AERONET data (see Methods). c Similar to (a) but for dust optical depth (DOD). d Difference between simulated SW DRE of dust using the MODERATE and STRONG hematite indices, along with the volume averaging method for the period of 2007–2011. No simulation was performed using the WEAK hematite index, as previous results (Fig. 2a) suggest it substantially underestimates the laboratory imaginary part of the complex refractive index of dust aerosols compared to the other two indices.

Full size image

The comparison between the modeled (visible band centered at approximately 0.53 µm) and AERONET-based (wavelength: 0.55 µm) absorbing DOD (Supplementary Fig. 6) somewhat confirms the above finding. Using the MODERATE or OPTIMAL index improved the most likely estimates (e.g., spatial correlation R = 0.65 and RMSE = 0.02 for MODERATE), compared to using the STRONG index (R = 0.53 and RMSE = 0.04), though both still tend to overestimate the retrieved absorbing DOD. This overestimation and the evaluation itself, however, could be imprecise, given that (1) the AERONET retrievals can have a bias toward cases with high aerosol optical depth and thus high absorbing DOD because high-quality retrievals of the absorbing optical depth are for aerosol optical depth exceeding a threshold value (approximately 0.4)44 and (2) our model may overestimate the retrieved DOD (Fig. 4c), i.e., the accuracy of the modeled absorbing DOD depends on both the modeled DOD (Fig. 4c) and SSA (Fig. 4a).

There are satellite-based estimates of DRE efficiency under clear-sky conditions at the top of the atmosphere (Supplementary Fig. 7: gray horizontal lines or short gray bars), which can be used to evaluate if the simulated values are consistent with observations45,46. Such comparison (Supplementary Fig. 7), though limited by several aspects, as previously summarized47, suggests that, in general, the combination of the MODERATE index and the volume averaging method and the other combinations do not reproduce the regional-mean retrievals (Supplementary Fig. 7; for regional definitions, see x-labels). This discrepancy is likely partially attributable to a bias in the modeled abundance of iron oxides within dust aerosols (Fig. 1 and Supplementary Fig. 8).

Unfortunately, all simulations based on existing global soil atlases10,11 cannot accurately reproduce laboratory mineralogy (Fig. 1 and Supplementary Fig. 8) and, thus, imaginary CRI of the aerosolized soil samples (Supplementary Fig. 9), despite the use of the most recent atlas11 that represents iron oxides more consistently with recent findings, such as the dominance of goethite over hematite for dust from West Africa27. The model tends to underestimate the volume fractions of iron oxides at some sites while overestimating them at others, regardless of whether freshly emitted or transported mineral aerosols are used for analysis (Supplementary Fig. 8). These inaccurate simulations partially indicate a large uncertainty in soil mineralogy described by the existing atlases3, although the representativity of such comparison itself could be questioned by the limited number of soils analyzed in the laboratory. We anticipate large uncertainty in soil mineralogy due to the limited number of direct measurements used to create those atlases. These measurements were subsequently extrapolated globally by assuming that mineral fractions measured within a specific soil type or unit are applicable to other regions where measurements are absent, but the same soil type or unit is found10,11.

Figure 1d (dark orange) presents the first results from the new space-borne instrument of Earth surface Mineral dust source InvesTigation (EMIT), which will produce an independent global atlas of soil mineralogy48 (access the first initial global maps of surface soil hematite, goethite, and kaolinite from EMIT at https://www.jpl.nasa.gov/news/nasa-sensor-produces-first-global-maps-of-surface-minerals-in-arid-regions; last accessed on 3 May 2024). Dust aerosol mineralogy, converted from the soil data using these first results (see Methods), shows a statistically (95% confidence level) better spatial distribution than previously existing atlases10,11, compared to the laboratory data (Fig. 1d). This improvement suggests that results from the EMIT project will potentially enhance the model’s ability to simulate dust mineralogy and, thus, spatial variability in the dust CRI, SSA, and DRE49.

Discussion

Limitations of the methodology

There are several limitations in our methodology and interpretation of the results, which we summarize as follows. First, the laboratory data does not provide size-resolved mineralogy. Therefore, we assumed that iron oxides are uniformly mixed with the other minerals across the entire size range. This assumption influences how to interpret the laboratory scattering and absorption used to derive the CRI of dust particles, creating structural uncertainty that the laboratory study42 omits. Additionally, the assumption of size-invariant composition is common to the AERONET retrieval algorithm50 and analyses of in situ and airborne measurements27,41.

Second, the combinations of the MODERATE (STRONG) index and the volume averaging method (Maxwell Garnett approximation) do not reproduce the imaginary dust CRI at the other wavelengths (Supplementary Figs. 10, 11) as well as they do at the critical wavelength (0.52 µm) where the incoming radiative fluxes at the tropopause typically peak (Supplementary Fig. 2). In addition to the crucial wavelength for shortwave DRE, we have also assessed the performance of the indices at four out of the seven wavelengths, although with less detail, as depicted in Supplementary Information. Supplementary Fig. 1, along with Supplementary Figs. 10–13, serves as a likely reliable indicator of the overall performance across all the seven wavelengths. When comparing the MODERATE and the other two indices with the OPTIMAL index, given the mixing rule, we find that the preferred MODERATE index excels at most wavelengths, including the wavelength emphasized in this study (Supplementary Fig. 1a). While the combinations of the MODERATE (STRONG) index and the volume averaging method (Maxwell Garnett approximation) may not perform as strongly as at the target wavelength, they still replicate observations no less effectively than other combinations at different wavelengths. However, even at the wavelength of 0.52 µm, the utilization of the volume averaging method and MODERATE index to model the optical properties of dust aerosols can only serve as a compromise solution. This is because the volume averaging method (1) might not be applicable to dust minerals that are nearly metallic (insoluble) from a physical perspective39 and (2) its use requires the dust particle to be a uniform blend of different components, whereas most dust particles consist of aggregates of varying mineralogical composition51 and/or distinct minerals52.

Third, our calculations of imaginary CRI and SSA disregard the various complex forms in which iron oxides can exist in dust aerosols. Specifically, contrary to the presumption that iron oxides are inherently embedded in the mineral lattice of illite plus smectite for the Maxwell Garnett approximation, scanning and transmission electron microscopy findings reveal two distinct forms of iron oxides, differentiated by their sizes34,35. Specifically, minute grains manifest as flakes on the surface of aluminosilicates or adhere within the interstices of clay-aggregate particles due to Brownian motion and electrostatic forces. Conversely, larger iron oxide grains exist within dust aerosols as aggregates that adhere to the surface of other dust minerals. In reality, the coexistence of the three distinct forms of iron oxides is also possible, a facet not explored in this study. The existence of these cases and their coexistence mean that dust aerosols can show complex morphologies that specific approximations cannot describe accurately. As such, there is a lack of rigorous justification14 of existing mathematical approximations that can represent the wide variety of particle morphologies53. In theory, even in scenarios where the Maxwell Garnett approximation is deemed appropriate, the retrieval of the refractive index of multi-mineral particles should be conducted through optical experiments using standard mineral samples. From this perspective, our results serve as a compromise solution for modeling dust optical properties on a global scale, considering particles with mineral components of varying proportions where index retrievals are not available for each individual particle.

Fourth, our calculations rely on limited laboratory data on aerosolized soil samples (Fig. 1a) and wavelengths (e.g., Supplementary Fig. 13). We thus encourage more extensive measurements to fully constrain the imaginary hematite CRI as a function of the mixing rule.

Furthermore, with the same required data (e.g., the mass or volume fraction and CRI of each mineral) to calculate the CRI of dust aerosols, the volume averaging method produces significantly more absorption at the 95% confidence level (Supplementary Table 3) compared to the Maxwell Garnett approximation (Fig. 2a versus Supplementary Fig. 3a). The latter is more consistent with Maxwell’s Equations, while the former approximates the Lorentz–Lorenz mixing rule for quasi-homogeneous mixtures (similar constituents in terms of CRI)54. However, our primary results suggest that the preferred imaginary hematite CRI at the mid-visible wavelength (i.e., 0.52 µm) changes with respect to the mixing rule. For example, when employing the volume averaging method, the MODERATE index outperforms the other previously reported imaginary CRIs for hematite in reproducing the imaginary CRI and SSA of the aerosolized dust samples in the laboratory (e.g., Fig. 2) and their sensitivity to iron oxides (e.g., Fig. 3). In contrast, when employing the Maxwell Garnett approximation, the STRONG index is preferred (Supplementary Figs. 3, 4). Therefore, the mixing rule and hematite CRI cannot be chosen independently due to the constraints of laboratory measurements.

Nevertheless, sensitivity studies show that the primary results presented here are not sensitive to many of the assumptions made in this study, such as the CRI for the matrix, chlorite, and dolomite (Supplementary Table 4), mixing states of dust minerals (Supplementary Fig. 14), and the distinction between hematite and goethite (Fig. 2 versus Supplementary Fig. 5). This is especially notable in the preferences of the MODERATE index against the other indices previously reported in the literature when used with the volume averaging method to reproduce the imaginary laboratory dust CRI.

Implications for constraining dust impacts on the Earth system

The observationally constrained optical properties will improve estimates of the direct perturbation of dust aerosols on the Earth’s energy budget via interaction with radiation (e.g., dust DRE), because of the importance of the amount and imaginary CRI of hematite3,13,22. We find that the choice of hematite indices alone can cause substantially different estimates of dust DRE (Fig. 4d and Supplementary Figs. 15b, 16), indicating potential impacts on the global energy budget. For example, changing from the STRONG to MODERATE index using the volume averaging method results in a stronger annual mean cooling by approximately 0.24 W m−2 (net DRE: shortwave plus longwave) on the global average under all-sky conditions at the top of the atmosphere in our model (Supplementary Fig. 15b). This amplitude change, primarily arising from the change in the shortwave DRE (Fig. 4d versus Supplementary Fig. 15b), is even larger than that resulting from (1) uncertainty in the soil abundance of hematite in either clay- or silt-sized categories, which contribute 0.2 and 0.1 W m−2, respectively3, to the shortwave DRE; (2) exclusion of very coarse dust aerosol particles (geometric diameter >10 µm)55, estimated at ~0.01–0.06 W m−2; and (3) underrepresentation of coarse dust aerosols between 5 and 10 µm in geometric diameter55, estimated at approximately 0.15 W m−2. For longwave DRE, iron oxides become less important that the other factors, such as the particle size and absorption by quartz and clays3,20.

It is worth noting that speciating dust by mineralogical composition in the model yields a shortwave dust DRE remarkably different from that calculated by using a globally uniform CRI of dust aerosols, in terms of both spatial distributions and global mean (Supplementary Fig. 17). This contrast highlights the importance of properly representing the contribution of regionally contrasted iron oxides (Fig. 1) to the spatial variations of dust optical properties (e.g., Fig. 2 and Supplementary Fig. 3). Additionally, employing a single climate model that uses the STRONG or WEAK hematite index combined with the volume averaging method could lead to an overemphasis or underemphasis of regional contrast and the importance of iron oxide contents to the dust DRE estimate. This is because the combination of the STRONG or WEAK hematite index with the volume averaging method tends to overestimate or underestimate the sensitivity of calculated dust optical properties to variations in iron oxide abundance in dust aerosols (Fig. 3).

Moreover, our results have important implications for other climate impacts due to desert dust, which are sensitive to the sign and distribution of the dust-radiation interaction. These include cloud burning effect, caused by the absorption of radiation by dust within or above clouds56,57, and the melting effect by dust on snow and glacier cover58,59,60,61 due to the dark color of dust particles relative to snow and ice grains (the surface-albedo feedback). Especially, the melting effect can be regionally important and highly uncertain in climate modeling62, which can then induce a series of consequences for multiple components in the Earth system, such as water resources63, ecosystems64, and climate changes (e.g., Northern Hemisphere warming65). The imaginary CRI of dust aerosols for wavelengths <~1.4 µm66 is one of the fundamental parameters determining how quickly the dust particles can melt the snow cover or glacier surface through surface darkening67. Estimates of these darkening and melting effects by dust in global climate models, such as the model employed here (not exactly the version we used but its officially released version), still utilize a globally uniform CRI for dust68, potentially introducing bias into the estimation. Our constraint on the imaginary hematite CRI and the mixing rule provides a basis for future advancements aimed at reducing bias by further considering dust speciation that includes hematite. Therefore, our results here have the potential to improve understanding of the regional to global warming by dust aerosols via the surface-albedo feedback69.

Our improved estimates of the dust optical properties also enable a better representation of the impact of dust on atmospheric circulations4,70 and the role mineral dust plays in weather prediction71 in coupled climate and weather-forecasting models. The feedback of dust aerosols differs depending on the sign of the perturbations to the energy budget at the surface and in the dust-lofting layer4,20, potentially altering the atmospheric stability72. These perturbations to the energy budget can also alter the horizontal temperature gradient, thereby affecting monsoon strengths and tropical cyclones73. We anticipate important implications of our findings for simulating how dust aerosols affect atmospheric circulation, particularly in regions near the “dust belt” (from North Africa through the Middle East and Central Asia to East Asia), where substantial changes to the dust DRE are observed (e.g., within the shortwave spectral range: Fig. 4d), particularly during monsoon seasons when dust outbreaks often occur74. As changes in meteorological fields can feed back into the simulation of the dust cycle72, improved modeling of dust optical properties based on speciated dust tracers and our constraints on the imaginary hematite CRI here can help better simulate the dust cycle while utilizing a prescribed soil mineralogy atlas and predicted atmospheric dynamics in the model.

Methods

Global aerosol modeling

The Community Atmosphere Model of version 6 (CAM6) is used to simulate the dust minerals (e.g., Fig. 1c and Supplementary Fig. 8, and those used in Supplementary Figs. 9, 10b, d–12b, d), optical properties (Fig. 4a–c and Supplementary Fig. 6), dust direct radiative effect (DRE) (Fig. 4d), and DRE efficiency (Supplementary Fig. 7). The model represents dust as mineral components (illite, kaolinite, smectite, quartz, feldspar, hematite, calcite, and gypsum) using a Modal Aerosol Module version 4 (MAM4) with four log-normal size modes (accumulation, Aitken, and coarse dust modes, and a primary carbonaceous mode). The dust model, which incorporates a physically-based scheme75,76 and was tuned toward the currently best estimate of the global mean dust optical depth (DOD: approximately 0.03) for the present climate, has undergone thorough evaluation against observed dust cycles47. The emission procedure of each mineral tracer within the three dust-containing modes was initialized using previously developed global soil atlases11,77 with additional modifications3,16. This procedure follows the brittle fragmentation theory78, which converts soil mineralogy to aerosol mineralogy. All global simulations using this model were conducted for the period of 2006–2011 with monthly model output frequency. The first-year simulation is excluded from the analysis as the model spin-up. The meteorological fields, including air temperature, relative humidity, and horizontal wind field, were nudged toward the Modern-Era Retrospective analysis for Research and Applications dynamics version2 (MERRA2) at a spatial resolution of 1.25° × 0.9° × 56 (longitude × latitude × vertical layers). These fields were updated on a 6-h relaxation time scale for each of the vertical layers. Anthropogenic emissions were taken from the Climate Model Intercomparison Program (CMIP6) inventory for the 2000s climate.

The rapid radiative transfer model (RRTMG) was used to calculate the radiative flux at each of the 56 vertical model layers per model hour at 16 longwave and 14 shortwave bands. The instantaneous dust DRE at the top of the atmosphere under all-sky/clear-sky conditions was diagnosed as the difference in net instantaneous fluxes per model hour with and without the presence of dust aerosol species for both shortwave and longwave bands79.

We adopted the assumption that all model iron oxides are hematite, while keeping the total volume fractions of iron oxides and other minerals unchanged. Although this approach does not substantially alter the relative comparison of the complex refractive index (CRI) of dust aerosols when calculated using various combinations of the imaginary hematite CRIs, it leads to a more pronounced difference in single scattering albedo (SSA) across the AErosol RObotic NETwork (AERONET) sites compared to imaginary CRI. This implies that SSA shows greater sensitivity to the amount of hematite compared to goethite than imaginary CRI does, with stronger hematite absorption enhancing this sensitivity. Consequently, solely representing both types of iron oxides with hematite, while keeping other parameters unchanged, results in a big difference in shortwave dust DRE of +0.10 W m−² under all-sky conditions at the top of the atmosphere3. Distinguishing between hematite and goethite and utilizing their respective imaginary CRI enhances dust cooling, given goethite’s lower absorption in the shortwave spectrum compared to hematite. This increased cooling is somewhat consistent with the comparison between Fig. 2 and Supplementary Fig. 5. Note that the 0.10 W m−2 difference was estimated based on Journet et al.’s soil representation of goethite and hematite mass fractions11, and the DRE contrast is based upon a single and contested measurement of the goethite CRI33. This study does not estimate how the different imaginary CRIs between hematite and goethite may affect the dust DRE here as it deviates from the primary objective and the importance of this difference has been emphasized in a previous study3.

Incorporating the Maxwell Garnett approximation to dust-speciated CAM6

The main purpose of this incorporation is to quantify the potential difference in the DRE estimate between different combinations of the mixing rules and imaginary hematite CRIs (e.g., Supplementary Fig. 16). We assume that iron oxides and other minerals, as well as other non-dust aerosol species, are spatially separated with no strong electrostatic interaction. This assumption excludes the case that the inclusion becomes resonant, as the Maxwell Garnett formula holds precisely only at the volume fraction of the inclusion <10−5. We acknowledge that this value, although not always the case, could still be much smaller than the volume fraction of iron oxides in dust-dominant grid boxes, which is well constrained, ranging between 0 and 10% by measurements19 and modeling3,16.

In corresponding model simulations, we combined illite and smectite as the matrix. Supplementary Fig. 18 illustrates the comparison between the selected matrix and other intrusions. See Supplementary Notes for detailed information on how we utilized this approximation to calculate the dust CRI.

Post-processing of Earth surface Mineral dust source InvesTigation (EMIT) retrievals, and the two existing soil atlases, C199910 and J201411

Since the laboratory mineral fractions are for aerosolized dust, we followed the steps below to convert soil mineralogy from EMIT retrievals and the two global atlases to aerosol mineralogy for the comparison shown in Fig. 1d:

  1. (1)

    Selecting pixels containing EIMT retrievals (ground-level resolution: 60 m), surface soil clay and silt fractions (horizontal resolution: on the order of approximately100 km), and C1999 and J2014 soil atlases (horizontal resolution: on the order of approximately100 km) that are closest to the sample sites (Fig. 1b). For detailed descriptions of the EMIT imaging spectrometer and on-orbit calibration, please refer to recent publications48,80.

  2. (2)

    Partitioning mineral fractions (Mi) from EMIT into the clay- and silt-sized categories based on the soil clay (Cf; diameter up to 2 µm) and silt (Sf; diameter ranging between 2–63 µm) fractions taken from the land model input while retaining the proportion of each mineral i assigned to each category (MiC or MiS):

    $$\left\{\begin{array}{c}{M}_{{iC}}={M}_{i}\frac{{C}_{f}}{{C}_{f}+{S}_{f}}\\ {M}_{{iS}}={M}_{i}\frac{{S}_{f}}{{C}_{f}+{S}_{f}}\end{array}\,.\,\right.$$
    (1)
  3. (3)

    Normalizing mineral fractions from EMIT obtained in step (2) such that the resulting fractions sum to unity. Since EMIT does not provide retrievals for feldspar and quartz, laboratory measurements for these minerals were used instead in the normalization process. EMIT reports mineral fractions in terms of the spectral expression of mineral signatures relative to that of a pure library mineral. Here, these mineral fractions are interpreted as mass fractions, although in practice, the two may not be perfectly correlated.

  4. (4)

    Converting iron oxides from different soil sources to those in aerosols, following the brittle fragmentation theory with the maximum dust size set as 20 µm in geometric diameter. This step is also applied to the C1999 and J2014 soil atlases.

Estimating uncertainty in calculating the imaginary CRI of dust aerosols

We accounted for uncertainty arising from laboratory-derived iron oxide fractions and the imaginary CRI of each mineral (Supplementary Table 1: a 44% relative change applied). Real CRI uncertainty, typically <8%, was not considered, as it is substantially smaller than the 16–75% range observed in the imaginary CRI. The total uncertainty was determined by the root-mean-squared sum of uncertainties stemming from these factors under independent assumptions. Given the unknown nature of the imaginary goethite CRI uncertainty, we opted not to differentiate between hematite and goethite. Instead, we applied a 44% relative change in the imaginary CRI and allocated 15% of the mass concentration to total iron oxides. This approach facilitates capturing a broad spectrum of plausible errors. Firstly, it accounts for the fact that laboratory-derived goethite mass concentrations exhibit an uncertainty of approximately 10%, which is less than the prescribed 15%. Secondly, any discrepancy resulting from the distinction between hematite and goethite was included alongside other sources of error in the calculation.

Calculating the SSA of dust aerosols using the Mie Theory

We calculated the SSA of dust aerosols at the wavelength of 0.52 µm (Figs. 2b, 3b and Supplementary Figs. 3b, 4b, 5b, 13c, d, 14) using the Mie Theory for spherical particles with the parameters for dust size distribution taken from Supplementary Table 1 of a recent publication22. Another key input is the CRI of dust aerosols, which was calculated by applying either the volume averaging method or the Maxwell Garnett approximation to the laboratory dust minerals without considering their potential size dependency. Both the dust size distribution and the minerals used vary spatially and represent dust aerosols transported over medium distances, reflecting global variability in the current climate22.

Estimating uncertainty in calculating the SSA of dust aerosols using the Mie Theory at each site

Uncertainty in direct inputs to the Mie Theory, such as the size distribution of dust aerosols (geometric diameter and standard deviation) and the CRI of each mineral, would propagate into uncertainty in the calculated dust SSA. In addition, potential errors in the measured mass fractions of minerals, based on which we calculated the CRI of dust aerosols, could also introduce uncertainty in the calculated dust SSA. To quantify the total propagated uncertainty, we conducted a total of 16 sensitivity tests in which we perturbed (increased or decreased) each of those inputs within the observed uncertainty range22 (Supplementary Table 1). Note that for sensitivity tests on CRI with the uncertainty range for imaginary CRI shown in Fig. 2a and Supplementary Fig. 3a, we did not perturb the real part, as it varies little compared to the imaginary CRI, and the associated uncertainty is typically small, less than 5%22. Then, we applied the root-mean-squared sum of the uncertainties induced by those factors to obtain the total uncertainty3,7,81, with independent assumption among all the direct and indirect input factors on each other.

Statistical metrics and significance tests

We utilized statistical metrics, such as slope, root mean square error (RMSE), and/or spatial correlation, to quantify the “distance” or relationship between calculations and observations (Figs. 1c, d, 2, 3, 4b and Supplementary Figs. 3–5, 6b, 8: right panels, and 9–14). The slope was determined using least squares regression. RMSE was computed as the Euclidean distance between the calculations and corresponding laboratory data at each site and single wavelength. The Pearson correlation coefficient was employed to assess spatial correlation. The corresponding null hypothesis test assumes that the samples are uncorrelated and normally distributed at the 95% confidence level.

A non-parametric Wilcoxon signed-rank test was also employed, as in previous studies82,83, to determine if the paired data is statistically different from each other (Supplementary Tables 2,3).

Bootstrapping method

Uncertainty in RMSE between calculated imaginary CRI/SSA and laboratory data (Fig. 2 and Supplementary Figs. 3, 5), as well as in the trend of calculated imaginary CRI and SSA on laboratory volume fractions of iron oxides (Fig. 3 and Supplementary Fig. 4) were estimated based on the results of bootstrapping iterations. In each iteration, a slope was obtained using randomly selected results from the sensitivity tests performed on each of the parameters that can change the calculated imaginary dust CRI (as explained in the previous section) at each of the 19 sites, along with the estimated uncertainty ranges of mineral volume fractions. Calculations were repeated a large number of times (>100,000) until the resulting slope showed minimal variation (<10%). The uncertainty in RMSE was similarly estimated through this iterative process.

The selection of the matrix and the determination of the CRI used for both the matrix and minerals with unknown CRIs

The results presented in the main text (control experiments) utilized illite CRI for the matrix (illite plus smectite) and kaolinite CRI for chlorite and dolomite when applying the Maxwell Garnett approximation to calculate the CRI of dust aerosols based on the laboratory mineral fractions, along with the corresponding SSA of dust aerosols. It is reasonable to test if those results vary considerably enough to lead to different conclusions when different assumptions are made (e.g., using kaolinite CRI for the matrix and chlorite and dolomite). Therefore, we conducted multiple sensitivity tests in which we repeated the calculations and analysis while applying different CRIs to the matrix, chlorite, and dolomite (left portion of Supplementary Table 4). In all these sensitivity tests, the CRI for each of the other minerals remains the same as in the control experiment.

Results from the sensitivity tests (right portion of Supplementary Table 4) in terms of the RMSE, the Pearson correlation coefficient (significance tested at the 95% confidence level), and the spatial regression slope suggest that the resulting CRI and SSA of dust aerosols, as well as the relationship between the imaginary dust CRI and iron oxide abundance in dust aerosols, do not show a strong response to different assumptions.

AERONET-derived dust optical properties

We process AERONET Version 3 Level 2.0 Almucantar50,84 hourly retrievals to extract optical properties for mineral dust on a monthly basis at the wavelength of 0.55 µm. We particularly aim to minimize contamination by carbonaceous absorbing aerosols, such as black or brown carbon, which may contribute to the absorption attributed to dust. Since dust is typically a coarse aerosol, we first remove all retrievals with fine volume fractions above 10%. Although sea salt aerosols may also be predominantly present at coarse sizes, they show a near flat (close to unity) SSA at visible wavelengths, whereas dust absorption increases towards short-visible and ultraviolet wavelengths85. Therefore, we can distinguish dust from sea salt aerosols by requiring an increasing SSA from 0.440 to 0.675 µm. Finally, the potential contamination of the selected dust events by absorbing carbonaceous aerosols is further reduced by filtering out the retrievals whose mean imaginary CRI at red-infrared wavelengths (0.675, 0.870, and 1.02 µm) is larger than 0.004286. This condition is expected to directly detect a strong presence of black carbon (and indirectly brown carbon, which is expected to coexist with black carbon), as it is the only species absorbing at these wavelengths86,87.

These filtering criteria21,88 were applied to the available hourly data from 2007 to 2011 to select dust-dominated measurements, although it is nearly impossible to completely remove all small contaminations by non-dust aerosols. For non-dust events, the DOD and absorbing DOD were set to zero before constructing the monthly means. The dust SSA was obtained as an extinction-weighted mean over the dusty scenes. The monthly means were then obtained for months with a minimum of 30 hourly measurements over the 5-year period.

Optimal estimation of hematite CRI

At each wavelength, we obtained two new sets of the hematite CRI (Supplementary Fig. 1: dodger blue and dark orange) using optimal estimation techniques to best fit the laboratory CRI of dust aerosols, considering a given mixing rule. For each site (j) and each wavelength (w), when using the volume averaging method, we calculated the CRI of dust aerosols (ymodel; m = 1 and 2 for real and imaginary CRI, respectively) based on the volume fraction (δ) and CRI (n) of each dust mineral (non-iron-oxides: i; iron oxides: FeOx), following

$${y}_{{{{{{{\mathrm{model}}}}}}},j,m,w}={\sum}_{i=1}^{7}{\delta }_{i,j}{n}_{i,m,w}+{\delta }_{{{FeO}}_{x},j}{{n}_{{{{{{{\mathrm{FeO}}}}}}}}}_{{x,}^{m,w}}$$
(2)

When using the Maxwell Garnett approximation, ymodel was obtained following Supplementary Eqs. 1–3 based on δ and spectrally resolved n for each dust mineral.

The final solution to this optimization model, the optimal CRI of iron oxides, was obtained to minimize the following cost function, a Chi-Square goodness of fit,

$${x}^{2}={\sum}_{m=1}^{2}\left[{{\sum}_{j=1}^{19}\left(\frac{{y}_{{{{{{{\mathrm{model}}}}}}},\, j, \, m}-{y}_{{obs},j,m}}{{\sigma }_{j,m}}\right)}^{2}+{p}_{m}\right],$$
(3)

where σ represents the uncertainty in each observation (yobs) at each site j for either real part or imaginary CRI, denoted by m; P is a penalty added to avoid negative results, which occurred at wavelengths of 0.59 and 0.66 µm.

The optimal CRI of iron oxides (resulting imaginary CRI/SSA and their relationship with iron oxide volume fractions shown in Figs. 2,  3 and Supplementary Figs. 3–5) was determined through a global search over a range bounded by the hematite CRI in the literature, assuming they bracket the “real” value we are trying to ascertain. This bounded condition took effect during the optimization at three wavelengths, 0.47, 0.59, and 0.66 µm. An additional constraint was imposed, ensuring that the goodness of fit approximates the total site number, which is 19. This constraint necessitates an increase in uncertainty in the observations from 20 to 36% except at 0.59 and 0.66 µm. The 95% confidence interval for the optimal value at each wavelength was determined by identifying the values for which the corresponding Chi-Square equals the minimum value plus four (e.g., black contour in Supplementary Fig. 19a), although the errors may not strictly follow a Gaussian distribution. These steps were repeated across each of the seven wavelengths and two mixing rules to obtain the spectral optimal hematite CRI, as shown in Supplementary Fig. 1. See Supplementary Fig. 19 for Chi-Square as a function of both parts of the CRI.

When applying this method to retrieve the optimal hematite CRI with the Maxwell Garnett approximation at wavelengths where there is no index previously reported for goethite (e.g., the wavelength of 0.37 µm), we obtained the index by assuming a logarithmic fit of the wavelength dependency. Separating the two parts of the CRI, such as using the real part of the CRI of hematite form that corresponds to the MODERATE index, so only needing to search the optimal imaginary CRI, yields similar results to those obtained by combining both parts in the retrieval (Supplementary Fig. 20b versus Supplementary Fig. 19b).