Introduction

Barrier islands are dynamic coastal landforms that provide protection from storms and high-energy waves to coastal infrastructure and ecosystems such as marshes, mangroves, oyster reefs, and seagrass meadows. This role is mainly controlled by barrier’s elevation and is thus a natural result of the competition between wind-driven sand accretion, which leads to dune formation and increases barrier’s elevation, and water-driven (mainly wave runup) dune overtopping that erodes the dunes and decreases barrier’s elevation1,2,3. The dunes that represent the highest natural feature on a barrier are the primary structure that dictates the effect of erosional processes on the island by mitigating the impact and reducing the frequency of storm overwashes4,5,6. Without dunes, a barrier island is susceptible to frequent coastal flooding7, which is expected to accelerate even faster than the global mean sea level rise in the near future8, and can become barren and potentially drown if sediment supply is low enough9,10. A barren barrier, in addition to the expected reduction of biodiversity given the lack of dunes and frequent flooding, would offer little protection to inland coastal infrastructure and ecosystems. As important, low-elevation and narrow barriers undergo a faster landward migration, or marine transgression, as more overwash events are able to transport sand from the beach to the backbarrier7, potentially exposing stored carbon-rich organic deposits from wetlands and coastal lagoons to high-energy waves at the nearshore11. Barrier migration can have a large impact on the size and characteristics of the coastal zone12 and could potentially shift the carbon budget of the entire coastal system from a net carbon sink to a carbon source13,14. Barrier elevation thus offers a good description of the barrier state, in which case the formation and post-storm recovery of coastal dunes provide a crucial indication of barrier resilience and ulterior dynamical response to external drivers.

Barrier island dynamics is a complex problem that involves the interaction of sediment transport, hydrodynamics, and vegetation across a wide range of spatial and temporal scales15,16. Simple models generally focus on the average planform dynamics using mass conservation but without resolving dune dynamics17,18,19,20,21,22. More complex process-based models23,24,25 can capture the effect of individual storm impacts on barriers and dunes, whereas large-scale models tend to focus on the long-term barrier response to sediment supply, storms, and SLR, but again greatly simplifying the dune dynamics and thus fail to capture the actual stochastic response of barrier elevation26,27,28,29,30,31,32. A common approach in all models is to resolve the barrier migration rate, which is crucial for the ulterior evolution of the barrier system, using a phenomenological estimation of sand fluxes due to storm overwashes26,27,32. Since, for a given storm, the occurrence and intensity of an overwash event are primarily determined by the barrier’s elevation, a consistent physical description of barrier migration requires resolving dune dynamics first.

The dynamics of barrier island elevation were recently investigated with a stochastic point model that resolved the competition between dune growth and water-driven vertical erosion that determines whether a barrier island has a dune or not at a given alongshore position33. The stochastic model has the advantage of analytically describing the phase space of the barrier elevation state, defined by the probability density function (PDF) of barrier elevation, in terms of two control parameters relating to quantities that can be measured remotely. These control parameters determine whether barriers are in a ‘high-barrier’ state with well-developed dunes, a ‘barren’ state devoid of dunes, and a ‘mixed’ state where dunes take longer to recover after erosion and thus washovers (i.e. the sand deposited by an overwash) tend to persist for some time33.

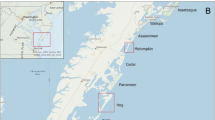
The probability distribution of barrier elevation in the Virginia Barrier Islands (VBI) (Fig. 1, see the “Methods” section) indeed shows the three types of barrier islands: ‘barren’ barriers with elevations close to the beach berm (~0.5 m) and lacking dunes, ‘high’ barriers with elevations around mature dunes (~2 m) as in the case of Hog island, and more complex ‘mixed’ barriers in between (e.g. South Metompkin). Given the external conditions are similar for all these islands and assuming similar sand availability, this leads to the question of what controls the transition from a ‘high’ barrier state, with complex dune and back-barrier ecosystems, to a barren state.

Fig. 1: Alongshore distribution of barrier elevation and barrier classification.
figure 1

a The study area comprises the Virginia Barrier Islands (VBI), where we analyzed five representative islands and divided Metompkin into two sections (North and South) with very different morphological characteristics (see the “Methods” section). b Alongshore distributions of barrier elevation h showing the three types of barrier islands classified based on their elevation: “Barren” islands (h ≲ 1 m) that lack vegetated dunes and are dominated by a beach berm with typically unvegetated overwash fans (c), “high” islands (h ≳ 1 m) with well-developed dunes stabilized by vegetation (d), and “mixed” islands with a broad distribution of elevations (e.g. South Metompkin). The distribution functions predicted by our stochastic model (Eq. (2)) are shown as solid lines in (b). c, d Map data: © Google, Landsat/Copernicus.

Full size image

Here, we answer this question and analyze its broader implications by spatially extending the stochastic point model and then quantitatively testing the model predictions using VBI data (see the “Methods” section).

Results and discussion

Stochastic model of coastal dune dynamics at a point

The stochastic model in ref. 33 describes the time evolution of the PDF of barrier elevation at a point (i.e. at a given alongshore position), where the barrier elevation h is defined as the highest elevation along a cross-shore transect on a barrier island. This model combines a deterministic wind-driven dune growth34 with stochastic erosion driven by high-water events35.

High-water events (HWEs) are defined by periods when total water levels (including wave runup) continuously exceed a given threshold and are well represented by a marked Poisson process with exponentially distributed marks35. The stochastic model assumes this probabilistic description, formally validated for HWEs overtopping elevations up to 0.5 m above the characteristic beach elevation35, can be extended to include the relatively low dunes in our study site, which is consistent with data and simulations of the return period of extreme events in Oregon35,36. During dune overtopping conditions, when the mark or size of the HWE exceeds the dune crest, the model assumes for simplicity that the dune is completely eroded up to a base elevation h0, which is thus defined as the maximum elevation after an overwash. Although, in reality, there can be partial dune erosion, this assumption captures the onset of the so-called ‘overwash regime’ in field data37 and makes analytical calculations possible by ignoring the detailed and complex morphodynamics of dune erosion.

The deterministic dune growth model is based on complex process-based simulations34 that resolve sand transport, wind aerodynamics, and its interaction with the topography, vegetation growth, and surface change, and that reproduces the shape and dynamics of real dunes34,38,39. Physical simulations34 showed that dunes grow up to a maximum height H, consistent with field data3,38. However, this maximum height is not necessarily constant40 but depends on slowly varying external conditions such as shoreline position38 and factors affecting the establishment and survival of dune-building vegetation as reflected in vegetation’s distance from the shoreline and elevation above water level39. After vegetation colonizes the back-beach and starts trapping wind-driven sand from the beach and assuming no water overtopping, the simulated dune grows to the maximum height H during a characteristic time Td following an exponential saturation curve of form \(H(1-\exp (-t/{T}_{{\rm {d}}}))\)34 consistent with data at different barrier islands3,4,38. The dune formation time Td characterizes the undisturbed dune growth in the absence of the dune’s crest erosion.

For simplicity, the stochastic model assumes that the colonization of the washover by ‘dune-building’ vegetation after an overwash is much faster than dune formation33. In that limit, Td can be written in terms of the maximum dune growth rate Gd as Td = (H−h0)/Gd34. The dune growth rate Gd is the function of the sand supply from the beach to the dune and, although it is treated as a constant in the model as supported by field data38, it is a complex quantity that depends on the availability of dry sand on the beach41, wind direction and intensity, and can be affected by dune toe erosion40.

The change dh in barrier elevation after a time interval dt is modeled by the stochastic equation33

$${{{\rm{d}}}}h=\left(\frac{H-h}{{T}_{{\rm {d}}}}\right){{{\rm{d}}}}t-\Delta h(h,t)$$
(1)

where Δh > 0 is the decrease in dune size after a random HWE33. Barrier elevation is assumed to be bounded by the maximum dune height H and the base elevation h0, and the maximum dune growth rate Gd is assumed to be constant over timescales of the order of a year, large enough to integrate daily and seasonal variations in wind regime and sand supply. Dune model’s parameters H, h0, and Gd will be estimated from the data.

The steady-state solution of Eq. (1) is given by the point PDF \({f}_{\xi }(\xi | {\lambda }_{0}^{+},{\overline{S}}^{+})\), describing the equilibrium distribution of the random variable ξ over a large enough time interval and at a particular alongshore position (see the “Methods” section, Eqs. (M1) and (M2)). The normalized barrier elevation ξ is defined as ξ = (h−h0)/(H−h0) and the two control parameters \({\lambda }_{0}^{+}\) and \({\overline{S}}^{+}\) are the frequency λ0 of HWEs overtopping the base elevation h0 rescaled by the dune formation time \({T}_{{\rm {d}}},{\lambda }_{0}^{+}={\lambda }_{0}{T}_{{\rm {d}}}\); and the average size \(\overline{S}\) of the overtopping HWEs rescaled by the maximum dune height relative to the base elevation, \({\overline{S}}^{+}=\overline{S}/(H-{h}_{0})\).

The comparison of the point PDF with an empirical distribution using real data requires a large number of observations frequently sampled overtime at the same alongshore location, which is exactly the opposite of how most field data is collected, where elevation is measured over large spatial scales roughly once a year. Therefore, the model has to be expanded alongshore (i.e. parallel to the shoreline) to take advantage of most available data.

Alongshore extension of the point model

In the absence of water-driven erosion and under finite sand supply from the beach, we assume that dunes can form everywhere along a barrier island. In a first approximation, we assume that wind and water forcing, as well as sand availability, are identical in the alongshore direction and that the spatial variations are limited to the randomness associated with preexisting morphology (excluding the dunes) and vegetation characteristics. In that case, only the maximum dune height H(y) and base elevation h0(y) would change spatially with the alongshore position y. By definition, the alongshore variations of the maximum dune height H(y) represent a simplified characterization of the dune morphology on a barrier island, such that a relatively uniform foredune ridge would be described by a narrow distribution of the values H(y) around the mean dune height, whereas a complex landscape with multiple ridges would be described by a wider distribution encompassing the variety of elevations. Similarly, the alongshore variations of the base elevation h0(y) would describe the alongshore morphology of superimposed washovers or eolian back-barrier deposits. Although both H and h0 can change alongshore randomly, we assume they remain relatively constant over timescales of the order of the dune formation time Td.

The spatial variation of H and h0 affects the control parameters of the point PDF which now depend on their local values. Although the change in \({\overline{S}}^{+}\) just follows its definition, the change in the rescaled frequency \({\lambda }_{0}^{+}={\lambda }_{0}{T}_{{\rm {d}}}\) is more subtle as both λ0 and Td depend on H and h0. Using the exponential distribution of the size S of HWEs35, the frequency λ0 of HWEs overtopping the base elevation h0 can be written as \({\lambda }_{0}={\lambda }_{{\rm {r}}}\exp (-{h}_{0}/\overline{S})\), where λr is the frequency of HWEs overtopping a reference beach elevation at which h0 = 0 by definition35. The undisturbed dune formation time is given by Td = (H−h0)/Gd.

Assuming for simplicity that the alongshore variations in H and h0 are random and can be approximated by a normal distribution \({{{\mathcal{N}}}}\) (in agreement with the data, Fig. 2), the alongshore PDF fh(h) is obtained by the integration of the steady-state solution fξ at a point (Eqs. (M1) and (M2)), conditioned by H and h0, over all possible values of the parameters:

$${f}_{h}(h) = {\int}_{\!\!\!{0}}^{h}{{{{\mathcal{N}}}}}_{{h}_{0}}({h}_{0})\left({\int}_{\!\!\!\!{h}}^{\infty }{{{{\mathcal{N}}}}}_{H}(H){f}_{h| H,{h}_{0}}(h){{{\rm{d}}}}H\right){{{\rm{d}}}}{h}_{0},$$
(2)

where the conditional PDF \({f}_{h| H,{h}_{0}}\) is

$${f}_{h| H,{h}_{0}}(h)=\frac{1}{H-{h}_{0}}{f}_{\xi }\left(\left.\frac{h-{h}_{0}}{H-{h}_{0}}\right\vert {\lambda }_{0}^{+},{\overline{S}}^{+}\right),$$
(3)

and the barrier elevation h(y) is a random variable now understood as the highest elevation along cross-shore transects at different locations y alongshore a barrier island.

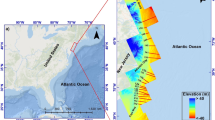
Fig. 2: Estimation of model parameters and stable equilibria in island dynamics.
figure 2

a–f Rate of elevation change G(y) = [h(y, 2017)−h(y, 2014)]/(3yr) for a given alongshore location y (dots) as a function of the initial alongshore elevation h(y, 2014) relative to the reference beach elevation (see the “Methods” section). The solid line is the average growth rate G(h). The red dashed line is the maximum dune growth rate Gd (see the “Methods” section). g–l Probability density function fs of elevations h with very small rates of change (∣G∣ < 2.5 cm yr−1). Solid black line is a fit with two Gaussians, the first one (in red) describes the alongshore distribution \({{{{\mathcal{N}}}}}_{{h}_{0}}\) of the base elevation h0. For Hog and South Metompkin (k and l), the second Gaussian (in blue) describes the alongshore distribution \({{{{\mathcal{N}}}}}_{H}\) of maximum dune elevations H (see the “Methods” section). In g–j, the Gaussian in gray has no clear interpretation. Red dots in a–f correspond to the lower-elevation stable equilibrium \({\overline{h}}_{0}\) defined by the mode of the red Gaussian in (g–l). In a–c, this equilibrium is consistent with the formal definition G = 0 and \({G}^{{\prime} } < 0\), as shown by the solid black line. The black dashed line in (a–d) shows the linear growth rate \(G(h)=({\overline{h}}_{0}-h)/(3\,{{{\rm{yr}}}})\). Blue dots in c–f correspond to the dune stable equilibrium \(\overline{H}\) defined either by the condition G = 0 and \({G}^{{\prime} } < 0\) or by the mode of the blue Gaussian (e and f). See the “Methods” section for more details.

Full size image

Assuming for simplicity that the local control parameters \({\lambda }_{0}^{+}(H,{h}_{0})\) and \({\overline{S}}^{+}(H,{h}_{0})\) can be approximated by their values at the mean maximum height \(\overline{H}\) and mean base elevation \({\overline{h}}_{0}\)

$${\overline{S}}^{+}=\overline{S}/(\overline{H}-{\overline{h}}_{0})$$
(4)
$${\lambda }_{0}^{+}={\lambda }_{{\rm {r}}}{{{{\rm{e}}}}}^{-{\overline{h}}_{0}/\overline{S}}(\overline{H}-{\overline{h}}_{0})/{G}_{{\rm {d}}},$$
(5)

they become independent of the local variations and recover their meaning as global control parameters of the alongshore distribution fh, the only function of the average properties along a barrier island.

By describing barrier elevation only by the maximum elevation along a cross-shore profile and simplifying vertical erosion to an all-or-nothing process, the stochastic model given by Eqs. (2) and (3) reduce the complex shape and dynamics of the barrier surface, including dunes, to a minimal physical description. Indeed, the steady-state alongshore elevation distribution fh only depends on the two control parameters (Eqs. (4) and (5)), defined over regional or island-based averages, and the alongshore distributions of the maximum dune height and base elevation, \({{{{\mathcal{N}}}}}_{H}\) and \({{{{\mathcal{N}}}}}_{{h}_{0}}\), respectively.

Estimation of model parameters

The average size \(\overline{S}\) and mean frequency λr of HWEs overtopping the reference beach elevation were estimated for the VBI as 0.3 m and 18 events/year respectively35. Therefore, Eqs. (2)–(5) require five parameters (\({G}_{{\rm {d}}},{\overline{h}}_{0},\overline{H}\) and standard deviations \({\sigma }_{{h}_{0}}\) and σH) to evaluate fh and compare it to the empirical alongshore distributions (Fig. 1).

A fundamental ingredient of the point model33, supported by an idealized dune building dynamics34, is that in the absence of dune erosion, dunes at a given alongshore position grow up to the maximum elevation H selected by the external conditions at that location, and there is a single stable equilibrium in the system: h = H. In that case, the point PDF can be approximated as a delta function fξ(ξ) ≈ δ(1−ξ) for a single alongshore location, which leads to \({f}_{h}(h) \, \approx \, {{{{\mathcal{N}}}}}_{H}(h)\) once alongshore fluctuations are taken into account (Eqs. (2) and (3)). As expected, in the absence of dune erosion the steady-state distribution of barrier elevation fh is just the alongshore distribution of maximum dune elevation \({{{{\mathcal{N}}}}}_{H}\) characterizing the alongshore morphology of mature dunes in the barrier.

In the absence of dune growth, either because of lack of eolian transport, sediment supply, or back-beach vegetation34 or because dune growth is negligible compared to erosion33, we expect water-driven transport (by waves and currents) to select a single equilibrium elevation of the barrier, the base elevation h0 (Fig. 2a–c). This water-driven equilibrium is called a beach berm in barren barriers (e.g. Fig. 1c). In that case, the point PDF becomes fξ(ξ) ≈ δ(ξ) and thus \({f}_{h}(h) \, \approx \, {{{{\mathcal{N}}}}}_{{h}_{0}}(h)\). That is, in the absence of dune growth the steady-state distribution of barrier elevation fh becomes the alongshore distribution of the base elevation \({{{{\mathcal{N}}}}}_{{h}_{0}}\) selected by a balance of water-driven erosion and deposition.

Since by definition neither H nor h0 change over time (at least over timescales of the order of a few years), we can estimate the distributions \({{{{\mathcal{N}}}}}_{{h}_{0}}\) and \({{{{\mathcal{N}}}}}_{H}\) by focusing on elevations with negligible growth rate in the VBI data (Fig. 2). In particular, we find that the distribution of steady-state elevations can indeed be well approximated by a Gaussian distribution (Fig. 2). The estimated parameters are shown in Table 1 (see the “Methods” section for further details, including the estimation of the maximum dune growth rate Gd). Interestingly, our estimated maximum dune growth rates Gd do not change much for such a diverse group of barrier islands and are roughly in the range of 0.2−0.4 m/yr, comparable to measurements from barrier islands in Florida and Texas3,4, and coastal dunes in Oregon38.

Table 1 Model parameters, control parameters and average barrier elevation for VBI
Full size table

Predicted steady states of barrier elevation

As discussed in the “Introduction” section, whether a barrier island has a dune or not depends on the competition between dune growth, including sand supply from the beach, and vertical water-driven erosion. For a given pair of control parameters (Table 1), the outcome of this competition is predicted by our model in two different but related ways. The first one is by the alongshore elevation distribution function fh at the steady state. In spite of the model simplicity and the several assumptions and approximations behind the estimation of the model parameters, the predicted PDF was obtained by numerical integration of Eqs. (2) and (3), capture the main characteristics of the empirical distributions for the three years analyzed (Figs. 1b and 3). Crucially, it reproduces the mode of the empirical distributions and, therefore, the central quality defining the barrier’s elevation state: whether the mode is closer to the mean base elevation \({\overline{h}}_{0}\), thus defining a ‘barren’ barrier, or closer to the mean maximum dune height \(\overline{H}\), thus defining a ‘high’ barrier. Barrier steady state is thus completely determined by the control parameters \({\lambda }_{0}^{+}\) and \({\overline{S}}^{+}\) that regulate the relative weight of the two potential modes of the steady-state point PDF fξ: a dune-less mode at h = h0 and the dune mode at h = H33. The resulting character of the point PDF is then extended to the alongshore distribution fh.

Fig. 3: Comparison with model predictions.
figure 3

Probability density function (PDF) of dune height (relative to the reference beach elevation, see the “Methods” section) for North Metompkin (a), Smith (b), Cedar (c), Parramore (d), South Metompkin (e) and Hog island (f), obtained from real data for the 3 years analyzed. Solid lines show the steady-state PDF (fh) predicted by the stochastic model from the parameters estimated for each island (Table 1).

Full size image

The second way to describe the barrier’s elevation state is by using the mean post-storm dune recovery time \({\overline{T}}_{{\rm {r}}}^{+}\), rescaled by the dune formation time. This recovery time is defined as the average time spent by the barrier elevation around the low-elevation mode at \({\overline{h}}_{0}\) after an overwash (Eq. (M3)) and can be interpreted as the average duration of a washover before the dune starts to grow (see the “Methods” section for the formal definition). By definition, when the rescaled recovery time is much larger than 1, dunes take very long to recover after erosion. In that case, the island is effectively dune-less (e.g. in a ‘barren’ state) and its alongshore elevation distribution function at the steady state will have a single mode at the average base elevation interpreted as a beach berm (e.g. Fig. 1b for Cedar island). For example, model prediction for Cedar is \({\overline{T}}_{\rm {{r}}}^{+} \sim 30\) (Fig. 4), which, after multiplying by the estimated average dune formation time (Td ≈ 6 years, Table 1), leads to a dune recovery time  of ~180 years. On the contrary, when the rescaled recovery time is less than 1, dunes do recover after an overwash, in which case the island will evolve towards a ‘high’ state with mature dunes. In this case, the alongshore elevation PDF at the steady state has a single mode at the average maximum dune height (see Fig. 1b for Hog Island). In between, barriers have widely distributed elevations combining mature dunes and washovers. Therefore, the analytical function \({\overline{T}}_{{\rm {r}}}^{+}({\lambda }_{0}^{+},{\overline{S}}^{+})\) essentially defines the phase space of the barrier state (Fig. 4).

Fig. 4: Transition from ‘high’ to ‘barren’ barrier islands.
figure 4

Barrier phase space showing the contour lines of the rescaled dune recovery time \({\overline{T}}_{{\rm {r}}}^{+}\) (see the “Methods” section) and the corresponding barrier classification as a function of the two control parameters. Symbols representing the islands are based on the values in Table 1. The dashed line shows a parametric phase curve illustrating the transition from a `high' barrier to a barren state as the base elevation changes from 1.5 m to 0 (left to right) while keeping all other parameters as for Hog Island.

Full size image

Plotting the values of the control parameters estimated for the VBI in the predicted phase space (Fig. 4) clearly shows that the transition to barren barriers in this region is essentially driven by a 30-fold increase in the rescaled frequency of HWEs (\({\lambda }_{0}^{+}\)). From its definition (Eq. (5)), the rescaled frequency is particularly sensitive to the mean base elevation \({\overline{h}}_{0}\) (it decreases exponentially with it) compared to other parameters such as the relative maximum dune height (\(\overline{H}-{\overline{h}}_{0}\)) or the maximum dune growth rate (Gd). Indeed, changing only \({\overline{h}}_{0}\) while keeping all the other parameters as estimated for Hog creates a phase curve (i.e. a path in the phase space) that describes a potential transition from Hog to South Metompkin and eventually Cedar, Smith, and North Metompkin (Fig. 4, dashed line). Therefore, in the VBI, the transition to a barren state seems to be mainly controlled by the mean base elevation of the barriers.

Robustness of model predictions

The most important model prediction is related to the steady state of the barrier island and thus only depends on the control parameters (Eqs. (4) and (5)). Parameters such as the standard deviations of the base elevation and the maximum dune height, or even the type of random distribution, certainly affect the shape of the alongshore PDF (Fig. 3) but not the position of the modes that define the barrier state. Interestingly, the transition to a barren state, as described by the rescaled dune recovery time in Fig. 4, depends weakly on the mean maximum dune height \(\overline{H}\). This is because, in a first-order approximation at the transition from ‘mixed’ to ‘barren’ states, the dune recovery time is only a function of the product of the control parameters33\({\lambda }_{0}^{+}{\overline{S}}^{+}\) and this product does not depend on \(\overline{H}\) (Eqs. (4) and (5)). As a result, the uncertainty in our estimations of the maximum dune height, in particular for barren barriers, has little impact on our final results. This extends to model simplifications such as neglecting shoreline change and ignoring vegetation characteristics and dynamics, which mainly affect the size and shape of mature dunes38,39,42. Furthermore, by focusing on post-storm dune recovery (which mainly depends on the erosion of proto-dunes2) and not on the erosion of mature dunes, our predictions are relatively insensitive to the way we model the probabilistic properties of extreme events, and our simplified description of the degree of dune erosion after overtopping.

Irreversibility of the barren state

VBI data suggest that the transition to a barren state takes place at \({\overline{h}}_{0}\approx 0.4\) m, that is when the mean base elevation \({\overline{h}}_{0}\) is determined by the beach berm and thus purely controlled by water-driven transport. As shown in Fig. 2a–c, this barrier elevation (h ≈ 0.4 m) is a relatively strong attractor of the water-driven dynamics as elevations up to twice or more tend to be eroded on average, in agreement with the predicted stochastic model dynamics. Indeed, the barren state is a stable state in the stochastic model precisely because erosion dominates dune formation for barrier elevations around the beach berm. This also suggests the barren state is irreversible as water-driven processes cannot increase the mean base elevation above the beach berm once dunes are eroded following a large storm.

Effect of sea level rise

The model insight into the fundamental role played by the mean base elevation (\({\overline{h}}_{0}\)) in controlling barrier state allows for a subtler mechanism by which sea level rise (SLR) can impact barrier islands. Since h0 is defined relative to a reference beach elevation tied to the water level35, in the absence of sand accretion at a scale larger than the dune width, \({\overline{h}}_{0}\) would just decrease with SLR over time until the barrier undergoes a transition to the lower elevation state (Fig. 5). Using the intermediate scenario for the average rate of relative sea level rise (RRSLR) in the study site from 2020 to 2050 (RRSLR ≈ 10 mm/yr)43 it would take  ~25 years for \({\overline{h}}_{0}\) to decrease 0.25 m (Fig. 5), which is the difference between the mean base elevation of South Metompkin, a ‘high’/‘mixed’ barrier, and Parramore, a relatively barren barrier (Fig. 4 and Table 1).

Fig. 5: Critical transition in barrier’s elevation and the onset of potential barrier loss driven by SLR.
figure 5

a Simulations of the steady-state stochastic dynamics, represented by the PDF \({f}_{h}(h| {\lambda }_{0}^{+},{\overline{S}}^{+})\) of barrier elevation h sampled four times per year (symbols), over the phase curve shown by the dashed line in Fig. 4. The parametric phase curve (\({\lambda }_{0}^{+}({\overline{h}}_{0}),{\overline{S}}^{+}({\overline{h}}_{0})\)) is a function of mean base elevation \({\overline{h}}_{0}(t)\), which itself changes with time due to SLR as \({\overline{h}}_{0}(t)=1.3\,{{{\rm{m}}}}-R\,t\). The rate R of relative SLR is assumed to be constant and equal to the average for the intermediate scenario estimated for the region from 2020 to 2050 (R = 10 mm/yr)43. All other parameters are taken as for Hog Island (Table 1). The rescaled dune recovery time \({\overline{T}}_{{\rm {r}}}^{+}\) over the phase curve (solid line) shows the critical slowing down of the dynamics as it approaches the critical transition to the low-barrier state, represented qualitatively by a tipping point. b–e Approximate basin of attraction of the two most probable equilibrium elevations, the mean maximum dune height \(\overline{H}\) and the mean base elevation \({\overline{h}}_{0}\), represented by the inverted PDF fh(h) and interpreted as a potential function44.

Full size image

More generally, by only decreasing \({\overline{h}}_{0}\), SLR effectively increases the rescaled frequency of erosional events (HWEs), decreases the dune recovery time, and thus drives a potentially irreversible transition to the ‘barren’ equilibrium state. As shown in Fig. 5, this shift in barrier equilibrium can take place in a couple of decades, which is almost certainly an underestimation because we are ignoring the expected increase in the frequency of wave-driven coastal flooding8.

Critical transition in barrier islands’ dune ecosystem

The loss of coastal dunes and the transition to a barren state, driven by changes in the rescaled frequency of HWEs (\({\lambda }_{0}^{+}\)) and exemplified by the phase curve in Fig. 4, is an example of critical transition in a complex stochastic system44 (Fig. 5). As the mean base elevation of the barrier decreases with SLR, \({\lambda }_{0}^{+}\) increases and external fluctuations in HWEs, and the internal randomness in the underlying morphology, force the barrier to explore different elevations at different frequencies. The frequencies are given by \({f}_{h}(h| {\lambda }_{0}^{+}(t))\) if changes are slow enough for the system to remain close to the equilibrium state, and can be used to infer the basin of attraction of the two main equilibrium elevations44 (Fig. 5b–e): the mean base elevation \({\overline{h}}_{0}(t)\), itself a function of time via SLR, and the mean maximum dune height \(\overline{H}\), which is selected by the interaction of the dune-building plant ecosystem and shoreline-related abiotic stressors34. As \({\overline{h}}_{0}(t)\) approaches the 0.5 m threshold suggested by the data (\({\lambda }_{0}^{+}\approx 20\)), the basin of attraction of \(\overline{H}\) becomes shallower and the recovery time greatly increases, in what is called a critical slowing down (Fig. 5d). For even lower values of \({\overline{h}}_{0}(t)\), the dune basin of attraction essentially disappears and the barrier crosses a tipping point with its state relaxing towards the ‘barren’ equilibrium as eroded dunes cannot recover (Fig. 5e). This stochastic picture both formalizes and generalizes a previous interpretation of barrier dynamics as bi-stable1 which is not a suitable description of a stochastic system.

In this context, the rescaled dune recovery time \({\overline{T}}_{{\rm {r}}}^{+}\)33, interpreted as the average time to escape the low-elevation basin of attraction, provides a metric to evaluate the critical slowing down that characterizes the system close to the tipping point44 and can thus formally describe the barrier’s resilience.

Implications for our understanding of barrier dynamics

Barrier islands and the dune and dune ecosystems on them are very complex systems coupling water and wind-driven sediment transport into the dynamic of different plant ecosystems under the influence of tides, waves, wind, and storms16. Here we showed that, in spite of this complexity, barrier elevation can be well described by a relatively simple physics-based stochastic model in terms of a few basic parameters: the frequency and average intensity of high-water events, the dune growth rate, the maximum dune height and the base elevation after an overwash. The last three, in particular, capture the complexity of the system in different ways. The alongshore distribution of the maximum dune height captures the morphology of mature dunes along with the eco-geomorphic processes controlling it, including the type and characteristics of ‘dune-building’ vegetation and the effects of shoreline change. Similarly, the alongshore distribution of the base elevation captures the outcome of overwashes, beach berm’ dynamics, and any preexisting morphology. Finally, the island-based maximum dune growth rate contains all the spatiotemporal complexity of sand transport, including sand availability, taking place on the bare surface between the shoreline and any dense vegetation layer. Interestingly, the apparent randomness of the alongshore distribution (over large enough spatial scales) suggests that only the mean values (for both maximum dune height and base elevation) have physical meaning and that minor alongshore variations due to the spatial complexity of the underlying processes can be characterized as random noise. This is in contrast to other approaches attempting to correlate all the details of the alongshore variation of dune and barrier morphology to many potentially relevant parameters acting over relatively small spatial scales45,46.

It is important to emphasize that the predictions from the stochastic model concern only the steady state of barrier elevation and not the barrier’s current state. A barrier can be classified as ‘barren’ based on the estimated control parameters and still have well-developed dunes (or vice versa). However, such a barrier would lack resilience since dunes cannot recover after erosion and thus, by definition, the barrier would remain barren. In this context, the very large return period of the extreme events (e.g. large storms) needed to completely erode meters-tall dunes can prove misleading because the relaxation to the ‘barren’ equilibrium can be greatly accelerated by shoreline erosion, which can erode dunes at a much faster rate. Shoreline erosion can then ‘push’ the system into the ‘barren’ equilibrium made possible by passive inundation under SLR, in which case we would expect more barren barriers in regions with larger erosion rate47,48. This mechanism would connect barrier resiliency to the local underlying geology and erosion rates48,49.

The barrier elevation state is also closely related to its migration rate, as a barrier in a ‘high’ state would barely migrate, essentially shrinking and sinking under SLR (albeit with considerable internal reorganization) until potentially transitioning into the ‘barren’ state where it would experience a maximum migration rate function of the underlying geology50. In fact, under some approximations, the solution of the stochastic model can be used to estimate the average overwash-driven sand flux across a barrier island33. This could improve the predictions of large-scale coastal models that don’t resolve the actual dune dynamics and could allow us to better understand the effect of the expected acceleration in barrier migration on the overall barrier system26,51. Therefore, although the transition into a ‘barren’ state does not necessarily lead to drowning, because a barrier island lacking dunes can still have a large marsh platform that prevents it from becoming a submerged shoal (as is the case with most of the barren islands in the VBI), identifying a change in barrier equilibrium from a ‘high’ to the ‘barren’ state could be the very first indication of a broader shift in the global coastal system.

Note that the stochastic model is not applicable to natural systems that violate the model’s assumptions, in particular where dunes are not eroded down to the base elevation when high water events (HWE) exceed the dune crest, or where the dune growth rate strongly changes spatially. These could include wide barriers with relatively complex and large dune systems, and barriers exhibiting spatially complex beach armoring. However, the model should capture the stochastic dynamics of the most narrow single-dune barriers, which are also the most vulnerable ones.

Placing barrier islands in the broader class of (eco)systems undergoing critical transitions52 has the potential to advance the theoretical understanding of coastal dynamics at different spatial and temporal scales, and lead to simpler large-scale coastal models suitable for inclusion into Earth system models53 and models coupling human-coastal system to natural and socioeconomic drivers54,55.

Methods

Extraction of alongshore barrier elevation data

Digital elevation models (DEM) of the Virginia barrier islands for three different years (2014, 2016, 2017) were obtained from the USGS Lidar scans (www.ncei.noaa.gov/maps/bathymetry/). The data, originally referred to as the NAVD88 datum, was shifted relative to a representative value of the beach elevation, 1.5 m, obtained from the analysis of high water events (HWEs) and related to the average wave run-up35. We use this reference beach elevation as an unbiased way to define the body of the islands that naturally excludes the back-barrier marshes and other low-elevation features unrelated to wave-driven transport (Supplementary Fig. 1). Homogeneous parts of each island were considered to ensure a stationary process with the help of features present in the DEM, for e.g. Metompkin island was split into two portions since the southern portion of the island presents a partial dune system whereas the northern portion lacks any dunes. Islands where shrubs were exposed to the shoreline due to coastal erosion were not considered for the analysis. Cross-shore lines were constructed on natural portions of the selected barrier islands at a constant spacing of 10 m using GIS software. For each cross-shore line (alongshore position y) and year (t), the barrier elevation h(y, t) was extracted as the maximum elevation along the cross-shore profile. Therefore, the alongshore elevation profile h(y, t) includes all possible features in the barrier island: beach berms, overwash fans, primary dunes (or foredunes), and secondary dunes. For narrow islands (i.e. islands without secondary dunes) this method extracts the dune height without the complexity involved in the precise determination of the foredune crest56. By definition a positive elevation (h(y) > 0) means the feature at y is above the reference beach elevation.

Steady-state point PDF

From the stochastic point model in ref. 33, the steady-state PDF of the rescaled barrier elevation ξ is

$${f}_{\xi }(\xi )={\left(\int_{\!\!\!\!{0}}^{1}\frac{\phi (\xi )}{1-\xi }{\rm {d}}\xi \right)}^{-1}\frac{\phi (\xi )}{1-\xi }$$
(M1)

where

$$\phi (\xi )=\exp \left[-{\lambda }_{0}^{+}{{{{\rm{e}}}}}^{-\frac{1}{{\overline{S}}^{+}}}\left({E}_{i}\left(\frac{1}{{\overline{S}}^{+}}\right)-{E}_{i}\left(\frac{1-\xi }{{\overline{S}}^{+}}\right)\right)\right].$$
(M2)

and the exponential integral is \({E}_{i}(x)=-\int_{-x}^{\infty }{x}^{-1}{{{{\rm{e}}}}}^{-x}{{{\rm{d}}}}x\).

The PDF fξ(ξ) has a minimum at \({\xi }_{\min }={\overline{S}}^{+}\ln {\lambda }_{0}^{+}\) and, therefore is, strictly bimodal for \(0 \, < \, {\xi }_{\min } < 1\).

Mean dune recovery time

The rescaled mean dune recovery time \({\overline{T}}_{{\rm {r}}}^{+}\) is defined as the mean excursion time below the minimum of the steady state (\({\xi }_{\min }\)) divided by the dune formation time Td. From33

$${\overline{T}}_{{\rm {r}}}^{+}=\frac{1}{\phi ({\xi }_{\min })}{\int}_{\!\!\!\!{0}}^{{\xi }_{\min }}\frac{\phi ({\xi }^{{\prime} })}{1-{\xi }^{{\prime} }}{{{\rm{d}}}}{\xi }^{{\prime} }.$$
(M3)

Outside the bimodal region, \({\overline{T}}_{{\rm {r}}}\equiv 0\) when fξ has a single high-elevation mode (\({\xi }_{\min }\le 0\) for \({\lambda }_{0}^{+}\le 1\)), and \({\overline{T}}_{{\rm {r}}}\to \infty\) when fξ has a single low-elevation mode (\({\xi }_{\min }\ge 1\) for \({\lambda }_{0}^{+}\ge {{{{\rm{e}}}}}^{1/{\overline{S}}^{+}}\), white region in Fig. 4).

Estimation of model parameters: base elevation

At the steady state we expect the PDF fs of stable elevations to be approximated as \({f}_{{\rm {s}}}(h)={a}_{0}{{{{\mathcal{N}}}}}_{{h}_{0}}(h)+(1-{a}_{0}){{{{\mathcal{N}}}}}_{N}(h)\) with normalization constant a0. This constant depends on the relative contribution of dune growth and erosion in the resulting stochastic dynamics, such that a0 ~ 0 when erosional processes dominate whereas a0 ~ 1 otherwise. However, the complexity of barrier island dynamics and the fact that elevation data for the rate calculation is three years apart, and therefore we are sampling over several realizations of the stochastic process, imply that deviations from the ideal form of fs are to be expected (Fig. 2).

In spite of the inherent uncertainty of this method, fitting fs by two Gaussians seems to capture the distribution \({{{{\mathcal{N}}}}}_{{h}_{0}}\) of base elevations, and thus \({\overline{h}}_{0}\) and \({\sigma }_{{h}_{0}}\), relatively well (solid red lines in Fig. 2). Indeed, for the ‘barren’ barriers (Cedar, North Metompkin and Smith) the corresponding mean base elevation \({\overline{h}}_{0}\) reproduces the lower (beach berm) equilibrium of barrier elevation, defined by the conditions G = 0 and \({G}^{{\prime} } < 0\) on the average growth rate function G(h) (red dots in Fig. 2a, b and c), and the growth rate can be well approximated by the linear function \(G(h)=({\overline{h}}_{0}-h)/\Delta t\), with Δt = 3 years (black dashed lines in Fig. 2a–d).

In Hog and Parramore, \({\overline{h}}_{0}\) correspond to a local minimum of G(h) (red dots in Fig. 2d and f), similar to South Metompkin (Fig. 2e).

The larger standard deviation for South Metompkin (Table 1) is due to the presence of several overwash fans with a relatively complex morphology as compared with the more uniform beach berm morphology in ‘barren’ barriers (Supplementary Fig. 1).

Estimation of model parameters: maximum dune height

The extraction of the distribution of maximum dune elevations \({{{{\mathcal{N}}}}}_{H}\) is more challenging as not all barriers have well-developed dunes. For Hog and South Metompkin, fs peaks at elevations  ~2 m and can be used to estimate \({{{{\mathcal{N}}}}}_{H}\), and thus \(\overline{H}\) and σH (blue lines in Fig. 2k and l). The other islands do not have a well-developed dune system and, therefore, the fitted higher elevation Gaussian (gray lines in Fig. 2g, i and j) cannot be used to properly estimate \({{{{\mathcal{N}}}}}_{H}\). Interestingly, the value \(\overline{H} \sim 2\) m from Hog is consistent with the dune stable equilibrium in Smith (blue dot in Fig. 2c), defined by the conditions G = 0 and \({G}^{{\prime} } < 0\) on the average growth rate function G(h) (solid black line in Fig. 2c).

In general, for islands other than Hog or South Metompkin, \(\overline{H}\) and σH are approximated by their values for Hog, which is assumed to be representative of a well-developed dune system in the region. For Parramore, we assume \(\overline{H}\) can be approximated by the dune equilibrium elevation (blue dot in Fig. 2d) and use the standard deviation of the fitted higher elevation Gaussian (gray line in Fig. 2j) as an approximation for σH.

Note that the larger standard deviation for South Metompkin (Table 1) reflects a complex morphology with primary and secondary relic dunes (Supplementary Fig. 1), which are included in the way we define the barrier elevation data. In contrast, the relatively narrow distribution in Hog reflects its single and relatively uniform dune ridge (Supplementary Fig. 1).

Estimation of model parameters: maximum dune growth rate

We estimate the maximum dune growth rate Gd as the average of the ten highest growth rates (excluding the maximum) for initial elevations above the typical beach berm (approximated here as 0.4 m) where the potential availability of dry sand and the presence of vegetation allows dune building (red dashed lines in Fig. 2a–f).