Introduction

Speleothems (secondary cave carbonates) are excellent climate archives that have high dating potential and provide a growing range of climate proxies, including trace elements1. Trace elements can be challenging to interpret, and a good understanding of how speleothems form, which processes may affect drip water and speleothem composition, and the source(s) of trace elements are essential for correct assignments of environmental processes to element dynamics. Drip water originates from rainfall that infiltrates the soil where it dissolves gaseous CO2 and forms carbonic acid. This is where drip water can leach trace elements from soil components, clay minerals, and other sediments2,3. The carbonic acid further dissolves the carbonate hostrock (usually limestone or dolostone) up to the point, when the drip water CaCO3 saturation index reaches zero. Host rock composition and mineralogy are other important factors affecting the drip water trace element composition4,5,6. When this drip water comes in contact with air that has a lower partial CO2 pressure than the drip water, CO2 starts to degas leading to supersaturation of the drip water with respect to carbonate and secondary CaCO3 precipitation. In principle, this can occur anywhere along the water flow path within the epikarst, fissures / cracks in the host rock, at the cave ceiling, or at the stalagmite surface. When CaCO3 precipitation occurs before the drip water reaches the stalagmite surface, the process is referred to as prior carbonate precipitation4 (PCarbP). PCarbP is expected to increase under drier conditions when infiltration decreases, which may result in lower drip rates and thus more time for CO2 degassing. The volume of air-filled voids within the epikarst/host rock may also increase under drier conditions. PCarbP affects drip water trace element to Ca ratios (Me/Ca) as the precipitated carbonate incorporates trace elements disproportionately with respect to Ca. PCarbP is the most often invoked process to link speleothem trace element (Me) variability to effective rainfall7,8,9,10,11,12,13. However, drip rate is not the only process controlling PCarbP, as changes in soil and cave air pCO2 might also be important as they exert control on the amount of CO2 that can degas from the water.

The uptake of Me from the drip water with respect to Ca by the CaCO3 precipitate is described by the trace element partitioning coefficient, i.e., DMe = (Me/CaCarbonate)/(Me/CaDrip water)14. Qualitatively, it is critical to know whether DMe is above or below one as this determines whether drip water Me/Ca ratios increase or decrease in relation to enhanced PCarbP. Quantitative approaches that can assess the effects of PCarbP on drip water and speleothem Me/Ca ratios require accurate values of DMe. Owen et al.15 developed CaveCalc as a tool to model the effects of PCarbP and Stoll et al.16 developed the Excel-based model “I-STAL”. Sinclair et al.17 found that a regression line through a log-log scatterplot of ln(Mg/Ca) versus ln(Sr/Ca) (drip water or speleothem) should have a slope of ca. 0.88 to indicate PCarbP. The slope can be directly derived from the trace element partitioning coefficients: s = (DSr−1)/(DMg−1). The uncertainty of this slope depends entirely on how well the DMe is constrained. Recently, Wassenburg et al.6 showed that PCarbP can be identified with variable slopes, ranging from 0.709 to 1.45. Examining and refining DMe, is thus essential to accurately identify PCarbP. Furthermore, when drip water Me/Ca ratios can be linked to drip rate through PCarbP, and drip rate can be linked to infiltration, refined DMe values may allow quantification of infiltration from speleothem trace elements.

The above-mentioned studies focused mostly on the effects of prior calcite precipitation (PCP). However, crystal structures and, thus, DMe differ between the two dominant mineralogies found in cave environments (calcite and aragonite). The two modes (1) PCP16,17 and (2) prior aragonite precipitation (PAP)18,19,20,21 thus affect drip water Me/Ca ratios differently. DMe of the larger cations U and Sr are >1 for speleothem aragonite20, but <1 for calcite6,22. The small Mg ion is excluded from both mineral phases, albeit much more so by aragonite. Therefore, increased PCP results in higher drip water Mg/Ca, Sr/Ca, and U/Ca ratios, whereas increased PAP leads to lower drip water Sr/Ca and U/Ca ratios, but higher Mg/Ca ratios. Increased PCP may also lead to higher drip water Ba/Ca ratios, but the effect of PAP on drip water Ba/Ca remains to be determined. Available estimates of speleothem aragonite partitioning coefficients range from 0.61 to 1.4820.

According to ref. 23, aragonite precipitation may occur in karst environments where drip water Mg/Ca ratios are high (>0.5), drip water pH is above 8.2, and the saturation index with respect to calcite is relatively low (<0.8). Caves overlain by dolostone or mixed limestone/dolostone bedrock are associated with high drip water Mg/Ca ratios, and such settings are conducive for both PCP and PAP. Other potentially important processes that affect drip water Me/Ca ratios include chemical weathering of silicate minerals, changing element sources24, water residence time in the karst aquifer4, and element transport25 and incorporation26 mechanisms. In this study, we focus on PCarbP as it is one of the most significant mechanisms that modifies drip water Me/Ca ratios.

We analyze drip water samples for Ca, Mg, Sr, Ba, and U concentrations collected in Grotte de Piste, Morocco, where both calcite and aragonite speleothems form27,28. The studied drip site is characterized by seasonally varying drip rates. Previous low-resolution cave monitoring data collected between January 2010 and August 2012 indicate some PCarbP signatures28. Here we use a high-resolution (i.e., 2–4 days) drip water trace element dataset to estimate aragonite DMe and identify a trace element(s) that reliably tracks PCarbP variability in aragonite speleothems. We derive an aragonite DSr value of ca. 1.31 ± 0.11 and a DU value of 1.76 ± 0.57, consistent with previous estimates20. Interestingly, the DBa value for aragonite mineralogies may have switched from >1 to <1 at this drip site. Precipitation rate seems to exert an important control on aragonite DBa, supporting the results from ref. 29. For aragonite speleothems that form under relatively constant drip rates and low aragonite SI drip waters (SIAr « 0.38), aragonite DBa < 1. Such samples may preferentially form under seepage flow drip sites and are ideal candidates to faithfully record PCarbP with its Ba concentrations because both calcite and aragonite DBa < 1. However, it is important to consider where PCarbP takes place. Higher carbonate precipitation rates occur when the CO2 partial pressure difference between drip water and air is large, which is more likely at the cave ceiling compared to the epikarst/aquifer environment above the cave. Furthermore, drip rate variations can control precipitation rates on the stalagmite surface. The Ba concentration in an aragonite speleothem will thus depend on (1) DBa for PCarbP occurring in the epikarst/aquifer above the cave, (2) DBa for PCarbP at the cave ceiling, and (3) DBa on the stalagmite surface in relation to drip-rate. If the speleothem precipitated from low CaCO3 supersaturated drip water, then the calcite and aragonite DBa values are similar, and Ba is the element least affected by the PCarbP mode and speleothem mineralogy.

Results and discussion

Setting

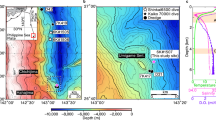
The cave site, Grotte de Piste, Morocco8,27,30, is located in the Middle Atlas mountain range (34°N, 4°W; Fig. 1), a region characterized by a Mediterranean climate with wet winters and dry summers. Local bedrock is characterized by Jurassic dolostones with limited limestone intervals27 resulting in high drip water Mg/Ca values. Both calcite and aragonite speleothems, as well as calcite–aragonite alternations within single speleothems, have been observed in this cave27,28. The studied drip site (GP14) has ca. 35–40 m of host rock overburden and is associated with aragonite stalagmite GP5, for which Mg, Sr, δ18O, and δ13C data were published earlier28,31. A stalactite was present above stalagmite GP5 but unfortunately broke off during the first attempt to collect drip water in 201028.

Fig. 1: Cave setting.
figure 1

Location of Grotte de Piste in the Middle Atlas mountain range of Morocco with 2015 annual rainfall (a) and Grotte de Piste cave cross-section with wet and dry season scenarios and how they affect aragonite DBa (b). The cave is located at 1200 m above sea level.

Full size image

Cave monitoring

For 2010–2012, drip rate, mean drip water pH, and drip water SI values were published in ref. 23, and drip water Mg, Sr, and Ca concentrations in ref. 28. From March 8, 2012, to August 22, 2012, drip rate was monitored with an automatic dripcounter28 (Fig. 2). In response to rainfall events occurring between March 29 and April 13, totaling 153 mm rainfall, drip rate increased from 0.40 drips/min on April 18 to a short-lasting peak of 1.40 drips/min on April 25 followed by a slow return to 0.40 drips/min 18 days later. The last rainfall event that year was on May 25, and the drip site dried out on August 8. The short-lasting peak in drip rate suggests that this drip site is partly fed by fracture flow. For determining rainfall amount thresholds to activate fracture flow or to determine water residence times, the drip counter would be required to remain installed over a longer period. With the data at hand, we characterize this drip site as seasonal with a quick response to a series of rainfall events.

Fig. 2: Monitoring data.
figure 2

Relation between cave air temperature, drip rate, rainfall (a), drip water Ca concentrations (b), and 234U/238U activity ratios (c). Drip rates represent an average value of 3 single measurements. Ca concentrations in b are monthly mean values based on 5–8 samples. Ca concentrations and U-isotopes in c represent individual samples. Ca concentrations were measured with ICPMS. Error bars in b are 1 standard deviation. In c the error bar for Ca is 1 RSD; for 234U/238U it is the absolute error. The data can be found in Table S1.

Full size image

Cave air temperature at the drip site shows seasonal changes with 12 °C during winter and 13 °C in summer from 2010 to 2012 (ref. 28, Fig. 2). The winter of 2015 was cooler by ca. 1 °C, but summer was similar to 2010–2012 (Fig. 2). CO2 concentrations vary between 450 and 4000 ppmv at the cave bottom, but are relatively stable at the drip site year-round at 666 ± 151 ppmv between 2010 and 201228. This is related to the drip site position on a higher level within Grotte de Piste.

From the end of February to June 2015, we used an automatic sampler to collect drip water samples every 2–4 days for subsequent trace element analysis. For the dry season between June and October 2015, one sample represents 10 days of collection. A total of 31 drip water samples were collected. The sampling period covers the transition from the wet winter to the dry summer season. Drip rates were recorded manually at bi-weekly intervals, but are presented as monthly means. For selected drip water samples (n = 10), we also analyzed the U isotope composition to assess potential changes in water residence times in the aquifer/epikarst.

Evidence for PCarbP

The presence of a stalactite above stalagmite GP5 is the first indication for PCarbP at drip site GP14. Changes in PCarbP can occur when infiltration of rainwater is variable, for example in response to rainfall seasonality. Lower drip rates due to reduced infiltration are expected to be associated with enhanced PCarbP. Enhanced PCarbP results in lower drip water Ca concentrations, which may explain the strong positive correlation with drip rate (r = 0.996, p < 0.01; Fig. 2b). Enhanced PCarbP is also expected when water residence times increase. A potential proxy for water residence time is U-isotopes because 234U is more easily leached from the bedrock compared to 238U due to the alpha-recoil effect during the decay of 238U2. Longer water residence times can thus lead to higher drip water 234U/238U ratios. We selected drip water samples with high and low Ca concentrations, corresponding to high and low drip rates, and observed a negative correlation between drip water Ca concentration and the 234U/238U ratio (Fig. 2c). This suggests that indeed, lower drip rates are associated with longer water residence times, and that PCarbP is a potential mechanism to explain the drip water Me/Ca ratios.

The effect of PCP on drip water Mg, Sr, Ba, and U concentrations is small because calcite DMg and DSr are considerably smaller than one. This results in a near vertical slope when plotting the modeled Ca vs Mg, Sr, Ba, and U drip water evolution for a PCP-dominated scenario (Fig. 3a–d). Considering analytical uncertainties for Mg, Sr, Ba, and U, the high Ca drip waters (>0.8 mmol/L) might be explained by PCP. However, we also observe a strong positive correlation between Ca and Sr for samples with Ca < 0.65 mmol/L (r = 0.99; p < 0.01; Fig. 3e), which warrants a more elaborate discussion.

Fig. 3: Drip water trace element concentrations compared to PCarbP evolution lines.
figure 3

a Ca vs Mg, b Ca vs Ba, c Ca vs Sr, d Ca vs U, all error bars are 1 RSD. Blue datapoints are affected by PCP, green data points are affected PAP. The continuous and dashed lines correspond to the evolution of the drip water composition as a consequence of PCP and PAP. The 2 standard errors of the slopes of the trendlines in e (Sr vs Ca) and f (U vs Ca) are 0.032 and 0.28. We use calcite DMg, and DSr from ref. 6, taking into account the effect of high calcite Mg/Ca ratios on calcite DSr, and temperature on calcite DMg. Calcite DBa and DU are from ref. 22. The aragonite DSr and DU values are from this study, 1.31 and 1.76, respectively. Since there is a switch from PCP to PAP in the epikarst/aquifer or at the cave ceiling and initial concentrations may not be constant, we select the drip water element composition of the sample with the highest Ca concentration for the group with Ca < 0.65 mmol/L as a starting point for the PAP model. The approach used to model the evolution of the drip water composition is described in the methods section. In b the red dashed ellipse indicates drip water samples affected by PAP with SIAr > 0.38. The data can be found in Tables S2 and S3.

Full size image

Different modes of PCarbP have been used to explain speleothem trace element concentrations, i.e., PCP and PAP18,21,28. These modes affect drip water Sr concentrations differently because aragonite DSr is close to one or larger20 and calcite DSr is much smaller22. PAP thus not only depletes the drip water of Ca but also Sr, explaining the observed positive correlation. Additional evidence for PAP comes from the positive correlation between U and Ca (r = 0.73; p < 0.01; Fig. 3f) for samples with Ca < 0.65 mmol/L. Similar to aragonite DSr, aragonite DU is larger than one20. PAP thus also explains the observed positive correlation between Ca and U for samples with Ca<0.65 mmol/L. Having established the presence of PAP for samples with Ca < 0.65 mmol/L, it appears that PAP does not affect Mg concentrations, nor does it dominate drip water Ba concentrations. Though this is expected for Mg as aragonite DMg is far below one20, the effect of PAP on Ba requires a detailed discussion. Overall, this high-resolution drip water dataset reveals a bimodal PCarbP behavior at a single drip site.

Factors controlling CaCO3 mineralogy

The switch from PCP to PAP along the water flow path can occur as a response to the changing drip water chemistry related to progressive PCarbP. From lab-controlled carbonate precipitation experiments, solution parameters that are suggested to control the mineralogy include Mg/Ca ratios32,33, temperature34, organic compounds35, drip water carbonate ion contents/pH36, and calcite saturation index (SICc)37. These factors were discussed in several studies23,37, but our data can provide new constraints on this topic.

Drip water Mg/Ca might be the most often invoked parameter to explain aragonite precipitation under atmospheric pressure conditions, and many lab-controlled experiments induce aragonite precipitation by increasing the Mg/Ca ratio of the solution. The presence of Mg2+ has been suggested to inhibit the precipitation of calcite by a so-called “template effect”32, or by the higher desolvation energy that is required for Mg compared to Ca38. Therefore, at a certain solution Mg/Ca ratio, the calcite saturation index becomes lower than for aragonite, which results in a switch to aragonite precipitation. Since the aragonite DMg value is at least one order of magnitude lower compared to calcite DMg, aragonite only incorporates very little Mg into its crystal lattice. It may thus be inferred that the aragonite saturation index is not affected by an increase in solution Mg/Ca ratios. However, there is a range of Mg/Ca ratios at which both calcite and aragonite may precipitate in cave environments (Fig. 4) indicating that Mg/Ca ratios are not the sole factor to control mineralogy.

Fig. 4: Occurrence of calcite and aragonite with respect to drip water Mg/Ca and calcite saturation index (SICc).
figure 4

Drip water SICc for GP-DR14 2015 was derived from a regression equation between drip water Ca concentration and SICc for the cave monitoring period 2010–2012. Earlier published drip water data from Natural Bridge Caverns58 (NBC1 and NBC2), Soreq Cave59 (SC), Père Noël Cave60 (PNC), DeSoto Caverns39 (DSC), Hollow Ridge Cave5 (HRC), Grotte de Clamouse61, Obstanser Eishöhle41, El Soplao and Torca Ancha Caves40, Heshang Cave62 (HS4 drip site) and Grotte de Piste23 are shown. Error bars on data from ref. 23 are 1 SD, and for GP-Dr14-2015, error bars are arbitrarily set to 0.1. The data can be found in Table S1.

Full size image

Ref. 37 clearly highlights the importance of the solution SICc as a contributing parameter, in addition to solution Mg/Ca. With higher SICc values, a higher Mg/Ca ratio is required to precipitate aragonite. We plotted the “aragonite only” and “1st occurrence of calcite” zones from ref. 37 and compared these with a compilation of data from cave environments to gain insight on what controls the CaCO3 mineralogy (Fig. 4). Within the “1st occurrence of calcite” zone, where ref. 37 provides only limited data, cave mineralogies are exclusively aragonite when SICc < 0.5. To provide SICc estimates for the 2015 drip waters, we use a linear regression between 2010 and 2012 drip water SICc23 and Ca concentrations (Table S1). This approach is supported by the strong positive correlation between SICc and Ca (r = 0.95, p < 0.01). We observe that the switch from PCP to PAP occurs very closely to the “aragonite only” boundary, which confirms the important role of the balance between drip water SICc and drip water Mg/Ca in determining the precipitating CaCO3 polymorph. In addition, we plot the range and mean Mg/Ca drip water for other published drip sites, for which the associated mineralogies are known, but no SICc is available. The highest mean drip water Mg/Ca ratio is associated with an aragonite stalagmite39, although other drip sites may temporarily have higher drip water Mg/Ca ratios. This may be explained by two reasons: 1) the calcite precipitated from drip waters with high SICc, or 2) the drip waters only maintained high drip water Mg/Ca ratios for a time-interval that is too short to initiate aragonite precipitation on a calcite substrate.

In addition to drip water Mg/Ca and SICc, temperature34 and drip water pH36 have been suggested to be important parameters. Higher temperatures and higher pH are suggested to be more favorable for aragonite precipitation. Higher pH results in a higher concentration of carbonate ions in the water, allowing for higher precipitation rates, that potentially induce aragonite precipitation36. Therefore, we plotted the same drip sites as in Fig. 4 (except for our 2015 drip waters) with drip water Mg/Ca, pH, and temperature (Fig. S1). In cave monitoring data, we observe an increased occurrence of aragonite with higher drip water pH. However, some of the laboratory experiments37 produce aragonite at much lower pH values of around 7.5 (Fig. S1) or even 6.3 (Table 1). The role of pH in CaCO3 polymorphism was also debated in ref. 40, which mentions that carbonate ion content is not only a function of drip water pH, but also total carbonate alkalinity. Another explanation for the observed relation between Mg/Ca and drip water pH in Fig. S1 is the inhibition of calcite precipitation with increasing drip water Mg/Ca allowing the drip water pH to increase further as a consequence of CO2 degassing. There is no clear evidence for a causal relation between drip water pH and aragonite precipitation. The role of temperature is also unclear, as aragonite actively precipitates at 0 °C in Obstanser Eishöhle, Austria41, but equally at 20 °C in laboratory experiments and subtropical caves, like Yok Balum, Belize42. A potential effect of organic compounds35 might explain aragonite precipitation at drip water Mg/Ca ratios as low as 0.5 mol/mol23.

Table 1 Overview of aragonite partition coefficients
Full size table

Within the cave environments presented in Fig. 4, the occurrence of aragonite seems at least partly linked to drip water Mg/Ca and SICc. PCarbP seems to be an important process as it affects both parameters. Progressive PCarbP lowers Ca concentrations and the calcite saturation index, but results in higher drip water Mg/Ca ratios. We suggest that the balance between Ca concentration (and SICc) and drip water Mg/Ca are the most important parameters for aragonite precipitation at drip site GP14. An important implication is that the amount of PCP required to induce PAP may change with either the initial drip water Mg/Ca or the initial SICc. Either way, a clear distinction can be made between the wet season, which is associated with faster drip rates and is dominated by PCP, and the dry season, associated with PAP.

Aragonite partition coefficients

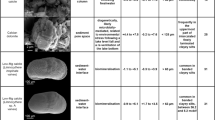
A vast body of literature on aragonite DMg, DSr, DBa, and DU has been published20,29,43,44,45,46,47,48,49,50,51 (Table 1). The laboratory experiments with low SI solutions29,44,51,52 generally agree that carbonate precipitation rates are an important parameter for DMe. Higher precipitation rates decrease DMe for lattice-compatible elements and vice versa for lower precipitation rates29,44. The solution composition may equally influence the DMe values, whereas solution pH will affect the speciation and desolvation (dehydration of aqueous elements). Here we provide new aragonite DSr and DU values and discuss the effects of PAP on drip water Sr, Ba, and U concentrations and Me/Ca ratios.

Aragonite D Sr

To ascertain that we discuss samples dominated by changes in PAP and not PCP, we use a Ca concentration of 0.65 mmol/L to distinguish between PAP and PCP-dominated drip water data. This threshold is based on the occurrence of the strongest positive correlation between Sr and Ca. The aragonite partition coefficient can be assessed by plotting the trace metal concentration on the y-axis and the Ca concentration on the x-axis for samples with Ca < 0.65 mmol/L (Fig. 3e). The slope of the linear regression line represents the Me/Ca change as a result of PAP. Dividing the slope by the mean drip water Me/Ca value gives the partition coefficient28:

$$S={dy}/{dx}$$
(1)
$$S={{\rm{Me}}/{Ca}}\left({\rm{Solid}}\right)$$
(2)
$${D}_{{\rm{Me}}}={{\rm{S/Me/C{a}}}}_{({{\rm{Solution}}})}$$
(3)

with “S” standing for “slope of linear regression line”. In Figs. 5 and S2, we show that this approach is applicable as long as DMe < 2, f > 0.4, and the range of the fraction of Ca (f) for the relevant drip water data is not too large. For small fractions of Ca remaining in the solution, this approach is not suitable as the slope of the modeled drip water evolution line changes too rapidly with the fraction “f”. For high DMe values, the slope is changing too rapidly as well. Additionally, the uncertainty of the slope of a linear regression line is larger than the standard deviation of the slope from the modeled drip water evolution lines. For example, the correlation between Sr and Ca concentrations in our dataset is exceptionally strong for Ca < 0.65 mmol/l, which results in a relatively small slope uncertainty (0.443 × 10−3 ± 0.016 × 10−3). However, even this small uncertainty is still large enough to induce considerable overlap with the average slope of the modeled PCarbP evolution lines for the same range of “f” (0.436 × 10−3 ± 0.169 × 10−4). Propagating the uncertainty of the linear regression (σ1) into the DMe uncertainty together with analytical uncertainties for Me (σ2), Ca (σ3), and the standard deviation derived from all PAP-affected drip water Me/Ca ratios (σ4), results in a conservative error estimate:

$$\Delta {D}_{{\rm{Me}}}={D}_{{\rm{Me}}}* \sqrt{{\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3}+{\sigma }_{4}}$$
(4)
Fig. 5: Modeled slopes of regression lines through Me to Ca plots as a consequence of PCarbP with respect to “f”, the fraction of Ca remaining in the drip water.
figure 5

Different partitioning coefficients and Me/Ca ratios were used (a–c). d Assessment of the potential offset between the real DMe and the calculated apparent DMe using the approach described in the paragraph “Aragonite DSr” if the estimated value of “f” is incorrect. We used a fixed Me/Ca ratio that corresponds to f = 60%. The real DMe is indicated by the point where the black dashed line (f = 60%) crosses the modeled apparent DMe. For a small range of “f” of ca. 20% and DMe < 2.0 the offset between the apparent DMe and the real DMe is relatively small. For example, if “f” is not 60% but 70% and the real DMe = 2.0, the apparent DMe = 2.3. The data can be found in Table S4.

Full size image

The aragonite DSr provided by this method is 1.31 ± 0.11. Our PCarbP model6 driven by the above mentioned DMe shows an approximate range of drip water Sr and Ca concentrations that can be explained by PAP. This exercise exemplifies the different effects of PCP and PAP on drip water Sr concentrations (Fig. 3c).

The DSr value derived here is 1.31 and agrees well with the previous estimate of DSr = 1.38 ± 0.53 (ref. 20). However, the aragonite DSr value from ref. 20 was calculated using a calcite DSr of 0.12 and the trace element concentrations of the calcite and aragonite transition within individual speleothems. Ref. 6 showed that calcite DSr depends on the calcite Mg/Ca ratio, but this effect was not accounted for in ref. 20. Recalculating the aragonite DSr value with a Mg/Ca-corrected calcite DSr and the same calcite to aragonite transitions gives a DSr value of 1.75 ± 0.67. This agrees within error with the present study and the formerly published value of 1.38, increasing confidence in our results. All of these values are >1 and higher than most laboratory precipitation experiments45,46,47,48. Brazier et al.44 confirmed the notion from ref. 20 that aragonite DSr depends on precipitation rates, with lower rates associated with higher aragonite DSr. The generally higher published aragonite DSr for cave environments can thus be explained by lower precipitation rates.

Aragonite D U

Although a positive correlation between Ca and U for samples with Ca < 0.65 mmol/L is an indication that PAP affected drip water U concentrations, the uncertainty in the slope of the trendline through the U vs Ca plot is relatively large compared to Sr. Also, analytical uncertainties in this range of U concentrations are considerably larger than for Sr and should be considered when attempting to derive an aragonite DU value. With the same approach as for aragonite DSr, we estimate a DU value of 1.76 ± 0.57, which is considerably lower but within error with the values suggested by ref. 6 (6.26 ± 4.54) and just below the lower end of ref. 21 (3.74 ± 1.13). Although this study shows once again that aragonite DU in cave environments is higher than one, the low value needs to be discussed.

Aragonite DU has been shown to be related to carbonate precipitation rates50, with higher DU values linked to higher aragonite precipitation rates. Considering that there was a stalactite at the drip site, PAP took place within the cave environment where drip water SIAr is expected to be higher compared to air-filled voids in the epikarst/aquifer. So that would result in higher aragonite DU values and not lower values.

Drip water pH is another factor that can control aragonite DU through U speciation. Ref. 50 discussed that within a pH range of 7.5–8 the CaCO3 preferred U-species (UO2(CO3)3) is most abundant. The studied drip site is characterized by high pH values of 8.5 ± 0.0523, which provides a possible explanation for the lower aragonite DU values. This is supported by the cave analog precipitation experiments from Day et al. with DU of 1.7 at a calculated pH value of 8.3 (see Table 1; personal communication). These results point to the importance of conducting cave monitoring to derive drip site-specific aragonite DU values. To test these effects systematically, cave-analog precipitation experiments are needed to address the large range in cave aragonite DU.

Aragonite D Ba

Ba in aragonite likely replaces the Ca cation within the crystal lattice, and variable incorporation mechanisms probably play only a minor role in determining DBa. Multiple precipitation experiments show that the aragonite DBa value may range from 2 to 3 (refs. 46,48). However, these values were found at high supersaturations. A recent precipitation experiment29 indicates that at low precipitation rates, aragonite DBa can be <1 (i.e., 0.2–0.8). This is supported by theoretical estimates that consider the ionic radius of Ba, giving a DBa value of 0.14 (ref. 49). Extrapolation of the equation from ref. 29 suggests that drip water aragonite saturation indices (SIAr) higher than 0.38 may result in DBa > 1. It is thus important whether PAP dominantly occurs within the epikarst, where SIAr is probably low, or at the tip of a stalactite, where cave ventilation reduces cave air CO2 concentrations, resulting in higher SIAr values. In the case of drip site GP14, where a stalactite was present, SIAr might have been sufficiently high to increase DBa > 1.

Calculations of SIAr from the regression between 2010 and 2012 SIAr and drip water Ca concentrations (Table S1) suggest that in 2015, drip water SIAr varied between 0.45 and 0.32 for PAP-affected drip waters. This implies that aragonite DBa might have switched from >1 to <1 at the cave ceiling. A significant positive correlation can indeed be observed for PAP-affected drip water for SIAr > 0.38 (r = 0.68, p < 0.05, Fig. 3b), but it is unlikely to relate this entirely to PAP because it requires an aragonite DBa of 3.68 ± 1.35 to explain the slope. Overall, Ba/Ca ratios are significantly negatively correlated to the Ca concentration (r = −0.49, p < 0.01) when all drip water samples are considered. This shows that Ba/Ca ratios are at least partly driven by the PCarbP-induced depletion of drip water Ca.

Non-PCarbP processes

Although we focus on PCarbP as a major process affecting drip water trace element concentrations, we observe significant scatter around the PCarbP evolution lines in Fig. 3, which hints at non-PCarbP mechanisms. Separate correlation tables for the drip water samples with Ca > 0.65 mmol/L and Ca < 0.65 mmol/L (Table 2) provide more comprehensive insights at non-PCarbP mechanisms. In PCP-affected waters, Mg, Sr, and U correlate positively with each other, but each element correlates negatively with Ca. At Grotte de Piste the main source of Mg is the dolostone host rock, and we believe this may also be the case for Sr and U. A possible explanation for the positive correlations is selective leaching that may be enhanced with increasing water residence times setting the initial Mg, Sr, and U concentrations. Alternatively, the mixing of waters originating from different flow paths through the aquifer, e.g., fast conduit/fracture flow vs seepage flow might result in different Ca, Mg, Sr, and U concentrations. The latter mechanism has also been invoked to explain some of the Sr variability in stalagmite GP528. Most likely, the negative correlations between this group of elements (Mg, Sr, U) and Ca result from a combination of these processes, with PCarbP being the dominant factor controlling Ca concentrations.

Table 2 Pearson correlations (regular font) with p-values (italics) for trace element concentrations in the drip waters affected by PCP and PAP
Full size table

Barium drip water concentrations seem unrelated to other elements (Table 2) suggesting a different source. Interestingly, Ba soil concentrations are 256–292 ppm, whereas soil Sr concentrations range between 66 and 75 ppm27. As alkaline earth metals, Sr and Ba are likely to behave similarly. Since Sr concentrations in the drip water are higher by one order of magnitude, the host rock clearly has a much lower Ba concentration than Sr. Combined with the lack of a correlation with other elements suggests that the Ba source is the soil above the cave.

Fig. 6: Trace element to Ca ratios compared to PCarbP evolution lines.
figure 6

The continuous lines represent PCP evolution lines. The dashed lines represent PAP evolution lines. Two lines for each PCarbP mode provide a range of values that can be explained by PCarbP. Starting points for the different lines are based on the relative uncertainty of the trace element analysis. a Ca vs Mg/Ca, b Ca vs Ba/Ca, c Ca vs Sr/Ca, d Ca vs U/Ca, all error bars are 1 RSD. The data can be found in Tables S2 and S3.

Full size image

Identification of PCP and PAP in aragonite speleothems

The drip water trace element to Ca ratios and the DMe values determine how speleothem trace element data reflect PCarbP along the water flow path and cave ceiling. To use trace elements from aragonite speleothems for the reconstruction of past hydrological conditions in the epikarst/aquifer, we require an element that responds to PCP and PAP in a similar fashion. In our drip water, the most similar response to PCP and PAP is seen in the Mg/Ca ratio (Fig. 6a). However, since Mg variability in aragonite speleothems depends strongly on carbonate precipitation rates50,51, incorporation mechanisms (detrital components53 vs crystal defect sites51), and effects from Mg-rich primary co-precipitating calcite27, this element is less suitable as infiltration tracer. Sr and U are equally ambiguous since a switch from PCP to PAP will lead to opposite signals in drip water Sr/Ca and U/Ca ratios (Fig. 6c, d). Such a reversal complicates the interpretation of speleothem aragonite trace element changes unless only one PCarbP mode dominates. A suitable parameter that can trace infiltration dynamics seems to be the Ba/Ca ratio. The question is whether an aragonite speleothem would also reflect the drip water Me/Ca ratios, and how PCP can be distinguished from PAP in an aragonite speleothem trace element record.

An important observation is that PCP and PAP occur at relatively high drip water SI values (Fig. 4). This indicates that most of the PCarbP likely occurs at the ceiling of the cave. This is also visible by the former presence of a stalactite above stalagmite GP5. As mentioned above, we suspect that PCarbP in the epikarst above the cave ceiling is limited due to higher pCO2 in air-filled voids vs cave air pCO2.

Speleothem GP5, which formed below the studied drip site, was analyzed for Mg and Sr concentrations in ref. 28,31. The stalagmite record covers the last 1000 years, and the period from 1000 to 1350 AD was interpreted as a “PAP-phase” because Mg and Sr were negatively correlated. As discussed earlier, aragonite Mg incorporation mechanisms are uncertain, and its partitioning coefficient should be used with caution to distinguish PCP from PAP. Here, we present new annually resolved trace element data (Mg, Sr, Ba, U) from aragonite speleothem GP5 (Fig. 7) to elucidate the PCarbP dynamics in Grotte de Piste.

Fig. 7: Speleothem GP5 proxies.
figure 7

Aragonite δ18O (a), and concentrations of U (b), Sr (c), Ba (d), Mg (e), and annual growth rate (f). The green rectangle indicates the period (1140–1364 AD) with a positive correlation between U/Ca and Sr/Ca (g) and a negative correlation between Sr/Ca and Ba/Ca (h). U/Ca and Ba/Ca do not show a strong correlation (i). The data can be found in Table S5.

Full size image

We highlight the period from 1140 to 1364 AD, which is characterized by a positive correlation between Sr and U (r = 0.67, p < 0.01), and a negative correlation between Sr and Ba (r = −0.67, p < 0.01). To identify whether the trace element variability could be explained by PAP, we use the “Sinclair test” with aragonite DSr and DU values that are within the uncertainty of those presented here. The slope of the regression through ln(Sr/Ca) vs ln(U/Ca) is 0.20, which can be reproduced with a DSr of 1.2 and DU of 2.0. The positive correlation between Sr and U cannot be explained by PCP, which would result in a regression slope of ca. 0.98 with calcite DSr of 0.166 and DU of 0.1422. The slope of the trendline through ln(Sr/Ca) vs ln(Ba/Ca) is −0.66, which can be reproduced using aragonite DSr of 1.2 and DBa of 0.7. An aragonite DBa value of 0.7 is realistic for high precipitation rates29. The “Sinclair test” shows that PAP is one possible explanation for the observed correlations between Sr, U, and Ba. However, U and Ba are only weakly correlated (Fig. 7i) which suggests that other processes affect these elements as well. In the case of speleothem GP5, the growth rate varies between 100 and 300 µm/a. Considering the seasonal characteristics of drip rate and the quick response to large rainfall events, these growth rates could easily be twice as high during winter or spring, affecting precipitation-dependent elements, such as Ba (ref. 29) and U (ref. 50). One particular phase in GP5 around 1250 AD with low Sr and U concentrations as well as high Ba and Mg values is associated with high growth rates. If the interpretation of PAP for 1140–1364 AD is correct, then the period around 1250 AD was dry. However, this seems contradictory to the high growth rates. Furthermore, faster growth could increase Ba and U concentrations, i.e., in the same direction as PAP for Ba, but in the opposite direction for U. Growth rate changes in aragonite speleothems may therefore mask PAP-induced correlations between Ba and U. With drip rate responding quickly to rainfall events it is also challenging to relate annual growth rate to mean annual infiltration. In addition, potential changes in the initial balance between drip water SICc and Mg/Ca may control how much PCP is needed to induce PAP that affects speleothem Me concentrations.

Although speleothem δ18O has been interpreted as a proxy for rainfall amount in north Morocco, a comparison with that record will not provide conclusive evidence. This initial interpretation was based on multi-proxy data from stalagmite GP28 from Grotte de Piste. It has been highlighted that δ18O values could be driven by several processes that would all force it in the same direction under the influence of rainfall variability, i.e., kinetic isotope effects, PCarbP, and potentially rainfall amount, which led to a robust interpretation of δ18O for speleothem GP2. A potential rainfall amount effect was shown by a negative correlation between rainfall δ18O values and amount. However, the rainfall δ18O data were derived from a mixture of monthly mean rainfall and rainfall events, and not annual mean rainfall δ18O. For this purpose, the monitoring period was too short. Considering these shortcomings, additional evidence is required to support the climatic interpretation of the GP5 trace element record, for example, additional speleothem records that cover the same time interval.

Implications for speleothem proxies

Our high-resolution drip water dataset allowed us to characterize the different responses of Mg/Ca, Sr/Ca, Ba/Ca, and U/Ca to both PCP and PAP. We showed that the interpretation of trace element concentrations in the aragonite speleothem that corresponds to the monitored drip site is not straightforward given large changes in speleothem growth rates. This study has important implications for the interpretation of aragonite speleothem trace element concentrations:

  1. 1.

    Both PCP and PAP may occur successively at the same drip site, potentially complicating the interpretation of Sr and U in aragonite speleothems;

  2. 2.

    PCP and PAP can be distinguished in aragonite speleothems by the “Sinclair test”. If dominated by PCP, a slope around 1 can be expected for the trendline through ln(Sr/Ca) vs ln(U/Ca). PAP, in contrast, would result in a much lower slope of ca. 0.2.

  3. 3.

    Slowly growing aragonite speleothems that form under low drip water SIAr («0.38) and a relatively constant drip rate (seepage flow drip sites) are ideal candidates to faithfully record PCarbP with Ba, independent of the PCarbP mode.

  4. 4.

    At drip sites that are not affected by PCarbP, drip rate may be the dominant control on aragonite speleothem Ba concentrations provided the initial drip water Ba/Ca is relatively constant.

Methods

Water sample collection and drip rate

31 drip water samples were collected using an autosampler developed at ETH Zurich, Switzerland by S.F.M. Breitenbach, Nicola Tisato, and Reto Seifert. Sampling was conducted between February and June 2015, with an approximate 3–4 days resolution. Because of slow drip rates resolution is approximately 10 days for the dry season from June to September. The correct functioning of the autosampler was checked by our local speleo-guides at bi-weekly intervals. The exact dates for each drip water sample are not determined because the autosampler intermittently malfunctioned, leading to skipped sampling vials or delayed progression to the next sampling vial. Therefore, drip rates cannot be exactly matched to specific drip water samples. Instead, we provide a mean drip rate for March, April, May, and the dry season (June–September) based on 3 single drip rate measurements. Shortly after collection, drip water samples were stored in a fridge in polypropylene bottles. They were acidified with 1 drop of ultra-pure HNO3 in February 2016.

Drip water trace element analysis

Drip water samples were initially analyzed with ICP-OES (Spectro Ciros Vision) in the Applied and Analytical Paleontology lab at the University of Mainz. Calibration was performed with a 28-element Carl Roth multi-element standard. Because of low Sr, Ba, and U concentrations, 27 samples were analyzed for a 2nd time at the IBS Center for Climate Physics (ICCP) Mass Spectrometry Laboratory in 2023. Drip water samples were analyzed using an Agilent 7900 Quadrupole Inductively Coupled Plasma Mass Spectrometer (ICPMS). Elemental analyses of drip water samples were carried out following the standard calibration approach described by Tadros et al.54 and Samanta et al.55. Toward that, multiple single-element (Ca, Mg, Sr, Ba, and U) standards (from Sigma-Aldrich and Merck) were mixed together with variable concentrations to prepare calibration standards. Calibration standards were mixed to minimize possible matrix effects during ICP-MS analysis. Standard solutions were analyzed after each batch of 6–7 drip water samples to correct any possible instrumental drift. To monitor the external reproducibility (precision) of the Morocco drip water samples, two samples were measured in replicates. However, due to sample volume constraints, repeat analysis of multiple samples was not possible. Therefore, we collected 600 ml of drip water from a cave in the Republic of Korea. The drip water was measured at regular intervals (n = 47) along with the Grotte de Piste drip water samples to monitor reproducibility. The average external precision of our elemental analysis with ICP-MS is better than 5% (0.5–6.9; n = 47). For U concentration analytical precision varies between 3.2 and 6.9% for these drip waters. However, considering that the Morocco drip water samples have one order of magnitude lower concentrations, we use a relative uncertainty of 2 RSD for U.

Evaporation correction

We observed that in 8 years of storage the water samples have undergone evaporation. Since the samples were already acidified, evaporation only affects the elemental concentrations. We calculated the relative increase in Ca concentration and used it as a correction factor for Ca, Mg, Sr, Ba, and U concentrations (Table S1). Subsequently, we compare the corrected Mg concentration with the results from 2016 and discard any samples (n = 1) with a larger offset of 5%, i.e., the approximate uncertainty of our ICPMS Mg measurements. This correction highly improves the correlations between 2016 ICP-OES and 2023 ICPMS Mg and Sr concentrations (Fig. S3). It also brings the ICPMS U concentrations in the same range as the multi-collector ICPMS data from Xi’an Jiaotong University. We are thus confident that our evaporation-corrected ICPMS data are accurate.

Uranium isotope measurements

U-isotope measurements were conducted at the Institute of Global Environmental Change of Xi’an Jiaotong University (China). All chemical procedures and measurements were performed under clean room conditions. The methodology comprised the following steps:

  1. 1.

    20 ml of drip water was weighed and spiked with 236U–233U–229Th.

  2. 2.

    After resting one day, the U isotope in the drip water was co-precipitated with Fe(OH)3, by adding FeCl3 solution and an ammonia solution;

  3. 3.

    Following the co-precipitation, the precipitate was separated using centrifugation and subsequently rinsed with super-clean water (18.2Ω)

  4. 4.

    The U isotope separation process utilized extraction chromatographic resin to remove Fe, Mg, and Th isotopes. Subsequently, U isotopes were then eluted using super-clean water and collected in a Teflon beaker;

  5. 5.

    The eluate was then evaporated until dry. To eliminate potential organic contaminants that might have co-eluted from the resin, the dry residue underwent digestion three times using an HNO3 and HF mixture prior to assessments.

U isotope ratios were measured using a Neptune Plus Multi-Collector Inductively Coupled Plasma Mass Spectrometer (MC-ICP-MS) with the high-efficiency Aridus sample introduction system. Both the standards and samples underwent dilution using a solution composed of 1% HNO3 and 0.1%HF to maintain a consistent concentration during isotopic measurements. The instrumental procedures are described in Cheng et al.56.

Laser ablation ICPMS trace element analysis

Trace elements in speleothem GP5 were measured with LA-ICPMS at the Max Planck Institute for Chemistry, Mainz, Germany. Analysis was conducted with a Thermo Finnigan Element II coupled to a New Wave UP213 laser ablation system. We used linescans with 5 µm/s speed, 100 µm round spot size, 10 Hz laser frequency, and an energy density of 11.80 J/cm2. We targeted the following isotopes: 25Mg, 43Ca, 86Sr, 137Ba, and 238U. 43Ca was chosen as an internal standard to convert Me/Ca ratios to concentrations. Glass reference material NIST612 and compressed powder MACS3 reference materials were used to calculate relative sensitivity factors and calibrate the data. Uncertainties are in the range of 5–10%. For more details on the methodology see refs. 20,57. In Fig. 7c, e the orange lines represent data published in ref. 28 that were analyzed with the same setup, but with spot analysis instead of linescans. Concentrations and trends between the two different techniques result in very similar results. Small differences could be explained by the spatial heterogeneity of the sample. The trace element data were binned into yearly time intervals to downscale the resolution and obtain annual trace element data.

PCarbP modeling

For modeling the evolution of the drip water compositions under the influence of PCP and PAP, we use the same approach as Wassenburg et al.6. In contrast to using a Rayleigh equation:

$${{\rm{Me}}}/{{\rm{Ca}}}={{\rm{Me}}}/{{\rm{Ca}}}_{0}* {f}^{({D}_{{{\rm{Me}}}}-1)}$$
(5)

with “Me/Ca0” representing the initial Me/Ca ratio in the solution and “f” the fraction of Ca remaining in the solution, our approach allows us to calculate the drip water elemental concentrations by using a stepwise approach. Another advantage of our modeling approach is that it is possible to change the DMe to simulate a switch from PCP to PAP along the drip water flow path. This is not possible when using the Rayleigh equation, since Me/Ca0 is fixed. Equations used for the stepwise approach:

$$\Delta {{\rm{Ca}}}={{\rm{Ca}}}_{0}-{{\rm{Ca}}}_{f}$$
(6)
$$\Delta {{\rm{Me}}}=\Delta {{\rm{Ca}}}* {{\rm{Me}}}/{{\rm{Ca}}}* {D}_{{\rm{Me}}}$$
(7)
$${D}_{{\rm{Me}}}=\Delta {{\rm{Me}}}/\Delta {{\rm{Ca/Me/Ca}}}$$
(8)

The steps of ΔCa are determined by “f” with a stepsize of 0.001%. The initial Me/Ca ratios for the PCP model correspond to the drip water sample with the highest Ca concentration. The initial concentrations for the PCarbP model that also includes a switch from PCP to PAP (i.e., the dashed lines in Fig. 3c–e) were tuned by using initial Sr and U concentrations to match the minimum and maximum Sr and U taking into account their uncertainties and PAP to start at a Ca concentration of just below 0.65 mmol/l. This is necessary to model the PAP evolution lines at a realistic value of “f”. This approach is justified by our acknowledgment that initial metal drip water concentrations are not constant (see section “non-PCarbP processes”). In Fig. S3 we demonstrate that our stepwise modeling approach provides highly similar Me/Ca ratios as the Rayleigh equation, independent of the DMe that is used.

2015 rainfall data Fig. 1a

The rainfall map (Fig. 1a) was produced using TRMM data from Giovanni’s online data system, developed and maintained by the Goddard Earth Sciences Data and Information Services Center (NASA GES DISC), and visualized with QGIS.