Introduction

Marine heatwaves (MHWs), defined as discrete, prolonged, extreme warm water events1,2 exert catastrophic impacts on marine ecosystems, affecting adversely fishery industry and social economy3,4,5,6,7. The intensity, frequency and duration of MHWs have increased significantly over most parts of the global ocean during the past several decades in response to the global warming8,9. These trends will be likely to persist or even become more evident in the future9,10,11. Due to the rising threat of MHWs, there are growing efforts dedicated to describing their features12,13,14, understanding their dynamical drivers15,16,17, monitoring their occurrence18, evaluating their predictability and making forecast19,20.

Current knowledge of MHWs globally is primarily confined to the sea surface, relying on up-to-date, satellite-measured sea surface temperature (SST)2,8,15. However, there is extensive evidence on the presence of MHWs below the sea surface (referred to as the subsurface MHWs hereinafter to distinguish them from the surface MHWs)21,22,23,24,25,26,27,28,29. For instance, MHWs at 150 m are detected in the Northeast Pacific based on a combination of Argo floats and ship-board measurements, and thought to impact fishes like salmons21. Long-term mooring observations in the coastal waters off southeastern Australia22 reveal the subsurface intensification of MHWs that are driven by local downwelling favorable winds and bring damages to benthic species such as coral, kelp and seagrass. Based on OOI Pioneer Array and fishing fleets, a subsurface MHW is detected in early 2017 on the Northeast U.S. continental shelf, affecting significantly on the ecosystem and commercial fishing industry23,24. Recently, a study25 based on the Tropical Atmosphere Ocean/Triangle Trans-Ocean Buoy Network buoys in the West Pacific, reports much stronger subsurface MHWs in the thermocline caused by downwelling, compared to the surface MHWs. More intense MHWs than surface MHWs have also been discovered along the continental shelves of North America26. These subsurface MHWs are likely to threaten the marine ecosystem no less severely than the surface MHWs, since a massive number of organisms live in the oceanic epipelagic zone extending down to 200 m30.

To facilitate timely management for alleviating the marine ecosystem stress and associated socioeconomic ramifications, monitoring the occurrence of subsurface MHWs becomes imperative. However, current capacity for direct detection of subsurface MHWs is strongly hindered by the sparse in situ temperature observations below the sea surface2. Satellite remote sensing provides high spatio-temporal resolution, extensive coverage, and nearly real-time ocean observations at the sea surface. Here we switch the lens and attempt to indirectly detect the subsurface MHWs by retrieving the subsurface temperature from the surface observations.

The relationship between the subsurface temperature and surface variables has recently been estimated using dynamical methods31,32,33,34 and statistical learning methods35,36,37,38. The dynamical methods are primarily based on the quasi-geostrophic (QG) dynamics39 to retrieve the subsurface temperature anomaly \({T}^{{\prime} }\) (relative to a climatological mean seasonal cycle) using the observable variables at the sea surface, i.e., SST anomaly (SSTA) and sea surface height anomaly (SSHA). However, some dynamical assumptions have to be made as the potential vorticity in the ocean interior is not observable. These assumptions, essentially empirical, differ substantially among different studies31,32,33,34, which makes the dynamical methods applicable only in specific regions under certain conditions.

Statistical learning, also known as machine learning, is free from dynamical assumptions and instead employs a data-driven way to predict \({T}^{{\prime} }\) from SSTA and SSHA. A variety of statistical learning methods with different levels of complexity35,36,37,38 have been applied, ranging from the classical ordinary least square (OLS) regression to the popular deep neural networks. However, statistical learning methods suffer from the bias-variance trade-off40. On the one hand, an overly simple model such as the OLS regression may not accurately capture the complicated relationship between \({T}^{{\prime} }\) and its predictors (i.e., SSTA and SSHA), leading to large estimation bias. On the other hand, highly flexible models such as the deep neural networks are subjected to large estimation variance and thus may cause overfitting, in addition to the lack of interpretability. Constructing an appropriate statistical model that provides accurate prediction by exploiting dynamical information is thus crucial for the detection of subsurface MHWs.

In this study, we first demonstrate a geographically and temporally varying linear relationship between \({T}^{{\prime} }\) and its predictors (i.e., SSTA and SSHA) by combining the ocean dynamics and optimal prediction theory in statistics. We then propose a statistical model to capture such relationship to retrieve \({T}^{{\prime} }\) from SSTA and SSHA, and finally detect subsurface MHWs based on the retrieved \({T}^{{\prime} }\). Application of our dynamics-guided statistical model to three ocean reanalysis datasets (See “Ocean reanalysis datasets” in Methods) confirms its consistent outperformance in detecting the subsurface MHWs over both the OLS regression and deep neural networks. We remark that our model, trained for one ocean reanalysis dataset, shows good performance when tested against another, despite the different numerical model configurations and data assimilation methods among the different ocean reanalysis datasets. It thus suggests that the relationship between \({T}^{{\prime} }\) and its predictors in different ocean reanalysis datasets is generally consistent with each other and should capture the relationship in reality. This lends support that our model learned from the ocean reanalysis datasets can also be used to detect the subsurface MHWs in the observations, helping in the near real-time monitoring of subsurface MHWs globally.

Results

Guidance of ocean dynamics on statistical learning

A statistical model consists of three components, i.e., the response, the predictors, and the relationship between the response and predictors40. Here we treat \({T}^{{\prime} }\) at some depth below the sea surface as the response. Once \({T}^{{\prime} }\) is obtained, whether an MHW occurs or not can be determined straightforwardly based on some prescribed threshold for \({T}^{{\prime} }\) (See “Definition of MHWs” in Methods). The predictors are chosen as SSTA and SSHA. Such choices are not only due to the availability of these variables in the observations but also their tight relationship with \({T}^{{\prime} }\). In particular, we will show that there is geographically and temporally varying linear dependence of \({T}^{{\prime} }\) on SSTA and SSHA according to the ocean dynamics. The mathematical derivations of the relationships are detailed in the Methods (See “Guidance of ocean dynamics and optimal prediction theory in statistics” in Methods).

Variations of satellite-measured SSTA and SSHA are dominated by oceanic mesoscale eddies41,42. The behavior of these eddies is largely governed by the QG dynamics that can be further divided into the surface and interior QG dynamics. Assume that density anomaly is dominated by temperature anomaly, which holds over most parts of the global ocean (Supplementary Fig. 1). On the one hand, the surface QG dynamics suggests a linear relationship between \({T}^{{\prime} }\) and SSTA. On the other hand, the interior QG dynamics combined with the optimal prediction theory in statistics suggests linear dependence of \({T}^{{\prime} }\) on SSHA. However, the dependences of \({T}^{{\prime} }\) on SSTA and SSHA are neither constant over space nor time but are affected by the Coriolis frequency and background stratification (See “Guidance of ocean dynamics and optimal prediction theory in statistics” in Methods). In particular, the strong seasonal variation of background stratification in the upper ocean should cause evident seasonality in the relationship between \({T}^{{\prime} }\) and SSTA according to the surface QG dynamics. The above dynamics information guides us to propose a geographically and seasonally varying coefficient (GSVC) linear regression model to capture such relationships (See “GSVC model” in Methods). In the GSVC model, the regression coefficients of \({T}^{{\prime} }\) onto SSTA and SSHA can vary with location and calendar day. Estimating the regression coefficient at each location and calendar day is achieved by borrowing the samples on its neighboring locations and calendar days.

It should be noted that we do not take into consideration the variation of relationship between \({T}^{{\prime} }\) and its predictors at interannual and longer time scales. The main reason is that the variation of upper-ocean background stratification is dominated by its seasonal cycle43. By neglecting the variations of regression coefficients at interannual and longer time scales, the GSVC model treats samples on the same calendar day in different years as replicates and is thus capable of reducing estimation variance at the expense of a minor increase in the estimation bias. Additionally, by assuming the regression coefficient to be the same every year, we can train the GSVC model using the historical data (e.g., the ocean reanalysis datasets) and apply it to the near real-time monitoring of subsurface MHWs.

Performance of the GSVC model in detecting subsurface MHWs

Ideally, the GSVC model should be trained and tested based on observational data. However, the sparsity of the observed \({T}^{{\prime} }\) prohibits such analyses. Instead, we use three different ocean reanalysis datasets as surrogates to evaluate the performance of the GSVC model (See “Ocean reanalysis datasets” in Methods). In this case, there are concerns on to what extent the ocean reanalysis datasets can faithfully capture the relationship between \({T}^{{\prime} }\) and its predictors in reality. Such uncertainty can be inferred from the inter-dataset differences of relationships among the three ocean reanalysis datasets, based on the premise that the differences of relationships between the ocean reanalysis datasets and observations should be comparable in magnitude to those among the different ocean reanalysis datasets. For this reason, we train the GSVC model for one ocean reanalysis dataset and test it against another. Accordingly, the resulting model test errors contain three components related to the variation of \({T}^{{\prime} }\) independent from the predictors, the inaccuracy of estimated relationship between \({T}^{{\prime} }\) and its predictors in some ocean reanalysis datasets, and the differences of relationships among the different reanalysis datasets.

To quantify the performance of the GSVC model in detecting the subsurface MHWs based on SSHA and SSTA, we use a scalar metric, the Matthews correlation coefficient (MCC)44, ranging from −1 to 1. The MCC has been demonstrated to be a reliable measure of quality of binary classification (MHW or not in our case) especially for imbalanced datasets45. It produces a high score only if the classifier leads to high values for all the four basic rates of the confusion matrix, i.e., the sensitivity, specificity, precision, and negative predictive value. (See “Computation of the Matthews correlation coefficient” in Methods).

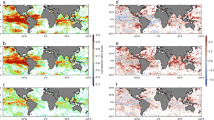
We first examine the performance of GSVC model in MHW detection at different depths. Figure 1 displays the distribution of the test MCC for MHW detection at 25 m, 50 m, 100 m and 200 m averaged over the 6 combinations of training and test datasets. At 25 m, the GSVC model has MCC values close to 1 over most parts of the global ocean. This is expected from a dynamical point of view, as \({T}^{{\prime} }\) at this shallow depth should vary coherently with SSTA via the surface QG dynamics41,46 and/or mixed-layer dynamics43. Indeed, using SSTA as a single predictor leads to almost identical MCC values at 25 m (Fig. 2a). As the depth increases, the values of MCC decrease but there is a still considerable fraction of the ocean showing high positive values of MCC. The fraction of ocean area with MCC > 0.3 is 94.5% at 50 m, 62.9% at 100 m and 40.2% at 200 m, respectively, suggesting that the GSVC model has skills in detecting subsurface MHWs across the oceanic epipelagic zone. The good performance of the GSVC model is also indicated by the high hit rate and low false alarm rate over the global ocean (Supplementary Figs. 2 and 3).

Fig. 1: Performance of the GSVC model in detecting the subsurface MHWs globally.
figure 1

Global distribution of the test MCC for MHW detection at 25 m (a), 50 m (b), 100 m (c) and 200 m (d) averaged over the 6 combinations of training and test datasets. Here the GSVC model is trained for one ocean reanalysis dataset and tested against another dataset, leading to 6 combinations of training and test datasets. The GSVC model is used first to predict subsurface temperature anomaly and then detect MHWs. The land is marked in dark gray and the continental margins are marked in light gray. Area where MCC is not significantly different from zero at the 95% confidence level is filled in white.

Full size image
Fig. 2: Importance of SSTA and SSHA for subsurface MHW detection at different depths.
figure 2

MCC values of the GSVC model with SSHA and SSTA (red), SSTA alone (blue), and SSHA alone (orange) as predictors at 25 m (a), 50 m (b), 100 m (c) and 200 m (d). Here the values are first averaged over the global ocean (58°S–58°N), and then over 6 combinations of training and test datasets. The errorbar is the standard error of the ensemble mean value of 6 combinations.

Full size image

Furthermore, the relative importance of two predictors, SSHA and SSTA, is investigated. The role of SSHA in predicting \({T}^{{\prime} }\) becomes more important as the depth increases, whereas the role of SSTA fades with the depth (Fig. 2). The MCC value derived from using SSHA as a single predictor approaches that from using both SSHA and SSTA, as the depth increases to 200 m (Fig. 2d). In contrast, using SSTA as a single predictor leads to severe model degrade at 200 m (Fig. 2d). Such patterns have clear physical interpretation. On the one hand, once the depth goes below the surface mixed layer, the strong background stratification in the pycnocline causes rapid decay of the surface QG modes with the increasing depth, so that SSTA has weaker imprint on \({T}^{{\prime} }\). On the other hand, the variation of \({T}^{{\prime} }\) generated by interior QG modes becomes dominant in the pycnocline32. Such variation is associated with the variation of SSHA through the hydrostatic balance.

Finally, it should be noted that the skill of the GSVC model for subsurface MHW detection varies geographically especially at the large depths, as evidenced by the geographical heterogeneity of the MCC (Fig. 1). At 100 m and 200 m, the low detection skill is primarily located in the eastern Atlantic and eastern Pacific, suggesting that SSHA is an insufficient predictor for \({T}^{{\prime} }\) in these regions. This might be partially due to the relatively stronger effects of subsurface salinity anomaly on density anomaly there than elsewhere, which makes the density anomaly less dominated by \({T}^{{\prime} }\) (Supplementary Fig. 1) and degrades the correlation between \({T}^{{\prime} }\) and SSHA.

Advantage of exploiting ocean dynamics in statistical learning

The proposal of the GSVC is guided by ocean dynamics. To examine how such guidance benefits the statistical learning outcomes, we compare the performance of the GSVC model for subsurface MHW detection with another two models that do not effectively exploit ocean dynamics. The first is the OLS regression model, one of the simplest but widely used statistical learning methods. Here the OLS model is trained at each grid point with samples at different times as replicates. This leads to a geographically varying but temporally constant relationship between \({T}^{{\prime} }\) and its predictors. The OLS model is actually a reduced case of the GSVC model (See “GSVC model” in Methods). The second is the convolutional neural network (CNN)47, one of the popular deep learning methods (See “Convolutional neural network” in Methods). It is a highly flexible model that can capture complicated nonlinear relationship between response and predictors. In this subsection, our principal interest is to compare the efficiency of the different statistical models in estimating the relationship between \({T}^{{\prime} }\) and its predictors. Therefore, rather than training and testing the models on the different reanalysis datasets, we divide each reanalysis dataset into training and test sets. This excludes influences of the discrepancy of relationships among the different reanalysis datasets. Nevertheless, we find that excluding such influences or not does not impact the rank of performance of statistical models (Fig. 3 and Supplementary Fig. 4).

Fig. 3: Comparison of performance of the different statistical learning methods in detecting the subsurface MHWs globally.
figure 3

The global mean (58°S–58°N) test MCC for MHW detection at 25 m (a), 50 m (b), 100 m (c) and 200 m (d) obtained from the GSVC (red), OLS (pink) and CNN (cyan) models. Here the test MCC for each reanalysis dataset is estimated via a 5-fold cross validation. The models are used first to predict subsurface temperature anomaly and then detect MHWs. Direct detection of MHWs based on the CNN model is shown in the dark blue bars. The errorbar is the standard error of the ensemble mean value of the 3 reanalysis datasets.

Full size image

The geographical and vertical distributions of MCC values for the OLS and CNN models are qualitatively consistent with those for the GSVC model (Supplementary Figs. 5–7). In particular, all the models have some skills for detecting MHWs except in the eastern Atlantic and eastern Pacific at 100 and 200 m. This lends further supports that the poor skills in these regions mainly result from limitations of the predictors rather than the relationships adopted by the statistical models. Despite the similar geographical and vertical distributions of MCC values among the models, the globally averaged MCC of the GSVC and OLS models are significantly larger than that of the CNN model at all the depths (Fig. 3). Given the simplicity of the OLS model, its outperformance over the CNN model is remarkable but understandable. The QG dynamics in combination with the optimal prediction theory suggest a linear relationship between \({T}^{{\prime} }\) and its predictors. It is natural that a linear model should be more efficient than a nonlinear model like the CNN model. In view that the advantage of the CNN model lies in its capability for capturing nonlinear relationship, we use the CNN model to detect subsurface MHWs directly by using a binary variable (MHW or not) as its response (Note that the dependence of MHWs on \({T}^{{\prime} }\) is nonlinear). However, this model does not outperform the GSVC and OLS models, either (Fig. 3).

As to the comparison between the GSVC and OLS models, they have similar performance at 200 m, whereas the GSVC model outperforms the OLS model at 25 m, 50 m and 100 m. This depth range generally coincides with the seasonal pycnocline where the seasonal variation of background stratification is most prominent43. A strong seasonal cycle of relationship between \({T}^{{\prime} }\) and SSTA is expected there according to the surface QG dynamics and mixed-layer dynamics. In specific, SSTA should play a more important role in determining \({T}^{{\prime} }\) in winter when these depths are generally within the deep mixed layer than in summer when the seasonal pycnocline is developed. Such a pattern is captured by the GSVC model (Fig. 4) but not so by the OLS model, leading to higher MCC values for the GSVC model than the OLS model.

Fig. 4: Seasonal cycle of relationship between subsurface temperature anomaly (\({T}^{{\prime} }\)) and sea surface temperature anomaly (SSTA) at 50 m.
figure 4

Here the relationship is computed as the regression coefficient of \({T}^{{\prime} }\) onto SSTA in the GSVC model with SSTA and SSHA as the predictors. The regression coefficient is averaged over the three reanalysis datasets (ECCO2, GLORYS, HYCOM) during December-February (a), March-May (b), June-August (c) and September-November (d). The land is marked in dark gray and the continental margins are marked in light gray.

Full size image

Discussion

With the increase of computational resources, there is a tendency to use more and more complicated statistical learning methods in oceanic studies and other scientific fields. However, more complicated methods, albeit more flexible, do not necessarily outperform the simpler ones due to the bias-variance trade-off issue40. In particular, complicated methods require large-volume training data, which are usually not available in oceanic studies. Therefore, developing methods with the optimal degree of complexity is thus crucial to enhance the efficiency of statistical learning. The optimal method depends on the true relationship between the response and predictors and is thus problem-specific.

This study proposes a dynamics-guided statistical learning method for detecting subsurface MHWs based on SSTA and SSHA and highlights how the usage of dynamical information can enhance the efficiency and interpretability of statistical learning. Combination of the ocean dynamics and optimal prediction theory in statistics demonstrates a geographically and seasonally varying linear relationship between \({T}^{{\prime} }\) and its predictors (SSTA and SSHA). This insight guides us to propose the GSVC model to capture such relationship. Benefiting from exploiting the dynamical information, the GSVC model has good skills in detecting MHWs in the oceanic epipelagic zone over many parts of the global ocean and outperforms both the classical OLS model and popular CNN model. More importantly, the superiority of the GSVC model has clear dynamical interpretation. On the one hand, the outperformance of the GSVC model over the OLS model is because the OLS is too simple to capture the geographically and seasonally varying relationship between \({T}^{{\prime} }\) and its predictors (SSTA and SSHA). On the other hand, it is superior than the CNN model as the latter is overly complicated. In particular, the CNN model has a highly complicated architecture aimed to handle the nonlinear relationship, whereas the ocean dynamics suggests a linear relationship.

Despite the superiority of the GSVC model, it has its own limitations. The GSVC model is developed based on the QG dynamics. The QG dynamics provides an appropriate dynamical framework for ocean mesoscale eddies41,42 but no so for submesoscale48 and coastal processes49. In regions where these processes dominate the variations of \({T}^{{\prime} }\), the GSVC model may be not effective in detecting subsurface MHWs. In particular, we caution the readers that the high MCC in the coastal regions shown in Fig. 1 does not necessarily suggest the good performance of the GSVC model for detecting coastal subsurface MHWs in reality. Instead, it is likely an artifact of the ocean reanalysis datasets, as the coastal processes are poorly represented in these datasets due to the insufficient resolution.

Even in regions where the QG dynamics governs the variations of \({T}^{{\prime} }\), there is still a lot of space to further improve the capability of statistical learning for detecting subsurface MHWs, especially in the regions where SSTA and SSHA are poor predictors of \({T}^{{\prime} }\). The improvement requires utilizing in situ subsurface measurements such as Argo floats50,51. These measurements can be merged with the predictions from SSTA and SSHA using the spatio-temporal statistical learning methods such as the kriging methods52. More subsurface in situ observations and advanced statistical learning methods exploiting dynamical information are crucial for enhancing the capacity of subsurface MHW monitoring and alleviating their induced ecosystem stress and socioeconomic ramifications.

Methods

Ocean reanalysis datasets

In this study, we use three ocean reanalysis datasets to identify subsurface MHWs. The first is the Estimating the Circulation and Climate of the Ocean, phase II (ECCO2) project53, version “cube 92.” It is obtained by using Green’s function approach and provides a three-day mean estimate of the physical ocean state on 0.25° × 0.25° regular grids from 1993 to 2020. The second is the Global Ocean Physics Reanalysis (GLORYS)54 product delivered from the Copernicus Marine Environment Monitoring Service. It is assimilated by means of a reduced-order Kalman filter and corrected based on a three-dimensional variational (3D-VAR) scheme, providing a daily mean 1/12° global ocean reanalysis from 1993 to 2020. The third is the Hybrid Coordinate Ocean Model (HYCOM)55 product covering the period from 1993 to 2012, which uses the Navy Coupled Ocean Data Assimilation (NCODA) system for 3DVAR data assimilation. It has a 3-h temporal resolution and a 0.08° horizontal resolution.

We bin-average the HYCOM data within each day and interpolate the ECCO2 data onto a daily basis. The spatial grids of the three reanalysis datasets are unified by interpolating each dataset onto regular grids with a horizontal resolution of 1° × 1° and vertical levels of 5 m, 25 m, 50 m, 100 m, and 200 m. The SST is approximated as the temperature at 5 m. The anomalies of SST, sea surface height and subsurface temperature \(T\) (SSTA, SSHA and \({T}^{{\prime} }\)) are computed by subtracting their respective climatological mean seasonal cycles over the entire period (1993-2020 for ECCO2 and GLORYS but 1993–2012 for HYCOM).

Definition of MHWs

MHWs are defined, following Hobday et al.1, as an abnormal warming event with \(T\) consecutively exceeding its seasonally varying 90th percentile \(\theta\) for at least 5 days. The baseline period for the computation of \(\theta\) is the entire period of the ocean reanalysis datasets (1993–2020 for ECCO2 and GLORYS but 1993–2012 for HYCOM). Note that \(T={T}^{{\prime} }+{T}_{c}\) and \(\theta =\theta ^{\prime} +{T}_{c}\) where \({T}_{c}\) is the climatological mean seasonal cycle of \(T\) and \(\theta ^{\prime}\) is the seasonally varying 90th percentile of \({T}^{{\prime} }\). As MHWs are defined based on \(T-\theta\) (Hobday et al.1), \({T}_{c}\) is irrelevant to MHWs and we can detect subsurface MHWs based on \({T}^{{\prime} }\) alone56. The value of \(\theta ^{{\prime} }\) is always computed from the “true” \({T}^{{\prime} }\) in the reanalysis dataset, no matter whether MHWs are identified based on the “true” \({T}^{{\prime} }\) or predicted \({T}^{{\prime} }\) from SSTA and SSHA.

Guidance of ocean dynamics and optimal prediction theory in statistics

In this subsection, we combine the ocean dynamics and optimal prediction theory to demonstrate a geographically and seasonally varying linear relationship between \({T}^{{\prime} }\) and its predictors (i.e., SSTA and SSHA). Under the QG approximation, the geostrophic streamfunction anomaly (\(\psi ^{{\prime} }\)) can be derived by inverting the potential vorticity (PV) anomaly under the surface and bottom boundary conditions39

$$\left(\frac{{\partial }^{2}}{\partial {x}^{2}}+\frac{{\partial }^{2}}{\partial {y}^{2}}+\frac{\partial }{\partial z}\frac{{f}^{2}}{{N}^{2}}\frac{\partial }{\partial z}\right)\psi ^{\prime} =q^{{\prime} } ,-H \, < \,z \, < \,0,$$
(1a)
$$f\frac{\partial \psi ^{{\prime} } }{\partial z}={b}_{0}^{{\prime} } (x,y,t),z=0,$$
(1b)
$$f\frac{\partial \psi ^{{\prime} } }{\partial z}=0,z=-H,$$
(1c)

where \(f\) is the Coriolis frequency, \(N\) is the background buoyancy frequency, \(q^{{\prime} }\) is the QG PV anomaly, \({b}^{{\prime} }=f\frac{\partial \psi ^{{\prime} } }{\partial z}=-(\frac{g}{{\rho }_{r}})\rho ^{{\prime} }\) is the buoyancy anomaly with \(g\) the gravity acceleration, \(\rho\) the density and \({\rho }_{r}\) the reference density value, and \({b}_{0}^{{\prime} }\) is the value of \({b}^{{\prime} }\) at the sea surface. In the following analysis, we assume \({b}^{{\prime} }\) is dominated by temperature anomaly \({T}^{{\prime} }\) so that \({b}^{{\prime} }\approx g\alpha T^{{\prime} }\) with \(\alpha\) the thermal expansion coefficient, which holds over most parts of the global ocean (Supplementary Fig. 1).

Eq. (1) is linear with respect to \(\psi ^{{\prime} }\), allowing \(\psi ^{{\prime} }\) to be decomposed into a homogeneous solution known as the surface QG (SQG) solution \({\psi }_{s}^{{\prime} }\) and a particular solution as the interior QG (IQG) solution \({\psi }_{i}^{{\prime} }\)41,42. Accordingly, \(b^{{\prime} }\) can be decomposed into \({b}^{{\prime} }={b}_{s}^{{\prime} } +{b}_{i}^{{\prime} }\) with \({b}_{s}^{{\prime} } =f\partial {\psi }_{s}^{{\prime} } /\partial z\) and \({b}_{i}^{{\prime} } =f\partial {\psi }_{i}^{{\prime} } /\partial z\) representing the buoyancy anomalies of SQG and IQG solutions, respectively. We next demonstrate \({b}_{s}^{{\prime} }\) depends linearly on SSTA and \({b}_{i}^{{\prime} }\) depends linearly on SSTA and SSHA.

The SQG solution is defined as

$$\left(\frac{{\partial }^{2}}{\partial {x}^{2}}+\frac{{\partial }^{2}}{\partial {y}^{2}}+\frac{\partial }{\partial z}\frac{{f}^{2}}{{N}^{2}}\frac{\partial }{\partial z}\right){\psi }_{s}^{{\prime} } =0,-H \, < \,z \, < \, 0,$$
(2a)
$$f\frac{\partial {\psi }_{s}^{{\prime} } }{\partial z}={b}_{0}^{{\prime} } (x,y,t),z=0,$$
(2b)
$$f\frac{\partial {\psi }_{s}^{{\prime} } }{\partial z}=0,z=-H.$$
(2c)

As evidenced from Eq. (2), \({\psi }_{s}^{{\prime} }\) depends linearly on \({b}_{0}^{{\prime} }\) (SSTA) and so does \({b}_{s}^{{\prime} }\). Moreover, it can be demonstrated that \({b}_{s}^{{\prime} }\), equal to \({b}_{0}^{{\prime} }\) at the sea surface, decays as the depth increases with decaying rate proportional to \(N/f\)41. These thus suggest a geographically and temporally varying linear relationship between \({b}_{s}^{{\prime} }\) and \({b}_{0}^{{\prime} }\) (SSTA).

The IQG solution is defined as:

$$\left(\frac{{\partial }^{2}}{\partial {x}^{2}}+\frac{{\partial }^{2}}{\partial {y}^{2}}+\frac{\partial }{\partial z}\frac{{f}^{2}}{{N}^{2}}\frac{\partial }{\partial z}\right){\psi }_{i}^{{\prime} } =q^{{\prime} } ,-H \, < \,z \, < \,0,$$
(3a)
$$f\frac{\partial {\psi }_{i}^{{\prime} } }{\partial z}=0,z=0,$$
(3b)
$$f\frac{\partial {\psi }_{i}^{{\prime} } }{\partial z}=0,z=-H.$$
(3c)

As \(q^{{\prime} }\) is unknown in reality, \({\psi }_{i}^{{\prime} }\) and hence \({b}_{i}^{{\prime} }\) cannot be derived deterministically. However, they can be predicted based on SSHA and SSTA if we switch our perspective from dynamical to statistical, as demonstrated below.

For now, we consider \({\psi }_{i}^{{\prime} }\) at some geographical location and time \(\left(x,y,t\right)\) as a vertical random process. In order to predict \({\psi }_{i}^{{\prime} }\), we decompose it as a linear combination of countable basis functions, that is,

$${\psi }_{i}^{{\prime} }={\sum }_{n=0}^{\infty }{\theta }_{n}^{{\prime} }{\left(x,y,t\right)F}_{n}\left(x,y,z,t\right),$$
(4)

where \({F}_{n}\) are specified basis functions in the vertical and the coefficient \({\theta }_{n}^{{\prime} }\) are random effects. Essentially, Eq. (4) is a statistical model for the vertical variability of \({\psi }_{i}^{{\prime} }\).

There are many ways to specify the basic functions but it is natural and useful to choose basic functions with clear physical meanings57. For this reason, the basic functions are chosen as the vertical modes in ocean dynamics39, i.e., the eigen functions of the following Sturm-Liouville problem

$$\left(\frac{\partial }{\partial z}\frac{{f}^{2}}{{N}^{2}}\frac{\partial }{\partial z}\right){F}_{n}+{\lambda }_{n}^{2}{F}_{n}=0,-H \, < \, z \, < \,0,$$
(5a)
$$\frac{\partial }{\partial z}{F}_{n}=0,z=0,$$
(5b)
$$\frac{\partial }{\partial z}{F}_{n}=0,z=-H,$$
(5c)

where \({F}_{n}\) is the eigen function (vertical mode) associated with the eigenvalue \({\lambda }_{n}\). The \({F}_{n}\) is a known function as both \({f}^{2}\) and \({N}^{2}\) are known in reality. In particular, \({F}_{0}\equiv 1\) with the eigenvalue \({\lambda }_{0}=0\) is the barotropic mode.

The advantage of using the vertical modes as the basic functions is that \({\psi }_{i}^{{\prime} }\) in reality can be approximated at a high level of accuracy by the first several vertical modes58

$${\psi }_{i}^{{\prime} }\approx {\sum }_{n=0}^{N}{\theta }_{n}^{{\prime} }{\left(x,y,t\right)F}_{n}\left(x,y,z,t\right).$$
(6)

We next utilize the dynamical constraints to construct an optimal predictor of \({\psi }_{i}^{{\prime} }\). Assuming no motions at the sea floor yields the first constraint:

$${\sum }_{n=0}^{N}{\theta }_{n}^{{\prime}} {\left(x,y,t\right)F}_{n}(x,y,-H,t)=0,$$

or equivalently

$${\theta }_{0}^{{\prime} }\left(x,y,t\right)=-{\sum }_{n=1}^{N}{\theta }_{n}^{{\prime} }{\left(x,y,t\right)F}_{n}\left(x,y,-H,t\right).$$
(7)

Substituting Eq. (7) into Eq. (6) gives rise to

$${\psi }_{i}^{{\prime} }={\sum }_{n=1}^{N}{\theta }_{n}^{{\prime} }{\left(x,y,t\right)G}_{n}\left(x,y,z,t\right),$$
(8)

where \({G}_{n}{\left(x,y,z,t\right)=F}_{n}(x,y,z,t)-{F}_{n}(x,y,-H,t)\).

The other constraint is related to SSHA and SSTA due to the hydrostatic balance, i.e.,

$${\psi }_{i}^{{\prime} }\left(x,y,0,t\right)={\sum }_{n=1}^{N}{\theta }_{n}^{{\prime} }{\left(x,y,t\right)G}_{n}\left(x,y,0,t\right)=\frac{g}{f}{SSHA}-{\psi }_{s}^{{\prime} }\left(x,y,0,t\right),$$
(9)

where \({\psi }_{s}^{{\prime} }\left(x,y,0,t\right)\) is a linear function of SSTA according to the SQG solution.

Typically, \({\theta }_{n}^{{\prime} },n=1\ldots N\) can be uniquely determined based on Eq. (9) only for \(N=1\)32. In reality where \(N \, > \,1\), \({\theta }_{n}^{{\prime} }\) is underdetermined and so is \({\psi }_{i}^{{\prime} }\). Nevertheless, from a statistical perspective, \({\psi }_{i}^{{\prime} }\) and further \({b}_{i}^{{\prime} }\) can be predicted based on the predictive distribution of \({\psi }_{i}^{{\prime} }\) given its physical constraint, i.e., Eq. (9).

We assume that \({{{\boldsymbol{\theta }}}}^{{\prime} }\equiv {({\theta }_{1}^{{\prime} },{\theta }_{2}^{{\prime} }\ldots {\theta }_{N}^{{\prime} })}^{T}\) is a N-dimensional Gaussian random vector with zero mean and covariance matrix \({\Sigma }_{N\times N}\equiv {{\rm{Cov}}}\left({{{\boldsymbol{\theta }}}}^{{\prime} }\right)\), denoted as \({{{\boldsymbol{\theta }}}}^{{\prime} } \sim {Gau}\left({{\boldsymbol{0}}}{{,}}{{\boldsymbol{\Sigma }}}\right)\), where the superscript T denotes the transpose. Let \(\pi ^{{\prime}} \equiv \frac{g}{f}{SSHA}-{\psi }_{s}^{{\prime} }(x,y,0,t)\), \({{\bf{G}}}\equiv {({G}_{1},{G}_{2}\ldots {G}_{N})}^{T}\) and \({{{\bf{G}}}}_{0}\equiv {{\bf{G}}}{|}_{z=0}\). Then we have \({{{\boldsymbol{\tau }}}\equiv ({\psi }_{i}^{{\prime} },\pi ^{{\prime}} )}^{T}={\left[{{\bf{G}}}{{,}}{{{\bf{G}}}}_{0}\right]}^{T}{{{\boldsymbol{\theta }}}}^{{\prime} }\), a 2-dimensional Gaussian random vector with covariance matrix \({\Omega }_{2\times 2}\equiv {{\rm{Cov}}}\left({{\boldsymbol{\tau }}}\right)={\left[{{\bf{G}}}{{,}}{{{\bf{G}}}}_{0}\right]}^{T}\Sigma \left[{{\bf{G}}}{{,}}{{{\bf{G}}}}_{0}\right]\). According to the property of multivariate Gaussian distribution, the conditional distribution of \({\psi }_{i}^{{\prime} }\) at some depth given \(\pi ^{{\prime}}\) is

$${\psi }_{i}^{{\prime} }{{|}}{\pi }^{{\prime} } \sim {Gau}\left(\mu ,{\sigma }^{2}\right),$$
(10)

with conditional mean and variance respectively being

$$\mu ={\Omega }_{12}{\Omega }_{22}^{-1}{\pi }^{{\prime} },$$
(11)
$${\sigma }^{2}={\Omega }_{11}-{\Omega }_{12}{\Omega }_{22}^{-1}{\Omega }_{21},$$
(12)

where \({\Omega }_{{ij}}\) corresponds to the component of \(\Omega\) at th i-th row, j-th column.

It can be proved that the optimal predictor of \({\psi }_{i}^{{\prime} }\)59, under the mean squared error loss, is the conditional mean given by Eq. (11). Accordingly, \(f\partial \mu /\partial z\) is the optimal predictor of \({b}_{i}^{{\prime} }\). Therefore, Eqs. (10) and (11) suggest that the optimal predictors of \({\psi }_{i}^{{\prime} }\) and \({b}_{i}^{{\prime} }\) depend linearly on SSHA and SSTA (note that \({\psi }_{s}^{{\prime} }(x,y,0,t)\) is a linear function of SSTA) but the relationship varies with location and time due to the geographical and temporal variations of \({F}_{n}\).

GSVC model

The ocean dynamics in combination with the optimal prediction theories suggest linear but geographically and seasonally varying relationships between \(T^{{\prime}}\) and its predictors (SSTA and SSHA). To capture such relationships, we propose a geographically and seasonally varying coefficient (GSVC) linear regression model,

$${T}_{k}^{{\prime} }\left({{{\boldsymbol{s}}}}_{i},{t}_{j}\right)={\beta }_{1}\left({{{\boldsymbol{s}}}}_{i},{t}_{j}\right){{SSTA}}_{k}\left({{{\boldsymbol{s}}}}_{i},{t}_{j}\right)+{\beta }_{2}\left({{{\boldsymbol{s}}}}_{i},{t}_{j}\right){{SSHA}}_{k}\left({{{\boldsymbol{s}}}}_{i},{t}_{j}\right)+{\beta }_{0}\left({{{\boldsymbol{s}}}}_{i},{t}_{j}\right)+{\varepsilon }_{k}\left({{{\boldsymbol{s}}}}_{i},{t}_{j}\right),$$
(13)

where \({{{\boldsymbol{s}}}}_{i}=({x}_{i},{y}_{i})\) is the geographical coordinate, \({t}_{j}\) is the calendar day, the subscript \(k\) represents the k-th year, \({\beta }_{1}({{{\boldsymbol{s}}}}_{i},{t}_{j})\) and \({\beta }_{2}({{{\boldsymbol{s}}}}_{i},{t}_{j})\) are the geographically and seasonally varying regression coefficients of \({T}_{k}^{{\prime}} ({{{\boldsymbol{s}}}}_{i},{t}_{j})\) onto \({{SSTA}}_{k}({{{\boldsymbol{s}}}}_{i},{t}_{j})\) and \({{SSHA}}_{k}({{{\boldsymbol{s}}}}_{i},{t}_{j})\) respectively, \({\beta }_{0}({{{\boldsymbol{s}}}}_{i},{t}_{j})\) is the geographically and seasonally varying intercept, and \({\varepsilon }_{k}({{{\boldsymbol{s}}}}_{i},{t}_{j})\) is a random noise with mean zero and independent from SSTA and SSHA. Here \({\varepsilon }_{k}({{{\boldsymbol{s}}}}_{i},{t}_{j})\) is a catch-all for what are missed in the GSVC model. Samples in different years are treated as replicates in the GSVC model, since \({\beta }_{1}\), \({\beta }_{2}\) and \({\beta }_{0}\) are identical for every year.

A simple way to estimate the regression coefficients including the intercept in Eq. (13) at \(({{{\boldsymbol{s}}}}_{i},{t}_{j})\) is minimizing the residual sum of squares (RSS) over the training dataset40:

$$\min {\sum}_{k}{\left({T}_{k}^{{\prime}} \left({{{\boldsymbol{s}}}}_{i},{t}_{j}\right)-{\hat{T}}_{k}^{{\prime}} \left({{{\boldsymbol{s}}}}_{i},{t}_{j}\right)\right)}^{2},$$

where \({\hat{T}}_{k}^{{\prime} }\) is the prediction of \({T}_{k}^{{\prime} }\) based on Eq. (13). However, the above minimization leads to a poor estimator of the regression coefficients, as there are only ~20 replicates available for estimation. A more efficient estimation method could be motivated from physical information. Note that the background stratification and Coriolis frequency vary smoothly in the spatio-temporal domain, suggesting that the regression coefficients should be similar at the proximate locations in the spatio-temporal domain. Accordingly, the regression coefficients at \(({{{\boldsymbol{s}}}}_{i},{t}_{j})\) can be estimated by borrowing the information from its neighborhood. In other words, the GSVC model can be fitted by locally weighted least squares:

$$\min {\sum}_{p}{\sum}_{q}{\sum}_{k}w\left({{{\boldsymbol{s}}}}_{i}-{{{\boldsymbol{s}}}}_{p},{t}_{j}-{t}_{q}\right){\left({T}_{k}^{{\prime} } \left({{{\boldsymbol{s}}}}_{p},{t}_{q}\right)-{\hat{T}}_{k}^{{\prime} } \left({{{\boldsymbol{s}}}}_{p},{t}_{q}\right)\right)}^{2},$$
(14)

where localization is specified by a spatio-temporal kernel function \(w({{{\boldsymbol{s}}}}_{i}-{{{\boldsymbol{s}}}}_{p},{t}_{j}-{t}_{q})\)52. By assigning a weight to samples in the neighborhood of the location \(({{{\boldsymbol{s}}}}_{i},{t}_{j})\), the kernel function reflects the different importance of these samples when estimating the regression coefficients at \(({{{\boldsymbol{s}}}}_{i},{t}_{j})\). In this study, we adopt a Gaussian kernel, i.e.,

$$w\left({{{\boldsymbol{s}}}}_{i}-{{{\boldsymbol{s}}}}_{p},{t}_{j}-{t}_{q}\right)=\exp \left(-\left[{\left(\frac{\varDelta x}{{\theta }_{x}}\right)}^{2}+{\left(\frac{\varDelta y}{{\theta }_{y}}\right)}^{2}+{\left(\frac{\varDelta t}{{\theta }_{t}}\right)}^{2}\right]\right),$$
(15)

where \(\left(\Delta x,\Delta y\right)={{{\boldsymbol{s}}}}_{i}-{{{\boldsymbol{s}}}}_{p}\), \(\Delta t={t}_{j}-{t}_{q}\), and \({\theta }_{x}\), \({\theta }_{y}\) and \({\theta }_{t}\) are the band widths determining the decay rate of \(w({{{\boldsymbol{s}}}}_{i}-{{{\boldsymbol{s}}}}_{p},{t}_{j}-{t}_{q})\) along the zonal, meridional and temporal axes, respectively. We remark that the GSVC model can be treated as a generalization of the geographically and temporally weighted regression model60 to deal with any number of replicates. Furthermore, the OLS model is a reduced case of the GSVC model with zero \({\theta }_{x}\) and \({\theta }_{y}\) but infinite \({\theta }_{t}\).

We set \(({\theta }_{x},{\theta }_{y})\) as \((2^{\circ } ,1^{\circ }\, )\) and \({\theta }_{t}\) as 60 days, large enough to include sufficient samples for estimation but small enough to capture the geographical and seasonal variations of regression coefficients caused by the varying background stratification and Coriolis frequency. Sensitivity tests suggest that changing the band widths within a reasonable range does not affect the performance of the GSVC model significantly. Finally, the value of \(w < 0.01\) is truncated as zero. This truncation has nearly no influence on the estimation but reduces the computational burden substantially.

Convolutional neural network

The Convolutional Neural Network (CNN) is one of the deep learning networks and has been widely used in marine research61,62,63. It has the capability for capturing nonlinear relationships within data. In this study, we use an end-to-end CNN model to detect the occurrence of subsurface MHWs, with SSTA and SSHA as inputs. The CNN model is implemented in two different approaches, depending on its output. In the first approach, the output is set as a binary variable to directly detect MHW occurrence, where one indicates the occurrence of MHWs and zero indicates the otherwise. It corresponds to a supervised classification learning model, referred to as CNN_cla. The second approach uses the CNN model to first learn \(T^{{\prime} }\) and then detect MHWs based on the learned \(T^{{\prime} }\). It corresponds to a supervised regression learning model, referred to as CNN_reg.

The CNN_cla and the CNN_reg share the same architecture, depicted in Supplementary Fig. 8. Based on the volume of available data, we first experiment with 2-layer, 3-layer and 4-layer CNN and ultimately choose a 3-layer-architecture CNN to prevent overfitting. In the proposed architecture, data normalization is employed at the start to effectively accelerate convergence and alleviate the vanishing gradient issue. The first two layers are convolutional layers with a filter size of 3° × 3° followed by a ReLU activation function for CNN_reg and a Sigmoid activation function for CNN_cla. Filters of different sizes are also tried but not adopted due their poorer prediction performance (Supplementary Table 1). The third layer is a fully connected layer essentially implemented as a convolutional layer, with an additional sigmoid function followed for CNN_cla to produce an output between 0 and 1 representing the probability of MHW occurrence. The output is classified as one (an MHW) if the probability is higher than 0.5 and zero (not an MHW) otherwise.

We use Python with Pytorch API to implement the above learning architectures. For optimization, the Adadelta64 is used, which adjusts the learning rate for each parameter individually and dynamically. As the relationship between the input and output is assumed to be invariant at the interannual and longer time scales, we experimented with different batch sizes and ultimately set a batch size of 365 samples for CNN_reg and 256 samples for CNN_cla. (Supplementary Table 2). The number of training epochs is set empirically as 100. The loss function is the mean squared error for CNN_reg and binary cross entropy for CNN_cla, respectively. Note that CNN_cla involves imbalanced binary classification as MHWs are rare events. For this reason, we give different weights to different classes in the loss function, i.e., 0.80 for the “one” class (an MHW) and 0.20 for the “zero” class (not an MHW), to make the model pay more attention to occurrence of MHW events. This weight leads to a better prediction performance compared to those derived from the weights (0.3, 0.7) and (0.1, 0.9) (Supplementary Table 3).

Computation of the Matthews correlation coefficient

The performance of a statistical model for binary classification (MHW or not in our case) can be evaluated based on the 2 × 2 confusion matrix40:

$${{\bf{M}}}=\left(\begin{array}{cc}{TP} & {FN}\\ {FP} & {TN}\end{array}\right),$$

where TP represents the true positives (i.e., the prediction from a statistical model correctly indicates the presence of an MHW), TN the true negatives (i.e., the prediction correctly indicates the absence of an MHW), FP the false positives (i.e., the prediction wrongly indicates the presence of an MHW), and FN the false negatives (i.e., the prediction wrongly indicates the absence of an MHW).

Although the confusion matrix provides a complete description on the performance of a statistical model, analyzing all the four components of the confusion matrix separately would be cumbersome. It is thus desirable to define a scalar metric that summarizes the confusion matrix. The Matthews correlation coefficient (MCC)44 has been proved to be an effective metric superior than the commonly used metrics like the accuracy and F1 score particularly for imbalanced class classification like MHW45. The MCC is calculated as

$${MCC}=\frac{{TP}\cdot {TN}-{FP}\cdot {FN}}{\sqrt{\left({TP}+{FP}\right)\left({TP}+{FN}\right)\left({FP}+{TN}\right)\left({FN}+{TN}\right)}}.$$
(16)

The MCC has a range of \([-{\mathrm{1,1}}]\). A score higher (lower) than zero indicates superior (inferior) performance than a random classification. It possesses class-exchange invariance and yields a high score only when predictions perform well in all the four components of the confusion matrix.

We employ a bootstrap method to test whether the value of MCC at some spatial location (Fig. 1) is significantly positive. First, we compute the probability p of MHWs estimated as the ratio of number of MHW days to the total number of days \({N}_{t}\). Then, we randomly pick up \({{pN}}_{t}\) days from the entire period, assign them as MHW days and compute the MCC. This random prediction is repeated for 5000 times and an empirical 95% confidence interval is computed. The MCC of a statistical model is thought to be significantly positive at the 95% confidence level if its value is higher than the upper bound of the 95% confidence interval of the MCC for random prediction.