Introduction

Seismic energy radiated during an earthquake may cause localized amplified shaking levels due to wave interactions with the terrain through which the seismic waves propagate1,2,3 (i.e., sedimentary basin or mountainous regions). The level of seismic amplification is linked to the characteristics of the media the seismic waves travel through, namely, material, structural features, and topography4. The latter interacts with seismic waves by trapping them within hills or mountains of a suitable geometry5,6. A suitable geometry refers to situations where topographic sharpness7 approximately matches the seismic wavelength8,9.

Topographic amplification has been quantified with peak ground motion velocities10 increasing up to 30%11, and crest-to-base spectral ratios up to 20%12. Trapped seismic waves due to constructive interference may also increase shaking duration13. This then translates into a cumulative kinetic energy up to 200% higher along hilltops and ridges as compared to mountain bases and flat areas14.

Amplification along hilltops may contribute to the genesis of coseismic slope failures4,15,16,17,18. This has been suggested for several earthquakes, including the 1994 Mw 6.7 Northridge19, the 2008 Mw 7.9 Wenchuan20, the 2010 Mw 6.2 Aysen Fjord16, the 2015 Mw 7.8 Gorkha21 and the 2016 Mw 7.0 Kumamoto22,23, among others. Sepúlveda et al.24, suggest that strong shaking led to landslide concentrations in low-susceptibility areas due to topographic amplification during the 1994 Northridge earthquake. Notably, their analyses were carried out at specific locations where strong-motion recordings were available. However, the availability of a dense seismic array is a common limitation in studies addressing the effect of topographic amplification on the occurrence of coseismic landslides9,12,25.

Alternatively, the link between topographic amplification and landslide occurrence can be investigated through ground motion simulations21,23. However, due to the numerical complexity and the limitation in available subsurface data, few studies have explored the use of such techniques in landslide research21,22,26,27,28,29,30, the Gorkha earthquake being one of the most common test sites. There, Gallen et al.31, suggest that the mismatch between landslide model predictions and observed coseismic landslides may be justified by unaccounted amplification. Dunham et al.21, note a spatial correlation between the distribution of large coseismic landslides and the footprint of hillslopes over which ground-motions may have been topographically amplified. Similar conclusions are drawn for other earthquakes in which high landslide densities are assumed to be generated by topographic amplification16,17,28,32,33,34. However, it should be stressed that amplification is not a requirement for coseismic landslide occurrence. Especially in the case of strong earthquakes, it is reasonable to assume that landslides may occur if ground shaking is sufficiently high, irrespective of potential ground-motion amplification effects23. This may be the reason why a standard methodology is not available yet to quantify and isolate the role of ground-shaking amplification in the occurrence of coseismic landslides29,35.

The devastating 2015 Mw 7.8 Gorkha earthquake not only generated strong shaking affecting densely populated settlements36, but also caused ~25,000 landslides over a large geographic area (28,344 km2), at distances even exceeding ~160 km from the epicenter37. Are some, or even many, of these landslides due to topographic amplification? If so, how are they spatially distributed with respect to the epicentral region? Here we aim to address these questions by combining numerical simulations and statistical analyses.

The 2015 Nepal earthquake generated peak ground accelerations (PGA) ranging from 0.1 g to 0.5 g38. These are typically considered sufficient to trigger landslides based on global observations (minimum failure thresholds above ~ 0.05 g29), even without topographic amplification.

Our numerical simulations and data-driven analyses attempt to isolate landslides that occur due to amplification from those that did not require amplification. We do so by generating synthetic waveforms through Spectral Element Method simulations39. These simulations include a data-constrained earthquake rupture process and consider cases with and without topography21. The respective Peak Ground Velocity (PGV) maps are shown in Fig. 1.

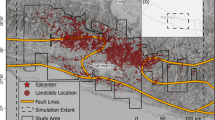
Fig. 1: Synthetic PGV maps overlaid by coseismic landslides.
figure 1

Maps of the study region, showing the area considered for ground motion simulations (rectangle in dashed lines) and the observed coseismic landslide distribution. Colors denote values of simulated PGV without topography (a) and (b) the difference in PGV when we run the simulation with topography. PGV values are computed at ~50,000 densely spaced receiver locations. CMT: Centroid Moment Tensor. PGV values are reported only for the area examined by Roback et al.61 for mapping landslides. Basemap source: Esri,USGS, and the GIS User Community.

Full size image

Results

Numerical analyses of landslide occurrences

The two sets of synthetic waveforms generated by High-Performance-Computing enabled numerical simulations with and without topography are injected in a subsequent experiment to predict coseismic failures through physics-based40,41 and data-driven42,43 models (for details on the procedure, see Method section). We label slope failures triggered in both cases as landslides that occurred even without topographic amplification (i.e., Non-Amplified Landslides, NAL). Those that were triggered uniquely due to topographic amplification, we refer to as Topographically-Amplified Landslides (TAL) in the remainder of the document.

This procedure relies on physics-based (PBM) and data-driven (DDM) susceptibility models. The former corresponds to a Newmark approach40,44 whereas the latter refers to a binomial Generalized Additive Model42. We then identify NAL and TAL using a ground-displacement threshold of 0.1 m for PBM and a probability threshold of 0.5 for DDM. These thresholds return 17% and 6% of TAL, for PBM and DDM, respectively, with respect to the overall landslide distribution.

Such differences are expected, as PBM and DDM are two completely different techniques, each one relying on different data. The PBM is based on the shear strength of hillslopes, incorporating the safety factor and given ground acceleration, while the DDM relies on various topographic proxies and PGV (details provided in the Method section). However, we should also stress that both techniques have been extensively tested and are widely used for slope stability assessments. Therefore, despite the percentage difference, TAL spatial density patterns obtained from PBM (Fig. 2a) and DDM (Fig. 2b) appear similar (Pearson’s correlation coefficient = 0.72). The similarity between TAL and DDM is particularly evident in the northeastern sector where the rupture process occurs later and shows relatively small coseismic slip (Fig. 2c). Conversely, a divergence between PBM and DDM can be observed in the northwestern sector.

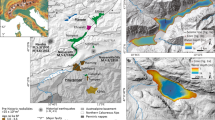
Fig. 2: Spatial density of TAL, NAL and rupture mechanism.
figure 2

Maps of the spatial distribution of Topographically Amplified Landslides (TAL) obtained from Newmark (a) and GAM (b) models. c Presents the finite fault model projected to the Earth surface. d Depicts the ensemble result together with the corresponding QQ-plot and correlation estimate. CMT Centroid Moment Tensor. Basemap source: Esri,USGS, and the GIS User Community.

Full size image

Overall, each model captures part of the process, and hence a single approach cannot be considered satisfying. We therefore combine the two spatial densities into an ensemble model (EM) by averaging the two landslide density maps (Fig. 2d). The idea behind EM is that areas with high estimated TAL density in both models may eventually stand out, while the landslide density signal at locations where the two outputs disagree would spatially fade away. In this process, individual modeling biases would also be smoothed out. In the remainder of the manuscript, further analyses will be based on the EM.

Insight into the amplification patterns

We measure differences in simulated PGV maps obtained from simulations with and without topography, for both NAL (Fig. 3a) and TAL (Fig. 3b). Locations that produced NAL show little to no variations in the respective PGV distributions, with (max density at ~ 0.30 m s−1) and without (max density at ~ 0.31 m s−1) topography. Conversely, locations where TAL occurred, exhibit a large shift in PGV, with maximum kernel densities ranging from ~ 0.15 m s−1 to ~ 0.40 m s−1. Without topography, seismic-wave propagation and corresponding wave-amplitudes are largely controlled by wave-propagation distance, while with topography, local amplifications due to hill-shapes are expected. This is likely the reason why NAL essentially exhibit analogous shaking levels, independent of whether topography is included or not in the simulations. Conversely, TAL appear originally associated with much lower PGV in simulations without topography, compared to the case including the topography.

Fig. 3: TAL and NAL according to simulations and relief.
figure 3

Kernel densities displaying the change in (a) Peak Ground Velocity (PGV) for non-amplified landslides (NAL) and (b) Topographically Amplified Landslides (TAL). The yellow color represents the density of PGV obtained from simulations without topography, whereas the pink color represents the density obtained from simulations with topography. c Presents the mean relief and the width of its 68% confidence interval, calculated radially from the CMT center at 500 m increments. The blue line refers to the kernel density estimation calculated based on the TAL spatial density shown in Fig. 2d.

Full size image

This observation is currently missing in the literature and suggests that amplification may be of limited importance for landslide occurrence near the epicenter. Subsequently, as distance increases, ground-motion amplification becomes more important. While seismic-wave energy dissipates with distance due to geometrical spreading, local topographic scattering may lead to localized constructive wave-interference and corresponding amplitude amplification even at larger epicentral distances. To further explore this spatial component and the influence of topographic variation/roughness as a potential variable controlling this behavior, we examine variation in both local mean relief and density of TAL as a function of distance to the epicenter (here referred to the CMT location, Fig. 3c). Our analysis shows that high TAL concentration away from the CMT epicenter is uncorrelated to surface roughness. This can be seen in the local mean relief as it remains unchanged with epicentral distance.

This observation is further explored in Fig. 4 in which we present landslide information as a function of distance and direction from the CMT epicenter using stacked barplots grouped radially around the epicenter. In Fig. 4a, we separately plot the densities of NAL and TAL. What stands out is that NAL are distributed across all radial distances. However, TAL become prominent from a minimum epicentral distance of ~40 km. Specifically, only 12.8% of TAL are located near the epicenter (~25 km45). Staked barplots documenting the slope steepness (cyan bars) do not present a preferential direction. An analogous illustration is provided in panel (b), where all coseismic landslides (NAL + TAL) are radially plotted against their associated PGV. The stacked barplots (red bars) highlight regions of strongest shaking in our simulations. A preferential direction appears, with PGV values increasing east-south-eastwards. However, when looking at the same information exclusively computed for all landslides, the largest PGV values are concentrated in the east-to- northeast direction within a ~40 km radial distance. In Fig. 4c, we complete this overview by plotting the amplification ratio computed from our simulated PGV values with and without topography. This simulation-based ground-motion amplification pattern covers the directions from northwest to east, being mainly located in areas ~25–90 km far from the source. Interestingly, the stacked barplot (light brown bars) reveals a similar angular directionality with the largest drop in elevation characterizing the local landscape from northwest to east.

Fig. 4: A radial view of TAL, NAL, shaking and landscape properties.
figure 4

Radial plots showing (a) the spatial distribution of TAL and NAL with respect to the CMT epicenter, b the spatial distribution of simulated PGV-values at all landslide locations c Spatial distribution of amplification ratios for all landslides. The radial stack plots in the outer rim represent the mean and 95th percentile of slope, PGV and amplification ratio, irrespective of the landslides. The radial distances to the CMT epicenter are represented in logarithmic scale.

Full size image

To confirm or reject the observations presented above, we perform four additional sensitivity tests by varying the ground motion simulations (details provided in the Method section), including: (1) considering a point source, (2) transforming the inferred on-fault slip distribution to follow a truncated exponential distribution46, (3) a decrease of on-fault slip by 25% and (4) an increase of on-fault slip by 25%. Each test leads to an individual EM, whose NAL and TAL distributions are summarized in a radial plot (Fig. 5).

Fig. 5: TAL, NAL and sensitivity ground motion analyses.
figure 5

Radial plots showing the spatial distribution of TAL and NAL with respect to the CMT epicenter for simulations with (a) a point source, and three modified versions of the original rupture according to (b) a truncated exponential slip distribution, (c) a 25% slip increase, and (d) a 25% slip decrease. The radial distances to the CMT epicenter are represented in logarithmic scale.

Full size image

Despite the variability of ground motion produced in each test, TAL still predominantly occupy the same radial sector (>40 km from the epicenter), as noticed in the original simulation shown in Fig. 4. What changes mostly is the sample size of the TAL population across each test. Specifically, the EM of the original simulation attributed 12% all coseismic landslides to the TAL case. As for the four successive tests shown in Fig. 5, from panel a to d, these respectively isolated 2%, 9%, 2%, and 18%. Below, we will present a conceivable physical interpretation of the dependence between topographic amplification and coseismic landslide occurrence, based on the original test presented in Fig. 4.

Discussion

To date, it is yet to be understood how topographic amplification contributes to large populations of coseismic landslides. We explore two missing elements: (i) quantifying coseismic landslides due to topographic amplification; (ii) locating the spatial extent at which this process exerts a substantial influence.

Recent studies have provided only indirect clues on these topics, often referring to modeling performance rather than an explicit quantification of TAL with respect to NAL. For instance, Chen and Wang23 notice a predictive improvement by accounting for amplification in their model, tested only for the rim of the Aso caldera and the shaking it experienced during the 2016 Kumamoto earthquake. Based on this, the authors emphasize the importance of topographic amplification, prescribing its inclusion for suitable landslide modeling. Here, we estimate the amplification contribution in the range between 6% (DDM) and 17% (PBM) of all landslides triggered by the Gorkha earthquake that shook Nepal in 2015, this being a statistically significant observation in both cases. Therefore, our findings are generally consistent with those of Chen and Wang23. However, our study includes a clear spatial connotation of ground-motion amplification and how this may relate to slope stability. While this has been partially addressed by Stoffel et al.47 by noting that coseimic rockfalls happen at large distances, our study comprises target simulations to numerically explain the available landslide observations.

Our analyses further elucidate on these spatial characteristics. We assess slope stability conditions by employing both physics-based and data-driven models across the entire area affected by landslides. This approach allows us to analyze multiple conditional factors simultaneously, without restricting our analyses to a bivariate framework. For example, Dunham et al.21, examined the spatial distribution of landslides triggered by the Gorkha earthquake concerning ground shaking and relief, noting that the highest landslide concentration did not coincide with the areas of greatest ground shaking in gentle topography. They also provided insight into the relationship between coseismic landslides and topographic amplification highlighting that the role of topography in landslide occurrences cannot be discussed in isolation from other variables that control hillslope stability.

Our findings are consistent with Dunham et al21. Our models consider several topographic, geologic and seismic variables together. As a result, we demonstrate that topographic amplification does not improve landslide prediction in the close epicentral distances (<~40 km). Conversely, ground-motion amplification contributes to an accurate classification of coseismic landslides in the far field, where experienced shaking levels are comparatively lower. In other words, our experiment highlights that the influence of topographic amplification is negligible if ground motion is high, whilst it becomes proportionally more relevant as ground-motion levels decrease (at least within a certain distance range). Dunham et al.21 also demonstrate that landslide frequency begins to increase at a close epicentral distance, around 50 km, and continues to rise with distance from the epicenter. In this context, we could argue that our findings are consistent, although their analyses focus on coseismic landslides as a whole rather than specifically addressing those triggered by topographic amplification.

Our findings have implications beyond the context of the Nepalese landscape and, they raise the question whether similar conclusions apply elsewhere and, if so, whether this is also valid across earthquakes of different magnitudes. To address this question, similar analyses, including earthquake simulations and slope stability assessments under varying topographic, seismic, and geological conditions, need to be conducted. In this context, further study areas could be selected based on two main criteria. One criterion is to focus on sites with high-quality and complete earthquake-induced landslide inventories48. The second criterion involves the accuracy of earthquake simulations, where a reliable earthquake source model and a dense seismic network are crucial for validating the simulation. Such sites could help explore the transferability of our approach to other areas.

This being said, a few challenges still remain. For instance, recognizing TAL and NAL solely on the basis of a scalar approximation of the ground motion time series may not capture the full complexity of the seismic interaction with a given landscape49,50. In this sense, additional shaking parameters or full ground motion waveform could be incorporated in future analyses.

Moreover, the frequency content of the simulations may also play a role. Topographic amplification is often related to topographic resonance, which can manifest at higher frequencies (>1 Hz). Beyond resonance, amplifications related to other processes (focusing, scattering, etc.) can be highest at higher frequencies10. That said, because the study presented here is largely dealing with the amplification of long-wavelength features (i.e., the Himalaya), the frequency range we generate should be sufficient to capture region-scale resonance effects. A question that may influence the validity of these results moving forward relates to the range of frequencies at which topography amplifies shaking, and whether this shaking is expressed in the range of frequencies that in turn influence landsliding. There is almost certainly some overlap, but quantifying that relationship for a given area and earthquake would be elucidating. For example, a mountain that amplifies 0.3 Hz shaking is probably not going to have much influence on a landslide that is sensitive to 2 Hz shaking. Conversely, a slope that amplifies 2 Hz shaking may not have much influence on the PGV from a source dominated by 0.25 Hz energy, but could strongly influence a local landslide sensitive to 2 Hz shaking.

Such considerations may also be landslide-type-dependent. In fact, the resonance frequency of deep-seated landslides differs from shallow ones, or depending on the material these slope failures developed into. Unfortunately, coseismic landslide inventories hardly provide a distinction between different landslide types51. An additional level of complexity is added when considering the quality and completeness of landslide inventories or and/or the geotechnical characterization of the landscape under consideration52,53,54.

Aside from these source of uncertainty to be addressed in future research, we conclude our analyses by highlighting that the role of topographic amplification relative to coseismic landslide occurrence has been mostly, if not exclusively, been explored so far for major earthquakes21,23,55,56,57,58,59. In light of our findings, we question whether topographic amplification may become more dominant for moderate and small earthquakes. In such cases, ground shaking would be less intense compared to stronger earthquakes and, therefore, might not be sufficient to trigger landslides in some instances. As a result, the contribution of topographic amplification could be more substantial for moderate and small earthquakes, especially in areas close to the fault rupture, when it comes to landslide occurrences. If confirmed, this hypothesis would imply that dedicated topographic-amplification studies may be required to suitably characterize the coseismic stability of landscapes exposed to moderate-magnitude earthquake shaking.

Another consideration to be made in the context of earthquake legacy effects60 relates to the questions, if topographic amplification mostly controls coseismic failures in the far-field and the how the local slope dynamics in the region proximal to the rupture are yet to be understood. In fact, if the system is mostly brought to the brink of failure, the amplification could still introduce permanent deformation at hillslopes that could fail during post-seismic phases. Such considerations open another field of research, mostly neglected thus far, corresponding to topographic amplification effects on subsequent earthquakes, rainfall, and snowmelt processes.

Methods

To understand the role of topographic amplification on landslide occurrence, we selected the case of the 2015 7.8 Mw Gorkha Earthquake, because of its magnitude and vicinity to the tallest mountains in the world, the large number of landslides (~25,000) regularly distributed along hanging wall37,61. In addition to the landslides triggered by the mainshock, an aftershock of magnitude Mw 7.2 occurred on 12th of May 2015. This also generated more than 3000 slope failures. This distinction between the coseismic landslides occurred in response to the main and after shocks is made available in the metadata of the inventory provided by Roback et al.61. This coseismic landslide inventory is the basis of our analyses in this work because of its completeness and accuracy, as well as its identified spatial locations of landslide initiation and deposition zones. As it is important for this research to include only the initiation zone where the topographic amplification can have an effect on the genesis of the failure mechanism. Moreover, we exclusively extract the landslide triggered in response to the mainshock.

This event is a well-studied earthquake, with several finite-fault rupture models62,63,64,65 and relatively complete landslide inventories37,66,67,68,69. We obtained the simulated and validated ground motion data at the topographic surface from Dahal et al.49 who used the kinematic finite-fault rupture model by Wei et al.64 to simulate ground-motions using a spectral element method Dahal et al.49 also used Synthetic Aperture Radar Interferometry and strong motion data to validate their ground motion simulation. Briefly, spectral element method employs polynomial equations to solve the weak form of the wave equation21,39 which enables the seamless integration of surface features and establishes it as a suitable technique for studying how seismic waves interact with topographical features. The kinematic source model Dahal et al.49 used for the simulation resolved up to 0.5Hz64 with the capacity to generate realistic seismic waves up to 1 Hz. We deem this frequency range sufficient for our analysis because the dominant frequency range of the Gorkha earthquake has been observed in the range between 0.25 and 0.3070. For landslides that occur far away from the Centroid Moment Tensor (CMT) location, most high frequency seismic waves attenuate before reaching those locations and our observation shows that landslides mostly occurred in 12–90 km distance from the location. Since there is no reliable 3D velocity structure available for the Himalayan region, Dahal and co-authors used a 1D velocity structure obtained from Mahesh et al.71. The extent of the simulation is shown in Fig. 1, and it has a depth of 35 km below mean sea level. Dahal et al.49 validated the simulated ground motion at the observed locations (seismic stations and permanent geodetic stations) by visually comparing the seismic waveforms as well as by calculating the Kristekova scores72, both of which show that up to 1 Hz frequency, the simulations are adequately represented. Moreover, they also validated the ground motion simulation in more spatially dense manner using InSAR data. Quantitatively, their validation approach for the fault model of Wei et al.64 showed the best fit in both InSAR and strong motion observation with correlation coefficient of 0.91 and Kristekova72 score of 6.28/10 (amplitude) and 6.87/10 (phase) at seismic station “CHLM” for north-south direction. At other seismic stations and directions, the Kristekova72 scores showed good fit with values above 4 in all cases.

Applying the same simulation setup, we also generated a “flat-earth” ground-motion scenario by neglecting topography. This is used to differentiate between topographically amplified and non-amplified ground motion signals, using the wavefield-adapted meshing technique73,74. Both meshes could resolve seismic waves up to 1.5 Hz and had the same velocity structure, spatial coverage, absorbing boundary, and resolution, with the only difference being the addition of topography and flat surface. The synthetic waveforms were recorded at the centroid of each landslide initiation location and the same number of locations without landslides which are at least 500 m away from the landslide locations and above 10° slope. The locations without landslides are used to fit the physically based and data driven models and to test their goodness on representing the landslide distribution for this event.

For the simulated ground motions we run the Newmark approach40,41,44 for both with and without topography simulations to obtain the ground displacement at the locations of interest. This approach first calculates the Factor of Safety (FoS) using Equation (1), given as

$${{{\rm{FoS}}}}=\frac{C}{{t}_{m}}\frac{1}{\left({\rho }_{r}g\right)\sin (\alpha )}+\frac{\tan (\varphi )}{\tan (\alpha )}-\frac{m\left({\rho }_{w}g\right)\tan (\varphi )}{\left({\rho }_{r}g\right)\tan (\alpha )}$$
(1)

which represents the stress over strain ratio and uses FoS to calculate critical acceleration (ac) using Equation (2),

$${ac}=({{{\rm{FoS}}}}-1)g\sin \alpha$$
(2)

The critical acceleration ac represents the threshold above which the slope starts to deform (which is the cumulative deformation known as the Newmark displacement). Note that \({FoS}\) stands for factor of safety, while \(C\) is cohesion, \({t}_{m}\) is landslide thickness, \({\rho }_{r}\) is rock and soil density, \(g\) is the acceleration due to gravity, \(\alpha\) is slope angle, \(\varphi\) is the internal friction angle, \(m\) is groundwater height, and, \({\rho }_{w}\) is the density of water. In Equation (2), \({{{\rm{ac}}}}\) is critical acceleration, \({{{\rm{FoS}}}}\) is the factor of safety, \(g\) is the acceleration due to gravity, and \(\alpha\) is slope angle.

This method requires geotechnical parameters that are not available at high resolution in the case of Nepal, hence we largely obtain these from literature (e.g., Gallen et al.31). Given the availability of slope information at 30 m resolution from Shuttle Radar Topography Mission (SRTM)75, we calculate spatially varying FoS-values under the assumption of constant rock and soil density of 2300 kg m−3, internal friction angle of 30°, water table height at 0 meters, and aggregated strength parameter of 15 kPa m−1 31. Once the FoS-distribtion is obtained, we use it to estimate ac. Deviating from the simplified Newmark approach applied by Gallen et al.31, instead of using peak ground velocity, we used the ac threshold obtained from the acceleration signal and calculated Newmark displacements by double-integrating the difference between acceleration amplitude in time at and ac, as prescribed by Newmark44 and demonstrated to be suitable in similar contexts41. Here, it is crucial to mention that the ground motion signal obtained in three directions was projected towards the slope direction before calculating the acceleration above ac. The equation to project the 3D ground motion data into the slope direction is shown by (3), where slope angle (\(\alpha\)) and aspect (\(\beta\)) are used to project the ground motion towards slope direction. Moreover the equation to calculate the Newmark displacement (D) is shown by (4), where the integration is performed from time 0 till the earthquake lasts (\({t}_{e}\)).

$${at}=\left(\left(\frac{a{t}_{x}}{\sin \left(\beta \right)}\right)+\left(\frac{a{t}_{y}}{\cos \left(\beta \right)}\right)* \cos \left(\alpha \right)\right)-\left(a{t}_{z}* \sin \left(\alpha \right)\right)$$
(3)
$$D={{\iint }_{\!\!\!t=0}^{{t}_{e}}}\left({at}-{ac}\right){dt}$$
(4)

Having computed the Newmark displacements, we used a threshold of 10 cm76,77 to classify our entire receiver array into landslide location and non-landslide location. The threshold of 10 cm is selected by evaluating the best fitting threshold values between 5 and 15 cm, which is commonly accepted value range in the literature. To identify the best fitting value, we tested different thresholds increasing by 0.5 cm and observed how well it can differentiate the observed landslide and no-landslide locations and selected 10 cm as it provided the best separation on the observed dataset. Then, to identify landslides caused by topographic amplification (TAL), we selected the observed landslides that had less than 10 cm displacement without topography (dnt) and above 10 cm displacement with topography (dt).The landslides caused without influence of topographic amplification (Non-Amplified Landslides, NAL) were classified as all the landslides which had dnt above 10 cm.

Even though the Newmark approach is widely used and considered a powerful tool for slope stability analysis, the geotechnical characterization of a large geographic area has always constituted one of its major limitations78,79. Therefore, we also employed a data-driven Generalized Additive Model (GAM)42 approach, whereby GAM is a statistical tool to model landslide presence and absence (susceptibility) by using various linear and non-linear covariate effects. To support the analyses, we included terrain characteristics namely, Slope Exposition and Steepness, Curvature, Topographic Position Index, and Elevation, together with the PGV obtained from both simulations. We did not include geology due to its coarse information. Similarly, we did not feature the precipitation as a landslide predictor because the earthquake occurred during the dry season in Nepal31.

We applied the GAM approach by fitting 70% of the receiver locations based on input variables and simulation-based PGV (with topography); for validation, we retained 30% of the receiver locations obtaining an Area Under Curve (AUC) value of 0.82, which demonstrates that the model produced excellent performance according to the classification standard proposed by Hosmer and Lemeshow80. Using the validated model, we calculated the probability of landslide occurrence for all receiver locations for both simulation cases, with and without topography. Similar to the Newmark approach, to identify landslides caused by topographic amplification (TAL), we selected the observed landslides that were initially estimated with a probability of landslide occurrence less than 0.5 in the analyses without topography and that only appeared estimated with a probability greater than 0.5 adding the topography to the analyses. As for the NAL, these were identified with locations where the probability was consistently above 0.5 both in the cases with and without topography. The value 0.5 is mainly selected because we have a balanced sample of landslide and no-landslide locations and in a probabilistic modelling of balanced dataset, 0.5 probability score should differentiate if it can be classified as a landslide or not. Moreover, to test this assumption quantitatively, we also used multiple thresholds ranging from 0.3 to 0.7, increasing by 0.5 each time to test how well this threshold fits the model with observed data and selected 0.5 as it was the best fit.

Statistical methods have limitations as they do not simulate the physical processes per se. Thus, to reduce such limitations from both the Newmark and GAM models and to obtain more reliable representative result, we generate an ensemble of the two81,82. To create the ensemble, we first calculated the spatial kernel density for 1 × 1 km2 area for both TAL and NAL and averaged their density at each grid point. The correlation in density between both methods for TAL was 0.72, showing that both methods agree for the majority of locations about the influence of topographic amplification.

To understand the spatial pattern of individual landslide locations (TAL and NAL) with respect to the seismic energy release, we calculated the distance and direction from the CMT location obtained from the United States Geological Survey (USGS)38. The reason to use centroid moment tensor instead of fault plane in calculating distance and direction is to understand the spatial patterns of TAL and NAL in relation to the largest seismic energy release83,84,85 which has a higher effect in the entire region as well as to have a uniformity in comparing landslides because there is no way to identify effect of each sub-fault on each landslide.

To assess the sensitivity of our observation, we extend the earthquake simulations (for both with and without topography cases) provided by Dahal et al.49. We do so by modifying the source model while keeping the mesh and sub-surface structure intact for four different cases. For the first sensitivity test, we run the simulation with the point source model obtained from the USGS38. In the second test, we modified the source model of Wei et al.64, and convert their slip distribution into truncated exponential, following Thingbaijam et al.46. For two additional tests, we increased and decreased the slip by 25%, respectively. These four scenarios were chosen to test how small change in slip may affect our results while keeping magnitude and fault geometry fixed. For reasons of consistency with respect to the reference model based on the synthetic waveform from Dahal et al.,49 the output produced by each sensitivity test is initially fed to a Newmark and GAM models and their individual results are later averaged into a modeled ensemble.