Introduction

Vertical diffusivity (Kv; coefficient of vertical mixing) is known to have a significant influence on the water mass transformation in the ocean and the strength of the global deep ocean circulation. A well-known estimate of the vertical diffusion coefficient was proposed in a classic paper by Munk1; based on the global balance of ocean tracers such as temperature, salinity, and radiocarbon (Δ14C), a typical Kv value at a depth of around 1000 m was estimated to be about 1 × 10−4 m2 s−1. However, many subsequent studies have shown that Kv values are spatially very heterogeneous2, and their heterogeneity significantly influences the global ocean deep circulation3. Hence, some attempts have been made to estimate the three-dimensional distribution of Kv from tracer distributions4,5,6, but these estimates are based on local balances and do not take into account the global heat and salinity balance. Therefore, other attempts to estimate Kv using an assimilated ocean general circulation model (OGCM) that satisfies the global balance have been also conducted7,8. However, its large computational cost makes long-term integration and application to steady-state balances difficult9, and therefore, estimation of vertical diffusion with a global ocean model is still challenging.

On the other hand, various observations have been made about the Kv value. The most reliable data can be obtained by direct turbulence measurements from shipboard observations, but currently the number of data is limited, creating the inability to determine global distributions from those data alone. In recent years, global-scale data with indirect estimates have been obtained via fine-scale parameterization, such as the compiled ship data by Kunze10 and the horizontal distribution estimates using Argo floats by Whalen et al. (2015)11. Various model parameterizations providing spatial Kv distributions have also been proposed and utilized in global ocean models12,13,14. Nevertheless, while some reported that these parameterizations improved the model’s reproducibility13, inconsistencies have also been highlighted between the model’s distributions and the aforementioned observational estimates15. Currently, comparisons between the distributions used in the model and the observation-based estimates have not been adequately verified.

Based on the above limitations, this study reports the inverse estimations of a global Kv distribution from tracer distributions using an approach combining OGCM and the steady-state tracer model. This study proposes a 3D distribution of Kv including the deep ocean that most realistically reproduces the steady-state distribution of observed temperature and salinity when used in an OGCM. Subsequently, we compared our results with direct turbulence measurement data from shipboard observations16 and wide-range observation data using fine-scale parameterization10,11, followed by discussions on the current understanding of Kv distributions in the global ocean.

Results

Ocean general circulation model (COCO) results

Fig. 1 shows the results of our OGCM (CCSR Ocean Component Model; COCO17) experiment before optimization. Our COCO experiment reproduced the meridional overturning circulation, temperature, and salinity distributions, which were as realistic as typical global OGCMs. The spatial distributions of our model bias from the observed temperature and salinity data are similar to those of the previously reported biases of OGCMs (e.g., Figs. 13 and 14 in Tsujino et al. 2020)18. For example, COCO result shows the high-temperature, high-salt bias in the mid-latitudes of the upper North Pacific (Fig. 1h, i), the low-temperature, low-salt bias in the upper Indian Ocean (Fig. 1k, l), and the high-salt bias in Antarctic Intermediate Water of the South Atlantic (Fig. 1e, f), which are also found in the state-of-the-art OMIP2 multi model mean result (Fig. S4). On the other hand, thanks to the relaxation of temperature and salinity to the observed climatology at high latitudes (see Methods), the biases due to the deep-water formation process were suppressed in our results. For instance, the high-temperature bias due to the insufficient reproduction of North Atlantic deep water overflow and the low-temperature low-salt bias due to problems with the deep-water formation processes in the Southern Ocean were all suppressed, resulting in smaller biases (especially in the deep ocean) than in the typical global OGCMs. Detailed description of the model biases and their comparison with state-of-the-art OGCMs (OMIP2 from Tsujino et al. 2020) are given in Section 3 of Supplementary Note.

Fig. 1: Results of initial COCO simulation.
figure 1

a The meridional overturning circulation (MOC) in the global ocean. b The zonally averaged distribution (left) and vertical profile (right) of potential temperature bias in the global ocean. c The same as (b) but for salinity bias in the global ocean. d–f The same as (a–c) but in the Atlantic Ocean. g–i The same as (a–c) but in the Pacific Ocean. j–l The same as (a–c) but in the Indian Ocean. Counter intervals are 2 Sv (106 m3s−1) for MOC. The units for temperature and salinity are °C and ‰, respectively. Results with the vertical diffusivity of T00 (Tsujino et al. 2000) are shown here.

Full size image

Adjoint calculation results from the steady-state tracer model (STAR)

To reduce the above-mentioned temperature and salinity biases of COCO, the vertical diffusivity (Kv) distribution was optimized by using the adjoint method with the tracer model STAR (see Method and Fig. S1b for the procedure). After about 2000 iterations in the adjoint method (2000 repetitions of step 1–4 in Fig. S1b), we obtained an optimal solution as the converged value (Fig. S7a); the initial vertically one-dimensional distribution (Fig. S7b) was optimized to have a 3D distribution (Fig. S7e, h, k, n). We observed significant reductions of the temperature and salinity bias at all locations after the optimization (Fig. S7) compared to the COCO results (Fig. 1).

Kv optimization via iterative calculations with COCO and STAR

In the above optimization by STAR, note that a dynamical inconsistency between the optimized Kv and the ocean circulation field remained. Namely, when the optimized Kv is used in COCO, the obtained ocean velocity field will not match that used in STAR. Therefore, in order to resolve the inconsistency, this study attempted a method that repeats the COCO calculation and the STAR optimization (see Method and Fig. S1c for the procedure). Figure 2 shows the results as black lines: the cost function’s evolution (Fig. 2a), the vertical Kv distributions (Fig. 2b), the temperature’s root mean square error (RMSE; Fig. 2c), and the salinity’s RMSE (Fig. 2d) for each iteration. In Fig. 2a, although we observed a discontinuous error increase in error near the 2000th iteration that corresponded to the error increase as a result of COCO recalculation, such discontinuities gradually became smaller after the second (around the 3200th iteration) and the third (around the 3500th iteration) COCO recalculations. This discontinuity almost disappeared after about five cycles of STAR and COCO, and we subsequently observed no further error decrease, confirming a successful convergence to the optimal solution. Thus, in this study, we considered the result after ten cycles of COCO and STAR as the optimal solution.

Fig. 2: Results of the optimization process using COCO and STAR from 6 different initial vertical diffusivities.
figure 2

a Cost function versus iteration number during the optimization. Note that discontinuities arose at each optimization cycle (i.e., at the timing of COCO recalculation with an updated vertical diffusivity). b Vertical profile of vertical diffusivity in the global ocean at each optimization cycle. c Vertical profile of root mean square error (RMSE) for the ocean potential temperature in the global ocean at each optimization cycle. d The same as (c) but for the ocean salinity. The results are shown with black line for T00 (Tsujino et al. 2000), red line for K0.1 (constant value of 0.1), green line for K1 (constant value of 1), blue line for S02 (St. Laurent et al. 2002), yellow line for O13 (Oka and Niwa, 2013), and purple line for dL20 (de Lavergne et al. 2020).

Full size image

Our optimal solution was confirmed to be modified from an initial profile by Tsujno et al. (2000)19 and have a somewhat smaller value around 1000–3500 m (Fig. 3). For the zonally averaged distribution, our optimal solution was generally similar to that obtained in STAR (Fig. S7), but with minor modifications. It was also revealed that the temperature and salinity biases (Fig. S10) were significantly reduced compared to the original COCO results (Fig. 1) and the error had been reduced to a same level as in the STAR optimization results (Fig. S7). Furthermore, while similar results as the first COCO calculation (Fig. 1) were maintained for the meridional overturning circulation (MOC; Fig. S10a, d, g, j), the maximum volume transport of the Atlantic MOC was increased (20.17 Sv→24.23 Sv), that of the Pacific MOC was weakened (11.45 Sv→9.62 Sv) and that of the Indian MOC was strengthened (4.45 Sv→6.30 Sv).

Fig. 3: The distributions of vertical diffusivity after optimization.
figure 3

a The zonally averaged distribution (left) and vertical profile (right) for the optimized vertical diffusivity in the global ocean. b The same as (a) but in the Atlantic Ocean. c The same as (a) but in the Pacific Ocean. d The same as (a) but in the Indian Ocean. Counter intervals are 0.2 cm2/s. Results from the initial vertical diffusivity of T00 (Tsujino et al. 2000) are shown here, and both initial (thin line) and optimized (bold line) values are displayed for the vertical profile. Regarding the vertical profile, observational estimates from Whalen et al. (2015) and Kunze et al. (2017) are also displayed with red and blue lines, respectively.

Full size image

Dependency of initial Kv distribution

As shown in Fig. 3, the optimized 1D vertical distribution of Kv did not differ significantly from the initial profile of Tsujino et al. (2000). There are two possible reasons for this. The first is the possibility that the obtained results were local solutions near the initial values, and the second is that the profile by Tsujino et al. (2000) was a vertical distribution close to the optimal solution. To evaluate these two possibilities, we performed experiments starting from various initial Kv distributions: a constant value of 0.1 cm2/s (K0.1), another constant value of 1 cm2/s (K1), a distribution based on the parameterization of St. Laurent et al. (S02)12, a distribution based on the TideNF case of Oka and Niwa (2013) (O13)13, and a distribution based on de Lavergne et al. (2020) (dL20)14. The results are shown with red (K0.1), green (K1), blue (S02), yellow (O13), and purple (dL20) lines in Fig. 2. The model error from the first COCO calculation differed depending on the initial distribution of Kv, with the initial values for the cost function being 1.15 for T00, 1.86 for K0.1, 2.06 for K1, 1.01 for S02, 0.90 for O13 and 0.89 for dL20. After optimization, the cost function values became 0.39 for T00, 0.38 for K0.1, 0.40 for K1, 0.39 for S02, 0.40 for O13, and 0.41 for dL20, confirming the relative similarity of the final values in all cases. This result means that the optimization worked well in all cases, regardless of the initial value of Kv. The vertical profiles of root mean square error (RMSE) of temperature and salinity (Fig. 2c, d) also indicated that the inter-case differences present in the initial values almost disappeared after optimization and converged to similar distributions. As the optimization process proceeded, the difference in the vertical profile of Kv depending on the initial values (Initial in Fig. 2b) became gradually smaller (Initial->cycle1->cycle2 in Fig. 2b) and revealed a convergence to a similar one regardless of the initial value (cycle 10 in Fig. 2b). Still, dependence on the initial value remained somewhat in the ocean deeper than 2000 m, which will be discussed later. The obtained optimized vertical profiles show a gradual increase with depth, regardless of various initial Kv profiles. This result supports the idea presented in the recent paper20 titled “Middepth Recipes,” which indicates that the vertical change of Kv is necessary to explain the observed stratification at mid-depth (between 1000 m and 3000 m) and that the frequently cited value of 1 cm2/s from “Abyssal Recipes”1 is representative only of the bottom of the mid depth. In summary, the vertical profile obtained in this study is considered as the global optimal solution rather than the local solution, and the vertical profile of T00 was also close to the optimal solution.

Hereafter, we will look at the horizontal distribution of the optimized Kv. For the horizontal distribution in the 500–1000 m upper layer (Fig. S14), a generally common distribution is obtained regardless of the initial value. For example, the value of Kv was as small as 0.1 cm2/s in many locations in the open ocean, with large values exceeding 1 cm2/s being limited in areas close to the coast, such as the Sea of Okhotsk and the Indonesian Sea, known for strong tidal mixing2.

The horizontal distribution at a depth of 1000–2000 m (Fig. S15) was also similar to the 500–1000 m distribution; namely, many areas had small values of about 0.1 cm2/s with large values being limited in areas close to the coast like the Indonesian Sea, the northeast Atlantic, and the northern Indian Ocean. These features were confirmed to be independent of the initial values. Locally, however, initial value dependence was observed, for example, near the areas with strong tidal mixing such as the Tuamotu archipelago in the South Pacific and the Kerguelen Plateau in the South Indian Ocean2. In cases where this information was included in the initial distribution, such as the O13 and dL20 cases, these strong local mixing regions remained in the distribution after optimization. Conversely, in the case of K0.1, K1, and T00 with horizontally uniform initial values, such local high Kv values are not well reproduced.

For the horizontal distributions at depths deeper than 2000 m (Fig. S16), the optimized distributions for the T00, K0.1, and K1 cases showed common features, such as high values at the central part of the Pacific Ocean and high (low) values at the eastern (western) side of the Atlantic Ocean. In addition to the above-mentioned characteristics, the information from the initial distribution also remained to a considerable extent in the post-optimized distribution for the S02, O13, and dL20 cases. Namely, the initial values of S02, O13, and dL20 were based on tidal mixing parameterizations containing strong vertical mixing near the seafloor locally (e.g., in the western Pacific region), with such initial distribution still being reflected in the post-optimized distribution. These results suggest more difficult inverse estimations for locally strong vertical mixing near the seafloor than in other ocean areas.

To further discuss the robustness of our results, we investigated other parameter dependencies through additional experiments (Table S1), in addition to the initial value dependence (InitKv) described above. Specifically, a parameter involved in the optimization (Wsalinity: the weight parameter of salinity error to calculate cost function), model parameters introduced for steady-state calculations ignoring seasonal variations (Rsfc: the parameter for restoring to the climatology in surface layers, and Rpolar: the parameter for restoring to the climatology at high latitudes), and model parameters for OGCM (Kiso: isopycnal diffusivity, and Kg: isopycnal thickness diffusivity) were also tested by changing these parameter settings. Note that only Kv is the parameter to be optimized and optimization of parameters other than Kv was not performed in this study and will be a future study. Results are shown and discussed in Supplementary Materials (refer to Figs. S17–20 and Section 6 of Supplementary Note). Investigations revealed that although some parameter dependence was observed, the overall Kv distribution after optimization was generally the same. These results suggested that the Kv distribution obtained in this study was an optimal solution that is independent of the initial values and selected model parameters, except that there was some dependence on the initial values in the deeper ocean (especially the spatial distribution at depths greater than 2000 m).

Comparison with the observation-based estimates

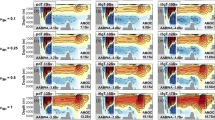
Finally, we compare our results with the observation-based Kv estimates: Whalen et al. (2015) based on temperature-salinity data profiles from Argo floats11, Kunze et al. (2017) based on the CTD data profiles from shipboard observations10, and Waterhouse et al. (2014) which is a compiled dataset of direct turbulent observations16. The results are shown in Fig. 4, in which our optimized results are illustrated for two cases: the case with an initial value of T00 (top panel) and that with dL20 (second from the top). For the distribution at 500–1000 m (Fig. 4a, d, g, j, m), the global characteristics show some similarities with the observed estimates. For example, very small values of about 0.1 cm2/s in most of the open oceans and large values localized near the coast are observed in both our results and the observed estimates. This was also found for the distribution at 1000–2000 m (Fig. 4b, e, h, k, n). Looking at the details of the distribution, our results showed high values around the Mediterranean Sea and the Red Sea, however, no such high values existed in the observational estimates. This could be due to model problems; insufficient representation of the high-salinity overflow process could have skewed our estimates. Another interpretation could be that the observational estimates referenced here missed some mixing processes in this ocean area.

Fig. 4: Comparison of this study’s vertical diffusivity with observation-based estimations.
figure 4

a The depth-averaged Kv distributions between 500 m and 1000 m obtained when T00 (Tsujino et al. 2000) was used as the initial value. b The same as (a) but for depth average between 1000 m and 2000 m. c The same as (a) but for depth average below 2000 m. d–f The same as (a–c) but when dL20 (de Lavergne et al. 2020) was used for the initial value. g–i The same as (a–c) but from the Argo-based fine-structure estimation of Whalen et al. (2015). j–l The same as (a–c) but from the ship-based fine-structure estimation of Kunze (2017). m–o The same as (a–c) but from the micro-structure observation of Waterhouse et al. (2014). The unit is cm2/s and the base-10 logarithmic scale is used for all figures. In (a–f), values in the polar regions where the relaxation of temperature and salinity to the observed climatology is applied are not shown.

Full size image

Regarding the distribution at depths greater than 2000 m (Fig. 4c, f, i, l, o), significant differences were observed between our results and the observational estimates, with our results showing an overall overestimation compared with the observational estimate. This was also confirmed from the vertical profiles in Fig. 3; our results increased with depth below 2000 m, contrasting Kunze et al. (2017)’s estimate that showed no such trend. Regarding horizontal distribution, our results showed large values close to 3 cm2/s in many regions (Fig. S13c–f), while such large values were rarely found in Kunze et al. (2017)’s estimate (Fig. S13l). Alternatively, Waterhouse et al. (2014), for which partial data existed, reported values exceeding 3 cm2/s off Hawaii and near the Drake Passage in the Southern Ocean (Fig. 13o). There are still large discrepancies among the observational estimates especially in the deep ocean (also note that data of Whalen et al. (2015) is completely missing below 2000 m). Our results suggested high values in the central Pacific and high (low) values in the western (eastern) side of the Atlantic, but these results are difficult to be confirmed from the current observational estimates, creating a gap for future studies.

Discussion

Although it has been difficult to optimize the vertical diffusion coefficients (Kv) directly using an assimilated OGCM due to the difficulty in applying it to steady-state calculations, this study overcame this technical difficulty by adopting a method combining OGCM and the steady-state tracer model. Consequently, this study succeeded in obtaining a 3D distribution of Kv including the deep ocean that most realistically reproduces the observed steady-state tracer distribution of temperature and salinity using an OGCM.

The distributions of Kv obtained in this study captured the basic characteristics of the observational estimates for the upper ocean, but we found significant differences in the estimated values in the deep ocean. Namely, this study estimated that the value of Kv in the deep ocean was large (close to 3 cm2/s) in many areas, which was significantly larger than the current observational estimates. In OGCM simulations, a value of Kv exceeding 1 cm2/s was usually assumed in the deep ocean; if a small Kv value consistent with the observational estimates was used in the model, previous studies pointed out that the simulated ocean deep circulation became weaker compared to the reality13,19. Therefore, this study clarifies that the inconsistency between the model-assumed and observation-based Kv distributions, which had been known empirically, certainly exists in the latest observation data and the model.

The difference between the two should be explained by issues in the current OGCM and/or by problems in the observation-based estimates. As for the former, while it has been confirmed that the model biases in temperature and salinity in our COCO OGCM used in this study are also common in the state-of-the-art OGCMs reported in OMIP2 (see Section 3 of Supplementary Note), further validation is needed to determine whether it is reasonable to correct these model biases through the optimization of Kv. For instance, optimizing model parameters other than Kv, such as isopycnal thickness diffusivity, should be explored and discussed in future studies. In addition, we plan to utilize various ocean tracers such as Δ14C in addition to temperature and salinity as an exciting extension of our optimization for future work. Specifically, it is worth investigating how useful ocean tracers are for constraining Kv (and other model parameter) distributions in the deep ocean. As for the latter, from an observational perspective, the estimate is not perfect due to measurement uncertainties, inaccuracies in methodological assumptions, and the intermittency of mixing events. Therefore, it is important to evaluate the validity of the assumptions made in Whalen et al. (2015) and Kunze et al. (2017), such as the assumption of the constant shear-to-strain variance ratio of 3. Furthermore, enhancing the direct turbulence observations reported in Waterhouse et al. (2014), which are currently available only in the limited ocean areas (Fig. 4m, n, o), is essential for obtaining more reliable data on a broader scale, particularly in the deep ocean. Additionally, it may also be necessary to examine whether the observed data, which are instantaneous values at a certain time and place, can be regarded as representative values in the model grid21. Further research from both model and observation would be needed to resolve the mismatch regarding the Kv values in the deep ocean.

Methods

Ocean general circulation model (OGCM): COCO

The OGCM used was COCO version 4.017. The model has 128 × 64 horizontal grids and 24 vertical layers. The surface heat and freshwater fluxes were diagnosed by 10-day damping restorations of the sea surface temperature and salinity toward the annual-mean observational climatology22, and the surface momentum flux was applied from the annual-mean wind stress data23. In addition to the surface forcing, the body forcing (i.e., 10-day damping restorations of the temperature and salinity in the internal ocean) to observational climatology22 is applied in high-latitude ocean (shown by the red-colored regions in Fig. S2a). Since seasonal variations were excluded from our simulation, this body forcing enabled us to realistically reproduce the deep-ocean temperature and salinity originating from the winter-season deep water formation. Note also that, since mixed layer parameterization was not applied here, we applied the body forcing in the near-surface ocean (0–190 m: 5 surface model layers) to realistically maintain the structure of the ocean surface mixed layer. Regarding the treatment of mesoscale eddies, the model employs isopycnal diffusion and isopycnal thickness diffusion parameterizations24. For the following discussion, it is important to note that no special parameterization or specific treatment has been applied to the exchange processes in marginal seas, such as the Mediterranean Sea and the Red Sea, or in narrow passages, such as the Bering Strait and the Indonesian Throughflow. The model is integrated for 5000 years and the last 1000-year time-averaged output was used as input data for the ocean tracer model.

Ocean tracer model: Sea Tracer Adjoint calculatoR (STAR)

In addition to OGCM, the ocean tracer model was utilized in this study. The ocean tracer model was developed here by the author and named “Sea Tracer Adjoint calculatoR (STAR)”. The model STAR consists of two parts: the forward calculation and the adjoint calculation, which are described in turn below.

In the forward calculation, the model solves the following steady-state ocean tracer equation:

$${{\rm{Tc}}}={{\rm{q}}},$$
(1)

where T is an advection-diffusion transport operator, c is the ocean tracer (temperature or salinity), and q represents the source/sink term of the ocean tracer (e.g., the sea surface heat and freshwater fluxes). As long as the operator T (and q) acts linearly on c, Eq. (1) can be discretized as a matrix form25. Therefore, we can obtain the vector c after solving the system of equations shown in (1) using a sparse matrix solver. Apart from the fact that the steady state is explicitly assumed, note that the Eq. (1) is the same as the following advection-diffusion equation:

$${{\rm{dc}}}/{{\rm{dt}}}={{\rm{adv}}}({{\rm{c}}})+{{\rm{dif}}}({{\rm{c}}})+{{\rm{q}}},$$
(2)

where adv is the advection term and dif is the diffusion term. The Eq. (2) is the same as that used in the tracer calculation routine of COCO. Therefore, if output data from COCO (e.g., ocean velocity fields) are utilized as input data to calculate Eq. (1) as input data, the same tracer distribution as COCO can be reproduced in STAR. It is crucial for our optimization that both tracer calculation in COCO and that in STAR become the same result. For this purpose, the same finite-difference discretization method (simple centered scheme) was used for the advection and diffusion terms in both COCO and STAR in this study.

In the adjoint calculation, value of model parameter (vertical diffusivity in this study) is systematically modified so that the model error (i.e., the cost function FC described later) becomes smaller. With updated model parameter obtained after the adjoint calculation, the next forward calculation is guaranteed that its model error becomes somewhat smaller than the previous forward calculation. We repeat the forward and adjoint calculations (Fig. S1b) until the model error becomes unchanged and reaches its minimum. Typically, after about 1000 iterations, an optimized distribution of the vertical diffusivity can be obtained. Details about the adjoint calculation can be obtained from previous papers such as Schlizer (1993)26 and DeVries and Primeau (2007)27.

Optimization of the ocean vertical diffusivity using COCO and STAR

In the STAR calculation described above, the ocean velocity distribution (which was originally calculated from COCO under the initial vertical diffusivity) was prescribed and assumed to be unchanged. In spite that the ocean circulation depends on the distribution of the vertical diffusivity, it means that the effect of the vertical diffusivity on the ocean circulation was neglected in optimization by STAR. In other words, the distribution of vertical diffusivity obtained from STAR and the ocean velocity field used in the tracer calculation were not physically consistent. To solve this problem, we again perform COCO calculation using the vertical diffusivity optimized by STAR. Note that the update of the ocean velocity by the recalculation of COCO causes the increase in the value of the model error; therefore, under the updated ocean velocity, we perform the further optimization of the vertical diffusivity by STAR. We repeat the calculation of COCO and STAR (Fig. S1c) until the vertical diffusivity becomes almost unchanged. Finally, after 10 times COCO and STAR recalculations, we obtain the optimized distribution of the vertical diffusivity that can minimize the temperature and salinity errors in a physically consistent way.

As described at the beginning of this paper, directly optimizing the vertical diffusion coefficient using an assimilated OGCM is difficult because applying it to a steady state requires long-time integration and its computational load is too high even with current computing power. The method described here successfully overcame such technical difficulties by explicitly assuming the steady state in tracer calculations, significantly reducing the computational cost.

Cost function

In this study, we define the cost function (FC) as the volume integral of temperature and salinity errors:

$${{\rm{F}}}_{{\rm{C}}}\,=\,\int ({{\rm{w}}}_{{\rm{Temp}}} \, * \, ({{\rm{T}}}-{{\rm{T}}}_{{\rm{obs}}})^{2}+{{\rm{w}}}_{{\rm{Salinity}}} \, * \, ({{\rm{S}}}-{{\rm{S}}}_{{\rm{obs}}})^{2}) \, \, {{\rm{dv}}},$$
(3)

where T and Tobs are the model and observed temperatures, S and Sobs are model and observed salinities, and wTemp and wSalinity are weights for temperature and salinity errors, respectively. In this study, the WOA13 climatology is used for Tobs and Sobs22. The error weight is defined from the uncertainty of the observational temperature and salinity climatology (Tobs_err and Sobs_err):

$${{\rm{w}}}_{{\rm{Temp}}}\,=\,(1/{{\rm{T}}}_{{{\rm{obs}}}{\_}{{\rm{err}}}})^{2}/{{\rm{V}}}_{{\rm{ocn}}},$$
(4)

and

$${{\rm{w}}}_{{\rm{Salinity}}}\,=\,(1/{{\rm{S}}}_{{{\rm{obs}}}{\_}{{\rm{err}}}})^{2}/{{\rm{V}}}_{{\rm{ocn}}},$$
(5)

where Vocn is the global ocean volume. Following Schmittner et al. (2009)28, Tobs_err and Sobs_err are defined as the sums of the standard error provided directly from the WOA13 dataset and mapping error. Note that Tobs_err and Sobs_err yield spatially variable distributions; their vertical profiles are shown in Fig. S2d and g, respectively. Finally, to suppress negative value of Kv, note that large penalty against the negative Kv is also additionally applied in the cost function.