Subsurface structure and impact process of Yilan Crater, northeastern China

Abstract

Yilan Crater is a newly discovered impact structure in Northeast China. However, the impact process and its subsurface properties have not been properly investigated yet. Here we employed multiple seismic methods to gain insight on its subsurface structures, based on an ultra-dense observation with 220 seismic nodes. We observed a clear site amplification within the circular region of the crater generated by loose sediment and impact-fractured rocks. The resulting bowl-shaped structure beneath the Yilan crater was further revealed by the ambient noise tomography and Horizontal-to-Vertical Spectral Ratio analysis. Multiple solutions for the impact velocity and diameter were found by a parametric investigation, while the impact energy is around 1 E17 Joules, likely representing one of the most significant impact events in the last 80,000 years. These findings offer new insights into the Yilan impact event and its potential effects on the surrounding environment, highlighting the need for further multidisciplinary investigations.

Introduction

Impact craters are among the most captivating geological features in the solar system and gather even greater attention when they are discovered on our planet. To date, the Planetary and Space Science Centre’s Earth Impact Database has documented nearly 200 craters (https://impact.uwo.ca/map/, last accessed on 04/01/2024). Impact craters capture the interest of both the scientific community and the general public. They serve as valuable laboratories for planetary scientific research, and provide a unique window to study the deep Earth rocks and minerals that are otherwise difficult to sample. These deep rocks can form during impact events, where extreme high-pressure and high-temperature conditions that are similar to those at depth within planetary interiors. Furthermore, craters offer a great opportunity to investigate the causal relationship between impact events and significant changes in paleontology and paleoenvironment¹.

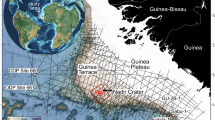
Yilan Crater, located in Heilongjiang Province Northeast China, is the second confirmed impact structure in China, following the Xiuyan crater in Liaoning Province (Fig. 1). Depending on the size, craters can be categorized as complex or simple². With its rim-to-rim diameter of 1.85 km, Yilan Crater falls within the definition of a simple crater. Early geological drilling conducted near its center revealed a 110 m thick cover of lacustrine sediments resting on a thick brecciated granite unit, primarily composed of unconsolidated granite clasts and fragments³. Furthermore, significant shock-metamorphic evidence, including shock-melted granite, planar deformation features in quartz, and shock-induced high-pressure mineral coesite, were also discovered^3,4. Carbon-14 dating on impact-produced charcoal from the crater fill suggests that the impact occurred ~49,300 ± 3200 years ago³. The surface topography of the crater exhibits an incomplete circular shape⁵ due to the absence of the rim on the southeastern side, while the other rim sections remain intact (Fig. 1).

Fig. 1: Geological information and distribution of seismic stations at Yilan Crater.

a Topography and station distribution (white triangles) at Yilan Crater. A drilling well at station YL0000 is marked with a red star. Profile YL07 is outlined for the later discussion. Blue circle indicates the rim of Yilan Crater. b Geological sketch map of the crater and surrounding areas (modified from Chen et al.³). c Location of the two documented craters in China (blue circles) (Data from Earth Impact Database https://impact.uwo.ca/map/).

Although previous studies discovered numerous shock-metamorphic evidence^3,4, no geophysical investigation has ever been performed on this area. In addition, most previous studies on Earth’s impact craters utilized active seismic methods and other types of geophysical imaging methods such as gravity or magnetic anomalies^2,5,6. As far as we know, no studies have utilized new methods such as passive seismic imaging with dense arrays. In order to investigate the subsurface structure of the crater and its formation process, we deployed a dense grid of seismic nodes in Spring 2023, primarily to record natural seismic ambient noise, but also to record any earthquake occurring locally and at remote distances (Fig. 1a). In this study, we mapped the seismic site response and investigated the subsurface structure using multiple methods, including amplification from earthquake recordings, ambient noise tomography, and Horizontal to Vertical Spectral Ratio (HVSR) of ambient noise. Subsequently, based on the crater depth estimated from the seismic data, we leveraged numerical modeling to infer the main dynamic properties of the impact process.

Results

Amplitude spectrum of earthquakes

Our first analysis focused on the amplitude spectrum of the vertical component of a local M3.1 earthquake on 2023/05/06 (Supplementary Table 1). Ascertaining which frequencies undergo amplification is challenging due to the similarity in shapes of the individual spectra (Supplementary Fig. 1). However, the spectrum along profile YL07 reveals a significant increase in amplitude at the central part of the profile, well localized within 0.5–10 Hz (Fig. 2b). Following this observation, we evaluated the integral of the spectrum from each station over this frequency range to compute the band-limited power associated with these signals. This feature provides an effective way to capture the local amplification and its geographical distribution. The amplification is significant near the crater center where the observed values are ten times higher than its surrounding areas (Fig. 2a).

Fig. 2: Amplitude ratios from the seismic obvervations.

a, c show the amplification as a map of the band-limited power of the recorded signals. The colors indicate the amplitude ratio between the value at each station and the station where the minimum value is obtained. Here, the value at each station represents the integral of the power spectrum summed over the 0.5–10 Hz frequency range for a local M3.1 earthquake (a), and over the 0.5–2 Hz range for the teleseismic event 2023/04/24 20:00:57.265 Mw 7.1 (c). b, d show the power spectrum as a function of the frequency and the location of the receivers along a selected profile YL07 (a).

Following the same strategy, we analyzed the vertical component of six teleseismic earthquakes. Typically, teleseismic earthquakes exhibit minimal high-frequency content due to inherent attenuation and absorption⁷. Supplementary Fig. 2 displays the spectrum recorded at 20 stations along profile YL07 for the event that occurred on 2023/04/24 20:00:57 UTC. The amplitude shows a rapid decay with increasing frequency except for a slight local increase observed around 0.6–0.8 Hz at the central stations in the profile. Next we computed the band-limited power over the frequency range of 0.5–2 Hz (Fig. 2c, d). At the crater’s center, the values are again higher, measuring twice as large as those in the surrounding peripheral areas. The corresponding waveform plots (Supplementary Fig. 3) of these events are direct evidence of such amplitude anomalies. Supplementary Fig. 4 shows that the amplification patterns are consistently observed across all the local and teleseismic events.

Velocity structure based on ambient noise tomography

Figure 3a shows the ambient noise cross-correlation functions (CCFs) of all station pairs, and Fig. 3b shows the corresponding average phase velocity at each subarray (for details, please refer to the “Materials and Methods” section and Supplementary Figs. 5–7). The average velocity inside the crater is clearly lower than the outside part. The 1-D Vs model beneath station YL0000 obtained upon inversion of the dispersion curve agrees well with the drilling data (Supplementary Fig. 8). The observed velocity profile is compatible with the well lithology, especially around the transition from sediment and granite clasts at a depth of 110 m (Supplementary Fig. 8d). To ensure that our results were independent of any arbitrary choice of the reference model, we performed three separate inversions using three different reference models (Supplementary Fig. 9). Figure 3c, d presents additional details of the velocity profiles across the crater, which clearly show its bowl-shaped structure. The velocity correlates well with the topography, with the high topography having the high velocity in the shallow part, and the center of the crater displaying the thickest low-velocity layer. The latter corresponds to the sediment and clast/breccia features. We should note that station density near the marigin of the array is low, resulting in insufficient effective dispersion curves to accurately invert the reliable velocity structure around the margin.

Fig. 3: Ambient noise cross-correlations and velocity distribution based on the ultra-dense observations.

a Ambient noise cross-correlation functions (CCFs) of the vertical-vertical component with a bandpass filter in the 0.5–10.0 Hz range. b Map of average phase velocity. c, d Velocity distribution along profiles A–A’ and B–B’.

Sediment thickness from HVSR curves

In order to determine the sediment thickness, we estimated the HVSR curves for each station (See the details in “Materials and Methods”). Figure 4a shows the distribution of the fundamental frequency f₀ over the area covered by the array. At the center of the crater, frequency values (<0.6 Hz, or −0.222 in log10 Hz scale) are visibly lower as compared to the relatively high values (>2 Hz, or 0.301 in log10 Hz scale) for stations located further away. To better emphasize such differences, we presented two selected HVSR curves at stations YL0710 and YL0000 (Fig. 4b), which are located near the center of the crater and at the drilling well, respectively. Notably, the curve at station YL0710 has a strong peak amplitude at 0.579 Hz, and the curve at station YL0000 has a relatively weak peak amplitude at 0.785 Hz. Station YL0718 at the rim of the crater has a spectral peak at 2.588 Hz. These values correlate well with a “bowl” model of the crater, where the low frequency at the center progressively increases toward the rim, as the sedimentary infill becomes thinner. The amplitude of the peak, on the other hand, decreases while moving away from the crater center, providing indirect evidence of a progressive reduction of the sediment-bedrock elastic impedance contrast.

Fig. 4: HVSR information and velocity models.

a Distribution of the observed fundamental frequency (f₀) across the investigated area. b HVSR curves from three selected stations YL0718, YL0710, and YL0000. c Velocity models at the center of crater inverted by fitting the dispersion curve with different reference models (Supplementary Fig. 9). The shaded area marks the velocity contrast that most likely corresponds to the sediment-rock transition. d Empirical relationships between fundamental frequency and sediment thickness. Station YL0000 behaves as the benchmark to determine the appropriate bounding relationships. (for further detail, please see Qin et al.¹⁰ and references therein).

The f₀ of the HVSR curve has been shown to correlate with the thickness of the low-velocity sediment layer (H)^8,9. However, establishing a local frequency-thickness relation is not possible without enough wells reaching the bedrock. An alternative approach is to use one of the relations existing in literature, although picking one would be rather arbitrary. Here we compiled 29 different empirical formulas from HVSR studies globally (Fig. 4d) and searched for a reasonable constraint¹⁰. As an example, station YL0000 is situated at the well site, where the thickness of sediments is known (H = 110 m). The fundamental frequency f₀ observed at this station is 0.785 Hz, and the (f₀-H) point for station YL0000 falls in between the curves of the empirical formulas^11,12 with the lowest uncertainty. We, therefore, used these formulas as upper and lower limits for our frequency-thickness conversion. In particular, with the fundamental frequency f₀ = 0.579 Hz obtained at the center point of the crater, these two formulas return an estimate of the sediment thickness in the range of 125–165 m, with a mean of 145 ± 20 m, higher than that of drilling site by 15–55 m. Similar evaluations for all remaining stations are found in the Supplementary Fig. 10. Comparatively, the three velocity models that fit the dispersion curve at YL0710, all show a similar interface around 125–150 m, regardless of the fact that they were obtained by inversions with three independent initializations (Fig. 4c, Supplementary Fig. 9). Thus, taking into account all sources of uncertainty, the obtained sediment thickness from HVSR analysis aligns well with the result from the ambient noise tomography, therefore ensuring a sufficient level of robustness for subsequent discussion.

Estimation of the impact process

The observed surface diameter of Yilan Crater is 1.85 km. The crater depth, as observed from the drilling well near station YL0000, close to the center of the crater, is 260 m (110 + 150 m, elevation difference between rim and drilling site)³. Notably, the depth is not the true crater depth, but rather the depth above the melt-breccia lens d_fr¹³. Our independent estimations based on the HVSR analysis and dispersion inversion (Fig. 4c, d) indicate a depth at the center point (YL0710) ranging between 275 (260 + 15) m and 315 (260 + 55) m with a mean of 295 (260 + 35) m.

To constrain the impact parameters responsible for the 1.85 km diameter of Yilan Crater, we performed a grid-search for the impactor diameter and pre-atmospheric-entry impact velocity using the online Earth Impact Effects Calculator (See the details in “Materials and Methods”). Since the impact speed at the top of Earth’s atmosphere ranges from the escape velocity (11.2 km/s) to the maximum possible velocity of 72 km/s¹⁴, we established a search range for the impact velocity from 10 to 70 km/s in steps of 5 km/s. For the impactor diameter, we searched in the 40 - 160 m range with an increment of 10 m. Since there is no information available on the nature of impactor, our parametric study considered two different density values: ρ = 3300 and ρ = 8000 kg/m³, compatible with a stony- and an iron-based asteroid, respectively. In addition, we considered three impact angles (α), namely 30, 45, and 60 degrees. Figure 5a–c show the result for an impactor density of 3300 kg/m³ and impact angles of 30, 45, and 60 degrees, respectively. Figure 5d–f show the same scenarios for an impactor density of 8000 kg/m³. If only considering the crater diameter (1850 m), the problem of estimating impactor velocity and diameter for the crater size is ill-posed and multiple equivalent solutions can be found. However, we observed that the residual kinetic energy of the impactor when it strikes the ground, which we refered to as the impact energy, is relatively constant across different solutions. For example, the impact energy for the case ρ = 3300 kg/m³ and α = 30° is 1.5–2 E17 Joules, it is 1.0–1.5 E17 Joules for α = 45°, and is ~1.0 E17 Joules for α = 60°. Comparatively when ρ = 8000 kg/m³, the impact energy is ~1.5 E17 for the α = 30° scenario, while the impact energy amounts to ~1.0 E17 Joules for the α = 45° case, and to ~0.75 E17 Joules for α = 60°. Overall, larger impact angle and denser impactor could induce the lower impact energy for the same crater size.

Fig. 5: Residual kinetic energy of the impactor at the ground in Joules as a function of impactor diameter and impact velocity at the top of the atmosphere.

a–c show the result for an impactor density of 3300 kg/m³ and impact angles of 30, 45, and 60 degrees, respectively. d–f show the same scenarios for an impactor density of 8000 kg/m³. Black contours indicate the estimated final crater diameter, while white contours indicate the impact energy. We marked the diameter of 1850 m.

It is important to emphasize that our analysis relies on several assumptions and has inherent limitations. The real cases may be more complicated¹⁵. In all realistic scenarios, the impactor speed when it strikes the ground is less than half the pre-entry speed and the impact energy is a relatively small fraction of the initial (pre-entry) kinetic energy of the impactor owing substantial deceleration in the atmosphere. Our estimation reported solely the effects of the ground impact based on the residual kinetic energy of the impactor. However, if a significant amount of energy is released in the atmosphere, the full effects may be more pronounced and encompass radiation from atmospheric entry and an additional blast from the ground impact¹⁴.

Discussion

Subsurface structures of Yilan Crater

In this study, significant ground motion amplification was observed at the central part of the crater, for both local and teleseismic earthquakes, and ambient noise (Figs. 2 and 3). Specifically, we observed a broader frequency band amplification (0.5–10 Hz) for local earthquakes, a narrower frequency band amplification (0.5–2 Hz) for teleseismic earthquakes, and a 0.5–1 Hz amplification for ambient noise (HVSR analysis). We attributed these site amplifications to the impact bowl-shaped structure of the crater, infilled with sediments and fractured rocks. The differences in the frequency ranges of amplification likely originated from different excitation mechanisms in these seismic sources and also frequency component difference due to, e.g., attenuations. Collectively, such an amplification can be attributed primarily to the lithology of the site, and especially to the velocity contrast between the slow sediment infill of the crater and the rock layers underneath.

Ground motion amplification due to site response is a well-documented phenomenon^16,17, influenced by various factors that affect the propagation of seismic waves in the near surface. Local geological conditions play a critical role in such amplification, including the presence of soft soils^18,19, shallow fault structures^20,21,22,23, sedimentary basins^24,25, and topographic/geometric effects^26,27. Among these factors, the presence and characteristics of low velocity layers are particularly influential in enhancing seismic wave amplification. For instance, Di Naccio et al.²⁸ investigated a site with fractured rock formations and observed significant seismic amplification. Similarly, Burjánek et al.²⁹ conducted experimental modeling and found marked amplification in fractured rock masses compared to intact rocks.

A 3D seismic velocity model from ambient noise tomography (Fig. 6) reveals additional details of shallow subsurface structures beneath the Yilan impact event. The center of crater has the thickest low velocity layer, forming a bowl-shaped structure. As expected, the meteoroid impact can fracture the rocks, forming breccia², lowering the overall velocity compared to the bedrocks surrounding the crater. Indeed, a breccia layer of 319 m was reported from the drilling well³, consistent with our findings.

Fig. 6: 3-D representation of Yilan Crater.

a 3-D velocity structure beneath the Yilan crater. b A schematic diagram illustrating the Yilan impact event and its subsequent effects in the surrounding region. Mammal fossils dating back to 48,000 years were found in this region.

Impact energy of Yilan Crater

Recently, Ren et al.³⁰ conducted a similar impact estimation on the genesis of Yilan Crater based on the iSALE-2D simulation code³¹. They suggested an impactor of diameter 120 m, striking the ground vertically at a speed of 12 km/s, with a relative error of 10.3%. It is worth noting that their conclusion is based only on considering two options as impact velocity; 12 km/s and 15 km/s, while an impactor angle of 90° is unlikely in real cases¹³. In comparison, our forward modeling provides a wide range of possible pre-atmospheric entry impactor diameter and speed scenarios (Fig. 5).

As noted before, although multiple solutions are equally plausible for the impact velocity and diameter if only the crater diameter is considered (1850 m), the impact energy is nevertheless stable (Fig. 5). As such, we limited this investigation to the interpretation of the impact energy. While several scenarios were investigated, in terms of density and impact angle, it is likely that the impactor rock was mostly mafic-ultramafic with a density of 3300 kg/m³¹⁴, and the most probable angle of impact was 45 degrees¹³. With this constraint, the estimated impact energy is ~1.0 E17 Joules. For an impact at the average pre-entry encounter speed with Earth of 20 km/s, the impactor diameter would be 106 m. In this case, atmospheric deceleration and disruption would slow the impactor to a speed of 10 km/s at the ground, implying that 3.0 E17 Joules was transferred to the atmosphere during entry. Compared with the Chicxulub crater, a large impact event on Earth (impact energy 5 E23 Joules⁶ that is believed to have had caused the Cretaceous–Tertiary (K–T) mass extinction^32,33, the energy of the Yilan event is more than six orders smaller. However, it is still ten times larger than that of the Barringer impact event³⁴. Using an empirical relationship³⁵, the energy yields equivalent to the seismic moment of a magnitude ~M5.5 Earthquake by taking into account the seismic efficiency of the impact event¹³. On the other hand, the crater diameter is a critical factor in assessing its impact event. In the last 80,000 years, Yilan Crater is among the strongest impact events around the world (Fig. 7), based on the comprehensive diameter information compiled in the Earth Impact Database. Finally, the crater depth estimated from our seismic analysis (295 ± 20 m) is shallower than most of the predicted crater depths (~400 m, Supplementary Table 2). One possibility is that Yilan Crater was produced by a closely separated collection of fragments, rather than a monolithic object as calculated by the program¹³. We also noted an interesting cluster of crater ages around 50,000 years (Fig. 7). Although some of their ages have large uncertainties, this apparent clustering around 50,000 years could be a subject of future research.

Fig. 7: Distribution of crater diameter and age.

Comparison of the diameter between Yilan and other craters in the last 80,000 years (Data from Chen⁵⁵ and https://impact.uwo.ca/map/). The error bars of crater ages are outlined.

With such a size, we expected that the Yilan impact event was significant enough to affect the living environment, at least on a local or regional scale. Numerous mammoth fossils have been discovered in this area, and a recent stable isotope analysis suggested that their age can be traced back to 48,000–42,000 years³⁶. This implies that the Yilan region already possessed suitable living conditions for large mammals at the time of impact; a hypothesis further confirmed by the analysis of impact-produced charcoal discovered in the drilling cores³. Further multidisciplinary investigations are needed to fully understand the detailed influence of the strong impact energy on the local environment.

Conclusions

The 220-station dense seismic array provides a unique opportunity to study the impact structure of Yilan Crater. Based on the systematic analysis of the spectral amplitudes of local and teleseismic earthquakes, and ambient noise, we identified a characteristic seismic amplification concentrated within the circular area of the crater, and directly connected to the litho-stratigraphic bowl-shaped structure of the crater and its sediment and fractured rock infill. Additionally, by parametric investigating the combinations of impactor density, diameter and impact angle, velocity as functions of the crater diameter and depth, we deduced that the residual kinetic energy of the impactor at the ground is of the order of 1 × E17 Joules, and equivalent to a magnitude M5.5 earthquake. This event is among the strongest impacts that occurred in the last 80,000 years and influenced the living conditions of the local environment. Our findings offer valuable insights into the impact process of Yilan Crater and provide essential guidance for future investigations into crater formation and related phenomena.

Materials and methods

A dense seismic array consisting of 220 stations equipped with three-component 5-Hz SmartSolo seismometers was deployed at Yilan Crater from April 10th to May 25th, 2023. The array comprised 12 parallel profiles (YL01-YL12), featuring 20 stations for the inner profiles, and 10 stations for the two outer profiles (Fig. 1). The distances between stations were set to 150 m within the central profiles and 300 m within the outer profiles, covering a target area of 3 × 3 km. Data was collected in continuous-acquisition mode at a sampling rate of 250 Hz. During our observation period, the China Earthquake Networks Center reported only one local earthquake (2023/05/06 02:19:43 UTC, M3.1, depth 8 km) located 190 km away from the array, while USGS’s NEIC earthquake catalog documented four teleseismic earthquakes with Mw > 7. Detailed information on the earthquakes analyzed in this study can be found in Supplementary Table 1.

Ambient noise cross-correlation

We obtained the ambient CCFs for all station pairs using the Python package NoisePy³⁷. The advantage of NoisePy is its fast and easy computation. The applied processing procedure is similar to that of Bensen et al.³⁸. First, we removed the mean, trend, and instrument response, and then resampled the vertical component data with 25 Hz. Subsequently, we band-pass filtered the data in the frequency band of 0.1–10 Hz. We divided the data into 120 s segments with a 60 s overlapping and applied spectral whitening. Finally, we computed the cross-correlation on the pre-processed waveforms and stacked them to obtain the final CCFs between station pairs (Supplementary Fig. 5).

The F-J method for dispersion curve extraction

The frequency–Bessel transform (F-J) method is an array-based surface wave analysis method designed for extracting dispersion curves from ambient noise CCFs³⁹. In this work, we utilized the package CC-FJpy⁴⁰ to conduct the F-J method for dispersion curve extraction. First we partitioned all the stations in the study area into overlapping small subarrays. For each subarray, we transformed the CCFs to obtain the corresponding F-J spectra and extract the dispersion curve. The effectiveness of the F-J method greatly depends on how the subarrays are partitioned. The commonly used approach is to employ a subarray with a fixed size and shape, sequentially moving it along the latitude and longitude coordinates to cover the entire study area. This partitioning method is suitable when the velocity structure beneath the subarrays exhibits gradual changes.

In our study, the central region had a high density of stations, while the peripheral regions had relatively sparse station coverage. Therefore, we used subarrays of size 0.006° × 0.006° for the central region and subarrays of size 0.012° × 0.012° for the peripheral regions. After processing all the subarrays, we found significant differences in the F-J spectrum corresponding to different regions. In particular, the F-J spectrum from subarrays located at the edges of the impact crater was worse and unable to provide effective dispersion curves. This complexity arises from the complex and variable subsurface velocity structure of the impact crater. To increase the number of dispersion curves, we divided the stations into those inside and outside the impact crater based on their locations and elevations. For the subarrays at the edges of impact craters, we further subdivided them into subarrays inside the crater and subarrays outside the crater, and calculated the F-J spectrum separately. For example, at Subarray_0203, which is located at the edge of the crater, using all the stations within the subarray yields to chaotic results in the F-J spectrum, making it impossible to obtain a useful dispersion curve (Supplementary Fig. 6a). In contrast, when we focused only on the stations located inside or outside the crater, the F-J spectrum reveals a clear fundamental mode dispersion curve (Supplementary Figs. 6b, c). Overall, this approach ensured relatively homogeneous subsurface structures within the subarrays and significantly improved the quantity of useful F-J spectrum.

Finally, we utilized a combination of the machine-learning-based DisperNet⁴¹ and manual adjustments to extract the dispersion curves. Specifically, we employed visualization tools to compare these curves with the F-J spectrum, which allowed us to systematically verify their smoothness and plausibility. Throughout this process, we carefully identified and corrected any outliers or anomalies, ensuring that the final results were both reliable and accurate. The subarray center inside the crater shows remarkable lower velocity than that of the subarray center outside the crater (Supplementary Fig. 7a, b). The sensitivity kernel indicates that the dispersion is mostly affected by the velocity structure in the shallow 300 m (Supplementary Fig. 7c).

Inversion of multimodal dispersion curves

After extracting the dispersion curves, we employed Broyden-Fletcher-Goldfarb-Shanno optimization^42,43 to invert 1-D Vs models. We established a reference velocity model at the center point of each subarray. For subarrays with a size of 0.006° × 0.006°, we set the model depth to 350 meters, while for subarrays with 0.012° × 0.012°, the model depth was set to 750 meters. Due to significant variations in underground velocity structures within the study area, we assigned different initial velocity values and layer thicknesses to the reference velocity models in different regions. For each center point of the subarray, we randomly generated 100 initial velocity models within a range of ±0.2 km/s around the reference velocity model. We then inverted the dispersion curve using these 100 initial velocity models. The inversion range for each depth was within the range of the initial model ±1.5 km/s. The final estimated Vs model was obtained by performing a weighted average over the best-fitting 50% of the inverted models. During inversion, we assumed a constant velocity ratio Vp/Vs = 2, and the density was updated according to the empirical relation given by Gardner et al.⁴⁴. Two examples of the inversion results are shown in Supplementary Figs. 8 and 9. Supplementary Fig. 8 shows the velocity model obtained beneath the drilling site, while Supplementary Fig. 9 shows the velocity model beneath the center of the crater. To overcome the effect of the reference models, we repeated the inversion using three different initial reference models. As it was foreseeable, the results of these three independent runs are different. Nevertheless they all capture a similar velocity transition at a depth around 125-150 m (Fig. 4c and Supplementary Fig. 9). Finally, we assembled the 1-D shear wave velocity models from all subarrays to construct a pseudo-3D velocity model for the entire study area.

HVSR analysis

In order to quantify the fundamental frequency for the stations within the impact crater we employed two different approaches. The first method consists of comparing the Fourier Amplitude Spectra for stations inside and outside the impact area as it is usually done in seismic response studies when soft-sediment versus hard-rock subsurface configuration⁴⁵, or when a damaged zone around a recent fault rupture is considered^20,46. The second method relies on computing the horizontal-to-vertical spectral ratio (HVSR) of ambient noise^47,48, which is effective for estimating the near-surface structure through the analysis of three-component microtremor recordings. The latter also allows one to obtain the sediment resonant frequency. HVSR curves are computed as the ratio of the Fourier Amplitude Spectra of the horizontal and vertical components from the microtremor record^49,50:

$${HVSR}=\frac{\sqrt{{U}_{E}\left(f\right)\times {U}_{N}\left(f\right)}}{{U}_{Z}\left(f\right)}$$

(1)

where ${U}_{E}(f)$, ${U}_{N}(f)$ and ${U}_{Z}(f)$ are the spectral amplitudes of the E-W, N-S, and vertical (Z) components of microtremors. Two most popular approaches are based on calculating either the geometric mean or the quadraticmean/squared average. Here, we chose the first approach to do the process as recommend by SESAME⁴⁹. Tens of minutes of recordings are usually sufficient to obtain reliable HVSR curves (Bignardi et al.^51,52). In order to minimize the impact of human activities even further, we based our HVSR computations on data sets of 2 h. The Python package “hvsrpy”⁵³ was used to compute the HVSR due to its advantages of automatically removing contaminated time windows.

After visual inspection, we discovered that the HVSR curve was in general more stable during the hours UTC 16:00–18:00 (local time 00:00–02:00 am), likely because of the reduced human activity at night-time. Data-cleaning such as removing time windows containing impulsive, short-term signals, which typically carry more information about their source rather than on the subsurface structure, greatly enhanced the quality of the HVSR peaks, while reducing the overall standard deviations (e.g., Supplementary Fig. 11). Subsequently, we averaged the HVSR curves obtained during the same time frame of every day to compute an enhanced average curve. We then identified the fundamental peak as the lowest-frequency peak and retained those satisfying the SESAME^49,50 reliability criteria.

It is well known that in a simplified 1D model comprising a homogeneous slow-velocity layer resting over a hard bedrock (i.e., high shear velocity), the fundamental vibration frequency (f₀) of the system could be derived from

$${f}_{n}=(2{{\rm{n}}}+1){V}_{s}/4H,n=0,1,2\ldots$$

(2)

$$wh{en}\; n=0,{f}_{0}={V}_{s}/4H$$

(3)

where V_s and H are the shear wave velocity and thickness of the sedimentary layer, respectively (e.g., Qin et al.¹⁰, and references therein). This relation entails a natural ambiguity in the interpretation of the fundamental peak, as one cannot determine the thickness of sediments without knowing the sediment’s velocity (and vice-versa). To address this issue, Ibs-von Seht & Wohlenberg⁸ proposed to leverage the sediment thickness measured at several wells drilled across the surveyed area to build a set of (f₀, H) pairs. They demonstrated that such points follow the relation H = b (f₀)^a (where a and b are constants to be determined). Such an empirical relation can then be leveraged to determine H across the same area directly from f₀, encompassing the need for V_s completely. To obtain a regression of sufficient quality they employed 95 wells. Unfortunately, in the most common case, there are not enough wells available, and building an ad-hoc correlation is not possible. In those cases (we have only one well available), one must resort to published formulas. As such, after a systematical analysis, we found two formulas that would offer the solution closest to our observation at the well. Equations from Liu and Shi¹¹ and Shi and Chen¹²:

$$H=91.93 \times {f}^{-1.066}({Shi}\, {{\& }}\, {{Chen}}^{12})$$

(4)

$$H=82.19 \times {f}^{-0.766}({Liu}\, {{\& }}\, {{Shi}}^{11})$$

(5)

Simulation of impact energy

Moving forward to the dynamics of the crater formation, an impact event involves a variety of physical and chemical processes occurring in a relatively short amount of time⁵⁴. These complex processes are influenced mainly by the impactor’s speed, size, density, and angle of impact. We leveraged the energy-based scaling algorithm proposed by Collins et al.¹³ to estimate the regional environmental consequences of an impact event similar to the one generating Yilan Crater.

The program (calculator) comprehensively assessed three principal aspects of impact process: (1) projectile dynamics during atmospheric passage, (2) thermal emissions from transient radiative phenomena (specifically the vapor plume, commonly referred to as the fireball), and (3) morphometric parameters of both the resultant crater structure and associated ejecta stratigraphy. The analysis further quantified energy dissipation mechanisms through atmospheric shockwave propagation for both terminal crater-forming impacts and upper-atmosphere airburst scenarios. Notably, the model formulation intentionally excluded ablation processes due to their negligible effect on sufficiently massive impactors capable of surviving atmospheric transit to generate craters. Progressive fragmentation mechanics were parameterized using the widely accepted pancake model framework, incorporating standard depth-to-diameter scaling relationships characteristic of simple crater morphology.

The detailed equations were described in Collins et al.¹³. Here we only present important ones to compute the crater diameter and impact energy at the ground:

$${Di}_{{fr}}=1.45125\times {\left(\frac{{\rho }_{i}}{{\rho }_{t}}\right)}^{1/3}\times {L}_{i}^{0.78}\times {V}_{i}^{0.44}\times {g}_{E}^{-0.22}\times {\sin }^{1/3}\theta$$

(6)

$${E}_{0}=\frac{\pi }{12}\times {\rho }_{i}\times {L}_{0}^{3}\times {V}_{0}^{2}$$

(7)

$$E=\frac{\pi }{12}\times {\rho }_{i}\times {L}_{i}^{3}\times {V}_{i}^{2}$$

(8)

where ${\rho }_{i}$ is the density of the impactor, ${\rho }_{t}$ is the density of the target (in kg/m³), L₀ and L_i is the impactor diameter before and after atmospheric entry (in m), V₀ and Vi is the impact velocity before the atmosphere and at the surface, $\theta$ is the angle of impact, ${g}_{E}$ is the Earth’s surface gravity (in m/s²), E0 is the initial kinetic energy of the impactor before atmospheric entry and E is the residual kinetic energy of the impactor when it strikes the ground, and Di_fr is the rim-to-rim diameter, respectively. The program allows one to compute the crater depth (d_fr), diameter (Di_fr), and residual kinetic energy (E), based on five inputs: impactor diameter (L₀), impactor density (${\rho }_{i}$), impact velocity before atmospheric entry (V₀), impact angle ($\theta$), and nature of the target (${\rho }_{t}$) (e.g., sedimentary rock, crystalline rock, or a water layer above the rock). We could set several possbilities for the impact density and angle. As the target type is known (i.e., crystalline rock), the only degrees of freedom left to determine are the pre-atmospheric-entry impactor diameter and velocity.

Finally, we followed Collins et al.¹³ to assume the “seismic efficiency” (the fraction of the impact energy (E) that ends up as seismic wave energy) is one part in ten thousand (1 × 10⁻⁴) to compute the seismic magnitude (M). The earthquake magnitude could be estimated as

$${{\rm{M}}}=0.67{\log }_{10}{{\rm{E}}}-5.87$$

(9)