Reconciling tracked atmospheric water flows to close the global freshwater cycle

Abstract

Atmospheric moisture flows play a vital role in the hydrological cycle, connecting evaporation sources to precipitation sinks. While high-resolution tracking models provide valuable insights, discrepancies arise comparing tracked flows to atmospheric reanalysis data. Here we reconcile tracked atmospheric flows with reanalysis data by means of the Iterative Proportional Fitting applied to the UTrack dataset (averaged over 2008–2017) aggregated within countries and ocean boundaries. It corrects country-scale discrepancies of up to 275% in precipitation and 225% in evaporation, adjusting bilateral flows by ~ 0.07 %, on average. The resulting dataset ensures that the total tracked moisture matches total precipitation at the sink and evaporation at the source annually. Remarkably, this procedure can be applied to any tracking model output and scale of analysis. The reconciled dataset enhances transboundary atmospheric water flows analysis, revealing that 45% of total terrestrial precipitation (~1.5 ⋅ 10⁵ km³yr⁻¹) originates from land evaporation (9.8 ⋅ 10⁴ km³yr⁻¹).

Introduction

A new view of global freshwater interconnectivity is emerging, where we understand that our collective pressure on the climate and biosphere impacts the stability of the entire global hydrological cycle¹. Any aspirations for sustainable water stewardship and governance must be based upon an understanding of how hydrological flows interact at local to global scales to shape the global freshwater cycle (^2,3). Such understanding implies reliable confidence in the estimation of freshwater teleconnections, making it crucial to frame atmospheric moisture flows within the global hydrological cycle. Atmospheric moisture flow is the transport of water vapour driven by wind and atmospheric circulation patterns and include large-scale phenomena such as atmospheric rivers, which play a significant role in transporting water, contributing to the long-term atmospheric moisture network. Climate change and land use (e.g., deforestation) are reshaping global moisture transport patterns^4,5 and influence the frequency, intensity and impacts of atmospheric rivers^6,7).

The last decades have seen many improvements in the field of atmospheric moisture tracking and the understanding of region- and country-scale connections. Dirmeyer et al.⁸ were the first to provide a global dataset of country-to-country flows of atmospheric moisture, building on the 3D-QIBT model, based on a quasi-isentropic back-trajectory algorithm^9,10 forced by reanalysis data at 1.9^∘ and 2.5^∘ resolution^11,12. Keys et al.¹³ shed new light on the transboundary governance of water by developing a typology for moisture flow relationships between nations, identifying their characteristics and enabling the classification of different possible governance principles. The work by Link et al.¹⁴, based on ERA-Interim reanalysis, presented the first grid cell-to-grid cell dataset of moisture flows, with a spatial resolution of 1.5^∘, including an analysis of the fate of evaporation and the origin of precipitation for several countries. Recently, Tuinenburg et al.¹⁵ applied the Lagrangian (trajectory-based) tracking model UTrack, which is forced with ERA5 reanalysis data¹⁵, and released a grid cell-to-grid cell dataset¹⁶ of monthly multi-annual means of atmospheric moisture flows (for 2008–2017) from any evaporation source to all its targets (i.e., precipitation) at a spatial resolution of 0.5 degrees with global coverage. Despite the growing efforts focusing on tracking atmospheric moisture flows, less attention has been given to guarantee the closure of the hydrological balance (i.e. the closure of the hydrological balance for its atmospheric component) on an annual scale and the consistency of the tracked moisture volumes with reanalysis data of precipitation (moisture reaching target cells) and evaporation (moisture departing from source cells).

In this study, we propose a framework to reconcile tracked atmospheric moisture flows, aggregated into a matrix M of bilateral connections between sources and sinks, with reanalysis data (i.e., a combination of past observations with weather forecasting models to generate consistent time series of multiple climate variables) through the Iterative Proportional Fitting (IPF) approach¹⁷. The IPF approach is a mathematical method which finds a new matrix M_IPF, being the closest to M, but with the row and column totals matching the targeted values¹⁸

Here we perform an exemplary case of application of the IPF to the UTrack dataset¹⁶, based on the Lagrangian atmospheric moisture tracking model by Tuinenburg and Staal¹⁵. The model tracks single moisture parcels from a column of water vapour at the source in forward direction (from location of evaporation to location of precipitation) until 99% of the original water content of the parcel is precipitated. Running at high spatial and temporal resolution and forced with ERA5 global reanalysis¹⁹, it is currently the state-of-the-art Lagrangian tracking of atmospheric moisture.

The proposed IPF method suits any scale of analysis, from cell to any cell-aggregated scale (e.g., city, country, region, continent). Here, we apply it to a country/ocean scale matrix of flows, aggregated within countries and ocean delineations, and to a sub-continent/ocean matrix, built upon sub-continental regions and ocean classification (see Methods).

Our post-processing framework provides a novel dataset of up-to-date bilateral moisture connections between countries, including oceans, aimed at helping countries manage their portion of the global water cycle. This information enhances the exploration of the role countries and regions play in the international network of atmospheric water flows and the global hydrological cycle, thus supporting global water governance with consistent and reliable data.

Results

The dichotomy between hydrologic reanalysis data and tracked volumes

The UTrack dataset provides for any location c (represented through a cell of 0.5^∘) a forward footprint matrix (i.e., the fraction of evaporation in c that reaches the downwind cells) and a backward footprint matrix (i.e., the fraction of precipitation in c that comes from evaporation in upwind cells).

Here, we study the annual atmospheric moisture flows at the national level and aggregate the single-cell moisture footprints (both forward and backward) to the country/ocean scale, hence obtaining two matrices of bilateral flows. We consider oceans as sourcing/receiving entities, thus handling them as countries.

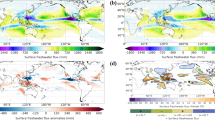
The bilateral structure of the country/ocean matrix allows us to evaluate the total precipitation (as imported volume) and total evaporation (as exported volume) of each country/ocean on the average annual scale, on both forward and backward approaches. When comparing the tracked volumes with reanalysis data, a dichotomy between the latter and the tracked volumes arises for both the backward and forward matrices. Specifically, estimated backward volumes result in deviations related to evaporation at the sources (Fig. 1a, b), whereas estimated forward volumes are associated with deviations in precipitation at the sinks (Fig. 1c, d).

Fig. 1: Deviations between ERA5 data and the UTrack estimates at country/ocean scale.

a Comparison between evaporation estimated by backward approach and ERA5 observations in mm per year, and b corresponding geography of the relative errors [%]. c, d The same, but referred to precipitation estimates obtained by forward approach.

Despite scatter plots suggesting a good correlation between the two data sets, significant percentage deviations both for evaporation (including transpiration over land) ET(from −50% to 225%) and precipitation P (from −50% to 275%) occur at the country/ocean scale. Notably, ET and P deviations at the country/ocean scale are typically out-of-phase, but with different magnitudes of relative deviations: ET overestimation corresponds to P underestimation—e.g., Greenland (+131%, −35%), Russia (+23%, −18%), Ecuador (+24%, −16%)—and vice versa, e.g., South Africa (-20%, +50%), Oman (-18%, +92%) and Spain (-15%, +34%). We observe deviations particularly pronounced in regions characterised by aridity – such as countries in Northern Africa, the Middle East, the Arabian Peninsula, and Antarctica – and in the Northern and Southern latitudes. Other relevant differences emerge in Eastern Africa and Southern Europe, where absolute deviations on evaporation in backward tracking are on average −250 mm ⋅ yr⁻¹ (Supplementary Fig. 1a). Conversely, in these regions, the absolute deviations in precipitation in forward tracking are on average +600 mm ⋅ yr⁻¹ and +200 mm ⋅ yr⁻¹, respectively (see Supplementary Fig. 1b).

A reconciliation framework for atmospheric moisture connections

We solve the dichotomy between country/ocean-scale tracked volumes and the ERA5 re-analysis shown in Fig. 1 by adopting the IPF method on both forward and backward matrices. The IPF procedure is a simple and parsimonious methodology that, given a low amount of information – i.e. topology of the network, an initial guess about the entries and the target row and column sums – assures a reliable degree of closeness between the initial and the final adjusted network²⁰. Accordingly, we re-scale the elements of the country/ocean matrix of moisture connections, so that the sum of rows and columns in the new matrix meets, respectively, the total precipitation and evaporation data provided by ERA5 at the country/ocean scale. We separately implement the IPF method on the forward flow matrix (F) and backward flow matrix (B) as they are estimated by UTrack, and obtain the IPF-reconciled matrices F_IPF and B_IPF. Due to different initial conditions, each single bilateral moisture connection shows a deviation, see Equations (10) and (11) both ante-IPF application – with an ${{{\rm{R}}}}_{log}^{2}$ of 0.9665 (Supplementary Fig. 2a) – and post-IPF application despite demonstrating an improved ${{{\rm{R}}}}_{log}^{2}$ of 0.9981 (Supplementary Fig. 2b). To address the remaining discrepancy between the two bilateral matrices, we average element-wise F_IPF and B_IPF and obtain a unified reconciled matrix M_IPF of moisture connections between countries/oceans.

The new mean matrix M_IPF shows a good correlation with the mean matrix before the IPF application (i.e., (F+B)/2) with an ${R}_{log}^{2}$ of 0.997 (Fig. 2a). This consistency demonstrates that the IPF algorithm adjusts the bilateral moisture flow matrix to meet ET and P constraints, but does not fundamentally change either the network’s topology nor does it significantly impact the largest flows, showing a flow-weighted average difference between the two matrices of 0.067%.

Fig. 2: Performance of the reconciliation approach on the network structure.

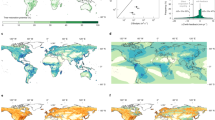
Comparison of bilateral flow changes ante- and post-Iterative Proportional Fitting (IPF) application for the composite matrix of forward and backward atmospheric moisture connections sourced from the UTrack dataset and aggregated at the country/ocean scale (a) density scatter plot of bilateral moisture volumes before (on the x-axis) and after (on the y-axis) the IPF application (values are plotted in logarithmic scale). The colour bar shows the normalized point density, scaled from 0 (lowest) to 1 (maximum observed density). b Scatter plot of the terrestrial moisture recycling (TMR) at the country scale before (on the x-axis) and after (on the y-axis) the IPF application. The circles’ size represents the volume of mean annual precipitation (2008–2017), while the circles’ colour indicates the relative change [%] of TMR before and after the IPF application.

To evaluate the performance of our reconciliation approach on the network structure, we assess how country-scale terrestrial moisture recycling (TMR) – i.e., the portion of terrestrial precipitation originating from land evaporation – is affected by the IPF application (Fig. 2b). On a country scale, Fig. 3b shows the TMR relative change after IPF and its spatial heterogeneity worldwide. Notably, the country-specific maximum relative change in TMR does not exceed 9% in absolute values, showing that the global balance of each country-specific network is not heavily affected by the IPF adjustments. The maximum positive relative change (8 to 9%) shown in Fig. 3b mainly occurs across countries in East Africa, whereas a maximum relative decrease in TMR is applied to Antarctica (−8%). These adjustments on TMR are not surprising if comparing the relative change in Fig. 2 with overestimation of evaporation and underestimation in precipitation shown in Fig. 1b and d, respectively.

Fig. 3: Maps of country-scale TMR and relative changes following IPF procedure.

a Terrestrial moisture recycling (i.e., precipitation percentage from terrestrial evaporative sources, TMR) obtained at the country scale and (b) relative change of TMR [%] at the country scale after the application of IPF.

Reconciled country-scale TMR values in Fig. 3a also represent valuable information for water and land governance, giving insight into terrestrial evaporation dependencies and self-resilience of a country for its precipitation. On a global scale, we find an average TMR of 45%, with highest amounts in Mongolia (95%), the Central African Republic (CAR) (88%) and Congo (87%), see Supplementary Table 1. These countries are located in major moisture recycling hubs where regional evapotranspiration plays a dominant role due to large-scale atmospheric circulation patterns and topographic influences^21,22,23. The lowest TMR, excluding small island nations, is found in Chile (4%), French Guiana (7%) and Portugal (9%), see Supplementary Table 1. These countries are all coastal, leading to high oceanic moisture sources, and either shielded by their orographic configuration from receiving continental moisture (Chile), or relatively small, reducing local recycling, which has been shown to be correlated to size of the sink region²⁴.

Balanced bilateral flows at the country scale

In this section, we provide evidence of the importance of post-processing and adjusting the tracked moisture volumes to match ERA5 data for two emblematic examples: South Africa and Brazil. South Africa shows a significant difference between the precipitation and evaporation estimated with UTrack and the ERA5 data (50%,-20%), whereas Brazil represents a well-studied example in the moisture recycling literature and exhibits a UTrack-ERA5 relative error in precipitation and evaporation of just 9% and-6%, respectively.

While the South African moisture evaporation is strongly directed to the Indian Ocean (453 km³yr⁻¹), the precipitation sources are more evenly distributed i.e., among the Indian Ocean (190 km³yr⁻¹), the South Atlantic Ocean (180 km³yr⁻¹), and several neighbouring countries. 75% of South Africa’s total precipitation is sourced by just ten connections, of which 20% originates from terrestrial evaporation from Botswana (58 km³yr⁻¹), Zimbabwe (38 km³yr⁻¹), Mozambique (34 km³yr⁻¹), and Namibia (28 km³yr⁻¹). Post-IPF volumes of precipitation show a monotonous decrease; the major relative changes occur for the Southern Ocean (-59%), Chile (-36%), and the South Pacific (-33%) (Fig. 4f) while major evaporation volumes (Fig. 4b, c) show an increasing trend, that peaks in Antarctica (+57%) and in the Southern Ocean (+42%). Despite a former relative error on precipitation and evaporation estimate of 50% and −20%, Africa’s key precipitation and evaporation flows are, on average, balanced by small adjustments, by −22% and +16%, respectively.

Fig. 4: Case example: South Africa – Moisture flow adjustments via IPF.

Major exports (evaporation) (a) and imports (precipitation) (d) and flows for South Africa after the IPF application. The size of the edges and the colour gradient represent the flows’ weight. Panels(b) and (e) show the resulting volumes of export and import after the IPF reconciliation, respectively. c, f Report their relative change [%].

In comparison to South Africa, the Brazilian network (Fig. 5) shows a narrower adjustment range: relative changes in its major 20 terrestrial connections vary from +39% (Brazil ⇌ Southern Ocean, 14 km³yr⁻¹) to-21% (Colombia⇌ Brazil, 40 km³yr⁻¹). Brazil supports the South American regional moisture recycling, which amounts to 1,4 ⋅ 10⁴ km³, larger than the strongest bilateral connection between oceans (South Pacific Ocean ↔ North Pacific Ocean, 1,36 ⋅ 10⁴ km³) (Fig. 6a), and exports moisture from its rain forest’s evaporation downwind to its western neighbors Fig. 5a). Its largest annual terrestrial bilateral connections are exports to Peru (780 km³yr⁻¹), Bolivia (510 km³yr⁻¹), and Colombia (460 km³yr⁻¹). These three major flows are changed by 16%, 8% and 18%, respectively, in contrast with the Brazilian export to the Southern Ocean, which reaches about +40% (Fig. 5c,e). In general, we observe that in the cases of South Africa and Brazil, the largest relative changes applied by the IPF re-balancing affect flows to the Southern Pole. This behaviour is not surprising, since the polar regions are among the regions mainly affected by precipitation/evaporation errors (Fig. 1, Supplementary Fig. 1) and consequently adjusted by the reconciliation framework (Fig. 3).

Fig. 5: Case example: Brazil – Moisture flow adjustments via IPF.

Major exports (evaporation) (a) and imports (precipitation) (d) and flows for Brazil after the IPF application. The size of the edges and the colour gradient represent the flows’ weight. b, e The resulting volumes of export and import after the IPF reconciliation, respectively. c, f Report their relative change [%].

Fig. 6: Atmospheric moisture connections among subcontinental land regions and oceans.

Moisture connections between subcontinental land regions (a) and involving oceans (b). The size and colour of the edges are proportional to the volume evaporated at the source and precipitating at the sink. In panel (a), the node colour indicates if the region is a net importer or exporter of atmospheric moisture from other terrestrial regions, excluding its domestic recycling; their size is proportional to the gross volume domestically recycled i.e., evaporation from the region that precipitates within the region boundaries. Insets show the geographical partitions.

Reconciled land and ocean flows of atmospheric moisture at sub-continental scales

The adjusted subcontinental matrix of atmospheric moisture connections, consistent with ERA5 reanalyses (Supplementary Fig. 3 and Supplementary Fig. 4c, d), is shown in the network in Fig. 6, divided into terrestrial interactions (panel a) and land-ocean interactions (panel b). The total annual precipitation and evaporation flows for subcontinents and oceans originating from the global (ocean-land) circulation are reported in Supplementary Table 2. Noticeably, when comparing Fig. 6a and b, the domestically recycled moisture-i.e., the volume of precipitation originating from terrestrial evaporation within the same regional boundaries-in South America (14,360 km³yr⁻¹) and North America (6500 km³yr⁻¹) is of the same order of magnitude as certain key oceanic moisture exchanges, such as those between the South and North Pacific Ocean (14,354 km³yr⁻¹) and between the South Atlantic and the Indian Ocean (5420 km³yr⁻¹).

Zooming in on the terrestrial interactions in Fig. 6a, absolute net importing and exporting hubs of terrestrially-sourced mean annual precipitation are highlighted. Among the net importers, Eastern Asia and Eastern Europe are major sinks of net imported precipitation from terrestrial sources (1990 and 1844 km³ per year, respectively), followed by Western Africa with 1000 km³. In terms of major bilateral connections, the strongest terrestrial moisture exchanges occur from Eastern Africa to Central Africa and from Southern Asia to Eastern Asia, with volumes of 1670 km³ and 1120 km³, respectively (Supplementary Table 3). The major ocean ↔ land flows are the ones from the South and North Atlantic Oceans to South America (8530 and 6360 km³) and from the Indian Ocean to Southeast Asia (6270 km³), while the largest land  ↔ ocean flows are from South America to the South Atlantic Ocean (3115 km³), from North America to the North Atlantic Ocean (1940 km³) and from Eastern Asia to the North Pacific Ocean (1940 km³), see Fig. 6b.

Looking at the domestic moisture recycling (DMR) – measured as domestic precipitation originating from domestic evaporation proportionally to total precipitation in the region– the highest values are exhibited by Central Africa (48%) and South America (44%). In terms of TMR, Central Africa, Central Asia and Eastern Europe show the highest values, with values of 79%, 74%, and 66%, respectively; these three regions are indeed the major sinks of net terrestrial precipitation (Supplementary Table 4).

Discussion and Conclusion

Despite having attracted much attention in the last years, little focus has been put on the consistency of tracked moisture volumes with re-analysis of atmospheric data of precipitation (in target cells) and evaporation (in source cells) nor on guaranteeing internal closure of the moisture balance. This clashes with the awareness that water balance closure is a pivotal factor in hydrological models for strengthening their robustness and enhancing their reliability, especially at global scales^25,26, and on detecting hydrological changes²⁷. The challenge of achieving water balance closure in global hydrological assessments is widely acknowledged (e.g.,^28,29,30,31). Studies such as Lorenz et al.³² have highlighted discrepancies in large-scale runoff estimates, emphasizing the need for improved methodologies to reconcile atmospheric and terrestrial water budgets. Similarly, Abolafia-Rosenzweig et al.³³ explored multiple closure techniques to improve hydrological budget assessments at river basin scales, highlighting uncertainties that remain despite advancements in satellite-based and model-derived datasets. In fact, it is in areas exhibiting high uncertainty where the IPF approach proves useful by providing significant adjustments, thus improving our understanding of the location and degree of the uncertainties, while ensuring internal water balance closure at multiple spatial scales.

The errors we observe (see Figs. 1– 2) are recognised by the moisture tracking community; e.g., such deviations are shown in a cell grid map of relative (-) and absolute error (mm ⋅ d⁻¹) in Tuinenburg et al.¹⁶. To fill this gap, we propose the IPF framework to reconcile moisture tracking outcomes with measured (here re-analysed) data. Our IPF approach successfully brings moisture flows to a fitted matrix of bilateral connections which is the closest to the initial one from a topological point of view, but with the total volumes matching the target ones. We here exemplified the capabilities of our approach by referring to UTrack (forward and backward) outcomes and working at annual, country/ocean and sub-continental/ocean scales. We find confirmation of the UTrack atmospheric tracking where IPF applies fewer changes (e.g., Australia, India, Central Europe and South America) while where UTrack shows higher errors in precipitation and evaporation estimates (Northern and Southern poles, oceans and arid regions), IPF introduces significant changes in the total annual water flows (ET and P) in the moisture tracking network.

Estimates in our study shed new light on the global hydrological cycle, closing the annual balance to 5.5 ⋅ 10⁵ km³ per year over the time window from 2008 to 2017. From the IPF-balanced matrix of moisture connections, we find that precipitation over land generated from terrestrial and ocean evaporation amounts to 7 ⋅ 10⁴ km³ and 9.3 ⋅ 10⁴ km³ per year, respectively (Table 1). The contribution of terrestrial evaporation to terrestrial precipitation, expressed as TMR, gives useful insights into land resilience, inter-dependencies and vulnerabilities. We find global annual TMR to be 45%, a percentage in between recent findings: van der Ent et al.³⁴ report 40% using forward tracking from WAM-2layers model, forced with ERA-Interim data at a 1.5^∘ resolution and Tuinenburg et al.¹⁶ find 51% using a backward approach in UTrack.

Table 1 Global atmospheric water flows from/to land and oceans based on the reconciled atmospheric moisture network

We analysed the quantitative flow dependencies between subcontinents and oceans to ensure the integrity of the global flow network after the IPF reconciliation and then assessed countries as either net importers/exporters of moisture as well as their TMR and DMR ratios. Our country scale hotspots of high TMR in Fig. 3a correspond to locations of high-intensity TMR values in grid-based maps presented in previous studies based on the UTrack dataset, such as Tuinenburg et al.¹⁶ and Posada-Marin et al.³⁵. Net import and net export information on terrestrial flows, as well as TMR and DMR ratios, are useful tools to enhance the applicability of inter-regional land use policies to safeguard atmospheric water flows as a common, public and transboundary good.

By closing the water balance in a state-of-the-art moisture tracking model output dataset, we offer an example of IPF application to hydrological modelling and take a step towards limiting the inherent uncertainties associated with large-scale moisture flow models and their data inputs. Furthermore, our reconciliation method and dataset could be applied to atmospheric river networks to ensure water balance closure and enhance the robustness of their analysis, providing a valuable tool for studying the significance and life cycle of these rivers within the global moisture flow network. However, Kampf et al.³⁶ emphasize that strict closure does not necessarily reduce uncertainties but rather redistributes them, pointing to the need for an “open water balance" approach that accounts for unknown or unmeasured fluxes. Other studies have addressed hydrological balance closure using different methodologies: Wong et al.³⁷ examined water balance closure in Canada via remote sensing and data assimilation, while Haddeland et al.³⁸ investigated the impact of time-step choices and energy budget assumptions on moisture flux reconciliation. The necessity of reconciling hydrological data was also stressed by Abolafia-Rosenzweig et al.³³, who compare different closure techniques in global river basins and underline the importance of methodological choices in achieving balance closure. Additionally, Hobeichi et al.²⁷ showed that long-term hydrological trends must be carefully validated when reconciling different datasets. Our approach differs by focusing on network consistency in global-scale moisture tracking, ensuring that adjustments preserve the underlying structure of atmospheric flows.

To evaluate the sensitivity of the IPF method to the scale of application, we analysed the fit of a subcontinent/ocean matrix, aggregated before re-balancing, against a subcontinent/ocean matrix aggregated after a re-balancing applied at the country/ocean scale, as shown in Supplementary Fig. 3. The high degree of alignment between the matrices (${R}_{l}^{2}log$ equal to 0.9998) and a mean deviation between their respective bilateral flows of 0.084% confirms that IPF effectively balances moisture flows across different spatial scales, with minimal deviation between the original and reconciled data. This demonstrates the robustness of the method with respect to the scale of application. This result enforces the general validity of the IPF application at different scales (Supplementary Fig. 4c, d). Given IPF’s effectiveness in closing the country scale annual balance while weighting the most affected areas by error, future efforts could be addressed to extend this mathematical approach to finer spatial and temporal scales (e.g., cell scale and month scale).

Though Tuinenburg and Staal¹⁵ tested the sensitivity of atmospheric moisture recycling to different model assumptions and explicitly show model-dependent uncertainties in estimates across the globe, addressing these limitations, so far, either falls out of scope or goes undetected in UTrack dataset applications (e.g.,^5,24,39,40). Further studies can take advantage of our framework to potentially apply it as a post-processing step to reconcile tracked flows (eventually sourced from any other tracking model) with reanalysis data, to any scale of application. In addition, this post-processing approach can help bring more clarity to the uncertainty in and between the different moisture tracking methods, the uncertainty of which still poses an issue for the moisture tracking community, though is currently being addressed through a model intercomparison initiative⁴¹.

Estimates balanced by IPF application, offer a pathway towards a more accurate and reliable understanding of water flows between major geographical and political boundaries, which is crucial for governance, policy and safeguarding of water resources^{13,40,42,43,44}, showing different insights into the reliance on either terrestrial evaporation from external or internal sources or on oceanic evaporation. Future studies can use our reconciled bilateral network to assess green water resources availability and resilience, and their role in human-ecological systems, delving into the economic importance of green water flows. Enhancing the evaluation of the amounts of atmospheric moisture across these scales can yield important geopolitical implications by analysing the network globally, and investigating its relation to other socio-hydrological flows, such as virtual water trade⁴⁵.

Methods

Framework

To reconcile the hydrological balance of atmospheric moisture connections - from sources to sinks, considering annual evaporation and precipitation volumes - we employ the Iterative Proportional Fitting (IPF) algorithm. This algorithm operates on the tracked precipitation (forward direction) and evaporation (backward direction) volumes, facilitating adjustments among sources and sinks. This method ensures that the total tracked atmospheric moisture equals the total precipitation at the sink and evaporation at the source on an annual basis.

The proposed approach can be applied to any scale of aggregation (from cell, to countries, regions and continents). In particular, here we chose the country/ocean and subcontinent/ocean scales.

Our framework entails five major steps: (i) Pre-processing and correction of input precipitation and evaporation data to achieve a closed 10-year water balance (Supplementary Fig. 5), (ii) Evaluation of forward and backward tracked moisture flows for an average year in the period 2008-2017 as annual imports of precipitation (P) and exports of evaporation (ET) at the country/ocean scale (Fig. 1), (iii) Application of the IPF method on the import-export matrices to adjust the discrepancy with ERA5 country/ocean scale data of total annual precipitation and evaporation Fig. 2, (iv) Aggregation of country/ocean matrices to subcontinental/ocean scale and IPF application at this scale of analysis, and (v) Validation of the IPF adjustment at the scale of application (Supplementary Fig. 3).

Data

The atmospheric moisture connection dataset used in the study is the UTrack dataset¹⁶, available at https://doi.org/10.1594/PANGAEA.912710 and accessible through sample scripts provided by the authors. The dataset is based on the Lagrangian atmospheric moisture tracking model UTrack¹⁵.

For each mm of evaporation, the model tracks 100 parcels of moisture throughout the atmosphere from their locations of evaporation to those of precipitation. The tracking is based on ERA5 hourly evaporation and precipitation, wind speed and the three-dimensional wind directions for 25 atmospheric layers in the troposphere at 0.25^∘ horizontal resolution (Copernicus Climate Change Service, C3S)¹⁶. The moisture tracking runs among all global grid cells including the oceans at 0.25^∘ spatial resolution and consists of three steps: (1) the release of moisture evaporated from the land surface into atmospheric moisture parcels, (2) the calculation of trajectories through the atmosphere for each parcel and (3) the allocation of moisture present in the parcels to precipitation events at the location of the parcel. In addition to the horizontal transport component, the model includes a probabilistic vertical transport scheme that distributes the moisture parcels vertically over 25 atmospheric layers. The parcels are tracked for up to 30 days or until only 1% of the original moisture remains. We refer to the original model development paper by Tuinenburg and Staal¹⁵ for a more in-depth model description.

The UTrack dataset is available for a reference average year y over the period 2008–2017, on a monthly basis (m) and at grid-cell resolutions of 0.5^∘ and 1^∘. Here, we source the dataset at a spatial resolution of 0.5^∘. In the dataset, the selection of a source cell s (location of evaporation) gives a global matrix of the monthly forward footprint, pf(s, t, m) of atmospheric moisture (i.e., the fraction of evaporation from the selected cell s to each target cell t, in the month m) and in reverse, selecting a target cell, t, (location of precipitation) gives the monthly backward footprint of atmospheric moisture, pb(s, t, m) (i.e., the fraction of precipitation in the cell t originating from the upwind evaporation in each source cell s).

Here, we reconstruct the bilateral moisture flows in cubic meters between any sources and sinks using (i) the UTrack monthly forward and backward footprint data of atmospheric moisture connections, i.e., pf(s, t, m) and pb(s, t, m)– described above – (ii) the monthly-averaged data of precipitation and evaporation at 0.25^∘ in the cell c for each year y from 2008 to 2017, namely P_ERA5(c, m, y) and ET_ERA5(c, m, y), expressed in meters per day from the ERA5 Climate Data Store (Copernicus Climate Change Service, C3S), and (iii) the cells areas a(c).

For consistency with the UTrack dataset, available at 0.5^∘ spatial resolution, P_ERA5(c, m, y) and ET_ERA5(c, m, y) are re-gridded at 0.5^∘ with bilinear interpolation through the CDO operator remapbil on a grid [(90,-90),(0,360)].

We calculate the area of the cell grid a(c) through the gridarea operator from the Climate Data Operators (CDO) software, a collection of many operators for standard processing of climate and forecast model data⁴⁶. The reference grid to calculate the area of each cell is the input data from the UTrack dataset at the spatial resolution of 0.5^∘.

ERA5 data pre-processing

Reanalysis products such as ERA5 are known to exhibit regional biases, particularly in areas with sparse observational data, such as the Southern Hemisphere, the tropics, and high-latitude regions^19,47,48. Studies have found that ERA5 tends to overestimate precipitation in some oceanic and tropical regions while underestimating it in arid and semi-arid areas⁴⁸. Despite these uncertainties and regional biases, which are not the focus of this study, the ERA5 dataset represents the most detailed available representation of the atmosphere¹⁶.

Though the ERA5 balance between precipitation and evaporation is relatively good for a twenty-year period from the mid-1990s¹⁹, the annual balance is not well closed in more recent years. Indeed, Tuinenburg et al.¹⁶ acknowledge the non-closure between precipitation and evaporation data from the global reanalysis as a source of error in the UTrack dataset itself¹⁶. To address the non-closure of the hydrological balance, we first analyse the difference between the ERA5 global precipitation and evaporation over the period 2008–2017, namely P_ERA5,g(y) and ET_ERA5,g(y), calculated as:

$${P}_{ERA5,g}(y)=\left[{\sum }_{c=1}^{{N}_{c}}{\sum }_{m=1}^{12}{P}_{ERA5}(c,m,y)\cdot a(c)\cdot d(m)\right]\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(1)

$$E{T}_{ERA5,g}(y)=\left[{\sum }_{c=1}^{{N}_{c}}{\sum }_{m=1}^{12}E{T}_{ERA5}(c,m,y)\cdot a(c)\cdot d(m)\right]\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(2)

where N_c is the total number of cells, 720 × 1440, namely 1’036’800, a(c) the area of the cell and d(m) the number of days in the month m.

Supplementary Fig. 5 shows that the annual balance between P_ERA5,g(y) and ET_ERA5,g(y) is not met along the reference period. Supplementary Table 5 reports the ratio and the relative error between P_ERA5,g(y) and ET_ERA5,g(y) for each year of our period of interest. In these ten years of reference, the relative difference between global evaporation estimates and precipitation ranges from -0.4% in 2008 to -1.8% in 2017.

The yearly relative difference is evaluated as:

$$\frac{E{T}_{ERA5,g}(y)-{P}_{ERA5,g}(y)}{{P}_{ERA5,g}(y)}\cdot 100\,\,[ \% ]$$

(3)

Since UTrack data are given as a multi-year average between 2008 and 2017, we calculate the global volumes of P_ERA5,g(y) and ET_ERA5,g(y) averaged over the number of reference years N_y (10):

$${\hat{P}}_{ERA5,g}=\frac{1}{{N}_{y}}{\sum }_{y=1}^{10}{P}_{ERA5,g}(y)\,\,[{{{\rm{m}}}}^{3}]$$

(4)

$${\hat{ET}}_{ERA5,g}=\frac{1}{{N}_{y}}{\sum }_{y=1}^{10}E{T}_{ERA5,g}(y)\,\,[{{{\rm{m}}}}^{3}]$$

(5)

where the ̂ recalls the time-average over the years 2008–2017.

We impose ${\hat{P}}_{ERA5,g}$ and ${\hat{ET}}_{ERA5,g}$ equal their 10-year average (equal to 5.50 ⋅ 10⁵ km³ yr⁻¹), obtaining the scaling factors α_P and α_ET as:

$${\alpha }_{ET}=\frac{{\hat{P}}_{ERA5,g}+{\hat{ET}}_{ERA5,g}}{2}\cdot \frac{1}{{\hat{ET}}_{ERA5,g}}\,\,[-]$$

(6)

$${\alpha }_{P}=\frac{{\hat{P}}_{ERA5,g}+{\hat{ET}}_{ERA5,g}}{2}\cdot \frac{1}{{\hat{P}}_{ERA5,g}}\,\,[-]$$

(7)

Obtaining α_P = 0.9971 and α_ET = 1.0029.

Scaling factors are used to re-scale the data of monthly precipitation and evaporation in the average year, ${\hat{P}}_{ERA5}(c,m)$ and ${\hat{ET}}_{ERA5}(c,m)$ as:

$${\overline{\hat{P}}}_{ERA5}(c,m)={\alpha }_{P}\cdot {\hat{P}}_{ERA5}(c,m)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(8)

$${\overline{\hat{ET}}}_{ERA5}(c,m)={\alpha }_{ET}\cdot {\hat{ET}}_{ERA5}(c,m)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(9)

UTrack atmospheric moisture flow reconstruction between source and sink cells

We reconstruct annual atmospheric moisture forward and backward flows (m³) sourcing for each month the forward footprint pf(s, t, m) and the backward footprint pb(s, t, m). Since the footprint of atmospheric moisture is dimensionless and $\overline{\hat{ET}}(c)$ and $\overline{\hat{P}}(c)$ are sourced in meters per day, we consider the area of each cell a(c), as in section 4, in squared meters, and the days in each month d(m) to obtain the cumulated atmospheric moisture volumes in cubic meters. Hereafter the generic cell c is referred to as s when it acts as a source cell, t when it acts as a target cell.

In the forward approach, we evaluate the average annual atmospheric moisture flow, ff(s, t), from a cell s (evaporation) to a matrix of cell t (precipitation) as:

$$ff(s,t)={\sum }_{m=1}^{12}\overline{\hat{ET}}(s,m)\cdot pf(s,t,m)\cdot d(m)\cdot a(s)\,\,[{{{\rm{m}}}}^{3}\,{{{\rm{yr}}}}^{-1}]$$

(10)

In the backward approach, we evaluate the average annual atmospheric moisture flow, fb_s,t, from a target cell t to a matrix of source cells s as:

$$fb(s,t)={\sum }_{m=1}^{12}\overline{\hat{P}}(s,m)\cdot pb(s,t,m)\cdot d(m)\cdot a(t)\,\,[{{{\rm{m}}}}^{3}\,{{{\rm{yr}}}}^{-1}]$$

(11)

where pb(s, t, m) is previously multiplied for the evaporation of each source cell s, as suggested in Tuinenburg et al.^16,49, thus reading:

$$pb(s,t,m)=\overline{\hat{ET}}(s,m)\cdot pb(s,t,m)\,\,[-]$$

(12)

Comparing the reconstructed flows in the two cases, we find that a deviation exists, namely:

$$f{f}_{(s,t)}\, \ne \, fb(s,t)$$

(13)

Integration to the country-scale

The spatial scale of this study is primarily set on national boundaries, thus we define a forward matrix F and a backward matrix B of size C × C, where C is the total number of countries and oceans (C=272). Each element of the forward (backward) matrix F (or B) represents the atmospheric moisture flow between an exporting country e and an importing country i, aggregated from the source-sink flows at the cell scale ff(s, t) and fb(s, t) defined in Equation (10) and Equation (11).

However, the conceptual framework and methodologies developed in this research are adaptable and meant to be applied across various scales, ranging from grid cells to other chosen geographical aggregations.

For the geographical delineation of the countries, we access the Administrative Units - Dataset from European Commission Eurostat (ESTAT) GISCO⁵⁰. Additionally, we choose to include major water bodies (oceans and seas) in the source/target mask to enable a more precise analysis of the oceanic sources of precipitation. The delineations of oceans and seas are taken from the Global Oceans and Seas Dataset of the Flanders Marine Institute⁵¹ and a delineation of the Caspian Sea from the SeaVoX Salt and Fresh Water Body Gazetteer (v19) of the British Oceanographic Data Centre⁵². Alterations to the shapefiles, namely the separation of Alaska and Hawaii from the US, the French overseas regions from France and mainland China from Taiwan, are performed in QGIS. Each of the vector shapefiles is rasterized and reformatted into a NetCDF raster masking the geographical delineations with a specific numeric ID for each delineated area using the gdal_rasterize and gdal_translate operators of the Geospatial Data Abstraction software Library (GDAL)⁵³. Subsequently, the three masks are combined while giving priority to the country mask by not overwriting cells with an existing country attribution. Finally, the country-ocean mask is re-gridded using nearest neighbour interpolation through the CDO operator remapnn to align with the coordinates of the UTrack dataset.

To allocate each forward and backward flow (i.e., ff(s, t), fb(s, t)) to a country/ocean scale bilateral connection in the matrices F(e, i) and B(e, i), we query in both cases if each source cell s falls in the boundaries of e and if the target cell t falls in the boundaries of i, and aggregate the flows as follows:

$$F(e,i)={\sum }_{s\in e=1}^{S}{\sum }_{t\in i=1}^{T}ff(s,t)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(14)

$$B(e,i)={\sum }_{s\in e=1}^{S}{\sum }_{t\in i=1}^{T}fb(s,t)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(15)

where S is the total number of source cells located in the country/ocean e and T is the total number of target cells located in the country/ocean i.

The structure of the bilateral matrix, allows us to compare element-wise the reconstructed flows in the two cases. By comparing the bilateral connections element-wise in F(e, i) and B(e, i), we find a deviation with an ${R}_{log}^{2}$ of 0.9965 (Supplementary Fig. 2a), due to Equation (13).

We also compare the gross precipitation (import) and evaporation (export) flows for each country/ocean both in the forward and backward case. Summing row-wise both F(e, i) and B(e, i) we get the export flow ET_U(e) from the exporting country/ocean e, which represents its annual tracked evaporation the UTrack dataset. Summing column-wise we obtain the import flow P_U(i) of the importing country/ocean i, which represents its annual tracked precipitation from the UTrack dataset. This reads in the forward case:

$$E{T}_{U}^{f}(e)={\sum }_{i=1}^{C}F(e,i)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(16)

$${P}_{U}^{f}(i)={\sum }_{e=1}^{C}F(e,i)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(17)

and in the backward case:

$$E{T}_{U}^{b}(e)={\sum }_{i=1}^{C}B(e,i)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(18)

$${P}_{U}^{b}(i)={\sum }_{e=1}^{C}B(e,i)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(19)

Comparing the flows of evaporation $E{T}_{U}^{f}(e)$ and $E{T}_{U}^{b}(e)$ obtained in Equation (16) and Equation (18) we observe that:

$$E{T}_{U}^{f}(i) \, \ne \, E{T}_{U}^{b}(i)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(20)

while comparing the flows of precipitation ${P}_{U}^{f}(e)$ and ${P}_{U}^{b}(e)$ obtained in Equation (17) and Equation (19) we find:

$${P}_{U}^{f}(i) \, \ne \, {P}_{U}^{b}(i)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(21)

To further understand the nature of this dichotomy, we assess the deviation of the tracked flows at the country/ocean scale $E{T}_{U}^{f}(e)$, $E{T}_{U}^{b}(e)$, ${P}_{U}^{f}(i)$ and ${P}_{U}^{b}(i)$ to ERA5 corrected data on precipitation and evaporation – i.e., ${\overline{\hat{P}}}_{ERA5}(c,m)$ and ${\overline{\hat{ET}}}_{ERA5}(c,m)$ (Equation (8), Equation (9)). To this aim, we integrate the cell-scale monthly data at the country/ocean and annual scales to obtain ${\overline{\hat{P}}}_{ERA5,C}(i)$ and ${\overline{\hat{ET}}}_{ERA5,C}(e)$, that reads

$${\overline{\hat{P}}}_{ERA5,C}(i)={\sum }_{c\in i=1}^{C}{\sum }_{m=1}^{12}{\overline{P}}_{ERA5}^{c}(c,m)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(22)

$${\overline{\hat{ET}}}_{ERA5,C}(e)={\sum }_{c\in e=1}^{C}{\sum }_{m=1}^{12}{\overline{ET}}_{ERA5}^{c}(c,m)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(23)

Where subscript C recalls country/ocean aggregation.

Comparing Equation (22) with Equation (17) and Equation (19), it emerges:

$${\overline{\hat{P}}}_{ERA5}(i) \, \ne \, {P}_{U}^{f}(i)$$

(24)

Conversely, comparing Equation (23) with Equation (16) and Equation (18):

$${\overline{\hat{ET}}}_{ERA5}(e) \, \ne \, E{T}_{U}^{b}(e)$$

(25)

These deviations are reported in Fig. 1.

Iterative Proportional Fitting (IPF) on the country/ocean scale bilateral atmospheric moisture flow matrix

To correct Equation (24) and Equation (25) we separately apply an IPF procedure and bi-proportionally adjust the import-export matrices F and B, re-scaling the rows and the columns by the minimum amount necessary, to respect the sum constraints ET_ERA5(e) and P_ERA5(i) until they converge toward a balanced matrix (^17,20).

The initial bilateral moisture matrix, F (or B), is adjusted with two coefficients, a row factor (r(e)) and a column factor (s(i)), which are obtained with an iterative procedure that progressively updates the initial matrix to obtain the final bilateral moisture matrix, F_IPF (or B_IPF), that satisfies the equations

$${\sum }_{i=1}^{C}{F}_{IPF}(e,i)={\overline{\hat{ET}}}_{ERA5}(e)\,{{\rm{and}}}\,{\sum }_{e=1}^{C}{F}_{IPF}(e,i)={\overline{\hat{P}}}_{ERA5}(i)$$

(26)

and

$${\sum }_{i}^{C}{B}_{IPF}(e,i)={\overline{\hat{ET}}}_{ERA5}(e)\,{{\rm{and}}}\,{\sum }_{e}^{C}{B}_{IPF}(e,i)={\overline{\hat{P}}}_{ERA5}(i)$$

(27)

The iterative procedure alternatively evaluates the row and the column factors as follows. For example, for the matrix F, at step n=1, s(i)ⁿ⁻¹=1 while r(e) is calculated to satisfy the row constraint, namely

$$r{(e)}^{n = 1}=\frac{{\overline{\hat{ET}}}_{ERA5}(e)}{{\sum }_{e=i}^{C}s{(i)}^{n-1}\cdot F(e,i)}$$

(28)

At step n=2, r(e) = r(e)ⁿ⁻¹ and s(i) is equal to

$$s{(i)}^{n}=\frac{{\overline{\hat{P}}}_{ERA5}(i)}{\mathop{\sum }_{e=1}^{C}r{(e)}^{n-1}\cdot F(e,i)}.$$

(29)

Once the full iteration is completed, it is possible to determine the final row (R(e)) and column (S(i)) coefficients, namely

$$R(e)=\prod_{n}r{(e)}^{n}\,{{\rm{and}}}\,S(i)=\prod\limits_{n}s{(i)}^{n}$$

(30)

Hence, the generic adjusted bilateral moisture flow reads

$${F}_{IPF}(e,i)=R(e)\cdot F(e,i)\cdot S(i)\,{{\rm{and}}}\,{B}_{IPF}(e,i)=R(e)\cdot B(e,i)\cdot S(i)$$

(31)

Where R(e) and S(i) are matrix-specific and, therefore, they will be different for matrix F and matrix B. At this point, Equation (26) and Equation (27) are satisfied and the dichotomies in Equation (24) and Equation (25) are solved.

The IPF application demonstrates an improved matching between each corresponding bilateral connection in F_IPF(e, i) and B_IPF(e, i), with ${{{\rm{R}}}}_{log}^{2}$ of 0.9981 (Supplementary Fig. 4b), especially for larger flows, with respect to ante-IPF matrices F(e, i) and B(e, i). However, due to different initial conditions for the bi-proportional fitting, still a weak discrepancy between F_IPF(e, i) and B_IPF(e, i) remains.

To address the remaining discrepancy between the two bilateral matrices, we evaluate the IPF performance in the two cases, comparing the F(e, i) with F_IPF(e, i) and B(e, i) with B_IPF(e, i), proving a similar behaviour in the two cases, as shown in Supplementary Fig. 4a,b. In light of the similar performance of the IPF application on F and B, we average element-wise F_IPF and B_IPF and obtain a unified reconciled matrix M_IPF of moisture connections between countries/oceans, as follows:

$${M}_{IPF}(e,i)=\frac{{F(e,i)}_{IPF}+{B(e,i)}_{IPF}}{2}$$

(32)

To compare M_IPF(e, i) with ante-IPF flows, we perform the same average in Equation (32) also for F(e, i) and B(e, i), obtaining a mean matrix ante-IPF application namely M(e, i), as:

$$M(e,i)=\frac{F(e,i)+B(e,i)}{2}$$

(33)

The new mean matrix M_IPF(e, i) shows a good correlation with the ante-IPF matrix M(e, i) (Fig. 2a) with ${R}_{log}^{2}$ of 0.997.

Integration at the sub-continental scale

Both F and B matrices are aggregated to sub-continent/ocean scale matrices F^r and B^r and adjusted as in section 4, by separately applying the IPF algorithm on both F and B and assess the performance of the application.

The integration to the sub-continental/ocean scale refers for lands to the regions scheme from the United Nation Statistics Division (UNSD,⁵⁴), though with respect to this classification, we aggregate Caribbeans to Central America for consistency of flows in the network. The classification for oceans refers to the Global Oceans and Seas Dataset of the Flanders Marine Institute⁵¹ and a delineation of the Caspian Sea from the SeaVoX Salt and Fresh Water Body Gazetteer (v19) of the British Oceanographic Data Centre⁵², identically to the country/ocean case analysis (section 4).

To allocate each country/ocean forward and backward flow (F(e, i), B(e, i)) to a subcontinent/ocean scale bilateral connection in the matrices F ^r(r_e, r_i) and B^r(r_e, r_i), we query in both cases if each exporter country/ocean e falls in the boundaries of the exporter subcontinent/ocean r_e and if the import country/ocean i falls in the boundaries of the importer subcontinent/ocean r_i, and aggregate the flows as follows:

$${F}^{r}({r}_{e},{r}_{i})={\sum }_{e\in {r}_{e}=1}^{R}{\sum }_{i\in {r}_{i}=1}^{R}\cdot F(e,i)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(34)

$${B}^{r}({r}_{e},{r}_{i})={\sum }_{e\in {r}_{e}=1}^{R}{\sum }_{i\in {r}_{i}=1}^{R}\cdot B(e,i)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(35)

where R is the total number of regions and oceans (equal to 33).

The same aggregation procedure applied to the cell scale ERA5 corrected data in Equations (22)– (23), is here performed to ERA5 country/ocean corrected data for the average year in the period 2008–2017, namely ${\overline{\hat{P}}}_{ERA5}(i)$ and ${\overline{\hat{ET}}}_{ERA5}(e)$, as follows:

$${\overline{P}}_{ERA5,R}^{c}({r}_{i})={\sum }_{i\in {r}_{i}=1}^{R}{\overline{\hat{P}}}_{ERA5}(i)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(36)

$${\overline{ET}}_{ERA5,R}^{c}({r}_{e})={\sum }_{e\in {r}_{e}=1}^{R}{\overline{\hat{ET}}}_{ERA5}(e)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(37)

Where the subscript R recalls the subcontinent/ocean regional aggregation. At this point, the gross import (precipitation) and export (evaporation) are assessed for each subcontinent/ocean element of F^r and B^r, as follows:

$$E{T}_{U}^{f}({r}_{e})={\sum }_{{r}_{i}=1}^{R}{F}^{r}({r}_{e},{r}_{i})\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(38)

$${P}_{U}^{f}({r}_{i})={\sum }_{{r}_{e}=1}^{R}F({r}_{e},{r}_{i})\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(39)

and:

$$E{T}_{U}^{b}({r}_{e})={\sum }_{{r}_{i}=1}^{R}{B}^{r}({r}_{e},{r}_{i})\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(40)

$${P}_{U}^{b}({r}_{i})={\sum }_{{r}_{e}=1}^{R}B({r}_{e},{r}_{i})\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(41)

Applying IPF to subcontinent/ocean scale bilateral atmospheric moisture flow matrix

The IPF procedure is applied at the subcontinent/ocean scale, following Equations (28)–(31), applied to the region/ocean matrices F^r and B^r.

IPF is applied separately on the two matrices, to get in one case the adjusted ${{{\bf{F}}}}_{IPF}^{r}$ which satisfies equations

$${\sum }_{{r}_{i}=1}^{R}{F}_{IPF}^{r}({r}_{e},{r}_{i})={\overline{\hat{ET}}}_{ERA5}({r}_{e})\,{{\rm{and}}}\,{\sum }_{{r}_{e}=1}^{R}{F}_{IPF}^{r}({r}_{e},{r}_{i})={\overline{\hat{P}}}_{ERA5}({r}_{i})$$

(42)

and in the other case the adjusted ${{{\bf{B}}}}_{IPF}^{r}$, which satisfies equations

$${\sum }_{{r}_{i}}^{R}{B}_{IPF}^{r}({r}_{e},{r}_{i})={\overline{\hat{ET}}}_{ERA5}({r}_{e})\,{{\rm{and}}}\,{\sum }_{{r}_{e}}^{R}{B}_{IPF}^{r}({r}_{e},{r}_{i})={\overline{\hat{P}}}_{ERA5}({r}_{i})$$

(43)

Post-IPF matrices ${{{\bf{F}}}}_{IPF}^{r}$ and ${{{\bf{B}}}}_{IPF}^{r}$ are compared against ante-IPF matrices F^r and B^r, to assess the changes brought by the IPF to the network at this scale of analysis. Panels c and d in Supplementary Fig. 4 show that also at the subcontinent/ocean scale, the IPF works likewise in the forward and backward cases. In light of this result, we calculate the mean matrix M^rante-IPF and ${{{\bf{M}}}}_{IPF}^{r}$post-IPF, as in Equations (33) and (32). Results shown in Fig. 6 refer to the adjusted mean matrix ${{{\bf{M}}}}_{IPF}^{r}$.

Inter-scale validation

The subcontinental scale analysis also serves as a validation procedure to evaluate the sensitivity of the IPF method to the scale of application. To this aim, we aggregate the post-IPF country/ocean matrix M_IPF, at a subcontinent/ocean scale matrix, ${{{\bf{M}}}}_{IPF}^{aggr,r}$, and analyse its fit with the adjusted subcontinental-ocean matrix ${{{\bf{M}}}}_{IPF}^{r}$ obtained in the previous section (see Equations (42)–(43)).

The subcontinent/ocean matrix ${{{\bf{M}}}}_{IPF}^{aggr,r}$ is aggregated from the adjusted country/ocean matrix M_IPF as follows:

$${M}_{IPF}^{r,post}({r}_{e},{r}_{i})={\sum }_{e\in {r}_{e}=1}^{R}{\sum }_{i\in {r}_{i}=1}^{R}\cdot {M}_{IPF}(e,i)\,\,[{{{\rm{m}}}}^{3}{{{\rm{yr}}}}^{-1}]$$

(44)

Matrices ${{{\bf{M}}}}_{IPF}^{r}$ and ${{{\bf{M}}}}_{IPF}^{aggr,r}$ are compared element-wise as:

$$\epsilon ({r}_{i},{r}_{e})=\frac{{M}_{IPF}^{r}({r}_{i},{r}_{e})-{M}_{IPF}^{r,post}({r}_{i},{r}_{e})}{{M}_{IPF}^{r}({r}_{i},{r}_{e})}\,\,[-]$$

(45)

The mean relative deviation reads

$$\overline{\epsilon }=\frac{{\sum }_{{r}_{i} = 1}\mathop{\sum }_{{r}_{e} = 1}^{R}{\epsilon }_{rel}({r}_{i},{r}_{e})}{\mathop{\sum }_{r = 1}^{R}{M}_{IPF}^{r}({r}_{i},{r}_{e})}\cdot 100\,\,[ \% ]$$

(46)

and gives $\overline{\epsilon }$ = 0.084%.

Estimates of bilateral flows in ${{{\bf{M}}}}_{IPF}^{r}$ and ${{{\bf{M}}}}_{IPF}^{aggr,r}$ are plotted against each other in Supplementary Fig. 3.