Introduction

Climate projections are based on a variety of Earth system model (ESM) simulations compiled in model intercomparison projects1. The accuracy of these simulations is key for progress in climate science and eventually affects the implementation of climate policies globally. The sixth phase of the Coupled Model Intercomparison Project (CMIP6) substantially contributed to the physical science basis of the Sixth Assessment Report (AR6) by the Intergovernmental Panel on Climate Change (IPCC)1,2. This phase includes the most advanced ESMs, simulating historical and future climates based on greenhouse gas and aerosol concentration scenarios outlined in the Shared Socioeconomic Pathways (SSP)3. Nonetheless, continuous efforts are needed to keep improving multi-model ensembles, as some models have been shown to not fully align with observational evidence or theoretical understanding4,5,6,7,8.

The land water available for evapotranspiration (ET)—here referred to as active land water (ALW)—links the global energy, water, and carbon cycles, and is thus key for accurate climate projections9,10,11. ALW denotes the combined water available in the soil profile—including surface water, soil moisture from both upper and deeper layers, accessible groundwater, and rock moisture – that collectively contributes to plant transpiration and surface evaporation. ALW primarily directs the available energy (net radiation) at the land surface, towards the evaporation of water9,12. This process not only affects the water cycle but also modulates the turbulent heat fluxes, thus impacting the climate system as a whole13. ALW also acts as a reservoir for precipitation and radiation anomalies, maintaining stability in the climate system12,14. Moreover, given that plants regulate photosynthesis and transpiration in response to water availability, ALW influences the global carbon cycle9.

When ALW drops below a critical threshold, the evaporative fraction of net radiation decreases, leading to an increase in the sensible heat fraction and ultimately in air temperature12,13. Once ALW is below that threshold, terrestrial vegetation can no longer maintain sufficient transpiration and evaporation, effectively entering a water-limited regime. Water limitation is estimated to affect evapotranspiration in 30% to 60% of the Earth’s land surface for most of the year15, and it is an important factor in the exacerbation of heat extremes. However, our understanding of the frequency of water limitation and its effects on ecosystems under climate change remains limited12. This is reflected in the representation of land-atmosphere interactions in climate models16,17. Recent research has suggested an overestimation of future warming across CMIP6 models5, plausibly connected to other documented biases in soil moisture6 through land-atmosphere interactions. This uncertainty affects our ability to determine whether we can limit global warming below the targets outlined in the Paris Agreement. It is therefore crucial to constrain these model ensembles with other evidence, such as historical trends and current climate observations.

Using simulations from the land surface model component of nine ESMs available within CMIP618 driven with observed atmospheric forcing, we show that the frequency of water-limited conditions for evapotranspiration is generally overestimated across models. Furthermore, we analyze how biases in the frequency of water limitation relate to active land water storage capacity (ALWSC) within the models. We conclude by discussing the reasons behind these model biases and the potential implications for climate projections on land.

Results and discussion

Biases in the frequency of water limitation

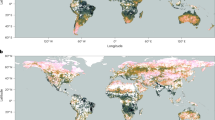
We focus on the land-hist experiment within the Land Model Intercomparison Project (LMIP), which consists of simulations of the land component of ESMs from CMIP6, driven by observational atmospheric forcing. Because LMIP simulations are forced with observational data, differences in the frequency of water limitation cannot stem from variations in precipitation or incoming radiation. This is not the case when using CMIP6 simulations from the historical scenario, where precipitation and radiation can differ among models. To quantify water constraints on evapotranspiration and photosynthesis, we study the evaporative fraction of net radiation (EF) as a function of total-column soil moisture from all nine ESMs available within LMIP. The variable ‘total soil moisture’ includes moisture from all soil layers2,19. On the other hand, given the challenges of directly observing EF and total soil moisture on a global scale, we use normalized remotely sensed solar-induced fluorescence (SIF) and TWS from GRACE to identify when vegetation is affected by insufficient water availability11. For models and observations, we first derive the critical water limitation threshold θcrit at every grid cell, and then compute the amount of time each grid cell remains beneath θcrit (see Methods).

We find that the frequency of water limitation is on average overestimated in CMIP6 models compared to observations by 14% over land, and up to 26% in the tropics (Figs. 1 and S1). Conversely, models often underrepresent the occurrence of water limitation in the Northeastern US and in central and northern Europe, and generally at high latitudes in the Northern Hemisphere. Grouping our results by IPCC regions generally supports these findings, with many regions showing an overestimation of frequency of water limitation in the models. The most affected regions include the Congo rainforest, Southern Africa, Australia, the Amazon, South and Southeast South America, and Eastern Central Asia (Fig. 2). We additionally analyze water limitation frequency when substituting GRACE TWS data with total soil moisture from two products (GLWS2.020 and GLDAS_CLSM025_DA1_D19,21,22) that assimilate GRACE TWS and exclude snow and water bodies on land (Fig. S2). Here, too, we find a similar overestimation of water limitation frequency by the models. Our results are also consistent when using CMIP6 simulations from the historical scenario instead of those from the land-hist experiment (Fig. S3).

Fig. 1: Global maps of frequency of water limitation.
figure 1

Pixel-specific critical water limitation thresholds (θcrit) were calculated to determine when plant water stress occurs. We show here the fraction of months with total-column soil moisture below θcrit. a θcrit determined with normalized SIF versus normalized TWS from GRACE (2007–2014). b θcrit calculated with EF vs normalized total-column soil moisture with LMIP-CMIP6 data (2007–2014). Dark blue pixels represent areas where water is rarely limiting, whereas dark red pixels represent areas that are almost always water-limited. Gray areas correspond to regions where our methodology could not be applied due to insufficient data points after applying a growing season filter (see Methods). White areas correspond to non-vegetated land (see Methods). The raw bias (Bias) was determined by subtracting the observed value from each model pixel-by-pixel and then calculating the mean of these differences globally across all pixels. Calculating the median bias instead of the mean yielded similar results (11% globally and 29% for the tropics). The land fraction (excluding gray and white pixels) affected by overestimation (Bias > 0) is 57%, and by underestimation (Bias < 0) is 40%. In the tropics, the corresponding overestimation is 78%, and the underestimation is 22%. For the absolute bias (|Bias|), we computed the mean after taking the absolute value of each pixel-wise subtraction. Biases were weighted to account for the latitudinal variation in grid cell area. Details of all datasets and normalizations can be found in Methods. The multi-model mean was calculated with models CESM2, CMCC-ESM2, CNRM-CM6-1, CNRM-ESM2-1, E3SM-1-1, EC-Earth3-Veg, IPSL-CM6A-LR, MIROC6 and UKESM1-0-LL.

Full size image
Fig. 2: Comparison of the frequency of water limitation across different IPCC regions based on LMIP-CMIP6 model simulations and observations.
figure 2

Region-wise evaluation of the frequency of water limitation, using observations-based estimates and corresponding LMIP-CMIP6 model simulations. We first derived the frequency of water limitation in every pixel and then computed the mean of these values within each IPCC region for model and observational data. We retained only IPCC regions that contained at least ten grid cells. a Vertical axis shows θcrit calculated using EF vs normalized total-column soil moisture from LMIP-CMIP6 data (2007–2014). Horizontal axis represents θcrit derived from normalized SIF and normalized TWS from GRACE (2007–2014). b IPCC reference regions. Details of all datasets and normalizations are provided in Methods. The multi-model mean was calculated with models CESM2, CMCC-ESM2, CNRM-CM6-1, CNRM-ESM2-1, E3SM-1-1, EC-Earth3-Veg, IPSL-CM6A-LR, MIROC6 and UKESM1-0-LL.

Full size image

The model overestimation of the occurrence of water limitation is confirmed when performing the same analysis with FLUXNET2015 observations, complemented with soil moisture simulated with a bucket-type soil water balance model driven by in-situ measurements23 (Figs. 3 and S4 and S5). For many ESMs, even a typically humid biome as the Amazon can experience water limitation for more than 30% of the days in a year (Fig. 3g, h, i, j). This pattern of water limitation is similar to that observed in a dry Mediterranean savanna (US-Ton, Fig. 3k–o). ESMs also overestimate the frequency of water limitation at multiple FLUXNET2015 stations in Australia, China, Italy, and the USA (Fig. S4). We use daily data from LMIP-CMIP6 (available only for four models) and we compare the ESM output to the FLUXNET2015 observations lying within the same grid cell (see Methods). The footprint of an eddy-covariance flux tower is much smaller than an ESM grid cell, and this could be a source of bias.

Fig. 3: Analysis of water limitation at three selected eddy-covariance sites.
figure 3

Evaporative fraction (EF) as a function of the active land water (ALW) in observations versus CMIP6 models. a, f, k, eddy-covariance measurements from the FLUXNET2015 dataset. b, g, l Data from UKESM1-0-LL. c, h, m Data from IPSL-CM6A-LR. d, i, n Data from EC-Earth3-Veg. e, j, o Data from CNRM-ESM2-1. When the decrease in the EF from its maximum value to the y-axis intercept was less than 0.3, we assigned a status of no water limitation (NA). The total soil moisture was normalized to ease the comparison between model outputs and the corresponding observed values (see Methods). GF-Guy is an evergreen broadleaf forest site situated in the coastal region of the north-western Amazon, in French Guyana. BR-Sa3, another site characterized by evergreen broadleaf forest, lies further south and inland in Brazil. US-Ton is an oak savanna woodland located near Sacramento, United States.

Full size image

These findings raise the question of whether the overestimation of the frequency of water-limited conditions stems from too little ALW available in the models, or from intrinsic model assumptions about how water availability influences land–atmosphere fluxes. In the next section, we compare ALWSC in models versus observational proxies, to assess whether biases in water storage capacity may be at the root of the discrepancies in the frequency of water limitation.

Modeled and observed active land water storage capacity

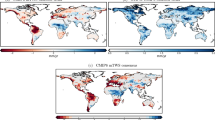
There are no direct observations of ALWSC that could be used to evaluate the models. The maximum cumulative water deficit (CWDmax), based on the annual maximum cumulative difference between evapotranspiration (ET) and precipitation (P)24,25,26 can be considered as a proxy for ALWSC, as it captures the depletion of ALW. To calculate the CWD with CMIP6 data, we directly used ET and P from LMIP-CMIP6 models. For the observational reference (referred to as SCWDX), we use the 80-year extreme CWD from a previous study27, determined using ET data derived from thermal infrared remote sensing via the Atmosphere-Land Exchange Inverse (ALEXI) product24,25 and precipitation reanalysis data from WATCH-WFDEI26. We find a model underestimation of ALWSC, especially in the wet tropics (Fig. 4). Grouping our results by IPCC regions reveals several regions where ALWSC is underestimated, i.e., South Asia, Central and South America, and Sub-Saharan Africa (Fig. S6). Using historical CMIP6 simulations instead of those from the land-hist experiment yields similar results (Fig. S7). It is important to note that SCWDX can be inaccurately low in areas that are not typically water-limited, as it relies on ET estimates derived from thermal infrared remote sensing. In addition, SCWDX accounts for snow accumulation and melt27, whereas this is not accounted for in the CWD estimate of the models, contributing to the differences in high-latitude regions.

Fig. 4: Comparison of active land water storage capacity (ALWSC) from LMIP-CMIP6 simulations against observations-based estimates.
figure 4

a ALWSC estimated with maximum CWD determined from ALEXI and WATCH-WFDEI observations (SCWDX) augmented using an extreme value distribution with an 80-year return period27. b ALWSC estimated with maximum CWD determined from 80 years of LMIP-CMIP6 data (1935–2014), to align with the methodology used for SCWDX. The land-hist simulation was used across CMIP6 models. White areas correspond to non-vegetated land (see Methods). The raw bias (Bias) was determined by subtracting the observed value from each model pixel-by-pixel and then calculating the mean of these differences globally across all pixels. For the absolute bias (|Bias|), we computed the mean after taking the absolute value of each pixel-wise subtraction. Biases were weighted to account for the latitudinal variation in grid cell area. Values exceeding 1000 mm are colored as 1000 mm for clarity. Details of all datasets and normalizations can be found in Methods. The multi-model mean was calculated with models CESM2, CMCC-ESM2, CNRM-CM6-1, CNRM-ESM2-1, E3SM-1-1, EC-Earth3-Veg, IPSL-CM6A-LR, MIROC6 and UKESM1-0-LL.

Full size image

As an alternative proxy for ALWSC, we also use the maximum annual depletion of total-column soil moisture (ΔSMmax) (see Methods). This is straightforward to obtain for the models, but difficult to derive from observations. We assume that the annual depletion in terrestrial water storage (ΔTWS) in observations from the Gravity Recovery and Climate Experiment (GRACE) is comparable to the depletion in total soil moisture from CMIP6 models10,11,28 (Fig. S8a, b). However, we note that this assumption is particularly problematic in regions with large annual variability in snow (e.g., high latitudes) or water bodies on land (e.g., the wet tropics, which contain large river basins), given that they contribute to the ΔTWS signal29,30. We thus additionally estimate ΔSMmax using two products (GLWS2.020 and GLDAS_CLSM025_DA1_D19,21,22) that assimilate GRACE TWS to simulate total soil moisture while excluding snow and water bodies on land (Fig. S8c–f). Results from GRACE ΔTWSmax suggest a much larger ALWSC, particularly in the Amazon, than what is represented in the CMIP6 models (Fig. S8a, b), whereas when compared to GLDAS_CLSM025_DAI_D (Fig. S8c, d) and GLWS2.0 (Fig. S8e, f), the bias in CMIP6 models is much smaller.

Overall, given the limitations of the observational estimates, it remains difficult to conclude how well ALWSC is represented in the ESMs. It is also conceivable that, during dry periods, the land component of the ESMs responds too strongly to water stress, reducing ET and thereby limiting further soil moisture depletion, which would decrease our model estimate of ALWSC. Thus, the overly frequent water-limited conditions in the models may not necessarily stem from an underestimation of the ALWSC; rather, they likely relate to how plant-available water is represented in the models, for instance, through assumptions about rooting depth or soil moisture stress functions. This is consistent with other studies pointing to a general overreliance on shallow rather than deep soil moisture in models31,32 and the stronger drying trends in projections of surface compared to deep soil moisture33.

Potential causes of biases between CMIP6 models and observations

Our analysis shows that CMIP6 models overestimate the occurrence of water limitation (Figs. 1 and 2), particularly in the tropics. The overestimation of the time under water limitation is consistent with previous studies suggesting that models underestimate ET in the tropics7, and across most regions during dry periods31,34,35,36.

Europe and North America emerge among the least biased regions when compared to observations (Figs. 1 and 2). This is probably due to the large availability of ground-based observations to constrain ESMs in these areas compared to the rest of the world. On the other hand, the Amazon and, in general, the wet tropics, are subject to the largest biases (Figs. 1 and 4). This supports previous findings that ESMs tend to overestimate water stress in the Amazon and do not adequately capture the positive sensitivity to atmospheric aridity in its most humid regions37 and at locations with a shallow water table38. This also potentially reflects the inadequate representation of tropical forest root traits in global models39. Given the key role of the Amazon for the global water and carbon cycles40,41, it is crucial to improve model accuracy when representing this region, also because the response of tropical rainforests to water limitation is one of the main uncertainties in ESMs42.

Among the nine LMIP-CMIP6 models available for this study, CESM2 has the most realistic representation of the soil-plant-atmosphere continuum, being the only model that represents water stress based on leaf water potential31,43,44. It explicitly accounts for plant hydraulics and calculates water potentials in soil, roots, stems, and leaves43. This enables plants in CESM2 to draw more water for transpiration from deeper soil layers compared to other ESMs43. This may explain why CESM2 is the model with the lowest raw bias (Figs. S1 and S9). CNRM-ESM2-1 and UKESM1-0-LL are among the models with the highest linear fit for the spatial pattern (R2) and lowest absolute bias (Figs. S1 and S9). This stronger performance may be linked to their more detailed treatment of land processes, including dynamic seasonality of leaf area index (LAI), interactive vegetation cover, and land use change, rather than relying on a fixed annual LAI cycle45. EC-Earth3-Veg ranks as one of the least accurate models in terms of water limitation (Fig. S1), even though it estimates ALWSC comparatively well (Fig. S9). This discrepancy likely stems from its limited accuracy in simulating EF (Fig. 3). MIROC6 has the highest overestimation of water limitation (Fig. S1), despite being the only model that overestimates ALWSC (Fig. S9). This is probably due to the model lacking a representation of terrestrial carbon-cycle processes and relying on prescribed vegetation properties (Table S1). These last two examples (with EC-Earth3-Veg and MIROC6) suggest that biases in water limitation are not necessarily related to biases in ALWSC. Overall, an accurate representation of water potentials, soil water uptake profiles, and LAI appears relevant for improving biases in water-limitation frequency and ALWSC.

Implications for predicting future climate on land

Our global comparison of state-of-the-art ESMs to observational estimates reveals an overestimation of water-limiting conditions. This bias hampers the model representations of both regional and global water cycles. For example, the Amazon is characterized by a high precipitation recycling ratio, as about one-third of the rainfall has previously evaporated from the Amazon itself46. In this and other regions strongly reliant on terrestrial ET, exaggerated ET suppression could result in excessive drought self-intensification and self-propagation12,47. Given that precipitation projections are uncertain due to both internal climate variability and the reliance on parameterizations at subgrid-scales1, it is crucial to improve model fidelity of ET to prevent an amplification of this uncertainty through unrealistic land–atmosphere interactions. As the global hydrological cycle intensifies in response to our warming climate48,49,50, biases in soil moisture-limitation of ET are likely to disproportionately affect the reliability of future projections.

Owing to the fundamental role of ALW in modulating not only water but also energy and carbon fluxes, model biases in water use and limitation propagate beyond the hydrological cycle. Soil moisture–temperature feedbacks are known to amplify hot extremes in most land areas51, which also emerges clearly in climate projections52,53. In fact, it has recently been shown that across much of Europe, air temperature increases are outpaced by even stronger soil temperature trends, suggesting that “the heat comes from below”54. It is challenging to reliably quantify the role of soil moisture–temperature coupling in a changing climate, but for certain regions, such as the wet tropics, including Amazonia, CMIP6 simulations point to a strong contribution of land feedbacks to extreme heat55. Recent work, again based on CMIP6 model experiments, indicates that strong land-atmosphere coupling will become more widespread under increasing atmospheric CO2, suggesting an amplification of future climate sensitivity to such feedbacks56. These findings distinctly rely on the ability of the CMIP6 multi-model ensemble to adequately capture the interactions between land and atmosphere, yet our results indicate systematic deficiencies with respect to how the land surface models make use of the available subsurface water and how they respond to drought conditions. As such, targeted efforts to improve the representation of these processes in climate models would likely enable more accurate projections of hot and dry extremes.

We remark that in certain regions, e.g., Eastern North America, Northern Europe, and India, the analyzed CMIP6 models underestimate the frequency of water limitation (Fig. 1). Consequently, in those regions, increases in both the occurrence and magnitude of future heatwaves could be underestimated by current state-of-the-art ESMs. Individual hot and dry events can undo several years’ worth of net carbon uptake at regional scales57, and global soil moisture variability has been shown to dictate the strength of the terrestrial carbon sink10,11,58, which in turn largely governs the fraction of anthropogenic CO2 emissions remaining in the atmosphere. Due to this inherent link between land carbon sequestration and climate extremes, model improvements of both subsurface water utilization and limitation could also reduce the intermodel uncertainty of carbon uptake and hence long-term climate projections.

In this study, we identify an overestimation of water limitation frequency across CMIP6 models compared to observations, and analyze how it relates to ALWSC, indicating a promising avenue for upcoming model development. Our analysis illustrates the challenges ESMs face in accurately capturing the specificities of the land water cycle, with implications for the simulated land water, energy, and carbon fluxes. Future work to refine land surface models is poised to benefit from a simulation environment that offers observational constraints to attribute model biases59, from novel proximal remote sensing techniques60, and from model outputs at higher temporal resolutions61. Insights from these developments can improve how models represent plant uptake and use of water across biomes and seasons.

Methods

Data sets

This study investigates how water limitation of evapotranspiration and ALWSC are represented across nine CMIP6 models (Table S1)2. We select these nine CMIP6 models because they were the largest set for which all required variables were available from the ETH Zurich CMIP6 next generation archive62. Our focus is on the land-hist experiment within the Land Model Intercomparison Project (LMIP), which consists of global land-only offline simulations driven with observational atmospheric forcing over a historical interval, improving snow and soil moisture estimates. Sharing the same configuration of historical simulations of the parent model within CMIP6, the land-hist experiment is conceived for diagnosing systematic biases within the land component of ESMs18.

We use the CMIP6 Land Model Intercomparison Project (LMIP) land-hist experiments to ensure that all models are forced by the same, observation-based meteorological inputs. This design removes a major source of inter-model variability—differing precipitation and incoming radiation—and helps us focus on how each land surface model responds to water limitation and regulates evapotranspiration (ET) and subsurface water storage. Although land-hist runs do not include land-to-atmosphere coupling, they do incorporate oceanic moisture fluxes implicitly through reanalysis-based forcing data. In contrast, fully coupled CMIP historical simulations include land–atmosphere–ocean feedbacks but have model-specific atmospheric forcing that can diverge substantially from observations, complicating the attribution of ET and water-storage biases to the land model itself. However, we should be aware that forcing LSMs with observed meteorological conditions can introduce other issues, because these models are typically tuned to run with their ‘native’ coupled atmosphere—one that may carry biases relative to observations (even disregarding internal variability). By using LMIP land-hist, we can more directly compare model performance against reference datasets under a common and realistic atmospheric forcing framework. As illustrated in the Supplementary Figs. (e.g., Figs. S3 and S7), our comparisons with the fully coupled CMIP6 historical runs show broadly consistent results, yet reinforce the added clarity in bias attribution when atmospheric forcing is fixed in the LMIP setup.

To benchmark CMIP6 models, we use several observational datasets. We use SIF from version 2.6 of the Global Ozone Monitoring Experiment-2 (GOME-2)63 as a proxy of photosynthetic activity (Fig. 1), consistent with previous studies41,63,64. Monthly means are calculated, retaining days when the effective cloud fraction is <30%41. SIF is a complementary process of photosynthesis, and it is thus directly related to the photosynthetic rate65. In addition, we use total water storage (TWS) data from the Gravity Recovery and Climate Experiment (GRACE)29. TWS accounts for soil moisture, groundwater, surface water, snow, and ice. To complement our analysis, we use eddy-covariance data from the FLUXNET2015 dataset66 together with soil moisture simulated with a bucket-type soil water balance model driven by in-situ measurements23. In Figs. S2 and S8, we also use two data products that assimilate GRACE TWS, namely: GLDAS_CLSM025_DA1_D19,21,22 and GLWS2.020. The key advantage of the GRACE dataset lies in its foundation on mass balance principles, ensuring its water balance aligns with that of CMIP6 models. Both CMIP6 models and GRACE operate on this principle, providing consistency in their approach to water balance, despite the CMIP6 models likely not capturing all physical processes contributing to land water storage variations. We use CMIP6 data from the ETH Zürich CMIP6 next generation (CMIP6ng) archive62, which adds extra validation for processed variables and consistency among files from different sources. We retained pixels with vegetated land using a global land cover dataset from MODIS67. To group the vegetated land pixels of the world in meaningful climatic regions (Fig. 2), we use the fourth version of the IPCC WGI reference regions68. Although the non-CMIP6 data products had higher spatial resolution, all datasets were resampled to the CMIP6 grid using area-weighted averaging. For land-cover data, after averaging, CMIP6 grid cell was classified as vegetated when more than 50% of its underlying high-resolution pixels were classified as vegetation. All analyses were performed using R Statistical Software69. To access all code and R packages used in this study, please refer to our published repository on GitHub and Zenodo (see “Data Availability” section).

Determining water limitation thresholds globally with monthly data

We studied the evaporative fraction (EF) as a function of the total-column soil moisture (SM, variable ‘mrso’) using monthly data from CMIP6 models. EF was calculated as the ratio of latent heat flux to net radiation:

$${EF}=\frac{{latent\; heat\; flux}}{{R}_{n}}=\frac{{{{\rm{hfls}}}}}{\left({{{\rm{rsds}}}}-{{{\rm{rsus}}}}\right)+({{{\rm{rlds}}}}-{{{\rm{rlus}}}})}$$
(1)

where “hfls” (W m−2) is latent heat flux from CMIP6 and “rsds,” “rsus,” “rlds,” and “rlus” were respectively incoming and outgoing shortwave radiation and incoming and outgoing longwave radiation (W m−2), also from CMIP6.

We retained data from all months with Rn > 75 W m−2 to focus on the growing season, effectively removing colder winter months at high latitudes. We then fitted a segmented linear regression with one breakpoint (i.e., “linear-plus-plateau model”70,71) to the EF vs SM relationship at each pixel, using R package “segmented”72. The pixel-specific estimate of the breaking point θcrit was determined by least-square fit; its value represents the SM threshold up to which EF increases linearly as a function of SM (water-limited regime)9,70,71. The percentage of time under SM limitation was calculated as the ratio of the number of months with SM < θcrit divided by the total number of months (Fig. S10b). Note that some pixels were excluded from the analysis (gray areas in Fig. 1), given that too little data points (fewer than 25, i.e., at least 2 years of data at monthly resolution) remained to fit the linear regression after applying the growing season filter. The global observational map shown in Fig. 1 was created with GOME-2 SIF63 data and TWS data from GRACE29 as a proxy of ALW. We focused on monthly data from the growing season by retaining months with SIF values greater than or equal to half of the pixel-specific SIF maximum11. This filter mainly excludes months when vegetation is not active at high latitudes, similarly to the Rn filter applied to the models. To derive a metric comparable to EF, we use SIF data divided by its pixel-specific maximum value, as in previous studies11,73. We then proceeded to calculate the frequency of water limitation as described above.

Total-column soil moisture and TWS values were scaled to the 0–1 unit interval using pixel-specific min-max normalization to allow for direct comparison between GRACE and CMIP6 datasets. Both model and observational analyses were limited to the period from January 2007 to December 2014 (8 years), based on the availability of the observational and modeled datasets.

We do not extend our analysis of water limitation to the intercept and slope from the segmented regression given the different variables used for the models and observations, as well as the high sensitivity of both the intercept and slope to the underlying assumptions of the segmented regression and the quantity of data points included in the analysis.

Determining water limitation thresholds at flux tower locations with daily data

We repeated the EF vs SM analysis outlined in the preceding section at the site-scale, using FLUXNET2015 daily data at selected sites (Figs. 3 and S4 and S5). We calculated EF using FLUXNET2015 data as \({EF}=\frac{{latent\; heat\; flux}}{{R}_{n}}\). Due to inconsistencies of measured soil moisture at several FLUXNET2015 sites36, we simulated soil moisture at eddy-covariance locations with SPLASH, a bucket-type soil water balance model based on a Priestley-Taylor formulation for ET estimation, with water-holding capacity set to 220 mm23,74. Soil moisture values were scaled to the 0–1 unit interval using pixel-specific min-max normalization to allow for direct comparison between FLUXNET and CMIP6 datasets. We focused on the growing season by retaining site-days with observed gross primary productivity (GPP) equal or greater than half of the site-specific maximum. We extracted EF and SM data at FLUXNET2015 locations using daily datasets from 2000 to 2014. We used daily LMIP-CMIP6 data (available only for models UKESM1-0-LL, IPSL-CM6A-LR, EC-Earth3-Veg, and CNRM-ESM2-1) and focused on the grid cells corresponding to the FLUXNET2015 sites for comparison. We determined the critical threshold θcrit and calculated the percentage of days when SM was less than θcrit relative to the total number of days. When the decrease in EF from its maximum value to the y-axis intercept was less than 0.3, we assigned a status of no water limitation (NA) to avoid misinterpreting noise as water limitation.

Estimating active land water storage capacity

We estimated ALWSC as the maximum cumulative water deficit (CWDmax). For the observational benchmark, we used CWDmax derived from an ET estimate based on thermal infrared remote sensing27, and precipitation from WATCH-WFDEI data. For the CMIP6 models, we derived the CWD as the annual cumulative difference in evapotranspiration (ET) and precipitation (P) at the monthly resolution, focusing on continuous dry periods, i.e., periods where the difference P–ET was negative27,36. We also assessed ALWSC by computing the long-term maximum annual soil moisture depletion in CMIP6 models, by using the total-column soil moisture (variable “mrso”) at the monthly resolution. This LMIP variable includes moisture from all soil layers in the model. In each grid cell, we estimated the maximum depletion of total-column soil moisture (ΔSMmax) by first calculating the difference between the highest and lowest total-column soil moisture monthly values in every year (Fig. S10a). We then identify the greatest annual difference across all analyzed years:

$$\Delta S{M}_{\max }={\max \left({\max \left({SM}\right)}_{{year}}-{\min \left({SM}\right)}_{{year}}\right)}_{{all} \, {years}}$$
(2)

For the maps in Fig. S8, we calculate the long-term maximum annual soil moisture depletion with estimates from GRACE, GLDAS_CLSM025_DA1_D19,21,22, and GLWS2.020. The calculation was performed for the years 2003–2014, when data were simultaneously available for the used products and CMIP6. GRACE was converted from cm to mm, whereas total-column soil moisture was already available in Kg m−2 (equivalent to mm H2O). To visualize regional biases in CMIP6 predictions, we grouped the results of Fig. 4 by IPCC climate reference regions68. We determined the mean of the ALWSC across all points within each region, using CMIP6 data. We then compared to the corresponding observational data for the same region (Fig. S6).