Introduction

Plate motions shape the Earth’s geography, control the distribution of volcanoes, earthquakes, and mineral resources, and have important effects on the evolution of life on Earth. Since the concept of plate tectonics was formulated in the 1960s, numerous studies have demonstrated that plate motions are generally affected by the negative buoyancy of subducted slabs (i.e., “slab-pull” forces), the potential energy gradient from the high topography of the ridges (i.e., “ridge-push” forces), and the shear traction at the base of plates (i.e., “asthenosphere-drive” forces)1,2,3. Plate velocity and deformation result from the balance of these driving forces. The detachment/ breakoff of a subducting slab is accompanied by a decrease of slab-pull force and the formation of a low-pressure zone in the asthenosphere4,5,6. In this scenario, asthenosphere flow regime could change from plate-driven Couette flow to the pressure-driven Poiseuille flow generated by lateral pressure and density variations within the asthenosphere7,8, which could then become the main plate-driving force9,10,11. However, the influence of slab detachment on plate kinematics and deformation under different tectonic settings remains poorly understood and has been mostly overlooked, although it could provide an important insight into plate motion.

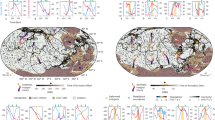
In recent decades, numerous observations have indicated that protracted convergence occurred after detachment of the subducted oceanic lithosphere (e.g., Alps, Anatolia, Zagros, Himalayas in the Tethyan belt)12,13,14,15,16. The pronounced post-breakoff uplift (>2.0 km) along the suture zones of the Tethyan collisional belt has been considered a typical geological feature of slab detachment17,18,19,20. Although the related plate-driving force remains debated, asthenosphere-lithosphere interaction by large-scale mantle flow due to mantle plume upwelling or slab sinking into the lower mantle could be strong enough for mountain building21,22,23,24. However, the uplift associated with slab detachment along the Tethyan orogenic belt is highly variable, showing pronounced in the Himalayas orogen but relatively modest in the Mediterranean-Carpathian and Zagros orogens (Fig. 1). Moreover, in modern active convergent plate margins (e.g., circum-Pacific subduction zones), episodes of slab detachment appear to have enhanced compression tectonics along the suture zones25,26,27, but only with minor uplift (<1.0 km) of overriding plates (Fig. 1). Because previous studies have mainly focused on whether basal mantle drag can drive sustained post-collisional plate convergence, the dynamic effect of slab detachment, especially considering the complex and variable nature of subduction-collision processes, has not been explicitly demonstrated yet.

Fig. 1: Tectonic expressions in various slab detachment scenarios.
figure 1

a Global topography and subduction zone distribution. Global topography data are from the ETOPO1 arc-minute global relief model (earth_relief_05m)66. Subduction zone geometries are based on the Slab 2 model67. The data of mid-ocean ridges are from the global tectonics package68. Slab detachment zones are labeled with numbers. The red lines represent spreading ridges. b Elevation and geological configuration of slab detachment zones. Error bars denote two standard deviations of the mean.

Full size image

Slab detachment may be achieved by developing tensile stresses in the hanging slab through, for example, subduction of a spreading ridge or of buoyant continental blocks5,28,29,30, which can further evolve into ridge-trench and continent-trench collision, respectively. In this study, we distinguish the tectonic settings of slab detachment into ridge-trench collision and continent-trench collision scenarios from a global perspective. Employing two-dimensional thermo-mechanical modeling, we then investigate the geological consequences of plate convergence driven by basal mantle flow induced by slab detachment in different tectonic scenarios. Our results emphasize the dramatic change of the plate-driving force from subduction-driven to asthenosphere-driven due to slab detachment and its various effects on plate motion and deformation in different geological settings.

Results

Modeling strategy and geodynamic scenarios

The numerical approach of the 2D thermo-mechanical simulation and the initial setup (Fig. S1) are described in detail in the Methods section31. It is important to note that the purpose of this work is not focused on exploring the origin or cause of slab detachment, but rather on the examination of its effects on geological and geophysical observables. The configuration of the numerical models is designed as a general representation of the incoming of buoyant continental blocks or mid-ocean ridges into the subduction zone, which is the main mechanism for slab detachment (Fig. 1). We identified four typical geodynamic situations based on the recent slab detachment events (<30 Ma), which can be categorized into two main types: spreading ridge-trench collision and continent-trench collision (Fig. 1). An important variable is the nature of the plate boundary on the subducting plate. The first geodynamic scenario is the ridge-trench collision without a weak plate boundary on the subducting plate, consistent with the Baja California Sur continental margin, where subparallel subduction of the Farallon-Pacific spreading ridge and slab detachment occurred at ca. 12 Ma25. The second is the ridge-trench collision with a mid-ocean ridge on the subducting plate, resembling the Southern Costa Rica and Chile continental margins, where the Cocos-Nazca ridge subduction and slab detachment took place at ca. 8 Ma26, and the slab detachment of the Nazca-Antarctic ridge subduction started ca. 5 Ma27. The third is the continent-trench collision with a weak boundary on the subducting plate. This case is analogous to the slab detachment in the Mediterranean-Carpathian region from ca. 30–20 Ma4. We also categorized the Zagros orogen as the third type, in which the Red Sea is an incipient sea basin32 and could be a continental rifting at ca. 10 Ma33. The last is the continent-trench collision with a mid-ocean ridge on the subducting plate, comparable with the slab detachment in the Himalayas orogen from ca. 25–13 Ma12,34.

Plate convergence in response to slab detachment

The flow field within the asthenospheric mantle and the induced motion and topographic evolution of the overlying plates for four different geodynamical settings are shown in Fig. 2. The detailed results about how the motion rate of the subducting plate and the topography of the suture zone evolve after slab detachment in these four different reference models are shown in Fig. S2. Mantle flow in our models is driven by slab subduction and the sinking of the detached slab. For the third geodynamical setting, we use an endmember model with a homogenous subducting plate. The effect of the plate boundary weakness (PBW) will be further shown in other sensitivity parameter tests.

Fig. 2: Reference models showing plate motion and deformation in response to slab detachment.
figure 2

a Ridge-trench collision without plate boundary weakness (PBW) on the subducting plate. b Ridge-trench collision with mid-ocean ridge on the subducting plate. c Continental-trench collision without PBW on the subducting plate. d Continent-trench collision with mid-ocean ridge on the subducting plate. The velocity profile on the top of each panel is obtained at the depth of y = 28 km (i.e., 8 km below the initial surface) in the model. Velocity is positive to the right and negative to the left. The upper and lower model snapshots display the onset of slab detachment and subsequent vigorous mantle flows, respectively. The time of the lower snapshot is relative to the upper snapshot. The bottom of each panel shows the topographic evolution over model time, with the green dashed line indicating the onset time of slab detachment. Color palettes at the figure base represent viscosity, mantle flow velocity, and elevation from left to right. MOR Mid-ocean ridge, RTC Ridge-trench collision, CTC Continent-trench collision.

Full size image

Figure 2a shows the model evolution of the first geodynamical scenario. Slab detachment induces vigorous mantle flow that is mainly focused beneath the ridge-trench collision zone. With a rheologically homogeneous subducting plate, the mantle suction force caused by slab detachment is insufficient to drive obvious deformation and movement of the subducting plate (Fig. S2a). When a mid-ocean ridge is prescribed on the subducting plate in the ridge-trench collision scenarios (Fig. 2b), plate convergence shows a much different evolution. Before slab detachment, the negative slab buoyancy produces active mantle flow (ca. 2 cm/yr) beneath the mid-ocean ridge (Fig. 2b). After slab detachment, the sinking of the detached slab induces corner flow around the trench, with the mantle flow increasing toward the trench. In this case, we can observe a trench-ward motion of the subducting plate with a maximum transient velocity of 7.3 cm/yr (Fig. S2b). The corresponding geological response is characterized by spreading acceleration of the mid-ocean ridge on the subducting plate. Even so, the topographic evolution of the overriding plate in the different ridge-trench collision models is similar (Fig. 2a, b), indicating that the difference in motion state of the subducting plate plays little role in shaping the surface topography. In addition, vigorous trench-ward horizontal mantle flow is discovered in these models at shallow depths beneath the ridge axis attached to the trench.

Figure 2c, d show the experimental results for continent-trench collision for the case of a rheologically homogeneous subducting plate and a subducting plate with a mid-ocean ridge, respectively. Because the continental lithosphere is mechanically attached to the subducting slab, the pull force of descending slabs drives the trench-ward motion of the subducting plate during the ongoing subduction. When slab detachment arises, the trench-ward motion rate of the subducting plate decreases sharply (Fig. S2c, d). Although obvious corner flow is activated beneath the trench, little to no continental plate motion occurs due to the stronger lithospheric resistance to plate movement than in the ridge-trench collision cases (Fig. 2c). The shear traction exerted by the horizontal mantle flow at the base of the plate may drive not only the plate motion but also the deformation of the overriding plate. In Fig. 2c, the topography of the overriding plate near the trench (< 400 km) only experiences a slight elevation after slab detachment (Fig. S2c). In contrast, an obvious uplift (up to ca. 6.0 km) of the overriding plate can be observed after slab detachment in Figs. 2d and S2d, which is much higher than those in the ridge-trench collision scenarios. In addition, the surface uplift in these models occurs around the suture zone, where the direction of horizontal mantle flow changes and generally extends less than 200 km away from the trench.

The mantle flow induced by slab detachment not only affects the subducting plate but also acts on the overriding plate. We hence present additional tests with a mid-ocean ridge prescribed on the overriding plate (Fig. S3). The results show an obvious trench-ward motion (ca. 8 cm/yr) of the overriding plate in the case of ridge-trench collision (Fig. S3a, b), consistent with the case with the mid-ocean ridge prescribed on the subducting plate (Fig. 2b). The topography of the suture zone shows a moderate but more widespread uplift (ca. 2 km) in the case of continent-trench collision (Fig. S3c, d). The presence of mid-ocean ridges on the subducting and overriding plates can result in an obvious uplift (ca. 8 km) in the case of continent-trench collision (Fig. S4). In summary, although simplified, these tests support the important role of slab detachment in driving plate convergence.

Effects of PBW on the subducting plate

PBW on the subducting plate has an important effect on plate motion (Fig. 2a, b) and deformation (Fig. 2c, d), as revealed by the geological responses in different ridge-trench and continent-trench collision models. To validate this result, we conduct a series of numerical experiments, including variable cooling ages of mid-ocean ridges and plate boundary types on the subducting plate.

In the ridge-trench collision scenarios, we vary the cooling age of mid-ocean ridges from 0 to 4 Myr (Fig. 3a, b), corresponding to an increase in ridge axis strength. The results show that the trench-ward motion rate of the subducting plate decreases from 7.3 to 1.2 cm/yr over the range of model parameters with increasing ridge strength (Fig. 3c). The trench-ward motion rate decreases rapidly for increasing cooling ages of mid-ocean ridges up to 2 Myr, and more slowly for older cooling ages. Moreover, we replace the initial setup of mid-ocean ridges on the subducting plate using a weak plate boundary. The result shows a nearly stationary subducting plate with the same subducting plate size when slab detachment occurs (Fig. S5a). Compared with the model without PBW on the subducting plate (Fig. 2a), we can see that PBW is a prerequisite to promoting the subducting plate motion during ridge-trench collision. In particular, the spreading ridge is a much more favorable plate boundary for mantle-driven plate convergence during slab detachment.

Fig. 3: Test models showing the effect of PBW on the subducting plate.
figure 3

a and b Initial ages of mid-ocean ridges on the subducting plate are 1 and 4 Myr, respectively. c Relationship between the maximum trench-ward motion rate and the initial cooling age of mid-ocean ridge. d and e Initial sizes of weak seeds on the subducting plate are 20 × 20 km2 and 30 × 30 km2, respectively. f Relationship between the maximum elevation and the initial size of weak seeds. The model snapshot depicts vigorous mantle flow conditions. Velocity profiles, topography evolution plots, and color palettes follow the conventions established in Fig. 2.

Full size image

In the continent-trench collision scenarios, subduction drag can reactivate the extinct ridge on the subducting plate forming new spreading ridge. Given that the initial model with an extinct ridge on the plate acts as a spreading ridge when slab detachment occurs, we test the effect of PBW by prescribing a variable size of weak seeds on the subducting plate (Fig. 3d, e). The larger the weak seed, the weaker the initial plate boundary. The results show that if the plate boundary breaks, the elevation at the suture zone remains almost identical to the model with a mid-ocean ridge on the subducting plate (Fig. 3f). In contrast, if the weak plate boundary does not break, the elevation at the suture zone is around 2.2 km, which is much higher than the model with a homogenous plate boundary. These results indicate that when slab detachment occurs, the mid-ocean ridge on the subducting plate can cause an obvious uplift at the suture zone, whereas weak plate boundaries on the subducting plate can only cause a moderate uplift along the suture zone.

Effects of the subducting plate size

The relationship between mantle-driven plate convergence and plate size is another point of interest. We therefore test a range of models with different ridge-trench distances in the ridge-trench and continent-trench collision scenarios (Fig. 4). In ridge-trench collision models (Fig. 4a, b), the trench-ward motion rate of the subducting plate increases as the ridge-trench distance decreases from 2000 to 1000 km (Fig. 4c). This phenomenon can also be observed in the ridge-trench collision model with a weak plate boundary on the subducting plate (Fig. S5). In addition, the increase in the rate of trench-ward motion is much more pronounced when the distance between the plate boundary and the trench is less than 1500 km. The results indicate that small-size plates are more likely to be driven by mantle flow during slab detachment. In continent-trench collision models (Fig. 4d, e), the elevation of the suture zone decreases slightly as the ridge-trench distance changes from 2000 to 1000 km (Fig. 4f). This indicates that large-sized plates are more likely to produce greater converging force between the subducting and overriding plates.

Fig. 4: Test models showing the effect of the subducting plate size.
figure 4

a and b Ridge-trench distance is 1500 and 1000 km, respectively, in the ridge-trench collision model. c Relationship between the maximum trench-ward motion rate and the ridge-trench distance. d and e Ridge-trench distance is 2500 and 1500 km, respectively, in the continent-trench collision model. f Relationship between the maximum elevation and the ridge-trench distance. The model snapshot depicts vigorous mantle flow conditions. Velocity profiles, topography evolution plots, and color palettes follow the conventions established in Fig. 2.

Full size image

Discussion and Conclusions

Slab detachment can transform the shear traction at the base of plates from resisting to driving plate motion, during which mantle drag could compensate for a part of the lost slab pull force. However, the basal drag under power-law rheological conditions is an order of magnitude lower than the slab pull force35,36,37, implying that there may be other factors inducing mantle-driven plate convergence. Li et al.24 suggested that the Cenozoic India-Asian collision could have been driven by the upper-mantle flow originating from the Neo-Tethyan slab detachment interacting with the thick Indian cratonic root and thereby enhancing both lithosphere-asthenosphere coupling and upper-plate compressional stress. In this study, we propose that the mantle-lithosphere-ridge interaction could have an important effect on the dynamic mechanism of plate convergence induced by slab detachment (Fig. 2). The obvious uplift of the overriding plate along the suture zone only occurs in the continent-trench collision scenario when there is a spreading ridge on the subducting plate (Fig. 3f). In contrast, the ridge-trench collision cannot induce obvious uplift of the overriding plate (Fig. 2a, b) but can drive the fast trench-ward motion of the subducting plate with a spreading ridge at the rear (Fig. 3c).

We interpret the experimental results in the light of force balance analysis (Figs. S6 and S7). The motion rate of the subducting plate is determined by the combined force (Fc) and the mass (i.e., plate size) of the subducting plate. When the subducting slab detaches, the motion of the subducting plate is driven by friction drag (Fdf) at the base of the lithosphere but resisted by boundaries of the subducting plate (Frt) and the suture zone (Frs). The basal drag exerted by the fast-moving asthenosphere is generally less than 20 MPa (Fig. S6e, f), and when integrated over the plate surface, it typically cannot overcome the overall strength of an unstretched lithosphere (Fig. S6c, d). However, when a spreading ridge is present on the subducting plate, the weakness of the ridge axis strongly reduces the lithospheric resistance (Fig. S6a, b) and the tectonic structure of the ridge axis can introduce additional driving forces, including the ridge push force associated with the potential energy gradient from the high topography of ridges (Fdp), and slab detachment-induced mantle flow pushing at the lithospheric step (Fdn). The net force (Fc) acting on the subducting plate can be expressed as \({F}_{c}={F}_{df}+{F}_{dn}+{F}_{dp}-{F}_{rt}-{F}_{rs}\). In the ridge-trench collision scenario, the mid-ocean ridge on the subducting plate results in relatively large plate driving-forces and relatively small plate resistances, and thus the net force acting on the subducting plate is larger than in other cases. Moreover, with the decreasing of plate size (Figs. S7a, c), the average thickness of oceanic lithosphere decreases due to the younger oceanic lithosphere (Fig. S7e), and the second invariant of the deviatoric stress tensor of the subducting plate increases (Fig. S7d). Thus, the smaller the plate size, the faster it will speed up (Fig. 4c). Correspondingly, the deformation and elevation of the suture zone are determined by the net force balance \({F}_{rs}={F}_{df}+{F}_{dn}+{F}_{dp}-{F}_{rt}-{F}_{c}\). In the continent-trench collision scenario, the blockage of the continent plate at the trench precludes the motion of the subducting plate and the net force acting on the suture zone is relatively low. This force reaches its maximum in the presence of mid-ocean ridges due to low Frt on the subducting plate (Fig. 4f). Besides, the elevation of the suture zone is slightly dependent on the subducting plate size, as a longer plate implies a greater extent of basal mantle traction, although this effect is relatively low (Fig. 4d, e). This may explain the phenomenon that the elevation of the suture zone increases slightly when the size of the subducting plate increases (Fig. 4f).

Although it is still difficult to reproduce the asthenospheric flow field, predictions from global mantle convection modeling may be the best constraint38,39,40,41. To reveal the effect of slab detachment on mantle flow, we further analyzed the spatial distribution of the magnitude and direction of horizontal mantle flow and its relationship to slab detachment. The horizontal flow field was estimated by the southward and eastward velocity components at 200 and 250 km depth (Fig. 5a–d) from the global mantle flow model of refs. 40,42. Figure 5a, b display the results from the model of ref. 42, which was calculated by estimating the relative importance of mantle density heterogeneity, surface plate motions, and net lithosphere rotation through the observation of azimuthal seismic anisotropy. The best-fitting model was determined by comparing the model predictions of asthenospheric anisotropy to a global data set of shear wave splitting measurements. Figure 5c, d show the horizonal flow component from the global mantle convection model that resolves the highly nonlinear rheology and plastic deformation of the mantle and combines global lithosphere and slab geometries, together with seismicity and tomography data40. The best-fitting model was determined by comparing the predicted surface plate velocities with geophysical observations. The major difference between the two models is the flow field at subduction zones, where the mantle flow velocities in Fig. 5c, d are much greater than that in Fig. 5a, b. This can be ascribed to the coupled plate-mantle system including mechanically coherent slabs and non-Newtonian rheology in Hu et al.40, which can better constrain the effect of slab pull. Despite this, both models show obvious trench-ward horizontal mantle flow along the slab detachment zones, except for the Baja California Sur continental margin (Location 1, Fig. 5a, c) which may be perturbed by the westward-subducting Pacific slab.

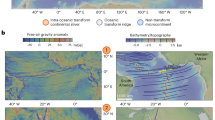
Fig. 5: Global mantle convection model showing the relationship between horizontal mantle flow and slab detachment.
figure 5

a and b Global mantle flow model of ref. 42 at 200 and 250 km depth, respectively. c and d Global mantle flow model of ref. 40 at 200 and 250 km depth, respectively. e and f Drag coefficient calculated from the model of (a and b). g and h Drag coefficient calculated from the model of (c and d). Black lines with arrows show the direction of mantle flow. Color palettes at the figure base represent (from left to right): horizontal mantle flow velocity (a–d), slab depth (a–h), and mantle drag coefficient (e–h).

Full size image

In order to quantify the effect of mantle drag versus plate drag, we compute the drag coefficient as the normalized difference between the sub-lithospheric velocity and the surface velocity in the direction of plate motion according to the method of ref. 41. The positive and negative values correspond to plate-driven and mantle-driven dominant drag, respectively. The results show obvious mantle-driven drag at the Chile continental margin (Location 3), slight mantle-driven drag at the Southern Costa Rica region (Location 2), and plate-driven drag at the Baja California Sur continental margin (Location 1) in ridge-trench collision zones (Fig. 5e–h). This may be attributed to the relatively young ( < 5 Ma) detachment time of the Nazca slab and the separation of Nazca slab from other subducting slab by mid-ocean ridges that avoid the effect of plate drag from the nearby subducting slab. By contrast, the detachment time of Cocos slab is ca. 8 Ma along the Southern Costa Rica region26 and the slab detachment area is small. In continent-trench collision zones, the model of Fig. 5e–h shows obvious mantle-driven drag at the Mediterranean-Carpathian and Zagros regions and slight mantle-driven drag along the Himalayas region. Because the main slab detachment time along the Tethyan orogens exceeds 10 Ma, it is too long to maintain mantle flow induced by slab detachment. The present mantle-driven drag at the Zagros region may come from the Afar mantle plume in the south. As previously studied, mantle plumes are also an important mechanism for driving plate motion22,43. Despite this, slab detachment of microplates at the Mediterranean-Carpathian region may produce the local strong mantle drag. For example, bathymetric mapping, high-resolution seismic reflection imaging, geodetic and earthquake data show that the ongoing convergence of the Sinai microplate with respect to Anatolia occurs in Cyprus, where a recent ( ~ 1 Myr ago) slab was detached along its sole converging plate boundary44.

We compare the modeling results with geological observations from ridge-trench collision and continent-trench collision zones. A typical ridge-trench collision case is the Izanagi-Pacific ridge subduction during the early Cenozoic (Fig. 6a), which has caused large-scale separation of the subducting Izanagi plate from the Pacific plate6,45. The 56–46 Ma magmatic gap formed across ca. 1500 km of the Eurasian continental margin among Japan, NE China, and Sikhote-Alin, Russian Far East well constrains the timing of slab detachment at 56 Ma27,46,47. At the time of slab detachment, the Farallon-Pacific full spreading rate increases from 75 ± 5 mm/yr at 57.6 Ma to 101 ± 5 mm/yr at 55.9 Ma48 (Fig. 6b). The key points are that the 57.6–55.9 Ma surge of the Pacific-Farallon plates spreading precedes the Izu-Bonin-Mariana (ca. 52 Ma)49 and Tonga-Kermadec (ca. 50 Ma)50 subduction initiation (Fig. 6b), and there are no indications of obvious changes in the Pacific plate absolute motion at this time51. Given that, an increase in Farallon absolute motion, either from the steepening of the subducting slab or development of east-dipping subduction, has been proposed to explain the acceleration of the Farallon-Pacific plates spreading during this period48. However, the demise of the Laramie orogeny at ca. 60 Ma indicates the steepening of the subducting Farallon slab is earlier than 56 Ma52,53. The development of east-dipping Farallon subduction through the closure of the Mezcalera and Angayucham basins is at ca. 55 Ma54, slightly lagging the time of the acceleration of the Pacific-Farallon plates spreading. Alternatively, the vigorous mantle flow triggered by slab detachment may provide additional forces that drive the Pacific plate toward the trench in the same direction shortly after the cessation of the Izanagi plate subduction and the corresponding acceleration of the Farallon-Pacific ridge spreading. This spreading acceleration is lower than our ridge-trench collision modes in Figs. 2b and 4c, possibly due to the relatively long ridge-trench distance.

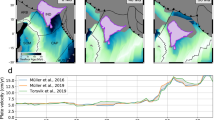
Fig. 6: Typical geological examples of ridge-trench and continent-trench collisions.
figure 6

a Plate reconstruction results45 showing the spatial distribution of Izanagi-Pacific and Farallon-Pacific spreading ridges at 55 Ma. b The spreading rate evolution of the Farallon-Pacific ridge48. IBM-SI = Izu-Bonin-Mariana subduction initiation; TK-SI = Tonga-Kermadec subduction initiation. c Topography and tectonic settings of the Tethyan orogenic belt. d The history of surface elevation change across56 Tibet and the spreading rate evolution of the Carlsberg ridge69. Gray-shaded areas denote the 95% confidence intervals for spreading rates.

Full size image

The Tethyan orogenic belt is the typical location where the continent-trench collision has occurred mainly in Cenozoic4,22,55. The presence of the Red Sea and the Indian Ocean spreading ridge promotes the penetration of the Arabia and India blocks into the Eurasian continent (Fig. 6c). Intensification of shortening from Late Miocene onwards produces the High Zagros, corresponding to slab detachment at ca. 10 Ma below the parts of Central Iran and eastern Turkey15. The India-Asia continental collision led to the eventual formation of the high (> 4 km) Tibetan Plateau (Fig. 6c). The uplift time of Tibet Plateau, which began at ca. 50–60 Ma, coincides with a sharp deceleration of the Carlsberg ridge spreading (Fig. 6d), suggesting an initial continental collision between India and Asia56,57. It is worthwhile to note that the India-Asia suture zone (Himalaya Mountains) was rapidly uplifted from <2 km to near-modern elevation from ca. 23 to 15 Ma (Fig. 6d), which is substantially delayed when compared with the time of initial collision along the India-Asia suture zone56,57,58,59,60. Slab suction induced by the slabs beneath East Asia8 may be important for the Himalayan uplift. However, the trench-ward (i.e., north-ward) mantle flow beneath the Indian plate61 indicates that the effect of mantle flow from East Asia may be minor. Previous studies indicated that the initial subduction of a large portion of the north-western India continent took place at 35 ± 5 Ma along a 1500 km-long suture zone, the slab breakoff started around 25 Ma and then propagated eastwards until the complete slab breakoff around 15 Ma34,62,63. The time of slab detachment is consistent with the rapid uplift along the Himalayas suture zone, which is accompanied by the slight fluctuation of the Carlsberg ridge spreading (Fig. 6d). Slab detachment could have caused a flatter slab that increased the coupling between the Tibet and India plates64. The buoyancy of the low-velocity zone above the flat slab facilitates maintaining the high elevation of Tibet Plateau64, but it does not explain the mechanism of rapid Himalaya uplift. By contrast, the rapid uplift along the Himalaya suture zone may be consistent with the mantle-driven plate convergence in our continent-trench collision models when there is a mid-ocean ridge on the subducting plate (Fig. 2d). Moreover, the difference in elevation between the Zagros and Himalayan collision zones (Fig. 1b) may be related to the plate boundary property (i.e., continent rifting versus spreading ridge) of the subducting plate during slab detachment (Fig. 3f).

Collectively, this study suggests that when subducting slabs are detached, the dominant force driving plate motion could switch from slab pull to mantle suction, during which the plate boundary, such as spreading ridges, controls the amount of plate convergence and the deformation of the overriding plate. The geological responses to this process are regulated by the mantle-lithosphere-ridge interaction, and a substantial difference exists between the ridge-trench collision and continent-trench collision scenarios. Nevertheless, it is also necessary to acknowledge the limitations of our study—the single slab detachment event in our model results in a short duration of mantle-driven plate convergence. While vertical plate deformation can be recorded by topography, short-duration rapid plate motion is hard to record. Future work with multiple slab detachment events that lasted for a long geological time will help to refine our understanding of the complex lithosphere-mantle interaction beneath collisional belts.

Methods

Model setup

High-resolution 2D models with a domain of 5050 × 1100 km distributed over 2001 × 301 nodal points are prescribed in the experiments (Fig. S1). In the x direction, the spatial resolution is 2.525 km. In the y direction, the spatial resolution varies from 2 km in less than 400 km depth to 7 km in more than 400 km depth. Each grid cell has 8 × 5 randomly distributed markers used to trace various material properties and temperatures. A total of 24 million makers are used in the calculation. The velocity boundary conditions are all free slip. A hanging slab nose is prescribed in our models to drive subduction and the formation of slab detachment without the presence of additional internal boundary velocity. To make the crust deform spontaneously, we implement a 20 km low viscosity “sticky” air overlain the crust to mimic a free surface. Erosion and sedimentation on the crustal surface are implemented according to the transport equation:

$$\frac{\partial {y}_{e}}{\partial t}={v}_{y}-{v}_{x}\frac{\partial {y}_{e}}{\partial x}-{v}_{s}+{v}_{e}$$
(1)

where ye is the vertical position of the erosion/sedimentation surface; vx and vy are the material velocity at the surface in x, y direction respectively; vs and ve are the sedimentation and erosion rates respectively, of which the values are applied by the following rules: vs = 0 and ve = 0.3 mm/yr when ye < 20 km, vs = 0.03 mm/yr and ve = 0 when ye ≥ 20 km.

For the initial compositional configurations, the continental plate incorporates a 20 km upper continental crust, a 10 km lower continental crust, and the underlying 70 km lithospheric mantle. The oceanic basin consists of 2.5 km-depth sea water, 2.5 km sediments, 3.0 km upper oceanic crust, and 7.0 km lower oceanic crust. The thickness of oceanic lithospheric mantle is determined by the half-space cooling model65, with a maximum thickness of 120 km. For simplicity, we set the hanging slab nose (i.e., subducting slab) using a unified thickness of 95 km, with 3 km upper oceanic crust and 7 km lower oceanic crust. A cambered weak zone is prescribed above the subducting slab at the mantle wedge region to decouple the subduction slab and the overriding plate. The initial thermal structure of continental lithosphere varies linearly from 0 to 650 °C from the surface to the crustal bottom and 650 to 1300 °C from the crust bottom to the lithosphere bottom. The initial thermal structure of oceanic lithosphere is applied using the half-space cooling model with ages ranging from 0 to 50 Ma. Beneath the lithospheric mantle, the initial temperature gradient is 0.5 °C/km. The presentation of the initial composition, temperature, and viscosity field of different models is in Fig. S1.

Governing equations

In this study, we use the I2VIS code to solve the momentum, continuity, and energy equations, that is,

Stokes equations:

$$\frac{\partial {\sigma {\prime} }_{xx}}{\partial x}+\frac{\partial {\sigma {\prime} }_{xy}}{\partial y} =\frac{\partial P}{\partial x}\\ \frac{\partial {\sigma {\prime} }_{yx}}{\partial x}+\frac{\partial {\sigma {\prime} }_{yy}}{\partial y} =\frac{\partial P}{\partial y}-g\rho (C,M,P,T)$$
(2)

Mass conservation is described by the incompressible continuity equation (extended Boussinesq approximation):

$$\frac{\partial {v}_{x}}{\partial x}+\frac{\partial {v}_{y}}{\partial y}=0$$
(3)

Heat conservation equations:

$$\rho {C}_{p}\left(\frac{DT}{Dt}\right) =-\frac{\partial {q}_{x}}{\partial x}-\frac{\partial {q}_{y}}{\partial y}+{H}_{r}+{H}_{s}+{H}_{a}+{H}_{L}\\ {q}_{x} =-k(T,P,C)\frac{\partial T}{\partial x},{q}_{y}=-k(T,P,C)\frac{\partial T}{\partial y}\\ {H}_{a} =T\alpha \frac{dP}{dt},{H}_{s}={\sigma }_{xx}^\prime{\dot{\varepsilon }}_{xx}^\prime+{\sigma }_{yy}^\prime{\dot{\varepsilon }}_{yy}^\prime+2{\sigma }_{xy}^\prime{\dot{\varepsilon }}_{xy}^\prime $$
(4)

where x and y are the coordinates along horizontal and vertical directions, respectively; vx and vy are velocity components; \({\sigma }_{ij}^\prime\) denotes deviatoric stress tensor; g is the gravitational acceleration; t is the time; ρ(C,M,P,T) is the density depending on composition(C), melt fraction (M), pressure (P), and temperature (T); q is the thermal heat flux; k(T,P,C)is the thermal conductivity depending on temperature, pressure, and composition; α is the thermal expansion coefficient; \({\dot{\varepsilon }}_{ij}^\prime\) is the deviatoric strain rate tensor; Hr is the radioactive heat production with a constant value for each rock; Ha is the adiabatic heating \(({H}_{a}=T\alpha (DP/DT))\); Hs is the shear heating; HL is the latent heating and is mainly invoked by partial melting below the mid-ocean ridges in our model.

For a given rock, the effective density (ρeff) is calculated according to the proportion of solid part and molten part.

$${\rho }_{eff} ={\rho }_{solid}-M({\rho }_{solid}-{\rho }_{molten})\\ {\rho }_{P,T} ={\rho }_{0}[1-\alpha (T-{T}_{0})][1+\beta (P-{P}_{0})]$$
(5)

where ρ0 is the standard density at P0 = 0.1 MPa and T0 = 298 K; the thermal expansion of all the rocks α = 3 × 10−5K−1; the compressibility of all the rocks β = 1 × 10−5 MPa−1.

Rheological model

The viscoplastic flow is adopted in this study. The non-Newtonian viscous creep follows the flow laws of the diffusion and dislocation creep, and depends on the temperature, pressure, and strain rate. The effective viscosity of the viscous deformation is the harmonic average between diffusion and dislocation creep.

$${\eta }_{vis}={\left(\frac{1}{{\eta }_{diff}}+\frac{1}{{\eta }_{disl}}\right)}^{-1}$$
(6)
$${\eta }_{diff}=0.5{A}_{D}{({\sigma }_{crit})}^{1-n}\exp \left(\frac{P{V}_{a}+{E}_{a}}{RT}\right)$$
(7)
$${\eta }_{disl}=0.5{({A}_{D})}^{\frac{1}{n}}{({\dot{\varepsilon }}_{\Pi })}^{\frac{1-n}{n}}\exp \left(\frac{P{V}_{a}+{E}_{a}}{nRT}\right)$$
(8)

where \({\dot{\varepsilon }}_{\Pi }\) is the second invariant of the strain rate tensor, which is defined as \({\dot{\varepsilon }}_{\Pi }=\sqrt{0.5{\dot{\varepsilon }}_{ij}{\dot{\varepsilon }}_{ij}}\); R gas constant, AD pre-exponential factor, Ea activation energy, \({V}_{a}\) activation volume, and n creep exponent. \({\sigma }_{crit}\) is the critical stress for transition from diffusion creep to dislocation creep.

Plastic deformation follows the Drucker–Prager yield criterion. The viscosity of the plastic deformation is calculated as follows:

$${\sigma }_{y}={C}_{o}+P\phi$$
(9)
$${\eta }_{plas}=\frac{{\sigma }_{y}}{2{\dot{\varepsilon }}_{\Pi }}$$
(10)

where \({\sigma }_{y}\) is yield stress, C0 cohesion, \(\phi\) effective internal friction coefficient. The effective viscosity of rocks \(({\eta }_{eff})\) is determined by the minimum viscosity of viscous and plastic deformation.

$${\eta }_{eff}=\,\min ({\eta }_{vis},{\eta }_{plas})$$
(11)

The physical properties of rocks used in this study are listed in Table S1.