Introduction

Dating back to the pioneering study of Manabe & Wetherald1 in 1975, scientists have recognized and agreed that the Arctic is warming faster than the global average in response to the increased greenhouse gases concentrations, a phenomenon known as Arctic amplification (AA). AA is consistently evident in paleoclimatic records2, recent observations3, and future climate model projections4. Understanding AA has been a long-standing and active research area because of its environmental, ecological, and societal implications for the coupled natural-human system within and outside the Arctic5, but explaining its causes is difficult. In this study, we seek to improve understanding of Arctic warming by reconstructing and attributing historical Arctic temperature trends and variability from a new perspective.

There is a warming asymmetry between winter and summer over the Arctic, with stronger winter warming than in summer6, and it has been suggested that Arctic sea ice loss plays a key role in setting this seasonal asymmetry7,8. Several different but related mechanisms have been proposed to explain this asymmetry: (i) a delayed seasonal warming manifesting through the surface albedo feedback, by which more solar energy is accumulated in the ocean during summer with less sea-ice and snow cover9 followed by more ocean heat released in the subsequent autumn and winter10; (ii) a weakened sea-ice insulation effect, by which reduced sea-ice cover and thickness lead to more ocean-to-atmosphere energy transport during winter7; and (iii) increased thermal inertia of the ocean surface layer, as the shift from perennial sea ice to seasonally ice-free ocean supports warmer surface temperatures later in the year, potentially causing peak winter warming11,12,13. However, with respect to mechanism (i), it is worth noting that AA can still be found in numerical experiments even without surface albedo changes14, implying that other processes are also active. Seasonal variations in other local climate feedbacks, such as the lapse-rate feedback, can also amplify winter warming15. Gravesen et al.16 suggested that Arctic warming above the lowermost part of the atmosphere cannot be primarily explained by snow and ice feedbacks and emphasized the importance of changes in atmospheric poleward energy transport (PET) on the Arctic warming aloft17.

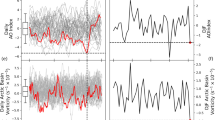
Atmospheric infrared sounder observations also show that the Arctic is becoming warmer and wetter18. PET associated with large-scale atmospheric circulations can substantially contribute to winter Arctic warming and sea ice loss by decreasing Arctic lower-tropospheric stability19 and increasing downward longwave radiation20. Figure 1 shows the time evolution of winter (December through February; DJF) area-averaged, normalized surface air temperature (SAT) anomalies, and the two factors identified as contributing to SAT warming: (1) the reduction of SIC, and (2) the increase in PET over the Arctic (70–90°N), based on the latest generation of European Centre for Medium-Range Weather Forecasts (ECMWF) reanalysis, ERA5 (Methods). Covariance among SAT, SIC, and PET might be impacted by the large trends over recent decades. Detrended time series and correlations (Fig. 1b) show similar relationships, although detrending those time series slightly decreases the correlation between SAT and SIC, SIC and PET, and to a lesser extent, between SAT and PET.

Fig. 1: Correlation among surface air temperature (SAT), sea ice concentration (SIC), and poleward energy transport (PET).
figure 1

a Standardized anomalies (relative to 1980–2024) of area-averaged DJF-mean SAT (red), reversed-sign SIC (blue), and PET (black) over the Arctic (poleward of 70°N). b Same as (a) but for detrended time series. The correlation coefficient (R) and the corresponding p-value are marked at the bottom of each panel.

Full size image

The rest of this article provides a new interpretation of factors helping to explain climate variability and changes over the Arctic during the boreal winter (DJF) by constructing a novel stepwise regression that utilizes the time series of PET, SIC, and atmospheric CO2 concentration to closely reproduce the Arctic tropospheric warming from 1980 to 2024. Using a dynamical adjustment method21, we demonstrate that ~80% of the variance in the PET time series during 1980-2024 can be explained by the component associated with atmospheric circulation patterns that we label as ‘dynamically induced’. The remaining 20% is likely influenced by other factors such as atmospheric thermodynamic processes, sea ice variations, ocean heat flux anomalies, and cloud radiative effects, which are not directly accounted for in the dynamical adjustment framework. We then show that observed SAT trends since the 1960s can be decomposed into factors associated with (i) a secular trend in those atmospheric circulation features (termed as ‘dynamically induced warming’), (ii) a trend in the dynamically adjusted SIC (i.e., SIC after removing the dynamically induced component), and (iii) a trend directly associated with increasing CO2. Dynamically-adjusted sea-ice loss (i.e., sea-ice loss after removing dynamically-induced components) contributes over half of the winter Arctic SAT increasing trend during 1959–2015 while dynamically-induced warming accounts for about one-fifth at the surface and up to 80% in the mid-troposphere. CO2 can explain the remainder of the trend. Our study contributes to the ongoing exploration of the drivers of amplified Arctic warming, an open question in climate science and global changes. While our findings agree with previous work, they offer a refined quantitative perspective on key factors influencing AA, emphasizing their relevance for improving climate models and predictabilities.

Results and discussion

Reconstructing winter Arctic tropospheric warming

Unlike the top-heavy warming signature found in the tropical troposphere22, the Arctic tropospheric warming has a bottom-heavy structure (Fig. 2a). Screen & Simmonds23 in 2010 tried to attribute this bottom-heavy warming structure by regressing the temperature field onto the SIC time series and concluded that sea ice loss played a leading role in the recent Arctic warming. However, subsequent results from global climate model experiments suggest that the effects of sea ice loss are primarily associated with the near-surface warming, whereas Arctic warming aloft is likely to be associated with other remote controls24,25,26. We have repeated the regression method in ref. 23 and confirm that the Arctic warming trend over the whole troposphere cannot be fully explained by the SIC reductions (Supplementary Fig. S1), especially when the regression coefficient is calculated using detrended data to eliminate concerns of two variables with large trends (Fig. S1b).

Fig. 2: Reconstruction and attribution of winter Arctic tropospheric temperature (T) trends during 1980-2024.
figure 2

a Observed (black dot) and regressed (red circle) trends (K decade-1) of area-averaged DJF-mean T over the Arctic (poleward of 70°N). All of trends are statistically significant at the 99% confidence level. b Contribution (%) of PET (black), PET-adjusted SIC (blue), and CO2 (red) indices to regressed T trends.

Full size image

Motivated by previous analyses, a simple physically based stepwise regression (Methods) has been constructed to better reveal possible contributions to Arctic wintertime tropospheric warming. Interestingly, trends of T time series derived from the stepwise regression framework (red circles in Fig. 2a) closely agree with the observed trends (black dots in Fig. 2a) based on ERA5 data. The correlation coefficients between regressed and observed time series show a bottom-heavy structure: gradual decreasing from ~0.95 in the lower troposphere to ~0.8 in the upper troposphere (red circles in Supplementary Fig. S2). Using stepwise regression, we decompose the Arctic tropospheric warming trend into contributions from three time series indices representing key climate drivers, namely, changes in PET, PET-adjusted SIC, and CO2 (Fig. 2b). The PET-adjusted SIC index describes the largest contribution (~50%) to warming near the surface. The PET-adjusted SIC contributions show a profile that decreases with height in the lower troposphere, reaches a local minimum near 600 hPa, and then increases aloft, implying a possible link between sea ice variability and temperature fluctuations in the mid to upper troposphere27. The peak of PET relative contributions at 600hPa is associated with the opposite vertical changes of specific humidity, which decreases with height, and meridional wind, which increases with height, across 70°N28. The CO2 increase plays a smaller role (≤ 18%) at most of vertical levels compared to the other two factors. The CO2 time series (not shown) follows a nearly linear trend with minimal interannual variability, so its regression coefficient mainly captures the residual long-term warming after accounting for the influences of atmospheric circulation and sea ice changes. Note that CO2 should be responsible for more warming than that shown in Fig. 2b, due to its indirect roles through driving sea ice loss and atmospheric circulation changes.

AA is a robust response to CO2 increases1,15, but the spatial pattern of CO2 radiative forcing is inhomogeneous and directly affects the PET under global warming29. While CO2 is considered as the primary forcing agent related to anthropogenic activities30, other factors, such as clouds and water vapor, also influences the climate response through feedback processes31,32. These unconsidered factors might help explain the slightly overestimated trends by our regression that uses a single homogeneous CO2 concentration in Fig. 2a. The excellent performance of this simple regression suggests that it has captured the most important factors connected with historical temperature changes during the Arctic winter. Nevertheless, we acknowledge that feedback processes involving water vapor and clouds are not explicitly represented, which maybe implicitly captured within the existing terms. Future work incorporating these additional feedbacks could provide further clarity.

Dynamical adjustment of the PET time series

Given the large interannual variability and the trend of the PET index which is less than 99% significant threshold (p-value = 0.03) in Fig. 1, and the strong influence of Northern Hemisphere (NH) teleconnection patterns on wintertime climate variations30,33, we hypothesize that the influence of PET on high-latitude temperature is largely explained by the dynamically induced component associated with atmospheric circulation patterns. To test our hypothesis, we first employ a regression and composite analysis and then apply a dynamical adjustment methodology30 based on partial least-squares regression34 (hereafter PLS-regression) to the PET time series, as described in Methods.

To investigate the spatial relationship between the PET index and the large-scale atmospheric circulation patterns, we first regress detrended DJF-mean sea level pressure (SLP) anomalies linearly onto a standardized (i.e. anomaly divided by the standard deviation) and detrended PET index (Fig. 3a). This map of fitted regression coefficients assumes an equal and opposite response to the atmospheric circulation anomalies between positive and negative phases of the standardized detrended PET index. To confirm this linear relationship, we obtain composite differences of detrended DJF-mean SLP anomalies (Fig. 3b) averaged over positive and negative years wherein the detrended PET index exceeds one standard deviation of the mean (Supplementary Fig. S3). Note that Fig. 3b is not sensitive to changes in number of positive and negative years used. The obvious similarity and high pattern correlation (0.83) over north of 20°N between Fig. 3a and b indicate that the relationship between the PET index and SLP field is approximately linear and this also demonstrates that the composite analysis is a simple but effective technique for exposing the relationship between PET and SLP. A common pattern in Fig. 3a and b is a negative anomaly center over the eastern North Atlantic surrounded by three regions known for atmospheric blocking (the North Atlantic, Ural Mountains, and eastern North Pacific). These blocking patterns have been recognized as playing an important role in the warm-air advection and cold-air outbreaks between the Arctic and mid-latitudes35,36,37, inducing strong poleward transport of moisture and heat.

Fig. 3: Relationship between PET time series and atmospheric circulation.
figure 3

a Regression coefficient of detrended DJF-mean sea level pressure (SLP in hPa) anomalies upon the standardized detrended PET index (black line in Fig. 1b) with 0.01 significance levels (stippling) during 1980-2024. b Composite difference of detrended DJF-mean SLP anomalies averaged over years wherein the standardized detrended PET index exceeds one standard deviation. The uncentered pattern correlation over north of 20°N between (a) and (b) is 0.83. c Raw (black), dynamically induced (blue), and residual (red) DJF-mean PET anomaly time series over the Arctic (poleward of 70°N). R2 is the square of correlation coefficient between black and blue lines.

Full size image

To further quantify the dynamically induced variability and changes in the PET time series during 1980–2024, we perform an SLP-based dynamical adjustment analysis. The analysis identifies the leading three PLS-regression predictors (i.e., the black lines in Supplementary Fig. S4b-d) and the corresponding patterns (i.e., SLP regression maps in Supplementary Fig. S5). Interpretation and physical meaning of the PLS-regression predictors and corresponding patterns are presented in detail in the Supplementary Discussion. We choose PLS-regression following ref. 21, as it provides a structured approach for identifying key explanatory variables in our analysis. Based on these connections between the mutually orthogonal PLS-regression predictors and well understood dynamical features, the dynamically induced component of the PET has been obtained by a multiple linear regression of the raw PET anomaly time series (black line in Fig. 3c) onto the three leading PLS-regression predictors. The total variance time series explained by the dynamically induced component (blue line in Fig. 3c) is 87%. These results are consistent with our hypothesis that PET are highly influenced by atmospheric circulation patterns. Residual PET variability not captured by the dynamic adjustment is likely influenced by other factors such as local thermodynamic processes, sea ice variations, ocean heat flux anomalies, and cloud-radiative effects, or may still be connected to the atmospheric circulation, but through non-linear interactions, or by higher order PLS-regression predictors which are not considered here.

Reconstruction and attribution of winter Arctic SAT variations since 1959

Reconstruction and attribution of winter Arctic SAT anomaly time series are the primary goal of this study. Motivated by the findings in Figs. 2 and 3 based on ERA5 data, we have extended our analysis using other datasets (Methods) back to the winter of 1958-1959, soon after direct measurements of CO2 were started in March of 1958 at Mauna Loa Observatory38. To accomplish this, we first apply the dynamical adjustment method to the time series of area-averaged DJF-mean SAT and SIC for 1959-2015 (Supplementary Discussion 2, Supplementary Figs. S6-S11). We then rebuild the observed SAT anomaly time series (black line in Fig. 4a) by the same stepwise regression used in Fig. 2 but replacing the PET index with the dynamically induced SAT component, and SIC after removing the dynamical influence. This substitution is made because while PET variability is largely dynamically induced (Fig. 3), it may also be affected by thermodynamic processes and ocean heat flux variations. Thus, using the dynamically induced SAT component directly ensures a more explicit attribution of atmospheric circulation-driven SAT changes. Figure 4 shows the total SAT time series (panel a; observed in black, and estimated by our regression in red), the dynamically induced component obtained from the dynamical adjustment (panel b), the SIC after removing the dynamically induced SIC (panel c; labelled as ‘dynamical-adjusted SIC’), and from CO2 variations (panel d). Interestingly, these three components, respectively, account for about 20%, 53% and 27%, respectively, to the total trend of the observed SAT time series during 1959–2015 (0.48 K decade-1 in Fig. 4a). This partitioning is broadly consistent with the surface-level results based on the ERA5 data from 1980–2024 (about 35%, 50%, and 15%, respectively; Fig. 2b). The time series deduced from the decomposition (red line in Fig. 4a) shows a high correlation (R = 0.91 before detrending and R = 0.84 after detrending) with the observed SAT time series during 1959-2015 and a small error (RMSD = 0.5). The regressed and observed SAT time series correlations are higher (R = 0.95 before detrending and R = 0.91 after detrending) during the satellite era (1979-2015) compared to the full time series, suggesting that observational accuracy may play a role in the analysis. To test if the findings for 1959–2015 remain robust in the context of more recent Arctic warming, we extend the SLP and SIC datasets by incorporating ERA5 data through 2024 (Fig. S12). To ensure continuity and minimize bias, we adjust the ERA5 fields using the 10-year monthly mean differences with 20CRv3 (for SLP, 2006–2015) and with NSIDC (for SIC, 2008–2017) before applying them to the extended period to 2024. The updated results remain consistent with the original findings. Namely, dynamically adjusted SIC still explains over 40% of the winter Arctic SAT warming, while the dynamically induced component increases modestly to ~38%. Since the potential effect of internal variability depends on the specific period and the choice of starting and ending years, we do not expect the relative contributions to be identical across different time intervals. However, the comparable contributions across different periods support the interpretation that these signals are largely robust.

Fig. 4: Reproduced Arctic winter SAT from 1959 to 2015.
figure 4

a Area-averaged DJF-mean SAT variations (K) over the Arctic (poleward of 70°N) based on the HadCRUT5 data (black) and reproduced by the stepwise regression (red) as described in the text. b–d Contributions to the regressed SAT from dynamically induced component, dynamically adjusted SIC, and CO2, respectively. e Mean (circle) and standard deviation (error bar) of SAT trends (K per decade) from 30-year moving windows based on observed (black) and regressed (red) anomaly time series in (a). f–h Same as red circle and error bar in (e) but based on individual time series in (b–d), respectively. The trends with 95% confidence interval of the corresponding time series are marked in (a–d). R is the correlation coefficient between black and red lines in (a) based on raw and detrended time series (R in parentheses). RMSD is the root-mean-square difference between black and red lines in (a). All trends (except for (b)) and correlations are statistically significant at the 95% confidence level.

Full size image

To further assess the robustness of this regression, we examine the trends of each time series in Fig. 4a–d using a sequence of 30-year (WMO standard climate normal period definition) moving windows that are incrementally shifted by one-year each. The mean and standard deviation of trends from the 28 moving windows (1959–1988, 1960–1989, ……, 1986–2015) are shown in Fig. 4e–h. They are 0.43 ± 0.3 (black in Fig. 4e), 0.42 ± 0.2 (red in Fig. 4e), 0.05 ± 0.12 (red in Fig. 4f), 0.24 ± 0.14 (red in Fig. 4g), and 0.13 ± 0.01 (red in Fig. 4h) K per decade. Overall, the component sensitive to dynamical variations (Fig. 4b, f) exhibits a large degree of variability and accounts for a large percentage of the standard deviation of trends from moving windows. These results suggest that our simple regression largely accounts for factors contributing to winter Arctic SAT historical trends.

CO2 has been identified as the primary driver of Arctic warming39, both through direct radiative forcing and indirect influences on atmospheric circulation and sea ice loss. The goal of our study is to disentangle the relative roles of internal and external processes contributing to the Arctic surface and tropospheric warming. To this end, we decompose the observed warming into contributions from atmospheric circulation, dynamically adjusted SIC, and the direct influence of CO2. While this framework does not provide causal attribution, it offers valuable insights into the mechanisms shaping observed Arctic warming. Although the extent to which circulation- and SIC-related warming components arise from internal variability versus external forcing remains uncertain, we hypothesize that these two components are largely related to internally generated and externally forced responses, respectively. Further quantifying the relative roles of internal variability and external forcing in these components represents an important direction for future research.

We have further tested the dependence of the results to the order of the stepwise regression (Figs. S13 and S14). As expected, when CO2 is considered first, a much larger portion of the lower tropospheric warming is attributed to CO2, including its indirect effects through altering atmospheric dynamics and SIC. However, in this way the specific contributions of these indirect mechanisms are unrevealed, reinforcing the rationale behind our decomposition method. The results confirm that CO2 remains the dominant driver of the historical Arctic SAT change as well as demonstrating the importance of explicitly resolving the intermediate processes that mediate its effects. The dominant contribution of PET to mid-tropospheric warming is likely in part due to internal variability and non-linear dynamical feedback that cannot be directly attributed to forcing agents.

As described in ref. 40, the dynamical adjustment method cannot distinguish between internally generated and externally forced contributions to the predictor (e.g., SLP) or predictand (e.g., SAT) fields. It is difficult to separate signal and noise using observations alone, but the large ensemble simulations based on climate models41, especially those in the Polar Amplification Model Intercomparison Project (PAMIP)42, can help to further address these issues in future research. The accurate reconstruction of historical Arctic warming by attributing it to three representative factors contributes to our mechanistic understanding of the causes of Arctic warming. However, it is important to acknowledge that other crucial feedback mechanisms, such as those through cloud and water vapor, as well as externally forced changes in SLP fields, are not directly considered in this analysis. These factors may also have played a significant role the observed Arctic warming trend. A more comprehensive inclusion of these local feedbacks and factors in future analyses could further improve predictions of seasonal-to-decadal changes in temperature and sea ice over the Arctic.

Methods

Climate data

ERA5, the fifth-generation ECMWF atmospheric reanalysis43, has been widely used in climate science community for its considerably high spatial resolution in both the horizontal (~31 km) and vertical (137 model levels from surface to 0.01 hPa) resolution. ERA5 provides hourly and monthly data through the Copernicus Climate Change Service (C3S) Climate Date Store (https://cds.climate.copernicus.eu/#!/search?text=ERA5&type=dataset). Here we use monthly averaged data provided by the C3S at 0.25° × 0.25° (longitude x latitude) horizontal resolution and 37 pressure levels from 1979 to 2024. The data we use include atmospheric temperature (T) at pressure levels, surface pressure, sea ice concentration (SIC), sea level pressure (SLP) and SAT. PET is calculated as the net difference between top-of-the-atmosphere radiative fluxes and surface energy fluxes, under the assumption that atmospheric heat storage is negligible over the timescale of the experiment15. We evaluate ERA5 against other observations for the time series of wintertime SAT (Supplementary Fig. S15) and SIC (Supplementary Fig. S16) over the Arctic in recent decades. Note that ERA5 reanalysis data are also potentially subject to some limitations, including a warm bias in near-surface temperatures relative to buoy observations in the Arctic, and a negative or upward bias in net surface longwave radiation44,45. However, since only the anomaly with respect to the whole time period is used in the analysis, this warm bias is less likely to have a significant impact on our main results as long as such warm bias is stable from year to year. Furthermore, recent studies46 suggest that ERA5-based temperature trends over the Arctic Ocean may actually be underestimated rather than overestimated. Nevertheless, our comparison of area-averaged DJF-mean SAT anomalies over the entire Arctic indicates that the warming trend in ERA5 is consistent with that observed in HadCRUT5.

Monthly mean atmospheric CO2 concentration measurements, started from March of 1958, at Mauna Loa Observatory, Hawaii38 are downloaded from https://gml.noaa.gov/ccgg/trends/data.html.

In Fig. 4 and relevant Supplementary Figs. (Supplementary Figs. S9-S11, S15, S16), we use three different sources of data (rather than ERA5) for SAT, SIC, and SLP fields, respectively, to extend our analysis to earlier years, including SAT as a collaborative product of the Met Office Hadley Centre and the Climatic Research Unit at the University of East Anglia (HadCRUT5), SIC provided by National Snow and Ice Data Center (NSIDC), and SLP provided by National Oceanic and Atmospheric Administration (NOAA)/Office of Oceanic and Atmospheric Research (OAR)/ Earth System Research Laboratory (ESRL), Physical Sciences Laboratory (PSL), Boulder, Colorado, USA, at https://psl.noaa.gov/data/gridded/data.20thC_ReanV3.html.

HadCRUT5 is a new version of the Had/CRU global historical surface temperature dataset from 1850 onwards47. We here use ensemble mean of HadCRUT.5.0.2.0 analysis gridded data which are on a 5° x 5° grid and available from the download page (https://www.metoffice.gov.uk/hadobs/hadcrut5/data/HadCRUT.5.0.2.0/download.html). The winter Arctic SAT time series from HadCRUT5 shows good agreement with that from ERA5 (Supplementary Fig. S15).

Gridded Monthly Sea Ice Extent and Concentration, 1850 Onward is a continuous sea-ice dataset for depicting historical sea ice variations48. The data cover the period of 1850–2017 on a 0.25° x 0.25° grid. We use SIC from version 2 of this dataset available at https://nsidc.org/data/G1001049. The evaluation work50 suggests that this dataset is more realistic and reliable than other long-term sea ice dataset. The winter Arctic SIC time series from this dataset is shown to be in good agreement with that from ERA5 (Supplementary Fig. S16).

The SLP field in the NOAA-Cooperative Institute for Research in Environmental Sciences (CIRES)-Department of Energy (DOE) Twentieth Century Reanalysis version 3 dataset (20CRv3) is on a 1° x 1° grid for the time period of 1836-201551. As described in ref. 21, the NOAA-CIRES-DOE 20CR data are not only back to the 1836 but also free of the spurious discontinuities. The 20CRv3 data have been systematically evaluated against observations, satellite products, and reanalysis products in ref. 52.

A novel stepwise regression for reconstructing temperature

We construct a simple physically based stepwise regression, expressed as:

$$T={\beta }_{1}\cdot {PET}+{\beta }_{2}\cdot \left({PET\; adjusted\; SIC}\right)+{\beta }_{3}\cdot {{{\mathrm{ln}}}}\left(\frac{{{CO}}_{2}}{278}\right)+\varepsilon$$
(1)

Each term and the regression coefficients (\(\beta\)) are quantified using the following procedure: (1) Forming the anomaly time series of area-weighted average of DJF-mean atmospheric temperature (T), PET, and SIC over the Arctic with respect to the whole period studied in the analysis; (2) Regressing T linearly onto PET to obtain the PET-induced T (i.e., the first term on the right-hand side of Eq. 1) with the residual T referred to as PET-adjusted T (i.e., by subtracting PET-induced T from the observed T); (3) Repeating the previous step with SIC to obtain PET-adjusted SIC and then regressing PET-adjusted T onto PET-adjusted SIC (i.e., the second term on the right-hand side of Eq. 1); (4) Regressing the final residual term, T − (PET-induced T) − (SIC-induced T), from (3) onto the natural logarithm of the ratio of DJF-mean atmospheric CO2 concentration to the pre-industrial CO2 level of 278 parts per million (ppm) (i.e., the third term on the right-hand side of Eq. 1); (5) Sum of PET-, PET-adjusted SIC-, and CO2- induced T in (2), (3), and (4), respectively, to form the regressed T time series. Except for regression in (4), all of regression coefficients are based on the detrended time series. \(\varepsilon\) denotes a residual term.

Although previous studies have shown that PET contributes greatly to Arctic temperature increases and sea ice reduction by transporting moisture and heat from lower latitudes into the Arctic19,53, the assumption that a statistical linkage between PET frequency and other variables implies causality may overestimate PET contributions to T and SIC.

Dynamical adjustment methodology

The dynamical adjustment based on partial least-squares regression34 (PLS-regression) has been well developed and used in recent studies21,40,54. It isolates the influence of atmospheric circulation changes on SAT variability and trends by removing temperature variations linked to spontaneous SLP anomalies. We apply this approach to the time series of area-average DJF-mean PET, SIC and SAT over the Arctic in the following steps.

Step 1: Forming the standardized time series of predictand Y (i.e., PET, SIC and SAT indices) and the standardized DJF-mean predictor X (i.e., SLP field) with respect to the whole period studied in the analysis.

Step 2: Creating a one-point map of correlation coefficient (denoted CC) between detrended X and detrended Y at each grid.

Step 3: Projecting X onto the weighted CC by the cosine of latitude over north of 20°N to form a time series and then be standardized (denoted Z, i.e., SLP-based PLS-regression predictor).

Step 4: Obtaining the residual X and Y by regressing Z out of both X and Y using ordinary least-squares regression.

Step 5: Repeating steps 2-4 using the residual X and Y to obtain more PLS-regression predictors until the successive PLS predictors can no longer explain an appreciable fraction of variance in the predictand time series.

Leave-one-out cross validation can be used to determine how many PLS predictors need to be used (see more details in ref. 40). Usually, the leading three PLS-regression predictors are used to obtain the dynamically induced component in the predictand time series40. Here we also choose to use three PLS-regression predictors through cross validation and the corresponding SLP patterns with clearly physical meaning as shown in Supplementary Fig. S5.

Trend, correlation, and statistical significance

All linear trends are based on ordinary least-squares regression. All correlation values represent Pearson correlation coefficients. Given the possible autocorrelation in the time series, the reduction of effective degrees of freedom due to autocorrelations has been considered for the significance test of trends and correlations using the effective sample size as described in ref. 55.