Introduction

Accurate and continuous spatiotemporal precipitation data are vital for advancing hydrological modeling, disaster monitoring, and water resource management, yet such data remain elusive in many parts of the world1,2,3,4,5,6. The latest report from the World Meteorological Organization reveals that 60% of national hydrological agencies face serious challenges in acquiring the data necessary for calibrating and validating flood forecasting systems7. Even more concerning, no country currently has access to the real-time, precise hydrological data needed to fully support evidence-based decision-making and proactive early interventions8. This deficiency in reliable data severely constrains further analytical efforts, particularly in the context of disaster mitigation9,10.

Ground rain gauges play an irreplaceable role in precipitation measurement, serving as the standard tool for obtaining point-scale hydro-meteorological data11. However, their distribution is often uneven and they are prone to damage, particularly in regions where accurate data is most needed12,13. While developed nations maintain relatively dense rain gauge networks, many developing countries—and those most in need of accurate precipitation data for flood and drought forecasting—face substantial deficits in ground-based measurement infrastructure14,15. Furthermore, the spatial representativeness of rain gauges is especially limited in capturing convective rainfall, which tends to be highly localized and variable16. Consequently, the extent of missing precipitation data varies widely, with some regions experiencing data gaps ranging from less than 1% to as much as 50–60%, and an average of approximately 30%17.

In recent years, deep learning techniques have emerged as promising tools to address the challenges of filling and correcting missing precipitation data18,19,20,21,22. Trained end-to-end on large datasets and bypassing explicit meteorological laws, these models are particularly effective at capturing the complex and nonlinear relationships among distributed ground-based sensors23,24,25,26,27. Notably, they excel in detecting low-intensity rainfall events, as indicated by metrics such as the Critical Success Index (CSI)28. However, despite these advancements, considerable uncertainties persist in estimating extreme precipitation events, particularly when accounting for the inherent temporal and spatial variability of global precipitation patterns. Although various imputation schemes have been proposed for specific hydrological contexts29,30,31,32,33,34,35,36, the development of universally applicable strategies that perform effectively across diverse regional scales remains a formidable challenge37,38,39.

Given the limitations of existing methods and the challenges of addressing precipitation data gaps on a regional scale, we propose a Global Spatiotemporal Precipitation Imputation and Correction model based on Regional-Scale Intelligent Optimization and Topography Analysis (GSPIC-RT). This model integrates multi-source precipitation data to bridge historical data gaps and enhance overall model performance. Central to GSPIC-RT is an intelligent spatial clustering module, designed to optimize regional-scale precipitation imputation by constructing bespoke models tailored to the unique variability patterns of each region. Furthermore, by incorporating topographic factors—crucial for understanding precipitation dynamics—we enrich the model’s input variables, thereby enhancing its capacity for physically grounded precipitation modeling.

Through rigorous evaluation, we demonstrate that the accuracy of precipitation data is closely linked to regional scale, with the judicious integration of topographic factors markedly reducing biases in precipitation estimates. The GSPIC-RT framework markedly improves the accuracy of strong precipitation data at regional scales, as evidenced by an increase of 0.11 (from 0.66 to 0.77) in the correlation coefficient (CC) index (a 17% increase) following the imputation and correction of Integrated Multi-satellite Retrievals for Global Precipitation Measurement-Early (IMERG-Early) satellite precipitation data. Additionally, the model achieves substantial reductions in root mean square error (RMSE) decreasing from 6.6 to 4.4 mm/day (a 33% reduction), and the relative bias (BIAS) declining from 27.74 to 3.94% (an 85.80% reduction). These results underscore the efficacy of GSPIC-RT in enhancing the quality and reliability of precipitation data, particularly in regions where it is most needed.

Results

The results are divided into three parts: optimization of regional-scale outcomes via the intelligent spatial clustering module, global view precipitation data imputation40 results and evaluation, and transfer learningr (see “Methods”) in typical missing data regions.

Regional-scale intelligent optimization

This section focuses on the application of the intelligent spatial clustering module within the GSPIC-RT model across global continents \(({60}^{\circ }{{{\rm{N}}}} \sim {60}^{\circ }{{{\rm{S}}}})\). This module is utilized for regional-scale intelligent optimization to enhance the accuracy of regional precipitation data imputation. The study area spans the global continent, where precipitation distribution exhibits pronounced regional and seasonal variations (Fig. 1a). Based on daily average precipitation data from the Climate Prediction Center Global Unified Gauge-Based Analysis of Daily Precipitation (CPC-Global), global precipitation exhibits latitudinal continuity, with abundant rainfall in tropical regions and scarce precipitation in mid to high latitudes (Fig. 1b). Observation of the global ground station density distribution reveals dense networks in areas like the United States (Fig. 1d), Mexico, and parts of South America, whereas regions in Africa, northeastern Europe, western China, and the Amazon see sparse distribution. It’s crucial to note the dynamic change in the number and density distribution of ground stations over time. Therefore, employing the intelligent spatial clustering module for regional-scale optimization and constructing independent precipitation imputation models for each region allows for better reflection and adaptation to regional precipitation variability.

Fig. 1: Basic information on the global precipitation dataset and the construction of regional-scale models.
figure 1

a Global continental division into four climatic regions based on the annual average precipitation volume from the Intergovernmental Panel on Climate Change dataset for the years 1891-2018. b Daily average precipitation volume from CPC-Global data for the years 2015–2018. c Global ASTER GDEM elevation data. d Spatial distribution of ground station density as of December 31, 2018. e Distribution of global spatiotemporal precipitation data imputation and correction model count. Original data provided in Supplementary Table 3. f Correlation analysis between topographic factors and precipitation volume, tested for significance at 0.01. Original data provided in Supplementary Table 4. g Optimized Clustering of Spring Precipitation Characteristics in the Northern Hemisphere. The subplot illustrates the relationship between the number of clusters (X-axis) and both the sum of squared errors (SSE, left Y-axis, in blue) and the silhouette coefficient (SC, right Y-axis, in red). The optimal number of clusters for each region is indicated by the SSE “elbow” point and the SC peak within each corresponding subplot. Northern hemisphere seasonal divisions: March-May as Spring, June-August as Summer, September-November as Autumn, and December-February as Winter69, showcasing regional and seasonal optimization of precipitation pattern clustering.

Full size image

In the global scope, 6420 research grids were constructed, each containing at least one real ground rain gauge station. Through the intelligent spatial clustering module (see “Methods” and Supplementary Methods), we obtained the optimal number of clusters k for each preliminary clustering field (Fig. 1g and Supplementary Fig. 5), ensuring optimal similarity in precipitation within regional scales for more pronounced precipitation characteristics. According to the global regional division results, models unique to each region were constructed, totaling 119 precipitation imputation models worldwide, with 71 in the Northern Hemisphere and 48 in the Southern Hemisphere (Fig. 1e). Further, based on the strength of the correlation between topographic factors (Fig. 1c)and precipitation volume within each region, different topographic factors were selected (see “Methods”). Figure 1f shows the correlation analysis results between topographic factors and precipitation volume across different climatic zones and seasons.

Global imputation results and evaluation

This section focuses on the results and evaluation of the constructed model’s global application. The model, by considering regional and temporal scales of precipitation processes, as well as incorporating auxiliary data such as topography, aims to enhance effectiveness during training, accurately addressing spatial and temporal missing issues of precipitation data at the regional scale.

For spatial data gaps in part of the ground-observed precipitation grid, we utilized the GSPIC-RT model to fill these missing data. By concatenating model-generated data with existing datasets, we achieved the construction of a complete, high-precision, and continuous ground precipitation dataset (Supplementary Fig. 6b).

In cases where ground-observed precipitation data were entirely missing, GSPIC-RT demonstrated its capability to accurately fill data voids (Supplementary Fig. 6f). This model successfully completed long-term missing data in the rainfall time series, providing a reliable tool for long-term and large-scale rainfall data prediction and analysis.Quantitative Evaluation and Analysis

Satellite rainfall estimates inherently contain substantial uncertainties due to sensor limitations, retrieval algorithms, and spatiotemporal mismatches, particularly in regions with complex terrain or sparse gauge coverage41,42. This underscores the importance of enhancing rainfall data accuracy through imputation and correction strategies. To address this challenge, we first examined spatial distributions of key evaluation indices, revealing critical patterns in regional precipitation variability(Fig. 2 and Supplementary Fig. 7). Subsequently, histogram analyses comparing evaluation metrics at the grid level quantitatively illustrated the substantial improvements achieved by the GSPIC-RT model(Supplementary Fig. 8). The results clearly indicate the consistent advantages of GSPIC-RT relative to IMERG, especially in regions experiencing higher precipitation. Additionally, monthly time series analyses of evaluation metrics (Supplementary Fig. 9) further validated GSPIC-RT’s superior performance in capturing monthly precipitation variations, significantly reducing systematic underestimations and effectively mitigating overestimations, especially during lower precipitation periods.

Fig. 2: Spatial distribution of daily precipitation evaluation metrics for IMERG-Early, IMERG-Final, and GSPIC-RT.
figure 2

a-i demonstrate that GSPIC-RT consistently outperforms IMERG-Early across all regions, with higher correlation (CC = 0.77, see Supplementary Table 5) and lower error (RMSE = 4.4 mm/d), significantly reducing the overestimation of precipitation (BIAS = 3.94%). Compared to IMERG-Final, which incorporates bias corrections using ground rain gauge data, GSPIC-RT shows notable improvements in regions with sparse ground station coverage, such as Indonesia, central Australia, Africa, northern South America, northeastern Europe, and western China (Fig. 1d), underscoring its reliability in data-scarce areas.

Full size image

The improved accuracy of GSPIC-RT was further confirmed through scatter plot analyses of precipitation data across four distinct climatic zones (Fig. 3a and Supplementary Fig. 10). Specifically, GSPIC-RT data consistently clustered closer to the 1:1 diagonal reference line, exhibiting the lowest RMSE and minimal deviations from ground-based reference datasets. This finding is further corroborated by the analysis of correlations and dispersions between satellite-derived and ground reference precipitation (Fig. 3b). Additional scatter plots and Taylor diagrams in the Appendix (Supplementary Figs. 11, 12) reinforce these results, with GSPIC-RT demonstrating the best performance during seasonal evaluations.

Fig. 3: GSPIC-RT is more accurate in reflecting actual precipitation conditions than both IMERG and GSPIC.
figure 3

a Scatter plots show daily precipitation amounts from GSPIC-RT over global land areas, in comparison with baseline precipitation data. The black dashed line represents the ideal consistency line (1:1 line). b Taylor diagrams of daily precipitation estimates for four climatic zones from January 2015 to December 2018, where closer proximity to the observation point (actual precipitation amount) indicates better model performance. c Distribution of global precipitation accumulation in 2018. d Box plots of daily precipitation product evaluation indicators, assessing the model’s performance in correcting near-real-time precipitation data across different precipitation intensities through CC, RMSE, and BIAS key evaluation indicators.

Full size image

GSPIC-RT shows marked improvements in regions with pronounced orographic precipitation enhancement, such as the mountainous west coast of the United States. By incorporating elevation, slope, aspect, surface roughness, and terrain ruggedness factors (verified through significance testing, p < 0.01), GSPIC-RT significantly enhances precipitation estimation accuracy compared to IMERG products. Specifically, daily-scale assessments along the U.S. West Coast indicate substantial improvements, with CC increasing from 0.53 to 0.76 and RMSE decreasing from 7.0 mm/day to 4.5 mm/day. The model also demonstrates enhanced skill in precipitation event detection, significantly reducing false alarms and enhancing the accuracy of early warnings.

To comprehensively evaluate the accuracy of precipitation data, we conducted detailed comparative analyses of various precipitation data across different climatic zones and seasons (see Supplementary Tables 5, 6), including IMERG-Early, IMERG-Final, and the Global Spatiotemporal Precipitation Data Imputation and Correction Model (GSPIC) series. In this series, GSPIC serves as the foundational model, GSPIC-T as the iterative version incorporating topographic factors, and GSPIC-RT includes the intelligent spatial clustering module. The comprehensive evaluation results show that GSPIC-RT precipitation data’s CC consistently ranges between 0.57 to 0.79, with an average CSI of 0.51, and lower ranges of RMSE and BIAS, performing most excellently. Particularly in semi-arid and arid zones, GSPIC-RT significantly reduced the overestimation of actual precipitation by IMERG-Final data.

GSPIC significantly reduces the overestimation of observed precipitation by IMERG satellite data, while unfortunately also enhancing its tendency for underestimation in humid regions. Supplementary Table 5 reveals that GSPIC and GSPIC-T exhibit BIAS values of –6.65% and –2.50%, respectively, due to global overcorrection of the originally low bias in humid regions. This suggests that the underestimation is caused by the neural network’s optimization strategy and that appropriately incorporating topographic factors helps to mitigate it. Notably, the scatter distribution in Fig. 3a demonstrates that GSPIC-RT exhibits the least deviation from ground observations in humid regions, corroborating the results in Supplementary Table 5. This improvement stems from the application of regional-scale intelligent optimization, which adjusts for prior underestimations and yields a positive BIAS of 3.10%, effectively correcting the systematic underestimation bias introduced by earlier models.

To verify the temporal consistency of infilled precipitation sequences, we analyzed monthly mean precipitation trends and their autocorrelation(Supplementary Fig. 13a–c and Supplementary Methods). Results clearly indicate GSPIC-RT accurately reproduces seasonal variations observed in ground-based CPC-Global data, effectively reducing the systematic overestimation of IMERG. Autocorrelation analyses reveal that GSPIC-RT maintains strong short-term positive correlations, transitions into intermediate-term negative correlations indicative of semi-annual cycles, and exhibits pronounced annual seasonality at lag 12 months, thus confirming that the infilled precipitation time series retains essential temporal dynamics. Spatially, the latitudinal precipitation distribution analysis(Supplementary Fig. 13d) further demonstrates that GSPIC-RT closely follows observed precipitation patterns, markedly improving estimates in critical rainfall regions and mitigating extreme biases observed in IMERG data.

To further enhance the robustness and credibility of our precipitation correction results, the Global Precipitation Climatology Project (GPCP) monthly precipitation dataset was selected as an additional ground-based benchmark for evaluating IMERG-Early, IMERG-Final, GSPIC, and GSPIC-RT precipitation products (see Supplementary Table 7). As shown in the table, GSPIC-RT outperforms the IMERG series in most evaluation metrics, demonstrating the reliability of the satellite precipitation correction product developed in this study.

Near-real-time precipitation data correction results

Initially, we validated the effectiveness of GSPIC-RT in filling in missing data at ground stations and its superiority in enhancing the accuracy and continuity of precipitation products. Notably, the model’s unique capability allows it to operate in real-time to correct near-real-time precipitation data, and this process does not rely on future precipitation data.

To conduct a comprehensive evaluation of GSPIC-RT’s overall performance in correcting near-real-time precipitation products, this study systematically assessed the accuracy of IMERG-Early and GSPIC-RT across different precipitation intensities based on the precipitation classification standards of the China Meteorological Administration (see Supplementary Table 8). Through box plot analysis (Fig. 3c), we observed that GSPIC-RT demonstrates higher CC and lower RMSE across all precipitation intensity intervals compared to IMERG-Early. Furthermore, the GSPIC-RT model excels in reducing anomalies in IMERG-Early data, especially in effectively correcting overestimation phenomena within the 0 ~ 6 mm/d precipitation interval and adjusting underestimation in the >6 mm/d precipitation interval, showcasing its notable capability in data correction.

The precipitation datasets used in this study—IMERG, CPC-Globa, and GPCP—exhibit substantial uncertainties due to sparse gauge coverage, satellite retrieval algorithm limitations, and methodological inconsistencies. For example, IMERG retrievals are highly sensitive to cloud regime and surface conditions, leading to terrain- and convection-related biases43. This spatial heterogeneity further exacerbates inter-product climatological discrepancies, sometimes exceeding 300 mm/year44. Even gauge-based climatologies show large systematic differences at identical locations, depending on the interpolation and merging methodologies employed, as highlighted in the recent World Climate Research Programme assessment.

Further, to fully reveal GSPIC-RT’s performance in detecting precipitation events, we employed quantitative evaluation indicators such as the Probability of Detection (POD), False Alarm Ratio (FAR), and CSI45,46 for an in-depth analysis of these two datasets (see Supplementary Fig. 15). The results reveal that, GSPIC-RT shows improved performance in monitoring moderate, heavy, and torrential rain compared (>10 mm/d) to IMERG-Early. Notably, its lower POD and higher CSI values suggest a well-calibrated trade-off between detection sensitivity and reliability, highlighting the model’s strength in accurately identifying high-intensity precipitation.

Additionally, we also calculated the cumulative precipitation amounts for various precipitation data (Fig. 3c and Supplementary Fig. 13a, b). The results, from a macro perspective, clearly show that all precipitation data exhibit an overestimation phenomenon regarding the total amount of ground reference precipitation. Notably, GSPIC-RT shows a lower degree of overestimation relative to other datasets, offering a more accurate reflection of ground-reference precipitation. While smoothing long-term variability, it more accurately captures the actual precipitation patterns. This finding not only further confirms GSPIC-RT’s outstanding performance in correcting real-time precipitation data but also provides timely and accurate data support for actual monitoring and early warning.

We explicitly addressed uncertainties originating from multiple data sources. For satellite data, we identified inherent biases and uncertainties in IMERG arising from sensor accuracy and algorithm assumptions. Ground-based observational uncertainties were managed by selecting temporally consistent CPC-Global data points. Topographic input uncertainties were minimized via rigorous significance testing and dimensionality reduction. We further employed a robust Monte Carlo cross-validation approach(see Methods) and introduced SHapley Additive exPlanations interpretability analysis(see Supplementary Methods and Supplementary Fig. 14) to quantify uncertainty propagation throughout the model. Additionally, validation using the authoritative GPCP dataset improved our assessment in tropical regions, confirming the reliability and uncertainty control capabilities of GSPIC-RT.

Model transfer in typical missing precipitation data regions

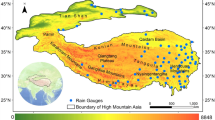
In this study, we selected representative precipitation data missing regions (the Tibetan Plateau, sometimes referred to as the world’s water tower47) to assess the model’s transfer adaptability in specific regional scales and high-resolution data conditions, thereby verifying its generalizability. Through comprehensive evaluation of the Global Satellite Mapping of Precipitation (GSMaP) series precipitation data (see Supplementary Figs. 16, 17 and Supplementary Table 9), we found that compared to GSMaP_MVK data, GSPIC-RT data’s CC increased from 0.35 to 0.69, RMSE decreased from 5.8 mm/d to 2.5 mm/d, and BIAS was reduced from 48.95 to 0.25%.

Further analysis of the spatial distribution of various precipitation data error evaluation indicators and classification statistical indicators in the Tibetan Plateau area (Fig. 4 and Supplementary Fig. 18) shows that GSPIC-RT data has higher CC and lower RMSE in this region, effectively improving the underestimation (in the west) and overestimation (in the east) situations of GSMaP series data. Over the Qaidam Basin, the GSPIC-RT product exhibits the lowest RMSE. Given the region’s extremely arid climate and predominance of high-intensity rainfall events, this result suggests not only reduced cumulative error due to prolonged dry periods but—more critically—the enhanced capability of the GSPIC-RT algorithm in detecting and quantifying sporadic heavy rainfall with higher accuracy and robustness compared to the GSMaP product.

Fig. 4: Spatial distribution of daily precipitation evaluation indicators for GSMaP_MVK, GSMaP_Gauge, and GSPIC-RT.
figure 4

a–c CC distribution. GSPIC-RT shows high CCs (>0.5) across most regions, with localized low CCs (<0.3) in southwestern Xinjiang. d–f RMSE distribution. GSPIC-RT exhibits lower RMSEs (<5 mm/d) over the Tibetan Plateau, showing a northwest-low to southeast-high pattern. g–i BIAS distribution. GSPIC-RT corrects GSMaP’s underestimation in the west and overestimation in the east, improving agreement with gauges.

Full size image

Especially in the Qaidam Basin, GSPIC-RT data shows the lowest RMSE, possibly due to the sparse precipitation in this area, leading to smaller overall errors. In terms of precipitation detection capability, compared to GSMaP series data, GSPIC-RT data exhibits higher hit rates and lower false alarm rates.

It is noteworthy that GSMaP_Gauge data show a specific circular distribution characteristic in spatial distribution, a phenomenon resulting from the fusion of interpolation algorithms and ground rain gauge data in GSMaP_Gauge, significantly enhancing accuracy in areas with dense ground observation networks. However, achieving high-precision correction of satellite precipitation products becomes a challenge in areas lacking ground rain gauge coverage. In contrast, GSPIC-RT data’s circular distribution characteristic in indicator spatial distribution is less pronounced than GSMaP_Gauge, but its coverage area for high-precision indicators is more extensive. This indicates that the GSPIC-RT model can effectively improve the accuracy of satellite precipitation data in areas lacking ground observation stations, providing more reliable precipitation data for these regions.

Supplementary Fig. 19 shows the daily precipitation data evaluation metrics for real-time correction of GSMaP_NRT by GSPIC-RT under different precipitation classification thresholds, with comprehensive evaluation metrics summarized in Supplementary Table 9. GSPIC-RT data’s deviation from actual precipitation is lower than GSMaP_RNT data, displaying higher overall performance. Within the 0–1 mm/d precipitation threshold, GSMaP_RNT underestimated ground reference precipitation, while GSPIC-RT data effectively improved this phenomenon. Especially for precipitation amounts greater than 2 mm, GSPIC-RT shows a strong correlation with ground reference precipitation, with the median value of the CC exceeding 0.8, and displaying lower errors across all levels of precipitation thresholds, demonstrating its high accuracy and reliability in estimating precipitation amounts.

Overall, the GSPIC-RT exhibits exceptional applicability in the Tibetan Plateau, providing high-precision precipitation products and significantly enhancing the capability to monitor heavy precipitation events. At the same time, the model maintains the real-time nature of precipitation data, offering crucial support for hydro-meteorological research and flood disaster prevention.

Discussion

Research into natural disasters, such as floods, necessitates localized, low-latency, and high-precision precipitation data48. The uneven global distribution of rain gauge stations, coupled with their susceptibility to damage, long-term data gaps, and systematic biases in satellite-derived precipitation estimates, highlights the urgent need to address gaps in ground-based observations and improve the accuracy of satellite precipitation products within a global precipitation information system. This challenge is particularly acute in regions with sparse rain gauge coverage and substantial data voids, such as the Tibetan Plateau—a hydrologically vulnerable area with limited research data49. In response to the World Meteorological Organization call for a robust global precipitation monitoring system, reducing uncertainties in rainfall estimates is essential for supporting international climate mitigation efforts and disaster preparedness.

When compared with 22 other global precipitation datasets, this dataset was found to perform best50. CPC-Global data are often considered the “ground truth” in global precipitation evaluations51. Thus, the closer the corrected and filled precipitation data results are to the CPC-Global dataset, the better the performance. However, the “truth” in rainfall observations remains inherently uncertain, especially for convective and shallow-cloud precipitation. Rainfall exhibits strong spatiotemporal variability, and even gauge-based climatologies can diverge notably due to differences in interpolation and merging methods52,53. Satellite estimates, though globally available, are further constrained by sensor limitations, retrieval algorithms, and gap-filling techniques such as morphing and reanalysis infilling54. These factors introduce considerable uncertainties, particularly in complex terrain or data-sparse regions. Accordingly, the accuracy assessments in this study should be interpreted in light of these underlying limitations.

The difficulties inherent in precipitation data imputation and correction stem from uncertainties in correction methodologies and the challenge of integrating physical principles with statistical techniques. Our approach combines conditional learning methods to develop multiple independent models, leveraging regional-scale intelligent optimization and topographic analysis. By training deep learning models in an end-to-end manner, we address these challenges, enabling efficient adaptation to different regional scales. These models effectively mitigate the temporal and spatial gaps in ground-based precipitation data while ensuring the timeliness of precipitation estimates—an issue that existing methods struggle to resolve.

The standard seasonal definitions may not optimally represent precipitation regimes in tropical monsoon regions due to asynchronous monsoon onset and retreat timings55. Nevertheless, our monthly-scale evaluations indicate GSPIC-RT consistently achieves superior performance across all months and significantly improves accuracy in high-precipitation regions, confirming the robustness of our approach despite seasonal definition limitations.

Our comprehensive evaluation and comparison of imputed and corrected data reveal several key insights and limitations.

First, the precision of precipitation data varies across regions, years, seasons, and precipitation intensities, with model uncertainty not explicitly quantified. Nonetheless, compared to other satellite rainfall datasets, our model exhibits robustness, particularly in accurately capturing the spatiotemporal distribution of precipitation, especially in arid regions and during summer rainfall events.

Second, while the GSPIC-T model reduces satellite-derived precipitation overestimation relative to ground observations, it introduces a tendency toward underestimation. The GSPIC-RT model effectively addresses this issue, significantly improving precipitation accuracy through temporal and spatial intelligent clustering and the strategic incorporation of topographic factors.

Third, satellite-derived precipitation data perform well in detecting light precipitation events but remain less reliable in capturing extreme rainfall. Our model reduces the false alarm rate for moderate to extreme precipitation events (>10 mm/d) while achieving higher CSI values, thus providing more accurate data for monitoring and early warning systems.

Finally, our model successfully fills gaps in ground-based data without relying on future precipitation information and corrects current satellite precipitation data in real-time. Across various precipitation intensity thresholds, the model’s corrected data consistently outperform near-real-time satellite estimates, offering higher precision for meteorological forecasting and disaster prevention research.

Looking ahead, efforts to further enhance the completeness and accuracy of precipitation data will focus on two key areas. First, the integration of additional physical principles, such as thermodynamics and dynamics, into the modeling framework. Second, the use of advanced high-resolution meteorological datasets, including temperature, humidity, and wind speed, for improved data fusion and correction. In conclusion, the GSPIC-RT model represents a notable leap forward in global precipitation data correction, providing a robust, real-time solution to the spatial and temporal gaps in precipitation data, particularly in regions with sparse ground observations.

Methods

This section elaborates on the specific methods employed in intelligent spatial clustering, model construction and training, hyperparameter tuning, and transfer learning.

Intelligent spatial clustering

We employ intelligent methods to select initial clustering centers, randomly choosing a sample point from the dataset \(X=\{{x}_{1},{x}_{2},{{\mathrm{..}}}.,{x}_{n}\}\) as the first cluster center \({c}_{1}\). For subsequent sample points\({x}_{i}\), calculate the shortest Euclidean distance to the already selected cluster centers and denoted by \(D(x)\). Using this distance, the probability \(P(x)\) of each sample point being selected as the next cluster center is calculated, with the point having the highest probability of becoming the next cluster center56.

$$P(x)=\frac{D{(x)}^{2}}{{\sum }_{x\in X}D{(x)}^{2}}$$
(1)

Continue until \({{{\rm{k}}}}\) cluster centers \(C=\{{c}_{1},{c}_{2},{{\mathrm{..}}}.,{c}_{k}\}\) are selected. Calculate the distance of each sample point \({x}_{i}\) in the dataset to the \({{{\rm{k}}}}\) cluster centers and assign it to the cluster with the shortest distance. For each cluster, update the cluster center \({c}_{i}=1/|{c}_{i}|{\sum }_{x\in c}x\) to represent the total number of sample points in the cluster. Repeat the calculation of distances and updating of cluster centers until the cluster centers no longer change.

In cluster analysis, determining the optimal number of clusters \({{{\rm{k}}}}\) is essential for ensuring high-quality clustering performance. Two widely used methods for evaluating cluster validity are the elbow method and the silhouette coefficient method57,58. The elbow method identifies the optimal number of clusters \({{{\rm{k}}}}\) by plotting the SSE against the number of clusters. The optimal cluster number corresponds to the ‘elbow’ point, where the SSE begins to level off significantly. SSE is calculated as follows:

$$SSE={\sum }_{i=1}^{k}{\sum }_{x\in {C}_{i}}{|x-{c}_{i}|}^{2}$$
(2)

where \({C}_{i}\) represents the set of all sample points with\({c}_{i}\) as the cluster center. The SC reflects the degree of closeness of the sample point to others in its cluster and the separation from points in other clusters. The SC ranges from −1 to 1, where values close to 1 indicate good clustering, values near 0 suggest overlapping clusters, and values approaching −1 indicate poor clustering. SC is calculated as follows:

$$SC(i)=\frac{b(i)-a(i)}{\max \{a(i),b(i)\}}$$
(3)

Wherein, \(a\) represents the average distance between sample point \(i\) and other sample points within the same cluster (intra-cluster density), while \(b\) denotes the average distance between sample point \(i\) and all sample points in the nearest cluster (inter-cluster separation). Given that topography and elevation impact precipitation, our feature set consists of elevation characteristics (DEM and MRDEM, refer to Fig. 5b for details) and annual average precipitation characteristics.

Fig. 5: GSPIC-RT precipitation correction and gap-filling model schematic.
figure 5

a Workflow of the GSPIC-RT precipitation correction and gap-filling model. b Schematic of terrain factor selection, including slope and aspect calculation formulas. Input dimensionality was limited to 5 or fewer to mitigate potential issues such as feature extraction challenges, increased training difficulty, overfitting, and reduced computational efficiency. Prior to model training, Z-Score normalization was applied to standardize raw data and eliminate scale differences. c Evaluation metrics for the inversion accuracy of precipitation products, with classification metrics (POD, FAR, CSI) used to assess the model’s predictive capability for precipitation events.

Full size image

Model construction and training

Our deep network model architecture is detailed in Fig. 5a. This architecture integrates conditional learning methods, leveraging the advantages of multiple hidden layers in neural networks(see Supplementary Methods). By employing an end-to-end training approach, the deep network model enhances the accuracy of satellite precipitation data correction and addresses spatiotemporal gaps in ground station precipitation data, all while ensuring the timeliness of precipitation data. We implemented intelligent spatial clustering to divide the globe into multiple regions, with each region constructing an independent precipitation gap-filling model. This approach allows for a more precise understanding of precipitation variability at regional scales. Additionally, we incorporated topographic factors closely related to precipitation to further improve the model’s ability to simulate physical mechanisms(see Fig. 5b).

Hyperparameter tuning

In situations with limited computational resources, we strive to obtain the optimal combination of hyperparameters in deep network models, adjusting parameters such as the number of neurons in hidden layers, learning rate, and Dropout parameters. Specifically, the initial parameter space for the number of neurons in hidden layers is set to \([32,64,128]\), for learning rate to \([0.1,0.01,0.001,0.0001,0.00001]\), and for Dropout to \([0.1,0.2,0.3,0.4]\). During model training, the Dropout regularization technique is employed to randomly reduce neurons in the network, thus lowering model complexity and enhancing its generalization capability to prevent overfitting(see Supplementary Methods). Fig. 5b more clearly presents the deep neural network structure and hyperparameter settings of our proposed precipitation imputation model. The standard for hyperparameter adjustment is based on universally optimal values obtained through random grid search algorithms.

Transfer learning

GSPIC-RT is designed as a global spatiotemporal precipitation gap-filling and correction model. Continuous, long-term, and accurate large-scale global datasets aid the learning of general precipitation characteristics. Thus, for smaller-scale regions with sparse ground-observed precipitation data, a transfer learning approach was employed to avoid overfitting59. Models were first trained on the global-scale dataset to capture general precipitation representations and then fine-tuned specifically for the regional Tibetan Plateau dataset.

Our intelligent optimization algorithm segments the globe into multiple areas, each with similar underlying precipitation patterns, allowing the model’s generative network to be transferred across different regions. The GSPIC-RT model is pre-trained on a large-scale global dataset and fine-tuned to high-resolution, small-scale region-specific datasets using the Adam optimizer, further details of which are provided in the supplementary methods.

Model evaluation

The performance of satellite precipitation products is primarily evaluated based on their inversion accuracy and capability to detect actual precipitation events. Initially, we employ multiple error assessment metrics to evaluate the inversion accuracy of satellite precipitation products, including the CC, RMSE, BIAS, Mean Absolute Error, and Absolute Bias (Fig. 5c). Subsequently, we use several classification statistical metrics to assess the model’s capability in predicting precipitation events, such as the POD, FAR, and CSI. The POD and FAR metrics represent the proportion of correctly detected precipitation events and the proportion of falsely detected precipitation events relative to all actual precipitation events, respectively. The CSI metric integrates both hit and false alarm rates, reflecting the overall detection capability of the satellite precipitation products for real precipitation events. Given that the standard detection resolution of ground rain gauges is 0.1 mm/h60, we set the threshold for precipitation events to 2.4 mm/d.

To mitigate the potential randomness in the results from a single split of the training and test sets, we employ the Monte Carlo Cross-Validation algorithm61,62 to evaluate our satellite precipitation correction model. The dataset was randomly split into training and testing sets in an 8:2 ratio, and the model underwent 10 independent training and testing sessions. The average of the multiple test results was taken as the final validation error of the model.

It is important to note that, during the dataset splitting process, some grids might never be selected for the test set, while others might be selected multiple times. To ensure the accuracy of the evaluation results, we only consider grids that have been selected at least once for evaluation. For grids selected multiple times, we average the corrected precipitation results from multiple corrections as the final outcome.

Data preparation

This study utilizes the Global Precipitation Measurement satellite precipitation data, ground reference precipitation data from the National Oceanic and Atmospheric Administration’s Climate Prediction Center, and NASA’s digital elevation models. The data processing procedures are detailed in the supplementary data section, including typical data-scarce area data from the Tibetan Plateau.

Satellite data

The IMERG satellite precipitation dataset, produced by the Global Precipitation Measurement mission, integrates multi-satellite observations, providing a comprehensive high-temporal and spatial resolution global precipitation dataset63. This dataset combines microwave, infrared, and radar observations from Global Precipitation Measurement satellites, offering 30-min temporal resolution and 0.1° × 0.1° spatial coverage from 90°N to 90°S64. However, satellite-derived precipitation is inherently an indirect measurement, subject to uncertainties arising from sensor limitations, retrieval algorithms, and particularly from gap-filling techniques such as reanalysis data infilling and the morphing algorithm65. These procedures introduce systematic biases and spatiotemporal uncertainties into the IMERG estimates66.

Ground data

Ground reference precipitation data are obtained from the Climate Prediction Center of NOAA, based on global daily precipitation analysis datasets from standard observation stations. The CPC-Global dataset includes reports from over 30,000 stations worldwide, with a spatial resolution of 0.5° × 0.5°, covering 90°N to 90°S. The accuracy and reliability of the CPC-Global dataset vary according to the density and spatial distribution of ground meteorological stations67.

The GPCP dataset integrates microwave remote sensing from low-Earth orbit satellites, infrared retrievals from geostationary satellites, and global ground-based rain gauge observations68. As a benchmark dataset for precipitation studies in tropical regions, GPCP helps reduce evaluation inaccuracies that may arise due to the poor performance of the CPC-Global dataset in tropical areas. The GPCP dataset provides a long-term precipitation time series from 1979 to the present, offering both monthly (2.5° × 2.5°grid) and daily (1° × 1°grid) temporal and spatial resolutions.