Direct human interventions drive spatial variability in long-term peak streamflow trends across the United States

Abstract

Understanding non-stationarity in annual peakflow is critical amid climate change and human interventions^1,2. We analyzed trends in peakflow across 3907 streamflow sites with a median record length of 80 years in the continental United States. Results showed that one-third of the sites have significant trends. Of these, two-thirds showed decreasing trends nationwide, while one-third showed increasing trends in the Northeast and Great Lakes regions. We found urbanization and water management as primary drivers, with agriculture and climate as secondary. Urbanization explained up to 62% of the variance in Texas-Gulf, 44% in California, and 32% in the Mid-Atlantic regions. Water management dominated in Tennessee (37%) and Ohio (30%) regions. Agriculture was most influential in the Great Lakes (17%) region, while climate contributed in the Rio Grande (15%) and California (11%) regions. Although the latest climate model provides many realizations, it inadequately captures direct human interventions in the water system.

Introduction

Globally, flooding poses the most pervasive risk among all climate-related disasters³. Floods cause significant economic losses in the United States (US), with an average cost of $4.4 billion annually between 1980 and 2023⁴. The Congressional Budget Office warns of rising costs due to flood-related damages that could soar to $54 billion annually by 2050 without effective mitigation⁵. These financial burdens, spanning immediate repairs and long-term recovery, emphasize the urgent need for robust strategies to address and lessen the economic fallout from flood disasters not only in the US but globally as well.

Understanding the complex relationship between climate change and flooding continues to be a critical challenge because of the varied flood generation mechanisms^2,6,7. With an intensified hydrological cycle due to global warming⁸, the anticipated increase in extreme precipitation events⁹ presents a potential risk of heightened flooding. Changing precipitation, snowfall, and evapotranspiration patterns in different regions have led to both increased and decreased flood discharges across Europe¹⁰. In the contiguous United States (CONUS), cohesive regions affected by multi-decadal climate oscillations have been identified, which shed light on the drivers behind flood variability, notably emphasizing the influence of natural climate variability in the western and southern regions¹¹. Another study¹² linked recent changes in flood risk to trends in basin wetness measured by the Gravity Recovery and Climate Experiment (GRACE) satellite.

Human interventions like urbanization and water management, e.g., dams and reservoirs, can rival or surpass the impacts of climate-driven changes on the water cycle¹³. Blum et al. found that a 1% increase in impervious cover raises annual flood magnitude by 3.3%, underscoring urbanization’s impact on flood risk. The recent USGS water cycle diagram highlights the human role in altering the water cycle¹⁴. However, their relative influences, including direction of change and spatial extent vis-à-vis natural climate variability, have yet to be studied comprehensively. This is particularly important when most streams are human-impacted¹⁵ (Fig. 1), leading to a disconnect between observations and climate model predictions (shown later). Villarini and Slater¹⁶ emphasized the need for attribution studies linking observed changes in flood risk to climatic and anthropogenic factors. Moreover, the extent to which the observed changes in flood risk exceed natural variability, as simulated by recent large-ensemble climate data experiments^17,18, remains unexplored, leaving a critical knowledge gap in the existing literature.

Fig. 1: Dominance of Human Activities in Hydrological Systems.

a Spatial distribution of USGS reference and non-reference gauges based on data from the GAGES-II and HCDN networks. Non-reference sites constitute 84% of all USGS stations. The labeled HUC2 regions correspond to major hydrological units across the United States: 01-New England, 02-Mid Atlantic, 03-South Atlantic Gulf, 04-Great Lakes, 05-Ohio River Basin, 06-Tennessee, 07-Upper Mississippi, 08-Lower Mississippi, 09-Souris Red-Rainy, 10-Missouri, 11-Arkansas-White-Red, 12-Texas-Gulf, 13-Rio Grande, 14-Upper Colorado, 15-Lower Colorado, 16-Great Basin, 17-Pacific Northwest, and 18-California. b Normalized maximum water storage capacity in reservoirs and dams within each watershed, represented by color intensity. c Box plots comparing normalized maximum water storage (%) between reference and non-reference sites for each HUC2 region. The y-axis is logarithmic to improve clarity and highlight data variation. Only regions with 10 or more reference or non-reference stations are included in the comparison.

The annual peak streamflow (hereafter, called peakflow) is the metric used to evaluate the annual daily maximum flow and its temporal changes, i.e., trends over the years. Our study presents a detailed assessment of the factors influencing observed peakflow trends across 3907 USGS sites spanning the CONUS (Figs. 1 and 2). Data length ranges from 60 to 110 years with a median of 80 years. The drainage area of the studied sites ranged widely from 31 sq. km. to 82,845 sq. km., with a median of 1166 sq. km. Additionally, we assessed the variance changes by comparing the latter 30-year period to the preceding 30 years¹⁹ (see Methods).

Fig. 2: Long-Term Annual Peak Streamflow Trends Across the United States.

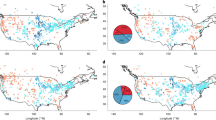
This map illustrates observed peak streamflow trends at 3,907 USGS stations across the United States. Open circles indicate insignificant trends with color representing the direction of the trend slope (blue for positive, red for negative, and grey for zero), while upward and downward arrows represent statistically significant (p-value < 0.05) increasing and decreasing trends, respectively, based on a non-parametric method. The trends are expressed as a percentage of the standard deviation over 60 years, where a 100% change corresponds to one standard deviation change within this time frame. Blue color indicates positive normalized trend slope and red color indicates negative trend normalized slope.

Results

Direct human interventions in the water cycle: watershed characteristics

Utilizing a collection of reference hydroclimatic network datasets, we contrasted the effects of climate change on the peakflow to those stemming from direct human interventions. The Hydro Climatic Data Network (HCDN)²⁰ and Geospatial Attributes of Gages for Evaluating Streamflow version II (GAGES-II)²¹ reference sites were minimally impacted by direct human interventions. GAGES-II was the superset, having a total of 620 reference sites that included 439 HCDN sites (Fig. 1). A total of 2830 GAGES-II non-reference sites were affected by direct human interventions, including dams, reservoirs (water management), and land-use changes. In addition, 457 other USGS sites were categorized as non-reference sites because they were not included in the HCDN or GAGES-II reference list.

The influence of direct human interventions was widespread, accounting for 84% of all the USGS sites analyzed in this study (Fig. 1). We evaluated the human impact by analyzing the watershed characteristics or attributes (see Methods). Further, we examined 18 large-scale regions within the CONUS using Hydrologic Unit Code level 2 (HUC2) watershed boundaries (Fig. 1). The normalized maximum water storage capacity behind the dams and reservoirs was 17.6 ± 1.4% of the annual average precipitation in the non-reference watersheds, compared to 0.9 ± 0.5% in the reference watersheds (Fig. 1c). Here, X ± Y denotes the mean plus or minus twice the standard error, calculated using data from all the USGS sites, encompassing 601 reference and 3254 non-reference sites across the conterminous United States (CONUS). We were unable to calculate watershed attributes for a minor portion (1.3%) of the USGS sites due to data gaps (see Method). Urbanization rates were twice as high (10.1 ± 0.6%) in the non-reference watersheds compared to the reference watersheds (4.4 ± 0.3%) (Supplementary Fig. 1).

At the CONUS scale, agricultural land use was moderately higher in the non-reference watersheds (22.3 ± 0.9%) than in the reference watersheds (18.0 ± 2.0%) (Supplementary Fig. 2). However, regional disparities existed. In the Ohio River Basin (HUC2# 5), agricultural land use was nearly twice as high in the non-reference watersheds (39.1 ± 3.1%; n = 306) compared to the reference watersheds (22.8 ± 7.2%; n = 48). In contrast, agricultural land use was generally comparable between the non-reference (31.5 ± 3.3%; n = 349) and reference watersheds (29.8 ± 7.3%; n = 61) in the Missouri River Basin. The climate impacts exhibited a similar pattern at the regional scale (Supplementary Figs. 3–6). For example, the Ohio River Basin exhibited comparable increases in annual maximum precipitation with values of 13.5 ± 2.0% (n = 306) for the non-reference watersheds and 10.9 ± 5.9% (n = 48) for the reference watersheds (Supplementary Fig. 3).

Long-term Trends in Peak Streamflow

A non-parametric Mann-Kendall trend analysis (see Method) at each site revealed regionally varying patterns in peakflow trends across the CONUS (Fig. 2). Statistically significant trends were found at approximately one-third of the USGS sites, with a larger proportion (21%) displaying decreasing trends compared to 13% displaying increasing trends. Stations with increasing trends were predominantly seen in the northeastern US and Great Lakes regions, and decreasing trends were seen in the Western, Central, and Southern US regions.

In the New England, Mid-Atlantic, and upper Midwest regions (HUC2# 1, 2, 4, 7, and 9), a higher proportion of USGS sites exhibited increasing trends compared to those showing decreasing trends. Notably, within the upper Mississippi River Basin (HUC2# 4), 32% of the USGS sites exhibited increasing trends while merely 6% demonstrated decreasing trends. Although most stream gauges began operation in the early to mid-20th century (median record length ~80 years), the observed trends likely reflect legacy impacts of land use changes that occurred during the 19th and early 20th centuries. For example, extensive artificial drainage—amounting up to 20% of the total land area in the Midwestern US occurred primarily in the late 19^th and early half of the 20th century²². Similarly, agricultural expansion peaked in the early 20th century, reaching 28% of land cover before declining to 22% in the latter half of the century²³. These changes reduced infiltration capacity and altered watershed hydrologic responses. Such legacy effects can persist for decades, continuing to influence runoff generation and streamflow long after the initial land use transformation^24,25,26. Additionally, given that the median data length is 80 years, it is likely that the dry conditions during the 1930s Dust Bowl also contributed to the observed increase in peak flow trends²⁷. A step increase in precipitation, notably observed in the Eastern US after the 1970s, was also acknowledged as a contributing factor²⁸. In contrast, an equal proportion of USGS sites (12.5%) within the lower Mississippi River Basin exhibited both increasing and decreasing trends.

In most of the HUC2 hydrological regions (12 out of 18), a decreasing peakflow trend was evident. Specifically, this pattern was noticeable across the Western, Central, and Southern US regions, including the Ohio River Basin. For instance, in the Upper Colorado River Basin (HUC2# 14), about 37% of the USGS sites showed decreasing trends, but less than 1% showed increasing trends. Such decreasing trends have been linked in the past to reduced snowpack²⁹ and various flow regulations, such as reservoirs and diversions that decrease peakflows during the snowmelt season³⁰. Surprisingly, despite an increasing trend expectation based on land use and climate change^28,31, the Ohio River Basin (HUC2# 5) exhibited 20.6% of the USGS sites with decreasing trends and 9.3% with increasing trends.

To confirm the trends from the individual Mann-Kendall test, the Regional Average Mann-Kendall (RAMK) test was used to synthesize the trends within each HUC2 region by examining the combined outcomes from the individual USGS sites (see Method). The results (Fig. 3a) show predominantly decreasing trends in the peakflow across CONUS when both the reference and non-reference USGS sites were considered.

Fig. 3: Regional Long-Term Annual Peak Streamflow (> 60 years).

a Regional trends for all USGS sites, b reference-only sites, and d non-reference sites. a, b, and d displays the Regional Average Mann-Kendall Z values, which assess the statistical significance of the trends by considering all individual sites within each HUC-2 region. A Z value < −1.96 or > 1.96 indicates statistically significant regional trends, with higher magnitudes of Z reflecting greater confidence in the trend (refer to Methods for details). Panels (c) and (e) depict the same data as Fig. 2, but is restricted to the reference and non-reference sites, respectively. Open circles indicate insignificant trends with the color representing the direction of the trend slope (blue for positive, red for negative, and grey for zero), while upward and downward arrows represent statistically significant (p-value < 0.05) increasing and decreasing trends, respectively, based on a non-parametric method. Regional trends are quantified using the Regional Average Mann–Kendall (RAMK) normalized Z-score, which is computed from the sum of site-level Mann–Kendall statistics (including both significant and non-significant sites) across the region (See Method). The regional trend significance thus reflects the net balance of increasing and decreasing site-level trends. Magnitude of trends are expressed as a percentage of the standard deviation over 60 years, where 100% change equates to one standard deviation change in this period. The reference sites include both the HCDN and GAGES-II reference sites, and the non-reference sites include the GAGES-II non-reference and other USGS sites.

We conducted an additional analysis using the reference only and non-reference only sites (Fig. 3b–e). The reference only sites (620 out of 3,907) primarily reflected the impacts of climate change (Fig. 3b, c). Notably, climate change led to substantial increasing trends in areas across the northern tier HUC2 regions, including New England, the Mid-Atlantic, the Great Lakes, Ohio River Basin, the Upper Mississippi River Basin, Missouri River Basin, and the Pacific Northwest (HUC2# 1, 2, 4, 5, 7, 10, and 17). Conversely, only two Southwestern regions, the Texas-Gulf and Rio-Grande (HUC2# 12 and 13), exhibited decreasing trends. The effects of climate change, particularly the prevalent increasing trends, aligned closely with past observed changes in precipitation. For example, in the literature, there is a documented increase of 10% or more in heavy precipitation events in the Northeastern and Midwestern US³². However, it was evident that the effects of climate change alone could not account for the predominantly decreasing trends in the peakflow (Fig. 3a).

A total of 3287 (out of 3907) non-reference sites encountered climate change and direct human influences. Among the non-reference sites, which included the GAGESII non-reference and other USGS sites, predominant decreasing trends were evident across the Western, Central, and Southern US regions (Fig. 3d, e). Our results were similar for the GAGESII non-reference only sites as well (not shown).

Direct human interventions over time have reversed climate-induced increasing trends, leading to predominantly decreasing trends in three northern-tier HUC2 regions: the Ohio River Basin, the Missouri River Basin, and the Pacific Northwest (HUC2# 5, 10, and 17 in Fig. 3). Specifically, the observed decreasing trends in the Ohio River Basin could be attributed to direct human interventions. For example, the z-value for the reference only sites was 4.71, while the corresponding value for the non-reference sites was −10.53. Consequently, an overall declining trend with a z-value of −8.52 was evident in the Ohio River Basin. Conversely, direct human interventions in the Upper Mississippi River Basin amplified the increasing trends, which potentially were linked to land use changes (to be determined later). The corresponding z-values for the reference only, the non-reference, and all the USGS sites were 2.63, 20.54, and 20.33, respectively, in the Upper Mississippi River Basin.

In the southern tier HUC2 regions, except for the Lower Mississippi River Basin (HUC2# 8), predominantly decreasing trends were caused by direct human interventions (Fig. 3d, e). The upper and lower Colorado River Basin and the Pacific Northwest exhibited predominantly decreasing trends that were observed solely in the non-reference sites. Additionally, direct human influences amplified climate-driven decreasing trends in the Texas-Gulf and the Rio Grande regions.

Field Significance Test

The Field Significance Test, using the False Discovery Rate (FDR) method³³, was applied to account for spatial dependencies among USGS sites. After considering spatial correlation, the proportion of sites with significant trends dropped from 33.9% to 23.7% for sites with more than 60 years of data (Table 1 and Supplementary Fig. 7). This reduction shows that some trends previously deemed significant are likely influenced by spatial dependencies rather than independent trends.

Table 1 Direct human interventions dominate the non-stationarity responses in peakflow across different datasets and metrics in the US for the long term (> 60 years)

Assessing the Impact of Variable Record Lengths

Our results are insensitive to variable record length across the USGS peak flow data. Analyses using a common time window from 1950 to 2014 (Supplementary Figs. 8–10) yielded results consistent with those presented in the main text (Figs. 2–4). As shown in Supplementary Table 1, approximately one-third (26.6%) of the sites exhibit statistically significant trends, with a larger share showing decreases (15.8%) compared to increases (10.8%). This pattern supports the broader finding that decreasing peak flow trends are more prevalent across the U.S. This robustness can be attributed to the use of long data records (≥60 years) and a non-parametric trend detection methodology, thereby minimizing the influence of short-term variability and data lengths on long-term trends.

Fig. 4: Drivers of spatial variability in long-term peakflow trends in the United States.

This figure depicts the statistically significant variances explained by climate factors (such as precipitation maximum increase, precipitation maximum decrease, precipitation mean increase, and precipitation mean decrease), land use factors (urbanization and agriculture), and water management aspects (normalized maximum storage) in each HUC2 region, which are shown on the x-axis. The y-axis represents the percentage of explained variances. The driving factors did not explain the significant variance in HUC2 regions 01, 08, 09, and 15 using the multiple linear regression model (see Methods); therefore, these regions are not shown.

Additional Testing of Non-stationarity

We employed two additional statistical metrics: the Levene test³⁴ to evaluate the changes in the variance and Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test³⁵ to assess non-stationarity (see Method). These tests afford insights into changes in higher-order statistical moments, complementing the evaluation of non-stationarity carried out by the Mann-Kendall trend test, which explicitly assesses changes in the mean. For instance, the KPSS test determines whether the time series exhibits stationarity (null hypothesis) or showcases a trend and/or structural break (alternative hypothesis)³⁵. Moreover, we assessed the robustness of our findings across different datasets, including HCDN, GAGESII, and other USGS sites.

The prevalence of direct human interventions in steering changes in the peakflow remained consistently evident across various datasets and in three of the four statistical metrics, as indicated in Table 1. Notably, a minority of HCDN (6.2%) and GAGESII reference sites (6.3%) exhibited significant decreasing trends in contrast to the higher percentages observed in the GAGESII non-reference sites (22.5%) and other USGS sites (31.3%), which confirmed the decreasing trends. Similarly, the changes in variances were less frequent in the HCDN (7.7%) and GAGESII reference sites (7.4%) compared to the GAGESII non-reference sites (18.6%) and other USGS sites (22.5%).

The KPSS test unveiled notably higher non-stationarity in the non-reference sites, such as 32.4% in the GAGESII non-reference and 40.9% in the other USGS sites, as opposed to reference sites such as the HCDN (14.8%) and GAGESII reference sites (14.7%). In contrast, the effects of climate change, which predominantly drove increasing peakflow trends, were marginally more prevalent in the reference datasets such as the HCDN (14.8%) and GAGESII reference sites (13.7%) compared to the non-reference datasets, such as the GAGESII non-reference sites (12.8%) and other USGS sites (12%).

Drivers of Spatial Variability in Long-term Peakflow Trends

We employed a multiple linear regression model to explore the spatial determinants behind the significant peakflow trends (1316 USGS sites) in the HUC2 regions (see Method). Our analysis focused on the climate, land use, and water management drivers. We examined how differences in precipitation trends, urban and agricultural land use, and water storage capacity impacted the peakflow trends (Figs. 1 and 2, and Supplementary Figs. 1 through 6). We aimed to discern whether or not human-influenced watersheds exhibited different trends compared to less-impacted ones within the same HUC2 region. The USGS sites with statistically significant trends (n = 1316) were included in the regression analysis following Singh and Basu³⁶.

In 14 of the 18 (HUC2 regions, statistically significant contributions from one or more drivers were identified (see Fig. 4). The climate, land use, and water management drivers collectively explained an average of 34.5% of the variance in trends across these 14 HUC2 regions, ranging from a minimum of 4% in the South Atlantic-Gulf region to a maximum of 66% in the Texas-Gulf region, highlighting the challenges in the attribution studies. Urbanization emerged as the most influential factor, explaining 15.8% of the variance, followed by water management (9.7%), agriculture (4.8%), and reduced annual maximum precipitation (2.3%). For categorization at the HUC2 level, contributions equal to or exceeding 20% were considered major, those ranging from 10% to 20% were considered moderate, and contributions less than 10% were deemed minor.

At the HUC2 level, urbanization emerged as the predominant factor, explaining major variances of 62%, 44%, and 32% in the Texas-Gulf, California, and Mid-Atlantic regions, respectively. Furthermore, urbanization contributed moderately to the explained variances in the Ohio River Basin (21.5%), Great Basin (18.8%), Upper Mississippi River Basin (17.7%), and Great Lakes region (11.2%). Additionally, urbanization played a minor role in explaining variances in the Missouri River Basin (6.5%), South Atlantic-Gulf region (4%), and Upper Colorado River Basin (2.6%).

Urbanization amplified the peak flow trends in most of the HUC2 regions where significant variance was found (9 out of 10), thus confirming a positive correlation between the normalized trend slope and urban extent. For example, three major urbanized HUC2 regions exhibited positive correlation values of 0.79 in the Texas-Gulf, 0.67 in California, and 0.57 in the Mid-Atlantic region. However, we found a negative correlation value of −0.43 between the urban areas and the normalized trend slope in the Great Basin region. This is likely due to its semi-arid climatic conditions and increased water withdrawals to meet urban water demands from cities such as Las Vegas³⁷.

Water management emerged as the second most influential driver, exerting significant influence with contributions of up to 37% in the Tennessee region, 30% in the Ohio River Basin, and 24% in the Upper Colorado River Basin. Additionally, water management made moderate contributions in the Arkansas-White-Red region (11.5%) and the Upper Mississippi River Basin (10.3%). Water management explained a minor fraction of variance in the Pacific Northwest (9.7%), Mid-Atlantic region (8.9%), and Missouri River Basin (4.9%).

Water management exhibited a mitigating effect on peak flow trends, confirming a negative correlation between the normalized trend slope and the water stored behind dams and reservoirs in the watershed. For example, three major water management-dominated HUC2 regions exhibited negative correlation values of −0.72 in Tennessee, −0.65 in the Ohio River Basin, and −0.51 in the Upper Colorado River Basin.

Agricultural land use emerged as the third significant driver, contributing to major variances in the Upper Colorado River Basin (28.6%) and moderate variances in the Great Lakes region (16.7%). Furthermore, agricultural land use explained minor fractions of variances in the Missouri (9.2%), Ohio (3.8%), Texas-Gulf (3.4%), Mid-Atlantic (3.1%), and Pacific Northwest (2.2%). Agricultural land use is extensive and relatively homogeneous across the reference and non-reference watersheds in the Midwestern US, encompassing the Ohio River Basin, Great Lakes, Upper Mississippi River Basin, Missouri River Basin, and Arkansas-White-Red regions (see Supplementary Fig. 2). Hence, agricultural land use did not emerge as a major determinant influencing spatial heterogeneities in peakflow trends in the Midwestern US. Agricultural land use exhibited a positive correlation with peak flow trends, with values of 0.54 in the Upper Colorado River Basin and 0.32 in the Great Lakes region.

Finally, climate emerged as the fourth significant driver with moderately decreasing influences in the Southwest (Rio Grande: 14.8 %, and California: 11.2%) and minor increasing influences in the Midwest (Great Lakes: 6.7%, Upper Mississippi: 4.8%, and Missouri: 4.6%). Additionally, the Arkansas-White-Red region exhibited a minor influence from three climate drivers: mean precipitation increase (7.7%), mean precipitation decrease (3.5%), and maximum precipitation decrease (2.8%). The Pacific Northwest region also exhibited a minor influence due to decreasing maximum precipitation (3.4%).

Role of Internal Climate Variability

The observed peakflow trends serve as a singular instance within a spectrum of equally plausible climate realizations due to unpredictable noise or internal climate variability in a climate model^17,18,38. We utilized the Community Earth System Model version 2 Large Ensemble (CESM2-LE)¹⁸ to assess whether the observed changes align with the range of variability simulated by CESM2-LE, which represents potential manifestations of large-scale climate variability. If the observed changes fall outside this simulated range, it strongly suggests a significant role of direct human interventions in the hydrologic system, which was one of our key findings.

We employed the Mann-Kendall trend test individually for each ensemble member at the grid scale of the climate models (~100 km × 100 km). Then, we consolidated a single ensemble result at the HUC2 level, representing the percentage of grid-cells manifesting significantly increasing or decreasing trends. By focusing exclusively on statistically significant trends, we compared the observed and CESM2-LE simulated trends that were outside the range of internal climate variability (by definition of significant trends). While modes such as ENSO, PDO, or AMO are not temporally synchronized between simulations and observations, long-term externally forced trends that exceed the range of internal variability can still be meaningfully compared. These results were then aggregated across all 90 ensemble members using a box plot to evaluate the spread of plausible trends arising from internal climate variability in the CESM2-LE (Fig. 5). This analysis underscored the impact of internal climate variability. To facilitate comparison, we also depicted our results from the first ensemble member only (open circle in Fig. 5), acknowledging its inherent limitation in capturing observations across most of the HUC2 regions. However, a comprehensive evaluation of the entire ensemble widened the prospects of accurately capturing the observed peakflow trends, particularly evident in the case of reference sites, which we discuss next.

Fig. 5: Climate model (CESM2-LE) evaluation for non-stationarity in peakflow.

Our climate model generally captured the observed trends and non-stationarity at the reference stations in 12 of the HUC-2 regions, whereas it failed to capture observations at the non-reference stations in 15 of the HUC-2 regions. The trends (Panel a) and KPSS non-stationarity test (Panel b) were evaluated using 90-member ensemble CESM2-LE data; and their spread, including the 5^th, 25^th, 50^th, 75^th, and 95^th percentiles are represented here using a box plot. Additionally, only the results from the first ensemble are also shown. The reference stations include both the HCDN and GAGES-II reference stations, and the non-reference stations include the GAGES-II non-reference and other USGS stations (c.f., Table 1, and Fig. 1a). The CESM2-LE data were analyzed for the 1950 to 2014 period (65 years, historical simulation). See Supplementary Fig. 11 comparing the USGS observation for the same period.

Despite its extensive 90-member ensemble, CESM2-LE exhibited deficiencies in reproducing observed peakflow trends in 15 of the 18 HUC2 regions (Fig. 5a). However, upon explicit examination of the reference sites, CESM2-LE adeptly reproduced the peakflow trends in 12 of the HUC2 regions. For example, urbanization significantly contributed to increasing trends in the Mid-Atlantic and California regions (Fig. 5), where 32% and 28% of all the USGS sites exhibited significantly increasing trends. Nevertheless, CESM2-LE failed to capture the observed level of trends falling outside the upper 95% range simulated by CESM2-LE, 26% and 18% respectively for the Mid-Atlantic and California regions (Fig. 5a). However, upon restricting the analysis to the reference sites, the observed level of trends decreased to 20% and 15% respectively, aligning with the CESM2-LE ensemble spread in both regions.

Similarly, the construction of dams and reservoirs over time has led to significantly decreasing peakflow trends in the Ohio River Basin (HUC2# 5 in Fig. 5). Once again, CESM2-LE’s upper 95% range (22%) failed to replicate the observed level of trends found at 30% of all the USGS sites in the Ohio River Basin (Fig. 5). However, CESM2-LE successfully reproduced the observed level of trends for 15% of the reference-only sites in the Ohio River Basin. A comparable outcome was observed in the Upper Colorado River Basin, where water management elucidated significantly decreasing peakflow trends found at 38% of all the USGS sites, while CESM2-LE’s upper 95% range only showed trends at 24% of all the grid cells (Fig. 5).

Additional non-stationarity metrics provided consistent insights, e.g., the KPSS test for non-stationarity (Fig. 5b). Notably, CESM2-LE demonstrated a greater capacity for capturing observations from the reference only sites compared to the human-impacted (non-reference sites). For instance, the 95% ensemble range of the CESM2-LE successfully encompassed the observed level of non-stationarity for the reference only sites in 14 of the HUC2 regions, in contrast to only three HUC2 regions for all the USGS sites. This result suggests that CESM2-LE was able to adeptly simulate the peakflow trends driven by climate change. However, due to the predominance of the observed changes resulting from direct human interventions, such as water management and urbanization, the processes were not well represented in the CESM2 model and faced challenges in accurately capturing the observed trends.

Peak Flow Trends in the Post-Dam Construction Period (1981 to 2021)

Given the significant impact of water management infrastructure on peak flow trends, our analysis specifically focused on the post-dam construction period (1981–2021). Notably, the majority (77%) of dams and reservoirs were completed before 1981 (Supplementary Fig. 12). Therefore, we hypothesized that during this period, climate change factors would emerge as the predominant drivers of peak flow trends.

The trends during the post-dam construction period align closely with climate-driven patterns, which are characterized by generally increasing trends in the eastern US and decreasing trends in the west (Fig. 6). The number of sites exhibiting significant trends and other non-stationary metrics decreased notably during the post-dam construction period compared to the long-term trends (Supplementary Table 2 vs. Table 1). For example, only 9.7% of USGS sites exhibited significant trends (5.8% increasing and3.9% decreasing) during the post-dam period, compared to 33.9% of sites showing significant trends over the long-term (> 60 years). Similarly, the proportion of USGS sites exhibiting non-stationarity decreased from 30.6% in the long-term analysis to 7.1% during the post-dam construction period. These results underscore the significant role of direct human interventions in shaping the observed long-term hydrological trends (Fig. 2).

Fig. 6: Peakflow Trends in the Post-Dam Construction Period (1981–2021).

a, c, and e display the Regional Average Mann-Kendall Z values for all the USGS sites, reference-only sites, and non-reference sites, respectively. These Z values indicate the statistical significance of the trends across the regions, with values < −1.96 or > 1.96 representing statistically significant trends. Higher magnitudes of Z correspond to greater confidence in the statistical significance (see Methods). b, d, and f illustrate the short-term (1981–2021) observed peak flow trends for all the USGS sites, reference-only sites, and non-reference sites, respectively. Open circles indicate insignificant trends with color representing the direction of the trend slope (blue for positive, red for negative, and grey for zero), while upward and downward arrows represent statistically significant (p-value < 0.05) increasing and decreasing trends, respectively, based on a non-parametric method. Regional trends are quantified using the Regional Average Mann–Kendall (RAMK) normalized Z-score, which is computed from the sum of site-level Mann–Kendall statistics (including both significant and non-significant sites) across the region (See Method). The regional trend significance thus reflects the net balance of increasing and decreasing site-level trends. Magnitude of trends are shown as percentages of standard deviation change over 40 years. The reference sites include both the HCDN and GAGES-II reference sites, and the non-reference sites include the GAGES-II non-reference and other USGS sites.

These observed trends also fall well within the range of internal variability simulated by the CESM2-LE large ensemble. For instance, 14.7% of the USGS sites in the Ohio River Basin exhibited significant trends, a proportion consistent with the CESM2-LE simulated range of 0 to 22.2% (Supplementary Fig. 13). In summary, when the effects of direct human interventions are minimized, e.g., by analyzing trends in the post-dam construction period, the CESM2-LE simulations captured the observed changes, highlighting the utility of large ensemble simulations in attributing climate-related variability to observed hydrological trends.

Discussion

By demonstrating the outsized influence of human interventions on peakflow trends, this study contributes to a more nuanced understanding of the observed trends in flooding. Previous investigations have either presented these trends as mixed¹³ or predominantly attributed them to climate-related factors alone^2,11. In contrast, our findings revealed that climate-only factors have intensified flooding in the northern half of the US. Whereas, direct human interventions, specifically water management, have counteracted the influence of climate-only factors across most of the US (refer to Fig. 2). Additionally, urbanization was found to have contributed significantly to the increased flooding in the Texas-Gulf, California, and Mid-Atlantic regions (Fig. 4). Agricultural land use also has contributed moderately to increased flooding, particularly in the Midwestern US. This study enriches the body of literature by emphasizing the impacts of direct human interventions on the hydrological system in the US³⁶ and globally¹.

Furthermore, in this study we conducted, for the first time, an assessment of the impacts of natural climate variability on the peakflow trends. Our findings highlight a crucial limitation in climate models in that they currently fail to accurately capture observed long-term trends due to process deficiencies. Notably, both water management and urbanization factors are inadequately represented in climate models. For example, CESM2 does not account for urban expansion³⁹, which has been a significant land use trend in recent decades⁴⁰. CESM2-LE therefore is not able to capture the observed trends in that area. Interestingly, upon excluding watersheds impacted by human activities, CESM2-LE’s ability to capture the observed trends (reference only) significantly improved. This observation underscores the importance of acknowledging the role of internal climate variability in elucidating observed trends at reference sites, a feat otherwise hindered by the constraints of a limited ensemble size.

Our results underscore the necessity of incorporating water management and urbanization effects to enhance prediction accuracy. We investigated the spatial determinants influencing the variability in the peakflow trends at a regional scale, specifically focusing on the HUC2 regions, which was an inherent limitation of this study. For example, when climate factors exhibited homogeneity across a region, they failed to elucidate the variability observed in the trends. At the same time, the observed trends manifested inhomogeneity within the HUC2 regions (Fig. 2). Consequently, we contend that human factors played a substantial role in shaping the observed long-term trends, as depicted in Fig. 2.

Methods

Streamflow data

We acquired long-term annual peak streamflow data to meet our needs from the USGS surface-water data web portal using the data length criterion of 60 years or more. This selection process yielded 3,907 USGS sites with a median data length of 80 years. A larger number of water management structures were constructed around 1960 and this longer data length allowed us to include the effect of these water management structures. Subsequently, we conducted trend and other non-stationary analyses individually for each USGS site using their peakflow time series.

The USGS sites were classified into reference and non-reference categories based on lists provided by the HCDN²⁰ and GAGES-II²¹ data, along with reference sites representing sites minimally impacted by direct human interventions. Among the 3,907 USGS sites, a subset of 620 sites met the criteria for reference sites, all of which were also identified as GAGES-II reference sites. Within this subset, 439 sites were additionally designated as HCDN reference sites. The remaining 3,287 sites were classified as non-reference sites, consisting of 2830 GAGES-II non-reference sites and 457 other USGS sites (Fig. 1a).

Updating the GAGES-II reference list

The GAGES-II dataset, published in 2011, was analyzed to determine whether its reference watersheds still met the criteria for reference status in 2021. The analysis revealed that new water management structures had been constructed in 47 out of 620 watersheds since 2008. However, these new storage additions accounted for less than 1% of the annual total precipitation, so these watersheds were retained as reference sites. Additionally, land cover data from 2008 to 2021 indicated that 98% of the reference sites experienced less than 1% urban growth. Based on these findings, we concluded that the reference sites still qualified for inclusion in the reference list.

Geospatial Analytics for watershed attributes (Anthropogenic Drivers)

We acquired watershed boundary shapefiles for each of the 3907 streamflow sites from the USGS’s Hydro Network-Linked Data Index (https://waterdata.usgs.gov/blog/nldi-intro/). Subsequently, we developed a Python program within the ArcGIS environment to clip a high-resolution raster dataset, such as land use data, to the respective watershed boundaries and to calculate the watershed attributes. The land use analysis utilized a high-resolution (30 m) National Land Cover Dataset for 2019 (NLCD 2019) to delineate present-day land cover types and their percentage of coverage within each watershed. Urban land cover, including Developed Open Space (NLCD Code: 21), Low Intensity (22), Medium Intensity (23), and High Intensity (24), were collectively categorized as Urban Land (Supplementary Fig. 1). Similarly, Pasture/Hay (81) and Cultivated Crops (82) were classified as Agricultural Land Use (Supplementary Fig. 2). Our land use analysis remained temporally static, assuming that human modifications in the watershed had transformed the land use from its pre-industrial natural vegetation condition. We hypothesized that varying degrees of land use change intensity can elucidate the spatial variability in peakflow trends at the HUC2 level.

Subsequently, we acquired high-resolution gridded (0.25° × 0.25°) daily precipitation observations from the National Oceanic and Atmospheric Administration (NOAA) Climate Prediction Centre (CPC) Unified Gauge-Based analysis, which contains all the available data from 1948 to 2021. We computed a gridded estimate of trends in both annual daily mean and maximum precipitation. Employing the GIS-based Python programming, we clipped the gridded precipitation trend estimates to the respective watershed boundaries, yielding the key attributes of the mean precipitation and the percentage of watershed areas exhibiting statistically significant increases or decreases in maximum and mean precipitation (Supplementary Figs. 3–6). The mean annual total precipitation depth values were utilized to normalize the water storage capacity, which is discussed in the subsequent section, while the remaining attributes were incorporated into the regression analysis that will be presented later.

The National Inventory of Dams (NID) dataset covers 88,509 dam sites across the CONUS, all of which were included in our analysis. Utilizing the GIS-based Python programming, we assigned the appropriate dams to each of the 3907 watersheds based on their geographical overlap with the watershed boundaries. Subsequently, we calculated the total maximum storage capacity by summing the maximum capacities of all the dams within each watershed. This total storage capacity was then normalized by the watershed-averaged mean annual total precipitation depth and watershed area. The resulting metric, which we called the normalized maximum storage capacity, represented the fraction of annual mean precipitation stored behind dams within a watershed. We employed this normalized maximum storage as a metric to assess the impacts of water management on the peakflow trends. Our hypothesis posits that varying degrees of water management intensity (Fig. 1b, c) can elucidate spatial variability in peakflow trends.

We intentionally omitted additional natural factors, such as topography, slope, and forested area, from our analysis to concentrate on uncovering the impact of climate change (specifically precipitation trends) and direct human interventions (land use and water management) on the peakflow trends. This focused approach allowed us to gain a clearer insight into the anthropogenic factors driving the peakflow dynamics. Moreover, we acknowledged the inverse relationship between forested areas and urbanization and agricultural land use change.

Mann-Kendall Trend test

We employed the non-parametric Mann-Kendall (MK) test^41,42 to evaluate the trends in peakflow. The MK test is based on the sign of change (Eq. 1) and offers several advantages: (1) it contains no prior assumption about the linear trend, (2) it has higher power in detecting a trend in non-normally distributed data^43,44, and (3) it is robust against outliers. We investigated the normality assumption using standard statistical testing including the Shapiro-Wilk test, the Anderson-Darling test, and the D’Agostino and Pearson’s tests, and found that the vast majority of the peakflow data (approximately 92%) of all the USGS sites did not adhere to normal distribution. Therefore, our utilization of the MK test was justified.

If ${x}_{1},{x}_{2},\ldots \ldots \ldots ..,{x}_{n}$ is a time series ($X$) of length n (in years), then the Mann-Kendall test statistic S is defined as:

$$S={\sum }_{i=1}^{n-1}{\sum }_{j=i+1}^{n}{sign}({x}_{j}-{x}_{i})$$

(1)

Here, ${sign}({x}_{j}-{x}_{i})$ takes values of −1, 0, or 1 depending on whether $({x}_{j}-{x}_{i})$ is less than, equal to, or greater than zero. The null hypothesis (${H}_{0}$) of the MK-test posits no trend in the time series. If ${H}_{0}$ is true, then S is normally distributed with zero mean ($E\left(s\right)=0$), and the variance of S depends on the sample size (n) as expressed below.

$${{\mathrm{var}}}\left(S\right)=\frac{n(n-1)(2n+5)}{18}$$

(2)

The significance of a trend is determined by comparing the standardized test statistics (${Z}_{{MK}}$) with that from the standard normal distribution at the desired significance level.

$${Z}_{{MK}}=\left\{\begin{array}{c}\frac{S-1}{\sqrt{{{\mathrm{var}}}(S)}}{if}S > 0\\ 0{if}S=0\\ \frac{S+1}{\sqrt{{{\mathrm{var}}}(S)}}{if}S < 0\end{array}\right.$$

(3)

If the probability yielded by ${Z}_{{MK}}$ fell below 2.5% or exceeded 97.5% then we rejected the null hypothesis at the 95% confidence interval. In this study, ${Z}_{{MK}}\le -1.96$ represented a declining trend, and ${Z}_{{MK}}\ge 1.96$ represented a statistically significant increasing trend.

Effect of serial correlation

The majority of peakflow data exhibit no serial correlation. We conducted an analysis using a one-year lag correlation metric and determined that 81% of all the USGS sites demonstrated serial independence in annual peak streamflow. This finding was consistent with a previous study⁴⁵ which concluded that serial dependence is primarily observed in annual minimum and mean flow data while peakflow events can be regarded as independent random events from year to year. The remaining 19% of our sites exhibited statistically significant serial correlation (Supplementary Fig. 14).

The presence of positive serial correlation reduced the effective sample size in the time series, leading to an underestimation of variance when employing conventional methods (e.g., Eq. 2), resulting in an erroneous identification of significant trends. We employed a variance inflation method suggested by Hamed and Rao⁴⁶ that adjusted the variance using the inflation factor (infl)

$${infl}=1+\frac{1}{n(n-1)(n-2)}{\sum }_{i=1}^{n-1}(n-i)(n-i-1)(n-i-2){r}_{i}$$

(4)

Here, ${r}_{i}$ is the statistically significant serial correlation at lag i of ranks of the observations. The variance calculated using Eq. 2 was multiplied by the inflation factor to obtain the adjusted variance $\left({{{\mathrm{var}}}(S)}^{* }={infl}* {{\mathrm{var}}}(S)\right)$, and the adjusted variance was used to calculate standardized test statistics (${Z}_{{MK}}$).

Trend magnitude

We computed the magnitude of the trend using the Theil-Sen approach (TSA)^47,48 as given below

$${TSA}={median}\left(\frac{{x}_{j}-{x}_{i}}{j-i}\right){for\; all}i < j$$

(5)

Then, we normalized TSA by the standard deviation of X at individual USGS sites; X is described in reference to Eq. 1. This step helped to compare the trends across different watersheds. It was then multiplied by 60 years to scale the normalized trend slope to a 60-year period, which provided a more practical understanding of the trend over a long period. Finally, the resulting value was converted to percentages which we found to be a more interpretable approach and often make it easier to communicate the results.

Regional Average Mann-Kendall (RAMK) test

We utilized the RAMK test⁴⁹ to assess trends at the HUC2 level, encompassing multiple USGS sites (Fig. 1a). In a HUC2 region containing m sites (1, 2, …m), the regional statistics are provided below:

$${S}_{R}={\sum }_{i=1}^{m}{S}_{i}$$

(6)

$${{\mathrm{var}}}{\left(S\right)}_{R}={\sum }_{i=1}^{m}{{\mathrm{var}}}{\left(S\right)}_{i}$$

(7)

Here, ${S}_{i}$ and ${{\mathrm{var}}}{\left(S\right)}_{i}$ represent the MK test S statistics and the variance of S at individual sites, respectively, as described in Eqs. 1 and 2. If the data exhibited serial correlation, we utilized the adjusted variance. Subsequently, we calculated the regional Mann-Kendall z statistic (Z_MK,R) using a similar equation to Eq. 3, but with ${S}_{R}$ and ${{\mathrm{var}}}{\left(S\right)}_{R}$. Finally, we compared Z_MK,R with the standard normal variate to determine the statistical significance of the regional trends.

Field Significance test for trends

To assess the field significance of trends across sites, we applied the False Discovery Rate (FDR) approach. First, p-values associated with the trends were extracted, i.e. the p-values derived from the Mann-Kendall test for trend detection. The p-values were then sorted in ascending order. Next, the global significance threshold (α = 0.05) was determined and the FDR-adjusted threshold was calculated for each p-value by dividing its rank (1 through K, where K is the total number of p-values) by the total number of tests (K), then multiplying by the global significance level. The formula for this threshold is:

$${{Threshold}}_{i}=\frac{i}{K}\times \alpha$$

(8)

where, i is the rank of the p-value, and K is the total number of tests (i.e., the number of sites).

The largest p-value that was less than or equal to its corresponding threshold was identified as the FDR cutoff value. In cases where no p-value met this condition, the FDR cutoff was set as the smallest p-value greater than the global significance threshold (α).

Following this, field significance was determined by comparing each original p-value to the FDR-adjusted threshold (P_FDR). Sites where the p-values were less than or equal to the FDR threshold were considered to have significant trends. The results of this field significance analysis indicated whether each site exhibited a significant trend after correction for multiple comparisons.

Levene test for variance

The dataset, spanning over 60 years, was partitioned into two subsets, each consisting of at least 30 years of data. Subsequently, the equality of the variance between these two subsets was assessed using the Levene test³⁴. The Levene test was preferred due to its lower sensitivity to deviations from normality assumptions, particularly evident in peakflow data. The test statistic (W) for Levene’s test was computed using the following expression:

$$W=\frac{\left(n-k\right)}{(k-1)}\frac{{\sum }_{i=1}^{k}{p}_{i}\left({z}_{i.}-{z}_{..}\right)}{{\sum }_{i=1}^{k}{\sum }_{j=1}^{{p}_{i}}{\left({z}_{{ij}}-{z}_{i.}\right)}^{2}}$$

(9)

Here, k represents the number of distinct groups (which is 2 in this study), ${p}_{i}$ stands for the number of values within the i^th group, and ${z}_{{ij}}$ denote the absolute deviation calculated as ${z}_{{ij}}=|{x}_{{ij}}-\bar{{x}_{i.}}|$, where $\bar{{x}_{i.}}$ represents the median of the i^th subgroup. ${z}_{i.}=\frac{1}{{p}_{i}}{\sum }_{j=1}^{{p}_{i}}{z}_{{ij}}$ denotes the group mean of the absolute deviations within the i^th group, while ${z}_{..}=\frac{1}{n}{\sum }_{i=1}^{k}{\sum }_{j=1}^{{p}_{i}}{x}_{{ij}}$ signifies the overall mean of the absolute deviation across all groups, and n is total number of observations in all groups. ${x}_{{ij}}$ indicate the time series with the j^th value in the i^th group. Levene test statistics, ‘W’ follows the F-distribution with k-1, and n-k degrees of freedom. The null hypothesis is rejected if the probability of ‘W’ is less than 0.05, corresponding to a 95% confidence level.

Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test for stationarity

We employed the KPSS test to assess the changing mean and variances in the peakflow time series⁵⁰. Specifically, we used the KPSS Level test that has following statistics:

$${KPSS}=\frac{1}{{n}^{2}}\frac{{\sum }_{i=1}^{n}{{v}_{i}}^{2}}{{\hat{\sigma }}^{2}(p)}$$

(10)

Where, ${v}_{i}={\sum }_{j=1}^{i}\left({x}_{i}-\bar{x}\right)$ represents the partial sum process of the residual $\left({x}_{i}-\bar{x}\right)$, and its variance is estimated as below:

$${\hat{\sigma }}^{2}\left(p\right)=\frac{1}{n}{\sum }_{i=1}^{n}{\left({x}_{i}-\bar{x}\right)}^{2}+\frac{2}{n}{\sum }_{j=1}^{p}{w}_{j}(p){\sum }_{i=j+1}^{n}\left({x}_{i}-\bar{x}\right)\left({x}_{i-j}-\bar{x}\right)$$

(11)

Here, p is the truncation lag taken as 1 because we used the annual peak streamflow time series; ${w}_{j}(p)$ is the weighting function that corresponds to the choice of a special window, e.g., the Bartlett window ${w}_{j}\left(p\right)=1-j/(p+1)$. If the KPSS test statistics (Eq. 11) were larger than the critical value suggested by Kwiatkowski et al.³⁵ corresponding to 0.05 significance level, then we rejected the null hypothesis.

The KPSS test has a null hypothesis that is similar to the MK test and Levene tests, namely that the time series is stationary. If evidence is found, the KPSS test will favor the alternate hypothesis of non-stationarity. The other two non-stationarity tests, namely the Augmented Dickey-Fuller (ADF) test, and the Phillips–Perron (PP) test have an opposite null hypothesis, i.e., the process is non-stationary or has a unit root. The ADF and PP tests favors the alternate hypothesis of weak stationarity³⁵, e.g., we found that by using ADF and PP, 99.9% of the sites had strong stationarity (not shown). Hence, we present here our results using only the KPSS test.

Multiple Linear Regression (MLR)

We employed a multiple linear regression (MLR) model to assess the impact of the anthropogenic drivers on the peakflow trends within a HUC2 region (Fig. 1b). The predictor (y) for the MLR model was the TSA trend normalized by the standard deviation of the peakflow time series at the respective USGS sites. All the USGS sites (10 or more), in a HUC2 region, exhibiting statistically significant trends were incorporated into the analysis. The set of predictants included four climate-related variables: changes in the areal coverage of maximum and mean precipitation (denoted as C1-C4), as well as two land use factors: agricultural land use (Agr) and urbanization (Urb). Additionally, we considered one water management factor: the normalized maximum storage capacity (NSC), as described below:

$$y={\beta }_{0}+{\beta }_{1}{C}_{1}+{\beta }_{2}{C}_{2}+{\beta }_{3}{C}_{3}+{\beta }_{4}{C}_{4}+{\beta }_{5}{Ag}+{\beta }_{6}{Urb}+{\beta }_{7}{NSC}$$

(12)

Here, β₀ is the intercept, and β₁ to β₇ are regression coefficients. We employed the linear model function within the R statistical software to fit the model. A driver was deemed significant if its associated regression coefficient demonstrated statistical significance at a 95% confidence level (p-value < 0.05). The variance explained by each driver is shown in Fig. 4. The intercept term (${\beta }_{0}$) is not shown.

Large Ensemble Analysis

The CESM2-LE is the latest generation climate and earth system model that provides a large ensemble simulation¹⁸. CESM2-LE employs a mix of macro- and micro-perturbations in initial conditions to create its ensemble. Macro perturbations are induced by four distinct phases of the Atlantic Meridional Overturning Circulation states, while infinitesimal perturbations (10⁻¹⁴) are applied to the initial atmospheric potential temperature states, resulting in a micro-perturbation ensemble¹⁸. Because of the chaotic nature of the climate system, any small or large initial condition perturbations quickly grow and saturate to a similar magnitude in 2-3 weeks after initialization⁵¹, providing 90 equally plausible long-term climate simulations. An extensive set of high-frequency outputs were archived. We employed the QRUNOFF output at daily frequency for the peakflow analysis. All of the available ensemble (=90), at the time of analysis, were included in the analysis.

QRUNOFF represents total runoff including surface and sub-surface runoff simulated by the Community Land Model version 5 (CLM5)⁵² with the land component in the fully coupled Community Earth System Model (CESM2). The CLM5 provides a comprehensive representation of the hydrological processes encompassing canopy interception, through-fall, multi-layer soil moisture dynamics, evapotranspiration, and surface and subsurface runoff processes. The model’s structure includes a nested subgrid hierarchy, facilitating the representation of diverse land cover types, vegetation classes, and agricultural land use and management practices within grid cells of typical size (1°×1°). Each grid cell can feature multiple soil columns, each with its vertically resolved profile of soil water and temperature. Soil columns serve as fundamental response units, discretized into up to 20 hydrologically active layers with spatially varying thickness, adjusting depths according to terrain characteristics such as mountainous or plain regions⁵³. CLM5 employs a TOMODEL scheme to parameterize surface runoff based on the fractional saturated area within each grid cell⁵⁴. The sub-surface drainage is a function of the water table depth which is determined based on the first soil layer above the bedrock, where the soil saturation fraction is less than 0.9⁵⁵.

Soil water is predicted using a one-dimensional Richard’s equation by integrating downward water movement over each layer with an upper boundary condition of the infiltration flux into the topsoil layer and a zero-flux lower boundary condition at the bottom of the soil column. The model incorporates a prognostic seasonal cycle for vegetation evolution, including leaf emergence, senescence, and vegetation height dynamics, using the Biome-biogeochemical cycle model^56,57. This seasonal evolution of plant functional types influences soil moisture distribution and runoff processes. Landscape heterogeneity is captured through a plant functional type tile structure. The model incorporates land use change using a land use change harmonization dataset⁵⁸. The CLM5 land-only simulation captures observed streamflow trends with high fidelity in the Southeastern US⁵⁹.

CLM5/CESM2 are the only global climate models³⁹ that incorporate urban land parametrizations by representing tall building districts; high, and medium density urban classes; and their thermal and imperviousness characteristics⁶⁰. Gray et al.³⁹ assessed the characteristics of urban runoff globally and found that urbanization increased total runoff and was sensitive to the urban class specification in the model. However, urban land cover does not change with time and is specified at the start of simulation, i.e., the pre-industrial era as the present-day urban cover extent. Hence, the effects of urbanization could not be discerned in the trend estimates.