On the optimum of the energy transfer efficiency in the generation of waves by subaerial landslides

Abstract

This paper studies the problem of the energy transfer from a subaerial landslide to the waves it produces, in two dimensions, with a thoroughly validated multiphase Navier-Stokes model. The completeness of the model and the large domain considered give access to the time evolution of the slide and water energy components up to the far field. Considering a configuration favoring high energy transfer efficiency, namely a triangular water slide lying at the free surface, the slide volume (per unit width) is varied. The results show that the transfer efficiency is reduced by dispersion for the smaller slides and by breaking for the larger ones, leading to the existence of a local optimum for an intermediate slide size. Starting from this point, a new optimum is obtained by varying the slide density and the slope angle. Hence, with a density of 1750 kg. m⁻³ and a slope of 30°, the efficiency reaches a value of 87% in the near field and 73% in the far field, which may be good approximates of the related maxima in two dimensions. Compared to the previous optimum case, considering a granular rheology or slides at higher elevations drastically decreases the efficiency.

Introduction

Impulse waves generated by subaerial landslides can occur in different environments such as rivers¹, mountain lakes or reservoirs^2,3, fjords⁴, bays⁵ or volcanic islands⁶. Subaerial slides are most of the time debris or rocks avalanche⁷ but other more fluidized slide types, such as debris flows⁸, pyroclastic flows⁹, or even snow avalanche¹⁰ may also generate waves. During the generation process, the initial potential energy of the slide is partly transferred to water waves which, in turn, can dissipate part of this energy by breaking¹¹, for instance or redistribute it by dispersion^12,13. Understanding these processes is key for a proper hazard assessment.

The energy transfer efficiency is usually defined as the ratio between the maximum wave energy obtained just after generation and the slide kinetic energy at impact. Submarine landslides are less efficient than subaerial landslides with maximum values of the order of 10%¹⁴. For subaerial slides, values between 25 and 50% are reported for solid slides¹⁵, while generally lower values (i.e., between 2 and 30%) are obtained for granular slides^16,17, except for very low values of the product FSM (with F slide Froude number, namely the ratio between the slide velocity and the local wave celerity, S slide thickness and M slide mass) for which the efficiency may exceed 2/3¹⁸. Higher slide elevations tend to decrease the efficiency¹⁷, as well as slide three-dimensionality^19,20. So far, there is no real link between the different efficiency values reported in the studies or attempt to explain, with physical reasons, the variability observed.

Moreover, the interpretation of these results should be made with care for two reasons. First, the definition of the efficiency may be different from one study to the other. For instance, different results may be obtained if the energy of the wave train or only the leading wave is considered. Second and more important, there is a non negligible uncertainty regarding the wave kinetic energy measurements involved in the wave energy computation. Usually, strong assumptions have to be made to assess the total wave energy such as kinetic and potential energy equi-repartition^16,17,19,20, solitary wave-like behavior¹⁵ or nil kinetic component during generation²¹. Nevertheless, the rare Particle Image Velocimetry measurements of the impulse wave kinetic energy performed to date²², show that the wave kinetic energy can actually be 1.4 larger than the corresponding potential energy.

Numerical models allow a direct access to the velocity field in the whole domain, thereby giving a more complete view of the energetic processes. If various advanced model types have been already applied to investigate this question^{11,23,24,25,26,27}, the results are still scarce, partly due to the limited number of cases studied. Another problem is the extent of the computational domain considered, usually too short to account for all of the wave transformation processes occurring up to the far field. Finally, turbulent energy dissipation, mostly induced by wave breaking, is not properly accounted for in the majority of the studies, while being critical in the energy budget.

The present work try to partly fill these gaps. The objective is to investigate numerically the energy transfers in cases maximizing these transfers. The last point is important as it helps reducing the numbers of cases to be studied and poses the question of the efficiency optimum, never addressed before. The final energy of the leading wave is considered the proxy for hazard assessment. This also differs from previous studies which rather focused on the wave energy at the time of maximum amplitude (i.e., just after generation). By progressively shaping the leading wave energy, the wave transformation processes play a role on the final efficiency value. Therefore, it is critical to properly resolve energy dissipation (mainly by breaking) and dispersion with the numerical model. Regarding this aspect, the present work greatly benefit from a recent extensive validation work²⁸, in which, special care was devoted to the accurate computation of the wave energy components. The validity of this model is also demonstrated by comparing the simulation results with new experimental data corresponding to the configuration studied in the present article (Section “Model validation”).

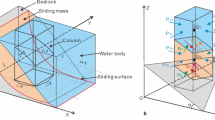
This configuration is displayed in Fig. 1. The computational domain is a two-dimensional prismatic tank, 20.3 m long and 1 m high. A 45° inclined plane, on the left side of the domain, drives the slide motion for the wave generation. The water depth h₀ is constant and equal to 20 cm. The extent of the domain, covers  ≈ 100h₀ to capture the wave transformation processes up to the wave stabilization zone (i.e., the far field). The slide, (volume (per unit width) V_s and initial height h_s) made up of water, is located adjacent to the water free surface, and therefore, enters the basin without initial speed. The use of water instead of a more realistic material for the slide, is justified by the research of a bounding value for the energy efficiency transfer (i.e., the maximum value possible). We will demonstrate in this paper that it, indeed, produces a very efficient energy transfer from the slide to the leading wave in the far field and subsequently allows, with varying the parameters of the problem, to look for the extremum. In the configuration presented in Fig. 1, we first vary the most influential parameter, the slide volume (per unit width) V_s (h_s varying from 0.5h₀ to 2.25h₀ with a 0.25h₀ step) and look for a local optimum in the energy efficiency. Then, the role of other parameters such as rheology, submergence, slope and density is further examined, and a first assessment of the global optimum is obtained.

Fig. 1: Slide cases considered in the study.

The water depth h₀, constant throughout the different simulations, is equal to 20 cm. The slide, of triangular shape and made up of water has a variable volume (per unit width) V_s controlled by the height h_s.

Results

The role of wave transformation processes in the energy transfer efficiency

In the configuration presented in Fig. 1, after generation, the waves are submitted to two main processes: dissipation by wave breaking and energy redistribution by dispersion.

In most of the cases, the wave generated breaks as illustrated in Fig. 2 for one of the largest slide (h_s = 2h₀). In Fig. 2 (a), the wave energy is gradually increasing until t^* ≈ 7, witnessing the generation phase. The ratio between the wave kinetic and the wave potential energy at the time of the wave energy maximum, $\frac{{E}_{k}}{{E}_{p}}\approx 1.8$, is very far from the classical equi-partition hypothesis (note that for smaller slide volumes, the results (not shown here) are closer to this assumption). Overall, the effect of breaking on the total wave energy evolution is very strong, dissipating the excess of kinetic energy up to a point where a stabilized ratio $\frac{{E}_{k}}{{E}_{p}}$ slightly larger than 1, typical of non linear waves²², is reached at t^* ≈ 50.

Fig. 2: Illustration of the breaking process for a relatively large slide volume case (h_s = 2h₀).

a Wave energy variation with (non dimensional) time. Solid line: wave train total energy E_k + E_p[J. m⁻¹] (black dots: fraction corresponding to the leading wave), “ × ”: wave train kinetic energy E_k[J. m⁻¹], “ + ”: wave train potential energy E_p[J. m⁻¹], dotted line: instantaneous dissipation rate in water ϕ_w[J. s⁻¹. m⁻¹] with the shaded area, the turbulent contribution to this dissipation rate. The colored vertical dashed lines in (a) refers to the time instant of the following panels (i.e., (b–e)). b–e Snapshots of the fluid interfaces, streamlines, and turbulent dissipation rate ϵ around the leading wave at different phases of the wave life for the same case as (a), with (b) Generation phase, (c) Transition, (d) Weak breaking and (e) Propagation phase.

Figure 2b–e shows the different stages of breaking analog to what is observed in the surf zone²⁹, with a transition phase (Fig. 2c) involving several splash-ups³⁰ associated with a maximum turbulent dissipation, a “weakly breaking” phase (Fig. 2d) with a lower dissipation rate and finally (Fig. 2e) a stabilized solitary-like wave.

Once freed from the slide influence, the evolution of the wave is totally dictated by its characteristics just after generation. At this point, the relative wavelength governs the amount of frequency dispersion that the initial wave will subsequently experience during its propagation. On the other hand, the Ursell number, defined as $Ur={a}_{1}{L}_{1}^{2}/{h}_{0}^{3}$ (with a₁ and L₁, respectively leading wave amplitude and apparent wavelength of the leading wave, from the wave face toe down to the second zero-crossing in the free surface profile), characterizes the wave nonlinearity. Large values will lead the wave to steepen through amplitude dispersion. These two parameters are represented on Fig. 3, respectively (a) and (b). According to the values obtained, the waves generated by small slides should undergo large frequency dispersion while on the contrary, large slides should generate very non linear waves and amplitude dispersion. This is confirmed on Fig. 3c, d, which show wave gauge signals for two different slide volumes and their respective wavelet scalograms (Fig. 3e, f). In the smaller slide case, while initially, the energy is localized in time (Fig. 3c, e), as the wave train progresses, a clear separation of the spectrum in two operates, with the higher frequencies arriving later. With the larger slide (Fig. 3d, f), if there is a slight frequency dispersion, the main process is a progressive strengthening of the energy at the crest by non linear effects (i.e., amplitude dispersion).

Fig. 3: Effect of dispersion and non linearity on the wave train transformation after generation.

a relative leading wave length. b Ursell number just after generation for the different slide cases studied. For two particular slide volume (per unit width) (× points on plots (a) and (b)), free surface time series (h_s = 0.75h₀ (c) and h_s = 2h₀ (d)) at the gauges position (g) (with zero crossings depicted by red crosses). The corresponding wavelet scalograms (h_s = 0.75h₀ (e) and h_s = 2h₀ (f)) using Morlet motherwavelet⁶² are plotted with the energy of the signal component at each time/frequency point in m². s⁻¹ as colorbar. The leading wave period is depicted by the gray color extent on the free surface plots, and by the horizontal pink ribbon (i.e., leading wave frequency  ± 10%) on the scalograms.

The energy transfer efficiency, accounting for the whole process from the initial slide start to the final leading wave energy, is now considered. One of the important idea developed in this paper, is that the output of this process is strongly dependent on the combined effects of breaking and dispersion. The former dissipates the waves generated by the larger slides, while the second redistributes the energy of the leading wave to the wave train in the case of the smaller slides. This interesting combination is illustrated in Fig. 4a. The results of the height cases simulated in this study are displayed in this panel in terms of non-dimensional initial slide volume per unit width ${V}_{s}/{{h}_{0}}^{2}$. As indicated previously, the slide initial height h_s was gradually increased from 0.5h₀ to 2.25h₀ with a 0.25h₀ step. The curve with the  × symbol shows that all the cases considered in this study are very efficient to generate the initial wave, with an efficiency between 60 and 70% comparable to the highest values reported in the literature¹⁸. However, when the subsequent wave transformation processes are taken into account (i.e., the curve with the triangle symbols), the conclusion changes drastically. The effect of dispersion (in purple), calculated as the difference between the final wave train energy and the final leading wave energy, is strong for the smaller slides and decreases with the slide volume (per unit width) increase. On the contrary, the energy dissipated by breaking (in red) is large for the large slides and decreases for smaller ones. As a result, the final energy transfer efficiency is higher for intermediate slides with a peak around 0.5 for the case h_s = 1.25h₀, which corresponds to an initial slide height slightly larger than the depth.

Fig. 4: Wave energy versus non dimensional slide volume per unit width ${V}_{s}/{{h}_{0}}^{2}$, with ${V}_{s}={{h}_{s}}^{2}/2$.

a relative wave energy (i.e., energy transfer efficiency) with  ×: maximum wave energy E_w,max/E₀ taken just after generation, '+': final wave train energy E_w,t=10s/E₀, ▴: final leading wave energy E_{leading−wave,t=10s}/E₀, with E₀ initial slide potential energy at rest calculated following equation (12) of Section “Methods”. The energy dissipated by breaking corresponds to the red area, the energy lost in dispersion to the purple area and the final remaining wave energy (t = 10 s) to the green area. In (a) the plot with the triangular markers represents the global efficiency of the energetic process. The black vertical dashed line locates the position of the local optimum with respect to the slide volume (per unit width). b absolute non dimensional wave energy with, •: final leading wave total energy and ▸: corresponding kinetic energy part. For comparison, the final leading wave amplitude to depth ratio is plotted in blue square symbols (■) with blue dashed line representing the limit a₁/h₀ = 0.6.

Efficiency is an important concept, but the absolute leading wave energy is the actual hazard. Here Fig. 4 (b) shows that, although the leading wave amplitude seems limited to the ratio a₁/h₀ ≈ 0.6^31,32 (note that the last point is slightly above 0.6, likely because the channel is not large enough for this case), the leading wave energy still increases with larger volumes without apparent limit. This increase is explained by larger wavelengths which seems no to be limited as the amplitude. This may be due to the geometry of the problem, the water body being limited in the vertical direction and unbounded in the horizontal direction.

Influence of rheology and submergence

In the results presented previously, the slide was composed of water in order to maximize the energy transfers. Moreover in the same vein, the slide was initially lying at the free surface level. In this section, we try to demonstrate the relevance of this previous configuration by comparing it with more elaborated rheology as well as introducing a slide elevation with respect to the free surface.

Considering the model presented in Section “Granular slide model”, with the same numerical and physical parameters, the effect of a more complex Coulomb granular rheology is investigated in the following. From a mechanical point of view, this type of rheology introduces locally higher viscosity values in the flow as compared to the water case. Consequently, it is logical to expect a lower efficiency. It is clearly what is observed on Fig. 5e, where different granular cases, with or without initial elevations are compared to the optimum water case determined so far. The snapshots show that the wave generated by any of the granular cases considered is smaller than in the optimum water case. Considering that the initial slide energy is higher in any of these cases due to either, higher elevation or higher density, the efficiency drops critically, by at least a factor three, in these three cases (i.e., (b), (c) and (d)) compared to the optimum water case (a). The model shows that this is due to higher dissipation in the slide, in the generation area in water or both of them.

Fig. 5: Influence of slide rheology and submergence on the energy transfer efficiency.

Left column: Granular slides. The slide volume (per unit width) is the same in all the cases (i.e., h_s = 1.25h₀). a–d Snapshots of the fluid interfaces, streamlines, and turbulent dissipation rate ϵ around the leading wave at four times (${t}_{1}^{* }$=3.5, ${t}_{2}^{* }$=8,${t}_{3}^{* }$=45, ${t}_{4}^{* }$=70), with (a) water slide with no initial elevation (i.e., h_l = 0), (b) same as (a) but the slide is granular and the density is 1575 kg. m⁻³, (c) same as (b) except h_l = h₀ and a density of 1000, (d) same as (c) but with a density of 1575 kg. m⁻³. e Wave energy versus slide initial energy E₀ for the four different cases. Right column: Newtonian slides (with h_s = 2h₀). Illustration of the decrease in efficiency when (f) increasing the slide viscosity (or decreasing the slide Reynolds number $R{e}_{s}=\frac{\sqrt{g\,{h}_{s}}\cdot {h}_{s}}{{\nu }_{s}}$) and (g) increasing the slide initial elevation. e, g curve symbols definition as in Fig. 4.

The effect of slide dissipation on the energy transfers can also be illustrated by simply increasing the viscosity value in a Newtonian slide. Note that this is only informative as the Newtonian law is too simple to describe the real phenomenon³³. Figure 5f shows the evolution of the energy transfer efficiency (i.e., E/E₀) with the slide Reynolds number $R{e}_{S}=\frac{\sqrt{g\,{h}_{s}}\cdot {h}_{s}}{{\nu }_{s}}$³⁴ for a slide case with h_s = 2h₀. The case on the right of this plot (i.e., Re_s around 10⁶) corresponds to a water slide. The decrease of efficiency (after generation as well as at the end of the channel) when decreasing the Reynolds number (i.e., increasing the slide viscosity) is obvious on this plot. The effect of slide initial elevation (also named submergence) is verified with a water slide of same surface. Figure 5g also clearly shows the efficiency decrease with higher submergence h_l. Interestingly, it is mainly the generation which is less efficient, the subsequent wave transformations processes acting more or less similarly for all the elevations considered. The model shows that this is due to a higher dissipation in the generation zone (crater formation, back breaking of the initial wave).

Influence of density and slope

In this section, the influence of density and slope is investigated. In Fig. 6a–d, the energy transfer efficiency is plotted against the slide density for the optimum slide found previously (h_s = 1.25h₀ and h_l = 0), which already had a very high overall efficiency (i.e., from the slide potential energy to the final leading wave energy) of 50 %. As for the slide volume (per unit width), the density effect on the efficiency is important. Considering the overall efficiency, an optimum with respect to the slide density (given the initial optimum volume) appears for a relative density of about 1.75. For this case, the energy transfer during generation ( × symbols) is extremely high (around 77%), and, in addition, the wave processes (dispersion and breaking) have a minimum effect. As a consequence, the leading wave energy keeps a very high value and the overall efficiency (around 68%) is the highest obtained for the slope of 45°. As a comparison, the case with a relative density of 2.5 has a better efficiency at generation (i.e., more than 80%) but then the dispersion and the dissipation strongly reduces the leading wave energy at the end of the domain.

Fig. 6: Effect of slide density and slope on the energy transfer efficiency.

Slide case: h_s = 1.25h₀ and h_l = 0. Top panels ((a–c)): Snapshots of the fluid interfaces, streamlines, and turbulent dissipation rate ϵ around the leading wave at the same times as Fig. 5 for different slide densities. d Wave energy versus slide initial energy E₀ for different slide densities. The black dashed vertical line shows the optimum case obtained with respect to the density. e–h Same as (a–d) (respectively) with a slide a density of 1750 kg. m⁻³ and varying the slope, keeping A_s constant. In (h), the red dashed vertical line shows the optimum case obtained in this study (i.e., a slope equal to 30°). d, h curve symbols definition as in Fig. 4.

Finally, in the last simulations presented in Fig. 6e–h, the slope effect is briefly studied considering the optimum slide volume (per unit width) and density, and keeping the same slide volume (per unit width) in all the cases. If the variation of the efficiency is weaker than for the density, an optimum value is nevertheless again obtained, this time for a slope of 30°. With this slope value, the efficiency at generation is 87% and the overall efficiency 73%. Note that for this case, even though the leading wave in the far field (Fig. 6e${{t}_{4}}^{* }$, seems smaller than for the two other slopes, the initial slide potential energy is also much smaller (64.5 J. m⁻¹ against 90 and 114, respectively), which gives overall a better efficiency for this case.

Discussion

The main findings of this study are listed hereafter and their significance discussed in the following:

• 1. during the process of wave generation and transformation, the wave kinetic energy can exceed the wave potential energy by a large amount,

• 2. after generation, the wave transformation processes, namely dispersion and breaking, can strongly affect the leading wave energy,

• 3. the energy transfer efficiency has an optimum. This paper gives the approximate value of this optimum and the slide characteristics associated.

This paper shows that, at the peak of the wave energy, during generation, the wave kinetic energy exceeds the wave potential energy with a ratio larger than 1.6 for the four largest slide cases plotted in Fig. 4. This is, for instance, the case in Fig. 2a, at t^* ≈ 7. This ratio then evolves toward a stable value in the far field, a little more than 1.1 in all these cases. These results align with the values previously measured with PIV²². For smaller slide volumes (i.e., the first four cases of Fig. 4), both components are almost equal at generation and in the far field (result not shown). Most of the previous results on the energy transfer efficiency have been obtained experimentally, considering the transfer at the maximum wave amplitude (i.e., just after generation) and assuming equi-repartition between the wave potential and kinetic energy^16,17,19,20. The present study shows that the validity of this assumption strongly depends on the case considered. For the four largest water slides of Fig. 4, the equi-repartition assumption would have lead to an underestimation of the actual energy transfer from 5 to 25%. Whereas for the smaller slide cases of Fig. 4, this hypothesis is true within 10%. Therefore, this work shows the need for a clearer identification of the configurations favoring the excess of wave kinetic energy, in order to correctly interpret past and future measurements. The model presented in this paper could be a valuable tool to conduct this particular research.

This work also highlights the critical role of the wave processes in the phenomenon, and in particular, the antagonist effects of dispersion and breaking in shaping the leading wave energy in the far field, the first decreasing efficiency for smaller slides and, the second, for larger slides. Most, if not all of the previous works on energy transfers, computed transfer rates between the slide, usually considering the slide kinetic energy at impact, and the wave, taking its amplitude when it is maximum, namely in the generation area. The work presented in this paper shows that this approach is not complete for an accurate hazard assessment. In particular, if the issues at risk are not directly in the generation area but at a slightly remote location, then the risk will strongly depend on the wave processes action. The present study shows that cases exist, for which the reduction of the wave energy by the latter is strong over a limited distance. For instance, in Fig. 4a, the case corresponding to a water slide with ${A}_{s}/{{h}_{0}}^{2}=2$ (or h_s = 2h₀) and h_l = 0, shows a large dissipation by breaking which stops around t^* = 30 (Fig. 2a). At this time, the leading wave is at a distance of about 40h₀ from the generation. For a case with a depth of 100 m, that would be at 4 km. Similarly, the most important reduction of amplitude by dispersion can occur quite rapidly as illustrated in Fig. 3c, e for the water slide corresponding to h_s = 0.75h₀ and h_l = 0. In this case, at x = 6 m (i.e., 30h₀), the reduction of the wave amplitude is already about 40%. For the same example of a depth h₀ = 100 m, that would be at 3 km.

This paper shows the probable existence of an optimum for the overall energy transfer (i.e., from the slide potential energy to the far field leading wave energy), for which the transfer efficiency is around 73% (and 87% just after generation). The efficiency corresponding to this optimum is larger than all the values reported in previous works¹⁴. Its exact value and the corresponding slide features are not yet completely determined, as this will require a rigorous optimum research on multiple parameters, which has not been performed here. Nevertheless, at this point of the study, the main influence of the most critical factors has been integrated (i.e., the primary influence of volume and density). Therefore, the conclusions of the present study are not expected to be much different with more computations. The first implications of this result is the probable bounding of the energy transfer efficiency to a value not too far from about 73% of the initial slide potential energy. This result could be used to obtain a first assessment of the risk in any given situation, by assigning a value to the maximum possible wave in the near and the far field. The second implication is the recognition of the slide type associated to this worst case. The study shows that it corresponds to a slide volume (per unit width) approximately equal to $0.8{{h}_{0}}^{2}$ with h₀ water depth, located close to the free surface, with a macroscopic density between 1500 and 2000 kg. m⁻³, a high water content (to favor minimal internal viscosity) and a slip surface inclined of about 30°.

Compared to this worst scenario, this study showed that the efficiency is reduced for other cases due to one or several of these factors:

• a slide rheology leading to a strong internal dissipation like in the granular rheology simulated in this paper. Here the simulation shows an efficiency divided by a factor 3 with values around 10 or 20% in phase with the literature^14,16. This also confirms the recent experimental results showing that a water slide case generates the highest wave amplitude compared to any other granular slides⁹.

• a large slide elevation. The latter increases the slide potential energy but does not necessarily produces a similar increase in the wave amplitude (Fig. 5). This is due to higher dissipation in the generation area as shown by this work as well as likely a lower generation efficiency due to supercritical slide Froude numbers.

• if fluidized slides close to the free surface are considered, a density or a volume which may be too low or too large. Regarding the slide volume (per unit width), compared to the optimum, smaller or larger slides are both less efficient due to dispersion or breaking, respectively. Whereas if the slide volume (per unit width) is optimum, then density may reduce or not the efficiency. According to Fig. 6d, compared to the optimum, lighter slides are less efficient in the generation, while heavier slides are more efficient at generation but the wave produced is then strongly affected by dispersion and breaking, and the overall efficiency is, therefore, comparatively reduced.

This classification of the cases helps to structure the knowledge, as compared to the current state of the art, and improves the understanding of the phenomenon. Nevertheless, despite their interests, these results should be taken with caution in a context of risk assessment. Indeed, the concept of optimum efficiency is not straightforward and therefore may potentially be wrongly interpreted. In this study, the efficiency is the ability to transform a given slide potential energy into wave energy. In this framework, the most efficient cases have been determined in this paper. Compared to these cases, other cases may be less efficient but nevertheless, generate larger waves in the near or far field, because their initial energy is simply larger. Hence, for instance, subaerial slides with high elevations have been classified as not very efficient here, but they still represent a paramount danger due to the large initial slide energy available. In the same vein, the case with a slope of 30° has been claimed the most efficient, but when compared with the corresponding (slightly) “less efficient” 60° slope slide case, the main wave generated by the first is obviously less energetic (Fig. 5). Yet, for these two cases, all the slide parameters are supposed equivalent (surface, density, initial position of the lower slide point with respect to the free surface, viscosity), but when varying the slope, keeping the slide volume (per unit width) constant, the potential energy is redistributed differently in both cases, inducing a much larger wave for the steeper slope. Therefore, the 60° slide case is both, a very efficient and a very dangerous case, due to its efficiency and its high potential energy.

In addition, this study has also a few other limitations stressed hereafter.

The simulations performed in this work are two dimensional and the initial water depth is constant. Those are strong assumptions compared to real events. In nature, there are cases where 3D effects may be neglected, where the slide lateral extent is of the same order as the one of the water reservoir width, like in fjords^35,36 or in mountain lakes, for instance. For such cases, the present work is valuable for identifying the most efficient slides in terms of energy transfers. On the other hand, in the case of volcanic island in the open ocean, 3D effects may be obviously more important^24,37. Pursuing this work in a 3D configuration is straightforward methodologically speaking, but the computational cost would be much higher. In this case, strategies optimizing the mesh could be employed. A fine mesh is, indeed, only required in the generation zone and where breaking occurs, which in 3D should be limited in space.

The energy transfer efficiency is calculated from the slide at rest to the leading wave in the far field. This approach assumes that the hazard is only function of the main wave energy which is not completely accurate. Indeed, the length and composition of the wave train are also important features as it influences the inundation time history. Wave recomposition may also occur in the opposite nearshore area due to bathymetry effects.

The granular slide simulations performed in this paper are based on a simple viscoplastic law supposed to describe the macroscopic behavior of the granular flow. Nevertheless, such a simple law do not include all the physical processes acting when a granular flow interacts with a water body. First, in reality, water flow within the grain may occur. This aspect is, for instance, better included in a recent multiphase Smoothed Particle Hydrodynamics model applied to the study of submerged landslides^33,38. Second, the flow in the porous medium may be only partially saturated requiring even more complex and heavier models to be employed³⁹. Nevertheless, in addition to the argument of the computation time, there are two physical justifications for the choice of this simple model. First, in most of the cases studied in this paper, the energy transfer to the wave is very quick, and at this time scale, the complex processes in the porous medium, may not really have time to significantly influence the generation stage. Second and most important, the point of Section “Influence of rheology and submergence” was to show the efficiency reduction compared to water slides. To this respect, it is likely, that the penetration of water between the slide grains would further reduces this efficiency⁹.

Methods

Governing equations

In this work, multiphaseInterFoam, the multi-phase solver of OpenFOAM, is used to simulate the flow composed of three immiscible phases (i.e., water, slide, and air). The governing equations are the incompressible Navier-Stokes equations with spatially varying density and viscosity and a VOF method to track the interfaces⁴⁰.

The phase-fraction of phase i is first defined as follows:

$${\alpha }_{i}(x,t)=\left\{\begin{array}{ll}1&{{{\rm{if}}}}\,{{{\rm{phase}}}}\,i\,{{{\rm{is}}}}\,{{{\rm{present}}}}\,{{{\rm{at}}}}\,x,t\\ 0&else.\end{array}\right.$$

(1)

The continuity and momentum equations respectively read:

$$\nabla \cdot {{{\bf{u}}}}=0,$$

(2)

$$\frac{\partial \rho {{{\bf{u}}}}}{\partial t}+\nabla \cdot (\rho {{{\bf{u}}}}{{{\bf{u}}}})=-\nabla p+\nabla \cdot (2(\mu +{\mu }_{t}){{{\bf{D}}}})+\rho {{{\bf{g}}}}+{f}_{\sigma i}.$$

(3)

with u the fluid local velocity, g the gravitational acceleration, p(x, t) the pressure field, ρ(x, t), μ(x, t) and μ_t the local fluid density, molecular dynamic viscosity and eddy viscosity, respectively. ${{{\bf{D}}}}=\frac{1}{2}(\nabla {{{\bf{u}}}}+{(\nabla {{{\bf{u}}}})}^{T})$ is the strain rate tensor, while f_σi = σ κ  ∇ α_i is the surface tension force, modeled as a continuum surface force⁴¹, in which σ is the surface tension at the interface and κ the local curvature of the interface.

In most of the cells, there is only one phase present. In this case, the density and viscosity affected to the cell corresponds to this phase. When the cell is crossed by one interface, the local mixture properties are computed by averaging among the existing phases. Therefore, in the whole domain, the local density and viscosity can be calculated following:

$$\rho (x,t)=\sum\limits_{i=1}^{N}{\alpha }_{i}(x,t)\,{\rho }_{i},$$

(4)

$$\mu (x,t)=\sum\limits_{i=1}^{N}{\alpha }_{i}(x,t)\,{\mu }_{i}$$

(5)

with N the number of phases, while ρ_i and μ_i are density and molecular dynamic viscosity of the ith phase.

The phase fraction value is updated at each time step thanks to the phase fraction advection equation given by:

$$\frac{\partial {\alpha }_{i}}{\partial t}+\nabla \cdot \left({\alpha }_{i}{{{\bf{u}}}}\right)+\nabla \cdot \left({\alpha }_{i}\sum\limits_{j=1,\,j\ne i}^{N}{\alpha }_{j}\,{u}_{r,ij}\right)=0\,.$$

(6)

Here u_r,ij is the relative velocity between phases. The last term is employed as a numerical technique to ensure a sharp and non-diffusive interface⁴². The phase volume fractions equation (Eq. (6)) is solved with the MULES (Multidimensional Universal Limited Explicit Solver) algorithm to ensure the conservation of sharp interfaces between a pair of phases⁴³.

The time and space computational domains are discretized into a finite number of time steps and cells to solve the governing equations. Spatial discretization is the standard Gaussian finite-volume integration method based on summing values on cell faces, which must be interpolated from cell centers⁴⁴.

Equations (2) and (3) are solved with the PIMPLE algorithm which takes care of the pressure-velocity coupling. The CFL_conv condition ensures the stability of the solution with respect to the convective terms of equation (3), by limiting the time step Δt as follows:

$$CF{L}_{conv}=\frac{| {{{\bf{u}}}}| \,\Delta t}{\Delta x} < 1$$

(7)

It is also important to respect a condition on the diffusive terms of equation (3) expressed as⁴⁵:

$$CF{L}_{diff}=\frac{(\mu +{\mu }_{t})\,\Delta t}{\rho \,\Delta {x}^{2}} < 1$$

(8)

In the simulations performed here, we impose a strong limit on the convective CFL (CFL_conv < 0.1) which is sufficient to indirectly respect equation (8).

The turbulence model used in the current study is a k-ω SST buoyancy-modified turbulence model⁴⁶. This model limits the spurious production of turbulent kinetic energy k usually observed with classical RANS models at the interfaces thanks to the new buoyancy term (G_b) added in the equation (see also the recent developments of refs. ^47,48 on this topic).

The governing equations for the turbulent kinetic energy k and the turbulent energy dissipation frequency ω read:

$$\frac{\partial \rho \,k}{\partial t}+\nabla \cdot (\rho \,k\,{{{\bf{u}}}})=\nabla \cdot \left(\left(\mu +{\sigma }_{k}\,{\mu }_{t}\right)\,\nabla k\right)+{P}_{k}-\rho \,{\beta }^{* }\omega k+{G}_{b},$$

(9)

$$ \frac{\partial \rho \,\omega }{\partial t}+\nabla \cdot (\rho \,\omega \,{{{\bf{u}}}})=\nabla \cdot \left(\left(\mu +{\sigma }_{\omega }\,{\mu }_{t}\right)\,\nabla \omega \right)+\frac{\gamma }{{\nu }_{t}}\cdot \\ G-\rho \beta {\omega }^{2}+2\rho (1-{F}_{1})\cdot \frac{{\sigma }_{\omega 2}}{\omega }\cdot \nabla k\cdot \nabla \omega .$$

(10)

with: $G=\rho {\nu }_{t}| \dot{\gamma }{| }^{2}$, P_k = min(G, 10ρβ^* kω), ${\nu }_{t}=\frac{{a}_{1}k}{max({a}_{1}\,\omega ,\sqrt{2}\,\dot{\gamma }\,{F}_{2})}\,$.

β^* and a₁ are equal to 0.09 and 0.31, respectively. F₁ and F₂ are blending functions (ϕ = F₁ϕ₁ + (1 − F₁)ϕ₂) which causes the model to behave as a k-ω model in the vicinity of the boundaries and as a k-ϵ model in the rest of the domain.

Model setup

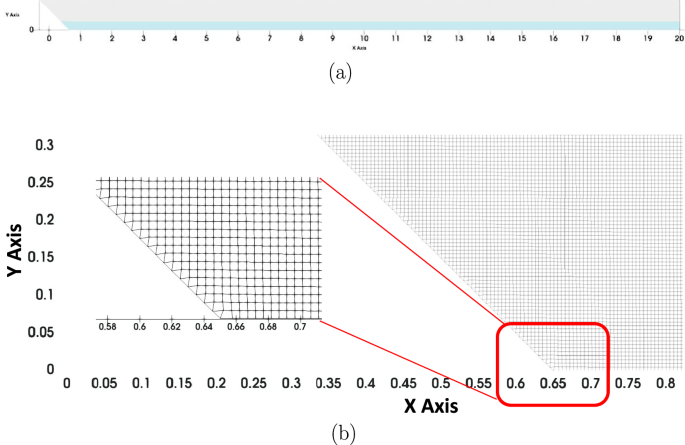
In the study conducted in this article, the computational domain is a two-dimensional prismatic tank, 20.3 m long and 1 m high (Fig. 7a). A 45° inclined plane, on the left side of the domain, drives the slide motion for the wave generation.

Fig. 7: Computational domain used for the numerical experiment.

a sketch of the numerical tank, (b) detailed view of the mesh arrangement around the slope.

The simulations are carried out with "multiphaseInterfoam" considering three phases (i.e., slide, water, and air). Each phase is initially located in the domain thanks to an individual phase fraction (e.g., "alpha.water" for water phase). In the basin, the water elevation (h₀) is constant and equal to 20 cm. The slide phase is placed over the slope and its characteristics (volume V₀ and initial height h_s) vary depending on the case. The empty space left by the two other phases is filled with air.

A uniform mesh is employed to avoid non-orthogonality and skewness of the mesh cells, which are both known to challenge most VOF algorithms. Taking into account the conclusions of the validation study and according to the wave features expected in our numerical experiment (observed between 0.01 and 0.27 m), we selected two cell sizes: 2.5 mm and 5 mm, each with an aspect ratio of one. The smaller mesh size, 2.5 mm, is applied in cases involving the smallest waves to ensure that the mesh resolution adequately captures the wave amplitude. The mesh is generated, first with "blockMesh" and, then with "snappyHexMesh". In total, It consists of a maximum of 1,251,120 hexahedral cells and 160 prism-shaped cells (Fig. 7b).

The walls, slope, and bottom boundary conditions are set to “noSlip” for the velocity field and zero-flux for the other fields. The top boundary is an open atmosphere boundary condition. The total duration of the simulation is set to 12 s. This is considered to be a sufficient duration to cover the full wave propagation through the tank in the majority of cases. The data output is carried out every 0.05 s. Other numerical methods and parameters, such as the turbulence model for instance, are chosen based on published recommendations²⁸. Table 1 summarizes the final model setup retained.

Table 1 Summary of model setup parameters used in the numerical experiment (teletype fonts for OpenFOAM specific parameters)

Length of the channel

With 20.3 m, the length of the channel represents 100h₀. In the interpretation of Fig. 4, it is assumed that the leading wave had reached the so-called “far field” zone at the end of the channel, which means that the main wave transformation processes have ceased. The examination of the turbulent dissipation rate ϵ allows to track the end of the breaking phase which, in our case, arises within the computation domain for all the cases (except the largest volume for which, there is still a slight dissipation remaining at the end of the domain as also witnessed by the value of the relative wave amplitude in Fig. 4b). On the other hand, dispersion affects the wave continuously with variable intensity and therefore, there is no real end of this process unlike wave breaking. Therefore, the length of the channel should account for most of the transformation. The evolution of the wave amplitude with the distance to generation has been measured in wave flumes^16,18,49. Note that generally, the domain considered is shorter than in the present study (i.e.,  ≈ 50h₀ or less). The attenuation is found dependent on the wave type which is consistent with the conclusions of the present work. The exponential attenuation coefficient reported in the literature are for instance^16,49, a = −0.4 for weakly nonlinear oscillatory waves and b = − 0.05 for nonlinear or the solitary waves, or an average value (including all wave type) of c = − 0.25. This gives an amplitude attenuation of 85%, 20% and 70% over the current computational domain for a, b and c, respectively. Over a domain of double extent (i.e., 200h₀), the corresponding attenuation would be respectively 88%, 24% and 74%. Consequently, as wave transformation is expected to be much slower beyond the domain limit, the computational domain extent appears sufficient to account for the quickest and most significant dispersion effects and the energy transfer efficiency results presented in Fig. 4 can be considered as relevant values.

Computation of energy and dissipation in each phases at time t

At each time step, the mechanical energy E_m of each phase m is the sum of the potential energy E_p,m and the kinetic energy E_k,m. The global kinetic energy of phase m is the sum of the mean flow kinetic energy and the turbulent kinetic energy within this phase:

$${E}_{k,m}(t)={\iint }_{A}{\alpha }_{m}(t)\,(\frac{1}{2}\,{\left\vert {{{\bf{u}}}}({{{\bf{t}}}})\right\vert }^{2}\,+k(t)){\rho }_{m}\,dx\,dy$$

(11)

with A denoting the computational area.

The potential energy of phase m is:

$${E}_{p,m}(t)={\iint }_{A}{\alpha }_{m}(t)\,g\,y(t)\,{\rho }_{m}\,dx\,dy$$

(12)

with y, the vertical coordinates of the point with respect to the water surface at rest.

The amount of energy dissipated at time t₁ is the integration in time of the energy dissipation rate Φ(t).

$${E}_{diss,m}({t}_{1})= \int_{0}^{{t}_{1}}\Phi (t)dt=\int_{0}^{{t}_{1}}{\iint }_{A}({\alpha }_{m}(t)\,{\mu }_{m}\,\dot{\gamma }(t)\dot{\gamma }(t)\,dx\,dy \\ +{\alpha }_{m}(t)\,\epsilon (t)\,{\rho }_{m}\,dx\,dy)\,dt,$$

(13)

where $\dot{\gamma }(t)$ denotes the scalar shear rate value in the cell. This dissipation is the sum of two components: the laminar dissipation and the turbulent dissipation.

For the energy components of the wave train, the integration in the horizontal direction starts from the slide tip²⁵. The potential energy of the wave field is therefore obtained by:

$${E}_{p,wave}(t)= {\iint }_{{x}_{slide-tip}}^{{x}_{end-channel}}{\alpha }_{w}(t)\,{\rho }_{w}\,g\,y(t)\,\,dx\,dy \\ -\int_{0}^{{h}_{0}}\int_{{x}_{slide-tip}}^{{x}_{end-channel}}\,{\rho }_{w}\,g\,y(t)\,\,dx\,dy,$$

(14)

The leading wave energy components are obtained by isolating the area concerned with a zero crossing method.

Model validation

As previously mentioned, a thorough validation of the multiphase solvers of OpenFOAM (i.e., interFoam and multiphaseInterFoam) has been previously published²⁸. In this paper, the phenomenon (i.e., impulse waves generated by fluid-like subaerial slides) was divided into elementary process, for which, a dedicated validation was, each time, performed. The following processes were studied: slide flow, wave generation and breaking, wave dispersion, energy conservation in a propagating wave, energy conservation in a breaking wave and dissipation in the turbulent bore. Table 2 displays all the cases with the reference set-up and the required number of cells, in the slide thickness or the wave height, depending on the case, to accurately resolve the case.

Table 2 Summary of the validations performed in ref. ²⁸

The originality of this validation work stands in the consideration of energy conservation or dissipation calculation. This aspect is rarely addressed in previous validation works, while it is crucial when the energy transfer from slide to wave is to be computed. It is shown that the breaking wave energy is acceptably conserved with the buoyancy modified k − ω SST turbulence model⁴⁶ but not with other more usual models such as the k − ϵ or the k − ω SST models. Additionally, the turbulent bore physical dissipation computed by the model was shown to tend to the analytical solution when decreasing the cell size. The minimum number of cells required to achieve these results are indicated in Table 2. The meshes used in the present paper have been chosen to respect these constraints on the number of cells.

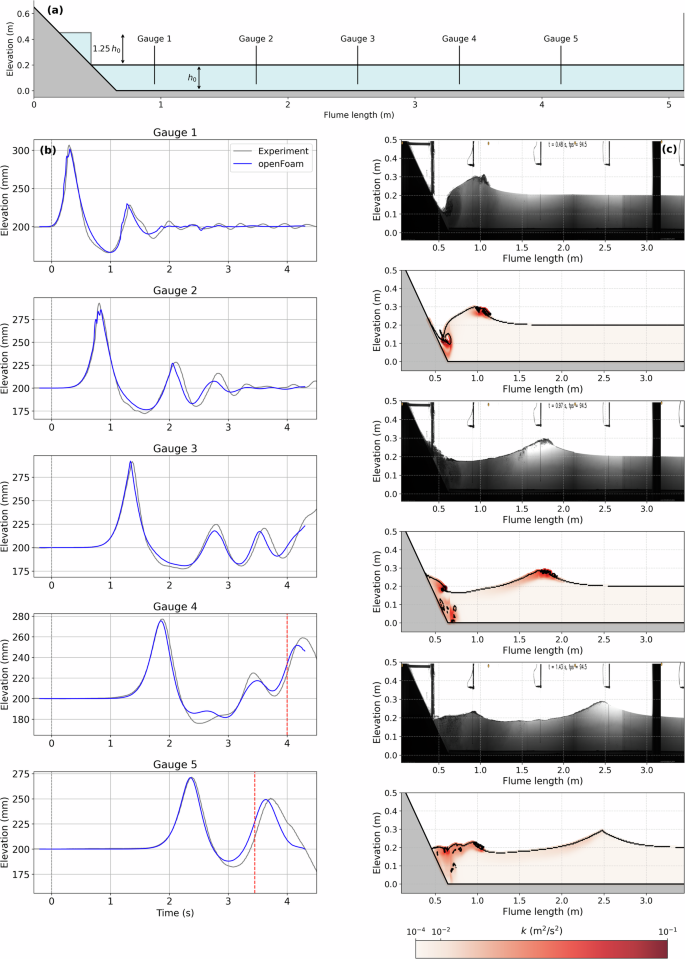
In order to demonstrate the validity of the model in the configuration studied in the present work, an experiment has been specifically conducted. The flume is 5.12 m long, 0.25 m wide and 0.65 m high (Fig. 8a). A pneumatically driven gate, positioned at x = 0.45 m, is used to release a water volume of triangular shape over a 45° slope as in the simulations presented in this article. The case considered for the experiment correspond to the optimum surface of Fig. 4 which features a slide height h_s = 1.25h₀ and no initial elevation (h_l = 0). The downstream depth h₀ is equal to 20 cm as in the simulations. Five wave gauges (HRWG-0105, HR Wallingford) were used to record the instantaneous water surface at an acquisition frequency of 100 Hz at different positions along the flume (Fig. 8a). Additionally, five cameras (Basler acA2000-165um) allowed to control the occurrence of wave breaking through the presence of foam in the movies as well as to capture the motion law of the lifting gate. The measurements were compared to a simulation performed with a model similar to the one presented in the results section, namely same numerical parameters and mesh resolution. The only differences are the domain considered (i.e., flume length of 5.12 m instead of 20 m) and the modeling of the gate motion²⁸. The latter is mandatory to accurately reproduce dam break flows over wet bottom as reported in earlier comparable studies^28,50. Finally, the experiment was conducted five times to check the repeatability. The wave gauge signals obtained were almost undistinguishable, therefore, in this section, only one run is presented.

Fig. 8: Validation of the model in the case of a water slide with the optimum surface found in Fig. 4 (corresponding to a slide height h_s = 1.25h₀).

a sketch of the experimental flume and gauge locations. b temporal evolution of the water surface at the five gauge positions and corresponding simulation results (the dotted red lines mark the times when the signal is affected by the wave reflection on the downstream boundary). c comparison of the camera and model snapshots for different wave breaking stages.

Figure 8b, c shows the comparison between the experiment and the simulation. Panels of column (b) allows to verify the model ability to generate the main wave accurately and compute its subsequent evolution in time, including the birth of the dispersive trail. In particular, the evolution of the leading wave amplitude and wavelength appears very similar to the data. The agreement is slightly less satisfactory for the leading wave back face and the amplitude of the trailing waves. Nevertheless, the numbers of trailing waves as well as their time evolution are overall respected. One important feature of this model is its expected capacity to reproduce the dissipation by breaking²⁸. The panels of column (c) shows the good behavior of the model regarding this aspect. The different phases of the process are indeed respected with, in the first two panels (starting from the top position), the breaking inception as a plunging breaker, in the two middle panels, the evolution toward a milder breaking in the data as in the simulation and finally, in the two bottom panels, the cease of the breaking at the same time and same position. The correct description of the breaking is obviously mandatory to get a good correspondence in amplitude as observed in the column (b).

Granular slide model

In Section “Influence of rheology and submergence”, granular slides are simulated to compare their efficiency to the reference water slide case. The rheological model used is a non-Newtonian Coulomb viscoplastic model⁵¹. This model has been first implemented in the solver interMixingFoam (OpenFOAM®) to study debris flow cases⁵² and later applied in multiPhaseInterFoam, to study waves generated by granular landslides⁵³. Computation results were successfully compared with experimental data involving subaerial and submarine granular slides. For the computations carried out in Section “Influence of rheology and submergence”, the same approach has been followed. The model and its parameterization are described in the following.

The slide material is considered to behave as a macroscopic non Newtonian phase with the following viscosity law⁵⁴:

$$\nu ={\nu }_{min}+sin(\delta )\frac{P}{| | D| | {\rho }_{b}}\times \left(1-ex{p}^{-{m}_{y}| | D| | }\right)$$

(15)

with ν_min the minimal kinematic viscosity, ∣∣D∣∣, norm of the strain-rate tensor, ρ_b slide bulk density, m_y a numerical parameter with units of seconds. This equation describes the granular flow as a non Newtonian rheological law with a yield stress equal to $P\sin \delta$. The parameter m_y is added to allow a smooth transition between yielded and unyielded areas of the flow⁵².

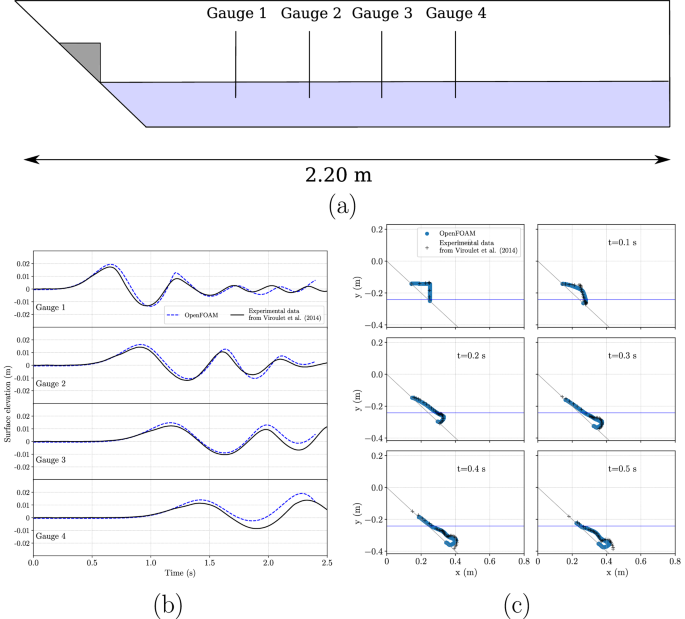
Figure 9 presents a validation of the model used in this study with respect to previous experimental data⁵⁵. Based on the parameters of the experiment, the following parameters values have been used in the simulation: ρ_b = 1575 kg ⋅ m⁻³, δ = 23°, m_y = 0.2 s, ν_min = 10⁻⁶ m² ⋅ s⁻¹. The figure shows the satisfactory match between data and simulation for the water free surface and the slide motion. The simulations presented in Section “Influence of rheology and submergence” used the same parameters as in this validation except case (d) which corresponds to the density of water.

Fig. 9: Validation of the granular model with respect to experimental data⁵⁵.

a sketch of the text case with gauges locations (respectively 0.702, 1.002, 1.302 and 1.602 m from the left water line). Comparison of surface elevation time series (b) and slide shape time evolution (c) computed and measured.