Main

Recent years have witnessed remarkable progress in the field of ab initio computation in combination with artificial intelligence1,2,3,4. For instance, neural-network force fields can facilitate ab initio molecular dynamics simulations at large length and time scales5,6,7,8,9 and have become almost indispensable in molecular dynamics simulations nowadays. There are also numerous deep learning models for studying various material properties10,11,12,13. Recently, fruitful progress has been achieved in the generalization of deep learning methods from atomic structure calculations to electronic structure calculations. For instance, machine learning offers a pathway for designing accurate density functionals14,15,16,17,18 as well as for predicting electronic properties, such as charge density and local density of states19,20,21,22,23,24,25,26,27,28,29,30,31. Deep learning methods have also been proposed to bypass the iterative solution of the Kohn–Sham equation of density functional theory (DFT) by directly predicting the converged DFT Hamiltonian under the atomic-orbital (AO) basis32,33,34,35,36,37,38,39,40,41,42,43. All these methods substantially expand the scope of theoretical and computational materials research towards unprecedented accuracy and efficiency.

When compared with other approaches, the deep learning DFT Hamiltonian method has several benefits33,34. First, eigenvalues and wavefunctions can be easily obtained from a one-shot diagonalization of the predicted sparse AO Hamiltonian matrix, from which all the DFT-based physical properties of materials can be derived. Furthermore, the method scales linearly with system size, and can be trained by DFT results for small-size structures and generalize to study unseen large-size structures with ab initio accuracy. The reason for these properties is that the AO Hamiltonian is a local and nearsighted physical quantity, which can be determined only by its nearby atomic environment44,45 (also see Supplementary Sections 1 and 2). Thus, methods of this kind can be designed to break the accuracy–efficiency dilemma in electronic structure simulations and are particularly useful for large-scale material simulations that would otherwise demand formidable computational resources. Similar to the role neural-network force fields are playing in today’s molecular dynamics simulations, it is highly possible that future electronic structure simulations will also be primarily based on deep learning models of the DFT Hamiltonian.

However, the deep learning DFT Hamiltonian method faces a critical issue related to basis functions. The Hamiltonian is a quantum mechanical operator, which can be expressed as a matrix if a particular basis set is chosen. Commonly used basis sets in DFT are plane waves (PWs) and AOs. Up to now, all neural-network methods for DFT Hamiltonians only support the AO basis, because PWs are spread over the entire space (Fig. 1a) and will destroy the aforementioned locality property. Nevertheless, PW-based methods usually offer higher accuracy than those using AOs because the PW basis can usually achieve fuller completeness and is also easier to converge. It is also favorable over the AO basis in terms of its simplicity and flexibility. In fact, the majority of DFT calculations for solids are done using the PW basis. In this context, generalizing deep learning electronic structure calculation to the PW basis would be of critical importance to future development of the field.

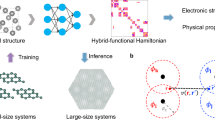
Fig. 1: Idea of the deep learning DFT Hamiltonian under the PW basis and its applications to twisted bilayer graphene.
figure 1

a, The PW basis offers high accuracy and flexibility, but deep learning electronic structure calculation methods require local basis sets. With the reconstruction method, local AO Hamiltonians are reconstructed from PW DFT output, thus deep learning methods are now able to interface with PW DFT. b, Practical workflow of the method. PW DFT results on a set of small, non-twisted structures are used to reconstruct Hamiltonians under the AO basis. A neural network trained on these reconstructed Hamiltonians can then be generalized to predict the Hamiltonians of large, twisted structures. c, Band structures of a perturbed 4 × 4 graphene supercell in the training set. Those obtained from diagonalization of the reconstructed AO Hamiltonian are compared with the PW DFT results. d, Band structure of twisted bilayer graphene at the magic twist angle θ = 1.08° with 11,164 atoms in the Moiré supercell. The bands labeled PW-NN correspond to those predicted by the neural network trained on Hamiltonians reconstructed from PW DFT results, and those labeled AO-NN correspond to the prediction of the neural network trained on AO DFT results from ref. 34. PW DFT results are from ref. 67.

Source data

Full size image

In this work, we propose a real-space reconstruction method to reconstruct AO Hamiltonians based on PW DFT results. It is orders of magnitude faster than the traditional method of directly projecting the PW Hamiltonian or wavefunctions. Moreover, we show that the AO Hamiltonians generated using our method not only can faithfully reproduce the PW electronic structure but also can be very easily learned by neural-network models. Thus, the critical problem of the deep learning DFT Hamiltonian under the PW basis is solved (Fig. 1a). The high accuracy and efficiency of our method is beneficial for the construction of more versatile and accurate deep learning electronic structure calculation methods, which not only makes them accessible to a much broader scientific community, but also greatly enhances their suitability for general applications.

Results and discussion

Theory

The PW Hamiltonian and the AO Hamiltonian are actually the same physical quantity expressed under different basis sets. In principle, once we have the PW Hamiltonian \({H}_{{\mathbf{k}}}({\mathbf{G}},{{\mathbf{G}}}^{{\prime} })=\langle {\mathbf{k}}+{\mathbf{G}}| \hat{H}| {\mathbf{k}}+{{\mathbf{G}}}^{{\prime} }\rangle\), we can always obtain the corresponding AO Hamiltonian \({H}_{i\alpha ,\;j\beta }=\langle {\phi }_{i\alpha }| \hat{H}| {\phi }_{j\beta }\rangle\) by a change of basis, which can then be flexibly learned by current neural networks for AO Hamiltonians. However, there are several different ways of doing this. In Supplementary Section 3, we present a detailed review of the possible methods from literature as well as previous attempts at deep learning electronic structure calculation under the PW basis. Here we will briefly discuss three methods to convert PW Hamiltonians to the AO basis, and more details can be found in Methods.

We would naturally think of using the projection method, which is widely used to bridge the gap between PWs and AOs. The projection method was initially developed to evaluate the quality of the AO basis set46,47,48 and has been adapted for various purposes, such as to analyze charge distribution and to interpret chemical bonding49,50,51,52,53,54,55. The projection method can also be modified to directly convert a Hamiltonian from the PW basis to the AO basis:

$${H}_{i\alpha ,\;j\beta }=\sum _{{\mathbf{k}}{\mathbf{G}}{{\mathbf{G}}}^{{\prime} }}\langle {\phi }_{i\alpha }| {\mathbf{k}}+{\mathbf{G}}\rangle {H}_{{\mathbf{k}}}({\mathbf{G}},{{\mathbf{G}}}^{{\prime} })\langle {\mathbf{k}}+{{\mathbf{G}}}^{{\prime} }| {\phi }_{j\beta }\rangle .$$
(1)

Here the PW basis is normalized in the Born–von Kármán (BvK) supercell: \(\langle {\mathbf{r}}| {\mathbf{k}}+{\mathbf{G}}\rangle =\exp (i({\mathbf{k}}+{\mathbf{G}})\cdot {\mathbf{r}})/\sqrt{N\varOmega }\), where k is a wavevector in the first Brillouin zone, G is a reciprocal lattice vector, N is the number of primitive unit cells forming the BvK supercell and Ω is the volume of the primitive unit cell. The AO basis function |ϕiα〉 is centered at atom i. There could be multiple basis functions (labeled by n) sharing the same angular momentum quantum number l and magnetic quantum number m. The index α is an abbreviation for n, l, m. Equation (1) will be referred to as the Hk(G, G′) projection method in this Brief Communication.

If the eigenvalues εnk and wavefunctions |ψnk〉 of the PW Hamiltonian are obtained, equation (1) can be further written as

$${H}_{i\alpha ,\;j\beta }=\sum _{n{\mathbf{k}}}\langle {\phi }_{i\alpha }| {\psi }_{n{\mathbf{k}}}\rangle {\varepsilon }_{n{\mathbf{k}}}\langle {\psi }_{n{\mathbf{k}}}| {\phi }_{j\beta }\rangle ,$$
(2)

where

$$\langle {\phi }_{i\alpha }| {\psi }_{n{\mathbf{k}}}\rangle =\sum _{{\mathbf{G}}}\langle {\phi }_{i\alpha }| {\mathbf{k}}+{\mathbf{G}}\rangle \langle {\mathbf{k}}+{\mathbf{G}}| {\psi }_{n{\mathbf{k}}}\rangle .$$
(3)

In this Brief Communication equation (2) will be referred to as the ψnk(G) projection method.

Although equations (1) and (2) offer straightforward ways of converting PW Hamiltonians to the AO basis, they suffer from low computational efficiency, and the reasons are as follows. Equation (1) involves two multiplications and summations over G, and the number of G vectors is usually very large. Equation (2) requires a large number of Bloch wavefunctions to converge. Moreover, they all scale cubically with respect to the number of atoms in the system (Methods), which limits their scope of applications.

In fact, we can leverage locality in real space to considerably speed up the calculation. The Hamiltonian \(H({\mathbf{r}},{{\mathbf{r}}}^{{\prime} })=\langle {\mathbf{r}}| \hat{H}| {{\mathbf{r}}}^{{\prime} }\rangle\) in real space under atomic units is56,57

$$\begin{array}{l}H({\mathbf{r}},{{\mathbf{r}}}^{{\prime} })=-\displaystyle\frac{1}{2}{\nabla }^{2}\delta ({\mathbf{r}}-{{\mathbf{r}}}^{{\prime} })+[{V}_{{\rm{Har}}}({\mathbf{r}})+{V}_{{\rm{xc}}}({\mathbf{r}})+{V}_{{\rm{loc}}}({\mathbf{r}})]\delta ({\mathbf{r}}-{{\mathbf{r}}}^{{\prime} })\\\qquad\qquad\ \;+{V}_{{\rm{nloc}}}({\mathbf{r}},{{\mathbf{r}}}^{{\prime} }),\end{array}$$
(4)

where the various terms correspond to the kinetic energy, the Hartree potential, the exchange–correlation potential and the local and non-local parts of the pseudopotential, respectively. In this Brief Communication we are only considering semilocal functionals for exchange and correlation. The three terms in the square bracket will be referred to as the total effective local potential: Veff(r) ≡ VHar(r) + Vxc(r) + Vloc(r), which is periodic over unit cells. Usually, PW DFT programs directly store Veff(r) or its Fourier transform Veff(G) in memory, and \({V}_{{\rm{nloc}}}({\mathbf{r}},{{\mathbf{r}}}^{{\prime} })=\langle {\mathbf{r}}| {\hat{V}}_{{\rm{nloc}}}| {{\mathbf{r}}}^{{\prime} }\rangle\) can be read from pseudopotential files. Once we have H(r, r′), we can calculate the AO Hamiltonian directly in real space as follows:

$${H}_{i\alpha ,\;j\beta }=\langle {\phi }_{i\alpha }| {-}\frac{1}{2}{\nabla }^{2}| {\phi }_{j\beta }\rangle +\int{{\rm{d}}}^{3}r\,{\phi }_{i\alpha }^{* }({\mathbf{r}}){V}_{{\rm{eff}}}({\mathbf{r}}){\phi }_{j\beta }({\mathbf{r}})+\langle {\phi }_{i\alpha }| {\hat{V}}_{{\rm{nloc}}}| {\phi }_{j\beta }\rangle ,$$
(5)

which will be referred to as the real-space reconstruction method in this Brief Communication. The first and last terms can be very efficiently calculated using two-center integral techniques58 (also see Methods). The most time-consuming part is the evaluation of the second term in the equation, which is integrated directly on an evenly spaced real-space grid. Since the AOs are local in real space, the integration region can be chosen such that both of the orbitals ϕiα(r) and ϕjβ(r) are non-zero. The number of grid points involved in the integration thus does not depend on the overall system size. Therefore, the time required to evaluate the above formula is proportional to the number of non-zero AO Hamiltonian matrix elements, which scales linearly with the number of atoms in the system. Although they are theoretically equivalent and will yield the same results when converged, the proposed real-space reconstruction method is much more efficient than the first two projection-based methods.

It is worth noticing that none of the three methods described in this Brief Communication depend on the specific form of the AO basis functions. They only need to be separable into radial and angular parts, and the radial function needs to go to zero after a certain cutoff radius. This degree of freedom allows us to systematically improve the quality of the reconstructed AO Hamiltonian by customizing the AO basis using modern techniques such as a numerical AO basis59,60,61,62. The most important design principle of the AO basis is that it must be compatible with the pseudopotentials used in the PW calculation, otherwise it is difficult for the reconstructed Hamiltonian to give an accurate description of the band structure.

Application to twisted bilayer graphene

The real-space reconstruction method provides a very efficient way to calculate the Hamiltonian under an AO basis set from PW DFT results. The resulting AO Hamiltonian not only can accurately reproduce the PW electronic structure, but also can be learned by neural networks, thus enabling deep learning electronic structure calculations under the PW basis. The effectiveness of this workflow depends on two factors: the quality of the reconstructed AO Hamiltonian, and the compatibility of the reconstructed Hamiltonian with deep learning methods. In our tests, the first is measured by comparison of the band structures of the AO Hamiltonian with those from direct PW DFT calculations. The second can be evaluated through checking the quality of the band structure predicted by the neural networks that learn from reconstructed AO Hamiltonians. In all calculations reported in this Brief Communication, PW DFT calculations are performed with the Quantum ESPRESSO package63 using norm-conserving pseudopotentials64. The results of these PW calculations are used to reconstruct AO Hamiltonians, where the AO basis is the numerical AOs generated using the SIESTA code59 for the same set of pseudopotentials. Details of the convergence tests we have performed on the effect of the sizes of AO basis sets can be found in Supplementary Section 4.

The most remarkable capability of the deep learning DFT Hamiltonian method is that neural-network models can be trained on small structures and generalized to predict the Hamiltonians of much larger structures. In the study of bilayer graphene, the training set consists of 300 4 × 4 bilayer graphene supercells with different stackings and random perturbation of each atom site. After we train the neural-network model on the reconstructed AO Hamiltonians from PW DFT results (Fig. 1b), we can use the model to systematically study Moiré twisted superstructures with arbitrary twist angle. We first benchmark the reconstructed Hamiltonian on one of the structures in the training set by plotting its band structure alongside those calculated using PWs. As shown in Fig. 1c, the two band structures agree very well. After training the neural-network model, we use it to study the well-known ‘magic-angle’ twisted bilayer graphene at θ = 1.08° with 11,164 atoms in a Moiré supercell. This system is of substantial interest to researchers because of the discovery of a series of correlated phenomena65,66, but is particularly challenging for electronic structure calculations because of its large system size and large-scale corrugation patterns. However, with the deep learning DFT Hamiltonian method available, the computational cost can be greatly reduced34 (also see Supplementary Section 5). As illustrated in Fig. 1d, the neural network trained on the reconstructed AO Hamiltonian manages to give very accurate predictions when compared with the PW DFT benchmark67, with an error of only a few millielectronvolts. Moreover, when the neural network is trained on reconstructed AO Hamiltonians from PW DFT output, the predicted band structure (PW-NN in Fig. 1d) has better agreement with the PW DFT results by Lucignano et al.67 compared to the case where the neural network is trained on Hamiltonians calculated by AO DFT34 (AO-NN in Fig. 1d). This shows that the deep learning Hamiltonian interfaced to PW DFT can indeed give results that have higher accuracy. This high accuracy, when combined with the flexibility and wide applicability of the PW method, will greatly enhance the capability of deep learning ab initio calculations and will be highly beneficial for future research.

Application to bilayer MoS2

The three previously discussed methods to obtain the AO Hamiltonian from PW DFT results are equivalent when converged, but the real-space reconstruction method (equation (5)) is the most efficient. Here we compare these three methods in the study of the bilayer MoS2 system (Fig. 2a). First we tested the reconstruction method on the AB-stacked bilayer unit cell consisting of six atoms, and the band structures obtained from the reconstructed AO Hamiltonian agree well with PW DFT results (Fig. 2b). We then plot the band structures given by the three different methods, and the results are shown in Fig. 2c. They are almost the same, except that the band structure given by the ψnk(G) projection method is slightly different from the other two because we are only using a finite number of bands in evaluation of equation (2).

Fig. 2: Application of the deep learning DFT Hamiltonian under the PW basis to study twisted bilayer MoS2.
figure 2

a, Schematic illustration of bilayer MoS2 with AB stacking. b, Band structures of the AB-stacked bilayer MoS2 unit cell. Those obtained from diagonalization of the reconstructed AO Hamiltonian are compared with PW DFT results. c, The band structures obtained from the AO Hamiltonians constructed using three conversion methods are compared with each other, and the results are almost the same. d, Comparison of the computation times among different conversion methods when studying bilayer MoS2 structures including varying numbers of atoms per supercell. The computation times of PW self-consistent field iterations until convergence (PW SCF) are also displayed as a reference. The H(r) reconstruction method scales linearly with system size and is much faster than the other two methods. e, Band structure of the fully relaxed θ = 6.01° twisted bilayer MoS2 with 546 atoms in the Moiré supercell. The neural-network-predicted band structure lies almost exactly on top of that diagonalized from the reconstructed Hamiltonian.

Source data

Full size image

We further compared the computation times of the three methods. The systems we have studied here are bilayer MoS2 structures with different numbers of atoms (unit cell with 6 atoms, 3 × 3 supercell with 54 atoms and Moiré twisted bilayer MoS2 at θ = 13.17° and 9.43° with 114 and 222 atoms). The CPU times are shown in Fig. 2d along with the time for PW self-consistent field calculation. Note that the time of diagonalization for PW wavefunctions for the ψnk(G) projection method is also included in the total CPU time for that method. As expected, the two projection-based methods show roughly cubic scaling. They are even more time consuming than the full self-consistent field calculation. Conversely, thanks to the locality of the AO basis, the real-space reconstruction method achieves linear scaling and can be several orders of magnitude faster than the projection methods. This acceleration will become more prominent when we investigate large-size materials. Therefore, our method will be essential when we want to construct large-scale training sets including various kinds of material and structures of different sizes to train accurate and versatile neural-network models, whereas the projection methods would not be affordable for this purpose in terms of computational cost.

Now, we follow the same workflow as illustrated in Fig. 1b and test the performance of the neural network on bilayer MoS2, which is a more challenging material system than bilayer graphene. PW DFT calculations are performed on 256 non-twisted 3 × 3 supercells of bilayer MoS2 with different stacking configurations and random perturbations of each atom site, and the neural-network model is trained on the reconstructed AO Hamiltonians. We test the generalizability of the neural network to a fully relaxed θ = 6.01° twisted bilayer MoS2 with 546 atoms in the Moiré supercell. Since the neural network is trained on reconstructed AO Hamiltonians, the predicted bands are compared with the bands of the AO Hamiltonian, and results are shown in Fig. 2e. The absolute energy differences are as small as 0.30 and 2.22 meV for the highest valence band and the lowest conduction band, respectively, where errors are averaged along the high-symmetry k path Γ–K–M–Γ. This is remarkable considering that only small non-twisted structures are included in the training set.

Discussion

Our approach to reconstruct an AO Hamiltonian from PW DFT results facilitates deep learning electronic structure calculations based on PW DFT results and combines the advantages of the PW method and the deep learning approaches. One direct impact of our work is that it makes the deep learning electronic structure method applicable for those who are already familiar with the PW method but have less experience in AO DFT. Another promising future application of our method is to build universal deep learning models that can handle diverse families of materials and give accurate predictions of their electronic structure. The model can take advantage of the numerous materials databases that have already been set up. In fact, most of the materials databases of solids are built using the PW method, and they are thus made accessible through our reconstruction method. Moreover, the applicable scope of our method is not limited to PW DFT only. The spirit of the change of basis can also be generalized to apply to any kind of implementation of Kohn–Sham DFT and interface it with deep learning approaches. Further, the PW methods are even more widely used to implement advanced methods beyond the DFT level, such as the density functional perturbation theory to study electron–phonon interactions68, the many-body perturbation theory (such as GW and GW-BSE methods) and time-dependent DFT for excited-state phenomena, and so on. Now, with our method to interface deep learning with PW methods, important generalizations of the deep learning approach to these advanced methods will become feasible in the foreseeable future.

Methods

Details of different ways to convert the PW Hamiltonian to the AO basis

The DFT Hamiltonian operator we are considering in this Brief Communication is given as equation (4) in the main text. Here, we will explain the non-local part of the pseudopotential \({V}_{{\rm{nloc}}}({\mathbf{r}},{{\mathbf{r}}}^{{\prime} })=\langle {\mathbf{r}}| {\hat{V}}_{{\rm{nloc}}}| {{\mathbf{r}}}^{{\prime} }\rangle\) in detail. It is constructed in a separable form known as the Kleinman and Bylander projectors69:

$${\hat{V}}_{{\rm{nloc}}}=\sum _{i\alpha \beta }\left\vert {p}_{i\alpha }\right\rangle {D}_{i\alpha \beta }\left\langle {p}_{i\beta }\right\vert ,$$
(6)

where the summation over atom sites i is carried out over all atoms in the whole BvK supercell, and this will apply to the remainder of this section unless otherwise stated. The projector function |piα〉 is centered at atom i and can be separated into radial and angular parts:

$$\langle {\mathbf{r}}| {p}_{i\alpha }\rangle ={R}_{inl}^{{\rm{proj}}}(| {{\mathbf{r}}}_{i}| ){Y}_{lm}({\hat{{\mathbf{r}}}}_{i}),$$
(7)

where ri ≡ r − Ri and Ri is the position of the ith atom. There could be multiple projector functions (labeled by n) sharing the same l and m. The matrix Diαβ is non-zero only for α = β and is not system dependent (that is, unchanged in different atomic environments) if we only focus on norm-conserving pseudopotentials70,71.

Here, we would like to discuss the locality of the Hamiltonian. The Hamiltonian in equation (4) is non-local (that is, it is non-zero when |r − r′| ≠ 0) because of the presence of the non-local projectors of the pseudopotential. However, the pseudopotential projector functions |piα〉 are, by construction, highly localized around each nucleus. Therefore, we would expect that the non-local part Vnloc(r, r′) is non-zero only within the core region. The nearsightedness of the Hamiltonian is closely related to its locality but is a different concept, which is discussed in Supplementary Section 2.

In practical DFT calculations, two common choices of basis functions for expanding the Hamiltonians and wavefunctions are PWs and AOs. In the remainder of this section, we will first briefly review the forms of the Hamiltonian matrix under both kinds of basis set. Then, we will discuss in detail the three methods of transforming a PW Hamiltonian to the AO basis mentioned in the main text. Finally, we will discuss an extension of our method to the projector augmented-wave (PAW) formalism72,73. Details of the numerical techniques used to speed up the calculations are deferred to the next section.

PW Hamiltonian

The PW basis we are using here is normalized in the BvK supercell:

$$\langle {\mathbf{r}}| {\mathbf{k}}+{\mathbf{G}}\rangle =\frac{1}{\sqrt{N\varOmega }}\exp (i({\mathbf{k}}+{\mathbf{G}})\cdot {\mathbf{r}}).$$
(8)

Under the PW representation, the Kohn–Sham equation is written as

$$\sum _{{{\mathbf{G}}}^{{\prime} }}({H}_{{\mathbf{k}}}({\mathbf{G}},{{\mathbf{G}}}^{{\prime} })-{\varepsilon }_{n{\mathbf{k}}}{\delta }_{{\mathbf{G}}{{\mathbf{G}}}^{{\prime} }}){\psi }_{n{\mathbf{k}}}({{\mathbf{G}}}^{{\prime} })=0,$$
(9)

where εnk is the Kohn–Sham eigenvalue, |ψnk〉 is the corresponding eigenstate, \({H}_{{\mathbf{k}}}({\mathbf{G}},{{\mathbf{G}}}^{{\prime} })=\langle {\mathbf{k}}+{\mathbf{G}}| \hat{H}| {\mathbf{k}}+{{\mathbf{G}}}^{{\prime} }\rangle\) is the PW Hamiltonian matrix and ψnk(G) = 〈k + G∣ψnk〉 is the wavefunction.

The Hamiltonian can be written under the PW basis56 as

$${H}_{{\mathbf{k}}}({\mathbf{G}},{{\mathbf{G}}}^{{\prime} })=\frac{1}{2}| {\mathbf{k}}+{\mathbf{G}}{| }^{2}{\delta }_{{\mathbf{G}}{{\mathbf{G}}}^{{\prime} }}+{V}_{{\rm{eff}}}({\mathbf{G}}-{{\mathbf{G}}}^{{\prime} })+{V}_{{\rm{nloc}},{\mathbf{k}}}({\mathbf{G}},{{\mathbf{G}}}^{{\prime} }),$$
(10)

where

$${V}_{{\rm{eff}}}({\mathbf{G}})=\frac{1}{\varOmega }{\int}_{\varOmega }{{\rm{d}}}^{3}r\,{V}_{{\rm{eff}}}({\mathbf{r}})\exp (-i{\mathbf{G}}\cdot {\mathbf{r}}),$$
(11)

and the integral is carried out within the primitive unit cell. Because Veff(r) is periodic over unit cells, it is convenient to discretize it on evenly spaced grid points in real space, and the Fourier transform can be efficiently calculated using the fast Fourier transform.

The last term in equation (10) is

$${V}_{{\rm{nloc}},{\mathbf{k}}}({\mathbf{G}},{{\mathbf{G}}}^{{\prime} })=\sum _{i\alpha \beta }\langle {\mathbf{k}}+{\mathbf{G}}| {p}_{i\alpha }\rangle {D}_{i\alpha \beta }\langle\; {p}_{i\beta }| {\mathbf{k}}+{{\mathbf{G}}}^{{\prime} }\rangle ,$$
(12)

where the Fourier transform 〈k + G∣piα〉 can be calculated efficiently using an algorithm described in the next subsection.

Finally, we would like to point out that the total effective local potential is the only term in equation (10) that is system dependent and needs to be obtained from self-consistent field iterations. The kinetic energy term is trivial, and the non-local pseudopotential term can be built from data read from the pseudopotential file. In practice, most of the PW DFT codes store the quantity Veff(G) or Veff(r) instead of the full Hamiltonian matrix, which substantially saves memory.

AO Hamiltonian

The AO basis functions are centered on atomic sites and are separated into radial and angular parts, similar to the projector function defined in equation (7):

$$\langle {\mathbf{r}}| {\phi }_{i\alpha }\rangle ={\phi }_{i\alpha }({\mathbf{r}})={R}_{inl}(| {{\mathbf{r}}}_{i}| ){Y}_{lm}({\hat{{\mathbf{r}}}}_{i}),$$
(13)

where the radial function Rinl(r) can, in principle, take any arbitrary form and still be compatible with our reconstruction method, which will be described in a later section. It only needs to be local, which means that it goes to zero after a certain cutoff radius. This degree of freedom allows us to systematically improve the quality of the reconstructed AO Hamiltonian by customizing the AO basis using modern techniques such as a numerical AO basis59,60,61,62. The most important design principle of the AO basis is that it must be compatible with the pseudopotential used in the PW calculation, otherwise it is difficult for the reconstructed Hamiltonian to give an accurate description of the band structure.

The Kohn–Sham equation under the AO basis is written as

$$\sum _{j\beta }({H}_{i\alpha ,\;j\beta }-{\varepsilon }_{n{\mathbf{k}}}{S}_{i\alpha ,\;j\beta }){\psi }_{n{\mathbf{k}},\;j\beta }=0,$$
(14)

where \({H}_{i\alpha ,\;j\beta }=\langle {\phi }_{i\alpha }| \hat{H}| {\phi }_{j\beta }\rangle\) is the Hamiltonian matrix, and Siα, jβ = 〈ϕiα∣ϕjβ〉 is the overlap matrix. Notice that we have to include the overlap matrix here because the AO basis functions are typically not orthonormal.

Reconstruction of AO Hamiltonian

In the main text, two projection-based methods are discussed: the Hk(G, G′) projection method (equation (1)) and the ψnk(G) projection method (equation (2)). Both methods scale cubically with system size, and here we will discuss the scaling of these two methods in detail. Equation (1) involves summations over two G vectors, and the summations are performed over all AO pairs (iα, jβ). The number of G vectors is usually very large, and is proportional to the system size. The number of orbital pairs (iα, jβ) within a certain cutoff radius is also proportional to the system size. Thus the projection has a scaling of O(N3), where N is the number of atoms in the unit cell. According to our tests, the typical calculation time for equation (1) is sometimes longer than that for a full self-consistent DFT calculation. The second method, using equation (2), involves the evaluation of equation (3), which also scales as N3, because number of AOs, number of G vectors and number of wavefunctions are all proportional to system size. Because equation (3) only involves one summation over G, this method is usually more efficient than the first one using equation (1). However, to converge the calculation of equation (2), we have to choose a relatively large n, which means we have to diagonalize the PW Hamiltonian for a large number of bands, including high-energy unoccupied bands that are typically not calculated by standard PW codes. Therefore, neither of the methods above is satisfactory in terms of efficiency.

In the main text, an efficient method is proposed to calculate the AO Hamiltonian directly in real space as equation (5). It can also be written as

$$\begin{array}{l}{H}_{i\alpha ,\;j\beta }=\langle {\phi }_{i\alpha }| {-}\displaystyle\frac{1}{2}{\nabla }^{2}| {\phi }_{j\beta }\rangle +\int{{\rm{d}}}^{3}r\,{\phi }_{i\alpha }^{* }({\mathbf{r}}){V}_{{\rm{eff}}}({\mathbf{r}}){\phi }_{j\beta }({\mathbf{r}})\\\qquad\qquad+\sum _{a\gamma \delta }\langle {\phi }_{i\alpha }| {p}_{a\gamma }\rangle {D}_{a\gamma \delta }\langle {p}_{a\delta }| {\phi }_{j\beta }\rangle ,\end{array}$$
(15)

where the terms 〈ϕiα|−½∇2|ϕjβ〉 and 〈ϕiα∣paγ〉 can be calculated very efficiently using the two-center integral technique58, which will be described in the next subsection. The second term in the equation can be calculated directly on an evenly spaced real-space grid, and the integration region can be chosen such that both of the orbitals ϕiα(r) and ϕjβ(r) are non-zero in the integration region. The number of grid points involved in the integration thus does not depend on the overall system size. Therefore, the time required to evaluate the above formula scales linearly with the system size. Here, we would like to note that sometimes we can not directly obtain Veff(r) from a PW DFT code, but have to convert Veff(G) to real space using the inverse of equation (11). This involves the fast Fourier transform, which scales as O(N log N), but we only have to do it once, and the pre-factor is so small that the time is negligible when compared with those of other parts of the real-space reconstruction method, at least up to a few thousand atoms.

As pointed out before, Veff(r) or Veff(G) is the only term in the Hamiltonian that requires self-consistent field calculations. The quantities ∣paγ〉 and Daγδ can be directly read from pseudopotential files. Therefore, for any material structure we are interested in, we only need to calculate Veff(r) with the PW DFT codes to use equation (5) to construct the AO Hamiltonian. Obtaining this quantity is also convenient because most PW DFT codes directly store Veff(r) or Veff(G) in memory.

Extension to the PAW method

Under the PAW formalism72,73, the all-electron wavefunction |Ψ〉 is connected to the smooth pseudo-wavefunction \(\left\vert \tilde{\Psi }\right\rangle\) by a linear transformation: \(\left\vert \Psi \right\rangle ={\mathcal{T}}\left\vert \tilde{\Psi }\right\rangle\). Since the wavefunctions are changed by a linear transformation, any operator \(\hat{A}\) in the PAW formalism is also changed according to the rule \(\tilde{A}={{\mathcal{T}}}^{\dagger }\hat{A}{\mathcal{T}}\). The Kohn–Sham equation still takes the same form:

$$(\tilde{H}-{\varepsilon }_{n{\mathbf{k}}}\tilde{S})\left\vert {\tilde{\psi }}_{n{\mathbf{k}}}\right\rangle =0,$$
(16)

where the Hamiltonian operator is

$$\tilde{H}({\mathbf{r}},{{\mathbf{r}}}^{{\prime} })=\left(-\frac{1}{2}{\nabla }^{2}+{\tilde{V}}_{{\rm{eff}}}({\mathbf{r}})\right)\delta ({\mathbf{r}}-{{\mathbf{r}}}^{{\prime} })+{\tilde{V}}_{{\rm{nloc}}}({\mathbf{r}},{{\mathbf{r}}}^{{\prime} }),$$
(17)

with

$${\tilde{V}}_{{\rm{nloc}}}=\sum _{i\alpha \beta }\left\vert {\tilde{p}}_{i\alpha }\right\rangle {\tilde{D}}_{i\alpha \beta }\left\langle {\tilde{p}}_{i\beta }\right\vert ,$$
(18)

and the overlap operator is

$$\tilde{S}=1+\sum _{i\alpha \beta }\left\vert {\tilde{p}}_{i\alpha }\right\rangle {\tilde{Q}}_{i\alpha \beta }\left\langle {\tilde{p}}_{i\beta }\right\vert .$$
(19)

Comparing equations (4) and (6) with equations (17) and (18), we can see that the PAW Hamiltonian takes exactly the same form as in the case where the norm-conserving pseudopotential is used, so equation (15) can still be used. The process of evaluating the terms in equation (17) will be different for the DFT codes, but this is beyond the scope of this Brief Communication. The only thing we have to be careful of here is that the matrix \({\tilde{D}}_{i\alpha \beta }\) is now system dependent and needs to be obtained self-consistently. Thus, apart from obtaining \({\tilde{V}}_{{\rm{eff}}}({\mathbf{r}})\), we also need the matrix \({\tilde{D}}_{i\alpha \beta }\) from the DFT code when we convert the PW Hamiltonian to the AO basis.

Numerical techniques

Fourier transform of orbitals

Here we consider the Fourier transform of orbitals that can be separated into radial and angular parts: \({\phi }_{i\alpha }({\mathbf{r}})={R}_{inl}(| {\mathbf{r}}| ){Y}_{lm}(\hat{{\mathbf{r}}})\). This will be useful when computing the Fourier transform of projector functions 〈k + G∣piα〉 or AOs 〈k + G∣ϕiα〉. Using the identity

$${\mathrm{e}}^{i{\mathbf{k}}\cdot {\mathbf{r}}}=4\uppi \mathop{\sum }\limits_{l=0}^{\infty }\mathop{\sum }\limits_{m=-l}^{l}{i}^{l}{j}_{l}(kr){Y}_{lm}(\hat{{\mathbf{k}}}){Y}_{lm}^{\,* }(\hat{{\mathbf{r}}}),$$
(20)

where \(r\equiv | {\mathbf{r}}| ,k\equiv | {\mathbf{k}}| ,\hat{\mathbf{r}}\equiv {\mathbf{r}}/r,\hat{\mathbf{k}}\equiv {\mathbf{k}}/k\) and jl is the spherical Bessel function of order l, we can rewrite the Fourier transform as

$${\phi }_{i\alpha }({\mathbf{k}})\equiv \int{{\rm{d}}}^{3}r\,{\mathrm{e}}^{-i{\mathbf{k}}\cdot {\mathbf{r}}}{\phi }_{i\alpha }({\mathbf{r}})={(-i)}^{l}{R}_{inl}(| {\mathbf{k}}| ){Y}_{lm}(\hat{{\mathbf{k}}}),$$
(21)

where the radial part can be obtained using a spherical Bessel transformation

$${R}_{inl}(k)=4\uppi \mathop{\int}\nolimits_{0}^{\infty }{\rm{d}}r\,{r}^{2}{j}_{l}(kr){R}_{inl}(r).$$
(22)

In practice, Rinl(k) can be computed on a radial grid up to certain energy cutoff. Then all three-dimensional Fourier transforms of the orbital can be calculated easily and very efficiently using spline interpolation. If the orbital is not centered at the origin, we only need to add an additional phase factor.

It is also worth mentioning the inverse transformation here:

$${R}_{inl}(r)=\frac{1}{2{\uppi }^{2}}\mathop{\int}\nolimits_{0}^{\infty }{\rm{d}}k\,{k}^{2}{j}_{l}(kr){R}_{inl}(k).$$
(23)

Two-center integrals

Integrals of the product of two orbitals centered at two different positions are used frequently in AO calculations. Here we discuss a very efficient way to calculate this kind of integral, following Sankey and Niklewski58. Consider two orbitals ϕiα(r) and ϕjβ(r) with α = (n1l1m1), β = (n2l2m2); their overlap integral is defined as

$$S({\mathbf{R}})\equiv \int{{\rm{d}}}^{3}r\,{\phi }_{i\alpha }^{* }({\mathbf{r}}){\phi }_{j\beta }({\mathbf{r}}-{\mathbf{R}}).$$
(24)

This integral in real space can be converted to the integral in Fourier space:

$$S({\mathbf{R}})=\int\frac{{{\rm{d}}}^{3}k}{{(2\uppi )}^{3}}\,{\phi }_{i\alpha }^{* }({\mathbf{k}}){\phi }_{j\beta }({\mathbf{k}}){\mathrm{e}}^{-i{\mathbf{k}}\cdot {\mathbf{R}}}.$$
(25)

Plugging in equations (20) and (21), we have

$$S({\mathbf{R}})=\mathop{\sum }\limits_{l=0}^{2{l}_{\max }}\mathop{\sum }\limits_{m=-l}^{l}{G}_{{l}_{1}{m}_{1},{l}_{2}{m}_{2},lm}{S}_{l}(| {\mathbf{R}}| ){Y}_{lm}(\hat{{\mathbf{R}}}),$$
(26)

with lmax = max{l1, l2}, Gaunt coefficients \({G}_{{l}_{1}{m}_{1},{l}_{2}{m}_{2},lm}\) defined as

$${G}_{{l}_{1}{m}_{1},{l}_{2}{m}_{2},lm}=\mathop{\int}\nolimits_{0}^{\uppi }\sin \theta \,{\rm{d}}\theta \mathop{\int}\nolimits_{0}^{2\uppi }{\rm{d}}\varphi \,{Y}_{{l}_{1}{m}_{1}}^{* }(\theta ,\varphi ){Y}_{{l}_{2}{m}_{2}}(\theta ,\varphi ){Y}_{lm}^{\,* }(\theta ,\varphi ),$$
(27)

and

$${S}_{l}(R)=\frac{{i}^{{l}_{1}-{l}_{2}-l}}{2{\uppi }^{2}}\mathop{\int}\nolimits_{0}^{\infty }{\rm{d}}k\,{k}^{2}{j}_{l}(kR){R}_{i{n}_{1}{l}_{1}}^{* }(k){R}_{j{n}_{2}{l}_{2}}(k).$$
(28)

In our calculations, Sl(R) is computed on a radial grid, so that all overlap integrals S(R) can be computed very efficiently using spline interpolation.

The above technique can be extended to calculate kinetic matrix elements

$$T({\mathbf{R}})\equiv \int{{\rm{d}}}^{3}r\,{\phi }_{i\alpha }^{* }({\mathbf{r}})(-\frac{1}{2}{\nabla }^{2}){\phi }_{j\beta }({\mathbf{r}}-{\mathbf{R}}),$$
(29)

with slight modifications to equation (28):

$${T}_{l}(R)=\frac{{i}^{{l}_{1}-{l}_{2}-l}}{4{\uppi }^{2}}\mathop{\int}\nolimits_{0}^{\infty }{\rm{d}}k\,{k}^{\,4}{j}_{l}(kR){R}_{i{n}_{1}{l}_{1}}^{* }(k){R}_{j{n}_{2}{l}_{2}}(k).$$
(30)

Preparation of datasets

Bilayer graphene dataset

The structures in the training set are the same as those used in ref. 33. There are 300 bilayer graphene 4 × 4 supercells with different interlayer stackings and random perturbations to atomic positions. The perturbations are uniformly distributed within ±0.1 Å along three Cartesian directions. The interlayer distance follows a normal distribution with mean 3.41 Å and s.d. 0.05 Å. The thickness of the unit cell along the non-periodic direction is chosen to be 20 Å. The PW DFT calculations are performed using the Perdew–Burke–Ernzerhof functional74 with the Quantum ESPRESSO package63 and norm-conserving Vanderbilt pseudopotential64. Energy cutoffs are 80 Ry for the wavefunctions and 320 Ry for the charge density. A 3 × 3 grid is used for the k sampling of the supercell. The double-zeta plus polarization (DZP) basis for the carbon atom with nodes is generated using SIESTA59, which includes two orbitals in the 2s shell, two orbitals in the 2p shell and one orbital in the 3d shell polarized from the 2p orbital.

Bilayer MoS2

PW DFT simulations are all performed with the Quantum ESPRESSO package using the Perdew–Burke–Ernzerhof functional with wavefunction cutoff 60 Ry and charge density cutoff 240 Ry. The unit cell is calculated using a 6 × 6 k sampling, and the mesh sizes are reduced for the supercells corresponding to the supercell sizes. The thickness of the unit cell along the non-periodic direction is chosen to be 20 Å. There are 256 3 × 3 supercells in the training set with different interlayer stackings and random perturbations to atomic positions. The perturbations are uniformly distributed within ±0.1 Å along three Cartesian directions. The average distance between the two Mo layers is 6.49 Å and the s.d. is 0.05 Å. The twisted structures are relaxed using the Perdew–Burke–Ernzerhof functional plus van der Waals interaction energy corrected using the DFT-D3 method75. The AOs are the standard split-norm DZP basis for Mo and S atoms generated by SIESTA. The orbitals for the Mo atom include one orbital in the 4s shell, one orbital in the 4p shell, two orbitals in the 4d shell, two orbitals in the 5s shell and one orbital in the 5p shell polarized from the 5s shell. The orbitals for the S atom include two orbitals in the 3s shell, two orbitals in the 3p shell and one orbital in the 3d shell polarized from the 3p orbital. One additional diffusion orbital in the 4s shell with cutoff distance 8.0 a.u. is added to the S atom to capture the interlayer hybridization.

Reconstruction from PW Hamiltonian to AO basis

The cutoffs for equation (5) of the two-center integrals are taken to be the same as the wavefunction cutoff used in the PW calculations. The sizes of the real-space grid for the real-space integrals in equation (5) are also taken to be the same as the size of the fast Fourier transform grid in the PW calculations. These are the same for all calculations in this Brief Communication.