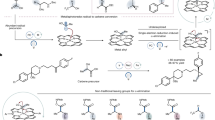
Abstract
Oxidative addition most commonly involves the addition of a substrate to a metal centre. This reaction is fundamental across synthetic chemistry and underpins numerous catalytic methods. In the textbook description of oxidative addition reactions, a net increase in the formal oxidation state of the metal occurs with simultaneous bond breaking at the substrate. The majority of known oxidative addition reactions, however, involve substrates bearing relatively electronegative elements (for example, hydrogen, carbon, nitrogen, oxygen and halogens) and there has been little discussion of how addition processes may fundamentally change if substrates were constructed from more electropositive elements. Here we show that the zinc–zinc bonded complex, Cp*ZnZnCp* (Cp* = pentamethylcyclopentadienyl), which is isoelectronic with dihydrogen, undergoes facile addition to the metal (or semi-metal) centres of a series of main group carbene analogues based on silicon, aluminium, gallium or indium. Reactions proceed with complete breaking of the zinc–zinc bond and an increase in the coordination number of the central metal from two to four. Our analysis suggests that these addition processes are not oxidative, but rather there is likely a continuum of redox outcomes spanning oxidative, redox neutral and reductive. The addition of Cp*ZnZnCp* to silicon(II) provides the most compelling case for a prototypical reductive addition process.

Similar content being viewed by others
Main
Oxidative addition1 and its microscopic reverse, reductive elimination, are fundamental steps in chemistry2,3. These steps are known to occur at discrete molecular complexes and at the surface of heterogeneous materials. Numerous value-added chemicals are created in catalytic processes that rely on oxidative addition and reductive elimination as key mechanistic steps. For example, catalysts that are used in hydrogenation typically operate by mechanisms in which metal sites react with dihydrogen (H2) by oxidative addition4,5. Oxidative addition of H2 to a metal site (M) involves donation of electron density from the σ-bond of H2 to an empty orbital of the metal, and back-donation from the metal site to the σ*-orbital of H2. Simultaneous depopulation of the σ-bond of dihydrogen with population of the σ*-orbital leads to breaking of the H–H σ-bond, which occurs with simultaneous making of two M–H σ-bonds and a change in the formal oxidation state at the metal from M to M2+. Similar processes can be found in textbook descriptions of mechanisms for hydrosilylation, hydroboration, isomerization, cross-coupling, hydroformylation and carbonylation2.
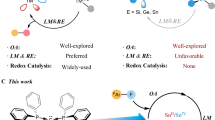
The description of this process as ‘oxidative’ is formalized in the International Union of Pure and Applied Chemistry (IUPAC) definition of oxidation state. Oxidation state is defined as the charge of the atom after its homonuclear bonds have been divided equally and the heteronuclear bonds assigned to the bonding partners according to the Allen electronegativity (Fig. 1a)6,7. In the case of dihydrogen, the underpinning assumption is that the hydrogen atoms are more electronegative than the metal site they are adding to, and as such the process is defined as oxidative from the perspective of the metal8. While a formalism, the description is intuitive and useful: it suggests a nucleophilic role of the hydrogen sites commonly involved in onwards steps (for example, migratory insertion). A philosophical question arises: if electron density in the M–H bond was to be shared evenly between the metal and hydrogen atoms, should the processes still be considered oxidative? Moreover, if the metal were more electronegative than hydrogen and the polarity of this bond reversed, Mδ−–Hδ+, would it be more suitable to describe this as a reductive addition? (Fig. 1b)3.
a, IUPAC definition of formal oxidation states based on division of heteronuclear bonds and assignment of electrons based on Allen electronegativity. b, Continuum of redox outcomes for addition of H2 and Zn–Zn bonds to metal (and semi-metal) centres. c, Frontier molecular orbitals and the isoelectronic relationship between H2 and Cp*ZnZnCp*.
In this paper, we describe the addition of Cp*ZnZnCp* to a series of main group carbene analogues, including silicon(II), aluminium(I), gallium(I) and indium(I) compounds. The Zn–Zn bond of Cp*ZnZnCp* can be considered to be isolobal to the H–H bond, with σ- and σ*-molecular orbitals constructed from overlap of 4s–4s atomic orbitals rather than 1s–1s (Fig. 1c)9,10,11,12. Previous studies have shown that Cp*ZnZnCp* reacts with transition metal complexes to form addition products13,14,15,16. In the current case, the addition reactions involve complete breaking of the Zn–Zn bond and construction of two new Si–Zn, Al–Zn, Ga–Zn or In–Zn bonds, resulting in an increase in the coordination number of the main group centre from two to four. In the case of the gallium(I), the process is reversible, with both addition and elimination accessible under ambient conditions. In the case of indium(I), the initial product of addition is unstable and cannot be detected spectroscopically because it undergoes further reaction to form a tetrametallic array.
Based on the Allen electronegativities of the elements involved and the IUPAC definition of oxidation state, these reactions are all formally described as reductive addition processes. A deeper analysis of the mechanism of addition and electronic structure of the products through computational methods suggests the situation is nuanced. While these reactions are perhaps best described by a continuum of redox outcomes, the case of addition to silicon(II) provides the most convincing data for a prototypical reductive addition process.
Results and discussion
Addition of Cp*ZnZnCp* to the heavier carbene analogues 1a–1c (E = Si, Al, Ga) in benzene or toluene solution resulted in the formation of 2a–2c (Fig. 2). These reactions were monitored by 1H NMR spectroscopy over a period of 10 min–5 h between 25 °C and 50 °C; in all cases product formation was indicated by a desymmetrization of the proton environments of the β-diketiminate ligand, along with an upfield shift of the methine resonance of the ligand backbone referenced against 1a–1c. In the case of 2a, the reaction was also characterized by a diagnostic 29Si NMR spectroscopy resonance observed at δ = +25.0 ppm, shifted upfield by Δδ = 63.4 ppm compared with the parent silylene 1a17. While 2a and 2b were generated cleanly in high yield, 2c formed as a 9:1 equilibrium mixture with 1c and Cp*ZnZnCp*. Variable-temperature 1H NMR spectroscopy studies were conducted on isolated samples of 2c dissolved in toluene-d8. Data were recorded across a −80 °C to +80 °C temperature range and showed that the equilibrium position shifts entirely toward 2c at lower temperatures18. A van’t Hoff analysis is consistent with the forward reaction having a Gibbs free energy of ΔG°298K = –4.7 kcal mol−1. The process is reversible, as confirmed by a crossover experiment between 2c and 1b which resulted in complete conversion to 2b and 1c.
A similar reaction between the indium(I) complex 1d (E = In)19 and Cp*ZnZnCp* did not led to isolation of the analogous compound 2d, but instead resulted in the generation of a tetrametallic complex 3 derived from a 2:1 reaction stoichiometry. 2d is proposed to be an intermediate is this reaction but was not stable enough to be observed spectroscopically or isolated. Related homometallic indium chains have been prepared through catenation of indium(I) complexes20. Additional experiments in which 1a–1d (along with the germanium analogue of 1a) were reacted with a series of complexes containing Zn–Zn and Mg–Mg bonds, under both thermal and photochemical conditions, failed to yield isolable products (Supplementary Tables 1 and 2).
2a–2c could be crystallized and isolated in 45–55% yield. In the solid-state, 2a–2c all demonstrated an approximate tetrahedral geometry at the silicon, aluminium or gallium centres (Fig. 3). The Zn–Zn distances are all in excess of 4 Å. These distances are beyond the sum of the covalent radii (Pyykkö, 2.36 Å (ref. 21); Pauling, 2.50 Å (ref. 22)) and are far greater than those experimentally determined in coordination complexes of Cp*ZnZnCp* with transition metal fragments which range from approximately 2.4 to 2.8 Å (refs. 12,13,14,15,23,24,25,26). The data suggest that complete breaking of the Zn–Zn bond occurs on reaction with the main group carbene analogue. The Si–Zn, Al–Zn and Ga–Zn distances in each compound are unsymmetrical and take values of 2.3268(6) and 2.3831(6) Å, 2.4102(9) and 2.4957(9) Å, and 2.3707(6) and 2.4576(6) Å, to the Zn2 and Zn1 atoms, respectively. All are within the sum of the covalent radii. Angles around the central main group element are distorted away from ideal tetrahedral geometry, the N–E–N angles are acute and range from 92.46(11)° to 101.12(9)°, while the Zn–E–Zn angles are more obtuse, taking values from 123.98(3)° to 133.84(2)°. 3 demonstrates an alternative structure comprised of an array of Zn–In–In–Zn metals with a centre of symmetry in the middle of the In–In bond. The In–Zn distance is 2.5360(4) Å, while the In–In distance is 2.7604(3) Å. The four metal atoms are coplanar, with the zinc sites adopting an anti-periplanar geometry with respect to the In–In bond.
Pathways for the addition of Cp*ZnZnCp* to 1a–1c were calculated by density functional theory (Fig. 4a). 1a–1c can all be considered low-valent complexes; each has an available lone-pair27. In all cases, the reaction is proposed to occur through formation of an intermediate Int-1, derived from coordination of the low-valent fragment to one of the zinc centres of Cp*ZnZnCp*. This coordination event is endergonic for both silicon and gallium (ΔG°298K = +4.8 to +9.7 kcal mol−1) but slightly exergonic for aluminium (ΔG°298K = −0.8 kcal mol−1). The Cp*ZnZnCp* moiety in Int-1 is both desymmetrized and polarized and the system is set up to reach the addition transition state, TS-1. TS-1 is a low-energy (ΔG‡298K = 2.3 to 17.5 kcal mol−1) three-centred transition state, reminiscent of those found in oxidative addition mechanisms for both main group and transition metal complexes (Fig. 4b)28,29,30,31. TS-1 appears late in the reaction pathway, with Zn–Zn bond breaking and Zn–E bond breaking almost complete as it is traversed. While formation of 2a–2c is calculated to be downhill, the gallium analogue is exergonic by only ΔG°298K = –5.5 kcal mol−1, consistent with the potential for this reaction to be reversible within the expected accuracy of the calculations. For 1d, a low-energy pathway for reaction with Cp*ZnZnCp* to form 2d followed by addition of a second equivalent of 1d to form the thermodynamic product 3 was identified (Supplementary Fig. 18).
In terms of the Allen scale of electronegativity, zinc (χZn = 1.59) is the least electronegative element in all these complexes. The main group centres that undergo the addition reaction are all more electronegative (χSi = 1.92, χAl = 1.61, χGa = 1.76, χIn = 1.66). Hence, based on the formal definition, these processes should be described as reductive additions. This definition, however, is fragile. The difference in electronegativity between aluminium and zinc is only 0.02 on the Allen scale, so small as to consider electron localization on either element insubstantial. The differences in electronegativities are also scale dependent (for example, Pauling, Mulliken–Jaffe, Alfred–Rochow). Hence, for aluminium, gallium and indium, the reactions could as well be described as oxidative or redox neutral (insertion) if the strict IUPAC definition was not followed. That said, silicon is more electronegative than zinc regardless of the electronegativity scale used, and hence this example may constitute a prototypical reductive elimination process.
The bonding in 2a–2c was interrogated through a suite of computational methods. There is no suggestion of any significant Zn–Zn interaction in these compounds. Atoms in molecules (AIM) treatment returned bond paths and associated bond critical points from the central main group element to each of the zinc atoms in 2a–2c, with no bond paths between the two zinc atoms themselves (Fig. 5a). Metrics associated with the bond critical points are consistent with their description as weak covalent bonds32. Independent gradient model based on Hirshfield partition (IGMH) analysis also supports an attractive covalent interaction with no or little Zn–Zn bonding (Fig. 5b)33. Natural bonding orbital analysis suggests that the E–Zn bonds in 2a–2c are best formulated as polar covalent interaction. Wiberg bond indices take average values of 0.68, 0.84 and 0.79 for the E–Zn bonds of 2a, 2b and 2c, respectively (Fig. 5c). In combination, the calculations support the proposal that complete Zn–Zn bond breaking occurs on addition to 1a–1c and these species are best formulated as tetrahedral four-coordinate complexes with zinc sites covalently bonding to the central atom.
a AIM plot of 2a showing Laplacian of electron density ∇2ρ(r) between silicon and zinc. b, Independent gradient model based on Hirshfield partition analysis of 2b. c, Wiberg bond indices for the E–Zn bonds in 2a–2c. d, Natural population analysis charges at key atomic sites on 2a–2c. e, AIM charges at key atomic sites in 2a–2c. f, NLMOs for the E–Zn bonds of 2a along with calculated coefficients for partitioning of NLMOs between E and Zn. g, Reaction of 2b with MeI. Ar, 2,6-di-iso-propylphenyl.
Additional computational analysis was undertaken to understand the polarization of the newly formed covalent bonds in 2a–2c. Although care should be taken to not convolute calculated atomic charges with formal oxidation states, in general the analysis suggests that the site of addition accumulates negative charge as the reaction proceeds. Natural population analysis charges show accumulation of negative charge on the central main group element of 2a–2c, with the zinc centres being the most electropositive sites in these molecules. For comparison, the calculated products from reactions between 1a–1c and H2 (refs. 34,35), a classical oxidative addition process, were also considered36,37,38. These species demonstrate greater charge separation than 2a–2c, consistent with a larger ionic contribution and the expected charge depletion at the main group centre and charge accumulation at the hydride ligands (Fig. 5d). Similar conclusions are drawn from inspection of fragment charges which consider delocalization of the charge across the supporting ligands (Supplementary Information). The analysis based on calculated AIM charges for 2a–2c is less definitive, with only the silicon analogue of the series demonstrating significant charge accumulation at the central main group metal (Fig. 5e). Natural localized molecular orbitals (NLMOs) were used to further interrogate the distribution of electron density between zinc and E. For 2a–2c, NLMOs describing the σ-bonding orbitals between the central main group element and zinc could be identified. In each case, these orbitals are polarized toward the central main group element (for example, silicon, aluminium, gallium or indium), having the largest coefficients on this element and smallest coefficients on zinc in the series; again the silicon analogue has the largest coefficients on the central atom (Fig. 5f).
In combination, the calculations suggest that 2a–2c contain polar covalent bonds that are polarized toward the central main group element (silicon, aluminium or gallium). As such, it could be expected that these species might be nucleophilic at this site. Addition of methyl iodide (MeI) to 2b over 16 h at 60 °C resulted in the formation of the corresponding dimethyl aluminium compound 1b-Me2 and Cp*ZnI as major reaction products. Although small amounts of Cp*ZnMe were also observed in this reaction, the implication is that the aluminium site of 2b is nucleophilic (Fig. 5g).
Conclusions
We report reactions of a Zn–Zn bonded complex, Cp*ZnZnCp*, with a series of main group carbene analogues bearing on low-valent silicon, aluminium, gallium and indium centres. In each case, the reactions occur with addition of the Zn–Zn bond to the low-valent centre, increasing the coordination number from 2 to 4. Although it is tempting to describe this as an oxidative addition process, the description is not strictly consistent with the IUPAC definition of oxidation state based on the Allen electronegativity scale. Formally these are reductive addition processes. Computational analysis of the reaction pathway and electronic structure of the products reveals a more nuanced picture, which is best considered by a continuum of redox outcomes ranging from oxidative through to reductive. The concept probably applies to transition metal as well as main group complexes1,2. Calculations on [Ni(PMe3)3(ZnCp*)(ZnMe)], originally reported by Fischer and co-workers15, suggest that this species shows increased charge build up at nickel compared with [Ni(PMe3)3(H)2] (Supplementary Figs. 68–71). Moreover, the three-fold addition of CpBeBeCp to [Ni(COD)2] to form [Ni(BeCp)6] was recently reported by Boronski and Aldridge39, and these authors describe the process as a ‘reductive addition’.
These results highlight the limitations of ‘normative scientific language’ in describing chemical reactivity. We suggest that addition reactions should not blindly be called oxidative. Rather it might be more constructive to consider a continuum of redox outcomes. In some special circumstances, such as the case of the addition of Cp*ZnZnCp* to a silylene complex reported herein, these may even be termed reductive addition processes.
Methods
Example procedure: preparation of 2a
In a glovebox, {DippNC(=CH2)CH(Me)NDipp}Si (20.0 mg, 0.045 mmol, 1 equiv.) and Cp*ZnZnCp* (18.1 mg, 0.045 mmol, 1 equiv.) were dissolved in C6D6 (0.6 ml) and transferred to a J. Young NMR tube. The reaction mixture was kept at 50 °C for 3 h. A 1H NMR spectrum was taken at this time point and showed the full conversion to 2a. The J. Young NMR tube was returned to the glovebox, the solvent was removed under vacuum and the crude product dissolved in 1 ml diethyl ether/n-pentane (1:10 v/v) mixture. The solution was filtered into a 4-ml vial and then placed in a freezer in the glovebox (−35 °C) for 2 days. Colourless crystals (2a) were successfully obtained. The filtrated crystals were washed with cold n-pentane (3 × 1 ml) and then dried in vacuo. Yield: 21 mg, 0.025 mmol, 55%.
1H NMR (C6D6, 298 K, 400 MHz) δ (ppm): 7.22–7.18 (m, 1H, ArCH), 7.16–7.14 (m, 1H, ArCH), 7.14–7.12 (m, 2H, ArCH), 7.12–7.10 (m, 1H, ArCH), 7.10–7.07 (m, 1H, ArCH), 5.55 (s, 1H, CH2CCHC(CH3)), 4.07 (s, 1H, NCCH2), 3.64 (hept, 3JH–H = 6.7 Hz, 1H, (CH(CH3)(CH3)), 3.48 (hept, 3JH–H = 6.8 Hz, 1H, (CH(CH3)(CH3)), 3.29 (s, 1H, NCCH2), 2.85 (hept, 3JH–H = 6.8 Hz, 1H, (CH(CH3)(CH3)), 2.84 (hept, 3JH–H = 6.8 Hz, 1H, (CH(CH3)(CH3)), 2.18 (s, 15H, CpMe), 1.55 (s, 15H, CpMe), 1.49 (s, 3H, NCCH3), 1.45 (d, 3JH–H = 6.7 Hz, 3H, (CH(CH3)(CH3)), 1.41 (d, 3JH–H = 7.0 Hz, 3H, (CH(CH3)(CH3)), 1.40 (d, 3JH–H = 6.8 Hz, 3H, (CH(CH3)(CH3)), 1.39 (d, 3JH–H = 6.9 Hz, 3H, (CH(CH3)(CH3)), 1.35 (d, 3JH–H = 7.0 Hz, 3H, (CH(CH3)(CH3)), 1.32 (d, 3JH–H = 6.9 Hz, 3H, (CH(CH3)(CH3)), 1.30 (d, 3JH–H = 6.7 Hz, 3H, (CH(CH3)(CH3)), 1.28 (d, 3JH–H = 6.9 Hz, 3H, (CH(CH3)(CH3)). 13C NMR (C6D6, 298 K, 101 MHz) δ (ppm): 153.1 (NCCH2), 149.2 (NC(CH3)), 148.4 (Ar-C), 148.3 (Ar-C), 147.3 (Ar-C), 146.3 (Ar-C), 142.6 (Ar-C), 126.6 (Ar-CH), 126.2 (Ar-CH), 124.7 (Ar-CH), 124.6 (Ar-CH), 124.5 (Ar-CH), 124.4 (Ar-CH), 109.7 (CpMe), 108.6 (CpMe), 105.0 (CH2CCHC(CH3)), 86.2 (NCCH2), 30.4 (CH(CH3)(CH3)), 30.3 (CH(CH3)(CH3)), 29.1 (CH(CH3)(CH3)), 28.7 (CH(CH3)(CH3)), 27.5 (CH(CH3)(CH3)), 26.9 (CH(CH3)(CH3)), 26.8 (CH(CH3)(CH3)), 26.1 (CH(CH3)(CH3)), 25.9 (CH(CH3)(CH3)), 25.8 (CH(CH3)(CH3)), 25.6 (CH(CH3)(CH3)), 25.0 (CH(CH3)(CH3)), 22.4 (NC(CH3)), 11.4 (CpMe), 10.1 (CpMe). 29Si NMR (C6D6, 298 K, 99 MHz) δ (ppm): 25.0 (s, Zn–Si–Zn). Analysis: Calculated (C49H70N2SiZn2): C, 69.57; H, 8.34; N, 3.31. Found: C, 69.50; H, 8.64; N, 3.09.
Data availability
Crystallographic data for the structures reported in this Article have been deposited at the Cambridge Crystallographic Data Centre, under deposition numbers CCDC 2350790 (2a), 2350788 (2b), 2350789 (2c) and 2410821 (3). Experimental procedures, details of calculations and spectroscopic data are available as Supplementary Information associated with this article, as are the cartesian coordinates for the density functional theory calculated stationary points (xyz).
References
Collman, J. P. & Roper, W. R. Preparation and oxidative addition reactions of a monomeric ruthenium(0) complex. J. Am. Chem. Soc. 87, 4008–4009 (1965).
Hartwig, J. F. (ed.). Organotransition Metal Chemistry. From Bonding to Catalysis (University Science Books, 2010).
Labinger, J. A. Tutorial on oxidative addition. Organometallics 34, 4784–4795 (2015).
Vaska, L. & DiLuzio, J. W. Activation of hydrogen by a transition metal complex at normal conditions leading to a stable molecular dihydride. J. Am. Chem. Soc. 84, 679–680 (1962).
Halpern, J., Okamoto, T. & Zakhariev, A. Mechanism of the chlorotris(triphenylphosphine) rhodium(I)-catalyzed hydrogenation of alkenes. The reaction of chlorodihydridotris(triphenylphosphine)rhodium(III) with cyclohexene. J. Mol. Catal. 2, 65–68 (1977).
Karen, P., McArdle, P. & Takats, J. Comprehensive definition of oxidation state (IUPAC recommendations 2016). Pure Appl. Chem. 88, 831–839 (2016).
‘Oxidation State’ in IUPAC Compendium of Chemical Terminology, 3rd ed. (International Union of Pure and Applied Chemistry, 2006), online version 3.0.1, 2019. https://doi.org/10.1351/goldbook.O04365
Mann, J. B., Meek, T. L., Knight, E. T., Capitani, J. F. & Allen, L. C. Configuration energies of the d-block elements. J. Am. Chem. Soc. 122, 5132–5137 (2000).
Resa, I., Carmona, E., Gutierrez-Puebla, E. & Monge, A. Decamethyldizincocene, a stable compound of Zn(I) with a Zn–Zn bond. Science 305, 1136–1138 (2004).
Río, D., del, Galindo, A., Resa, I. & Carmona, E. Theoretical and synthetic studies on [Zn2(η5‐C5Me5)2]: analysis of the Zn–Zn bonding interaction. Angew. Chem. Int. Ed. 44, 1244–1247 (2005).
Grirrane, A. et al. Zinc−zinc bonded zincocene structures. synthesis and characterization of Zn2(η5-C5Me5)2 and Zn2(η5-C5Me4Et)2. J. Am. Chem. Soc. 129, 693–703 (2007).
Ayala, R., Carmona, E. & Galindo, A. The dizinc bond as a ligand: a computational study of elongated dizinc bonds. Inorg. Chim. Acta 470, 197–205 (2018).
Bollermann, T., Freitag, K., Gemel, C., Seidel, R. W. & Fischer, R. A. Reactivity of [Zn2Cp*2] toward transition metal complexes: synthesis and characterization of [Cp*M(ZnCp*)3] (M = Ni, Pd, Pt). Organometallics 30, 4123–4127 (2011).
Freitag, K. et al. The σ‐aromatic clusters [Zn3]+ and [Zn2Cu]: embryonic brass. Angew. Chem. Int. Ed. 54, 4370–4374 (2015).
Freitag, K. et al. Zn···Zn interactions at nickel and palladium centers. Chem. Sci. 7, 6413–6421 (2016).
Hidalgo, N., Romero-Pérez, C., Maya, C., Fernández, I. & Campos, J. Reactivity of [Pt(PtBu3)2] with zinc(I/II) compounds: bimetallic adducts, Zn–Zn bond cleavage, and cooperative reactivity. Organometallics 40, 1113–1119 (2021).
Driess, M., Yao, S., Brym, M., Wüllen, Cvan & Lentz, D. A new type of N-heterocyclic silylene with ambivalent reactivity. J. Am. Chem. Soc. 128, 9628–9629 (2006).
Ganesamoorthy, C., Bläser, D., Wölper, C. & Schulz, S. Temperature‐dependent electron shuffle in molecular group 13/15 intermetallic complexes. Angew. Chem. Int. Ed. 53, 11587–11591 (2014).
Hill, M. S., Hitchcock, P. B. & Pongtavornpinyo, R. Solid- and solution-state structures of indium ‘alkene analogues’. Dalton Trans. 731–733 (2007).
Hill, M. S., Hitchcock, P. B. & Pongtavornpinyo, R. A linear homocatenated compound containing six indium centers. Science 311, 1904–1907 (2006).
Pyykkö, P. & Atsumi, M. Molecular single‐bond covalent radii for elements 1–118. Chem. Eur. J. 15, 186–197 (2008).
Pauling, L. Atomic radii and interatomic distances in metals. J. Am. Chem. Soc. 69, 542–553 (1947).
Cadenbach, T. et al. Twelve one‐electron ligands coordinating one metal center: structure and bonding of [Mo(ZnCH3)9(ZnCp*)3]. Angew. Chem. Int. Ed. 47, 9150–9154 (2008).
Cadenbach, T. et al. Molecular alloys, linking organometallics with intermetallic Hume–Rothery phases: the highly coordinated transition metal compounds [M(ZnR)n] (n ≥ 8) containing organo-zinc ligands. J. Am. Chem. Soc. 131, 16063–16077 (2009).
Chen, M., Jiang, S., Maron, L. & Xu, X. Transition metal-induced dehydrogenative coupling of zinc hydrides. Dalton Trans. 48, 1931–1935 (2018).
Jiang, S. et al. Synthesis and reactivity of triangular heterometallic complexes containing Zn–Zn bond. Inorg. Chem. 61, 8083–8089 (2022).
Parkin, G. Valence, oxidation number, and formal charge: three related but fundamentally different concepts. J. Chem. Ed. 83, 791 (2006).
Villegas-Escobar, N., Gutiérrez-Oliva, S. & Toro-Labbé, A. Catalytic mechanism of H2 activation by a carbenoid aluminum complex. J. Phys. Chem. C 119, 26598–26604 (2015).
García‐Rodeja, Y., Bickelhaupt, F. M. & Fernández, I. Understanding the oxidative addition of σ‐bonds to group 13 compounds. Chem. Eur. J. 22, 13669–13676 (2016).
Schoeller, W. W. & Frey, G. D. Oxidative addition of π-bonds and σ-bonds to an Al(I) center: the second-order carbene property of the AlNacNac compound. Inorg. Chem. 55, 10947–10954 (2016).
Zhang, X. & Cao, Z. Insight into the reaction mechanisms for oxidative addition of strong σ-bonds to an Al(I) center. Dalton Trans. 45, 10355–10365 (2016).
Matta, C. F. & Boyd, R. An Introduction to the Quantum Theory of Atoms in Molecules (Wiley-VCH, 2007).
Lu, T. & Chen, Q. Independent gradient model based on Hirshfeld partition: a new method for visual study of interactions in chemical systems. J. Comput. Chem. 43, 539–555 (2022).
Roy, M. M. D. et al. Molecular main group metal hydrides. Chem. Rev. 121, 12784–12965 (2021).
Stoelzel, M., Präsang, C., Inoue, S., Enthaler, S. & Driess, M. Hydrosilylation of alkynes by Ni(CO)3‐stabilized silicon(II) hydride. Angew. Chem. Int. Ed. 51, 399–403 (2012).
Chu, T., Korobkov, I. & Nikonov, G. I. Oxidative addition of σ-bonds to an Al(I) center. J. Am. Chem. Soc. 136, 9195–9202 (2014).
Morris, L. J., Rajeshkumar, T., Okumura, A., Maron, L. & Okuda, J. Solvent‐dependent oxidative addition and reductive elimination of H2 across a gallium–zinc bond. Angew. Chem. Int. Ed. 61, e202208855 (2022).
Seifert, A., Scheid, D., Linti, G. & Zessin, T. Oxidative addition reactions of element–hydrogen bonds with different polarities to a gallium(I) compound. Chem. Eur. J. 15, 12114–12120 (2009).
Boronski, J. T., Crumpton, A. E. & Aldridge, S. A crystalline NiX6 complex. J. Am. Chem. Soc. 146, 35208–35215 (2024).
Acknowledgements
We are grateful to the European Research Council (101001071) for funding to MRC. We thank P. Haycock and S. Elliott for assistance with NMR experiments, and R. Kong for initial preparation of 1a.
Author information
Authors and Affiliations
Contributions
W.Y. conducted all experimental and computational work. A.J.P.W. collected and refined single-crystal data. M.R.C. directed the research project. All authors were involved in writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Synthesis thanks Roland Fischer, Robert Mulvey and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Peter Seavill, in collaboration with the Nature Synthesis team.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Experimental details, Supplementary Figs. 1–71 and Tables 1–144.
Supplementary Data 1 X-ray
crystallographic data for 2a, CCDC 2350790.
Supplementary Data 2
X-ray crystallographic data for 2b, CCDC 2350788.
Supplementary Data 3
X-ray crystallographic data for 2c, CCDC 2350789.
Supplementary Data 4
X-ray crystallographic data for 3, CCDC 2410821.
Supplementary Data 5
Computational coordinates.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, W., White, A.J.P. & Crimmin, M.R. Reactions of a Zn–Zn bond with main group carbene analogues as a prototypical case of reductive addition. Nat. Synth 4, 995–1000 (2025). https://doi.org/10.1038/s44160-025-00790-y
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s44160-025-00790-y