Introduction

The exploding growth of the Internet of Everything (IoE) ecosystem1 has unleashed the generation of a tremendous amount of raw data, demanding high-speed, low-power processing. In this landscape, typical von Neumann computers, characterized by their processing architecture, have met an efficiency road-block2, struggling with data bottlenecks and energy constraints. Consequently, bio-inspired computing has emerged as an unconventional and promising route, aiming to circumvent inherent limitations of traditional systems3. This approach, drawing on the complex mechanisms of biological organisms, offers parallel processing capabilities and adaptability, potentially transforming the way we handle the escalating data challenges in the IoE era. Towards this route, photonic integrated circuits can offer a proliferating hardware platform for neural network implementation, based on merits such as multiplexing-assisted parallelism, low power consumption, large-scale integration, and low latency4,5,6.

One of the most common types of neural networks used for processing IoE generated visual data is convolutional neural networks (CNNs)7. Highly acclaimed for their ability to extract features from large datasets in a hierarchical manner, CNNs owe much of their effectiveness to their unique distinctive layered structure. Typically, CNN architectures consist of three types of layers: convolutional, pooling, and fully-connected layers (FCLs). The convolutional layers apply multiple sets of weights (kernel filters) to the input for feature detection, transforming the data into a feature map. Subsequently, the pooling layers reduce the dimensionality of the feature maps by computing the maximum or the mean of a local patch of units in one or several feature maps. Finally, the FCLs integrate the processed features, performing high-level reasoning to facilitate the final decision-making or classification task.

A key issue with CNNs lies in their high computational and power demands for convolutional operations, which often consume up to 90% of the network’s execution time8. This has led to a focus on optimizing these operations in various hardware architectures, including traditional graphics processing units (GPUs)9, memristors10, and lately photonics11. These technologies primarily aim to enhance the efficiency of digital matrix-to-vector multiplications (MVMs) which are necessitated to execute the convolutional operations in CNNs. In this context, integrated photonic solutions such as micro-ring resonator (MRR) banks based on the broadcast-and-weight protocol12, coherent MRR networks13, photonic tensor cores14,15, cascaded fixed Mach-Zehnder interferometers (MZI)16, and combined MRR-MZI networks17 risen as low-power MVM accelerators able to reach more than 1.27 tera-operations per joule.

The adaptation of the MVM-based approach into the photonic domain introduces considerable challenges. One primary issue is the necessity for extensive offline numerical simulations during high-speed weight adaptation in training13,17. These simulations are meant to emulate the behavior of photonic hardware but often lead to power inefficiency and make photonic MVMs prone to errors in weights and digital-to-analogue converter (DAC) components’ resolution. These errors arise from discrepancies between the actual physical parameters of the chip and those assumed in the simulations. Additionally, current scalability constraints of photonic platforms limit the number of total MVMs that can be executed in a single pass, increasing the total execution time of these systems. Therefore, as the resolution and/or size of visual data increases, the number of processing passes on the same integrated photonic chip might also increase the total processing time and energy consumption. Recent attempts in the electronic domain to address these constraints have utilized phase-change components for in-memory computing18, enabling precise control over a substantial number of weights. However, even in these optimized cases, such approaches still demand extensive off-chip training and additional circuitry.

In19, the operational principles of an unconventional integrated photonic accelerator were presented. The proposed system, namely OSS-CNN, is comprised of two main components: an analog pre-processor, which utilizes high-speed passive photonic and opto-electronic devices for feature extraction, nonlinear transformation and dimensionality reduction and a digital post-processor, in which a simple feedforward neural network is employed to associate the analog outputs with their corresponding class labels. The uniqueness of this acceleration approach stems from the adoption of an optical spectrum slicing (OSS) technique, which employs parallel passive optical filter nodes with distinct characteristics (bandwidth, central frequency) to perform analog-domain convolutions with the optical signal. Although the use of analog photonics as a preprocessor in convolutional tasks is not new, previous architectures that exploited this approach followed the MVM approach for the convolutional stage12,17,20.

In contrast, OSS-CNN uses each filter node as an analog convolutional operator, interacting with the modulated signal through a continuous-valued transfer function or impulse response in the spectral or temporal domain to extract different spatial features from the input tensors. Unlike MVM-based approaches, the number of optical nodes in OSS-CNN is determined by the number of distinct characteristic nodes required to efficiently decompose the signal, rather than the size of the visual dataset. Furthermore, the use of a single photoreceiver after each node to appropriately average the output time-traces before digitization reduces the number of data and the overall power consumption of the system. This method results in a simple and minimal design in terms of employed photonic and electronic components, and the associated power footprint. The combination with a straightforward time-multiplexed encoding of visual data into the optical signal allows convolution operations of any size to be performed through a single pass, freeing the photonic hardware from the need to physically replicate the required MVMs. Compared to other advanced photonic CNN architectures evaluated on the MNIST handwritten digits task21, the OSS accelerator has theoretically shown equivalent state-of-the-art precision, comparable computational density and increased efficiency in terms of power consumption19.

In this work, the transition of the OSS acceleration approach into the domain of reprogrammable photonics is explored. The photonic front-end of the OSS-CNN system is experimentally validated using a reconfigurable silicon photonic chip (SmartLight)6,22, with the OSS nodes now implemented using reconfigurable integrated filters. In our previous work, we demonstrated the OSS-NN concept using only numerically simulated ideal, lossless Butterworth filters19. Moreover, in this study, the OSS-CNN is benchmarked against a conventional digital CNN architecture, evaluating not only classification accuracy but also end-to-end power consumption for the same task, thereby highlighting the energy efficiency advantages of this approach. In specific, the first section of this document briefly analyzes the operational characteristics and performance of an ideal OSS-CNN system, characterized by no losses and the use of ideal Butterworth filters, and moves onto the analysis of an OSS-CNN system implemented within a reconfigurable photonic chip. Numerical simulations conducted using the physically accurate iPronics’ SmartLight emulation platform indicate that the proposed OSS accelerator even when implemented on a reconfigurable photonic platform notably can improve performance on benchmark datasets such as MNIST by at least 5.3% in accuracy, when utilized prior to a basic feedforward neural network. The subsequent section documents the experimental validation of the OSS accelerator on a reconfigurable silicon photonic chip, achieving a state-of-the-art 97.7% accuracy with only 3 OSS nodes while maintaining the same number of data samples at its output as the input visual data. The final section compares the reconfigurable OSS-CNN directly to a digital equivalent single-layer CNN implemented on a state-of-the-art GPU. The exploration of performance and total power consumption for both architectures is conducted in relation to the depth of the feedforward neural network employed at their back-end. Even though the OSS accelerator exhibits slightly inferior precision compared to the single-layer CNN, it achieves a substantial reduction in total power consumption during the training stage by 30%.

Results

Architecture, Principle of Operation, and Simulated OSS System

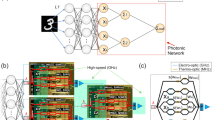
In Fig. 1, the generic OSS architecture is depicted. The process begins with encoding the input tensors onto the intensity of an optical carrier at 1550 nm using a Mach-Zehnder modulator. This step translates the spatial information of the input into the temporal domain by converting the tensor values into one-dimensional vectors, as will be explained later. The core of this architecture comprises multiple parallel OSS nodes, each consisting of bandpass optical filters (e.g., MRRs, asymmetric MZIs, etc.). Conceptually, applying the filter’s transfer function in the frequency domain is analogous to convolving the signal with the filter’s impulse response in the temporal domain. As a result, the proposed nodes function as continuous-valued analog convolutional kernels, each characterized by unique complex impulse responses determined by their distinct spectral characteristics, effectively interacting with the incoming time-traces. Unlike conventional CNNs, these kernels operate not with discrete weights but with continuous-valued transfer functions applied to the signal’s spectrum, or equivalently, with complex impulse responses in the temporal domain. These values can be considered as arbitrarily controlled but are coarsely tuned through the filter’s hyperparameters, which correspond to the parameters forming the impulse response of the OSS filters. For instance, the impulse response of a first-order filter can be expressed as follows:

$$h\left(t\right)={2\pi f}_{c}{e}^{-t\left({2\pi f}_{c}-j2\pi {f}_{m}\right)},\,t \, > \, 0$$
(1)

where \({f}_{m}\) and \({f}_{c}\) correspond to the central and the cut-off frequency of the filter respectively. Consequently, the continuous convolution of the input optical signal with this impulse response of each node can be represented as:

$$y\left(t\right)={\int }_{\!\!\!0}^{t}x\left(\tau \right)h\left(t-\tau \right)d\tau ,\,t \, > \, 0$$
(2)

where \(x(t)\) is the input optical signal, \(h(t)\) is the impulse response of the OSS filter and \(y(t)\) is the output optical signal. As depicted in the red and green insets of Fig. 1, varying the frequency detunings from the optical carrier and/or adjusting the filter bandwidths for each node results in diverse impulse responses in the complex domain. This diversity is evidenced by the differentiation in the discretized in-phase (I) and quadrature (Q) plots for each node.

Fig. 1: Schematic diagram of the OSS-CNN architecture.
figure 1

a Conversion of a MNIST digit image (number “3” as an example) into an analog time series following a patching and flattening operation for serialization into a one-dimensional digital vector and digital-to-analog conversion. b The photonic analog preprocessor of the optical spectrum slicing convolutional neural network (OSS-CNN) system includes a continuous wave laser source and a Mach-Zehnder modulator, which imprints the analog time series onto the amplitude of the optical signal. The signal is then equally split and processed by the OSS nodes (performing convolutional operations) and subsequent photodiodes (performing nonlinear and average pooling operations). c The digital postprocessor of the OSS-CNN consists of an analog-to-digital converter (ADC) that digitizes the outputs from the photoreceivers, controlling the degree of digital compression at the input of the feedforward neural network. A single or two-layer dense neural network with a softmax activation at the output layer classifies the digitized OSS node outputs into MNIST labels. d, e Schematic illustrations of the transfer functions of two filter nodes set at different positions within the optical signal’s spectrum and their corresponding discretized in-phase and quadrature (I–Q) diagrams, showing the different complex values applied through their impulse responses in the temporal domain. f, g Reconstructed images from the digitized outputs of the different slicing OSS nodes in (d, e), depicting the different spatial features extracted from the digit “3” image by changing the central position of each node.

Full size image

In contrast to MVM-based schemes that require extensive simulations to train and implement kernel weights through photonic devices, our approach optimizes the characteristics of the filter nodes. By adjusting the central frequencies and a common bandwidth for each node, we achieve optimal decomposition of the optical signal features. After photodetection and digitization, this allows a simple feedforward neural network to attain high accuracy. Additionally, the receptive field of each analog kernel node, representing the spatio-temporal window of application, can be fine-tuned by manipulating the bandwidth and filter order. For instance, wider bandwidth filters result in a faster exponential decay in the impulse response, thereby covering fewer pixels in each convolutional operation. Conversely, changing the filter order alters its steepness and the shape of the impulse response, subtly modifying the applied complex responses.

As also illustrated in Fig. 1, this generic scheme includes photodiodes and an analog-to-digital converter (ADC) following each node. The photoreceivers apply a nonlinear transformation to the OSS outputs due to the square law detection and average them over a specified time window. The rate of the ADC determines the degree of digital data compression at the output, which will be discussed in subsequent sections. The digitized signals from the nodes are then flattened and fed into a trainable readout layer implemented in the digital domain. This digital classifier is a simple software-based feedforward neural network with a softmax activation function at the output layer and an Adam optimizer23. Consequently, the proposed scheme preprocesses information directly in the analog domain, performing feature extraction through the OSS nodes and nonlinear activation and temporal averaging through the photodiodes, and is followed by a conventional yet lightweight digital back-end.

In this study, the acceleration capabilities of the OSS technique were initially examined through simulations. Ideal-generic Butterworth filters, on one hand and a reconfigurable photonic mesh emulator, on the other hand, were used. The primary goal of this investigation was to determine the maximum potential of the approach (ideal system) and then make direct comparisons with real-world implementations, emphasizing the impact of various physical constraints.

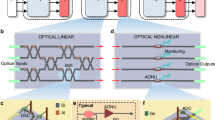
For the photonic circuit, we employed the reconfigurable photonic hardware platform, SmartLight processor22, developed by iPronics. Its software development kit accounts for various physical non-idealities of the photonic circuit, such as limited phase-tuning resolution and optical coupling errors, with most of these effects automatically managed and mitigated by control algorithms, whereas nonlinear effects are not considered. SmartLight comprises a two-dimensional integrated photonic waveguide mesh arranged in a hexagonal topology, where each side of the hexagons incorporates a programmable unit cell (PUC). Each PUC includes a Mach-Zehnder interferometer, forming a 2×2 reversible gate with independent control over the splitting ratio and phase response. To achieve the desired operation for each PUC, external electrical signals are applied to one or both of the PUC’s phase shifters, enabling precise amplitude and phase control of photonic signals between the two waveguide arms. This is facilitated through thermo-optic tuning, as each waveguide arm is equipped with a thermal actuator (heater).

For the implementation of OSS nodes within this mesh, each node is configured as a single MRR in an add/drop configuration (as illustrated in Fig. 2), consisting of eight PUCs in total. One PUC was programmed to operate in the cross-state, guiding the optical signal from the input into the waveguide loop. Two additional PUCs served as tunable couplers, enabling light to be coupled into and out of the MRR. The remaining five PUCs were configured in the bar state to form the MRR cavity. Furthermore, the central frequency detuning of the MRR resonance, relative to the optical carrier, was precisely tuned by adjusting the second phase shifter of a PUC within the optical cavity, controlled via an external electrical signal. This setup allowed each MRR to selectively interact with specific spectral regions of the input signal, effectively operating as a distinct analog kernel filter.

Fig. 2: Implementation of each optical spectrum slicing (OSS) node as a first-order micro-ring resonator (MRR) within the reconfigurable photonic mesh.
figure 2

The design utilizes eight programmable unit cells (PUCs): one PUC is set in the cross state (black) to guide light from the input port into the MRR loop, two PUCs act as tunable couplers (green) to couple light into and out of the loop, and the remaining five PUCs are set in the bar state (orange) to direct light within the loop and toward the output port (the drop port of the MRR). The central frequency of the MRR is tuned by utilizing a second phase shifter of a PUC within the loop, enabling the processing of different regions of the input signal spectrum.

Full size image

Furthermore, the resonant properties of the MRR filters allow them to act as optical integrators over specific time windows24, or in spatial terms, receptive fields, on the convolved analog responses. Consequently, the output time-traces from the OSS filters involve both the application of continuous-valued complex responses and a proper integration of their outputs, resembling the generation of feature map elements in CNNs.

To assess the scheme’s efficiency, the focus is placed on the conventional benchmark task of classifying the handwritten digits of the MNIST dataset, consisting of 60,000 images for training and 10,000 for testing. Instead of extensive digital preprocessing, a simple patching and flattening technique was utilized, preserving the spatial relationships of pixel values in both horizontal and vertical orientations, to convert each image into a one-dimensional (1D) vector (refer to Note 1 and Fig. 1 of Supplementary Information for more details). The pixel serialization process is based on 4 × 4 patches which yielded the best results in terms of accuracy for the MNIST task across all cases.

Ideal optical filters: numerical simulations

In the ideal node case, a state-of-the-art 128 GS/s DAC25 was considered to feed the pixel data into the system, with the mean input power of the intensity-modulated optical carrier maintained at 20 mW. This power level, accounting for the contributions of thermal and shot noise in the photoreceivers, ensured a minimum electrical signal-to-noise ratio (SNR) of 53 dB at each receiver node. Beyond this threshold, no further performance improvements were observed. The effect of the patching size (ΜxΜ), the number of OSS nodes (N) and the OSS filter characteristics(fc, fm) were investigated alongside the total input power and the sampling rate of the ADCs to identify the conditions under which classification accuracy, parameter minimization, throughput, and power consumption are optimized. The bandwidth and the central frequencies of the bandpass filters were initially set as to uniformly cover the input’s signal single-sideband spectrum depending on the number of OSS nodes, which were explored for \(N=2\) up to\(\,20\). For example, at a 128 GS/s pixel rate, with an intensity-modulated optical carrier and 5 OSS nodes, the filters cut-off and central frequencies are respectively set to \({f}_{c}=6.4\,\)GHz and \({f}_{m}=6.4,\,19.2,\,32,\,44.8,\,57.6\,\)GHz. Furthermore, the 3 dB bandwidth of the photodetectors following the OSS nodes was set to be inversely proportional to the patch size, enabling the retrieval of an average over its temporal duration (refer to Note 2 and Eq. 1 of Supplementary Information for additional details). Figure 3 illustrates the classification accuracy of the OSS-CNN as a function of the compression ratio (CR) for a different number of ideal Butterworth filter nodes with a single FCL as its digital classifier. The CR, a key metric of digital parameter reduction achieved by the OSS-CNN, is defined as the ratio between the size of the input tensor and the input size of the back-end neural network (see Note 2 and Eq. 2 of Supplementary Information for more details).

Fig. 3: Classification accuracy of the optical spectrum slicing convolutional neural network (OSS-CNN) as a function of the compression ratio (CR) and the number of OSS nodes utilized.
figure 3

The results correspond to an ideal OSS-CNN configuration, featuring ideal Butterworth filter nodes without chip losses, a single fully-connected layer (FCL) as its digital classification back-end, a modulation rate of 128 GS/s, and a patch size of 4 × 4.

Full size image

As a baseline, feeding all MNIST image pixels directly into a digital FCL with softmax activation achieved an accuracy of 92.6% (Fig. 3—black points). The classification accuracy of the OSS-CNN is observed to scale inversely with the CR and the beneficial impact of employing more OSS nodes becomes more evident at smaller compressions. The highest accuracy with a single dense layer back-end, ~98%, was achieved using 7 OSS filters (Fig. 3—orange points), and augmenting the number of nodes beyond this did not result in further improvements. Notably, even with increased CR, only a mild performance degradation is observed for the OSS scheme. For instance, at a CR of 4, the performance exceeds that of the standalone dense layer, reaching a maximum of 94.6% with 3, 5, and 7 OSS nodes (refer to Fig. 3), compared to the 92.5% achieved by the standalone FCL at this level of compression. It should be noted here that for the baseline case (no OSS preprocessing), the different CR scenarios were obtained by averaging the MNIST image values over varying pixel windows. Specifically, a CR of 4 corresponds to division and averaging across a 2 × 2 pixel window, while a CR of 2 entails averaging between two consecutive pixels. Therefore, it becomes apparent that the utilization of OSS prior to the dense layer consistently enhances classification accuracy across all cases, with the OSS scheme surpassing the maximum accuracy of the standalone readout even with a limited number of nodes and substantial compression. This improvement can be attributed to the efficient extraction of differentiated spatio-temporal features from each image by the photonic front-end, even with coarse tuning of the filters’ response. Consequently, the OSS preprocessing not only facilitates an enhancement in classification accuracy for the single-layer neural network but also provides a valuable dimensionality reduction.

SmartLight emulator: numerical simulations

As the next step, the SmartLight emulator was employed to implement the OSS scheme. The processes of data serialization, signal detection, and digital processing remained consistent with those described earlier. However, instead of ideal Butterworth filters, hardware-relevant filter implementations were employed, considering the properties of the PUCs within the SmartLight emulator. The configuration of the add/drop MRR filter nodes used is depicted in Fig. 2, with the coupling coefficients set to \({k}_{1}={k}_{2}=0.05\) (Fig. 2—green). As mentioned above, configuring each OSS node in the waveguide mesh requires a total of nine thermal actuators: two within a PUC inside the MRR loop to control the node’s central frequency, and one for each of the seven additional PUCs comprising the node. Figure 4a illustrates the power spectrum of an intensity-modulated optical signal, with a mean power of 13 dBm, carrying a MNIST image. Figure 4b shows the power responses from the drop ports of five OSS nodes implemented using the SmartLight emulator. These OSS nodes were configured to uniformly “slice” the single sideband of the signal’s spectrum. As observed in Fig. 4b, setting the insertion losses for each PUC to 0.2 ± 0.02 dB results in an approximate total loss of 12 dB at the drop port of each OSS node. The input pixel rate was set to 10 GS/s to match the fixed 10 GHz free spectral range of the photonic mesh filters, ensuring that each filter interacts exclusively with a single region of the optical spectrum. Finally, it is important to note that the bandwidth of the mesh-implemented OSS nodes is not an unrestricted hyperparameter. Due to the fixed length of the PUCs, the mesh filters exhibit a fixed 3 dB bandwidth of ~0.9 GHz. For a detailed discussion of the constraints imposed by the reprogrammable photonic processor on the implementation of the OSS-CNN, please refer to Note 3 of the Supplementary Information.

Fig. 4: Spectrum of a modulated MNIST image and optical spectrum slicing (OSS) node responses.
figure 4

a Normalized optical power spectrum of an intensity-modulated optical carrier, centered at 1550 nm, with a MNIST image and a 10 GS/s pixel rate, b Power responses from the drop ports of five SmartLight-implemented OSS nodes, set as to uniformly “slice” the single side-band of the optical spectrum.

Full size image

Figure 5 illustrates the relationship between mean input optical power and classification accuracy for a 5-node OSS implemented on the waveguide photonic mesh, using a 4 × 4 patch serialization. The comparison is drawn against the maximum accuracies represented by black dashed lines for a standalone FCL and by blue dashed lines for an ideal 5-node OSS setup (no losses, optimum bandwidth, and an SNR exceeding 53 dB for each node). The peak accuracy recorded for the chip-implemented OSS, at an input power of 20 dBm, stands at 96.7%, reaching an equivalent performance to the ideal OSS-CNN (96.9% with 5 optimized nodes). This slight variance can be attributed to the fixed bandwidth of the photonic-chip filters, which deviates from the optimal bandwidth for processing the MNIST dataset. The analysis also reveals that the OSS-CNN system demands a minimum of 16 dBm power to align closely with the ideal OSS’s accuracy. Falling below this threshold leads to performance drops, attributed to the cumulative losses in nodes which increase the noise susceptibility of their outputs. Consequently, the digital signals produced by nodes with lower SNRs become less distinct across different images, complicating the classification task for the single-layer readout. Lastly, it should be noted that absent noise constraints, the impacts of limited hyperparameter tuning resolution (for instance, a 16-bit DAC for phase adjustment) and the non-variable bandwidth on the system’s efficacy are minimal.

Fig. 5: Classification accuracy of a SmartLight-implemented 5-node optical spectrum slicing convolutional neural network (OSS-CNN) in relation to the mean input power, using a 4 × 4 image patching and a 10 GS/s pixel rate.
figure 5

For comparison, the maximum accuracy achieved by a standalone fully-connected layer (FCL) and that of a 5-node OSS-CNN configuration based on ideal Butterworth filters are also shown.

Full size image

Experimental validation

The experimental setup is illustrated in Fig. 6. A laser, centered at 1550 nm with an input power of 13 dBm, was connected to an intensity modulator. The data processing speed reached ~7.6 million images per second, with data serialization following the same methodology described earlier (refer to Note 4 of Supplementary Information for additional details). Within the photonic chip, an MRR filter, as shown in Fig. 2, was employed as a single OSS node. Measurements were performed sequentially by varying the resonant frequency of the MRR relative to the carrier, enabling the recording of 15 equivalent OSS node responses (see Note 4 and Fig. 3 of Supplementary Information for more details).

Fig. 6
figure 6

The experimental setup of the optical spectrum slicing convolutional neural network (OSS-CNN).

Full size image

To compensate the optical losses both before and within the SmartLight processor, the setup incorporated two erbium-doped fiber amplifiers (EDFAs), while a bandpass filter was positioned prior to the photodetector to mitigate noise introduced by the EDFAs. The amplified output signal was directed to a 20 GHz photodiode and a real-time oscilloscope operating at 25 GS/s. The recorded digital signal was resampled to match the initial image vector dimensions, and temporal average pooling was applied digitally (refer to Note 4 and Fig. 4 of Supplementary Information for more details). As previously, a single dense-layer feedforward neural network was initially utilized as the system’s back-end classifier. Its input size varied based on the number of digital samples per processed image, which depended on the size of the average pooling procedure, while the output size corresponded to the 10 MNIST classes. Finally, a softmax activation function was applied to the FCL to transform the outputs into class probabilities.

The classification process included the analysis of combinations of outputs from 2, 3, and 5 distinct filter positions to discover the maximum accuracy achievable by the experimental OSS-CNN. To identify the baseline accuracy, modifications were made to the experimental setup by omitting the photonic processor and the second EDFA. As a result, the modulated signal passed through the first EDFA, the bandpass filter, and the photoreceiver and was resampled at 12 GS/s after the oscilloscope. The digitized time-traces were subsequently normalized and fed directly into the FCL, which underwent training with an Adam optimizer and a learning rate set at 0.01. Figure 7 illustrates the peak classification accuracies attained by the experimental OSS system, correlating them with the number of distinct filter position outputs fed into the single-layer classifier. Analyzing the outputs from two filter positions yielded a maximum accuracy of ~95.7% at a CR of 1, achieved by combining the filter at the carrier frequency (0 GHz detuning) with a filter detuned by 2.5 GHz. The utilization of three filter positions, specifically at 0, 2.5, and 7 GHz detunings, produced the most advantageous results, achieving a top accuracy of 95.87% with a CR of 1. It is important to note that, to maintain a CR of 1 in each case, different undersampling rates were utilized. For instance, for the two-filter OSS-CNN, the sampling rate was adjusted to extract 392 samples at the output of each OSS node’s ADC, while in the three-filter case, the rate was modified to deliver 261 samples per node. Notably, the precision achieved with 3 OSS nodes exceeded the highest experimental performance reported for state-of-the-art photonic CNN accelerators, such as14,15. Lastly, incorporating outputs from five distinct filter positions did not further enhance accuracy, peaking at 95.76% with the inclusion of five filter positions.

Fig. 7: Precision of the experimental optical spectrum slicing convolutional neural network (OSS-CNN) with respect to the number of nodes.
figure 7

The bar graphs depict the maximum classification accuracy achieved by the experimental OSS-CNN for varying numbers of distinct filter position outputs, which were used as inputs to a digitally implemented single fully-connected layer classifier.

Full size image

The classification accuracy of the experimental OSS system with a single-layer readout, for the three most effective filter positions in relation to the CR is depicted in Fig. 8. This is compared against the baseline accuracy, as indicated by the black dashed line in the figure. To provide context for these experimental findings, two scenarios featuring simulations of ideal OSS nodes are also incorporated in the figure. The first scenario demonstrates a generic solution in which the central frequencies of the nodes are fixed to uniformly cover the single sideband spectrum of the optical signal, as shown by the blue plot in Fig. 8. The second scenario examines a configuration in which the central frequencies of the filter nodes are considered as free hyperparameters for the system. In more detail, an investigation was executed with the aid of the ‘Optuna’ hyperparameter optimization framework26, aiming to maximize the precision of an ideal 3-node OSS-CNN. The optimization task in this framework is usually defined by specifying the hyperparameter search space and an objective function to minimize or maximize. Additionally, advanced algorithms such as the Tree-structured Parzen Estimator (TPE) and CMA-ES are utilized to intelligently navigate the search space, offering a more efficient solution than traditional methods such as random or grid search. In this work, the bandwidth and central frequencies of the OSS filters were examined as hyperparameters, with the latter being able to take any value within the single sideband spectrum of the input signal. A TPE algorithm was employed to predict promising hyperparameter combinations based on past trial outcomes that would maximize the classification precision which was set as the objective function. The patch size was set to 4 × 4, the input power at 20 mW and the sampling rate was adjusted to extract two samples per patch. The optimum setup emerged for \({f}_{m}\) values of 6, 22, and 27 GHz, and \({f}_{c}\) equal to 5 GHz and is depicted by the green plot in Fig. 8. In both ideal OSS scenarios, the method employed for extracting digitized sequences from each OSS node was the same as the experimental post-processing procedure. The OSS node outputs were processed through a simulated 20 GHz photodiode and a digital 4th-order Butterworth filter, adjusting its bandwidth to match the digital sample count at the FCL input, as per the experimental setup.

Fig. 8: Performance comparison of experimental and ideal optical spectrum slicing convolutional neural networks (OSS-CNNs).
figure 8

Classification accuracy of the experimental OSS system (red plot) with a single fully-connected layer back-end, evaluated across the most effective filter positions (0, 2.5, and 7 GHz) as a function of the compression ratio (CR). The baseline accuracy is represented by the black dashed line. Additionally, two scenarios of an ideal 3-node OSS-CNN are included: one with fixed node central frequencies uniformly distributed across the single sideband spectrum (blue plot) and another optimized for the MNIST task with central frequencies set to the most effective positions (green plot).

Full size image

The capabilities as well as the robustness of the OSS preprocessing are highlighted in Fig. 8. First, it is observed that the classification accuracy of the experimental setup consistently surpasses the baseline accuracy, particularly in cases with lower CRs. The peak accuracy, observed at 95.9% with a 1-FCL classifier, surpasses the baseline system accuracy by 4.3%. This notable performance improvement not only confirms the efficiency of the SmartLight-based OSS as an accelerator but also outperforms the experimental results of other state-of-the-art photonic schemes, as referenced in refs. 14,15. Secondly, it is evident that the experimental OSS manages to maintain a higher level of accuracy compared to a standalone FCL fed with the entire MNIST image data, even in scenarios involving substantial data compression/averaging. For example, the experimental OSS-CNN achieved an accuracy of 94.1% with a CR of 4 and ~94.7% with a CR of 2, surpassing the baseline by 1.5% and 2.1% respectively. Therefore, even with the presence of losses, the amplified spontaneous emission introduced by the EDFA and the fixed bandwidth of the SmartLight-implemented nodes, the OSS was able to deliver efficient parameter reduction. Thirdly, when comparing the experimental OSS to the ideal OSS-CNN models, the experimental OSS’s accuracy demonstrated a trend similar to the ideal cases, inversely scaling with the CR up to a CR of 1, beyond which a slight decrease in accuracy was noted for CR = 0.5. A noticeable difference between the ideal and experimental setups was seen in the rate at which accuracy decreased as the CR increased. This declination in the experimental OSS’s performance can be attributed to two main reasons. Firstly, the bandwidth of the filters implemented in the SmartLight processor deviates from the optimal bandwidth required for this specific task. Secondly, considering the vast array of possible combinations of three filters from all 15 distinct filter position outputs, our investigation was limited to only those combinations that included the filter positions yielding the best outcomes in the 2-node scenario (0 and 2.5 GHz detunings). Lastly, comparing the ideal OSS-CNN configurations, it is observed that the performance of the generic OSS setup, where the central frequencies of the nodes uniformly filter the single-sideband spectrum of the input signal, is slightly worse than that of the OSS setup with optimized filter positions tailored for the specific task. For instance, in the optimized OSS scenario, the peak accuracy attained was 97.2% at a CR of 1, which only slightly decreases to 96.9% at a CR of 4. Conversely, in the generic OSS scenario, the highest observed accuracy was 96.5% at a CR of 1, dropping to 95.9% at a CR of 4. This depicts the OSS-CNN’s ability to achieve sufficient precision in machine vision tasks by uniformly covering the single side-band of the input spectrum, without the need to know the optimum filter positions. It should be noted that, with sufficient input power, comparable performance was also achieved in numerical simulations realizing 3-node OSS-CNNs in the SmartLight emulator.

Performance comparison with a respective digital CNN

In this section, a performance evaluation compares the OSS accelerator with a conventional digital CNN architecture, which features a single convolutional-nonlinear-pooling stage. For the classification back-end, two scenarios are depicted: a single FCL equipped with a softmax activation function and configurations including an additional hidden dense layer, while adding a second hidden layer did not enhance performance in any case. Table 1 presents a detailed comparison of key characteristics and metrics for three architectures: the optimally simulated 7-node OSS accelerator, a corresponding single-layer digital CNN utilizing the same number of kernel filters, and the optimal 3-node experimental OSS. The digital back-ends of the OSS schemes, as well as the entire single-layer CNN, were implemented on the TensorFlow platform27 using an NVIDIA GeForce RTX 2080 Ti GPU28. To obtain the maximum classification accuracy for each scheme, an investigation was conducted using the “Optuna” platform with respect to the number of nodes per layer, learning rate, batch size, and the activation function of the hidden layer. In the case of the single-layer CNN, the size of the kernels and the pooling were also investigated. Table I details the number of hidden FCLs, units per layer, and the classification accuracy for the optimal setup of each architecture. Additionally, the average power consumption of the graphics card (\({\bar{P}}_{{GPU}}\)) during the training procedure is depicted for each architecture. These values were derived from monitoring the mean thermal design power percentage (TDP%) during the training process for each approach. In general, TDP% is a metric that indicates the GPU’s power usage and thermal load. Given that the TDP of the GPU used in this study is 250 W, the TDP percentage was calculated using the GPU-Z monitoring utility29. The average TDP percentage was computed over 100 training epochs with a consistent learning rate and batch size for both architectures.

Table 1 Performance comparison of SmartLight OSS-CNN and a respective digital CNN architecture
Full size table

The information from Table 1 reveals that adding a second dense layer at the back-end, the simulated OSS exhibited a maximum accuracy of 98.6%, marginally lower than the performance of the respective single-layer CNN, which scored 99.1%. This same difference in precision is also observed with one dense layer, with the optimized digital CNN recording a 98.6%. Regarding the experimental OSS, it is clear that the introduction of an additional dense layer boosted its accuracy from 95.9% to 97.7%, thus narrowing its performance gap to under 1% compared to the simulated OSS, which utilized more nodes, and to only 1.4% compared to a fully optimized noiseless digital system. However, the OSS-CNN displayed a notable advantage in energy efficiency. Specifically, for both the simulated and experimentally produced inputs for the digital back-end, the OSS-CNN reduced the average power consumption of the graphics card by a substantial 33% for configurations with one and two FCLs. This can be attributed to the fact that the pre-processor effectively decouples the convolutional, nonlinear, and pooling stages from the digital domain, considerably reducing the computational workload of the GPU, which must handle all stages in the single-layer CNN.

For instance, in a traditional setup, each of the 7 × 7 kernel filters within the convolutional layer of the digital CNN performs convolutions at 22 × 22 positions across each MNIST image when striding with a step of 1. Therefore, on a single pass, each kernel filter executes \(2\cdot 7\cdot 7\cdot 22\cdot 22=47,432\) operations for each MNIST image, encompassing both multiplications and additions. Collectively, all seven kernels in the convolutional layer execute a total of 332,024 operations. Additionally, the subsequent single-layer feedforward network with 10 units handles 16,940 operations, derived from 847 multiplications and additions per unit. Thus, the model processes ~348,964 operations in one forward pass, not including the operations from the pooling layer. Conversely, in the OSS accelerator, the scope of forward and backward pass computations during the training process is limited to the depth of the digital back-end classifier. For example, in the single FCL case, with 10 units and an input size of 1372 (total samples per MNIST image at the output of the 7 OSS nodes), a total of \(10\cdot {\mathrm{1372}}\cdot 2={\mathrm{27,440}}\) operations are executed in a single forward pass. Hence, ~92% fewer computations are executed within the GPU with the OSS preprocessing, not accounting for the backpropagation operations during training, which typically amount to twice the number of forward pass computations, as well as the power consumption from memory accesses and data transfers between memory and GPU30.

To compare the OSS-CNN with this conventional digital CNN architecture in terms of end-to-end power consumption, it is necessary to consider not only the GPU’s power consumption but also that of the opto-electronic pre-processor and the digital post-processor components. The formula for calculating the total power consumption of the OSS-CNN can be given by:

$${P}_{{total}}={P}_{{LD}}+{P}_{{DAC}}+{P}_{{OSS}}+{P}_{{ADCs}}+\,{\bar{P}}_{{GPU}}$$
(3)

where \({P}_{{LD}}\) is the power consumption of the laser source, \({P}_{{DAC}}\) is the power of the front-end DAC, \({P}_{{OSS}}\) is the total power consumption of the OSS stage, and \({P}_{{ADCs}}\) is the total power draw of the ADCs. Based on31, the power consumption of a laser diode is given by:

$${I}_{{LD},{driv}}=\frac{{P}_{{LD},{opt}}}{{\gamma }_{{LD}}}+\,{I}_{{LD},{thr}}$$
(4)
$${P}_{{LD}}=\,{V}_{{LD},f}{{\rm{\cdot }}}{I}_{{LD},{driv}}$$
(5)

where \({V}_{{LD},f}\) is the diode bias voltage, \({I}_{{LD},{driv}}\) is the diode current, \({P}_{{LD},{opt}}\) is the optical power of the laser, \({\gamma }_{{LD}}\) is the slope efficiency and \({I}_{{LD},{thr}}\) is the threshold current. For a typical continuous-wave 1550 nm laser diode emitting at 16 dBm32, the values are as follows: \({V}_{{LD},f}=1.8\) V, \({I}_{{LD},{thr}}=8\) mA, and \({\gamma }_{{LD}}=0.29\) mW/mA. Therefore, the estimated power consumption of the laser diode is ~262 mW. Similarly, the power consumption for a state-of-the-art front-end DAC operating at 50 GS/s is about 243 mW33. For a 7-node OSS-CNN designed for this task and implemented on a silicon-on-insulator platform, the power consumption of the OSS stage can be calculated by factoring in the power used by both the MRR phase shifters and the DACs that control them. Each micro-electro-mechanical-system-based phase shifter consumes less than 0.1 mW34, while the low-power DACs driving them consume ~2.5 mW35. Therefore, the total power consumption to retain the phases of all seven nodes is 18.2 mW. Additionally, the power consumption for seven high-performance ADCs operating at 6 GS/s (aligned with the 4 × 4 patching in Eq. 3) amounts to ~105.7 mW36. Based on Eq. 3, the total power consumption of the application-specific OSS accelerator can reach up to 34.9 W, representing a substantial reduction of up to 30% compared to a single-layer CNN, which typically requires an average of 50 W of GPU power for training on the MNIST task. Similarly, for a 7-node OSS-CNN implemented on the SmartLight processor, consideration must be given to the booster EDFA, along with two components related to the nine thermal actuators associated with each MRR node: 1.3 mW for maintaining the PUC’s state37 and 2.5 mW for the DACs driving the actuators35. Consequently, the total power consumption for all seven OSS nodes in the mesh (7 × 9 = 63 actuators) is calculated at 239.4 mW, while the power draw of a state-of-the-art C-band booster EDFA is at 1.5 W38. Therefore, the total power consumption of the SmartLight OSS-NN is ~36.6 W, indicating that, even within a reconfigurable photonics platform, power consumption may increase by up to 27% compared to a digital CNN.

Finally, a comparison in terms of training time between the OSS and the digital CNN was also performed. In specific, ten iterations of the training procedure were executed for each architecture to calculate their mean training time and the average number of epochs required for convergence, maintaining the same training parameters but varying the initial weight values. For the OSS with a single-layer back-end, the average training time per iteration was ~224 s, with an average of 754 epochs needed for convergence. This contrasts markedly with the single-layer CNN using also a 1-FCL back-end, which required only about 17 s per iteration and 60 epochs on average. This difference can be attributed to noise introduced by the photoreceivers in the OSS, as well as to representation overheads at the output of the OSS nodes caused by phase-shifting or beam-splitting errors during photonic processing and by the analog-to-digital conversion. With a more complex 2-layer classifier at its back-end, the OSS scheme demonstrated notably improved efficiency, taking on average ~28 s per iteration and 96 epochs, reducing the difference to the single-layer CNN with a 2-FCL back-end to less than 4 s in training time and 10 epochs for convergence (24 s per iteration and 86 epochs on average). It is evident that by adding a second dense layer, the classifier was able to converge considerably faster, comparably to the noiseless digital CNN, due to its increased capacity to learn more complex representations from data that included noise and variations introduced by the OSS processing stages.

Conclusions

This work proposes an analog accelerator based on an integrated photonic reconfigurable platform, circumventing the issues that arise in hardware architectures adopting the MVM approach. Utilizing a single processing pass of the photonic chip, minimal external/internal memory, and minimal electro-optic/opto-electronic conversions, the hardware-friendly technique enables convolutional operations to be performed by optical filter-nodes without requiring fine control or elaborate training. Additionally, the OSS accelerator implements other key CNN operations, such as nonlinear transformation and pooling, in the analog domain without processing latency. Numerical results confirmed the scheme’s ability to achieve a classification accuracy of 98.6%, closely matching the performance of full-scale digital networks. Experimental validation using iPronics’s SmartLight reconfigurable photonic mesh achieved an accuracy of 97.7%, outperforming state-of-the-art photonic implementations on the MNIST dataset. More importantly, the proposed scheme confirms its accelerator properties by drastically reducing the total power consumption by 30% compared to its respective standalone digital neural network. The experimental performance and the reduced power consumption is substantiating the role of photonic accelerators as promising sub-systems for large-scale hybrid machine learning schemes.

Methods

Single-dimensional image vector formation (1-D vector)

A simple preprocessing step was employed to transform each image into a one-dimensional (1D) vector prior to imprinting onto the optical carrier. The preprocessing started by diving each image into evenly sized 4 × 4 pixel regions, known as patches. These two-dimensional patches were then serialized into 1D vectors using two distinct flattening methods: row-wise and column-wise. First, the row-wise flattening method was applied to each patch, converting the pixel values within rows into a continuous sequence. Subsequently, the column-wise flattening method was applied, creating another sequence based on the pixel values within columns. The row-wise flattened vectors of all patches were concatenated sequentially, followed by the concatenation of the column-wise flattened vectors. Finally, the two resulting vectors were concatenated into a single 1D vector for each image. This approach preserved spatial relationships of pixel values in both horizontal and vertical dimensions, enabling the optical filters to process this information effectively. As a result, the 1D vector of each image had a length of 2 × 784 = 1576, which is double the size of the original MNIST image representation.

Photoreceiver functionality and data compression in the OSS-CNN

The photoreceivers in the optical spectrum slicing (OSS) system perform two key functions commonly found in CNNs, but implemented in the analog domain: nonlinear activation and average pooling. Through their square-law behavior, the photoreceivers provide a nonlinear activation function to the optical outputs of the OSS nodes. Additionally, they are configured with a 3 dB bandwidth that is inversely proportional to the patch size, expressed by the equation:

$${{BW}}_{{PD}}=\frac{{PR}}{M\cdot M}$$
(6)

where \({PR}\) represents the pixel rate (modulation rate) of the input signal, and \(M\times M\) corresponds to the patch size. This configuration allows the photoreceivers to generate an average value for each time window, which aligns with the size of the patches (\({M}^{2}\) pixels). These averages are produced at the output of each photodiode as the optical signal propagates.

The system’s sampling rate at the ADCs serves as another important hyperparameter, as it determines the level of digital data compression performed by the OSS-CNN. The CR is a useful metric for quantifying parameter reduction in the system. It is defined as the ratio of the size of the input tensors to the input size of the back-end neural network, and is expressed as:

$${CR}=\frac{H\,\cdot \,W\,\cdot \,C}{{N}_{{nodes}}\,\cdot \,{N}_{s}}$$
(7)

where \(H\), \(W\) and \(C\) represent the height, width, and number of channels of the input tensors, respectively (e.g., 28 × 28 × 1 for MNIST images), \({N}_{{nodes}}\) is the number of employed OSS nodes and \({N}_{s}\) the number of digital samples at the output of each OSS node.

MNIST dataset processing and optimization in the OSS-CNN

The entire MNIST dataset of handwritten digits, comprising 60,000 training images and 10,000 testing images, was processed by the OSS-CNN system in both simulations and experiments. Prior to processing, the MNIST images were converted into one-dimensional vectors and sequentially imprinted onto the intensity of a 1550 nm optical carrier via a Mach-Zehnder modulator after digital-to-analog conversion. These optical signals were then processed by the OSS nodes. After photodetection and analog-to-digital conversion, the digitized outputs corresponding to a single image were combined into a vector. Each vector is stored as a row in a matrix, forming the classification dataset for the digital classifier at the back-end. The dataset was split into training and testing subsets consistent with the MNIST dataset structure, with 10% of the training dataset further allocated for validation. The OSS outputs of the MNIST training images were used to train the classifier, while the outputs of the testing images were used for evaluation.

The digital classifiers employed at the back-end in both the simulated and experimental OSS-CNNs were fully-connected feedforward neural networks with one or two layers. The output layer contained 10 units corresponding to the MNIST digit classes, with a softmax activation function. The networks were compiled through the PyTorch platform39 using the Adam optimizer and the categorical cross-entropy loss function, with accuracy used as the evaluation metric. To enhance training efficiency, an early stopping mechanism was implemented, halting training if the validation loss did not improve for 25 consecutive epochs. The best-performing model, based on validation loss, was used for inference. The Optuna optimization framework was employed to determine the optimal configurations for the neural networks. Specifically, a TPE algorithm within the framework was utilized to predict the best parameter combinations based on prior trial outcomes, with testing accuracy set as the objective function. For both single-layer and two-layer dense network configurations, the optimization process explored parameters such as the learning rate (ranging from 0.0001 to 0.01), training batch size (50, 125, 250), and testing batch size (25, 50, 125). For the two-layer network, additional parameters were considered, including the hidden layer activation function (sigmoid, tanh, or ReLU) and the number of hidden layer units, which ranged from 20 to 120. A maximum of 100 trials was conducted for each case to ensure robust exploration of the parameter space.

This optimization framework was also applied to the digital single-layer CNN to identify the optimal parameter combinations for maximizing inference accuracy. The number of kernel filters was fixed at 7, consistent with the number of nodes of the OSS-CNN that achieved optimal results in simulations. In addition to optimizing standard parameters such as the learning rate, batch size, and nonlinear activation function, the Optuna framework also explored kernel filter sizes (ranging from 2 × 2 to 5 × 5), stride values (1–5), and pooling layer sizes (2 × 2 to 5 × 5). Optuna was further employed to optimize the front-end hyperparameters of a 3-node OSS-CNN, enabling a direct comparison with the experimental 3-node OSS-CNN for the MNIST task. The optimization process focused on maximizing the classification accuracy of a single dense-layer back-end by adjusting the 3-dB bandwidth of the OSS filters (kept consistent across all nodes and explored within a range of 0.5–4 GHz) and the central frequency of the filter (allowed to vary freely within the single sideband of the optical spectrum, spanning from 0 to 6 GHz at a 12 GS/s pixel rate). Other front-end parameters were held constant during this optimization, including the patch size (4 × 4), input power (20 mW), the 3-dB bandwidth of the photodiodes (calculated using Eq. 6), and the sampling rate (configured to extract two samples per patch).

Reconfigurable OSS-CNN experiment

The experimental setup of the reconfigurable OSS-CNN system for the MNIST classification task utilized a laser emitting light at a wavelength of 1550 nm and an input power of 13 dBm. The laser output was connected to an intensity modulator, which received the serialized one-dimensional MNIST image vectors from a 12 GS/s arbitrary waveform generator, corresponding to a maximum processing speed of ~7.6 MImages/s. The modulated optical signal was subsequently amplified using a booster EDFA to raise the power level to 19 dBm, compensating for −19 dB losses incurred up to this stage and an additional 6 dB insertion loss from the following photonic reconfigurable SmartLight processor22. A MRR filter was configured inside the photonic waveguide mesh of this processor to function as the OSS node, implemented through eight photonic unit cells (PUCs) with coupling coefficients set to 0.1. Frequency shifts within the MRR cavity were enabled by an additional phase shifter integrated into one of the PUCs, allowing interaction with distinct spectral components of the input signal to facilitate the OSS process. The OSS stage was performed sequentially, with the transfer function of the MRR underwent controlled frequency shifts. The output signal was recorded for each of 15 distinct spectral positions (from 0 to 7 GHz, in 0.5 GHz steps), effectively monitoring the filter’s response at these intervals. After exiting the drop port of the MRR, the optical signal was further amplified using a second EDFA, increasing the power level by ~20 dBm. To mitigate noise introduced by the EDFA and ensure efficient photodetection, a bandpass filter was positioned immediately after the amplifier, setting the optical power at the input of the subsequent photoreceiver within the range of 0–1.85 dBm. The photodetection stage utilized a 20 GHz photodiode to convert the optical signal into an electrical signal, which was captured with a 25 GS/s oscilloscope and resampled at 12 GS/s to match the dimensions of the original image vectors. Following resampling, the signals were digitally processed using a 4th-order Butterworth filter, consistent with the simulation methodology for temporal average pooling.