A high-precision 1 × 15 infrared temperature measurement linear array based on thermopile sensors

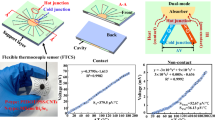
Abstract

In applications such as those in the semiconductor industry, precise temperature measurements with low power consumption are crucial. This article presents a novel noncontact temperature measurement method with low power consumption and high precision, and a thermopile sensor-based linear array for surface temperature measurements is used in semiconductor manufacturing and temperature calibration applications. The array consists of 15 thermopile sensors, a negative temperature coefficient (NTC) thermistor, an FPGA control board with a fiber optic interface, and a motion module. Moreover, the total power consumption of the board is less than 1.5 W. On the FPGA control board, a multiparameter temperature compensation algorithm is used to address intrinsic temperature differences and consistency errors among the sensors. Compared with the traditional two-point calibration method, the temperature measurement accuracy of the proposed method reaches 26 mK in the temperature range of 293–303 K, the maximum repeatability error of the sensor is less than 5.5 mK, and the non-uniformity error between 15 sensors is less than 11.9 mK. The array and its replicas were subjected to more than 6 h of rigorous testing, demonstrating their high stability, with the reduction in accuracy not exceeding 1.5 mK.

Introduction

High-precision noncontact temperature measurement methods are critical in various industrial and scientific applications because of their advantages, such as their noncontact nature, fast detection speed, and lack of harmful radiation^1,2. The increasing demand for accurate and reliable thermal monitoring in fields such as chip manufacturing, materials processing, and biomedical research has driven the development of advanced infrared temperature measurement techniques^3,4,5,6,7,8. Noncontact temperature measurement methods have several advantages over contact temperature measurement methods, including faster response times, noninvasive operations, and the ability to measure moving or inaccessible objects⁹. However, despite the significant progress made in this field, challenges remain in obtaining high-precision temperature measurements while maintaining low power consumption.

Low power consumption is a crucial consideration in the design of infrared temperature measurement systems. The increasing prevalence of portable and battery-powered devices, as well as the need for energy efficiency in industrial settings, has highlighted the importance of minimizing power consumption^10,11,12. Low-power operation not only extends the operational lifetime of the measurement system but also reduces heat generation, which can significantly affect the accuracy of temperature measurements¹³. Furthermore, low-power designs enable the integration of temperature measurement systems into a wide range of applications, including wearable devices, wireless sensor networks, and remote monitoring systems^14,15.

However, limitations related to measurement accuracy and sensor consistency must be addressed for existing noncontact temperature measurement methods^16,17,18. Commercial infrared temperature sensors, such as the Amphenol sensor ZTP-188MA and the Heimann sensor HMM series, provide an accuracy of ±1 K (273–303 K). The temperature sensors used in the ASML (Advanced Semiconductor Material Lithography) were manufactured by MKS Instruments, Inc., USA. The company’s MultiTherm 2000 temperature controller offers a temperature measurement resolution of 0.01 K, a repeatability better than 0.1 K, and an accuracy of ±0.8 K (273–303 K). While these accuracies may be sufficient for certain applications, they are insufficient in scenarios demanding higher precision¹⁹. Moreover, ensuring consistency among sensors becomes a significant challenge when multiple sensors are used in an array configuration. Variations in sensor characteristics and manufacturing tolerances can lead to discrepancies in temperature readings across the entire array²⁰. To address these issues, researchers have explored various calibration techniques and compensation algorithms. In refs. ^21,22,23, automatic calibration methods for infrared temperature measurements were proposed, achieving an accuracy of ±1 K. In refs. ^24,25,26, various temperature compensation methods were employed, reaching a measurement accuracy of 0.2 K. However, these methods are not suitable for scenarios with high accuracy requirements. In refs. ^{27,28,29,30,31,32}, machine learning approaches were applied to calibrate temperature sensors, effectively improving measurement accuracy. Nevertheless, the complexity and computational overhead of these methods may hinder their practical implementation in low-power systems.

In this paper, we present a high-precision, low-power 1 × 15 infrared temperature measurement array designed to address the aforementioned challenges, achieving both low power consumption and high-accuracy temperature measurements. In our system, we integrate thermopile sensors, negative temperature coefficient (NTC) thermistors, an FPGA-based control board, and a multiparameter temperature compensation algorithm to enable precise temperature measurements across multiple sensors while maintaining low power consumption. The thermopile sensors are employed to capture the surface temperature of the target object, whereas the NTC thermistors are used to collect the board temperature to compensate for temperature measurement errors. The FPGA control board facilitates efficient data acquisition, processing, and communication, and the embedded multiparameter temperature compensation algorithm compensates for temperature variations among the sensors, with both temperature compensation functions for individual sensors and consistency compensation functions among sensors. By adopting various low-power design techniques, the total power consumption of the board is less than 2 W, making it suitable for a wide range of applications.

The development of this high-precision, low-power infrared temperature measurement array has significant implications for various industries and research fields. By enabling accurate and reliable noncontact temperature monitoring, our approach can enhance process control, quality assurance, and scientific investigations. The array’s compact form factor and low power requirements make it suitable for integration into portable devices, remote sensing platforms, and industrial automation systems. Furthermore, the modular design of the array allows for scalability and customization to meet specific application requirements.

In the following sections, we present the technical details of our proposed infrared temperature measurement array. We discuss the sensor selection and characterization process, FPGA-based control board architecture, and temperature compensation algorithm. Additionally, we present the experimental setup, calibration procedures, and performance evaluation results. Finally, we explore the potential applications and future directions of this technology.

Methods

Infrared temperature measurement theory for thermopiles

The theoretical foundation of the total radiation thermometry method is the Stefan–Boltzmann law. With this method, the temperature is determined by utilizing the functional relationship between the radiant exitance of a thermal radiator over the entire wavelength range and its temperature. The mathematical expression of the Stefan–Boltzmann law is as follows:

$${M}_{B}(\lambda ,T)=\sigma {T}^{4}$$

(1)

In the equation, ${M}_{B}(\lambda ,T)$ represents the radiant exitance of an ideal black body, measured in units of ${{\rm{W}}}\,\cdot{{\rm{cm}}}^{-2}$. $\sigma$ denotes the Stefan–Boltzmann constant, which has a value of $\sigma =5.67051 \times {10}^{-8}{{W}}\,{{{m}}}^{-2}\,{{{K}}}^{-4}$. $T$ signifies the thermodynamic temperature, expressed in units of Kelvin (K). According to the Stefan–Boltzmann law, the surface of any object at a temperature above absolute zero continuously radiates energy outwards.

Thermoelectric modules are thermal-to-electric conversion devices that operate on the basis of the Seebeck effect, also known as the first thermoelectric effect. These modules consist of N pairs of thermocouples connected in series, where each pair is formed by joining an N-type semiconductor material with a P-type semiconductor material, constituting the fundamental building blocks of the thermoelectric module. According to the definition of the Seebeck effect, when two dissimilar metallic materials are joined to form a closed-loop circuit, an electric current is generated within the loop if there is a temperature gradient at the junction. With the advancement of semiconductor physics, P-type and N-type semiconductor materials with distinct Seebeck coefficients have been shown to exhibit Seebeck effects. In P-type semiconductor materials, a high concentration of holes at the hot end causes positive charges to flow towards the cold end along the concentration gradient. Conversely, in N-type semiconductor materials, electrons at the hot end have higher energies and velocities, leading to a rapid flow of electrons towards the cold end, whereas at the cold end, the flow of electrons is sparse and slow. Consequently, a thermoelectric potential difference, denoted as ${V}_{out}$, arises between the junction points of the P-type and N-type semiconductor materials at the cold junction. The mathematical expression for this potential difference is as follows:

$${V}_{{{out}}}={T}_{{{diff}}}({\alpha }_{A}-{\alpha }_{B})={T}_{{{diff}}}{\alpha }_{AB}$$

(2)

where ${\alpha }_{A}$ and ${\alpha }_{B}$ represent the Seebeck coefficients of the P-type and N-type semiconductor materials, respectively, ${\alpha }_{AB}$ is the difference in the Seebeck coefficients of the two materials, and ${T}_{diff}$ is the temperature difference.

The field of view (FOV) of a thermoelectric module refers to the angular measurement determined via signal detection, which involves the use of a blackbody to emit radiation at a set temperature T in an environment with a specific temperature T at a fixed distance from the sensor. The voltage signal ${V}_{\theta }$ is then measured and normalized ($\frac{{V}_{\theta }}{{V}_{\max }}$), and the corresponding rotation angle within a 0.5 range is taken as the device’s FOV angle, as illustrated in Fig. 1.

Fig. 1: Equipment working principle diagram.

In the given configuration, $l$ denotes the distance between the sensor and the blackbody, measured in meters, and $\theta$ represents half of the FOV angle and corresponds to the angle of rotation when a cross-sectional element $ds$ of the FOV is taken. $R$ is the distance from the detector to the maximum extent of the FOV on the blackbody surface when considering a small area $ds$, measured in meters, and $\varphi$ is the angle around the axis of the FOV cone.

In the case of an ideal FOV, a sensor with a detection area of 1.2 mm² is employed to determine the magnitude of infrared radiation. The computation of the blackbody radiative power within the FOV necessitates the utilization of the thermal radiation detection model, as illustrated in Fig. 1. This model is instrumental in quantifying the sensor’s capacity to capture blackbody radiation emissions, a critical parameter in the evaluation of infrared detection systems.

In Fig. 1, the definitions are as follows:

$$\begin{array}{c}r=l\,\tan \theta \\ R=\frac{l}{\cos \theta }=l\,{\mbox{sec}}\theta \\ ds=dr\cdot rd\varphi =l\,{{\mbox{sec}}}^{2}\,\theta d\theta \cdot l\,\tan \theta d\varphi ={l}^{2}\,\sin \theta \,{{\mbox{sec}}}^{3}\theta d\theta d\varphi \end{array}$$

(3)

In the given configuration, $l$ denotes the distance between the sensor and the blackbody, measured in meters, and $\theta$ represents half of the FOV angle and corresponds to the angle of rotation when a cross-sectional element $ds$ of the FOV is taken. $R$ is the distance from the detector to the maximum extent of the FOV on the blackbody surface when considering a small area $ds$, measured in meters, and $\varphi$ is the angle around the axis of the FOV cone.

Assuming that each elemental area $ds$ of the blackbody heat source radiates energy uniformly in all directions within a hemisphere of radius $R$, centered on itself, the radiance reaching the sensor can be described as follows:

$$\begin{array}{c}M(\lambda ,T)=\frac{{M}_{b}(\lambda ,T)\cdot ds}{2\pi {R}^{2}}\\ =\frac{\sigma {T}^{4}\cdot {R}^{2}{l}^{2}\,\sin \theta \,{{\mbox{sec}}}^{3}\theta d\theta d\varphi }{2\pi {l}^{2}{{\mbox{sec}}}^{2}\theta }=\frac{\sigma {T}^{4}\,\sin \theta {{\mbox{sec}}}\theta d\theta d\varphi }{2\pi }\end{array}$$

(4)

For a sensor with a sufficiently small receiving area A, the radiant power ${d}_{P}$ received is calculated as follows:

$${d}_{P}=M(\lambda ,T)\,A\,\cos \theta =\frac{\sigma {T}^{4}\,A\,\sin \theta d\theta d\varphi }{2\pi }$$

(5)

Within the FOV, taking $\theta$ as half the FOV angle, the total radiant power $P$ received by the sensor is calculated as follows:

$${P}_{obj}=\int dP={\int }_{0}^{2\pi }d\varphi {\int }_{0}^{\theta }\frac{\sigma {T}^{4}\,A\,\sin \theta }{2\pi }d\theta =2{\varepsilon }_{obj}\sigma A{T}^{4}{\sin }^{2}\frac{\theta }{2}$$

(6)

Then, the radiance M of a sensor with a radiating surface area A and an external FOV angle of $2\theta$ can be defined. Treating the sensor as a point radiative source, the solid angle corresponding to the FOV is defined as follows:

$$\Omega =2(1-\,\cos \theta )$$

(7)

Assuming that the radiant energy within this solid angle remains constant, the radiative power (W/m²) of the sensor is defined as follows:

$${M}_{S}(\lambda ,T)={\varepsilon }_{S}\sigma {T}_{S}^{4}$$

(8)

The power ($P$) received by the sensor is independent of the distance ($l$) between the sensor and the object. The larger the receiving area of the sensor and the greater the FOV angle are, the more radiant energy the sensor can collect. The Seebeck effect can then be utilized to establish a mapping relationship between the temperature and the pressure difference across the hot and cold junctions, allowing for temperature measurements. In practical applications, factors such as ambient humidity, changes in ambient temperature, the thermal design of the thermopile drive circuit, and the emissivity of the object being measured can all be sources of error. In the subsequent experiments, we thoroughly considered the impact of these factors on the temperature measurement accuracy and proposed a multiparameter temperature compensation algorithm to achieve high-precision infrared temperature measurements.

Temperature compensation algorithm

Traditional two-point calibration temperature compensation algorithm

The commonly used reference radiation source methods include one-point calibration, two-point calibration, and multipoint calibration algorithms. However, the one-point calibration method cannot simultaneously calibrate the offset and gain coefficients of the sensor, making it unsuitable for practical systems. Although multipoint calibration methods improve the calibration accuracy, the computational complexity and calibration workload are both increased, especially when there are many sensors.

On the other hand, the two-point calibration method overcomes the limitations of the one-point calibration method by allowing simultaneous calibration of both the offset and gain coefficients. Moreover, the two-point calibration method has a lower computational complexity than the multipoint calibration method, making it more suitable for sensor calibration. In this study, the infrared thermopile sensor was calibrated with the two-point calibration method by conducting experiments with a reference radiation source. The output response values of each sensor at different temperatures within the operating temperature range were obtained. After the calibration process, the calibrated outputs of each sensor were collected. The two-point calibration method effectively addresses the issue of simultaneously considering the offset and gain coefficients of the sensor. With this calibration method, two target temperatures are selected as calibration points, and a linear relationship is assumed between the sensor’s output response and the target temperature.

The output of the thermopile can be formulated as follows:

$${V}_{OUT}=\sigma \varepsilon {S}_{0}{\sin }^{2}\frac{\theta }{2}({T}_{obj}-{T}_{amb})$$

(9)

where ${V}_{OUT}$ represents the output voltage of the thermopile, ${S}_{0}$ is the sensitivity coefficient of the infrared sensor, $\sigma$ is the Stefan–Boltzmann constant, $\varepsilon$ is the emissivity of the object, $\theta$ is the optical field angle of the sensor, ${T}_{obj}$ is the temperature of the object’s surface, and ${T}_{amb}$ is the ambient temperature.

Two target temperatures, ${T}_{a}$ and ${T}_{b}$, are selected within the dynamic response range of the sensor. The actual response outputs, $V({T}_{a})$ and $V({T}_{b})$, of the two sensors at these temperatures are obtained. Then, Formula (12) is used to derive the relationship between the sensor’s output response and the temperature at ${T}_{a}$ and ${T}_{b}$. Assuming that the calibrated gain coefficient of the sensor is $m$ and that the calibrated offset coefficient is $n$, we have:

$$\begin{array}{c}{T}_{a}-{T}_{na}=mV({T}_{a})+n\\ {T}_{b}-{T}_{nb}=mV({T}_{b})+n\end{array}$$

(10)

On the basis of Formula (13), we can derive:

$$\begin{array}{c}m=\frac{({T}_{a}-{T}_{na})-({T}_{b}-{T}_{nb})}{V({T}_{a})-V({T}_{b})}\\ n={T}_{a}-{T}_{na}-m\cdot V({T}_{a})={T}_{b}-{T}_{nb}-m\cdot V({T}_{b})\end{array}$$

(11)

Multiparameter temperature compensation algorithm

In contrast to the two-point calibration method, the multiparameter compensation method accounts for the influence of the emissivity and environmental temperature of the measured object and linearly compensates for temperature measurement errors between sensors. The multiparameter compensation model is shown in Fig. 1.

During the temperature measurement process, several factors significantly influence the measurement results, including the cold junction temperature reference of the thermopile, the lack of uniformity among the thermopile sensors, drifts in the thermopile voltage response curve, the ambient temperature, the measurement distance, and the FOV. The electromotive force measured by the thermopile must be corrected when the cold junction temperature is not 273.15 K:

$$E(t,{t}_{0})=E(t,{t}_{n})+E({t}_{n},{t}_{0})$$

(12)

where $E({t}_{n},{t}_{0})$ represents the thermoelectric potential when the cold junction temperature is 273.15 K and the hot junction temperature is ${t}_{n}$. The lack of uniformity among the sensors is corrected via the linear calibration method:

$${E}_{1}(t,{t}_{0})=aE(t,{t}_{0})+b$$

(13)

Where coefficients a and b represent the calibration coefficients generated when linearly calibrating the detector. In addition, the influence of the emissivity of the object being measured on the thermopile temperature measurements must be considered. If a calibrated infrared temperature measurement device is used for temperature measurements under ideal conditions, assuming that the measured object is a blackbody, the actual measured signal is obtained after the sensor thermally interacts with the measured object, with an emissivity of ${\varepsilon }_{obj}$.

When sensors are used to measure the surface temperature of the object being tested, for the same ${P}_{in}$, according to the blackbody radiation formula, we have:

$${P}_{in}=\sigma {\varepsilon }_{S}K({\varepsilon }_{obj}\cdot {T}_{obj}^{4}-{T}_{n}^{4})$$

(14)

where $K=2AF{\sin }^{2}\left(\frac{\theta }{2}\right)$ is a constant, ${P}_{in}$ is the thermal radiation absorbed by the semiconductor material of the sensor, ${\varepsilon }_{obj}$ is the surface emissivity of the object being tested, ${\varepsilon }_{S}$ is the surface absorption rate of the sensor, ${T}_{obj}$ is the surface temperature of the object being tested, and ${T}_{n}$ is the ambient temperature during the transmission process.

When sensors are used to measure the surface temperature of a blackbody, for the same ${P}_{in}$, we have:

$${P}_{in}=\sigma {\varepsilon }_{S}K({\varepsilon }_{b}\cdot {T}_{b}^{4}-{T}_{n}^{4})$$

(15)

where ${\varepsilon }_{b}$ represents the emissivity of the blackbody surface and ${T}_{b}$ represents the set temperature of the blackbody surface. To express the relationship between the voltage response of the thermoelectric material and the temperature of the object being tested, we need to use the following formula:

For example, under the same ambient temperature ${T}_{n}$, for the same sensor voltage signal $\Delta V$, we have:

$$\left\{\begin{array}{c}\Delta V={\int }_{{T}_{c}}^{{T}_{h}}({S}_{B}(T)-{S}_{A}(T))dT=S\cdot \Delta P=S\cdot \sigma ({T}_{h}^{4}-{T}_{c}^{4})+800\\ \Delta V=\Delta P\cdot S=\sigma {\varepsilon }_{S}K({\varepsilon }_{obj}\cdot {T}_{obj}^{4}-{T}_{n}^{4})\cdot S \hfill \end{array}\right.$$

(16)

where ${S}_{A}$ and ${S}_{B}$ are the Seebeck coefficients of two thermoelectric materials, which are constant and do not change with temperature. ${T}_{h}$ represents the temperature at the hot end, and ${T}_{c}$ represents the temperature at the cold end.

$$\Delta V=\Delta P\cdot S=\sigma {\varepsilon }_{S}K({\varepsilon }_{b}\cdot {T}_{b}^{4}-{T}_{n}^{4})\cdot S$$

(17)

According to the blackbody radiation formula, the amount of thermal radiation emitted by the hot end of a sensor at thermal equilibrium is equal to the amount of thermal radiation absorbed, which can be formulated as follows:

$${P}_{in}=\sigma {\varepsilon }_{S}K({\varepsilon }_{obj}\cdot {T}_{obj}^{4}-{T}_{n}^{4})=\sigma {\varepsilon }_{S}K{T}_{h}^{4}={P}_{out}$$

(18)

Here, ${\varepsilon }_{b}=1$, and ${T}_{b}$ is the converted blackbody temperature. In addition, we have:

$$\sigma {\varepsilon }_{S}K({\varepsilon }_{obj}\cdot {T}_{obj}^{4}-{T}_{n}^{4})=\sigma {\varepsilon }_{S}K(V/S\cdot \sigma +{T}_{c}^{4})$$

(19)

where ${\varepsilon }_{obj}$, ${T}_{n}$ and ${T}_{c}$ are all known. When the environmental variables, including the nonzero correction at the sensor’s cold junction and the zero drift correction of the sensor, are incorporated, the relationship between the standard blackbody temperature and the sensor voltage difference is as follows:

$${T}_{obj}^{4}=\frac{(V/(S\cdot \sigma )+{T}_{c}^{4}+{T}_{n}^{4})}{{\varepsilon }_{obj}}$$

(20)

where ${\varepsilon }_{D}$ is the emissivity of the photosensitive surface of the detector. Combining Eq. (24) with Eqs. (2) and (9) yields:

$${T}_{obj}={\left(\frac{1}{{\varepsilon }_{obj}}(a{E}^{4}+b{E}^{3}{T}_{c}+c{E}^{2}{T}_{c}^{2}+dE{T}_{c}^{3}+\beta ({T}_{c}^{4}+{T}_{n}^{4})+\gamma )\right)}^{1/4}$$

(21)

Therefore, by measuring the output voltage of the sensor and using multivariate linear fitting, the $\alpha$, $b$, $c$, $d$, $\beta$, and $\gamma$ values of the 15 sensors can be calculated separately while correcting for the lack of uniformity among the 15 sensors during the fitting process.

System design

Design strategies for enhancing the thermal insulation of circuit boards

The thermopile-based temperature measurement array system comprises several core modules including a thermopile sensor array, PCB circuit board, dual-stage thermal insulation assembly (primary and secondary shields), oxygen-free copper thermal conduction plate, and precision linear guide rails. The hierarchically designed dual-stage thermal insulation system, consisting of primary and secondary shields, establishes a highly stable thermal environment through effective thermal isolation, significantly mitigating measurement interference caused by ambient temperature fluctuations. This innovative thermal insulation architecture, combined with the superior thermal conductivity of the copper conduction plate, ensures enhanced measurement accuracy and long-term system stability.

The thermal design primarily focuses on three critical components: the dual-stage insulation assembly and the copper thermal conduction plate:

Fabricated from high-strength aluminum alloy with hard-anodized surface treatment, the primary shield demonstrates enhanced structural integrity, corrosion resistance, and optimized thermal conductivity. Its innovative hollow-cavity design achieves weight reduction and low thermal mass while maintaining mechanical robustness. Internally integrated precision guide pillars ensure component alignment and secure fixation while minimizing parasitic thermal conduction paths, thereby establishing a stable thermal foundation for the measurement system (as illustrated in Fig. 2a).

Fig. 2: System structure rendering of thermopile temperature measurement array.

a Overall structure of temperature measurement system and rendering of testing environment; b Rendering of the first level thermal insulation cover structure of the temperature measurement array; c Rendering of copper thermal conductive plate and supporting base structure.

Machined from high-transparency acrylic polymer, the secondary shield exhibits three distinctive advantages: (1) The intrinsically low thermal conductivity of acrylic effectively blocks environmental heat exchange; (2) Optical transparency enables real-time visual monitoring of array operation and positional calibration; (3) The structural configuration accommodates measurement array displacement while maintaining thermal isolation efficiency.

This multifunctional thermal management component serves dual purposes as both structural support for the primary shield and high-efficiency heat distributor. Engineered with precision-machined interfaces ensuring optimal thermal contact, it leverages copper’s exceptional thermal conductivity (400 W/m · K) for rapid heat dissipation. The integrated thermal control system incorporates thermoelectric coolers (TECs) at both ends and ±0.1 °C-accuracy PT100 sensors, forming a closed-loop temperature regulation network that maintains plate temperature within ±0.3 °C of setpoint. Notably, the innovative integration of polytetrafluoroethylene (PTFE) insulation modules at guide rail interfaces effectively suppresses thermal bridging through their ultralow thermal conductivity and superior mechanical properties. This multiscale thermal management strategy achieves unprecedented baseline temperature stability for the thermopile array, ensuring reliable measurement accuracy across diverse environmental conditions (as shown in Fig. 2c).

This integrated thermal architecture demonstrates significant advancements in precision temperature measurement systems, particularly suitable for applications requiring high stability in thermally dynamic environments.

Because equipment heating is mainly an issue for FPGA modules and their supporting hardware circuits, to minimize the impact of the heat generated by the circuit boards on the accuracy of the thermopile sensors, the boards were divided into a data processing board and a sensor detection board. These boards were connected by a flexible flat cable (FFC), which was insulated with glass wool. The thermal imaging results after 2 h of board operation are shown in Fig. 3a. Figure 3b, c respectively shows clear schematic diagrams of the circuit board for comparison, with Fig. 3b showing the front and Fig. 3c showing the back. The image shows that the thermal insulation is very effective; the temperature of the sensor detection board was essentially unaffected by the heat generated by the data processing board, thus greatly reducing the thermal influence on the sensor detection results. To mitigate the impact of environmental humidity on the temperature measurement accuracy, clean, dry air was continuously introduced into the environment during the experiment. All experiments mentioned in this article were conducted in a constant temperature and humidity ultra clean room, and the dry air supplied was also provided by the laboratory’s inherent standard gas channel. The purpose of introducing dry air is to reduce environmental humidity and isolate the influence of water vapor in the testing environment. As for its impact angle on the sensor detection board, the entire experimental conditions were carried out in a clean environment with constant temperature and humidity, and dry air was introduced to ensure constant temperature. This strengthened the heat convection between the surface of the sensor board and the outside world, preventing heat accumulation on the surface of the sensor board and ensuring its temperature stability, which had a positive impact on the performance of the sensor board.

Fig. 3: Infrared image comparison during system operation.

a Infrared image of the effect of the insulation on the performance of the board; b Front circuit rendering of the board; c Back circuit rendering of the board.

Low-power design

Four measures are employed to constrain the power consumption of the board to within 1.5 W:

• (1) Selection of DC‒DC switching power supply chips with low quiescent current, automatic operating modes, and high conversion efficiency: the primary power supply chips are all highly efficient, highly integrated switching power supply chips, including MPM3630GOV-P, MPM3840GQV-P, and MPM38111GR-P. For circuits with stringent noise requirements on the power supply, linear regulators or voltage reference chips such as TPS7A8101DRBT and REF35120QDBVR are used.

• (2) Utilization of integrated chips with lower operating voltages and reduced power consumption: the selected peripheral functional chips could be powered with a low voltage of 1.8 V. Examples include OT705050MJBA4SL (crystal oscillator), MX25U12835FM2I-10G (FLASH), and low quiescent current, low-power consumption chips such as INA333AIDGKR (instrumentation amplifier), REF35120QDBVR (voltage reference chip), and AD7980BCPZ-RL (ADC). The chosen chip, XC7A50T (FPGA), has resources, functionalities, and pin counts that precisely meet the system requirements.

• (3) Reduction in the operating voltage within the permissible range of the power supply input: the supply voltage is reduced by 5% within the allowable range. All FPGA BANKs are powered by a low voltage of 1.8 V. The I/O pins of the ADC and RS485 chips can operate at 1.8 V.

• (4) Rational allocation of the power supply: appropriate power chips were selected on the basis of the voltage drop, load size, and efficiency. The power distribution within this system is illustrated in Supplementary Information. The power chips were chosen according to the voltage drop and load size requirements to maximize the conversion efficiency. For example, the core components of the FPGA, INT and AUX, which have relatively high current consumption, are powered by the MPM3840, which has high efficiency under heavy loads. The serial transceiver, which requires less current, is powered by the MPM38111GR-P chip, which has high efficiency under light loads. Since ADCs, operational amplifiers, and analog front‒end circuits have high demands for noise suppression, high-PSRR LDOs and voltage reference chips were selected. A system with a minimal LDO voltage drop has lower power consumption.

This thermometer has a working mode and a sleep mode. All circuit modules are powered on and operate in the working mode. The power consumption of the thermometer operating in working mode is shown in Table 1.

Table 1 Operating power of the temperature measurement array

The total power consumption of the circuit operating in working mode is less than 1.5 W. The detector- and instrument amplifier-related circuits on the detector board consume less than 0.04 W, so most of the power is used by the FPGA board. The FPGA board is connected to the detector board via the FPC, which can minimize the heat transfer from the FPGA board to the detector board.

In sleep mode, the optical port and 16-channel ADC enter standby mode, whereas the other circuit modules operate normally. As preheating is necessary after powering on the sensor, the temperatures of the board and the external environment need to stabilize before the maximum temperature measurement accuracy can be achieved. During testing, half an hour to an hour of preheating is needed to reach the ideal state. Before stabilization, due to the instability of the board and sensor, the measurement results may fluctuate within a certain range, which affects the measurement accuracy. Therefore, the detector-related circuit remains powered on in sleep mode so that measurements can start without waiting for the system to preheat. A wake-up command can be sent through the RS485 interface to restore the circuit to normal operation.

The power consumption of the system operating in standby mode is shown in Table 2.

Table 2 Standby power of the temperature measurement array

The total power consumption of the circuit operating in standby mode is less than 0.5 W. Experimental data shows that the background temperature of the sensor needs to gradually increase from the initial ambient temperature (22 °C) to the stable operating temperature (26.0 ± 0.5 °C) to ensure optimal stability of the thermoelectric potential output by the thermoelectric stack array. If preheating is insufficient, the temperature fluctuation in the first 10 min is close to ±0.5 °C; After sufficient preheating, the temperature drift of the system can be controlled within 15 mK within 6 h. Although this process is time-consuming, it is a necessary foundation for achieving mK level accuracy. To optimize the availability of practical application scenarios, the system has introduced a low-power standby mode. In this mode, the core circuit of the detector is continuously powered (with a power consumption of 0.5 W) to maintain the temperature stability of the sensor board, while the data acquisition and amplification module is turned off (saving 1 W of power consumption). This design enables the system to instantly wake up (response time <1 s) and maintain an accuracy of 20 mK, effectively avoiding the operational burden of repeated preheating, especially suitable for industrial testing scenarios that require frequent start stop. The comparison with existing equipment further highlights the performance advantages of this solution. For example, although the commercial infrared thermometer HORIBA IT-470 does not require preheating (can work in <5 min), its steady-state accuracy can only reach ±0.1 K, and there is no significant difference in measurement error between the initial stage and after preheating. In contrast, the accuracy of this system during preheating (50 mK) is significantly better than that of such devices, while the accuracy after sufficient preheating (15 mK) is closer to scientific grade instruments (such as FLIR A35’s 30 mK), but the power consumption is reduced by about 50% (1.5 W vs. 3.2 W).

Thermopile signal conditioning circuit: principles and parameter calculations

The signal conditioning circuit for thermopile detectors, as depicted in Supplementary Information, which shows the readout circuit and two-stage amplification circuit of the detector. The voltage signal of the Thermopile module is amplified in the first and second stages before entering the ADC chip for reading, this facilitates the amplification of the detector’s output signal through a dual-stage amplifier configuration prior to analog-to-digital conversion (ADC) sampling.

In the initial amplification stage, an instrumentation amplifier, specifically the INA333, is employed, with the gain factor contingent upon the resistance value of R2; a 200 Ω resistor corresponds to an amplification factor of 500. The output voltage from the first-stage amplifier can be calculated as follows:

$${V}_{{{OUT}}1}=500({V}_{{{TP}}+}-{V}_{{{TP}}-})+{V}_{{{REF}}}$$

(22)

If the temperature detected by the thermopile is lower than the ambient temperature, the differential voltage (${V}_{{{TP}}+}-{V}_{{{TP}}-}$) has a negative value. To address this issue and ensure a consistently positive output voltage, a bias voltage is introduced via pin 5. In this design, a voltage reference chip provides a 1.2 V output, which is subsequently reduced to 0.4 V through a resistive network to serve as the bias voltage.

In the second amplification stage, an LTC6081 operational amplifier is employed in a noninverting proportional amplification circuit, and the output voltage is calculated as follows:

$${V}_{{{OUT}}2}={V}_{{{OUT}}1}\left(\frac{R5}{R4}+1\right)$$

(23)

Incorporating the design parameters of the circuit into the formula yields:

$${V}_{{{OUT}}2}=1000({V}_{{{TP}}+}-{V}_{{{TP}}-})+0.8$$

(24)

According to the characteristics of the thermopile detector, when the ambient temperature is equivalent to the detection temperature, ${V}_{{{TP}}+}-{V}_{{{TP}}-}=0{{\rm{V}}}$, resulting in a ${V}_{{{OUT}}2}$ value of 0.8 V. If the detection temperature exceeds the ambient temperature, ${V}_{{{TP}}+}-{V}_{{{TP}}-} > 0{{\rm{V}}}$, resulting in ${V}_{{{\rm{OUT}}}2}$ exceeding 0.8 V. Conversely, if the detection temperature falls below the ambient temperature, ${V}_{{{TP}}+}-{V}_{{{TP}}-} < 0{{\rm{V}}}$, leading to a ${V}_{{{OUT}}2}$ value that is less than 0.8 V.

Because the maximum voltage of the ADC is 2 V, it is important to ensure that the detector output, after amplification, covers the voltage range of the ADC as much as possible. Assuming that V_OUT2 is 0 ~ 2 V, the difference in the detector output voltage is −0.8 ~ 1.2 mV. When the ambient temperature is 25 °C, the target detection temperature corresponding to the detector output of −0.8 ~ 1.2 mV is approximately 17 ~ 38 °C. The actual target temperature that needs to be detected in this design is 20 ~ 30 °C. Considering that changes in the environmental temperature can result in variations in the detector output, the measurement temperature range must be increased appropriately. In this design, a magnification factor of 500 × 2 is used to meet the detection requirements.

Result

In the experimental phase, the infrared high-precision temperature array was calibrated using the HGY-50×50 standard blackbody (specific parameters of the blackbody are detailed in Supplementary Table 2) radiation source developed in-house by our research group. The parameters of the blackbody radiation source are shown in Supplementary Information, and the parameters of the thermopile sensors used in the temperature array are listed in Supplementary Information. Since the actual operating range of the temperature array is 295.15–300.15 K, the temperature range of the standard blackbody radiation source was set to 293.15–303.15 K. The temperature array was calibrated within this temperature range. Next, the calibration results of the two-point calibration method are compared with those of the multiparameter compensation method.

Traditional two-point calibration temperature compensation algorithm

Firstly, conduct an analysis of traditional methods³³. Our experimental framework is divided into two different stages. (1) Retain the traditional multi-point linear fitting method (11 temperature points, 20–30 °C) as the control group for single sensor calibration. (2) Array level non-uniformity correction: subsequently, the two-point method (23 °C/27 °C) is used to address the inter sensor variations of the entire linear array. As shown in Table 3, the traditional two-point calibration method was used to evaluate and verify the calibration results using a temperature measurement array and a blackbody radiation source. Using this method, eleven temperature points from 293.15 K to 303.15 K were selected for calibration. The traditional polynomial fitting method was used, and after fitting, the linear array was non uniformly corrected using two-point calibration at two temperature points of 297.15 K and 300.15 K. The responses of 15 sensors were recorded separately. (Note: During testing, the voltage response of the NTC thermistor does not fluctuate by more than 20 mV around 1470 mV.).

Table 3 Data required for calibration

The temperature inversion formula is

$$T=m\cdot (a\cdot {V}_{OUT}+b)+n$$

(25)

Where m and n are non-uniform fitting coefficients, while a and b are polynomial fitting coefficients. The calculation of a and b here comes from least squares fitting, while the calculation of m and n will be discussed in the “Methods” section later. Using the temperature measurement array calibrated with the two-point calibration method, the blackbody temperature was set to 293.15–303.15 K with a step size of 1 K. The maximum absolute error reached 1.57 K, and the average error was 0.4258 K, indicating relatively large errors.

Multiparameter temperature compensation algorithm

The temperature of the standard blackbody radiation source was adjusted to 293.15 K, 295.15 K, 297.15 K, 299.15 K, 301.15 K, and 303.15 K. The voltage responses of the detector at these temperatures and the temperature of the board at the corresponding measurement point were recorded. The recording results are shown in Fig. 4a. Given a blackbody emissivity of 0.998, a mathematical model was theoretically established to fit the data, and the fitting result represents the calibration result of the detector for a blackbody source. The voltage values output by the 15 sensors and the NTC thermistor (used to monitor the environmental temperature) were recorded at each temperature point. Each voltage value was the average of 10 sets of temperature data taken within 10 ms before and after the measurement to ensure the validity of the calibration data. The data averaging and acquisition processes were performed via computer software. Figure 4b shows the voltage values output by the temperature measurement array and the voltage values of the NTC thermistor measured at each temperature point. As the temperature of the test object increased, the voltage values of the sensors increased. Moreover, as the environmental temperature increased, the temperature of the NTC thermistor increased, resulting in a decrease in the resistance of the thermistor and a corresponding decrease in the voltage output by the NTC thermistor. Since the environmental temperature at each temperature point was different, compensation for the environmental temperature was necessary when calibrating the temperature‒voltage relationship.

Fig. 4: The temperature‒voltage relationship.

a The temperature‒voltage relationship after determining the detector parameters. b The temperature‒voltage relationship after parameter fitting.

The “regress” function in MATLAB 2020 was used to fit the collected temperature data according to the mathematical model described in Formula (24). Table 4 shows the software fitting parameters. The calculated ${R}_{2}=0.999$ indicates the good fit of the proposed model.

Table 4 Data required for calibration

The fitted parameters were then substituted into Formula (24) and programmed into the FPGA. This allowed the FPGA to directly output high-precision temperature data with appropriate compensation. The calibrated temperature measurement array was further evaluated and tested with a standard temperature measurement instrument.

The calibration and verification of the performance of the high-precision infrared temperature array were performed with an actual test object (15 mm × 15 mm fused quartz plate with a Cr coating), and the results were referenced to those observed with a standard instrument.

Test system

The experimental system is shown in Fig. 5. Figure 5a shows the overall experimental system, including a constant-temperature water bath (FLUKE 7011, Refrigerated Temperature Calibration Baths), a power supply, a temperature measurement instrument (FLUKE1586A, a calibrated thermometer with an accuracy of 0.001 K), test equipment and a computer. Figure 5b shows the components of the testing equipment. The test object was placed on a copper heating plate (⑥) and attached to the copper base in a constant-temperature water bath. Pure water was added to the water bath to partially immerse the copper block; then, the water bath was heated. The temperature measurement array was isolated from the environment with a thermal insulation cover (②) to reduce the influence of the external temperature on the temperature array. The entire test setup was further isolated from the environment with an acrylic cover (⑤) to minimize the impact of environmental factors on the performance of the system. The PT1000 sensor (①) linked to the fluke thermometer was attached to the surface of the test object via tin foil tape to enable accurate contact temperature measurements of the test object. Owing to the temperature difference between the set temperature of the refrigerated temperature calibration baths and the actual temperature of the measured object, the temperature value measured by the PT1000 device was taken as the actual temperature measurement result. The temperature measurement array system was fixed on a bracket to align with the test object (⑦), and the measuring height was adjusted within a small range without affecting the sensor’s FOV. The measuring height was controlled within 41.65 mm ± 10 mm via a sliding rail. The horizontal position (③) and height (④) of the temperature measurement array were adjusted via the sliding rail.

Fig. 5: Standardized testing environment for temperature measurement systems.

a Overall experimental system; b Composition of the testing equipment.

Owing to the time required for the water bath to heat the surface of the test object uniformly, the temperature of the constant-temperature water bath was set with a temperature controller. Starting at 293.15 K, the temperature was increased by 1 K every hour until it reached 303.15 K. The temperature measured by the PT1000 contact thermometer was considered the actual surface temperature of the test object. The temperature values output by the 15 sensors and the NTC thermistor (used to monitor the environmental temperature) were recorded at each temperature point. As shown in Fig. 6a, the results obtained with the PT1000 temperature sensor were compared with those obtained with the infrared measurement array to determine the temperature measurement error. The horizontal axis represents the average temperature values of the PT1000 sensors at different test points, and the vertical axis represents the temperature measurement results of the 15 recording channels in the temperature measurement array.

Fig. 6: Error analysis of measurement results of the calibrated temperature measurement array for the test object.

a Fitting error under different channels and temperatures. b Absolute error at a single channel or temperature. The pink shaded area represents the maximum upper and lower error of 10 repeated measurements of the temperature of multiple channels at a single temperature point. The brown area represents the maximum upper and lower errors of 10 repeated temperature tests conducted on a single channel at multiple temperature points. c All the temperature data measured within the 6-h period.

Figure 6b depicts the errors of a single sensor (ch7) undergoing multiple tests at 11 temperatures and a sensor with 15 channels at a fixed temperature (299.15 K) for each channel. The y-axis represents the absolute error between the measured temperature and the standard temperature, and the curve width represents the repeatability error of multiple repeated tests. The absolute temperature measurement error does not surpass 25 mK compared with the results of the calibrated standard temperature measurement apparatus.

In addition, the temperature measurement array was continuously powered for 6 h, and temperature rise and fall cycling tests were conducted. The collected data were used to evaluate the system’s repeatability, sensor nonuniformity, and stability. Figure 6c shows all the temperature data measured within the 6-h period. A temperature point in the testing environment that was completely stable around the 150th minute was selected when the temperature of the test object was 295.15 K. A data acquisition board was used to collect temperature data 100 times for storage and analysis (i.e., 100 data points for each channel). Thus, we obtained 1500 data points. The maximum (${T}_{\max }1 \sim {T}_{\max }15$) and minimum (${T}_{\min }1 \sim {T}_{\min }15$) values were obtained from the 100 data points of each channel separately. $|{T}_{\max }-{T}_{\min }|={S}_{e}$. ${S}_{e}$ represents the repeatability error of the entire circuit board. T_max1 represents the maximum value among the 100 temperature data collected by the first thermopile sensor, similarly T_max15 represents the maximum value among the 100 temperature data collected by the 15th thermopile sensor, T_min1 represents the minimum value among the 100 temperature data collected by the first thermopile sensor, and T_min15 represents the minimum value among the 100 temperature data collected by the 15th thermopile sensor. For each thermopile sensor, subtracting the minimum temperature value from the maximum value of the 100 temperature data collected represents the repeatability error of the sensor test, that is, the error of each repeated collection. So each sensor calculates a repeatability error, with the first path being Se1, the 15th path being Se15, and the rest being the same. The 15th channel has the worst repeatability performance with a repeatability error of 5.5 mK, while the 7th channel has the best performance with a repeatability error of 2.8 mK. The repeatability errors of the sensors in the remaining channels are between these two. In addition, the standard deviation distribution of temperature data measured by each sensor (D1 ~ D15) was also calculated. The difference between the maximum and minimum errors between the 15 sensors was 11.9 mK, indicating that the control of non-uniformity errors between the channels of the line sensor has reached a high level. Additionally, the sensors exhibited stable performance and maintained good accuracy and uniformity during the 6-h continuous operation. In the 6-h test, by comparing the maximum error between the measured values and the true values at each temperature point before and after 6 h, the decrease in the temperature measurement accuracy did not exceed 1.5 mK (the change in the temperature of the constant-temperature water bath was less than 0.7 mK).

Discussion

In the 1 × 15 temperature measurement array designed in this study, the influence of environmental factors and the self-heating of the circuit board on the temperature measurement module is considered, enhancing the accuracy of the infrared temperature measurement array. Moreover, a multiparameter method is employed to compensate for the temperature of the measurement array, and the compensation results are compared with those of the two-point calibration method for the same temperature measurement array. The results demonstrate that the use of the multiparameter temperature compensation method can significantly improve the accuracy of the infrared temperature measurement array. This study provides new approaches for algorithms and the thermal design of circuit boards to comprehensively increase the accuracy of infrared temperature measurement arrays. Moreover, the proposed approaches were applied in semiconductor manufacturing and temperature calibration applications and could be used in other fields.

In this study, the calibration of thermopile sensors is based on a self-developed multi parameter temperature compensation model, aiming to simultaneously solve the problems of calibration, environmental temperature compensation, and sensor array non-uniformity correction. The calibration experiment is conducted within the temperature range of 20–30 °C (with a step size of 1 °C and a total of 11 calibration points), covering typical industrial application scenarios. During the calibration process, a high-precision blackbody radiation source (HGY series, emissivity 0.998 ± 0.002, temperature stability ±0.05 mK) was used as the reference. 100 sets of voltage temperature data were collected at each temperature point, and the Seebeck coefficient, radiation coupling coefficient, and non-uniformity compensation matrix were back calculated using the least squares fitting and nonlinear optimization algorithm (Levenberg Marquardt). This method integrates the traditional step-by-step calibration process into a unified framework, improving calibration efficiency to 30% of traditional methods while ensuring that the maximum error in the entire temperature range is controlled within ±0.03 K (Fig. 6b). In response to long-term stability issues, this study validated the reliability of the system through 6-h continuous testing. The experimental data shows that the drift of temperature measurement error with time does not exceed 1.5 mK (Fig. 6c). In response to this, we discussed the temperature drift problem in different usage scenarios based on different situations: in high-precision scenarios (error ≤30 mK): It is recommended to recalibrate every 6 months, Under conventional precision scenarios (error ≤50 mK): it can be extended to calibrate once a year, In addition, to extend the lifespan of the sensor, we propose practical suggestions: enabling sleep mode during non working hours (turning off the amplifier circuit, standby power consumption less than 0.5 W) can improve the average lifespan of the sensor; If the working environment is harsh (temperature >50 °C or humidity >80%), it is recommended to shorten the calibration cycle to 3 months.

Notably, the multiparameter fitting method and thermal design of the circuit boards in this study represent preliminary explorations for further improving the accuracy of infrared temperature measurement arrays. In future research, we will consider more factors that may influence the accuracy of infrared temperature measurement arrays, such as the slight temperature difference between the two ends of the sensor detection board and the temperature difference between the internal and external environments after thermal insulation. Additionally, we will explore further enhancements in the real-time performance of temperature measurement arrays.

Conclusion

Improving the accuracy of infrared temperature measurement sensors is crucial for expanding their applicability. This paper presents a board in which both thermal design and low power consumption were considered. In addition, a multiparameter temperature compensation algorithm is presented to increase the accuracy of infrared temperature measurements. An extensive dataset including 100,000 temperature measurements was collected for experimental comparison. The postcompensation results indicate that compared with the traditional two-point temperature compensation method, the proposed method improved the accuracy from 1.7 K to 25 mK, representing an enhancement of 97.47%. Moreover, sensor consistency errors are compensated for and reduced to 15.9 mK. Therefore, the proposed design and method are appropriate for scenarios in which more precise temperature measurements are required. Furthermore, the infrared temperature array designed in this study was applied in semiconductor manufacturing and blackbody calibration applications. After 6 h of continuous operation, the decrease in the temperature measurement accuracy did not exceed 1.5 mK.