Introduction

Non-destructive testing (NDT) is essential in industries such as aviation and construction1,2. Professionals often use NDT methods to assess the safety and condition of materials, components, or complete structures without causing any damage or alterations3,4,5. The primary goals of NDT include maintaining strict safety standards, preventing potential structural failures, and efficiently managing maintenance expenses. Eddy current testing (ECT) is a highly favored NDT technique due to its accuracy and rapid inspection capabilities. Inspectors place a specially designed excitation coil near the material surface, which induces ECs within the material. Any defects, like cracks or corrosions, interfere with these currents and produce noticeable changes in the electromagnetic signals received by the detection coil. Inspectors interpret these changes carefully to identify and assess the size and location of the defects6,7,8. A major advantage of ECT is its ability to perform inspections without physically touching the object. Based on the working principle of the ECT, two essential conditions must be satisfied for effective crack detection: first, the EC field induced by the ECT sensor within the test specimen must be sufficiently sensitive to clearly reflect disturbances caused by cracks; second, the ECT sensor must effectively detect variations in the secondary magnetic field resulting from the distortion of these ECs by cracks9,10,11.

The first condition is influenced by several factors, including the sensor coil configuration, the frequency of the excitation signal, the electromagnetic properties of the specimen being measured12, and the distance and relative position between the sensor and the test specimen. Among these factors, the coil structure plays the most decisive role, as it directly affects the penetration depth and spatial distribution of the EC field generated within the test specimen. Recently, many studies have proposed innovative design solutions that effectively meet these conditions. For example, flexible eddy current array (FECA) sensors have been fabricated by soldering parallel and staggered coils onto flexible printed circuit board (FPCB)13, FECA sensors have been applied to detect sub-surface defects in hollow shafts14,15, new FEC sensors utilizing a two-coil square excitation configuration combined with a multi-detection array have been developed to enhance crack detection capabilities16, and FEC sensors with a serpentine array design, based on the superposition principle and etched directly onto a flexible circuit board with a bidirectional curved structure, have been introduced to improve detection performance17. Additionally, by actively adjusting the direction of the EC field in the time domain, rotating field EC sensors have demonstrated the ability to significantly reduce the issue of uneven sensitivity when detecting short cracks oriented in different directions18,19. However, due to the limitation of wiring space, the number of turns in the coil of the FEC sensor is small, resulting in weak sensing signals. Therefore, solutions such as employing a multi-layer structure to increase the density of wire turns or integrating a signal amplification circuit directly at the measurement area to compensate for the low signal intensity have been implemented. However, the multi-layer structure affects the flexibility of the FECA sensor.

To meet the second condition, the effective collection of secondary magnetic fields caused by ECs disturbed by cracks primarily relies on highly sensitive sensing elements. Among the existing methods, many sensors utilize the giant magnetoresistance (GMR)20,21,22 and tunneling magnetoresistance (TMR)23,24,25 effects to enhance measurement sensitivity. For example, a novel TMR-based eddy current probe with double-cylinder magnetic shielding was proposed for high-sensitivity inspection of non-ferromagnetic metals26. However, since these elements are typically packaged in chip form27, the flexibility of the sensors is significantly limited. This makes them unsuitable for testing curved surfaces, reducing their applicability in industrial environments, where adaptability to the shape of the measured object is highly required. Recent developments have explored innovative sensing architectures to address similar limitations. For instance, a zero-magnetic zone sensing structure was proposed to achieve high-resolution defect visualization by suppressing background interference and enhancing spatial resolution across the sensing plane28. Additionally, a neuromorphic-induced electrodynamics model was recently introduced to support intelligent reinforcement-based actuation and sensing, demonstrating adaptive learning capabilities in complex environments29. These works highlight the ongoing trend toward highly sensitive, spatially adaptive, and intelligent sensor systems.

Therefore, to improve the performance of the FECA sensor, this study develops a novel FECA sensor consisting of 6 bendable channels for crack detection in weld zones of steel structures. The excitation coils of the 6 channels are connected in series to apply a high frequency excitation current. In addition, the detection coil is strategically interleaved with the excitation coil on the same plane to eliminate lift-off effects and interact with ECs at their peak intensity location, thereby enhancing crack detection capability in test specimens. This study also develops a real-time FECA measurement system incorporating the proposed FECA sensor and a Lock-in amplifier implemented in LabVIEW to replace traditional high-cost hardware Lock-in amplifiers. The sensor’s performance was validated through experiments detecting surface and sub-surface cracks in weld zones from various steel structures.

Results

Challenges of the ECT and proposed FECA sensor design

A theoretical model describing the operating principle of the ECT sensor is shown in Fig. 1a. When an alternating current flows through the excitation coil, it generates a primary magnetic field. When the ECT sensor is placed near a conductive material, the electromagnetic induction phenomenon generates EC inside the test specimen. These ECs further generate a new magnetic field, often called a secondary magnetic field, which has an opposite direction to the primary magnetic field. The presence of cracks or defects disrupts the EC, resulting in a change in the voltage or impedance of the sensor coil.

Fig. 1: Proposed FECA sensor for ECT.
figure 1

a Principle of ECT sensor. b Effect of excitation frequency intensity on EC penetration depth. c Proposed FECA sensor with 6 channels. d Design and specifications of FECA sensor.

Full size image

In the ECT method, there are two main factors to consider: penetration depth and lift-off (distance from sensor to test specimen surface), which directly affect the ability to detect and evaluate cracks. For the first factor, the excitation frequency determines the penetration depth of the EC into the test specimen, as shown in Fig. 1b. Specifically, the penetration depth \(\delta\) is determined by the following formula:

$$\delta =\frac{1}{\sqrt{\pi f\mu \sigma }}$$
(1)

where \(f\) is the excitation frequency, \(\mu\) is the permeability of the material, and \(\sigma\) is the conductivity. From this formula, as the frequency increases, the penetration depth decreases, the ECs are more concentrated at the surface of the test specimen, which helps detect surface cracks effectively. Conversely, as the frequency decreases, the ECs can penetrate deeper into the test specimen, allowing subsurface cracks to be detected, but the resolution decreases due to decreased signal-to-noise ratio (SNR) in the signal. For the second factor, lift-off reduces the signal amplitude due to the decrease in the intensity of the induced magnetic field in the test specimen. As lift-off increases, the induction effect of the ECs decreases, reducing the sensitivity to crack detection.

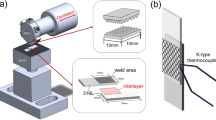
Conventional FECA sensors have a small number of turns in the excitation coil due to the limited wire space13,30, resulting in a weak sensing signal. Some solutions, such as using a multilayer structure to increase the turn density16,31, can reduce the flexibility of the sensor. To overcome this problem, we developed a novel FECA sensor with six bendable channels (Fig. 1c). This sensor has the excitation coils of the six channels connected in series, enabling a higher excitation frequency, thereby enhancing the weak EC signal caused by the limited number of turns in conventional FECA sensors. Furthermore, the sensor has only one layer, which maintains the flexibility of FECA sensor. In addition, the detection coils are strategically interwoven with the excitation coil on the same plane (Fig. 1d), which eliminates the lift-off effect and optimizes interaction with ECs at the location of maximum intensity, thereby enhancing crack detection in the test specimen. The excitation coil (orange) is manufactured according to strict design specifications, with a width of 100 \({{{\rm{\mu }}}}{{{\rm{m}}}}\) and thickness of 3 \({{{\rm{\mu }}}}{{{\rm{m}}}}\). Meanwhile, the detection coil (blue) is designed with a smaller size, having a width of 50 \({{{\rm{\mu }}}}{{{\rm{m}}}}\) and a thickness of 3 \({{{\rm{\mu }}}}{{{\rm{m}}}}\), suitable for effectively collecting magnetic field signals. The distance between the two coils is fixed at 35 \({{{\rm{\mu }}}}{{{\rm{m}}}}\) to ensure optimal interaction between the excitation field and the measurement signal. For each channel, both the excitation coil and the detection coil have 25 turns, resulting in a total of 150 turns for the excitation coil in the entire system. Each channel measures approximately 10 mm × 10 mm, as shown in Fig. 1d. The selection of the coil sizes is not only considered for technical requirements but also for optimizing the overall structure of the sensor. This design makes the system compact, easy to integrate into practical applications, especially in industrial environments, where a suitably sized device is required while still ensuring high measurement performance. The principle of the proposed FECA sensor is detailed in Supplementary Note 1 and Supplementary Fig. S1.

LabVIEW-based Lock-in amplifier

We have developed a custom LabVIEW-based Quadrature Lock-in Amplifier to achieve real-time, multi-channel signal processing, something typically not feasible with conventional commercial lock-in hardware. Figure 2 illustrates the Lock-in amplifier operation for a channel. In ECT, a Lock-in amplifier is used as a specialized tool to capture and analyze small signals hidden within noise by synchronizing the measured signal with a reference signal of known frequency and phase32, as shown in Fig. 2a. Typically, the induced signal obtained from an ECT probe is very weak, particularly when detecting small defects or operating under large lift-off conditions, causing ambient noise to easily mask the desired signal. In such cases, the Lock-in amplifier functions to extract only the signal component matching the frequency of the excitation signal while suppressing most background noise33. This significantly improves the SNR, enhancing the ability to detect and quantify minor defects such as cracks or corrosion in conductive materials. However, a major limitation of commercial Lock-in amplifiers is their high cost, coupled with their capability to process only one signal channel at a time. This makes implementing multi-point, multi-sensor measurement systems in ECT complex and costly, especially for applications requiring simultaneous data collection from multiple locations. For this reason, this study developed a multi-channel Lock-in amplifier programming solution using LabVIEW software.

Fig. 2: Lock-in amplifier operation for a channel.
figure 2

a Block diagram of Lock-in amplifier. b LabVIEW-based Lock-in amplifier program.

Full size image

The Quadrature Lock-in Amplifier (QLA) simultaneously determines the amplitude and phase of very small signals obscured by background noise. The QLA operates by demodulating the input signal using two orthogonal reference signals, typically sine and cosine functions. In practice, the phase of the measurement signal can fluctuate or shift relative to the reference signal due to factors such as system delays or non-ideal measurement conditions. To overcome this problem, QLA allows the signal to be acquired independently of the phase change, thereby providing higher stability and reliability compared to the traditional lock-in method using only one reference signal.

In this study, we implemented a digital QLA system using LabVIEW instead of a hardware-based solution for easier deployment, flexibility, and adaptability. Figure 2b describes the signal processing steps performed inside a lock-in amplifier program. Initially, we obtained the input signal waveform \(S(t)\) and the reference signal waveform \(R(t)\) from the acquisition process. Using the “Get Waveform Components” node, the data values of these waveforms, denoted as \({S}_{s}\left(t\right)\) and \({R}_{r}(t)\), are extracted. In theory, the input signal \({S}_{s}\left(t\right)\) is split and independently multiplied by both the reference signal \({R}_{r}\left(t\right)\) and its 90° phase-shifted counterpart. However, in this case, the Hilbert transformer is used to generate the 90° phase-shifted version of \({R}_{r}(t)\), where \({R}_{r}\left(t\right)=\cos ({{{\rm{\omega }}}}{{{\rm{t}}}})\) with \(\omega =2\pi f\), as expressed in Equation 2.

$$h\left(t\right)={{{\mathcal{H}}}}\left\{{R}_{r}\left(t\right)\right\}=\frac{1}{\pi }{\int }_{-{\infty }}^{{\infty }}\frac{{R}_{r}\left(\tau \right)}{\pi \left(t-\tau \right)}d\tau$$
(2)

This integral can be challenging to evaluate directly, so in the Hilbert node, the frequency domain representation is often utilized for more straightforward computation. Algorithm describes the details of the Hilbert transform process applied to \({R}_{r}\left(t\right)\). In the frequency domain, the Hilbert transform introduces a phase shift of −90° (or \(-\frac{\pi }{2}\) radians) to the positive frequencies and +90° (or \(+\frac{\pi }{2}\) radians) to the negative frequencies. This can be expressed as multiplication by \(-{jsgn}(f)\) in the frequency domain, where \({{\mathrm{sgn}}}(f)\) is the sign function. The symbol \(\delta\) denotes the Dirac delta function.

Hilbert Transform of \({S}_{r}(t)\)

Fourier Transform of \(\cos \left(\omega t\right)\)

\({{{\mathcal{F}}}}\left\{\cos \left(\omega t\right)\right\}=\pi \left[\delta \left(f-\frac{\omega }{2\pi }\right)+\delta \left(f+\frac{\omega }{2\pi }\right)\right]\)

Apply Hilbert transform to \({{{\mathcal{F}}}}\left\{\cos \left(\omega t\right)\right\}\)

\(H(f)=-{jsgn}(f){{{\mathcal{F}}}}\left\{\cos \left(\omega t\right)\right\}\)

Where sgn (f) is the sign function, which is sgn of (f) \(=\left\{\begin{array}{c}1{for}f > 0\\ 0{for}f=0\\ -1{for}f < 0\end{array}\right.\)

The transformed function

\({{{\mathcal{F}}}}\left\{h(t)\right\}=H(f)=-j\frac{1}{2}\delta \left(f-\frac{\omega }{2\pi }\right)+j\frac{1}{2}\delta \left(f+\frac{\omega }{2\pi }\right)\)

Inverse Fourier Transform

\({{{{\mathcal{F}}}}}^{-1}\left\{H(f)\right\}={{{\mathcal{H}}}}\left\{{R}_{r}\left(t\right)\right\}=h\left(t\right)=\sin \left(\omega t\right)\)

After obtaining the 90° phase-shifted copy of \({R}_{r}(t)\), we multiply the input signal \({S}_{s}(t)\) with two reference signals, resulting in the in-phase component \(I(t)\), as shown in Equation 3, and the quadrature component \(Q(t)\), as shown in Equation 4. Then, the AC & DC Estimator node applies to the Hanning window to sufficiently separate AC energy from the DC component. This step is crucial because it ensures that the measured amplitude corresponds to the actual modulated signal rather than any steady state offset. The outputs of the AC extractor, resulting in \(X=I(t)\) and \(Y=Q(t)\), represent the signal as a vector. The amplitude \({{{\mathcal{R}}}}\) is easily computed from \(I(t)\) and \(Q(t)\) by applying the Re/Im to Polar node, as shown in Equation 5.

$$X=I\left(t\right)={S}_{s}\left(t\right) {{{\bullet }}} \cos \left(\omega t\right)$$
(3)
$$Y=Q\left(t\right)={S}_{s}\left(t\right) {{{\bullet }}}\sin \left(\omega t\right)$$
(4)
$${{{\mathcal{R}}}}=\sqrt{{X}^{2}+{Y}^{2}}$$
(5)

Real-time FECA measurement system

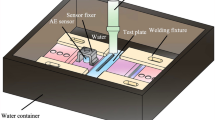
Figure 3 illustrates a schematic diagram of the real-time FECA measurement system. In this setup, a signal generated from the signal generator is transmitted through a high-speed bipolar amplifier, which provides the excitation current to the excitation coil of FECA sensor. The test specimen depicted in the figure represents a weld zone area, where the FECA sensor is positioned to detect cracks. The DAQ is directly connected to a computer with LabVIEW software installed, which has integrated into the Lock-in amplifier program based on LabVIEW. This program plays an important role in processing and displaying real-time signals. Through this program, detection signals from 6 channels are quickly analyzed and displayed visually, supporting the process of evaluating and detecting cracks accurately and effectively during the measurement process.

Fig. 3: Real-time FECA measurement system integrated with a LabVIEW‑based lock‑in amplifier.
figure 3

A signal from the synthesizer generator is fed to a high‑speed bipolar amplifier, which drives the excitation coil of the Flexible Eddy Current Array (FECA) sensor placed over the weld zone of the test specimen. The sensor outputs six detection channels that are conditioned by operational amplifiers and digitized by the Data Acquisition (DAQ), then processed and displayed in real time by a LabVIEW-based lock-in program on the computer.

Full size image

As shown in Fig. 1b, the FECA measurement system is used to evaluate surface and sub-surface cracks of the test specimen. When evaluating surface cracks, the system uses a high excitation frequency, resulting in the EC density being concentrated mainly at the surface layer of the test specimen. In this case, the intensity of the detected signal is relatively large, strong enough to be transmitted directly to the DAQ device and the LabVIEW-based Lock-in amplifier program without the need for an operational amplifier. However, when evaluating sub-surface cracks of the test specimen, it is necessary to use a low excitation frequency to increase the penetration depth of the EC. At that time, the EC density inside the test specimen decreases, resulting in a very small detection signal intensity, which is easily mixed with background noise. Therefore, the use of an operational amplifier is necessary to amplify the signal and eliminate noise, ensuring the best quality of the DAQ input signal. The detailed structure and operating principle of this amplifier are described in Supplementary Note 2 and Supplementary Fig. S2.

Experimental results of crack detection in test specimens from various steel structures

The experimental results on two flat test specimens (low carbon steel SS400) with cracks located at the surface of the weld zones, as shown in Fig. 4, clearly illustrate the ability to detect cracks of different orientations using the proposed measurement system. The scanning direction of the FECA sensor was aligned along the direction of the weld zone. This scanning process can be referred to in Supplementary Movie 1. The crack dimensions are illustrated specifically in Fig. 4a, where the symbol L represents the length, W represents the width, and D represents the depth of the cracks. For surface cracks, it is necessary to use high excitation frequency (500 kHz) to concentrate the EC density primarily in the specimen’s surface layer. As a result, the signal obtained from the detection coils are sufficiently large, allowing the real-time FECA measurement system (Fig. 3) to operate without requiring an operational amplifier. With the real-time FECA measurement system, the scanning of the weld zone was performed manually with the FECA sensor, so an encoder could not be used to accurately determine the crack signal location. To ensure the accuracy of the crack signal graph, the signals obtained from the 6 channels were manually aligned so that the crack signal was accurately reproduced. In this process, the x-axis value of the measurement result graph was defined as “distance,” which depends on both the scanning speed and scanning duration. Since the scanning was performed manually, the scanning velocity could not be precisely controlled, resulting in a non-uniform variation in distance values in each scan.

Fig. 4: Experimental results with flat test specimens.
figure 4

a Test specimen #1 (left) has cracks S1 and S2 perpendicular to the weld zone direction, and test specimen #2 (right) has cracks S3 and S4 parallel to the weld zone direction. b Measurement results for test specimen #1 with cracks S1 and S2. c Measurement results for test specimen #2 with cracks S3 and S4.

Full size image

For test specimen 1 in Fig. 4a (left), cracks S1 and S2 are perpendicular to the weld zone direction. Therefore, a larger number of sensors pass directly through the crack zone, increasing the ability to record the peak signal, where the EC density changes the most. This is shown by the voltage signal obtained, with a large amplitude of about 0.3 V for crack S1 and about 0.1 V for crack S2 (Fig. 4b) and is also visually illustrated by the 2D image showing a high magnitude of the crack signals. In contrast, in specimen 2 in Fig. 4a (right), cracks S3 and S4 are oriented parallel to the weld zone, resulting in a significant reduction in the number of sensors passing directly through the crack zone (only 2 sensors pass through crack S3, and 1 sensor passes through crack S4). This increases the likelihood that the cracks are located only at the edges of the sensors rather than the central region where the EC density changes the most. As a result, the detected signal amplitude is significantly lower, about 0.15 V for crack S3 and about 0.07 V for crack S4. This difference clearly shows the influence of the crack orientation on the detection ability and the clarity of the obtained signal. However, the signals in the measurement channels in both cases are stable, with channels 3 and 4 showing the clearest crack signal, confirming the high accuracy and sensitivity of the measurement system in the central channels. This clearly demonstrates the ability of the measurement system to accurately distinguish and locate cracks in different orientations and also suggests that cracks-oriented perpendicular to the weld zone are easier to detect and locate than those oriented parallel.

Figure 5 shows the experimental results on a curved specimen (low carbon steel SS400), demonstrating the crack detection capability of the FECA sensor system under complex geometric conditions. The scanning direction of the FECA sensor was aligned along the direction of the weld zone. The specimen was coated with a zinc (Zn) layer with a thickness of about 20–30 μm to simulate the corrosion protection layer commonly found in industrial steel structures (details of the specimen structure are presented in the Methods section). Four artificial cracks were created at a depth of about 0.5–1.0 mm from the test specimen surface, as shown in Fig. 5a. The scanning process for this specimen can be seen in Supplementary Movie 2. Since the cracks are located inside the weld zone, a low excitation frequency (5 kHz) is used to increase the EC penetration depth, as explained in Fig. 1. As a result, the signal obtained from the detection coil is quite low in intensity, requiring the real-time FECA system (Fig. 3) to operate with a signal amplifier. In the laboratory, due to equipment limitations, three operational amplifiers were used corresponding to the three channels of the FECA sensor.

Fig. 5: Experimental results with curved test specimen.
figure 5

a Test specimen #3 has cracks C1, C2, C3 and C4. b Measurement results for test specimen #3 with cracks C1, c C2, d C3, and e C4.

Full size image

The signals obtained from the measurement channels (Fig. 5b–e) clearly show the presence of cracks with characteristic amplitudes, confirming the effective detection capability of the sensor even under non-ideal contact conditions caused by the curved surface. Notably, the signal at the crack location has a lower amplitude than the background, in contrast to the phenomenon observed in Fig. 4 for surface cracks. This can be explained as follows: in Fig. 4, when examining a surface crack on an uncoated Zn steel sample, a high excitation frequency (500 kHz) was applied to limit the penetration depth of the EC. The crack interrupts the surface EC, which reduces the secondary magnetic field at that location and leads to an increase in the total magnetic field. Therefore, the signal at the crack exceeds the background, resulting in a positive amplitude. In contrast, for the cracks inside the weld area in Fig. 5, the sample, which has a Zn coating, was excited with a low frequency (5 kHz) to ensure that the penetration depth of EC through the coating to the weld area. In the absence of cracks, the EC can still penetrate deeply and generate a stable secondary magnetic field at the surface. However, the presence of a sub-surface crack weakens the EC in that area, leading to an increase in surface EC density. This increases the secondary magnetic field at the surface and results in a decrease in the total magnetic field at the sensor. As a result, the signal obtained at the crack location is smaller than the baseline and has a negative value. Detailed analysis of this phenomenon is presented in Supplementary Note 4 and Supplementary Fig. S4.

Figure 6 presents the experimental results obtained from a low carbon steel (SS400) test specimen with a weld area containing crater cracks. Unlike the previous test specimens, the surface of the weld area exhibits natural roughness caused by the welding process, resulting in uneven geometric deformations. Crater cracks typically form at the ends of welds due to uneven shrinkage and stress concentration during cooling. These cracks are generally small, propagate in random directions, and are often buried beneath the surface or combined with complex surface deformations, making their detection particularly challenging using conventional eddy current testing methods. However, as shown in the scan results, the FECA sensor successfully captured abnormal signals corresponding to the crater crack locations, despite the influence of the rough surface. Crack-related signal peaks are clearly distinguishable from background signal fluctuations caused by surface roughness, owing to the high spatial resolution and signal stability of the FECA sensor system. These results demonstrate that the FECA sensor can not only detect small, multidirectional cracks but also maintain stable detection performance even in the presence of complex surface geometries. To further verify the performance and versatility of the proposed FECA sensor, additional experiments were conducted on aluminum and flat steel specimens containing cracks of various orientations and dimensions. These tests confirmed the sensor’s ability to detect both large and small cracks with high spatial resolution across different materials and conditions. Detailed results and analysis are presented in Supplementary Note 5 and Supplementary Figs. S5 and S6. This highlights the system’s strong potential for practical applications in non-destructive testing of real-world weld areas, where small defects and surface irregularities are commonly encountered.

Fig. 6: Experimental FECA scan of an SS400 weld zone containing crater cracks.
figure 6

Top image: Photograph of the weld seam; red boxes mark visually identified crater crack regions (scale bar = 10 mm). Middle row (four panels): Close‑ups of the crater crack areas. Heat map: 2D distribution of detection voltage along the scan (distance axis) for six FECA channels; red arrows indicate crater crack positions. Bottom graph: Detection voltage profiles versus distance for Channels 1–6.

Full size image

Discussion

In summary, this study presents a cost-effective, flexible, and accurate approach to weld zone inspection using ECT. The combination of the novel FECA sensor design and real-time LabVIEW-based signal processing provides a solid foundation for scalable and adaptable NDT systems in structural health monitoring applications. The experimental results confirm the high sensitivity and flexibility of the proposed FECA sensor and measurement system in detecting surface and sub-surface cracks in the weld zone under various geometric conditions. Compared to conventional FECA sensors, which are often limited in the coil number of turns and signal strength due to design constraints, the novel design with six bendable channels and series-connected excitation coils significantly enhances the EC signal strength. This innovation addresses one of the major limitations of conventional flexible FEAC sensors, low sensitivity due to limited excitation field strength. Furthermore, the alternating arrangement of the excitation and detection coils on a single plane eliminates the lift effect and allows the sensor to acquire signals at the location of the EC peak intensity. This configuration not only enhances the ability to detect cracks but also maintains the flexibility of the sensor, making it particularly suitable for inspecting welds in complex-shaped structures such as curved pipes or tank walls. This effectiveness is evidenced by successful crack detection in both flat and curved test specimens, even with Zn coatings simulating industrial corrosion protection layers.

The developed LabVIEW-based Lock-in amplifier contributes to the practicality of the system by providing real-time multi-channel signal processing at a lower cost. Unlike commercial Lock-in amplifiers, which are limited to single-channel detection and are often expensive, the software-based solution enables efficient synchronous detection of weak signals buried in noise. However, the system currently relies on manual scanning, which limits the accuracy of spatially mapping crack locations due to non-uniform scanning speeds. The lack of an integrated encoder also affects the ability to reproduce spatial signal alignment between different measurements. In future work, combining an automated scanning mechanism with a position tracking function will enable precise crack localization. Additionally, while the current system demonstrates reliable detection of artificial cracks, further validation on real-world corrosion or fatigue weld zones is required to evaluate its performance in more complex industrial environments.

Compared to other eddy current-based detection methods, such as those utilizing GMR or TMR sensors, the proposed FECA measurement system offers several practical advantages. While GMR and TMR sensors provide high magnetic sensitivity, they are typically packaged in rigid chip forms and are limited to single-point detection, making them less suitable for inspecting large or curved areas such as weld zones. Additionally, systems like the TMR-based probe with double-cylinder magnetic shielding are mainly optimized for non-ferromagnetic materials and lack structural flexibility26. In contrast, the FECA sensor developed in this study features a fully flexible and compact design, enabling effective detection of surface and sub-surface cracks on both flat and curved steel structures. Furthermore, the integration of a multi-channel lock-in amplifier implemented in LabVIEW and a custom-built analog signal conditioning circuit enhances real-time performance while significantly reducing system cost. These innovations position the proposed system as a practical and scalable alternative for structural health monitoring in real-world industrial environments.

Methods

FECA sensor manufacturing

The FECA sensor was designed by the authors and ordered for manufacturing through FCM Co., Ltd., Japan. The FECA sensor fabrication method was carried out using the excitation coil and the detection coil on a 50 μm-thick polyimide (PI) substrate covered with a copper (Cu) layer with a target thickness of about 3 μm. In this method, the line width of the excitation coil is 100 μm and that of the detection coil is 50 μm, with a distance between the two coils of 35 μm. The connecting PADs are squares with sides of 1 mm, laser-machined with a diameter of 30 μm at 7 points on each PAD to ensure accuracy and good contact. The induction coil PAD is arranged on the right side, extending up to 300 mm in length to facilitate the connection of the measurement signal. This process enables the FECA sensor to achieve high sensitivity and resolution while maintaining stable performance under demanding measurement conditions.

FECA measurement system setup

An AC sinusoidal excitation current was supplied by a synthesizer generator (WAVE FACTORY WF1984, NF Co., Japan) with an amplitude of 2 Vp-p. The excitation frequency was set to 500 kHz for the test specimens #1 and #2, and 5 kHz for the test specimen #3. This signal was subsequently amplified 20 times using a high-speed bipolar amplifier (HSA42011, NF Co., Japan), reaching an amplitude of 40 Vp-p before being applied to the excitation coil of the FECA sensor. On the receiving side, the system utilized six channels to acquire sinusoidal signals from the detection coils for specimens #1 and #2, and three channels for specimen #3 (each channel was connected to an individual operational amplifier). The acquired signals were then input into channels AI 1 to AI 6 of the data acquisition device (NI USB-6363), while a reference signal from a dedicated output of the synthesizer generator was fed into channel AI 0. All signals were processed using a LabVIEW-based Lock-in amplifier, which enabled accurate extraction of the voltage amplitude from the detection coils. The processed signals were then displayed as 2D plots and stored on a computer. To ensure accurate signal acquisition across multiple channels, especially under varying excitation frequencies, the sampling rate per channel was carefully determined based on the total bandwidth of the DAQ device. A detailed discussion of the sampling strategy, including calculations for sampling time steps, frequency allocation per channel, and waveform validation at 5 kHz and 500 kHz, is presented in Supplementary Note 3 and Supplementary Fig. S3.

Test specimen manufacturing

The test specimens containing surface cracks were fabricated from low carbon steel (specifically SS400 of Japanese Industrial Standards) to accurately simulate defects commonly found in weld zones in practical applications. The cracks were introduced using the Electrical Discharge Machining (EDM) method, which enables the creation of narrow cracks with precisely controlled geometries and dimensions.

For the curved specimen with cracks in the weld zone, it underwent a hot-dip galvanizing process in which the entire sample was immersed in molten zinc (Zn) to form a durable protective coating. The total Zn layer had a thickness estimated at 20–30 μm. Finally, the surface was finished to ensure flatness, uniformity, and readiness for measurement.