Introduction

Railway infrastructure forms the backbone of freight transportation systems around the globe, supporting sustainable economic growth and community resilience1,2. Their failure can lead to substantial cascading events and disruptions across socio-economic systems and communities3,4. Globally, railway infrastructure has, in many cases, reached or exceeded its intended lifespan, while climate change is aggravating its condition by accelerating the ageing of these assets5,6. Additionally, the current traffic loads are much higher than what the infrastructure was originally designed for, causing further damage and increasing vulnerability7. Climate-induced compound hazards such as floods, storms, and extreme temperatures are projected to have an increasing impact on railways, further exacerbating their vulnerability6,8,9. For instance, based on ensemble means of seven climate scenarios, Alfieri et al. (2015)10 estimated that the expected annual damage (EAD) to European railways is projected to increase by 255, 281, and 310%, under 1.5 °C, 2 °C, and 3 °C warming scenarios, respectively. This challenge is particularly acute in coastal regions, where the interplay of extreme events superimposed on long-term trends, such as higher sea levels, heavier precipitation, and changing storm seasonality, causes more frequent and severe coastal flooding. These compound events and concurrent extremes increase the probability of low-likelihood, high-impact outcomes11,12. This poses a formidable threat to railway networks, which are often connected to ports, oil refineries, and other industrial infrastructure along coastlines. The interdependencies among these systems mean that disruptions in the railway network can cascade, leading to profound operational and economic impacts across multiple sectors13,14, exacerbating the overall vulnerability of the region, sometimes with impacts on the global supply chain and economy2,15. Given the increasing frequency and intensity of climate-related events along with the scarcity of resources, practical strategies are needed to predict and mitigate the impacts on railway networks as well as support efforts to rapidly restore services and minimize disruptions9,16. Effective probabilistic methods are essential to project uncertain post-disaster recovery trajectories and probe alternative interventions, thus minimizing resource misallocation17,18.

In recent years, railway resilience has been analyzed from various perspectives, with variations in stressors, recovery assumptions, performance measures, spatial scale and uncertainty treatment9,19. For instance, Woodburn (2019)2 leverages empirical data from past railway disruptions to assess the economic consequences of extreme weather events on rail freight traffic levels. Similarly, Lamb et al. (2019)20 conduct an economic risk analysis of Britain’s railway network, focusing on flood-induced bridge scour and leveraging historical damage data. Bi et al. (2024)21 examines the resilience of London’s urban rail transit system using network modeling and dynamic recovery processes to estimate economic losses. Besinović et al. (2022)22 conducts a passenger-centered railway network resilience assessment under deterministic, non-extreme disruption scenarios, utilizing optimization techniques. Likewise, Tang et al. (2023)23 focus on the optimal recovery of passenger railway networks, focusing on earthquake-induced disruptions and passenger rerouting. More recently, Ilalokhoin et al. (2025)24 conducted a nationwide railway flood risk assessment in Great Britain, evaluating direct asset damages, train and passenger disruptions, and economic losses without explicitly simulating post-disaster recovery. Despite these advancements, a critical gap remains: the absence of a resource-aware probabilistic framework to assess the resilience of railway infrastructure systems against climate-driven extreme hydraulic hazards. In particular, there is a need to integrate tailored damage and restoration functions for railway components affected by coastal hazards while capturing the diverse network-level functionality recovery trajectories under varying resource availability and allocation scenarios. Furthermore, such a framework should systematically account for the multiple sources of uncertainty inherent in resilience modeling25,26.

Moreover, modeling functionality recovery—a key aspect of resilience assessment—can be approached from various perspectives, each with inherent challenges. A realistic approach considers what is likely to occur in a post-disaster situation, where decisions regarding resource allocation are typically decentralized, ineffectively informed, and executed suboptimally27,28. An optimistic perspective examines what should or could be achieved with the most optimal allocation of available funds and resources23,29. An inquisitive approach explores how changes in resource availability or assumptions about their allocation affect recovery outcomes. Existing methods that otherwise attempt to rigorously account for the damaging effects of hazards on railway infrastructure make overarching assumptions regarding such features. For example, some assume fully available restoration resources or optimal allocation, thus falling short in reflecting real-world conditions30,31. Others that broadly emphasize the notion of resource-constrained recovery of infrastructure assets32,33 often fail to contextualize the framework with physics-informed damage and restoration models, or are not adept at handling the complexity of real-world railway networks. This complexity arises from both the high number of components and the extended recovery time horizon, requiring computationally intensive modeling methods that often hinder efficient resource allocation for building resilience into these systems34. Furthermore, in a coastal setting with a changing climate, some studies have highlighted the vulnerability and exposure of railway infrastructure to the effects of sea-level rise (SLR)18,35. However, the impact of different SLR projections on hazard stressors (e.g., surge) and consequently on resilience estimates for railway systems remains insufficiently explored, representing a gap in the literature that this work aims to bridge.

We introduce, for the first time, a probabilistic framework to evaluate the resilience of railway infrastructure systems subjected to compound climate hazards that manifest themselves by SLR and extreme hydraulic hazards as a result of hurricanes. This framework goes well beyond the current state of the art of traditional resilience assessments that comprise the synthesis of fragility and recovery modeling. With a distinct contribution to resilience, we explicitly account for variations in resource availability and allocation. We incorporate uncertainty in hazard, fragility, and restoration inputs. Thus, this paper enables a risk-informed, nuanced, and practical evaluation of resilience that empowers a decision-maker to probe a range of outcomes. The proposed framework introduced in the “Methods” section models the impact and subsequent functionality recovery through a five-stage approach that entails: (i) defining the infrastructure inventory and typology of railway corridors, bridges and embankments, and compound hazard intensity measures for variable scenarios of SLR, (ii) estimating damage states and initial functionality loss for railway assets, (iii) estimating link restoration costs and times, (iv) modeling resource allocation and recovery trajectories, and (v) obtaining resilience indicators. Next we utilize a case study to illustrate the applicability and value of the probabilistic resilience framework. The case study concerns the railway freight network in Mobile and Baldwin Counties, Alabama, subjected to five adopted storm scenarios that couple Hurricane Katrina’s hindcast with four SLR projections. Along the way, this work contributes by adapting fragility and restoration models for a diverse portfolio of multi-span railway bridges with varying characteristics, demonstrating the data needs and practical applicability of the proposed methods, and shedding light on resilience outcomes for alternative SLR scenarios and resource allocation strategies.

Methods

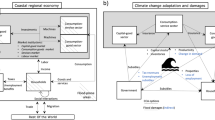
This section outlines the proposed framework for evaluating the resource-constrained resilience of railway networks subjected to extreme compound hydraulic hazards, as illustrated in Fig. 1. The framework stands out in two key ways. First, it follows a systematic approach, utilizing rigorous component-level probabilistic models, including physics-based damage models and expert-informed restoration models, to predict network-level damage and functionality recovery. Second, it explicitly incorporates the complexities of post-disaster recovery by integrating constraints and uncertainties related to resource availability, aiming to more accurately reflect real-world recovery efforts. Uncertainties are propagated via Monte Carlo simulation as the impact of compound coastal hazards is assessed across component, link and network levels, with network functionality \(F(t)\) measured in terms of the ability to transfer goods between origin-destination (OD) node pairs. The analytical stages of the proposed framework are described in the following subsections.

Fig. 1
figure 1

Flowchart depicting the five analytical stages of the proposed resilience framework.

Full size image

Asset inventory and hazards

In defining the inventory input (see step I in Fig. 1) for the resilience modeling framework, four primary assets, hereby named “components”, are identified: bridges, embankments, cut-slopes and rail tracks. Components are defined as discrete infrastructure elements susceptible to damage from the considered hazard event. For each component, key details that are compiled and defined include their location, structural or site parameters, aligned with fragility and restoration model requirements, and operational parameters, e.g., cargo-transfer capacity. Let \(N\) denote an infrastructure system of interconnected components, which in this study is the railway network. Let \({{{\mathcal{C}}}}\) be the set of infrastructure components within this system. \(N\) is abstracted using the graph \(G={{{\mathscr{(}}}}{{{\mathscr{L}}}},{{{\mathscr{N}}}}{{{\mathscr{)}}}}\), where \({{{\mathscr{L}}}}\) is the set of network links and \({{{\mathscr{N}}}}\) is the set of network nodes. Links represent railway corridors and nodes represent intersections. Furthermore, each component is associated with a specific link, thus, the set of components associated with link \(l\) is represented by \({{{{\mathcal{C}}}}}_{l}\), which is a subset of \({{{\mathcal{C}}}}\). The network topology is represented by the adjacency matrix \({{{\boldsymbol{A}}}}\), which indicates whether there is a link connecting the corresponding nodes in graph \(G\).

Regarding the hazard input, within the scope of this study, two hazard effects are considered: (i) scour causing damage to bridge foundations and embankments; and (ii) deck unseating in bridge spans due to hydraulic forces. While these effects can be triggered by diverse hydraulic hazards, such as heavy rainfall, tropical cyclones, or tsunamis, the critical hazard information for resilience modeling lies in the parameters describing hazard intensity at each component’s location, herein denoted as intensity measures (\({IM}\)). For the case study in this work, SLR is identified as the primary stressor impacting the system, while hurricane hazards act as secondary stressors. These hazards are compound, or multi-hazard, events involving various concurrent effects, such as surge, wind, and wave phenomena. Specifically for railway assets, two \({IM}\) are identified as critical: surge-induced flood elevation (\(S\)) and wave characteristic height (\({H}_{w}\)). For bridge fragility analysis due to deck unseating, both of these parameters are involved. For scour-induced fragility to embankments and bridge foundations, only the flood inundation depth \(S\) is utilized.

Damage states and functionality loss influencing railway resilience

The initial disaster impact on the system is measured in terms of functionality loss \(L\), including impact at the component level (\({L}_{c}\)), link level (\({L}_{l}\)), and network level (\({L}_{N}\)). To this end, for each iteration and each component, the first step consists of assessing component vulnerability by retrieving the relevant hazard intensity measure (\({IM}\)) and component fragility model, to obtain the probability of exceedance for each damage state \(P({DS}\ge d{s}_{n})\) (see Step II in Fig. 1). We adopt fragility models from the literature and appropriate adaptations for application in the case study were conducted where needed. For embankments, the fragility model introduced by McKenna et al. (2021)36 is utilized, which considers as \({IM}\) the water intensity measure (\({WIM}\)), defined based on embankment height and groundwater table depth. The model considers three damage states (minor, moderate and complete). The failure mode associated with these \({DS}\) is exceedance of limit vertical displacements at the road surface. For bridges, damage likelihood due to scour effects and hydraulic forces on foundations is assessed using the fragility models introduced in Argyroudis and Mitoulis (2021)37, which were developed considering foundations for a three-span bridge archetype, along with four damage states (minor, moderate, extensive and complete). Since the case study includes multi-span bridges, the original models are here adapted by considering a fragility factor \({n}_{k}\) to scale the vulnerability based on the number of spans that are prone to scour damage, i.e., the ones over water. The hazard \({IM}\) is the scour depth, which is calculated using the guidelines provided in the HEC-18 manual38. The probability of deck unseating is evaluated for each bridge span, utilizing the parameterized fragility model presented by Balomenos et al. (2020)39. This parameterized approach enables damage analysis across a diverse portfolio of bridges with varying characteristics, aligning with the diversity observed in the case study analyzed in this work. Details about these calculations and adaptations are presented in Supplementary Method 1.

Once the probabilities associated with each damage state \(P[{DS}\ge d{s}_{n}]\) are obtained for all components, the damage states \({DS}\) are realized for each iteration. Then, the initial functionality of each component after the event (at time step \(t={t}_{0}\)) is given by:

$${F}_{c}\left({t}_{0}\right)=\left\{\begin{array}{cc}1 & {{{\rm{if}}}}\,{DS}={{{\rm{no\; damage}}}}\\ 0 & {{{\rm{otherwise}}}}\end{array}\right.$$
(1)

For bridges, \({F}_{c}\left({t}_{0}\right)=1\) if no damage is observed as a result of scour or unseating effects. This binary definition arises from the stringent safety measures in railway networks, where even minimal damage most often results in the complete closure of bridges or embankments until the completion of restoration. Consequently, at the link level, the initial post-event functionality \({F}_{l}\left({t}_{0}\right)\) is estimated by considering bridges and embankments in a series system, yielding:

$${F}_{l}\left({t}_{0}\right)={\prod}_{c\in {{{{\mathcal{C}}}}}_{l}}{F}_{c}({t}_{0}).$$
(2)

Lastly, the initial post-event network functionality \({F}_{N}\left({t}_{0}\right)\) is measured in terms of network flow capacity, obtained considering the link initial post-event functionalities \({F}_{l}({t}_{0})\), as follows:

$${F}_{N}\left({t}_{0}\right)=\frac{{f}_{\max }({t}_{0})}{{f}_{\max }({t}_{u})},$$
(3)

where \({f}_{\max }({t}_{0})\) indicates the maximum flow between the OD nodes after the disaster ocurrence, which is normalized by the maximum flow in pre-event conditions \({f}_{\max }({t}_{u})\). \({f}_{\max }(t)\) captures the influence of deteriorated links on the overall network ability to accommodate flows, and is measured for a single shipment in this case study. A shipment is specified as a flow demand between a pair of OD nodes. The subsequent functionality loss \(L\) is derived by subtracting the initial post-event functionality \(F\left({t}_{0}\right)\) from the pre-event functionality \(F\left({t}_{u}\right)\). Assuming complete functionality in pre-event conditions, that is \({F}_{c}\left({t}_{u}\right)=1\), the subtraction yields:

$$L=1-F\left({t}_{0}\right)$$
(4)

Depending on whether we analyze a component, link or the network, we can use \({F}_{c}\left({t}_{0}\right)\), \({F}_{l}\left({t}_{0}\right)\) or \({F}_{N}\left({t}_{0}\right)\) in Eq. 4 to yield \({L}_{c}\), \({L}_{l}\) or \({L}_{N}\), respectively. Since partial component and link functionality is not deemed possible under the aforementioned assumptions, functionality loss \(L\) implies complete functionality loss for components and links. The assumptions established thus far within this proposed framework are adaptable to suit more intricate applications. For example, functionality could be represented as a continuous variable when needed, or distinctions could be made regarding pre-event functionality, diverging from the assumed original functionality of the undisturbed system.

Link restoration costs and times

The impact modeling process (Step I in Fig. 1) yields two key outputs: the component’s damage state \({DS}\) and functionality loss \({L}_{c}\). Based on these, restoration costs and times for each damaged component are estimated using restoration models, which provide probabilistic descriptors (mean and dispersion for the adopted normally-distributed model) for these parameters (Step III in Fig. 1). This stage introduces an additional layer of uncertainty into the resilience modeling process. For embankments, the restoration model proposed by Zormpas (2022)40 is leveraged, and its statistical parameters are presented in Table 1. For bridges, the restoration models presented by Mitoulis et al. (2021)41 are adopted, for both scour and unseating effects. Similar to fragility models, this restoration model is adapted for application in the case study by factoring the restoration times to translate the statistical parameters derived for three-span bridge archetypes to the multispan bridges of the case study. This restoration model provides parameters for various restoration tasks, which are selectively adopted for scour and unseating effects. Further details about these models and the adaptation process are presented in Supplementary Method 2.

Table 1 Restoration model parameters for three-span bridges and embankments
Full size table

The restoration models provide repair costs in terms of cost ratios \({d}_{c}\), which are then translated into absolute terms (monetary values) by multiplying them by the component replacement cost \({Q}_{c}\), yielding the component restoration cost as \({D}_{c}={d}_{c}{Q}_{c}\). The restoration duration of a damaged component is modeled by two stages: (i) the idle time \({T}_{c}^{i}\), which accounts for the time required for preparatory tasks, before commencing repairs; and (ii) the repair time \({T}_{c}^{r}\), which represents the time required for the execution of the repair tasks. The restoration models provide parameters to estimate each of these times, and in the case of bridges, for each failure mode. Since for bridges, scour damage and deck unseating are possible to occur simultaneously, guidelines to account for the interaction of these effects, while avoiding overestimation of repair times, are introduced in this work (see Supplementary Method 2).

Partial functionality is not deemed possible for the railway network links defined in this study, as it is assumed that operators will refrain from allocating resources to only a portion of damaged components within a link. This approach allows for the estimation of restoration costs and times at the link level by integrating heuristics. These simplifications can be construed as a preliminary resource allocation within each link, aiming to streamline the subsequent decision-making process. By leveraging the correlation between component interventions within a link, this method considerably reduces the number of decision variables during resource allocation. Once \({D}_{c}\) is realized at each iteration for each component within a link \(l\), and considering the above-mentioned assumption, the restoration cost \({D}_{l}\) for each non-functional link \(l\) is estimated as:

$${D}_{l}={\sum}_{c\in {{{{\mathcal{C}}}}}_{l}}{D}_{c}$$
(5)

Furthermore, once \({T}_{c}^{i}\) and \({T}_{c}^{r}\) are realized at each iteration, two heuristic-based assumptions are incorporated for translation to the link level. First, the idle time for each non-functional link is considered as the maximum idle time of its components, assuming that preparatory tasks can take place in parallel. Therefore, the link idle time \({T}_{l}^{i}\) is given by:

$${T}_{l}^{i}=\max ({T}_{c}^{i}),{{{\rm{for}}}}\,\forall \,c\in {{{{\mathcal{C}}}}}_{l}$$
(6)

Second, the repair time for each non-functional link is considered as the sum of the repair times of its components, assuming that components within a link are repaired in sequence. Therefore, the link repair time is given by:

$${T}_{l}^{r}={\sum}_{c\in {{{{\mathcal{C}}}}}_{l}}{T}_{c}^{r}$$
(7)

Ultimately, the restoration time for each non-functional link \({T}_{l}^{R}\) is given by:

$${T}_{l}^{R}={T}_{l}^{i}+{T}_{l}^{r}$$
(8)

These assessed link restoration costs and times (\({D}_{l}\) and \({T}_{l}^{R}\), respectively) are then input to the resource allocation modeling process to determine which links are intervened in each iteration, considering resource constraints and allocation optimality.

Resource allocation modeling shapes recovery trajectories

Here we model how decision-makers in conjunction with operators allocate their limited resources for infrastructure restoration tasks amidst uncertain and strained post-disaster situations (Step IV in Fig. 1). We investigate three allocations scenarios: optimal, sub-optimal and random, to cover a range of possible scenarios. The optimal and random allocation scenarios are intended to serve as lower and upper bounds of a more nuanced sub-optimal allocation, respectively.

(i) Optimal allocation: First, we obtain an optimistic resilience estimate (upper bound). Resources are allocated by solving a linear mixed-integer programming (LMIP) problem, which maximizes the flow between the OD nodes across the time horizon, subject to resource availability \(B\), expressed in terms of budget available for restoration tasks. The optimization parameters are the set of damaged links \({{{{\mathscr{L}}}}}^{D}\) for each iteration, the restoration cost and times for each of these links (\({D}_{l}\) and \({T}_{l}^{R}\), respectively), as well as the pre-event link capacity \({C}_{l}({t}_{u})\). The decision variables are which damaged links to intervene, represented by the binary variable \({\delta }_{l}\) (\({\delta }_{l}=1\) if intervened, \({\delta }_{l}=0\) otherwise), and the flow along each link at each time step \({f}_{l}(t)\). The constraints are classed into three groups: capacity constrains, budget constraints and functionality constraints, which are all linear (see further in Supplementary Method 3). While, in principle, the optimization problem could be formulated as a nonlinear program, given the emphasis of this work on real-world applicability, a linear formulation is preferred due to its computational efficiency, ease of implementation with free and open-source solvers, and scalability with network size. Once solved, the optimal values of \({\delta }_{l}\) and \({f}_{l}(t)\) are obtained, as well as the optimal maximum flow between OD nodes at each time step, denoted as \({f}_{\max }^{{{{\rm{opt}}}}}(t)\), which is then used to derive the optimal functionality recovery trajectory \({F}_{N}^{{{{\rm{opt}}}}}(t)\) by adapting Eq. 3.

(ii) Sub-optimal allocation: Second, considering that the network functionality is defined in terms of ability to satisfy flow demands, a flow-based betweenness centrality approach is taken in this study to model how decision-makers perceive the importance of each damaged link in a partially-informed sub-optimal manner. Specifically, the flow betweenness centrality measure \(B{C}_{l}\) introduced in Newman (2005)42 is here adopted and defined as:

$$B{C}_{l}=\frac{{\sum }_{\sigma \tau {{{\mathscr{\in }}}}{{{\mathcal{S}}}}{{{\mathcal{T}}}}}{I}_{l}^{(\sigma \tau )}}{\left(1/2\right){n}_{n}({n}_{n}-1)}$$
(9)

where \({I}_{l}^{(\sigma \tau )}\) is the flow traveling along link \(l\), when considering a unit of flow at source node \(\sigma\) and removing it at target node \(\tau\), \({n}_{n}\) is the number of nodes in the network and \({{{\mathcal{S}}}}{{{\mathcal{T}}}}\) is the set of source-target pairs. Therefore, \(B{C}_{l}\) is the average of the flow over all source-target pairs \(\sigma t\). This approach is chosen based on a comparison with other heuristics-based methods, such as shortest path betweenness centrality, eigenvector centrality, closeness centrality, and DomiRank43. The comparative analysis, presented in Supplementary Note 2, shows that flow-based betweenness centrality outperforms other strategies in the majority of scenarios. This method was originally derived using an electric circuit analogy, assuming that a current flow entering a node will be distributed among its connected links (resistors) inversely proportional to their resistance42. Translated to the context of flow of goods for railway networks in this study, this implies that shorter links will offer less “resistance”, and will thus tend to “absorb” more flow than longer links. Considering that in absence of more complete information, shippers tend to choose shorter paths when routing flow, \(B{C}_{l}\) is taken here as a ranking criteria for sub-optimal allocation. Several algorithms can be used to solve for \({I}_{l}^{(\sigma \tau )}\), both exact and approximate depending on network complexity. In this work the approach relies on a recursive removal of row-column pairs of the matrix resulting from substracting the weighted adjacency matrix from the degree matrix, followed by the inversion of said matrix. Complete details can be found in Newman (2005)42. At each iteration, for the set of damaged links \({{{{\mathscr{L}}}}}^{D}\), the available budget \(B\) is assigned sequentially to these links, from highest to lowest \(B{C}_{l}\) measure, until the budget limit is reached, producing the binary decision variable \({\delta }_{l}\) for each damaged link. Once resources are allocated, the sub-optimal values of \({\delta }_{l}\) are used to derive the sub-optimal network functionality recovery trajectory \({F}_{N}^{{{{\rm{sub}}}}}(t)\), by determing the maximum network flow \({f}_{\max }(t)\) at each time step, considering the temporal availability of each damaged link (depending upon decision \({\delta }_{l}\) and restoration time \({T}_{l}^{R}\)). \({f}_{\max }(t)\) is obtained using the network flow model implemented in the “NetworkX” Python package, which leverages the max-flow min-cut theorem44. \({F}_{N}^{{{{\rm{sub}}}}}(t)\) is then used to calculate the associated resilience indicators defined in Step V.

(iii) Random allocation: Lastly, to consider pessimistic resilience estimates (lower bound), a random allocation approach is taken by assigning resources to damaged links randomly until the available budget \(B\) is depleted. The decision variables \({\delta }_{l}\) are realized for each iteration, and the network functionality \({F}_{N}^{{{{\rm{ran}}}}}(t)\) is obtained for each time step using the same network flow approach as for sub-optimal allocation. Theoretically, a lower bound would be obtained by solving the LMIP problem defined for the optimal allocation, but minimizing the objective function. However, this situation is unlikely to be observed in real-world situations, thus a random allocation is deemed more representative as a lower bound for the purposes of this work, representing an “uniform” or “oblivious” decision-making.

Quantifying resilience by indicators

In the previous step, network functionality recovery \({F}_{N}(t)\) is derived for each iteration, considering three allocation methods. Next, these recovery processes are characterized using resilience indicators aimed at capturing key features in the non-linear temporal evolution of system-level functionality. The ultimate goal is to enable well-informed decision-making. In this work, we utilize two resilience indicators (Step V in Fig. 1). First, the resilience index \({R}_{N}\) proposed by Frangopol and Bocchini (2011)45 is used to characterize the evolution of the functionality recovery across the complete time horizon, and is defined as:

$${R}_{N}=\left(\frac{1}{{t}_{h}}\right){\int }_{{t}_{0}}^{{t}_{0}+{t}_{h}}{F}_{N}\left(t\right){dt},$$
(10)

where \({t}_{0}\) is the time at which disruption occurs, \({t}_{h}\) is the time horizon for the analysis, and \({F}_{N}\left(t\right)\) is the network functionality at time \(t\) after disruption. Second, time to recovery \({R}_{\phi }\) is defined as the time required to reach at least functionality \(\phi\), and is mathematically defined as:

$${R}_{\phi }=\min \left(\left\{t{{{\rm{| }}}}{F}_{N}\left(t\right)\ge \phi \right\}\right).$$
(11)

For instance, \({R}_{0.50}\) is the minimum time required to reach at least 50% of system functionality \({F}_{N}(t)\), which can inform resilience in terms of meeting flow demands. Scenarios with different network capacity recovery trajectories \({F}_{N}\left(t\right)\) may exhibit similar recovery times \({R}_{\phi }\) for demand levels lower than the full network capacity. The choice of resilience indicators depends on several factors, for example, stakeholder perspectives and minimum recovery requirements46, and the proposed resilience modeling framework allows for other functionality-based indicators to be readily implemented if necessary.

Results

This section presents a case study analysis of railway network resilience, applying the proposed framework from Fig. 1 to the railway network within the Mobile-Baldwin counties, in Alabama, USA. The same methodology with fit-for-purpose adjustments can be applied in other locations or even to other infrastructure systems. Regarding uncertainty propagation, a Monte Carlo analysis for the series of chained models described in the “Methods” section is conducted with 1,000 iterations, considering as convergence criterion a 2% error threshold for the mean network resilience index at a 95% confidence interval.

Case study

An overview of the case study scenarios, highlighting their key features, is provided herein. The railway system components considered in this study are bridges and embankments, with data compiled from public sources and available in Tafur et al. (2025)47. Cut slopes were excluded due to Alabama’s flat terrain. Railway tracks were excluded, given their lack of detailed physics-based fragility models and their lower exposure to wave-induced damage, which primarily affects shoreline tracks—a small portion of the network. Flooding impacts on inland tracks are expected to be less severe, with faster restoration than embankments and bridges. Given the severity of the most extreme hazard scenario, 19 railway bridges within Mobile-Baldwin counties are identified as prone to flood-induced damage as a result of SLR and hurricane effects. Their main characteristics are presented in Table 2. For fragility assessment purposes, two bridge structural typologies are defined, isolated bridges with bearings (Type I) and integral bridges (Type II). Type I represents bridges where the superstructure rests on bearings, whereas Type II represents integral structures, where super- and sub-structure are connected monolithically. Each bridge is assigned a specific structural typology through visual recognition, utilizing both aerial and ground-level imagery from Google Earth48. The bridge replacement costs were obtained considering a 3000 $/m2 unit cost, based on 2023 unit replacement costs for Alabama highway bridges provided by the U.S. Federal Highway Administration49, with adjustments to account for higher construction costs in railway infrastructure. Since information about bridge foundations is not available from public sources, we simulated two cases for all bridges: weak and robust foundations. In this study, “weak foundations” refer to shallow foundations, while “‘robust foundations” refer to deep foundations. This approach allows us to assess the lower and upper bounds of their vulnerability as the foundation type is a critical vulnerability factor for bridges exposed to floods, in addition to the type of superstructure and substructure connection. Additional details are available in Supplementary Note 1.

Table 2 The railway bridges of the case study
Full size table

Each bridge is assumed to have two embankments, one located at each approach, with each embankment being 50 meters long. The case study includes 100 links and 85 nodes, defined as described in the “Methods” section. Figure S4 in Supplementary Note 1 presents the network topology. The origin of the flow of goods is set to the Port of Mobile location, and the destination nodes are designated as five key locations marking the junctions with the national railway network. Each component (bridges and embankments) is assigned to the appropriate link based on their location. For the purposes of this study, it is assumed that the restoration of rail tracks will not control the restoration time (i.e., bridge and embankment restoration times and costs will largely exceed those of rail tracks as the latter can be supplied at short notice). Furthermore, five hazard scenarios are defined based on Bilskie et al. (2016)50, who simulated hurricane-driven storm surge inundation for current and future sea-level conditions. These scenarios include one Hurricane Katrina hindcast (the severe event of 2005) under base sea level conditions (of year 2015), denoted as SLR-0, as well as Hurricane Katrina coupled with four sea level rise projections (SLR−1 to SLR-4). The intensity of these SLR projections is described in Table 3.

Table 3 Hazard scenarios considered for the case study
Full size table

One key feature of these simulations is that they incorporate projected topographic changes in the environment. The dataset provides water elevation estimates of the surge-driven inundation. The inundation heights for each component are obtained by subtracting the ground elevation from the surge elevation. Ground elevation data is obtained from USGS Lidar DEM (digital elevation models)51, for years 2016–2019. For the bridge deck uplift analysis, due to the lack of wave data, the representative wave height (\({H}_{w}\)) is modelled probabilistically using a uniform distribution. The lower bound is set to 0, and the upper bound is defined as the surge height \(S\) multiplied by a factor of 0.51. This approach is based on the provisions in Section 5.4.4 of the ASCE-7 guidelines for calculating wave loads during flooding52. Further details about the case study definition and the complete dataset used for the analyzes are available in Supplementary Note 1.

SLR impacts hazard impact severity

This section presents the main results of the hazard initial impact modeling on the network assets under the five hazard scenarios defined (SLR-0 to SLR-4) and two bridge foundation cases (weak and robust). Initial impact is herein defined as the short-term detrimental hazard effects on system functionality, before recovery begins, also denoted in the literature as “functionality drop”. The results are categorized into two key areas: functionality losses and direct economic losses. The probability of functionality loss \(P\left[F\left({t}_{0}\right)=0\right]\) for each component is quantified using the framework introduced in the “Methods” section, based on the simulated damage state of the component. Figure 2 shows the probability of functionality loss for the 19 bridges along with the hurricane-driven flood intensity for the five SLR scenarios, considering robust foundations. The spatial distribution of bridge vulnerability reveals that five bridges exhibit a high probability of functionality loss, even for the least severe hazard scenario (SLR-0).

Fig. 2: Initial hazard impact results for the case study.
figure 2

a–e Probability of bridge functionality loss \(P\left[F\left({t}_{0}\right)=0\right]\) represented by colored dots, for the five hazard scenarios. f Boxplots showing the direct losses considering weak and deep bridge foundations, in terms of loss ratios. Loss ratio is defined as the direct loss divided by the replacement cost. In the boxplots, the central box represents the interquartile range, with the median marked by an inner horizontal line. The whiskers extend to the smallest and largest values within 1.5 times the interquartile range from the lower and upper quartiles, respectively. Base map from OpenStreetMap © OpenStreetMap contributors. Data available under the Open Database License.

Full size image

Direct losses were estimated using component damage states and restoration models, based on the proposed framework. For the purpose of this study, these direct losses are considered to stem solely from repair costs. The total replacement cost for all exposed assets is estimated at $75.38 million. Figure 2.f shows the distribution of the obtained direct loss ratios for all assets (19 bridges and 38 embankments) using boxplots. The effects of SLR are evident, with the expected direct losses increasing as SLR intensity rises. For instance, in the robust foundation case, the median loss ratio increases from 0.08 without considering SLR to 0.41 with 2.0 meters of SLR, reflecting the exacerbation of storm impacts due to climate-related effects. For bridges with shallow foundations, the median direct losses range from 0.27 to 0.55, indicating a twofold increase from SLR-0 to SLR-4. Overall, these results provide insight into the physical and economic exposure faced by railway owners and insurance providers under varying SLR scenarios and bridge typologies.

Resource availability and allocation decisions critically influence resilience

Given the network’s disrupted state, the subsequent analysis focuses on evaluating how resource availability and allocation decisions influence the simulated recovery trajectories of network functionality, leveraging the proposed resilience framework introduced in the “Methods” section. For each realized disrupted state from the previous stage, we simulate allocation decisions using three methods (proxies for decision-making cases): optimal, sub-optimal, and random, alongside varying resource availability represented by an available budget ratio \(b\) ranging from 0.01% to 100% of the entire system replacement cost. Once the available resources are allocated, we derive the post-disaster functionality recovery \({F}_{N}(t)\) for the five hazard scenarios defined previously.

Figure 3 illustrates the functionality recovery results for four values of \(b\), encompassing scenarios SLR-0, SLR-2 and SLR-4, and considering the three allocation types. \(b\) is shown to be up to 23.4%, as this represents an approximate point at which the network begins to show full recovery within the defined horizon. The findings suggest that it is crucial to consider allocation optimality within certain ranges of resource availability when modeling the recovery trajectory of network functionality. This range varies according to hazard intensity and foundation type. For instance, in Fig. 3, for robust foundations at \(b\) = 11.3%, the three allocation types yield similar expected values of \({F}_{N}(t)\) under current sea level conditions, yet this changes notably as SLR intensity increases. On the most severe hazard scenario (SLR-4), random allocation produces drastically lower values of functionality metrics, for values \(b\) = 3.8% to \(b\) = 23.4%, when compared to optimal and suboptimal allocations. This highlights the considerably low functionality values when an uninformed allocation is considered in the recovery modeling.

Fig. 3: Results for post-event network functionality.
figure 3

Temporal evolution of mean network functionality \(E[{F}_{N}(t)]\), for budget ratios \(b\) = 1.3, 3.8, 5.5, 11.3, and 23.4%; and SLR-0, SLR-2 and SLR-4 scenarios, considering optimal, suboptimal and random allocations. The red arrows illustrate the widening gap over time between network functionality results obtained using optimal (upper limit) and random (lower limit) allocations. These results consider robust (deep) foundations.

Full size image

Overall, considerable differences in functionality estimates among different allocation types are observed at low levels of budget availability (e.g., b > 10%). However, for higher budget levels (e.g., >20%), these differences diminish, except in the SLR-4 scenario. In SLR-4, a budget of 1.3% results in no functionality recovery regardless of the allocation type used, suggesting a lower bound on the budget below which it is impossible to restore any damaged component, making the choice of allocation type trivial. This lower bound depends on the severity of the hazard. Moreover, in the majority of results shown in Fig. 3, the similarity between recovery trajectories produced by different allocation types varies over time. Initially, they yield similar functionality estimations that dissipate as time progresses, reflecting the high non-linearity inherent in complex networked systems. For instance, the red arrows in Fig. 3 indicate that for low hazard severity (SLR-0), sub-optimal allocations produce functionality estimates within approximately 20% of the upper and lower bounds (optimal and random, respectively). This difference increases to around 50% for SLR-2 and collapses for SLR-4, where restoration becomes more resource-demanding. The similarity in functionality estimations across different allocations during the early stages is due to the fact that, regardless of the number of damaged components allocated for restoration, there is always an aggregated system-level downtime caused by the individual component-level downtimes. These observations highlight the clear need for the proposed framework, as operators make recovery decisions based on limited resources.

In freight transportation networks, it is important not only to assess functionality evolution, but also to gauge the likelihood of meeting specific demand levels at given points in time. This is particularly crucial for railways, where tolerances to damage are very low and full recovery is required as soon as possible to mitigate negative feedback loops and prevent cascading failures. Moreover, this metric explicitly incorporates the uncertainty about the recovery trajectory that amasses and uncertainties in the model chain compound. Figure 4 depicts the temporal evolution of the probability of meeting certain functionality demand \(\phi\), represented by \(P[{F}_{N}\left(t\right)\ge \phi ]\). These results offer an additional perspective on system reliability, as expected functionality in Fig. 3 may be driven by values below 1, signifying incomplete recovery. For instance, for SLR = 2.0 m, meeting demand \(\phi =1\) is unfeasible for any allocation type, despite, for example, expected functionality hovering around 0.75 (for \(b\) = 23.4%). These results probabilistically illustrate network reliability concerning meeting freight demands, with various probabilities obtained depending on the network’s anticipated stress levels.

Fig. 4: Results for post-event likelihood of meeting flow demands.
figure 4

Temporal evolution of probability of meeting demand \(\phi\), denoted as \(P[{F}_{N}\left(t\right)\ge \phi ]\); for budget ratios \(b\) = 1.3, 3.8, 5.5%, 11.3, and 23.4%; and SLR-0, SLR-2 and SLR-4 scenarios, considering optimal, suboptimal and random allocations. These results consider robust (deep) foundations.

Full size image

To characterize functionality recovery trajectories, the resilience index \({R}_{N}\) is computed. This index seeks to encapsulate the complete recovery trajectory across the 500-day time horizon into a single metric, aiming to condense the time dimension for comparison purposes. Figure 5 presents resilience index results for a complete range of budget availability \(b\) (0.01% to 100%), allocation types, and foundation scenarios. While Figs. 3 and 4 illustrate the temporal evolution of post-disaster functionality for specific cases, Fig. 5 encompasses a broader array of budget and allocation scenarios, illustrating resilience index for higher budget levels. These represent optimistic situations where infrastructure restoration is prioritized and extensively funded. Notably, for robust foundations and the least severe hazard scenario, considerably higher resilience values are expected for similar budget availability across all allocation types. Conversely, in the most severe scenario, more similar resilience outcomes are anticipated, with the influence of foundation type on system resilience diminishing substantially.

Fig. 5: Results for network resilience considering three allocation types.
figure 5

Available budget ratio \(b\) vs. mean network resilience \(E[{R}_{N}]\) for different allocation types (optimal, suboptimal and random), and for hazard scenarios SLR-0 and SLR-4, considering a weak foundations and b robust foundations.

Full size image

Another key observation arises from the results for weak (shallow) foundations. Within the range of 3% <\(b\) < 20%, an uninformed random allocation produces resilience values for the least severe hazard (SLR-0) that are lower than the resilience estimations for the most severe hazard (SLR-4) under optimal and sub-optimal allocations. This underscores the detrimental effects of lacking planning strategies for resource allocation, which exacerbates the impacts of hazards during recovery.

SLR influences railway system resilience

Having explored the influence of resource availability and allocation types in the section above, this section presents the results of system resilience indicators for the five defined hazard scenarios and two foundation types under specific resource-related conditions. For these results, we assume a medium-optimistic allocation, represented in this work by the sub-optimal allocation introduced in the “Methods” section. This assumes that operators will lack sufficient tools to allocate resources optimally, but will have some form of prioritization criteria in place for allocating restoration resources. For other applications, different allocation types may be utilized, as examined in the “Discussion” section. Thus, the available budget ratio \(b\) represents the resources available for disaster response, and the resulting resilience indicators \({R}_{N}\) reflect the expected system resilience under these given resource-related conditions. A resilience index of 1 signifies that the system recovered instantaneously from the disruption, while 0 represents a scenario with no recovery. It is reasonable to observe indices lower than 1, but still high, in scenarios with substantial budget availability. Figure 6(a,b) shows the resilience index for all hazard scenarios and both foundation types.

Fig. 6: Results for key resilience indicators across all hazard scenarios.
figure 6

a,b Available budget ratio vs mean network resilience \(E[{R}_{N}]\). c,d Time to recovery \({R}_{\phi }\), for three functionality levels \(\phi\) (0.50, 0.75 and 1.00). The results consider sub-optimal allocation for the defined five hazard scenarios. In the boxplots, the central box represents the interquartile range, with the median marked by an inner horizontal line. The whiskers extend to the smallest and largest values within 1.5 times the interquartile range from the lower and upper quartiles, respectively.

Full size image

Under the assumption that bridges have shallow foundations, the most optimistic resource availability produces an expected resilience index of 0.58 for SLR-0 scenario and 0.49 for SLR-4, indicating low resilience from the perspective of returning to pre-event functionality levels. Conversely, for the robust foundation scenario (Fig. 6b), we observe considerably higher expected resilience values for SLR-0, SLR-1 and SLR-2. However, for the most severe scenarios (SLR 1.2 m and 2.0 m), similar resilience indices are expected. When compared to current sea level conditions, for SLR = 0.5 m, the expected resilience indices show reductions of 20–25%, depending on the available budget. The two most severe SLR scenarios (1.2 m and 2.0 m) result in further reductions of 35% to 55%, highlighting the substantial impact of more extreme compound hazards due to SLR on system resilience, even under ideal budget conditions. A key observation from these results is the diminishing returns due to the non-linearity of the budget-resilience relationship. For robust foundations along with SLR scenarios 0.5, 1.2, and 2.0 m, diminishing returns emerge at about 10–20% of the total replacement cost. For shallow foundation scenarios, this range is about 25% to 30%.

Another key resilience indicator for high-level planning is the expected time to achieve certain functionality levels \(\phi\), which can be tied to demand expectations to assess system reliability from a flow-of-goods perspective. Panels c and d in Fig. 6 show the results for the time to recovery \({R}_{\phi }\) for both foundation types. These results illustrate the effects of SLR intensity on the expected times to reach three functionality levels (\(\phi\) = 0.50, 0.75, and 1.00). An overall trend shows median recovery times increasing with SLR scenario severity. Specifically, the median time to reach functionality \(\phi\) = 0.50 increases from 150 days to 250 days from the least to most severe scenario for shallow foundations. For the specific case of \(\phi\) = 1.00 for SLR = 2.0 m, the boxplot shows a flattened distribution, indicating that in all iterations, the time to achieve full functionality equals or exceeds the considered time horizon (500 days), suggesting recovery with very low resilience. For robust designs, median recovery times to \(\phi\) = 0.50 are shorter (50 and 220 days for SLR-0 and SLR-4, respectively), indicating a more resilient system. However, SLR still causes median recovery times to increase by a factor of 4.4. These times are expected to increase by a factor of 2.5 for \(\phi\) = 0.75 (from 150 to 370 days) and 1.67 for \(\phi\) = 1.00 (from 300 to 500 days), when comparing SLR-0 and SLR-4. Regarding uncertainty, the results suggest that for the current sea level conditions SLR-0, even though median recovery times are shorter compared to SLR scenarios, these estimates show considerably larger dispersion for most cases, as indicated by the interquartile ranges in the boxplots. This is most evident for the weak (shallow) designs, where for SLR-4 the system components experience extensive damage, often reaching maximum restoration costs and times in most iterations, with low dispersion. As hazard severity decreases, median recovery times also decrease, but the dispersion increases. This is due to the more diverse variation in damage spatial distribution and recovery costs and times, as the system does not reach the maximum possible damage. For robust foundations, this trend is somewhat dissipated, and only observed clearly for \(\phi\) = 1.00, suggesting more consistent aggregated uncertainty across hazard scenarios, thanks to proactive design considerations.

Discussion

The complexity of resource availability and allocation decisions profoundly influences the resilience of railway networks. From a resilience modeling perspective, our study demonstrates that optimal allocation can substantially enhance estimations of railway network resilience by strategically prioritizing intervention of damaged infrastructure components, thereby maximizing functionality recovery over a given time horizon. However, achieving such optimal allocation in real-world post-disaster conditions is often unlikely due to limited information, time constraints, and computational challenges, at least with the current state of knowledge relying on traditional infrastructure assessments. This suggests that modeling recovery of infrastructure systems considering sub-optimal allocation decisions, while less efficient, provides more realistic resilience estimations that align better with the decision-making processes observed during post-disaster recovery in past events28. Our framework offers high flexibility across multiple dimensions and leverages heuristics to reduce computational complexity, aiming to bridge a notable gap in resource-aware frameworks for modeling resilience of complex freight networks, such as railway systems. It considers uncertainties stemming from hazard mechanisms, physical responses, and human decisions, thereby incorporating greater nuance into resilience estimations.

For resilience planning, a task of paramount importance is to be aware of the recovery capabilities of a system to establish a baseline for evaluating the benefits of mitigation policies. Our analysis provided evidence that under certain ranges of resource availability, considering optimal allocation to model recovery trajectories may lead to an overestimation of the actual recovery capabilities of the system. This may result in the erroneous assumption that a system or certain components do not require mitigation policies, potentially introducing socio-economic inequities if the available resources or allocation optimality is not appropriately characterized. However, modeling allocation decisions in an optimal manner provides valuable insights into upper bounds and optimistic scenarios, which are still valuable for evaluating or steering mitigation policies. The optimization approach presented in this work enables computationally feasible optimal allocation of resources by leveraging the binary nature of functionality in railway system components. This algorithm aims to identify the set of components to be restored that maximizes resilience over a given time horizon. This allows policymakers to explore the upper bounds of their return on investment in terms of expected resilience for various resource-availability scenarios, given the hazard exposure and asset inventory of a railway system portfolio. Overall, our framework allows for probing and incorporating resource-related parameters, including their uncertainty, to support a risk-informed evaluation of mitigation policies and enhance railway network resilience.

In disaster response situations, our analysis reveals that while optimal disaster response strategies produce the highest resilience indicators and should be pursued whenever possible, heuristic-based sub-optimal strategies still achieve considerable functionality restoration. These sub-optimal strategies considerably outperform the uninformed decision-making scenario, represented in this work by the random allocation. This underscores the importance of having a disaster response strategy in place to allocate funds effectively during disaster response, even if these strategies are not optimal. For example, identifying prioritization strategies beforehand can allow policymakers and officials to deploy resources more quickly after a disaster by reducing the time required to evaluate allocations, thereby minimizing idle times in repair activities. Additionally, the diminishing returns observed in resilience improvements with increasing budget allocations suggest that satisfactory resilience levels can be achieved with a fraction of the replacement cost, thereby optimizing the return on investment in disaster response or resilience-enhancing measures. Our framework can support the implementation of these heuristic-based sub-optimal strategies, offering a viable alternative for policymakers when the conditions necessary for developing optimal strategies are not met.

Concurrent and sequential disasters are critical considerations for future resilience practice, which can be addressed through appropriate adaptations and inputs within the proposed framework. Initially, hazard modeling serves as a foundational input, enabling the consideration of concurrent and sequential disasters. The developed framework can then assess resilience variations under consecutive events, simulating back-to-back or increasingly frequent disasters driven by climate change. For example, by incorporating the fragility of already damaged components, it can capture the compounded impact of subsequent events. Additionally, more stringent budget constraints can be integrated to reflect the financial strain imposed by recurring extreme events, allowing for a more comprehensive evaluation of resilience under evolving hazard conditions.

Lasty, our findings reveal a subtle effect in which, as the severity of SLR conditions increases, even optimal allocation strategies result in marginal improvements in resilience compared to sub-optimal and random approaches. This effect is especially pronounced at the extremes of resource availability: very low resources lead to poor resilience outcomes, while high resource availability tends to yield the highest possible resilience outcomes, regardless of the allocation strategy. This is because high resources facilitate reconstructing large parts or the entirety of infrastructure, which is almost independent of the damage. The study also highlights that the initial functionality drop is primarily influenced by the physical vulnerability and hazard exposure of railway components, while subsequent functionality trajectories are largely governed by resource constraints and allocation decisions. This underscores the critical need for robust infrastructure design and proactive planning to mitigate the SLR and compound hazard effects, as they greatly affect the overall recovery process by lowering the starting point in the recovery trajectory. These pre-disaster measures are crucial regardless of the available resources for post-disaster restoration or how they are allocated. While they may lead to an increase in construction costs, this is often insignificant compared to the potential losses following a severe disaster.

Conclusions

The significance of this study lies in its potential to substantially improve the resilience of railway infrastructure systems. Given the limited availability of fragility and restoration data and the uncertainties in resources availability, the proposed framework provides more nuanced resilience estimates that can reflect the reality of coastal climate and hazard-exposed networks. This enhances the ability to inform decision-making and resource allocation strategies aimed at enhancing the resilience of critical infrastructure. By offering a more nuanced and resource-aware assessment of recovery capabilities, this framework helps avoid overestimation of a system’s recovery capabilities, supporting pursuit of resilience enhancement policies that are both effective and economically feasible. The implications of our study extend to regional resilience planning, where the framework can guide decision-makers on the most effective resource allocation strategies under various budget constraints and hazard scenarios.

While our framework offers considerable value and applicability, there are areas that present opportunities for further investigation. Firstly, our study focuses solely on budget constraints as the primary resource for recovery. In reality, factors such as labor availability and logistical support also play crucial roles53,54. Future research should incorporate these additional resource-related constraints to provide a more comprehensive assessment of post-disaster recovery capabilities. Secondly, the quantification of resilience indicators could be improved by explicitly characterizing and propagating uncertainty sources other than those considered in this study, and by validating the recovery results with historical data from past events55. In this regard, future studies may focus on gathering such data in collaboration with governmental and non-governmental organizations involved in disaster response. Thirdly, the use of a linear optimization method—selected here due to the need for iterative simulations to support uncertainty propagation—could be further expanded in future research through the application of higher-fidelity approaches, such as nonlinear or multi-objective optimization techniques. While linear optimization was chosen here for its tractability, lower computational complexity, and broader solver availability, nonlinear methods may be feasible in certain cases, particularly when high-performance solver licenses are accessible and deterministic scenarios are being analyzed.

The study’s findings also highlight the importance of robust infrastructure design and proactive planning to mitigate the effects of compound climate-driven hazards. By mitigating the initial functionality drop and improving recovery trajectories, robust design and planning can profoundly enhance system resilience. The insights provided by this study can inform resilience enhancement strategies and ensure that infrastructure systems are better equipped to withstand and recover from future hazards. Lastly, it is worth noting that the data revolution in smart cities will, in the future, provide high-quality information that can be effectively leveraged by the framework in this study. This presents notable potential for continually updating and improving resilience quantification of railway networks among other infrastructure, and opportunities to further steer high-confidence optimal resource allocation in post-disaster scenarios.