Introduction

Through experience, people learn links between their behaviors and the outcomes they produce, including which actions lead to which kinds of costs or benefits in which situations, on average. For example, across repeated experiences, someone might learn how much seasoning they like on their pasta, which floors of a parking garage will have available spaces on the weekend, or what type of social media post gets the most engagement. This sort of learning can be modeled using a reinforcement learning framework1, which formalizes the relationship between the expected and actual rewards of an action in terms of a reward prediction error (RPE). In humans and other species, these learning signals are reflected in the activity of subcortical structures in the brain2,3,4 and known to guide behavior. More positive prediction error increases the likelihood of repeating the action, whereas more negative prediction error reduces the likelihood of repeating the action. Interestingly, people often perform actions whose rewards are not theirs alone but are instead distributed across themselves and others, whether choosing what kind of cake to order for a birthday party or choosing a driving route for a group road trip. How does the social distribution of rewards affect learning? Despite progress in characterizing the reinforcement learning processes, on the one hand, and people’s preferences for the social distribution of resources, on the other, whether and how the social distribution of rewards impacts reinforcement learning is not well understood.

Although research on reinforcement learning has predominantly treated rewards as fixed (i.e., rewarding versus not rewarding; punishing versus not punishing), there is growing interest in characterizing contextual influences on valuation during reinforcement learning in a more flexible and continuous manner5,6,7,8. In particular, a number of studies have documented the effects of aspects of social context on learning. For example, social contexts can serve as information sources for learning, including through observational learning or advice-taking9,10,11,12. There is also evidence that social context can serve as reward or punishment itself (e.g., smiling or positive feedback; ref. 13,14,15,16), modulate the value one places on rewards received by others17,18, and shape the degree to which people learn vicariously from others’ rewards or punishments19,20,21. Still, little is known about (whether and) how social context influences the basic non-social reinforcement learning process when rewards are shared.

In parallel, research on social decision-making has characterized people’s preferences for how resources should be divided between themselves and others. Overall, people display social preferences for equity and fairness by making decisions that promote equal and fair distributions of resources, respectively22, suggesting that people generally derive greater value from equal (or fair) distributions of resources than unequal ones, but if resources are divided unequally, people generally prefer to receive the larger share. Yet this preference can be moderated by contextual factors, such as social distance23 and social group membership24,25. In particular, recent evidence suggests that perceptions of others’ traits, such as their warmth and competence, changes the value people place on particular divisions of resources across themselves and other people: the more warm the recipient, the less value people derive from advantageous inequity, i.e., receiving more than the other person, whereas the more competent the recipient, the less value people derive from disadvantageous inequity, i.e., receiving less than the other person25,26.

To what extent do patterns of social valuation, observed during decision-making, extend to impact reward signals during learning? Outside the social domain, differences between subjective value measured during reward-based learning versus decision-making suggest the non-triviality of this question. For example, during learning, individuals show range adaptation: that is, they demonstrate no meaningful advantage to learning when the rewards at play are in the range of $100 in magnitude than when rewards (differ by the same proportions but) are in the range of $10 in magnitude27,28,29. Yet during decision-making, people demonstrably value actions that generate $100 over those that generate $10. Likewise, although individuals generally value advantageous over disadvantageous inequity during decision-making, it could be the case that subjective value shows adaptation to the inequity context. If so, individuals exposed only to (various levels of) advantageous inequity and individuals exposed only to (various levels of) disadvantageous inequity would learn equally well from the best split percentage to which they are exposed, even though individuals in the advantageous context are exposed to better split percentages overall.

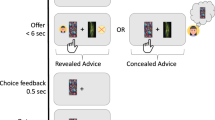
In the current studies, we addressed these questions by adapting a computerized, non-social reinforcement learning task from Collins and Frank (2012)30 to accommodate manipulations of the inequity of the reward (distributions across the learner and a partner, by percentage) and the social identity of the partner (Fig. 1). We chose this task paradigm because it can isolate contributions of lower-level reinforcement learning processes (versus executive processes) to performance while accommodating parametric modulations of inequity along with manipulations of partner identity. In 3 studies, participants had opportunities to learn the reward of stimulus-action pairs (images and button presses) under conditions of (in)equity in the social distribution of the rewards. One button press generated the largest reward, another generated the smallest reward, and a third generated an intermediate reward. Participants played 8 independent blocks of the task. In each block, they were first shown the set of images they would encounter in that block (5 images per block in Studies 1 and 2; 2 images per block in Study 3), followed by a piece of information about the partner with whom the rewards would be split during that block (e.g., “a nurse”). Then, on each trial, the participant saw an image on the screen and chose which of 3 eligible buttons on the keyboard to press (j, k, or l), within 1.5 s. Following the button press, a feedback screen displayed how much money they and the other person gained (e.g., You: $.30; Nurse: $.70). In each block, 12 trials per image were intermixed in a random order, for (5 images × 12 trials =) 60 trials per block in Studies 1 and 2 and (2 images × 12 trials =) 24 trials per block in Study 3. The total reward to be split across the participant and the partner depended on the button press: for each image, one button deterministically generated the highest reward (e.g., $2), another deterministically generated the intermediate reward (e.g., $1), and a third deterministically generated the lowest reward (e.g., $0). Inequity type was manipulated between subjects, such that each participant was either assigned to the advantageous condition (they always gained more than 50%) or the disadvantageous condition (they always gained less than 50%). Within each inequity type, specific split percentages were manipulated within subjects. To implement this, each image corresponded to a specific reward split between the participant and the partner (unbeknownst to participants). For example, for one participant in one block, the car image was always associated with the participant receiving 30% of the money and the other person receiving 70%.

Fig. 1: Example task.
figure 1

A, B The task was grouped into 8 independent blocks. Before each block, participants saw all stimuli they may encounter, and the occupation of the social target that would receive a share of the reward. A shows the block structure of Studies 1 & 2, where people had to learn about 5 stimuli per block. B shows Study 3, where the cognitive load was reduced by only learning about 2 stimuli per block. C, D Trial structures: Each image stimulus would appear for 12 trials in total and corresponded to one percentage of the split. The trials for all 5 stimuli were randomly shuffled. C shows the trial structure of Studies 1 & 3 where each action generated a fixed total reward ($0, $1, or $2), which was then split between the participant and the social target. D shows the structure of Study 2, where each action generated a fixed reward to the participant ($0, $1, or $2). The reward went to the social target, and hence the total reward depended on the specific percentage of the split. In all studies, both the participant and the social target would gain more (hypothetical) money if the participant learned quickly to press the button that generates the highest reward.

Full size image

In Study 1, the total amount of reward (summing the participant's and the partner’s reward) was held constant across inequity conditions, varying the amount the participant personally received. In Study 2, the amount that a participant received was held constant across inequity conditions, varying the total amount of reward summing across the participant and the partner. In Study 3, in light of prior research suggesting that cognitive load may dampen social information processing31,32, we reduced the total number of stimulus-action pairs in order to reduce cognitive load during learning, allowing for the possibility that effects of social information may be elevated in such cases. In all studies, we varied the identity of the partner by informing the participant of their occupation (e.g., Nurse), following past studies25,26,33 and collected participants’ ratings of the perceived warmth and competence of people with these occupations, both following the learning task and in an independent set of participants34. The occupation information remained the same within each learning block.

We raise 3 possible, not mutually exclusive hypotheses about the ways in which social contextual information might shape reinforcement learning. First, reinforcement learning may operate on objective rewards during learning (such as the total reward generated by different stimulus-action pairings). Second, reinforcement learning may be shaped by the degree of social inequity of the reward (i.e., how much more or less of the reward the participant receives than the partner). Third, reinforcement learning may be shaped by the perceived traits of the partners with whom rewards are shared. We formalized these hypotheses into 4 computational models and tested their fit to participants’ data. Two models formalize the first hypothesis, assuming only effects of objective reward, with no effect of social inequity or identity on reinforcement learning (baseline RL models). The baseline model in Studies 1 and 3 only learned from the total reward because, by experimental design, the total reward did not depend on the inequity manipulation. In Study 2, the baseline model only learned from the amount of reward given to the participant because Study 2 was designed such that the total reward amount depended on the inequity manipulation, while the reward given to the participant did not depend on the inequity manipulation. To formalize the second hypothesis, we constructed an inequity-weighted reinforcement learning model (IRL), which assumes that the rewards of both the learner and the target, along with the (signed) difference between them, affect learning. To formalize the third hypothesis, we created a social perception-weighted reinforcement learning model (SPRL), which assumes that the perceived traits (warmth and competence) of the social target combine with inequity to impact learning. This model builds upon our findings in social decision-making that perceptions of others’ traits modulate people’s preferences for (or against) inequity25,26. Here, we applied the utility function from our previously developed social perception-weighted model of social valuation to calculate the reward signal (Q-value) for reinforcement learning (see “Methods” section). By comparing the fits of each of these models to participants’ learning behavior, we can distinguish among the different hypotheses about whether and how social contextual information impacts reinforcement learning. All procedures were conducted in a manner approved by the Institutional Review Board at the University of Pennsylvania (protocol #831852).

Methods

Study 1

Participants

Participants (N = 99) were recruited through the University of Pennsylvania’s SONA platform and earned undergraduate psychology class credit for their online participation. 5 participants were excluded for a response rate below 80%, leaving us with 94 participants for analysis and modeling. 41 participants were randomly assigned to the advantageous condition (Mage = 19.63, 32 women, 8 men) and 53 participants were randomly assigned to the disadvantageous condition (Mage = 19.79, 35 women, 16 men, 2 self-described). Demographic information was collected in a self-report survey after the experiment. All procedures were conducted in a manner approved by the Institutional Review Board at the University of Pennsylvania (protocol #831852). Informed consent was obtained from all participants before their participation. The study was not preregistered.

Experimental procedure

After choosing to participate in the SONA system, participants proceeded to a new browser window to start the experiment, which was coded in PsychoPy35, converted to PsychoJS, and hosted on Pavlovia (pavlovia.org). On each trial of the experiment, the participant viewed a stimulus image on the screen and chose which of three possible keys to press in response; this action would generate some amount of monetary reward. Crucially, the monetary rewards obtained would ostensibly be split between them and another person, making it possible to manipulate inequity. We used images from Collins et al. (2017)36 as stimuli in our task.

The task consisted of 8 blocks of trials. A trial was the smallest unit of the task where participants saw a stimulus (in this case, an image) presented on the screen and pressed a key in response. A block was a collection of trials run one after another. Our experiment had one between-subject manipulation, one between-block manipulation, and one within-block manipulation. Between subjects, we manipulated inequity type. We assigned each participant randomly into either an advantageous condition, where the participant received more than half of the reward, or a disadvantageous condition, where the participant received less than half of the reward. We chose to manipulate inequity type between subjects for two main reasons. First, this allowed for a stronger test for the absolute effect of inequity type on learning. If each participant had experience with both advantageous and disadvantageous splits, any difference between the two conditions could have arisen due to anchoring effects. Second, the between-subject design kept the duration of the experiment within a range that minimized concerns about data quality. Similarly, given that learning on a non-social version of this task is already documented30,36, we chose not to include a non-social learning condition in the current study. Between blocks, we manipulated the social group membership of the partner (social target). Before each block, participants were told the occupation of the social target (Taxi Driver, Nurse, Judge, Computer programmer, Dancer, Plumber, Politician, or Secretary). These 8 occupations were selected to cover as widely as possible the range of warmth and competence ratings according to ref. 25. Each occupation was randomly assigned to one of the 8 inequity blocks. Within a block, each stimulus image corresponded to a different percentage of the split. For example, if the stimulus on the screen was an image of a lotus, 30% of the reward generated by the keypress would go to the participant, whereas if it was an image of a tree, the participant would get 0% of the reward. There were 5 unique stimuli in each block, corresponding to 100%, 90%, 80%, 70%, and 60% of the reward in the advantageous condition, and 0%, 10%, 20%, 30%, or 40% in the disadvantageous condition.

Each block was a learning problem independent of the others, using distinct sets of images. At the beginning of each block, the screen presented all 5 images that the participants would encounter in that block. 12 iterations of each stimulus were interleaved throughout each block.

Within each block, the trial structure was as follows: the trial began with an inter-trial interval of 1.5 s during which only a white cross was displayed at the center of the screen. Next, participants viewed one of the learning stimuli on the screen, which was continually displayed either until the participant responded with one of the three possible actions ("j”, “k”, or “l”), or if 1.5 s had elapsed. Each possible action generated either $0, $1, or $2 as a monetary reward. For each particular stimulus, two different keys could not generate the same reward amount. For any two stimuli in the same block, there was at least one key that generated different rewards for either stimulus. Upon pressing the key at each trial, participants would see on the screen how much reward they had received and how much reward the other person had received. The respective reward amount was determined by multiplying the generated reward by the split percentage corresponding to the stimulus. However, if the reaction time exceeded 1.5 s, the screen instead displayed the message “please respond faster”, and if the response was faster than 0.15, the response would not register, and the participant must press the key again. The feedback stayed for 2 s before transitioning to the next trial.

To become familiarized with the tasks, participants first read through the instructions, which informed participants that each key generated either $0, $1, or $2 as total reward, but part of it would be split with another person. The instructions also emphasized that participants should imagine the rewards were actual money. We did not explicitly state that the goal of the task was to get as much reward as possible, in which case participants may deliberately ignore social information and solely focus on the total reward. In order to elicit how participants would naturally incorporate social information with rewards, we stated merely that paying more attention could help them get more rewards. Participants then performed one practice block, which had the same structure as a regular block in the task but used a different set of images, and participants were told to receive 50% of the generated rewards while the remainder went to a singer (which was an occupation not used in the main task). After the entire experiment, participants were redirected to Qualtrics (qualtrics.com) to complete a short demographic survey where we also listed the 8 occupations that they had encountered during the task and asked them to rate from 0 to 100 how warm and how competent they perceived each of the occupations (see Fig. S3). The order of these questions in which we presented to participants on Qualtircs, was randomized. Because the social perception rating was always collected after the learning task, we confirmed that there was no evidence the between-subject manipulation systematically biased participants’ ratings of warmth or competence in any of the 3 studies through t-test (Study 1: tcompetence(679) = −0.81, p = 0.421, d = −0.06, 95% CI = [−0.20, 0.08]; twarmth(705) = −1.76, p = 0.079, d = −0.13, 95% CI = [−0.27, 0.01]; Study 2: tcompetence(595) = 0.42, p = 0.671, d = 0.03, 95% CI = [−0.12, 0.18]; twarmth(625) = 0.83, p = 0.407, d = 0.06, 95% CI = [−0.09, 0.21]; Study 3: tcompetence(744) = −1.05, p = 0.296, d = −0.08, 95% CI = [−0.22, 0.07]; twarmth(753) = −0.88, p = 0.382, d = −0.06, 95% CI = [−0.21, 0.08]).

Study 2

Participants

Participants (N = 100) were recruited through the University of Pennsylvania’s SONA platform and earned undergraduate psychology class credit for their online participation. 9 participants were excluded for a response rate below 80%, leaving us with 91 participants for analysis and modeling. 55 participants were assigned to the advantageous condition (Mage = 19.87, 37 women, 16 men) and 36 participants were assigned to the disadvantageous condition (Mage = 20.03, 28 women, 8 men). Demographic information was collected in a self-report survey after the experiment. All procedures were conducted in a manner approved by the Institutional Review Board at the University of Pennsylvania (protocol #831852). Informed consent was obtained from all participants before their participation. The study was not preregistered.

Experimental procedure

After choosing to participate in the SONA system, participants proceeded to a new browser window to start the experiment, which was coded in PsychoPy35, converted to PsychoJS, and hosted on Pavlovia (pavlovia.org). The experimental design was identical to that of Study 1, with an important exception: in Study 2, the amount of reward given to the participant was held constant across split conditions. Consequently, the total amount of rewards generated may vary. Therefore, we accordingly modified the instruction. We did not inform the participants that each key generates either $0, $1, or $2; we just told them that each key may generate a different amount of total reward. In actuality, each key generated the amount of total reward such that the amount given to the participant was either $0, $1, or $2. The total reward was thus either $0, $1 divided by the percentage of split to the participant, or $2 divided by the percentage of split to the participant. Because the 0% was not mathematically possible under this new design, we replaced it with 50%.

Study 3

Participants

Participants (N = 100) were recruited through the University of Pennsylvania’s SONA platform and earned undergraduate psychology class credit for their online participation. 5 participants were excluded for a response rate below 80%, leaving us with 95 participants for analysis and modeling. 47 participants were assigned to the advantageous condition (Mage = 19.76, 29 women, 17 men) and 48 participants were assigned to the disadvantageous condition (Mage = 19.92, 23 women, 23 men, 1 self-described). Demographic information was collected in a self-report survey after the experiment. All procedures were conducted in a manner approved by the Institutional Review Board at the University of Pennsylvania (protocol #831852). Informed consent was obtained from all participants before their participation. The study was not preregistered.

Experimental procedure

After choosing to participate in the SONA system, participants proceeded to a new browser window to start the experiment, which was coded in PsychoPy35, converted to PsychoJS, and hosted on Pavlovia (pavlovia.org). The experimental design was identical to that of Study 1, with one important exception: to reduce cognitive load, we reduced the total number of stimuli to 2 unique stimuli per block (rather than 5), where each stimulus corresponded to 90% or 70% in the advantageous condition, and 10% or 30% in the disadvantageous condition.

Regression analyses

Full regression predicting rewardingness of action

We ran the following mixed-effect linear regression for each of the 3 studies:

$$rewardingness \sim iteration* split* inequity* warmth* competence+(1| subject)$$
(1)

where rewardingness denotes the reward amount independent of the manipulation of social distribution ($0, $1, or $2). iteration denotes how many iterations the stimulus has appeared in a particular learning block (1, 2, ..., 12). split denotes the percentage of the reward given to participants themselves (0, 0.1, 0.2, ..., 1). inequity is a categorical variable denoting whether the participant is in the advantageous inequity condition or the disadvantageous inequity condition. warmth denotes the participant’s rating on the perceived warmth of the social target (1–100). competence denotes participant’s rating of the perceived competence of the social target (1–100). subject denotes the participant ID that we use as a random intercept. Before passing into the regression model, we standardized rewardingness, iteration, warmth, and competence across the entire data set, and we also standardized split within the advantageous or disadvantageous conditions so that it is not confounded with inequity.

Regression by separate inequity type

We ran the following mixed-effect linear regression for both the advantageous condition and the disadvantageous condition in each of the 3 studies:

$$rewardingness \sim iteration* split* warmth* competence+(1| subject)$$
(2)

All variables were standardized, and we removed the split condition where the participant received 0% in Study 1 and the split condition where the participant received 50% in Study 2, as they might serve as edge cases that drove the results in the full regression model.

Regression predicting reaction time of action by trial

We ran the following mixed-effect linear regression for each of the 3 studies, and the results were referenced in Supplementary Fig. S1:

$$rt \sim iteration* split+(split| subject)+(split| inequity)$$
(3)

rt denotes the reaction time at each trial. Both participant ID and inequity type were included as random intercept and split as randomly slope, allowing the effect of the split to potentially differ across participants. Before passing into the regression model, we standardized rt and iteration across the entire data set, and we also standardized split within the advantageous or disadvantageous conditions so that it is not confounded with inequity.

Regression predicting trial-by-trial model comparison

We ran the following mixed-effect linear regression for each of the 3 studies:

$${{\Delta }}WAIC \sim iteration* inequity+(1| subject)$$
(4)

where iteration was centered by subtracting 5 from it. ΔWAIC denotes the trial-by-trial difference in WAIC between two computational models, showing how much one outperformed the other in fitting the participant data.

Procedures

For the regression analyses, we tested the impact of different task variables by performing mixed-effect linear regression analysis using the R function mixed in the package afex37. All numeric variables were scaled before being passed into the regression model, and all interaction terms were included. The package afex conducts significance testing on regression coefficients by comparing the fit of the full model with the truncated model without that regressor through a χ2 test. To conduct a Wilcoxon test, we used the wilcox_test function from the package rstatix. To conduct a two-sample t-test, we used the t_test function from the package rstatix. For both tests, we averaged within participants first, so the sample sizes are the number of participants in each condition, and both are two-sided tests.

Computational models

All of our candidate models were adaptations of a typical reinforcement learning model1. The model relies on two main variables representing the task environment. The first one is the state s ∈ S, where S represents the full stimulus/state space within a block (i.e., all the possible images that could appear). In our experiment, ∣S∣ = 5 except in Study 3, where ∣S∣ = 2. The second variable is the action a ∈ A, where A is the full action space. In our experiment, ∣A∣ = 3 because there were three possible buttons to press as a response to the instrumental learning task. The algorithm proceeds in two stages, as introduced in the introduction: the value updating stage and the policy formation stage. In the value updating stage, for stimulus s and action a on trial t, the model estimates an expected value (i.e., the Q-value) Q(st, at) by performing an update using the delta rule (Equation (6); ref. 38):

$${{{{\boldsymbol{Q}}}}}_{t+1}({s}_{t},{a}_{t})={{{{\boldsymbol{Q}}}}}_{t}({s}_{t},{a}_{t})+\alpha {\delta }_{t}$$
(5)
$${\delta }_{t}={r}_{t}-{{{{\boldsymbol{Q}}}}}_{t}({s}_{t},{a}_{t})$$
(6)

where α represents the learning rate and Qt represents an ∣S∣ × ∣A∣ matrix encoding all Q-values given a trial t. Q0 is initialized as a uniform matrix of the expected values of random guessing. \(\delta \in {\mathbb{R}}\) is the reward prediction error, and rt ∈ {0, 1, 2} is the reward received at trial t.

In the policy formation stage, Q-values are transformed by the Softmax function into a policy, i.e., a vector of probabilities of taking each action (represented by \({\overrightarrow{\pi }}_{t}\)).

$${\overrightarrow{\pi }}_{t}=p(\overrightarrow{A}| {s}_{t})=Softmax({{{{\boldsymbol{Q}}}}}_{t}({s}_{t}),\beta )=\frac{{e}^{\beta {{{{\boldsymbol{Q}}}}}_{t}({s}_{t})}}{{\sum }_{a\in A}{e}^{\beta {{{{\boldsymbol{Q}}}}}_{t}({s}_{t},a)}}$$
(7)

where β ∈ [0, ∞) represents the inverse softmax temperature. Finally, we allow all Q-values to decay back to the initial Q-values with a decay rate (ϕ ∈ [0, 1]) to capture subjects’ forgetting process.

$${{{{\boldsymbol{Q}}}}}_{t+1}({s}_{t},{a}_{t})={{{{\boldsymbol{Q}}}}}_{t}({s}_{t},{a}_{t})+\phi ({{{{\boldsymbol{Q}}}}}_{0}({s}_{t},{a}_{t})-{{{{\boldsymbol{Q}}}}}_{t}({s}_{t},{a}_{t}))$$
(8)

Naive

The naive model is just the same reinforcement learning model as described above, where the inequity and social target information are entirely discarded. This model instantiates the hypothesis that participants only learn by the total amount of reward generated and ignore how the reward is split afterward. In Study 2, just like in Study 1, the naive model is the model that only learns based on the total reward, but the total reward is dependent on the split by experimental design: \({r}_{t}\in \{0,\frac{1}{{p}_{t}^{\,{{\rm{self}}}}},\frac{2}{{p}_{t}^{{{\rm{self}}}\,}}\}\) and ∀ a ∈ A, \({{{{\boldsymbol{Q}}}}}_{0}({s}_{t},a)=\frac{1}{{p}_{t}^{\,{{\rm{self}}}\,}}\). This model still instantiates the hypothesis that participants only learn by the total amount of reward generated and ignore how the reward is split afterward. The baseline model reported in the main task for Studies 1 and 3 was the naive model since the total reward was independent of the split condition.

Selfish

The selfish model instantiates the hypothesis that participants only learn by the amount of reward given to themselves. It is the same as the naive model except it only uses the amount of reward given to self:

$${\delta }_{t}={r}_{t}* {p}_{t}^{\,{{\rm{self}}}\,}-{{{{\boldsymbol{Q}}}}}_{t}({s}_{t},{a}_{t})$$
(9)

where pt denotes the percentage of the reward given to the participant at that trial, and Q0 is initialized to be the percentage of the split corresponding to the trial where a new stimulus first appears: if \(\forall {t}^{{\prime} } < t,{s}_{{t}^{{\prime} }}\ne {s}_{t}\), we have ∀ a ∈ A,

$${{{{\boldsymbol{Q}}}}}_{0}({s}_{t},a)={p}_{t}^{\,{{\rm{self}}}\,}$$
(10)

In Study 2, the concept of the selfish model is the same. Because in Study 2, we ensure the reward given to self does not depend on \({p}_{t}^{\,{{\rm{self}}}\,}\), \({r}_{t}* {p}_{t}^{\,{{\rm{self}}}\,}\in \{0,1,2\}\) and Q0(st, a) = 1. The baseline model reported in the main text for Study 2 was the selfish model.

IRL

The inequity-weighted model (IRL) instantiates the hypothesis that the degree of inequity of how the reward is split between the participant and the social target shapes how the reward is represented39. We formalize the effect of inequity using the Fehr–Schmitt utility function40:

$${u}_{t}={r}_{t}* \left({p}_{t}^{\,{{\rm{self}}}}+\gamma * \left({p}_{t}^{{{{\rm{target}}}}}-{p}_{t}^{{{\rm{self}}}\,}\right)\right)$$
(11)

where in our task, \({p}_{t}^{\,{{\rm{target}}}}=1-{p}_{t}^{{{\rm{self}}}\,}\) is simply the percentage of reward given to the recipient, and the inequity weight\(\gamma \in {\mathbb{R}}\) controls the influence of the inequity. In the disadvantageous inequity condition, positive γ means that the participant finds it more rewarding if the other person obtains more reward than themselves. Negative γ means that the participant finds it less rewarding if the other person obtains more reward than themselves. In the advantageous inequity condition, positive γ means that the participant finds it less rewarding if the other person obtained less reward than themselves. Negative γ means that the participant finds it more rewarding when the other person obtains less reward than themselves. If γ = 0, it means the participant only cares about the reward given to themselves and is indifferent to the inequity. In general, γ captures in what direction and to what extent a participant deviates from a purely selfish agent and cares about inequity in the reward distribution. The delta rule thus becomes

$${\delta }_{t}={u}_{t}-{{{{\boldsymbol{Q}}}}}_{t}({s}_{t},{a}_{t})$$
(12)

Q0 is initialized to be the expected utility corresponding to the trial where a new stimulus first appears: if \(\forall {t}^{{\prime} } < t,{s}_{{t}^{{\prime} }}\ne {s}_{t}\), we have ∀ a ∈ A,

$${{{{\boldsymbol{Q}}}}}_{0}({s}_{t},a)={p}_{t}^{\,{{\rm{self}}}}+\gamma * ({p}_{t}^{{{{\rm{target}}}}}-{p}_{t}^{{{\rm{self}}}\,})$$
(13)

We initialized Q0 differently for different split conditions because initializing Q0 with a flat value significantly undermines the ability of the model to capture the key effects of learning. We confirmed this by simulating the winning model with a flat initialization of Q0 on the Study 3 data and showed that it failed to produce the split effect that was produced by human participants in the disadvantageous condition (Fig. S9).

SPRL

The social perception-weighted model (SPRL) instantiates the hypothesis that not only does the degree of inequity shape how the reward is represented, but the sensitivity to the inequity further depends on the social perception of the recipient’s identity. We adopt the social preference model from ref. 25 to capture the effect of warmth and competence on the inequity weighting parameter:

$$\gamma ={\gamma }_{0}+{\gamma }_{w}* w+{\gamma }_{c}* c$$
(14)

where w is the warmth rating and c is the competence rating that we collected in the post-task survey. The rating scale we used for the survey was from 0 to 100. For the stability of modeling fitting, we rescaled the social perception ratings into [−0.5, 0.5]. \({\gamma }_{0},{\gamma }_{w},{\gamma }_{c}\in {\mathbb{R}}\) are respectively the base weight, warmth weight, and competence weight.

Modeling procedure

We fitted all model parameters using hierarchical Bayesian methods. Compared to the traditional maximum likelihood estimation, not only does the Bayesian fitting method give us a full posterior distribution over the fitted parameters (instead of simply one point estimate), but it also yields a superior parameter and model recovery41,42. The population-level priors for all model parameters were carefully tuned to be as uninformative as possible while avoiding divergence during fitting:

$${{{\boldsymbol{\alpha }}}} \sim \,{{\rm{Beta}}}\,(\alpha =1,\beta =1)$$
$${{{\boldsymbol{\beta }}}} \sim \,{{\rm{Gamma}}}\,(\alpha =3,\beta =0.5)$$
$${{{\boldsymbol{\phi }}}} \sim \,{{\rm{Beta}}}\,(\alpha =2,\beta =15)$$
$${{{{\boldsymbol{\gamma }}}}}_{{{{\boldsymbol{w}}}}},{{{{\boldsymbol{\gamma }}}}}_{{{{\boldsymbol{c}}}}} \sim \,{{\rm{Normal}}}\,(\mu =0,\sigma =1)$$
$$\,{{\rm{In Study \, 1:}}}\,{{{\boldsymbol{\gamma }}}},{{{{\boldsymbol{\gamma }}}}}_{{{{\bf{0}}}}} \sim \,{{\rm{Normal}}}\,(\mu =0.5,\sigma =3)$$
$$\,{{\rm{In Study \, 2:}}}\,{{{\boldsymbol{\gamma }}}},{{{{\boldsymbol{\gamma }}}}}_{{{{\bf{0}}}}} \sim \,{{\rm{Normal}}}\,(\mu =0,\sigma =3)$$
$$\,{{\rm{In Study \, 3:}}}\,{{{\boldsymbol{\gamma }}}},{{{{\boldsymbol{\gamma }}}}}_{{{{\bf{0}}}}} \sim \,{{\rm{Normal}}}\,(\mu =0.5,\sigma =1)$$

We performed fitting using the Python PyMC4 package version 4.1.343 via the no-U-Turn sampler, which was the state-of-the-art Markov-chain Monte Carlo sampling method to estimate parameter posteriors. For each model, we ran 3 chains of 1000 tuning samples (which were discarded) and 2000 kept samples used to estimate the posterior distributions. Therefore, in total, 6000 samples were used to represent each parameter’s posterior distribution. For diagnostic checks, we required \(\hat{R}\le 1.01\), BFMI ≥0.2 for all chains, a sufficiently large effective sample size (ESS ≥400) for all parameters, and that no divergences were observed. Besides these computational diagnostics, we also performed prior predictive checks to make sure that the priors had a reasonable level of informativeness, demonstrated that the fitting procedure could recover parameters that we generated from the prior distributions, and ensured that each model overall fit best to the data simulated by themselves, not by other candidate models (model recovery). For prior predictive checks and model validation (Figs. 2, S2), we simulated each model 20 times per subject. For parameter recovery (Figs. S5, S6, S7) and model recovery (Tables S3, S4), we only simulated each model once per subject. We fit the data to various computational agents with different learning parameters and compared them using the Widely Applicable Information Criterion (WAIC;44). All point estimates of parameter values per participant were the mean of the fitted posterior distributions, and different parameters are minimally correlated across subjects (Fig. S8). The human data used for model fitting did not include the first iteration because the learning performance should be at chance level at the first iteration and thus was not informative for model fitting.

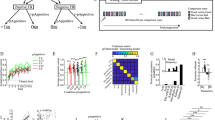
Fig. 2: Main behavioral results for Study 1 & 2.
figure 2

A, B learning curve of Study 1 (n = 41 in advantageous condition and n = 53 in disadvantageous condition) and Study 2 (n = 55 in advantageous condition and n = 36 in disadvantageous condition). Participants overall converged on generating a higher total reward. Curves reflect the rewardingness of actions as a function of the number of times that each stimulus was presented, plotted separately for each split condition (percentage of reward given to the participant). Dashed lines are the simulated learning curve by the best-fitting SPRL model. C overall rewardingness of actions averaged within the advantageous and disadvantageous conditions. People generated fewer rewards under disadvantageous inequity, where they received a smaller share of the reward. D overall entropy of actions averaged within the advantageous and disadvantageous conditions. People’s actions were less deterministic under disadvantageous inequity, where they received a smaller share of the reward. This suggests that people were not simply voluntarily choosing less rewarding actions but indeed had more uncertainty during learning. All error bars reflect the s.e.m.

Full size image

Results

First, we confirmed that participants were able to learn the stimulus-action-reward mappings across the course of the experiment (Figs. 2, 4). We ran a mixed-effect linear regression with the average rewardingness of actions as the dependent variable (equation (1), Tables S5–S6). The average reward generated by participants in response to a stimulus increased with the number of stimulus appearances, as suggested by the significant positive main effect of stimulus iteration (Study 1: b = 0.105, χ2(1) = 551.94, p < 0.001, 95% CI = [0.0962, 0.1138]; Study 2: b = 0.108, χ2(1) = 541.39, p < 0.001, 95% CI = [0.0989, 0.1171]; Study 3: b = 0.253, χ2(1) = 1235.72, p < 0.001, 95% CI = [0.2389, 0.2671]). These results indicate that, overall, participants succeeded in learning the stimulus–response–reward mappings.

Inequity in reward distribution affects learning performance

Although participants succeeded overall in learning, so as to generate more reward across the course of the experiment, we observed a significant main effect of inequity type on reward (Figs. 2, 4). Specifically, across all three studies, participants obtained significantly lower overall reward in the disadvantageous inequity condition (equation (1), Tables S5–S6) than the advantageous inequity condition (Study 1: b = 0.134, χ2(1) = 12.00, p < 0.001, 95% CI = [0.0582, 0.2098], Study 2: b = 0.178, χ2(1) = 18.51, p = <0.001, 95% CI = [0.0969, 0.2591], Study 3: b = 0.143, χ2(1) = 16.83, p < 0.001, 95% CI = [0.0747, 0.2113]). Additionally, we observed a significant interaction between iteration and inequity type (equation (1), Tables S5–S6), such that participants learned more slowly in the disadvantageous condition (Study 1: b = 0.022, χ2(1) = 24.47, p < 0.001, 95% CI = [0.0133, 0.0307], Study 2: b = 0.043, χ2(1) = 85.58, p < 0.001, 95% CI = [0.0339, 0.0521], Study 3: b = 0.008, χ2(1) = 1.18, p = 0.278, 95% CI = [−0.0064, 0.0224]). There are at least two possible explanations for the observation that participants generated lower rewards in the disadvantageous condition. One possibility is that participants learned less well which stimulus-action combinations were most rewarding. Another possibility is that participants deliberately chose actions that generated lower overall reward in these conditions. To distinguish these possibilities, we compared the overall Shannon entropy of participants’ choice in the advantageous condition with the entropy in the disadvantageous condition. Shannon entropy is a measurement of how deterministic (or how stochastic) a random variable is. The higher the entropy is, the less deterministic participants’ choices are. If the sole reason for participants generating less reward in the disadvantageous condition was that they deliberately chose the less rewarding actions, we would not see any difference in the entropy between advantageous and disadvantageous conditions. Their actions would be equally deterministic in both conditions, but deterministic towards more rewarding actions in the advantageous condition. However, we did identify a significantly higher entropy in the disadvantageous condition through Wilcoxon test (Study 1: U = 784, p = 0.021, Study 2: U = 667, p = 0.009, Study 3: U = 434, p < 0.001), suggesting that participants’ choices were indeed less deterministic in the disadvantageous condition (Figs. 2, 4). The SPRL model was also able to simulate this effect in entropy (Fig. S4). We discuss more in depth some other possible interpretations in the Supplementary (Section S1; Fig. S1). Put together, this behavioral evidence suggests that learning was more disrupted in the disadvantageous inequity condition. We further confirmed this result by comparing the fitted learning rate parameter of the baseline reinforcement learning models (Figs. 3, 4). Wilcoxon test supports that the learning rates of participants in the disadvantageous condition are lower than those in the advantageous condition (Study 1: U = 1578, p < 0.001, Study 2: U = 1520, p < 0.001, Study 3: U = 1823, p < 0.001).

Fig. 3: Modeling results of Study 1 (n = 41 in advantageous condition and n = 53 in disadvantageous condition) and Study 2 (n = 55 in advantageous condition and n = 36 in disadvantageous condition).
figure 3

A, B The trial-by-trial difference in WAIC between the better fit model and the worse fit model increases over the course of learning, suggesting the effect of social information enhances over learning. B Also suggests that the effect of inequity was stronger under disadvantageous inequity. C Fitted weight of the competence and warmth rating: no clear directional effect of the perceived warmth or competence in Studies 1 and 2. D Fitted learning rate of the baseline model: further confirms the behavioral result that people learned more slowly under disadvantageous inequity. Each dot represents a point estimate for one subject obtained as the mean of the posterior distribution of the parameters. All error bars reflect the s.e.m.

Full size image

Learning performance is more sensitive to the self-other difference in reward under disadvantageous inequity

We also found a significant positive main effect of the split percentage on the reward generated by participants (Study 1: b = 0.089, χ2(1) = 393.78, p < 0.001,95% CI = [0.0802, 0.0978], Study 2: b = 0.054, χ2(1) = 136.65, p < 0.001,95% CI = [0.0449, 0.0631], Study 3: b = 0.044, χ2(1) = 38.68, p < 0.001,95% CI = [0.0301, 0.0579]). This suggests that participants overall learned better when they earned a higher percentage of the reward. We also found a significant interaction effect, suggesting that the effect of split percentage was stronger in the disadvantageous condition (Study 1: b = −0.043, χ2(1) = 93.58, p < 0.001,95% CI = [−0.0517, −0.0343], Study 2: b = −0.047, χ2(1) = 102.25, p < 0.001,95% CI = [−0.0561, −0.0379], Study 3: b = −0.030, χ2(1) = 17.44, p < 0.001,95% CI = [−0.0441, −0.0159]).

To further explore this interaction effect, we fit two mixed-effect linear regression separately in the advantageous and disadvantageous conditions (equation (2), Tables S7–S8). In the disadvantageous condition, we removed the split condition in Study 1 where the participant obtained 0% of the reward, and in Study 2 where the participant obtained 50%, to make sure the effect was not solely driven by these extreme conditions. Across 3 studies, we observed a significant positive effect of split (Study 1: b = 0.058, χ2(1) = 16.77, p < 0.001,95% CI = [0.0302, 0.0858], Study 2: b = 0.068, χ2(1) = 15.62, p < 0.001,95% CI = [0.0343, 0.1017], Study 3: b = 0.064, χ2(1) = 9.16, p = 0.002,95% CI = [0.0226, 0.1054]). In the advantageous inequity condition, however, a significant effect of split is found only under reduced cognitive load, in Study 3: (Study 1: b = 0.018, χ2(1) = 1.53, p = 0.216,95% CI = [−0.0105, 0.0465], Study 2: b = −0.008, χ2(1) = 0.38, p = 0.538,95% CI = [−0.0334, 0.0174], Study 3: b = 0.046, χ2(1) = 4.45, p = 0.035, 95% CI = [0.0033, 0.0887]). Through trial-by-trial comparison of the computational models (Fig. 3), we confirmed in Studies 1 & 2 that the inequity-weighted model outperforms the baseline model more so in the disadvantageous condition (Study 1: t(57.3) = −3.43, p = 0.001, d = −0.713, 95% CI = [−1.063, −0.363], Study 2: t(36.2) = −2.30, p = 0.027, d = −0.492, 95% CI = [−0.935, −0.049]). The comparison in Study 3 is not significant, but may be due to the reduced power as a result of fewer split conditions (t(50.7) = −1.51, p = 0.137, d = −0.310, 95% CI = [−0.714, 0.094]). Model simulation also showed that the best-fitting model (SPRL) was able to qualitatively reproduce the effect of split percentage (Figs. 2, 4), but the baseline models were not able to reproduce the effect (Fig. S2).

Effects of inequity arise early during learning and grow as learning continues

Through model comparison in Studies 1 & 2, we see that the inequity-weighted model outperforms the baseline model as early as the 4th iteration of the stimulus (Study 1: t(93) = 3.54, p < 0.001, d = 0.365, 95% CI = [0.158, 0.572], Study 2: t(90) = 2.25, p = 0.027, d = 0.236, 95% CI = [0.026, 0.446]). The effect also increases over time (Fig. 3). We tested this using a mixed-effect linear regression with the model-fit metrics as the dependent variable (equation (4), Tables S11–S12). In both Studies 1 & 2, we see a significant positive main effect of stimulus iteration (Study 1: b = 0.004, χ2(1) = 86.25, p < 0.001,95% CI = [0.0032, 0.0048], Study 2: b = 0.002, χ2(1) = 49.42, p < 0.001,95% CI = [0.0014, 0.0026]), suggesting the inequity-weighted model outperforms the baseline more in later learning trials. Additionally, the effect is stronger under disadvantageous inequity, as suggested by the significant interaction effect (Study 1: b = −0.004, χ2(1) = 79.48, p < 0.001,95% CI = [−0.0049, −0.0031], Study 2: b = −0.002, χ2(1) = 42.54, p < 0.001, 95% CI = [−0.0026, −0.0014]).

Social partner identity impacts learning more systematically when cognitive load is reduced

We examined whether the perceived warmth and competence of the social partner affected how the social distribution of reward influenced learning. In Study 1 and Study 2, we observed mixed evidence. On the one hand, the full SPRL model, which integrates social perception ratings, prevailed as the best-fitting computational model (Fig. 3; Table S2). On the other hand, the fitted weight parameter of perceived warmth and competence was not significantly different from 0 (Fig. 3; Table S1). In Study 1 and Study 2, these coefficients were not significantly different from 0 in the advantageous condition (Study 1: tcompetence(40) = −0.736, p = 0.466, d = −0.115, 95% CI = [−0.423, 0.193]; twarmth(40) = 1.45, p = 0.155, d = 0.226, 95% CI = [−0.085, 0.537], Study 2: tcompetence(54) = 0.320, p = 0.75, d = 0.043, 95%CI = [−0.222, 0.308]; twarmth(54) = 0.502, p = 0.618, d = 0.068, 95% CI = [−0.197, 0.333]) or the disadvantageous condition (Study 1: tcompetence(52) = 0.050, p = 0.96, d = 0.007, 95% CI = [−0.263, 0.277]; twarmth(52) = 0.296, p = 0.768, d = 0.041, 95%CI = [−0.230, 0.312], Study 2: tcompetence(35) = −0.570, p = 0.572, d = −0.095, 95% CI = [−0.423, 0.233]; twarmth(35) = 1.52, p = 0.136, d = 0.253, 95% CI = [−0.077, 0.583]).

However, in Study 3 where the cognitive load is reduced (Fig. 4), we found a significant positive effect of both perceived warmth and perceived competence (Table S1) in the disadvantageous condition on the rewardingness of actions (tcompetence(47) = 2.25, p = 0.029, d = 0.325, 95% CI = [0.038, 0.612]; twarmth(47) = 3.34, p = 0.002, d = 0.482, 95% CI = [0.194, 0.770]). Similarly, mixed-effect linear regression (equation (1), Tables S5–S6) also revealed a significant main effect of both perceived warmth and perceived competence on the rewardingness of actions during learning (bcompetence = 0.031, χ2(1) = 12.10, p < 0.001, 95% CI = [0.0135, 0.0485]; bwarmth = 0.042, χ2(1) = 25.52, p < 0.001, 95% CI = [0.0257, 0.0583]). The overall effect of perceived warmth was stronger in the disadvantageous condition (b = −0.069, χ2(1) = 69.34, p < 0.001,95% CI = [−0.0852, −0.0528]). The overall effect of perceived competence was also stronger in the disadvantageous condition (b = −0.028, χ2(1) = 9.77, p = 0.002,95% CI = [−0.0456, −0.0104]). Notably, these effects remained significant when we ran the same regression on simulated data from the SPRL model with the fitted parameter values (Tables S13–S14). Moreover, they disappeared when using data simulated by the IRL model, which ignored information about perceived warmth and competence (Tables S13–S14).

Fig. 4: Results of Study 3 (n = 47 in advantageous condition and n = 48 in disadvantageous condition).
figure 4

A Learning curve. B, C Overall rewardingness of actions and action entropy averaged within the advantageous and disadvantageous conditions. Replicating Study 1 and Study 2, people learned worse under disadvantageous inequity. D, E The trial-by-trial model comparisons. The SPRL model significantly outperformed the models without considering social perception ratings, confirming the elevated effect of social perception in Study 3. Moreover, the effect is also stronger under the disadvantageous condition. F, G Fitted learning rate of the baseline model and effects of social perception of the SPRL model: replicating Studies 1 and 2, the learning rate was lower under disadvantageous inequity. However, we saw a significant positive effect of both perceived warmth and perceived competence in the disadvantageous condition, suggesting that the effect of social perception is enhanced under a smaller cognitive load during learning. Each dot represents a point estimate for one subject obtained as the mean of the posterior distribution of the parameters. All error bars reflect the s.e.m.

Full size image

Similar to the effect of inequity, the effect of social perception on learning also increases over the course of learning, but the increase is stronger under disadvantageous inequity. We support this again with mixed-effect linear regression on the model comparison metrics (equation (4), Tables S11–S12) where we see a positive main effect of stimulus iteration (b = 0.001, χ2(1) = 14.65, p < 0.001, 95% CI = [−0.0852, −0.0528]) and also a significant effect of its interaction with inequity type (b = −0.0008, χ2(1) = 4.53, p = 0.033, 95% CI = [−0.0015, −0.0001]). One possible interpretation of these results is that the perceived warmth and competence did shape how inequity affects learning across all three studies, but individual differences in the nature of this effect precluded its detection in model-free, group-level analyses in Studies 1 and 2. In Study 3, where cognitive load was reduced, we found evidence for a more systematic effect of social perception on learning at the group level.

Discussion

People often rely on learned reward contingencies to guide their decisions, making factors that impact the learning process important precursors to decisions. Through a reinforcement learning task, we found that inequity of the distribution of reward across oneself and another person, as well as the identity of that person, shaped people’s ability to learn from rewards.

First, people learned faster and more successfully overall when they received the larger share of the reward (compared to the other person) than when they received the smaller share of the reward (compared to the other person), even controlling for the overall reward size to self (Study 2). This result is especially potent given that we manipulated inequity type between subjects, ruling out the possibility that participants could have contrasted different inequity conditions and adjusted their internal learning incentives accordingly. Moreover, this shows that the impact of inequity (advantageous vs disadvantageous) on valuation during learning does not show range adaptation to the possible range of the degree of inequity27. In other words, disadvantageous inequity decreases the value of the rewards without needing a separate reference condition in which the same participants experience advantageous inequity. In this way, the effect of disadvantageous versus advantageous inequity on learning can be thought of as “absolute” rather than “relative”.

Second, people were more sensitive to the specific percentage of the reward given to themselves when that percentage was less than (compared to when it was more than) 50%. For example, the difference between receiving 20% and 40% of the reward (a 20% difference) was greater, in terms of its impact on learning, than the difference between receiving 60% and 80% (also a 20% difference). This could be because disadvantageous inequity prompts people to be more sensitive to the split percentage. We note that this finding is especially striking as it was replicated in Study 2, in which impaired learning under disadvantageous inequity cannot be explained by the amount of reward personally received by the participant because that amount was held constant. In this study, more total reward (across the participant and the partner) is actually generated in the disadvantageous condition than in the advantageous condition, yet participants still learn less effectively in this condition. In other words, participants’ learning seems to be more driven by social comparison than by total welfare during the learning task. Future studies could explore a within-subject manipulation on the design of Study 2, where a tradeoff between inequity and total reward exists. It would be especially interesting to see to test the possibility that split percentage may have a non-continuous effect on learning across the range from 0% to 100%.

Third, a more systematic effect of social perception on learning emerged when cognitive load was reduced. We saw a significantly positive effect of perceived warmth and competence on learning under the disadvantageous condition only in Study 3, where the stimulus space was reduced from 5 to 2. Because the parameter recovery result in Study 3 did not seem to differ substantially from Studies 1 and 2 (Figs. S5–S7), it is unlikely that this difference arose because the social perception weight parameters were harder to recover in Studies 1 and 2 compared to Study 3. Moreover, it is worth noting that the SPRL model, which incorporates social perception as well as inequity information, emerged as the best-fitting model to participants’ behavior even in Studies 1 and 2. This may suggest that while perceived warmth and competence have somewhat idiosyncratic effects on learning across individuals when the task is especially taxing (perhaps due to different reliance on heuristics and/or different levels of working memory capacity), these effects are more systematic when cognitive load is reduced. These possible interpretations are preliminary and open to more direct investigation in future research.

We would like to highlight some broader implications of this study. First, the observation that disadvantageous inequity hampers learning in an absolute sense-i.e., without requiring direct comparison to advantageous inequity-speaks to the potential importance of the current findings in ecological settings, where a given instance of learning from shared rewards is likely to be characterized by a single type of inequity. Second, the finding that social contextual information shapes reinforcement learning adds on to the body of evidence that the reinforcement learning system, despite long being considered a low-level implicit cognitive system, is impacted by higher-level cognition – in this case, social cognition30,45,46. Third, our studies contribute to a growing trend toward integrating models of cognition and models of economic behavior25,26,47,48,49. We tested experimentally how the distribution of rewards impacts reward values relevant to learning and designed formal models that make it possible to characterize this impact.

Finally, these findings point to a possible gap between subjective value constructed during social decision-making and social learning that warrants further investigation50,51,52,53,54. Although research on social decision-making has shown that others’ perceived warmth and competence have different effects on people’s equity preferences25, the current studies found that perceived warmth and competence both had the same positive effect on reinforcement learning. This gap may be due to how group processes, such as social status, impact valuations differently during learning than descriptive decision-making. Future research is needed to further investigate how contextual effects on valuation during social decision-making relate to contextual effects on learning from shared rewards.

Limitations

One potential limitation of this study is the hypothetical nature of the monetary reward as well as the social partner. Participants were asked to imagine that the rewards were real and that a portion was actually given to another person. Research comparing real to hypothetical monetary rewards generally finds consistent patterns of behavior across the two contexts55,56, and when they differ, hypothetical contexts typically have smaller effects57. In particular, although there is sometimes an overall shift from hypothetical to real rewards (e.g., in mean levels of generosity), manipulated factors (e.g., inequity, target identity) typically have similar effects in both contexts25,26. We also acknowledge that all participants are young adults in the United States, leaving open questions about the degree to which findings from our sample generalize to people situated within different socioeconomic systems.