Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Review Article
  • Published:

Opportunities and challenges of graph neural networks in electrical engineering

Nature Reviews Electrical Engineering volume 1, pages 529–546 (2024)Cite this article

Subjects

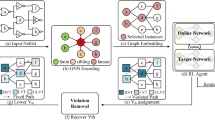
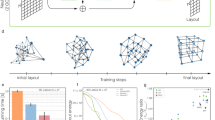
Abstract

Graph neural networks (GNNs) are a class of deep learning algorithms that learn from graphs, networks and relational data. They have found applications throughout the sciences and made significant strides in electrical engineering. GNNs can learn from various electrical and electronic systems, such as electronic circuits, wireless networks and power systems, and assist in solving optimization or inference tasks where traditional approaches may be slow or inaccurate. Robust learning algorithms and efficient computational hardware developed and tailored for GNNs have amplified their relevance to electrical engineering. We have entered an era in which the studies of GNNs and electrical engineering are intertwined, opening to opportunities and challenges to researchers in both fields. This Review explores applications of GNNs that might generate notable impacts on electrical engineering. We discuss how GNNs are used to address electrical automatic design, as well as the modelling and management of wireless communication networks. Additionally, we delve into GNNs for high-energy physics, materials science and biology. Presenting the applications, data and computational challenges, the need for innovative algorithms and hardware solutions becomes clear.

Key points

  • Graph neural networks (GNNs) hold immense potential for harnessing data power to effectively tackle a range of application challenges in electrical engineering.

  • Research in information science and cutting-edge hardware within electrical engineering offer valuable insights into the practical implementation of GNNs, overcoming their limitations related to model reliability and computational efficiency.

  • GNNs find extensive applications in various scientific domains, including physics, materials science and biology. Electrical engineering methodologies can enhance GNN performance in these fields and, potentially, lead to significant impacts in science.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Application of graph neural networks in electronic design automation.
Fig. 2: Graph modelling and performance evaluations of graph neural network-enhanced resource allocation in wireless multi-hop networks.
Fig. 3: Visual representation of a collision event at the Large Hadron Collider and several graph neural network tasks.
Fig. 4: Molecular and crystal graphs and a chronological overview of graph neural networks used in material design.
Fig. 5: The ubiquity of networks (or graphs) in biological systems.

Similar content being viewed by others

References

  1. Tanenbaum, A. S. Computer Networks (Pearson Education India, 2003).

  2. Shannon, C. E. Claude Elwood Shannon: Collected Papers (IEEE, 1993).

  3. Akpakwu, G. A., Silva, B. J., Hancke, G. P. & AbuMahfouz, A. M. A survey on 5G networks for the Internet of Things: communication technologies and challenges. IEEE Access 6, 3619–3647 (2017).

    Article  Google Scholar 

  4. Silver, D. et al. Mastering the game of Go without human knowledge. Nature 550, 354–359 (2017).

    Article  Google Scholar 

  5. Devlin, J., Chang, M.-W., Lee, K. & Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. In Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (eds Burstein, J. et al.) 4171–4186 (ACL, 2019).

  6. OpenAI et al. Gpt-4 technical report. Preprint at arXiv https://doi.org/10.48550/arXiv.2303.08774 (2023).

  7. Gori, M., Monfardini, G. & Scarselli, F. A new model for learning in graph domains. In Proc. 2005 IEEE International Joint Conference on Neural Networks Vol. 2 729–734 (IEEE, 2005).

  8. Scarselli, F., Gori, M., Tsoi, A. C., Hagenbuchner, M. & Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 20, 61–80 (2008).

    Article  Google Scholar 

  9. Kipf, T. N. & Welling, M. Variational graph autoencoders. In NIPS Workshop on Bayesian Deep Learning (NIPS, 2016).

  10. Shen, Y., Shi, Y., Zhang, J. & Letaief, K. B. A graph neural network approach for scalable wireless power control. In 2019 IEEE Globecom Workshops 1–6 (IEEE, 2019).

  11. Chowdhury, A., Verma, G., Rao, C., Swami, A. & Segarra, S. ML-aided power allocation for Tactical MIMO. In 2021 IEEE Military Communications Conference 273–278 (IEEE, 2021).

  12. Chowdhury, A., Verma, G., Rao, C., Swami, A. & Segarra, S. Unfolding WMMSE using graph neural networks for efficient power allocation. IEEE Trans. Wirel. Commun. 20, 6004–6017 (2021).

    Article  Google Scholar 

  13. Li, B., Verma, G. & Segarra, S. Graph-based algorithm unfolding for energy-aware power allocation in wireless networks. IEEE Trans. Wirel. Commun. 22, 1359–1373 (2022). This paper discusses the use of the algorithm unrolling framework to address the power allocation problem in the application of GNNs in wireless networks.

    Article  Google Scholar 

  14. Wang, Z., Eisen, M. & Ribeiro, A. Learning decentralized wireless resource allocations with graph neural networks. IEEE Trans. Signal. Process. 70, 1850–1863 (2022).

    Article  MathSciNet  Google Scholar 

  15. Shen, Y., Zhang, J., Song, S. H. & Letaief, K. B. Graph neural networks for wireless communications: from theory to practice. IEEE Trans. Wirel. Commun. 22, 3554–3569 (2023).

    Article  Google Scholar 

  16. Owerko, D., Gama, F. & Ribeiro, A. Optimal power flow using graph neural networks. In 2020 IEEE International Conference on Acoustics, Speech and Signal Processing 5930–5934 (IEEE, 2020).

  17. Owerko, D., Gama, F. & Ribeiro, A. Predicting power outages using graph neural networks. In IEEE Global Conference on Signal and Information Processing 743–747 (IEEE, 2018).

  18. Donon, B. et al. Neural networks for power flow: graph neural solver. Electr. Power Syst. Res. 189, 106547 (2020).

    Article  Google Scholar 

  19. Ustun, E., Deng, C., Pal, D., Li, Z. & Zhang, Z. Accurate operation delay prediction for FPGA HLS using graph neural networks. In 2020 IEEE/ACM International Conference On Computer Aided Design (ICCAD) 1–9 (IEEE, 2020).

  20. Xie, Z. et al. Preplacement net length and timing estimation by customized graph neural network. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 41, 4667–4680 (2022).

    Article  Google Scholar 

  21. Liu, M. et al. Parasitic-aware analog circuit sizing with graph neural networks and bayesian optimization. In 2021 Design, Automation & Test in Europe Conference & Exhibition (DATE) 1372–1377 (IEEE, 2021).

  22. Guo, Z. et al. A timing engine inspired graph neural network model for pre-routing slack prediction. In Proc. 59th ACM/IEEE Design Automation Conference 1207–1212 (ACM, 2022).

  23. Yang, Z. et al. Versatile multi-stage graph neural network for circuit representation. In Proc. 36th International Conference on Neural Information Processing Systems 20313–20324 (Curran Associates Inc., 2022).

  24. Shlomi, J., Battaglia, P. & Vlimant, J.-R. Graph neural networks in particle physics. Mach. Learn. Sci. Technol. 2, 021001 (2020). A timing engine inspired graph neural network model for pre-routing slack prediction.

    Article  Google Scholar 

  25. Duarte, J. & Vlimant, J.-R. Graph neural networks for particle tracking and reconstruction. In Artificial Intelligence for High Energy Physics 387 (World Scientific, 2022).

  26. DeZoort, G., Battaglia, P. W., Biscarat, C. & Vlimant, J.-R. Graph neural networks at the Large Hadron Collider. Nat. Rev. Phys. 5, 281 (2023).

    Article  Google Scholar 

  27. Fung, V., Zhang, J., Juarez, E. & Sumpter, B. G. Benchmarking graph neural networks for materials chemistry. npj Comput. Mater. 7, 84 (2021).

    Article  Google Scholar 

  28. Reiser, P. et al. Graph neural networks for materials science and chemistry. Commun. Mater. 3, 93 (2022).

    Article  Google Scholar 

  29. Baek, M. et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science 373, 871–876 (2021).

    Article  Google Scholar 

  30. Dauparas, J. et al. Robust deep learning–based protein sequence design using ProteinMPNN. Science 378, 49–56 (2022).

    Article  Google Scholar 

  31. Stokes, J. M. et al. A deep learning approach to antibiotic discovery. Cell 180, 688–702 (2020).

    Article  Google Scholar 

  32. Hamilton, W., Ying, Z. & Leskovec, J. Inductive representation learning on large graphs. In Proc. 31st International Conference on Neural Informaton Processing Systems 1025–1035 (Curran Associates Inc., 2017).

  33. Veličković, P. et al. Graph attention networks. In International Conference on Learning Representations (ICLR, 2018).

  34. Battaglia, P. W. et al. Relational inductive biases, deep learning, and graph networks. Preprint at arXiv https://doi.org/10.48550/arXiv.1806.01261 (2018).

  35. Defferrard, M., Bresson, X. & Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Proc. 30th International Conference on Neural Information Processing Systems 3844–3852 (Curran Associates Inc., 2016).

  36. Bronstein, M. M., Bruna, J., LeCun, Y., Szlam, A. & Vandergheynst, P. Geometric deep learning: going beyond Euclidean data. IEEE Signal. Process. Mag. 34, 18–42 (2017).

    Article  Google Scholar 

  37. Chien, E., Peng, J., Li, P. & Milenkovic, O. Adaptive universal Generalized PageRank graph neural network. In International Conference on Learning Representations (ICLR, 2021).

  38. Wang, X. & Zhang, M. How powerful are spectral graph neural networks. In Proc. 39th International Conference on Machine Learning 23341–23362 (ICML, 2022).

  39. Corso, G., Cavalleri, L., Beaini, D., Liò, P. & Veličković, P. Principal neighbourhood aggregation for graph nets. In Proc. 34th International Conference on Neural Information Processing Systems 13260–13271 (Curran Associates Inc., 2020).

  40. Hornik, K., Stinchcombe, M. & White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 2, 359–366 (1989). This fundamental work presents the architecture of GNNs, showing how it can be represented and implemented in a message passing process.

    Article  Google Scholar 

  41. Xu, K., Hu, W., Leskovec, J. & Jegelka, S. How powerful are graph neural networks? In International Conference on Learning Representations (ICLR, 2019).

  42. Morris, C. et al. Weisfeiler and Leman go neural: higher order graph neural networks. In Proc. 33rd AAAI Conference on Artificial Intelligence 4602–4609 (AAAI, 2019).

  43. Maron, H., Ben-Hamu, H., Shamir, N. & Lipman, Y. Invariant and equivariant graph networks. In International Conference on Learning Representations (ICLR, 2019).

  44. Li, P., Wang, Y., Wang, H. & Leskovec, J. Distance encoding: design provably more powerful neural networks for graph representation learning. In Proc. 34th International Conference on Neural Information Processing Systems 4465–4478 (Curran Associates Inc., 2020).

  45. Bouritsas, G., Frasca, F., Zafeiriou, S. & Bronstein, M. M. Improving graph neural network expressivity via subgraph isomorphism counting. IEEE Trans. Pattern Anal. Mach. Intell. 45, 657–668 (2022).

    Article  Google Scholar 

  46. Kipf, T. N. & Welling, M. Semi-supervised classification with graph convolutional networks. In International Conference on Learning Representations (ICLR, 2017).

  47. Chen, D. et al. Measuring and relieving the over-smoothing problem for graph neural networks from the topological view. In Proc. AAAI Conference on Artificial Intelligence 3438–3445 (AAAI, 2020).

  48. Topping, J., Di Giovanni, F., Chamberlain, B. P., Dong, X. & Bronstein, M. M. Understanding over-squashing and bottlenecks on graphs via curvature. In International Conference on Learning Representations (ICLR, 2022).

  49. Alon, U. & Yahav, E. On the bottleneck of graph neural networks and its practical implications. In International Conference on Learning Representations (ICLR, 2021).

  50. Chen, K., Hu, J., Zhang, Y., Yu, Z. & He, J. Fault location in power distribution systems via deep graph convolutional networks. IEEE J. Sel. Areas Commun. 38, 119–131 (2019).

    Article  Google Scholar 

  51. de Freitas, J. T. & Coelho, F. G. F. Fault localization method for power distribution systems based on gated graph neural networks. Electr. Eng. 103, 2259–2266 (2021).

    Article  Google Scholar 

  52. Arjona Martínez, J., Cerri, O., Pierini, M., Spiropulu, M. & Vlimant, J.-R. Pileup mitigation at the Large Hadron Collider with graph neural networks. Eur. Phys. J. Plus 134, 333 (2019).

    Article  Google Scholar 

  53. Li, T. et al. Semi-supervised graph neural networks for pileup noise removal. Eur. Phys. J. C. 83, 99 (2023).

    Article  Google Scholar 

  54. Luo, Y. et al. A network integration approach for drug–target interaction prediction and computational drug repositioning from heterogeneous information. Nat. Commun. 8, 573 (2017).

    Article  Google Scholar 

  55. Yu, Z., Huang, F., Zhao, X., Xiao, W. & Zhang, W. Predicting drug–disease associations through layer attention graph convolutional network. Brief. Bioinform. 22, bbaa243 (2021).

    Article  Google Scholar 

  56. Farrell, S. et al. Novel deep learning methods for track reconstruction. In International Workshop Connecting The Dots (2018).

  57. Ju, X. et al. Performance of a geometric deep learning pipeline for HL-LHC particle tracking. Eur. Phys. J. C 81, 876 (2021).

    Article  Google Scholar 

  58. DeZoort, G. et al. Charged particle tracking via edgeclassifying interaction networks. Comput. Softw. Big Sci. 5, 26 (2021).

    Article  Google Scholar 

  59. Wu, N., Yang, H., Xie, Y., Li, P. & Hao, C. High-level synthesis performance prediction using GNNs: Benchmarking, modeling, and advancing. In Proc. 59th ACM/IEEE Design Automation Conference 49–54 (ACM, 2022).

  60. Schütt, K. et al. SchNet: a continuous-filter convolutional neural network for modeling quantum interactions. In Proc. 31st International Conference on Neural Information Processing Systems 992–1002 (Curran Associates Inc., 2017).

  61. Wu, Z. et al. MoleculeNet: a benchmark for molecular machine learning. Chem. Sci. 9, 513–530 (2018).

    Article  Google Scholar 

  62. Xie, T. & Grossman, J. C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120, 145301 (2018).

    Article  Google Scholar 

  63. Qu, H. & Gouskos, L. ParticleNet: jet tagging via particle clouds. Phys. Rev. D 101, 056019 (2020).

    Article  Google Scholar 

  64. Guo, J., Li, J., Li, T. & Zhang, R. Boosted Higgs Boson jet reconstruction via a graph neural network. Phys. Rev. D 103, 116025 (2021).

    Article  Google Scholar 

  65. Eisen, M. & Ribeiro, A. Optimal wireless resource allocation with random edge graph neural networks. IEEE Trans. Signal. Process. 68, 2977–2991 (2020).

    Article  MathSciNet  Google Scholar 

  66. Owerko, D., Gama, F. & Ribeiro, A. Unsupervised optimal power flow using graph neural networks. In 2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 6885–6889 (IEEE, 2024).

  67. Nachmani, E. & Wolf, L. Hyper-graph-network decoders for block codes. In Proc. 33rd International Conference on Neural Information Processing Systems 2329–2339 (Curran Associates Inc., 2019).

  68. Cammerer, S., Hoydis, J., Aoudia, F. A. & Keller, A. Graph neural networks for channel decoding. In 2022 IEEE Globecom Workshops 486–491 (IEEE, 2022).

  69. Chen, T. et al. Learning to optimize: a primer and a benchmark. J. Mach. Learn. Res. 23, 8562–8620 (2022).

    MathSciNet  Google Scholar 

  70. Monga, V., Li, Y. & Eldar, Y. C. Algorithm unrolling: interpretable, efficient deep learning for signal and image processing. IEEE Signal. Process. Mag. 38, 18–44 (2021).

    Article  Google Scholar 

  71. Zhao, Z., Verma, G., Rao, C., Swami, A. & Segarra, S. Link scheduling using graph neural networks. IEEE Trans. Wirel. Commun. 22, 3997–4012 (2022).

    Article  Google Scholar 

  72. Zhao, Z., Verma, G., Swami, A. & Segarra, S. Delay-oriented distributed scheduling using graph neural networks. In 2022 IEEE International Conference on Acoustics, Speech and Signal Processing 8902–8906 (IEEE, 2022).

  73. Zhao, Z., Verma, G., Rao, C., Swami, A. & Segarra, S. Distributed scheduling using graph neural networks. In 2021 IEEE International Conference on Acoustics, Speech and Signal Processing 4720–4724 (IEEE, 2021).

  74. Kahng, A. B., Lienig, J., Markov, I. L. & Hu, J. VLSI Physical Design: From Graph Partitioning to Timing Closure 312 (Springer, 2011).

  75. Callister Jr, W. D. & Rethwisch, D. G. Fundamentals of Materials Science and Engineering: An Integrated Approach (Wiley, 2020).

  76. Erdős, P. & Rényi, A. On random graphs I. Publ. Math. Debr. 6, 290–297 (1959).

    Article  Google Scholar 

  77. Makhzani, A., Shlens, J., Jaitly, N., Goodfellow, I. & Frey, B. Adversarial autoencoders. Preprint at arXiv https://doi.org/10.48550/arXiv.1511.05644 (2015).

  78. Xu, M. et al. Geodiff: a geometric diffusion model for molecular conformation generation. In International Conference on Learning Representations (ICLR, 2022).

  79. Vignac, C. et al. Digress: discrete denoising diffusion for graph generation. In International Conference on Learning Representations (ICLR, 2023).

  80. Mercado, R. et al. Graph networks for molecular design. Mach. Learn. Sci. Technol. 2, 025023 (2021).

    Article  Google Scholar 

  81. Bilodeau, C., Jin, W., Jaakkola, T., Barzilay, R. & Jensen, K. F. Generative models for molecular discovery: recent advances and challenges. Wiley Interdiscip. Rev. Comput. Mol. Sci. 12, e1608 (2022).

    Article  Google Scholar 

  82. Jin, W., Barzilay, R. & Jaakkola, T. Junction tree variational autoencoder for molecular graph generation. In Proc. 35th International Conference on Machine Learning 2323–2332 (ICML, 2018).

  83. Mirhoseini, A. et al. A graph placement methodology for fast chip design. Nature 594, 207–212 (2021).

    Article  Google Scholar 

  84. Cheng, R. et al. The policy-gradient placement and generative routing neural networks for chip design. In Proc. 36th International Conference on Neural Information Processing Systems 26350–26362 (Curran Associates Inc., 2022).

  85. Chen, T., Zhang, G. L., Yu, B., Li, B. & Schlichtmann, U. Machine learning in advanced IC design: a methodological survey. IEEE Des. Test 40, 17–33 (2022). This review covers the integration of deep learning tools with conventional optimization algorithm frameworks to enhance the resolution of signal and image processing tasks through data-driven approaches.

    Article  Google Scholar 

  86. Sánchez, D., Servadei, L., Kiprit, G. N., Wille, R. & Ecker, W. A comprehensive survey on electronic design automation and graph neural networks: theory and applications. ACM Trans. Des. Autom. Electron. Syst. 28, 1–27 (2023).

    Article  Google Scholar 

  87. Zhang, J. et al. Fine-grained service offloading in B5G/6G collaborative edge computing based on graph neural networks. In IEEE International Conference on Communications 5226–5231 (IEEE, 2022).

  88. Ma, Y., He, Z., Li, W., Zhang, L. & Yu, B. Understanding graphs in EDA: from shallow to deep learning. In Proc. 2020 International Symposium on Physical Design 119–126 (ACM, 2020).

  89. Agnesina, A., Chang, K. & Lim, S. K. VLSI placement parameter optimization using deep reinforcement learning. In 2020 IEEE/ACM International Conference On Computer Aided Design (ICCAD) (IEEE, 2020).

  90. Lu, Y.-C., Pentapati, S. & Lim, S. K. The law of attraction: Affinity-aware placement optimization using graph neural networks. In Proc. 2021 International Symposium on Physical Design 7–14 (ACM, 2021).

  91. Lu, Y.-C., Siddhartha, N., Khandelwal, V. & Lim, S. K. Doomed run prediction in physical design by exploiting sequential flow and graph learning. In 2021 IEEE/ACM International Conference On Computer Aided Design (ICCAD) 1–9 (IEEE, 2021).

  92. Kirby, R., Godil, S., Roy, R. & Catanzaro, B. CongestionNet: routing congestion prediction using deep graph neural networks. In 27th International Conference on Very Large Scale Integration (VLSI-SoC) 217–222 (IEEE, 2019).

  93. Maji, S., Budak, A. F., Poddar, S. & Pan, D. Z. Toward end-to-end analog design automation with ML and data-driven approaches. In Proc. 29th Asia and South Pacific Design Automation Conference 657–664 (IEEE, 2024).

  94. Zhu, K., Chen, H., Liu, M. & Pan, D. Z. Tutorial and perspectives on MAGICAL: a silicon-proven opensource analog IC layout system. IEEE Trans. Circuits Syst. II: Express Br. 70, 715–720 (2023).

    Google Scholar 

  95. Kunal, K. et al. ALIGN: Open-source analog layout automation from the ground up. In Proc. 56th Annual Design Automation Conference 2019 1–4 (ACM, 2019).

  96. Wang, H. et al. GCN-RL circuit designer: transferable transistor sizing with graph neural networks and reinforcement learning. In 57th ACM/EDAC/IEEE Design Automation Conference 1–6 (IEEE, 2020).

  97. Dong, Z. et al. CktGNN: circuit graph neural network for electronic design automation. In International Conference on Learning Representations (ICLR, 2023).

  98. Zhang, G., He, H. & Katabi, D. Circuit-GNN: graph neural networks for distributed circuit design. In Proc. 36th International Conference on Machine Learning 7364–7373 (ICML, 2019).

  99. Ren, H., Kokai, G. F., Turner, W. J. & Ku, T.-S. ParaGraph: layout parasitics and device parameter prediction using graph neural networks. In 2020 57th ACM/IEEE Design Automation Conference (DAC) 1–6 (IEEE, 2020).

  100. Li, Y. et al. A customized graph neural network model for guiding analog IC placement. In Proc. 39th International Conference on Computer-Aided Design 1–9 (ACM, 2020). This groundbreaking work discusses the application of GNNS and RL to EDA, solving the global placement problem in chip design and outperforming the state-of-the-art method for this task.

  101. Chen, H. et al. Universal symmetry constraint extraction for analog and mixed-signal circuits with graph neural networks. In 2021 58th ACM/IEEE Design Automation Conference (DAC) 1243–1248 (IEEE, 2021).

  102. Cao, W., Benosman, M., Zhang, X. & Ma, R. Domain knowledge-infused deep learning for automated analog/radio-frequency circuit parameter optimization. In 59th ACM/IEEE Design Automation Conference 1015–1020 (ACM, 2022).

  103. Shi, W. et al. RobustAnalog: fast variation-aware analog circuit design via multi-task RL. In Proc. 2022 ACM/IEEE Workshop on Machine Learning for CAD 35–41 (ACM, 2022).

  104. Luo, Z.-Q. & Zhang, S. Dynamic spectrum management: complexity and duality. IEEE J. Sel. Top. Signal. Process. 2, 57–73 (2008).

    Article  Google Scholar 

  105. Chowdhury, A., Verma, G., Swami, A. & Segarra, S. Deep graph unfolding for beamforming in MU-MIMO interference networks. IEEE Trans. Wirel. Commun. 23, 4889–4903 (2023).

    Article  Google Scholar 

  106. Shi, Q., Razaviyayn, M., Luo, Z.-Q. & He, C. An iteratively weighted MMSE approach to distributed sumutility maximization for a MIMO interfering broadcast channel. IEEE Trans. Signal. Process. 59, 4331–4340 (2011).

    Article  MathSciNet  Google Scholar 

  107. Tassiulas, L. & Ephremides, L. Stability properties of constrained queueing systems and scheduling policies for maximum throughput in multihop radio networks. IEEE Trans. Autom. Control. 37, 1936–1948 (1992).

    Article  MathSciNet  Google Scholar 

  108. Joo, C., Sharma, G., Shroff, N. B. & Mazumdar, R. R. On the complexity of scheduling in wireless networks. Eurasip J. Wirel. Commun. Netw. 2010, 418934 (2010).

    Article  Google Scholar 

  109. Dimakis, A. & Walrand, J. Sufficient conditions for stability of longest-queue-first scheduling: second-order properties using fluid limits. Adv. Appl. Probab. 38, 505–521 (2006).

    Article  MathSciNet  Google Scholar 

  110. Joo, C. & Shroff, N. B. Local greedy approximation for scheduling in multihop wireless networks. IEEE Trans. Mob. Comput. 11, 414–426 (2012).

    Article  Google Scholar 

  111. Gurobi Optimization. Gurobi optimizer reference manual. Gurobi https://www.gurobi.com/wp-content/plugins/hd_documentations/documentation/9.0/refman.pdf (2020).

  112. Paschalidis, I. C., Huang, F. & Lai, W. A message-passing algorithm for wireless network scheduling. IEEE/ACM Trans. Netw. 23, 1528–1541 (2015).

    Article  Google Scholar 

  113. Zhao, Z., Swami, A. & Segarra, S. Graph-based deterministic policy gradient for repetitive combinatorial optimization problems. In International Conference on Learning Representations (ICLR, 2023).

  114. Zhao, Z., Radojicic, B., Verma, G., Swami, A. & Segarra, S. Delay-aware backpressure routing using graph neural networks. In 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 4720–4724 (IEEE, 2023).

  115. Rusek, K., Suárez-Varela, J., Almasan, P., Barlet-Ros, P. & Cabellos-Aparicio, A. RouteNet: leveraging graph neural networks for network modeling and optimization in SDN. IEEE J. Sel. Areas Commun. 38, 2260–2270 (2020).

    Article  Google Scholar 

  116. Li, B. et al. Learnable digital twin for efficient wireless network evaluation. In 2023 IEEE Military Communications Conference (MILCOM) 661–666 (IEEE, 2023).

  117. Deiana, A. M. et al. Applications and techniques for fast machine learning in science. Front. Big Data 5, 787421 (2022).

    Article  Google Scholar 

  118. Sirunyan, A. M. et al. Particle-flow reconstruction and global event description with the CMS detector. J. Instrum. 12, P10003 (2017).

    Article  Google Scholar 

  119. Pata, J., Duarte, J., Vlimant, J.-R., Pierini, M. & Spiropulu, M. MLPF: efficient machine-learned particle-flow reconstruction using graph neural networks. Eur. Phys. J. C 81, 381 (2021).

    Article  Google Scholar 

  120. Kieseler, J. Object condensation: one-stage grid-free multi-object reconstruction in physics detectors, graph and image data. Eur. Phys. J. C 80, 886 (2020).

    Article  Google Scholar 

  121. Di Bello, F. A. et al. Reconstructing particles in jets using set transformer and hypergraph prediction networks. Eur. Phys. J. C 83, 596 (2023).

    Article  Google Scholar 

  122. Pata, J. et al. Scalable neural network models and terascale datasets for particle-flow reconstruction. Preprint at arXiv https://doi.org/10.21203/rs.3.rs-3466159/v1 (2023).

  123. Sirunyan, A. M. et al. Pileup mitigation at CMS in 13 TeV data. J. Instrum. 15, P09018 (2020).

    Article  Google Scholar 

  124. Strandlie, A. & Frühwirth, R. Track and vertex reconstruction: from classical to adaptive methods. Rev. Mod. Phys. 82, 1419 (2010).

    Article  Google Scholar 

  125. Chatrchyan, S. et al. Description and performance of track and primary-vertex reconstruction with the CMS tracker. J. Instrum. 9, P10009 (2014).

    Article  Google Scholar 

  126. Elabd, A. et al. Graph neural networks for charged particle tracking on FPGAs. Front. Big Data 5, 828666 (2022).

    Article  Google Scholar 

  127. Huang, S.-Y. et al. Low latency edge classification GNN for particle trajectory tracking on FPGAs. In 2023 33rd International Conference on Field-Programmable Logic and Applications (FPL) 294–298 (IEEE, 2023).

  128. Duarte, J. et al. Fast inference of deep neural networks in FPGAs for particle physics. J. Instrum. 13, P07027 (2018).

    Article  Google Scholar 

  129. FastML Team. fastmachinelearning/hls4ml. Github https://github.com/fastmachinelearning/hls4ml (2023).

  130. Xuan, T. et al. Trigger detection for the sPHENIX experiment via bipartite graph networks with set transformer. In Machine Learning and Knowledge Discovery in Databases 51–67 (Springer, 2023).

  131. Moreno, E. A. et al. JEDI-net: a jet identification algorithm based on interaction networks. Eur. Phys. J. C 80, 58 (2020).

    Article  Google Scholar 

  132. Mikuni, V., Nachman, B. & Shih, D. Online-compatible unsupervised non-resonant anomaly detection. Phys. Rev. D 105, 055006 (2022).

    Article  Google Scholar 

  133. Que, Z. et al. LL-GNN: Low latency graph neural networks on FPGAs for high energy physics. In ACM Transactions on Embedded Computing Systems 1–28 (ACM, 2024). This extensive review discusses the integration of powerful machine learning methods into a real-time experimental data processing loop to accelerate the scientific discovery.

  134. Duarte, J. et al. FPGA-accelerated machine learning inference as a service for particle physics computing. Comput. Softw. Big Sci. 3, 13 (2019).

    Article  Google Scholar 

  135. Krupa, J. et al. GPU coprocessors as a service for deep learning inference in high energy physics. Mach. Learn. Sci. Technol. 2, 035005 (2021).

    Article  Google Scholar 

  136. Bogatskiy, A. et al. Lorentz group equivariant neural network for particle physics. In Proc. 37th International Conference on Machine Learning 992–1002 (ICML, 2020).

  137. Gong, S. et al. An efficient Lorentz equivariant graph neural network for jet tagging. J. High Energy Phys. 7, 030 (2022).

    Article  MathSciNet  Google Scholar 

  138. Tsan, S. et al. Particle graph autoencoders and differentiable, learned energy mover’s distance. In Advances in Neural Information Processing Systems (NIPS, 2021).

  139. Atkinson, O., Bhardwaj, A., Englert, C., Ngairangbam, V. S. & Spannowsky, M. Anomaly detection with convolutional graph neural networks. J. High Energy Phys. 8, 080 (2021).

    Article  Google Scholar 

  140. Hao, Z., Kansal, R., Duarte, J. & Chernyavskaya, N. Lorentz group equivariant autoencoders. Eur. Phys. J. C 83, 485 (2023).

    Article  Google Scholar 

  141. Govorkova, E. et al. Autoencoders on field-programmable gate arrays for real-time, unsupervised new physics detection at 40 MHz at the Large Hadron Collider. Nat. Mach. Intell. 4, 154–161 (2022).

    Article  Google Scholar 

  142. Gong, W. & Yan, Q. Graph-based deep learning frameworks for molecules and solid-state materials. Comput. Mater. Sci. 195, 110332 (2021).

    Article  Google Scholar 

  143. Bapst, V. et al. Unveiling the predictive power of static structure in glassy systems. Nat. Phys. 16, 448–454 (2020). This fundamental work demonstrates the potential of FPGA-implemented deep learning models for achieving ultra-high inference efficiency in particle physics.

    Article  Google Scholar 

  144. Chen, C., Zuo, Y., Ye, W., Li, X. & Ong, S. P. Learning properties of ordered and disordered materials from multi-fidelity data. Nat. Comput. Sci. 1, 46–53 (2021).

    Article  Google Scholar 

  145. Jang, J., Gu, G. H., Noh, J., Kim, J. & Jung, Y. Structure-based synthesizability prediction of crystals using partially supervised learning. J. Am. Chem. Soc. 142, 18836–18843 (2020).

    Article  Google Scholar 

  146. Chen, C., Ye, W., Zuo, Y., Zheng, C. & Ong, S. P. Graph networks as a universal machine learning framework for molecules and crystals. Chem. Mater. 31, 3564–3572 (2019).

    Article  Google Scholar 

  147. Gasteiger, J., Groß, J. & Günnemann, S. Directional message passing for molecular graphs. In International Conference on Learning Representations (ICLR, 2020).

  148. Choudhary, K. & DeCost, B. Atomistic line graph neural network for improved materials property predictions. npj Comput. Mater. 7, 185 (2021).

    Article  Google Scholar 

  149. Chen, C. & Ong, S. P. A universal graph deep learning interatomic potential for the periodic table. Nat. Comput. Sci. 2, 718–728 (2022).

    Article  Google Scholar 

  150. Batzner, S. et al. E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials. Nat. Commun. 13, 2453 (2022).

    Article  Google Scholar 

  151. Schütt, K., Unke, O. & Gastegger, M. Equivariant message passing for the prediction of tensorial properties and molecular spectra. In Proc. 38th International Conference on Machine Learning 9377–9388 (ICML, 2021).

  152. Thölke, P. & De Fabritiis, G. TorchMD-NET: Equivariant transformers for neural network based molecular potentials. In International Conferenc on Learning Representations (ICLR, 2022).

  153. Liao, Y.-L. & Smidt, T. Equiformer: Equivariant graph attention transformer for 3D atomistic graphs. In International Conference on Learning Representations (ICLR, 2023).

  154. Unke, O. T. et al. Machine learning force fields. Chem. Rev. 121, 10142–10186 (2021).

    Article  Google Scholar 

  155. Musil, F. et al. Physics-inspired structural representations for molecules and materials. Chem. Rev. 121, 9759–9815 (2021).

    Article  Google Scholar 

  156. Choudhary, K. et al. Unified graph neural network force-field for the periodic table: solid state applications. Digit. Discov. 2, 346–355 (2023).

    Article  Google Scholar 

  157. Zunger, A. Inverse design in search of materials with target functionalities. Nat. Rev. Chem. 2, 0121 (2018).

    Article  Google Scholar 

  158. Gebauer, N., Gastegger, M. & Schütt, K. Symmetry adapted generation of 3D point sets for the targeted discovery of molecules. In Proc. 33rd International Conference on Neural Information Processing Systems 7566–7578 (Curran Associates Inc., 2019).

  159. Xie, T., Fu, X., Ganea, O.-E., Barzilay, R. & Jaakkola, T. Crystal diffusion variational autoencoder for periodic material generation. In International Conference on Learning Representations (ICLR, 2022).

  160. Lyngby, P. & Thygesen, K. S. Data-driven discovery of 2D materials by deep generative models. npj Comput. Mater. 8, 232 (2022).

    Article  Google Scholar 

  161. Wines, D., Xie, T. & Choudhary, K. Inverse design of next-generation superconductors using data-driven deep generative models. J. Phys. Chem. Lett. 14, 6630–6638 (2023).

    Article  Google Scholar 

  162. Chanussot, L. et al. Open Catalyst 2020 (OC20) dataset and community challenges. ACS Catal. 11, 6059–6072 (2021).

    Article  Google Scholar 

  163. Gene Ontology Consortium. The Gene Ontology resource: 20 years and still going strong. Nucleic Acids Res. 47, D330–D338 (2019).

    Article  Google Scholar 

  164. Jumper, J. et al. Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 (2021).

    Article  Google Scholar 

  165. Kryshtafovych, A., Schwede, T., Topf, M., Fidelis, K. & Moult, J. Critical assessment of methods of protein structure prediction (CASP) — Round XIV. Proteins: Struct. Funct. Genet. 89, 1607–1617 (2021).

    Article  Google Scholar 

  166. Ingraham, J., Garg, V., Barzilay, R. & Jaakkola, T. Generative models for graph-based protein design. In Proc. 33rd International Conference on Neural Information Processing Systems 15820–15831 (Curran Associates Inc., 2019).

  167. Luo, J. & Luo, Y. Contrastive learning of protein representations with graph neural networks for structural and functional annotations. Pac. Symp. Biocomput. 2023, 109–120 (2023).

    Google Scholar 

  168. Gelman, S., Fahlberg, S. A., Heinzelman, P., Romero, P. A. & Gitter, A. Neural networks to learn protein sequence–function relationships from deep mutational scanning data. Proc. Natl Acad. Sci. USA 118, e2104878118 (2021).

    Article  Google Scholar 

  169. Chen, T. et al. HotProtein: A novel framework for protein thermostability prediction and editing. In International Conference on Learning Representations (ICLR, 2022).

  170. Gao, Z. et al. Hierarchical graph learning for protein–protein interaction. Nat. Commun. 14, 1093 (2023).

    Article  Google Scholar 

  171. Lu, W. et al. TANKbind: Trigonometry-aware neural networks for drug–protein binding structure prediction. In Proc. 36th International Conference on Neural Information Processing Systems 7236–7249 (Curran Associates Inc., 2022).

  172. Gainza, P. et al. De novo design of protein interactions with learned surface fingerprints. Nature 617, 176–184 (2023).

    Article  Google Scholar 

  173. Ho, J., Jain, A. & Abbeel, P. Denoising diffusion probabilistic models. In Proc. 34th International Conference on Neural Information Processing Systems 6840–6851 (Curran Associates Inc., 2020).

  174. Watson, J. L. et al. De novo design of protein structure and function with rfdiffusion. Nature 1–3 (2023).

  175. Stärk, H., Ganea, O., Pattanaik, L., Barzilay, R. & Jaakkola, T. EquiBind: Geometric deep learning for drug binding structure prediction. In Proc. 39th International Conference on Machine Learning 20503–20521 (ICML, 2022).

  176. Qian, W. W. et al. Metabolic activity organizes olfactory representations. eLife 12 (2023).

  177. Morselli Gysi, D. et al. Network medicine framework for identifying drug-repurposing opportunities for COVID-19. Proc. Natl Acad. Sci. USA 118, e2025581118 (2021).

    Article  Google Scholar 

  178. Li, S. et al. MONN: a multi-objective neural network for predicting compound–protein interactions and affinities. Cell Syst 10, 308–322 (2020).

    Article  Google Scholar 

  179. Zitnik, M., Agrawal, M. & Leskovec, J. Modeling polypharmacy side effects with graph convolutional networks. Bioinformatics 34, i457–i466 (2018).

    Article  Google Scholar 

  180. Satorras, V. G., Hoogeboom, E. & Welling, M. E(n) equivariant graph neural networks. In Proc. 38th International Conference on Machine Learning 9323–9332 (ICML, 2021).

  181. Townshend, R. J. et al. ATOM3D: Tasks on molecules in three dimensions. In 35th Conference on Neural Information Processing Systems (NIPS, 2021).

  182. Hoogeboom, E., Satorras, V. G., Vignac, C. & Welling, M. Equivariant diffusion for molecule generation in 3D. In Proc. 39th International Conference on Machine Learning 8867–8887 (ICML, 2022).

  183. Guan, J. et al. DecompDiff: Diffusion models with decomposed priors for structure-based drug design. In Proc. 40th International Conference on Machine Learning 11827–11846 (ICML, 2023). This article discusses the application of graph learning models to biology, presenting unprecedentedly high accuracy in predicting protein structures.

  184. Luo, S., Guan, J., Ma, J. & Peng, J. A 3D generative model for structure-based drug design. In Proc. 35th International Conference on Neural Information Processing Systems 6229–6239 (Curran Associates Inc., 2021).

  185. Liu, M., Luo, Y., Uchino, K., Maruhashi, K. & Ji, S. Generating 3D molecules for target protein binding. In Proc. 39th International Conference on Machine Learning 13912–13924 (ICML, 2022).

  186. Peng, X. et al. Pocket2Mol: Efficient molecular sampling based on 3D protein pockets. In Proc. 39th International Conference on Machine Learning 17644–17655 (ICML, 2022).

  187. Guan, J. et al. 3D equivariant diffusion for target-aware molecule generation and affinity prediction. In International Conference on Learning Representations (ICLR, 2023).

  188. Wang, J. et al. SCGNN is a novel graph neural network framework for single-cell RNA-seq analyses. Nat. Commun. 12, 1882 (2021).

    Article  Google Scholar 

  189. Li, H. et al. Inferring transcription factor regulatory networks from single-cell ATAC-seq data based on graph neural networks. Nat. Mach. Intell. 4, 389–400 (2022).

    Article  Google Scholar 

  190. Cheng, F. et al. Network-based approach to prediction and population-based validation of in silico drug repurposing. Nat. Commun. 9, 2691 (2018).

    Article  Google Scholar 

  191. Cheng, F., Kovács, I. A. & Barabási, A.-L. Network-based prediction of drug combinations. Nat. Commun. 10, 1197 (2019).

    Article  Google Scholar 

  192. Jin, W. et al. Deep learning identifies synergistic drug combinations for treating COVID-19. Proc. Natl Acad. Sci. USA 118, e2105070118 (2021).

    Article  Google Scholar 

  193. Ge, Y. et al. An integrative drug repositioning framework discovered a potential therapeutic agent targeting COVID19. Signal. Transduct. Target. Ther. 6, 165 (2021).

    Article  Google Scholar 

  194. Zhou, Y. et al. CGC-Net: cell graph convolutional network for grading of colorectal cancer histology images. In 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW) 388–398 (IEEE, 2019).

  195. Wu, Z. et al. Graph deep learning for the characterization of tumour microenvironments from spatial protein profiles in tissue specimens. Nat. Biomed. Eng. 6, 1435–1448 (2022).

    Article  Google Scholar 

  196. Liu, Z., Li, X., Peng, H., He, L. & Philip, S. Y. Heterogeneous similarity graph neural network on electronic health records. In 2020 IEEE International Conference on Big Data 1196–1205 (IEEE, 2020).

  197. Choi, E. et al. Learning the graphical structure of electronic health records with graph convolutional transformer. In Proc. 34th AAAI Conference on Artificial Intelligence 606–613 (AAAI, 2020).

  198. Fey, M. & Lenssen, J. E. Fast graph representation learning with pytorch geometric. In ICLR 2019 Workshop on Representation Learning on Graphs and Manifolds (ICLR, 2019).

  199. Wang, M. et al. Deep graph library: a graph-centric, highly-performant package for graph neural networks. Preprint at arXiv https://doi.org/10.48550/arXiv.1909.01315 (2019).

  200. Sarkar, R., Abi-Karam, S., He, Y., Sathidevi, L. & Hao, C. FlowGNN: A dataflow architecture for real-time workload-agnostic graph neural network inference. In 2023 IEEE International Symposium on High-Performance Computer Architecture (HPCA) 1099–1112 (IEEE, 2023).

  201. Huang, G. et al. Machine learning for electronic design automation: a survey. ACM Trans. Des. Autom. Electron. Syst. 26, 1–46 (2021).

    Article  Google Scholar 

  202. He, Z., Wang, Z., Bail, C., Yang, H. & Yu, B. Graph learning-based arithmetic block identification. In 2021 IEEE/ACM International Conference On Computer Aided Design (ICCAD) 1–8 (IEEE, 2021).

  203. He, S. et al. An overview on the application of graph neural networks in wireless networks. IEEE Open. J. Commun. Soc. 2, 2547–2565 (2021).

    Article  Google Scholar 

  204. Zitnik, M., Sosič, R. & Leskovec, J. Prioritizing network communities. Nat. Commun. 9, 2544 (2018).

    Article  Google Scholar 

  205. Hu, W. et al. Strategies for pre-training graph neural networks. In International Conference on Learning Representations (ICLR, 2020).

  206. Tishby, N., Pereira, F. C. & Bialek, W. The information bottleneck method. In Proc. 37th Annual Allerton Conference on Communication, Control and Computing 368–377 (1999).

  207. Miao, S., Liu, M. & Li, P. Interpretable and generalizable graph learning via stochastic attention mechanism. In Proc. 39th International Conference on Machine Learning 15524–15543 (ICML, 2022).

  208. Iiyama, Y. et al. Distance-weighted graph neural networks on FPGAs for real-time particle reconstruction in high energy physics. Front. Big Data 3, 598927 (2021).

    Article  Google Scholar 

  209. Wu, H. & Wang, H. Decoding latency of LDPC codes in 5G NR. In 2019 29th International Telecommunication Networks and Applications Conference (ITNAC) 1–5 (IEEE, 2019).

  210. Wang, Z. et al. GNN-PIM: A processing-in-memory architecture for graph neural networks. In Conference on Advanced Computer Architecture 73–86 (Springer, 2020).

  211. Huang, Y. et al. Accelerating graph convolutional networks using crossbar-based processing-in-memory architectures. In 2022 IEEE International Symposium on High-Performance Computer Architecture (HPCA) 1029–1042 (IEEE, 2022).

  212. Liang, S. et al. EnGN: a high-throughput and energy efficient accelerator for large graph neural networks. IEEE Trans. Comput. 70, 1511–1525 (2020).

    Article  Google Scholar 

  213. Choi, E., Bahadori, M. T., Song, L., Stewart, W. F. & Sun, J. GRAM: Graph-based attention model for healthcare representation learning. In Proc. 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 787–795 (ACM, 2017).

  214. Sajadmanesh, S., Shamsabadi, A. S., Bellet, A. & Gatica Perez, D. GAP: Differentially private graph neural networks with aggregation perturbation. In Proc. 32nd USENIX Conference on Security Symposium 3223–3240 (USENIX Association, 2023).

  215. Chien, E. et al. Differentially private decoupled graph convolutions for multigranular topology protection. In Proc. 37th International Conference on Neural Information Processing Systems 45381–45401 (Curran Associates Inc., 2023).

  216. Cao, Y. & Yang, J. Towards making systems forget with machine unlearning. In 2015 IEEE Symposium on Security and Privacy 463–480 (IEEE, 2015).

  217. Chien, E., Wang, H. P., Chen, Z. & Li, P. Langevin unlearning. In Privacy Regulation and Protection in Machine Learning Workshop (ICLR, 2024).

  218. Chien, E., Pan, C. & Milenkovic, O. Efficient model updates for approximate unlearning of graph-structured data. In International Conference on Learning Representations (ICLR, 2023).

  219. Mironov, I. Rényi differential privacy. In 2017 IEEE 30th Computer Security Foundations Symposium (CSF) 263–275 (IEEE, 2017).

Download references

Author information

Authors and Affiliations

  1. Electrical and Computer Engineering, Georgia Institute of Technology, Atlanta, GA, USA

    Eli Chien, Mufei Li, Cong Hao & Pan Li

  2. Physics, University of California San Diego, San Diego, CA, USA

    Anthony Aportela & Javier Duarte

  3. Computational Science and Engineering, Georgia Institute of Technology, Atlanta, GA, USA

    Kerr Ding, Shuyi Jia, Victor Fung & Yunan Luo

  4. Electrical and Computer Engineering, University of Texas Austin, Austin, TX, USA

    Supriyo Maji & David Pan

  5. Electrical and Computer Engineering, Rice University, Houston, TX, USA

    Zhongyuan Zhao & Santiago Segarra

  6. Electrical and Computer Engineering, University of Illinois Urbana-Champaign, Champaign, IL, USA

    Olgica Milenkovic

Authors
  1. Eli Chien
    View author publications

    Search author on:PubMed Google Scholar

  2. Mufei Li
    View author publications

    Search author on:PubMed Google Scholar

  3. Anthony Aportela
    View author publications

    Search author on:PubMed Google Scholar

  4. Kerr Ding
    View author publications

    Search author on:PubMed Google Scholar

  5. Shuyi Jia
    View author publications

    Search author on:PubMed Google Scholar

  6. Supriyo Maji
    View author publications

    Search author on:PubMed Google Scholar

  7. Zhongyuan Zhao
    View author publications

    Search author on:PubMed Google Scholar

  8. Javier Duarte
    View author publications

    Search author on:PubMed Google Scholar

  9. Victor Fung
    View author publications

    Search author on:PubMed Google Scholar

  10. Cong Hao
    View author publications

    Search author on:PubMed Google Scholar

  11. Yunan Luo
    View author publications

    Search author on:PubMed Google Scholar

  12. Olgica Milenkovic
    View author publications

    Search author on:PubMed Google Scholar

  13. David Pan
    View author publications

    Search author on:PubMed Google Scholar

  14. Santiago Segarra
    View author publications

    Search author on:PubMed Google Scholar

  15. Pan Li
    View author publications

    Search author on:PubMed Google Scholar

Contributions

E.C., M.L., A.A., K.D., S.J., S.M., Z.Z., J.D., V.F., Y.L., D.P., S.S. and P.L. researched data for the article. All authors contributed to the discussion of the content. E.C., M.L., A.A., K.D., S.J., S.M., Z.Z., C.H., O.M. and P.L. wrote the article. E.C., M.L., A.A., K.D., S.J., S.M., Z.Z., J.D., V.F., Y.L., D.P., S.S. and P.L. reviewed and edited the article.

Corresponding author

Correspondence to Pan Li.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Reviews Electrical Engineering thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chien, E., Li, M., Aportela, A. et al. Opportunities and challenges of graph neural networks in electrical engineering. Nat Rev Electr Eng 1, 529–546 (2024). https://doi.org/10.1038/s44287-024-00076-z

Download citation

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s44287-024-00076-z

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics