Introduction

Floods are causing increasing human and economic losses worldwide, with regional differences, and India is expected to experience indirect economic losses greater than the global average1,2. Moreover, the impact of floods has been severe in the country, with 113,390 human casualties reported between 1975 and 2015, averaging 2765 deaths per year3. The intensification of heavy precipitation events is likely due to an increase in atmospheric water holding capacity by 7% per 1 °C of warming, and this is playing a significant role in flood occurrence. However, the response of land surfaces at different scales can modulate the flood responses4. Given the significant impact of floods on human lives, infrastructure, and economic development, a comprehensive understanding of the changing nature of flooding using a long instrumental record is necessary for understanding the flood generation mechanisms, water resources planning and management, flood risk analysis and reduction, and assessment of climate change impacts5,6.

Many attempts have been made globally to explore the changes in flood hazard based on large-scale hydrological models7,8,9. However, these studies may not be able to correctly assess actual variability in flood occurrences, may have high uncertainty, and are inherently subject to the limitations of global hydrological models10,11. Moreover, regional patterns cannot be precisely inferred from global-scale studies. Many times, the intensification of extreme precipitation events globally12,13 is used as a proxy for assessing flood hazard14. However, caution must be exercised as many global and regional studies have reported decreasing trends in streamflow despite the increase in extreme precipitation15,16,17. This diverging trend of precipitation and streamflow highlights the complex nature of flood generation and the impact of multiple factors18,19. Studying streamflow trends—magnitude and timing—from past observational records is one of the best approaches to derive the hypothesis on changing flood hazard at any spatial scale6,15,20,21. However, the availability of good-quality, long and consistent observed streamflow data is necessary for such an analysis. Since such data are not widely available, large-sample studies at large spatial scales are limited to the developed regions of the world where long-term observation data exist. A few global studies exploring trends in streamflow magnitude14 and timing6, have used limited data from Asia, Africa, Eastern Europe, and South America (except Brazil). But due to some reasons, limited /no data was used from India, one of the worst-affected regions from recent hydrometeorological disasters. In India, a long series of observed streamflow data exists at limited gauging sites. Out of these, a large number of sites fall in the river basins whose data are classified, and hence, it is very difficult for researchers to collect the data, conduct analysis and obtain useful results.

Chug et al. (2020) found that the frequency of extreme flow events has doubled in North India during 1980–2003, with a statistically significant rising trend in annual maximum flows. This change in streamflow is likely to have been caused by increasing precipitation extremes during the summer and winter seasons. Das et al. (2022) examined the changing trends in annual maximum flows during 1966–2015 at 38 gauging stations in the Godavari catchment of India and found increasing trends in the northern stations located in the Wainganga, Wardha and Indravati sub-basins. At the same time, declining trends were observed in the upstream, central and downstream parts of the Godavari catchment. However, most reported observational studies in India concerning streamflow trends are catchment-scale22,23,24,25,26 or regional-scale21,27,28,29 and have relied on point data but not catchment-scale attributes. Moreover, the heterogeneity of catchment characteristics, analysis periods, chosen hydrological indices, and methods influences their conclusions. Consequently, they are limited in their ability to provide holistic information on the changing nature of flooding in the country.

Non-availability of observed data of adequate fidelity for the whole country and due to the reasons mentioned earlier, a comprehensive study describing the changing magnitude and timing of riverine floods at a pan-India scale does not exist in the scientific literature. Therefore, there is a pressing need for a cohesive, nationwide, consistent, and thorough investigation of flooding trends and their underlying mechanisms. This study has conducted a homogeneous and comprehensive analysis of flooding magnitude and timing trends and their causative mechanisms at a pan-India scale to facilitate improved understanding, management, and mitigation of riverine floods. This study was taken up after a painstaking effort to collate four decades of data from 173 gauge stations spread across the country, making it the most spatially representative, large-sample observational study in India.

Results

Regional patterns of change in the magnitude and timing of floods

Monsoon season accounts for ~80% of India’s annual rainfall30,31 and floods are a common occurrence in this season. In this study, 85% of the floods identified across all stations were recorded during the monsoon season between June and September. Our analysis reveals clear regional patterns in the changing nature of the magnitude and timing of floods across India. Figure 1 shows a decreasing trend in flood magnitude across most of the country during the monsoon season, which is also evident at the annual scale (Fig. S1 in Supplementary File). Specifically, 74% (128) of the gauging stations exhibited a decreasing trend in flood magnitude, out of which 47 catchments displayed a statistically significant decreasing trend with at least a 90% confidence level (CL). In contrast, only 26% (45) of the gauging stations out of a total of 173 across the country showed an increasing trend, and only four catchments among them are statistically significant with 90% CL.

Fig. 1
figure 1

Trends in a flood magnitude and b timing in monsoon (June-September) between 1970 and 2010 based on the Theil-Sen slope estimator and the Mann–Kendall test with 95% and 90% confidence levels (CL), i.e., p < 0.05 and p < 0.1, respectively. The inset figure in (a) with a blue border in the right lower corner corresponds to flood magnitude trends in pre-monsoon (March-May) over Hotspot M2. The inset figure in (a) with a green border in the right upper corner corresponds to the significant trends (red-decreasing; grey-no trend) in gridded monsoon mean precipitation over Hotspot M1 between 1970 and 2010 based on the Modified Mann–Kendall test (p < 0.05)80. Annual and other seasonal trends are available in the Supplementary File.

Full size image

Many factors, both natural and human-induced, influence river flooding at a location over an extended period of time. Natural factors such as climate change9,20 and natural hazards such as earthquakes and landslides can reshape river courses, leading to changes in flow pattern32. Further, human-induced changes, such as urbanization33, land use and cover alterations34, soil and water conservation measures such as check dams, and engineering projects such as dam construction35,36, can significantly modify flood generation in catchments and contribute to changes in flood dynamics. In particular, dams are constructed to mitigate flooding, but if they are improperly operated, they may aggravate flooding. Studying the complex interplay of all these factors with observed flooding trends is beyond the scope of this study. Nevertheless, we have made efforts to identify any potential relationships between changing precipitation patterns, soil moisture levels, and observed flooding variables in the identified hotspots. Hotspots are regions with a considerable number of gauge stations that do not have dams in their catchment and have a cluster of strong, distinct trends with a high percentage of change and statistically significant at 90% CL. A cluster of catchments with a strong decreasing trend, i.e., a high percentage of change per decade at a 95% CL (p < 0.05), was observed over the central region of the Ganga basin (Hotspot M1) during the monsoon season (Fig. 1) with an average decrease of 17% per decade. At the same time, a consistent decreasing trend in the magnitude of floods over the Narmada basin is observed in monsoon, possibly due to the construction of dams in this region during the study period37. Blöschl et al. (2019) reported a similar high decrease in flood discharges in western Russia at 18% per decade between 1960–2010.

In contrast, the West flowing rivers from Tadri to Kanyakumari (Chaliyar, Periyar, Bharathapuzha, Vamanapuram, etc.) in the Malabar coast (Hotspot M2) showed an increasing trend at an average rate of 8% per decade in pre-monsoon (March–May months) floods in the region (inset in Fig. 1a). In the Marathwada region of the Deccan plateau, which has been experiencing severe droughts in recent times38,39, river flows were found to be decreasing at an average rate of 8% per decade during the monsoon season and 31% in pre-monsoon, based on data from three stations in the region.

In terms of flood timing, the cluster of catchments covering the lower Yamuna basin (Hotspot T1, Fig. 1b) located southwest of Ganga showed a decreasing trend (12 locations out of the Hotspot T1 have statistically significant trend with at least 90% CL) across the monsoon, i.e., a shift towards an earlier calendar day, or floods occurring early. In contrast, catchments in the upper Ganga (Hotspot T2) exhibit a significant trend towards later floods (floods are delayed). On an annual scale, catchments in the southern region of the country tended to experience floods later, whereas those in the central region had earlier flood occurrences. Similarly, Fang et al. (2022) reported delayed flood timing in other monsoon zones, including Africa, the Amazon, and Japan. Moreover, regions dominated by the southwest monsoon in Southeast Asia, such as the Mekong catchment, Sumatra, Peninsular Malaysia, Borneo, Java, and the Tonle Sap Lake in Cambodia, as well as the Yangtze River valley in China, have experienced shifts in flood timing and other characteristics40,41, and these changes are projected to intensify in the region in the future under extreme climate change42.

Evolution of floods and their drivers

We focus on the gauge stations in the hotspots to infer the causes of changes in flood magnitude and timing. Given that multi-day precipitation and soil moisture have been identified as the primary drivers of flooding in India19,43, we studied the long-term evolution of these drivers using a ten-year moving average filter, jointly with flooding variables, and temperature as a proxy for a warming climate. The patterns in the evolution of flood discharge and drivers (Fig. 2) and the statistical significance between them (Table 1) demonstrate that the decrease in flood magnitude over central Ganga (Hotspot M1) is associated with the decline in precipitation and soil moisture, highlighting the crucial role of precipitation and soil moisture in flood generation. In fact, the role of soil moisture in runoff generation has been recognized in existing studies across the globe41,44,45,46. In addition, the temporal occurrence of flood in M1 follows precipitation and soil moisture (Fig. S3) confirming their importance in setting flood magnitudes across the region. Moreover, a significant decreasing trend at a 5% significance level in monsoon mean precipitation is observed between 1970 and 2010 over most grid points in Hotspot M1 (inset in Fig. 1a). This clearly suggests the crucial role of precipitation behind decreasing flood magnitudes over this region. The decrease in the annual and monsoon precipitation over central Ganga, as reported in studies by Bollasina et al. (2011) and Roxy et al. (2015), is attributed to factors such as Indian Ocean warming and the presence of atmospheric aerosols in the region.

Fig. 2: Long-term temporal evolutions of flood magnitude along with its drivers for hotspots with clear regional patterns.
figure 2

The data represents observed floods (blue), peak 5-day precipitation (orange), peak monthly soil moisture (green), and peak monthly temperature (red). Solid lines show the median, and the shaded region shows the variability within the hotspots (25th and 75th percentiles). All data were subjected to a 10-year weighted moving average filter.

Full size image
Table 1 Spearman’s rank correlation coefficient (r) between hotspot medians of the annual series of flood discharge and timing with their drivers
Full size table

Conversely, the increase in flood magnitude over the West flowing rivers from Tadri to Kanyakumari basin in the Malabar coast of the country (M2) (inset in Fig. 1a) can be attributed to the increasing magnitude of precipitation during the pre-monsoon. Notably, the flood magnitudes over the catchments of Hotspot M2 show a clear pattern and strong positive correlation (Spearman rank correlation coefficient r = 0.88) with precipitation, indicating that an increase in the magnitude of precipitation leads to an increase in flood discharge. This observation is further supported by the evolution plot of the day of flood occurrence and precipitation during the same period over M2 (Fig. S3), which also suggests that early occurrence of precipitation leads to early pre-monsoon floods over M2. Since rivers in M2 region do not receive any snow, all floods are rainfall-generated, and temperature does not seem to have any direct influence on floods. Intense pre-monsoon rains over the catchments of the West flowing rivers across M2 have been reported in recent articles and published studies47,48,49. Moreover, when the positive dipole mode index (DMI) and the positive ENSO index (SOI) coincide, an observed increase in positive rainfall anomaly during 1991–2020 was noticed over the southwest Indian peninsular region48.

On the other hand, the timing of floods in the two hotspots, the lower Yamuna basin (T1) and upper Ganga basin (T2) exhibit a close correlation with the pattern of the observed precipitation. In the lower Yamuna basin (located in the southwest of the Ganga basin) (T1), earlier precipitation leads to early floods, while delayed precipitation results in later floods over the upper Ganga basin (T2). In the entire Himalayan belt, including the Upper Ganga basin, rainfall contributes significantly more to streamflow than snowfall and glacier melt50. Moreover, substantial evidence suggests a strong correlation between precipitation extremes and streamflow in the T2 region22,51,52. Figure 3 shows the variations in flood timing and its drivers for hotspots T1 and T2, displaying a good match. Existing studies in the Southeast Asia region provide additional evidence that alterations in monsoon dynamics are affecting flood characteristics40,41,42. Together, these studies lend support to the hypothesis that regional changes in flood behavior in India are manifestations of broader climatic influences that are similarly impacting other monsoon-dominated basins.

Fig. 3: Long-term temporal evolutions of flood timing along with its drivers for hotspots with clear regional patterns.
figure 3

Please refer to the caption of Fig. 2 for the description of the plots.

Full size image

Changes in 100-year flood discharge

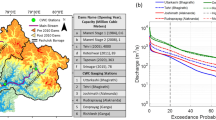
To further investigate the impact of these changes on observed flows in the context of flood management, we estimated the trend in 100-year flood discharge between 1970 and 2010 based on statistical flood frequency analysis. Our analysis reveals that regional trends in observed annual floods (Fig. S1), and nonstationary 100-year return period flood discharge are almost similar (Fig. 4). The inference from Fig. 4a is that the 100-year flood discharge has decreased by more than half during these 40 years at many locations in the Western and central Ganga basin. Consequently, the frequency of the 1970 100-year flood will increase in these regions (Fig. 4b). In contrast, a few stations in the Upper Ganga basin and the southwest of the country show an increase in the 1970 100-year flood discharge and a decrease in the frequency of its occurrence.

Fig. 4
figure 4

Estimated (a) percentage change in the magnitude of 1970 100-year flood discharge in 2010 and (b) return period in 2010 for the 1970 100-year flood discharge. Grey-colored points represent stationary stations.

Full size image

Relationship between floods and catchment characteristics

We investigate the first-order relationship between the trends in the magnitude and timing of floods and associated specific geographical or climatic characteristics. To examine the role of climate, catchments are categorized based on the dominant Köppen-Geiger climate class (i.e., covering more than 50% of the catchment area). There are 88 Tropical climate-dominated catchments, 43 temperate, 34 Arid, and 2 polar, among others. Since there are only 2 Polar catchments, and 6 catchments do not have any specific dominant climate in them, they are not considered in this analysis. While the 50% threshold ensures that the assigned climate class represents the majority of a catchment, we acknowledge that some catchments may experience mixed climatic influences. However, this threshold has been widely used in previous studies18,53 and provides a reasonable balance between classification simplicity and climate representation. Conducting sensitivity tests for varying thresholds is beyond the scope of this study, but could be explored in future research.

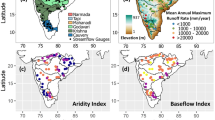
Figure 5a depicts a significant decrease in flood magnitude over arid climates during all seasons. No specific pattern is inferred regarding shifts in timings in any particular climate class (Fig. S4). The decrease in flood magnitude in arid regions can be attributed to climate change54,55 and various anthropogenic activities26,29. Drylands are more sensitive to global warming and its impact, leading to increasingly arid conditions54,55.

Fig. 5
figure 5

a Percentage of catchments with decreasing and increasing trends in flood magnitude in each climate over different seasons. b Drainage area vs. percentage change in flood magnitude per decade based on the Theil-Sen slope estimator over all the catchments. Points are color-coded based on the mean elevation of the catchment. The background is color-coded based on the size of catchments: small (<1000 sq.km.), medium (1000–10,000 sq.km.), and large (more than 10,000 sq.km.). c Heatmap of Spearman correlations between various anthropogenic characteristics, change in flood magnitude per decade (%), and drainage area.

Full size image

Interestingly, there exists a clear relationship between the catchment area and the observed percentage change in flood magnitude per decade (Fig. 5b). The flood magnitudes over larger catchments are decreasing at higher rates, and as the catchment size decreases, the rate of change is also decreasing. And it is predominantly an increasing trend in small catchments (area less than 1000 sq.km.), which have implications for flash floods, potentially due to their greater sensitivity to localized intense precipitation events and reduced capacity to attenuate flood peaks through natural storage56. This pattern can be attributed to several specific anthropogenic factors, as evidenced by our correlation analysis (Fig. 5c). Population count (−0.33) and total storage volume of all dams in the catchment (−0.32) show the strongest negative correlations with percentage change in flood magnitude, indicating their role in reducing flood peaks in larger catchments as more people will use more water and higher storage volume will absorb more flood water. The construction of large dams and reservoirs, which are more prevalent in larger catchments as seen in Fig. 5c, with a strong correlation of 0.67 between drainage area and the total storage volume of all dams in the catchment, has been shown to attenuate flood peaks in existing studies35,36,57. Moreover, existing studies have demonstrated that anthropogenic water withdrawals can significantly reduce annual discharge in major river systems58,59, which are generally high in larger catchments due to high population as seen in Fig. 5c. The Human Development Index (HDI) shows a slight positive correlation (0.17), potentially indicating that development patterns may introduce complex interactions with flood dynamics through improved infrastructure, more paved area, and altered drainage systems60.

No specific pattern is observed between the trend of flood magnitude and the mean elevation of the catchment, suggesting that the mean elevation of the catchment has no direct influence on the changing nature of flood magnitude. Similarly, from Fig. S5 in Supplementary File, neither the catchment area nor the mean elevation of the catchment has any notable relationship with the trends of flood timing. However, elevation can indirectly influence flood timing through several hydroclimatic mechanisms. Climate warming has significantly altered the rain-snow transition zone in high-elevation regions globally, with precipitation increasingly falling as rain rather than snow61,62. For the Indian subcontinent specifically, Ombadi et al. (2023) project substantial snowfall declines by 2070–2100 compared to 1971–2000: 30–50% in the Indus Basin, 50–60% in the Ganges, and 50–70% in the Brahmaputra. These changes can advance spring/pre-monsoon flood peaks by several weeks in snowmelt-dominated regions63. Additionally, orographic effects in mountainous catchments create complex precipitation patterns that respond uniquely to changing climate conditions. For instance, a study on high-altitude catchments in the Alps in Austria64 showed greater sensitivity to temperature-driven changes in snowmelt timing than lower-elevation catchments, potentially altering flood timing and characteristics.

While our current analysis using mean elevation did not identify clear patterns, future studies could benefit from incorporating more catchments from high-altitude regions in the Indus, Ganga, and Brahmaputra basins, and examining more nuanced elevation metrics such as hypsometric curves, elevation distribution, or specific elevation bands where rain-snow transitions occur. These approaches could better capture the complex relationships between elevation and flood timing in a changing climate.

Discussions

This study sheds light on the decreasing flood magnitudes across three-fourths of the country, with a notable 17% per decade decline in the Ganga basin. Additionally, it highlights distinct regional patterns in flood timing, underscoring the complexity of flood dynamics in India. If these changes in flood magnitude and timing trends are not fully understood and accounted for, significant economic and environmental consequences could emerge, given that reservoir filling, ecosystems, and communities are adapted to the typical seasonal flooding patterns. For instance, diminished flood magnitudes can lead to lower reservoir fillings, adversely impacting water supply, irrigation, and hydropower generation. Additionally, earlier-than-expected floods, such as those seen in the Upper Ganga region, can result in catastrophic outcomes since the entire flood management system, including preparatory activities, will need to be redesigned. Increasing discharges and early floods on the Malabar coast (Hotspot M2) in the pre-monsoon season may have severe implications for agriculture, as it is a significant crop harvesting time.

By focusing on hotspots, we identify the critical role of multiday precipitation and soil moisture patterns in driving changes in flood characteristics in these regions. Our analysis reveals that decreasing flood magnitudes in the Central Ganga basin (M1) are strongly linked to declining soil moisture and monsoon precipitation. Existing studies suggest that these declines in precipitation are influenced by Indian Ocean warming and atmospheric aerosols in the region. Conversely, increasing flood magnitudes in the Malabar coast (M2) are associated with intensified pre-monsoon rainfall, a trend consistent with recent studies highlighting enhanced pre-monsoon precipitation under positive DMI and ENSO conditions. Moreover, early precipitation in the lower Yamuna basin (T1) and delayed precipitation in the Upper Ganga basin (T2) have led to earlier and later floods in these regions, respectively, reinforcing previous findings that link precipitation patterns with streamflow dynamics in the Himalayan belt. These timing shifts mirror similar trends in monsoon-dominated basins, such as the Mekong, where monsoon variability has altered seasonal flood regimes. Additionally, it is observed that geographical and climatic factors play pivotal roles, with arid climates experiencing significant decreases in flood magnitudes. Notably, our analysis reveals a distinct pattern in which the decline in flood magnitudes becomes more pronounced as catchment area increases.

These findings and insights on changes in the magnitude and timings would enhance our scientific understanding of flood dynamics in India and play a crucial role in flood risk management and mitigation strategies tailored to the diverse regional characteristics of the country. Moreover, similar shifts in flood magnitude and timing have been observed in other monsoon-dominated regions, reinforcing the notion that these trends could also be part of a broader hydrologic response to large-scale and increased climate variability and anthropogenic influences. Future research should further investigate the role of large-scale climate indices in modulating flood characteristics, disentangle the multidimensional drivers of flood changes to assess their relative contributions and interactions, and examine the agricultural and other socioeconomic consequences of these shifting flood regimes. Adopting a holistic approach—integrating improved forecasting systems, sustainable land-use planning, and climate-resilient water management strategies—will be essential to mitigate the long-term impacts of evolving flood patterns, both in India and globally.

Methods

Data

  • Streamflow: A good quality time series of streamflow for a considerable period is vital for change detection studies65. The observed streamflow data used in this study were obtained from the Central Water Commission (CWC) of India. For this study, only those gauge stations were selected that had at least 30 years of data with a minimum of 350 daily values each year, ensuring robustness66. This requirement also meets the data availability criteria for trend analysis, which states that stations considered should have at least 70% of the years in the study period. The years from 1970 to 2010 were selected as the common period for the analyses due to the availability of the maximum data that met the above criteria, ensuring optimal spatial representativeness. Additionally, using data from a common period facilitates intercomparison among catchments. Based on these criteria, 173 gauge stations are selected, ensuring considerable representation of the catchments covering diverse physiographic characteristics. Moreover, extreme data indices are very sensitive to missing data. Hence, extensive efforts have been made to obtain, curate, and collate the long-term streamflow time series datasets over the country. In some cases, CWC estimates the peak flows by using rating curves. Hence, the peak flow data may have uncertainty of about 10–15%.

  • Catchment characteristics: Shapefiles were generated for the catchments corresponding to the 173 gauge stations by considering the location of gauge stations as their outlet/pour point. Next, shapefiles were used to compute the catchment area and catchment-scale variables from the raw gridded datasets. The mean elevation over the catchments was calculated utilizing the shapefiles and SRTM void-filled DEM data of 3 arc-second (~90 m) resolution.

  • Precipitation and Temperature: The global ERA5 reanalysis hourly precipitation and 2 m temperature data are aggregated to daily and average monthly values, respectively, and used to compute the catchment-scale precipitation and temperature over all the catchments in this study. ERA5 gridded products have been available from 1959 to the present at a resolution of 0.25° × 0.25°. Reanalysis integrates model data with global observations to create a global dataset that is full and consistent67. Though the India Meteorological Department (IMD) precipitation and temperature datasets also cover the given period, their spatial extent is limited to the national boundary of India. This is a catchment-scale study, and the catchments of some gauging stations in the Ganga basin (which are included in this study) fall outside the territory of India. Hence, the IMD observation dataset is not suitable for this study. Apart from this, it has been observed in the previous studies that ERA5 precipitation and temperature products are consistent with the observational record68,69,70 and outperform other reanalysis products for hydrologic applications in India71.

  • Köppen-Geiger climate classes: Köppen-Geiger climate classes are useful for combining climatic conditions determined by several variables and their seasonality. In this study, we used the main climates of the Köppen-Geiger map produced by Kottek et al.72, which is processed utilizing mean monthly precipitation and temperature data for the years 1951 to 2000 from the Global Precipitation Climatology Centre (GPCC) and the Climatic Research Unit (CRU) of the University of East Anglia, respectively.

  • Soil moisture: Catchment-scale monthly mean soil moisture is derived using Climate Prediction Center (CPC) soil moisture V2 data products from Physical Science Laboratory (PSL). This data is available at a resolution of 0.5° x 0.5° on a monthly scale for the period 1948 to present.

  • Anthropogenic: The HDI is a comprehensive index that is often used by various international organizations to assess the development status of an area, with higher scores indicating greater development. In this study, the average HDI for catchments is derived from global gridded HDI data73. To further analyze anthropogenic impacts, we calculate the urban area percentage in each catchment using the Global Human Settlement (GHS) - Settlement Model grid (SMOD)74. This involves computing the total area of urban clusters from the GHS-SMOD dataset relative to the catchment’s total area. Additionally, we utilize the Global Reservoir and Dam Database (GRanD)75 to obtain the total storage volume of all dams in each catchment. Lastly, we estimate the population in each catchment using the Gridded Population of the World (GPW) dataset76, which is available at a resolution of 30×30 arcseconds. This dataset provides a detailed spatial distribution of population, allowing us to better understand demographic pressures on catchments.

Identifying floods

To examine trends in flood magnitude and timing, we employed the block maximum approach, which involves dividing the time series data into predefined blocks (full year and seasons) and extracting the peak daily discharge value within each block for every stream gauge station. Specifically, we identified annual and seasonal peak discharges for every year and their corresponding occurrence day of the year (ordinal day: 1 for January 1 and 365 [or 366] for December 31) from daily streamflow time series data for the entire analysis period. Peak discharge serves as a metric for flood magnitude, while the day of the year on which it occurs indicates flood timing. This approach is widely adopted in flood studies5,6,20,77 and aligns with policy and infrastructure frameworks78,79 due to its straightforward interpretation, cross-basin comparability, practical significance, and statistical rigor. While focusing on annual or seasonal peaks may underrepresent catchments with multi-peak flood regimes, this approach ensures consistency and minimizes biases arising from heterogeneous flood data availability across stations. Moreover, considering a single flood event per year or season is particularly advantageous when analyzing seasonal floods, as it allows for more meaningful definitions of climatological averages for flood timing and magnitude at decadal scales77.

Changes in flood magnitude and timing

To evaluate the changing nature of flooding magnitude and timing at individual catchments, we have employed two well-known statistical methods a) the modified Mann-Kendall test80,81,82 and b) Theil-Sen’s Slope Estimator83. The Mann-Kendall test is a nonparametric method to find the monotonic trend in time series data. It has been widely used in various hydrometeorological time series trend analyses84, including groundwater85, streamflow5,14, and precipitation86,87. In this study, trends were evaluated at both 5% and 10% significance levels to ensure a comprehensive assessment. While the 5% level provides stronger statistical confidence, the 10% level helps identify weaker yet potentially important and hydrologically meaningful trends, allowing for a more explanatory approach. A 5% significance level rejects the null hypothesis (no monotonic trend) when the p value is below 0.05, whereas a 10% level extends this threshold (0.05–0.10) to capture additional emerging trends.

Complementing the Mann–Kendall test, the Sen-slope estimator was used to find the magnitude of trends in terms of percentage per decade using Eq. 1. This allows trend estimates comparison between catchments of different sizes and climates and diminishes model biases trends88,89,90. The Sen-slope estimator has also been widely used in various hydrometeorological time series trend analysis20,88,89.

$${T}_{c}=\frac{{\tau }_{c}}{{\underline{x}}_{c}}\times 10\,{years}\times 100$$
(1)

\({T}_{c}\) is the trend at catchment c in units of percent per decade, \({\tau }_{c}\) is the Theil‐Sen slope estimator, and \({\underline{x}}_{c}\) is the mean of the index time series.

While these methods provide robust trend estimates, it is important to acknowledge potential uncertainties in trend analysis. Such uncertainty may arise from data quality, time series length, and methodological choices. Although confidence intervals could further quantify variability in the Theil-Sen slope estimates, the estimator is inherently robust to outliers and non-normality, making it a reliable tool for hydroclimatic trend detection. Additionally, this study employs the modified Mann-Kendall (MK) method to account for serial correlation80, which effectively reduces the influence of autocorrelation in time series data, ensuring that trend significance is not overestimated due to persistence effects35.

Changes in 100-year flood discharge

The observed trends in flood magnitude suggest potential changes in the 100-year flood discharge20,91. The 100-year flood discharge was estimated for each station by employing generalized extreme value (GEV) distribution, which combines the Gumbel, Fréchet, and Weibull distributions into a single continuous probability distribution. GEV distribution is one of the most widely used distributions in flood frequency analysis due to its flexibility in modeling extremes92. The probability distribution function of the GEV distribution for the block maxima is given by Eq. 2:

$$F\left(z\right)=\exp \left[{-\left\{1+\tau \left(\frac{z-\mu }{\sigma }\right)\right\}}^{\frac{-1}{\tau }}\right]$$
(2)

\(\mu\) is the location parameter, \(\sigma\) is the scale parameter, \(\tau\) is the shape parameter. These parameters were estimated from the annual maximum flood discharge using the MLE (Maximum Likelihood) method. The ‘extRemes’ package in R93 environment was used to fit a GEV distribution to data on floods with 100-year return periods. A log-link function was implemented to ensure a positive scale parameter. For this study, location and scale parameters were modeled as linear functions of the covariate time (t) (Eq. 3), as empirically supported by existing studies94,95,96. We use a linear trend over time because it is easy to interpret, simple, and provides a reasonable first-order approximation of gradual flood changes over time94,95,96. Additionally, more complex functional forms, such as nonlinear trends or explicit climate covariates, often introduce additional uncertainty and may not necessarily improve predictive performance.

$$\mu \left(t\right)={\mu }_{o}+{\mu }_{1}t;\sigma \left(t\right)={\sigma }_{o}+{\sigma }_{1}t$$
(3)

\({\mu }_{o}\), \({\mu }_{1}\), \({\sigma }_{o}\), and \({\sigma }_{1}\) are the estimated coefficients. The shape parameter τ was assumed to be constant because including a covariate for the shape parameter introduces excessive estimation errors97.

The following four types of models were fitted to the flood data:

  1. 1.

    Stationary model: both location and scale are considered constant.

  2. 2.

    Nonstationary location model: the location parameter varies with time, while the scale parameter remains constant.

  3. 3.

    Nonstationary scale model: the location parameter is constant, while the scale parameter is a function of time.

  4. 4.

    Fully nonstationary model: both the location and scale parameters vary with time.

Finally, the Akaike information criterion (AIC) is used for selecting the optimal GEV model, as it is a versatile and reliable tool suitable for both stationary and nonstationary data98. The model with the least AIC value of all four fits was declared the best-fitting GEV distribution, and based on this distribution, the changes in the magnitude of 100-year floods with time were computed.