Optimal field-free magnetization switching via spin-orbit torque on the surface of a topological insulator

Abstract

We present an optimal field-free protocol for current-induced switching of a perpendicularly magnetized ferromagnetic insulator nanoelement on the surface of a topological insulator. The time dependence of in-plane components of the surface current, which drives the magnetization reversal via the Dirac spin-orbit torque with minimal Joule heating, is derived analytically as a function of the switching time and material properties. Our analysis identifies that energy-efficient switching is achieved for vanishing damping-like torque. The optimal reversal time that balances switching speed and energy efficiency is determined. When we compare topological insulators to heavy-metal systems, we find similar switching costs for the optimal ratio between the spin-orbit torque coefficients. However, topological insulators offer the advantage of tunable material properties. Finally, we propose a robust and efficient simplified switching protocol using a down-chirped rotating current pulse, tailored to realistic ferromagnetic/topological insulator systems.

Introduction

Spin-orbit torque (SOT), a torque based on the conversion of charge current to spin current and interface spin accumulation via spin-orbit interaction, provides an efficient mechanism for electrical control of magnetization^1,2,3,4. Magnetization switching is an important application of the SOT^5,6 as it can be assigned to represent logical operations in nonvolatile information technologies. The challenge is to minimize the energy cost of the switching. An SOT-induced magnetization reversal can be realized by applying an in-plane current in a heavy-metal (HM) layer on which a switchable ferromagnetic (FM) element is placed. In this case, the SOT can originate from the inverse spin galvanic effect^7,8,9 and the spin Hall effect^{10,11,12,13,14} in the HM. Both mechanisms of such HM SOT give rise to fieldlike (FL) and dampinglike (DL) torques, whose geometrical forms coincide with those of the spin-transfer torque⁴. Conventional switching protocols rely solely on the DL SOT and utilize a unidirectional current^15,16, inherently requiring the application of an external magnetic field to achieve deterministic magnetization reversal^2,3,17. However, switching with much lower current densities can be achieved by using both in-plane components of the current¹⁸, also allowing for a field-free operation.

Analysis based on the optimal control theory has previously revealed a theoretical limit for the minimum energy cost of the SOT-induced magnetization reversal in the FM/HM system, identified the corresponding optimal switching current pulse as a function of the reversal time and relevant material properties, and uncovered a sweet-spot ratio of the FL and DL torques which allows one to achieve a particularly efficient switching by a down-chirped rotating current pulse¹⁹. The optimization of magnetization switching protocols is both fundamentally interesting and technologically important, as it enables the identification of the right combination of material properties for energy-efficient applications.

Topological insulators (TIs), i.e., materials characterized by an insulating energy gap in the bulk and gapless edge or surface states protected by time-reversal symmetry^20,21,22,23, represent a promising alternative to HM systems in the context of electrical control of magnetization²⁴. The spin-momentum locking of the Dirac electrons at the surface of a TI results in a large charge-spin conversion, thereby enabling a significant SOT on an adjacent FM²⁴, hereafter referred to as Dirac or TI SOT. Remarkably, such SOT has a different geometrical form compared to the one found in HM systems²⁵, affecting the magnetization dynamics²⁶. It is therefore interesting to explore how much the Dirac SOT-induced magnetization dynamics can be optimized and whether using TI systems offers benefits for achieving energy-efficient magnetization switching.

In this article, we present a complete analytical solution to the problem of energy-efficient magnetization switching in an FM insulator nanoelement with perpendicular magnetic anisotropy (PMA) by means of Dirac SOT realized in TI systems. We show that the optimal switching protocol, i.e., the protocol that minimizes the energy cost associated with Joule heating, involves both in-plane components of the surface current whose time dependence is determined by the materials’ properties and the switching time. In this optimal scenario, the magnetization reversal is deterministic and does not require any external magnetic field. We obtain noteworthy exact dependencies concerning the optimal switching and compare them with the results obtained earlier for the HM systems¹⁹. We demonstrate that the best scenario for magnetization switching is realized for vanishing DL Dirac SOT. For realistically small DL SOT, the optimal switching is achieved in a particularly simple protocol involving a down-chirped rotating current, which can be readily generated in experimental setups. Finally, we discuss various possibilities to tune the SOT coefficients to achieve the most efficient switching. We conclude that TI systems offer a convenient and robust platform for energy-efficient magnetization control, providing several advantages over other systems.

Results

Model

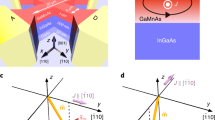
The simulated PMA nanoelement placed on the surface of a TI is illustrated in Fig. 1. The magnetic moment of the nanoelement is reversed by a surface current via Dirac SOT. The nanoelement is assumed to be small enough that its magnetization remains essentially uniform during the reversal process (single-domain), as is the case for free nanocrystalline Y₃Fe₅O₁₂ particles with a critical size of about 190 nm²⁷, but not so small that quantum correlations become significant²⁸, allowing the classical spin dynamics to remain a valid phenomenological model. We also assume the nanoelement to be a ferromagnetic insulator so as to ensure that the current flows mostly via the TI host²⁴. The energy E of the system is defined by the orientation of the nanoelement’s magnetic moment with respect to the anisotropy axis, which is perpendicular to the surface of the TI (see the reference frame in Fig. 1),

$$E=-K{s}_{z}^{2},$$

(1)

where s_z is the out-of-plane component of the normalized magnetic moment $\vec{s}$ and K > 0 is the anisotropy constant. We aim to identify the optimal current pulse that reverses the magnetic moment from s_z = 1 at t = 0 to s_z = − 1 at t = T, with T being the switching time. Both the amplitude and the direction of the current $\vec{j}$ on the surface of the TI are allowed to vary in time:

$$\vec{j}(t)=j(t)\left[\cos \psi (t),\sin \psi (t),0\right].$$

(2)

Fig. 1: Energy-efficient switching of a PMA nanoelement on a topological insulator.

The magnetization switching in the nanoelement is driven by Dirac spin-orbit torque induced by an optimal 2D electric current pulse (${\overrightarrow{j}}_{m}$) flowing at the surface of a topological insulator substrate. The calculated optimal control path for switching, with α = 0.1, ξ_D = ξ_F, and T = 50τ₀, is shown with the green line. The directions of the normalized magnetic moment $\overrightarrow{s}$ and the optimal current ${\overrightarrow{j}}_{m}$ are indicated by the blue and red arrows, respectively.

The efficiency of reversal is naturally defined by the amount of Joule heating generated in the resistive circuit during the switching process²⁹. In particular, the optimal reversal is achieved when the cost functional

$$\Phi =\mathop{\int}\nolimits_{0}^{T}| \vec{j}{| }^{2}dt,$$

(3)

is minimized. This optimal control problem is subject to a constraint imposed by the zero-temperature Landau-Lifshitz-Gilbert (LLG) equation describing the dynamics of the magnetic moment induced by the Dirac SOT²⁵:

$$\begin{array}{ll}\dot{\vec{s}}\,=\,-\gamma \vec{s}\times \vec{b}+\alpha \vec{s}\times \dot{\vec{s}}\\ \qquad+\gamma {\xi }_{F}\vec{s}\times (\vec{j}\times {\hat{e}}_{z})+\gamma {\xi }_{D}{s}_{z}(\vec{s}\times \vec{j}).\end{array}$$

(4)

Here, γ is the gyromagnetic ratio, α is the damping parameter, ${\hat{e}}_{z}$ is the unit vector along the z axis, and $\vec{b}$ is the anisotropy field: $\vec{b}\equiv -{\mu }^{-1}\partial E/\partial \vec{s}$, with μ being the magnitude of the magnetic moment. The third and the fourth terms on the right-hand side of Eq. (4) represent the FL and DL components of the SOT, respectively, where we note a fundamental difference in the geometrical form of the DL component from that realized in FM/HM systems ($\propto \vec{s}\times [\vec{s}\times (\vec{j}\times {\hat{e}}_{z})]$)⁴. The coefficients ξ_F and ξ_D can be written in terms of microscopic parameters of the system^4,25. Both ξ_D and ξ_F are assumed to be independent of $\vec{s}$. The validity of this assumption is discussed in Section “Tunability of SOT coefficients”. Moreover, the effect of the Oersted field generated by $\vec{j}$ is neglected in Eq. (4) as it is by 3-4 orders of magnitude smaller than the typical anisotropy field (see Supplementary Note 6).

In what follows, we focus on how the ratio of the SOT coefficients influences the switching cost. Using the approach from our previous study¹⁹, we introduce the following parametrization:

$${\xi }_{F}=\xi \cos \beta ,\qquad {\xi }_{D}=\xi \sin \beta ,$$

(5)

where $\xi =\sqrt{{\xi }_{F}^{2}+{\xi }_{D}^{2}}$ is the magnitude of SOT and β is a dimensionless parameter characterizing the proportion between its components.

Optimal magnetization switching

To find the optimal switching current ${\vec{j}}_{m}(t)$ (throughout this article, quantities indexed with m represent optimal values corresponding to the minimum energy cost of switching), we first express Φ in terms of the switching trajectory and then minimize it so as to find the optimal control path (OCP) ${\vec{s}}_{m}(t)$ for the switching process; after that, ${\vec{j}}_{m}(t)$ is derived from the OCP. A similar procedure was applied previously in the context of magnetization switching induced by an applied magnetic field³⁰ and SOTs in HM systems¹⁹. Here, we briefly report the main expressions, but a complete analytical solution can be found in Supplementary Note 1.

We first notice that the direction ψ of the optimal switching current [see Eq. (2)] can be written as a function of the spherical coordinates θ and φ of the magnetic moment $\vec{s}$ (see Fig. 1 and Supplementary Note 1):

$$\psi =\varphi -\arctan \left[\frac{\cos \theta \left(\alpha \cos \beta +\sin \beta \right)}{\cos \beta -\alpha\,{\cos }^{2}\theta \sin \beta }\right].$$

(6)

It follows from Eqs. (4) and (6) that the time-dependent amplitude of the optimal current can be expressed in terms of θ and $\dot{\theta }$ as

$$j={j}_{0}\frac{\left(1+{\alpha }^{2}\right){\tau }_{0}\dot{\theta }+\alpha \sin \theta \cos \theta }{\sqrt{(1+{\alpha }^{2}{\cos }^{2}\theta )(1-{\sin }^{2}\theta \,{\sin }^{2}\beta )}},$$

(7)

where j₀ = K(μξ)⁻¹ and ${\tau }_{0}=\mu {\left(2K\gamma \right)}^{-1}$. Equation (7) indicates that the current amplitude is the lowest for β = 0 and β = π leading to the most energy efficient switching. On the other hand, for β = π/2 and β = 3π/2 the switching is impossible as the current amplitude is infinite at the top of the energy barrier (θ = π/2). This is a consequence of the geometrical form of the Dirac SOT, for which the DL torque vanishes for an in-plane orientation of the magnetic moment. Notably, the current amplitude is independent of the azimuthal angle φ. As a result, the energy cost of switching, Φ, is a functional of the polar angle θ alone, which simplifies the minimization.

We are interested in minimizing the cost functional Φ defined in Eq. (3) with the boundary conditions of θ(0) = 0, θ(T) = π. The solution to the corresponding Euler-Lagrange equation for θ(t) is expressed in terms of Jacobi elliptic functions³¹. Subsequently, j_m(t) is obtained from Eq. (7). Next, φ_m(t) is calculated via direct integration of the equation of motion and ψ_m(t) is obtained using Eq. (6). Regardless of the system parameters, the OCP always crosses the energy barrier θ_m = π/2 at t = T/2 which is a result of a more general symmetry ${\theta }_{m}\left(T/2+{t}^{{\prime} }\right)=\pi -{\theta }_{m}\left(T/2-{t}^{{\prime} }\right)$, for $0\le {t}^{{\prime} }\le T/2$.

According to Eq. (6), the current rotates following the magnetic moment as it precesses around the anisotropy axis, gradually changing its frequency. The exact expressions for the frequency and amplitude are quite complex (see the Supplementary Note 1 for details), but an analytical expression for the average current amplitude has a relatively simple form:

$$\langle {j}_{m}\rangle =\frac{2\left(1+{\alpha }^{2}\right){\mathcal{K}}\left[{\sin }^{2}\beta +{\alpha }^{2}{\cos }^{2}\beta \right]}{\xi \gamma T},$$

(8)

where ${\mathcal{K}}[x]=\mathop{\int}\nolimits_{0}^{\pi /2}dr{\left(1-x{\sin }^{2}r\right)}^{-1/2}$ is the complete elliptic integral of the first kind. Note that the average current is independent of K. Similar to our earlier findings on the average current¹⁹ and magnetic field³⁰, the independence of 〈j_m〉 from K arises from the cancellation of the anisotropy field’s relaxation contribution during the switching process. Specifically, this field opposes switching for θ < π/2 but facilitates reaching the final state for θ > π/2, leading to a net null effect. However, the anisotropy does affect the amplitude of the optimal current: for large K, j_m(t) is a sharp (localized in time) and large pulse, while for small K, it becomes time independent.

For α = 0, Eq. (8) matches the average current $\langle {j}_{m}^{{\rm{HM}}}\rangle$ obtained in ref. ¹⁹ for FM/HM systems. Assuming the same values of ξ and T for both FM/HM and FM/TI systems, the ratio $\langle {j}_{m}\rangle /\langle {j}_{m}^{{\rm{HM}}}\rangle$ stays close to unity for α < 10⁻² and for β values in the range $[0,\frac{\pi }{2})$. However, for α > 10⁻², 〈j_m〉 can become much smaller or much larger than $\langle {j}_{m}^{{\rm{HM}}}\rangle$, depending on the value of β. The analytical expression for $\langle {j}_{m}\rangle /\langle {j}_{m}^{{\rm{HM}}}\rangle$ and its dependency on α and β are given in the Supplementary Note 3 and Supplementary Fig. 2, respectively.

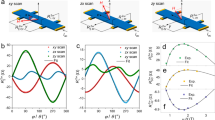
Figure 2 shows the j_m(t) profiles as functions of the reduced time t/T for various values of the switching time T, considering vanishing DL torque (β = 0). As α increases, the difference between the maximum and minimum values of j_m becomes more pronounced. These extremal values of j_m occur at specific points in time: the maximum at t/T = 1/4 and the minimum at t/T = 3/4. For zero damping, the current amplitude is time independent.

Fig. 2: Optimal switching current.

a–c Calculated amplitude of the optimal switching current as a function of time for several values of the damping parameter and switching time, as indicated in the legend; (d) Calculated magnitude and in-plane components of the optimal switching current as functions of time for T = 60τ₀ and α = 0.1. In all cases β = 0, which corresponds to the lowest energy cost of switching. The color scale, ranging from dark to bright, represents increasing total switching time.

Minimum energy cost of magnetization switching

As in the previously studied cases^19,30, Φ_m monotonically decreases with T and demonstrates two distinct asymptotic behaviors. For short switching times, $T\ll \left(\alpha +1/\alpha \right){\tau }_{0}$, the contribution from the internal dynamics driven by the anisotropy becomes negligible and the solution approaches that of a free magnetic moment, resulting in

$${\Phi }_{0}=\frac{4{(1+{\alpha }^{2})}^{2}{{\mathcal{K}}}^{2}[1-(1+{\alpha }^{2}){\cos }^{2}\beta ]}{{\xi }^{2}{\gamma }^{2}T}.$$

(9)

On the other hand, for T → ∞ the energy cost approaches a lower limit of

$${\Phi }_{\infty }=\frac{4\alpha K(1+{\alpha }^{2})\ln \left[(1+{\alpha }^{2}){\cos }^{2}(\beta )\right]}{\gamma \mu {\xi }^{2}\left[(1+{\alpha }^{2}){\cos }^{2}(\beta )-1\right]}.$$

(10)

The intersection of these asymptotics gives an optimal switching time T_opt for which a balance between switching speed and energy efficiency is achieved. When β = 0, T_opt (see Supplementary Note 2) coincides with that found for FM/HM systems¹⁹, which has the simple approximate form

$${T}_{{\rm{opt}}}\approx \frac{(1+{\alpha }^{2}){\pi }^{2}}{2\alpha }{\tau }_{0},$$

(11)

correct within 2.5% for 0 < α ≤ 1. Note that Eq. (11) implies that T_opt≥ π²τ₀ ≈ 10τ₀ when α = 1. For arbitrary values of β, T_opt can differ significantly from that obtained for the FM/HM case, especially if α → 1 and/or β → π/2. A complete comparison between the optimal switching times for both Dirac and HM SOT, considering various values of α and β, can be found in Supplementary Fig. 1.

Φ_m as a function of the inverse switching time is shown in Fig. 3, where we assume the optimal values of β ($\beta =-\arctan \alpha$ for FM/HM¹⁹ and β = 0 for FM/TI). As can be seen in the inset, the energy efficiencies of switching are very similar for both SOT types. This can be explained by the fact that the optimal switching relies mostly on the FL torque in both cases, and its form is the same in the models describing FM/TI [Eq. (4)] and FM/HM¹⁹ systems. However, the former presents only a slightly higher cost for switching because, in an FM/HM configuration, the DL torque can compensate for relaxation, whereas in an FM/TI system with Dirac SOT it cannot. For typical values of α, and even larger (see Supplementary Note 5), this difference in switching cost between the Dirac and HM SOT is small (≈4% when α = 0.3). At the same time, topological insulators, a priori, have the advantage of channeling the whole current through the surface instead of in the bulk, while electrons present a spin orientation fixed by their direction of motion (although real materials may exhibit some bulk conduction due to unintentional doping from vacancies, antisite defects, and other imperfections³²). This leads to an increased spin-torque efficiency, as demonstrated by experiments^24,33.

Fig. 3: Dependence of the minimum energy cost of magnetization switching on switching time.

Calculated minimum energy cost Φ_m of magnetization switching induced by Dirac SOT as a function of 1/T for various values of the damping parameter as indicated in the legend. Dotted and dashed lines show the long and short switching time asymptotics, respectively. Inset: comparison of Φ_m for the Dirac and HM spin-orbit torques for α = 0.3. In all cases, β is chosen to minimize the switching cost: β = 0 for Dirac SOT and $\beta =-\arctan \alpha$ for HM SOT.

Away from the optimal regime of β = 0, i.e., when ξ_D becomes finite in Dirac-SOT systems (expected to be common experimental situations), an optimal protocol still exists; in this case, both Φ_m and ${\vec{j}}_{m}$ can be directly calculated with the Supplementary Code available in Zenodo³⁴.

There is a strong dependence of Φ_m on the β parameter, as shown in Fig. 4. As predicted from Eq. (7), we obtain the lowest energy cost for β = 0 and β = π, while for β = π/2 and β = 3π/2 the cost diverges to infinity, indicating that switching is not possible using just SOT. Unlike the HM SOT, the optimal value of β and the value at which switching becomes impossible are independent of α for TI SOT. Nevertheless, both cases exhibit very similar dependencies of the switching cost on β. However, they are offset by $\Delta \beta =\arctan \alpha$ relative to one another, due to the differing geometrical forms of the DL torque component.

Fig. 4: Dependence of the minimum energy cost of magnetization switching on the ratio of the SOT coefficients.

The calculated minimum energy cost of magnetization switching Φ_m as a function of β for α = 0.3 and T = 20τ₀ (black lines) and T → ∞ (blue lines), considering two different spin-orbit torques: Dirac (solid lines), and HM SOT (dashed lines). The red dotted line corresponds to the ratio of the DL and FL parameters ratio at which no switching occurs for the HM SOT.

Tunability of SOT coefficients

Having analyzed the lowest energy cost and corresponding currents ${\vec{j}}_{m}(t)$ and identified the optimal ratio of the SOT coefficients β = 0, we now link β to the physical parameters of an FM/TI system and briefly explore their potential tunability.

The coefficients of the SOT acting on a magnet as a result of current flowing at the surface of a TI are given by the following equations²⁵:

$${\xi }_{F}\approx e\rho \frac{{J}_{xc}\tau {\varepsilon }_{F}}{\pi {\hslash }^{2}{v}_{F}\gamma },\,{\rm{and}}\,{\xi }_{D}\approx -e\rho \frac{2{J}_{xc}^{2}}{\pi \hslash {v}_{F}{\varepsilon }_{F}\gamma },$$

(12)

where e > 0 is the elementary charge, ℏ the reduced Planck constant, J_xc the exchange coupling between the FM and the TI, τ the charge carrier scattering time, and ε_F and v_F are the Fermi energy and Fermi velocity, respectively. The exchange parameter describes the coupling between the magnetization of the FM and the out-of-equilibrium Dirac state spin density on the surface of the adjacent TI. This is an interface property that depends on the specific materials used, but it can also be tuned by interface engineering^35,36. When J_xc/ε_F ≪ 1, both ξ_F and ξ_D become approximately independent of the magnetization state²⁵; this regime can be achieved in real systems (see discussion in Supplementary Note 5). In turn, the sample composition and quality determine both τ and v_F. Here, we assume an electric field $\vec{E}=\rho \vec{j}$, where ρ is some relevant surface resistivity. Interestingly, in a normal 2D system with Rashba spin-orbit coupling (SOC), the SOT takes the same form as in Eq. (12) when J_xc ≪ α_Rk_F, with α_R being the Rashba coupling parameter³⁷.

Comparing Eqs. (5) and (12) reveals that the β parameter is connected to the microscopic quantities through the following equation:

$$\tan (\beta )=\frac{-2{J}_{xc}\hslash }{{\varepsilon }_{F}^{2}\tau },$$

(13)

and the magnitude of the total SOT is given by

$$\xi =\left| \frac{{J}_{xc}}{\pi \hslash {v}_{F}}\frac{e\rho }{\gamma }\right| \sqrt{{\left(\frac{{\varepsilon }_{F}\tau }{\hslash }\right)}^{2}+{\left(\frac{2{J}_{xc}}{{\varepsilon }_{F}}\right)}^{2}}.$$

(14)

The β parameter does not explicitly depend on v_F, but ξ is, however, inversely proportional to v_F. By applying strain³⁸, or external gate voltages³⁹, the value of the Fermi velocity can be modified, and in some cases made asymmetric³⁸. The torque parameters in Eq. (12) only contain the Fermi surface contribution, relevant when the Fermi energy is in the gap. For ε_F closer to bulk bands, additional terms appear due to, e.g., hexagonal warping – which can be thought of as the counterpart of the cubic Dresselhaus coupling –^40,41, and spin-transfer torque due to bulk states^41,42,43, but these are beyond the scope of this article.

The β parameter depends on J_xc, τ, and ε_F, as shown in Eq. (13). A way to tune the exchange coupling and electron scattering time is by choosing different materials or via interface engineering^35,36. For example, τ can be controlled by selecting different impurity types, which create distinct scattering potentials²⁵. In turn, J_xc can be tuned by shifting the Fermi level⁴⁴. Finally, ε_F can be readily controlled in TIs by gate voltages, through electron density changes, or even light pulses⁴⁵; in HM systems, however, the Fermi energy is fixed.

In case of FM/HM systems, the ratio between the torque coefficients can be obtained from the model of an FM two-dimensional electron gas with Rashba SOC. This approach is commonly used as an archetypal free-electron model for SOT in ultrathin FM layers sandwiched between two distinct nonmagnetic materials³⁷. Within this model, the relationship between the torque coefficients in the context of the β-parametrization [see Eq. (5)] is determined by the following equation:

$$\tan ({\beta }^{{\rm{HM}}})=\frac{{J}_{xc}{\hslash }^{3}}{2{\varepsilon }_{F}\tau {\alpha }_{R}^{2}{m}^{* }},$$

(15)

where m* is the effective charge carrier mass. Here, the difference in the parametric dependence in Eqs. (13) and (15) is due to the distinct density of states in TI and HM systems; in particular, ${D}_{{\rm{TI}}}({\varepsilon }_{F})=\frac{1}{2\pi }\frac{{\varepsilon }_{F}}{{\hslash }^{2}{v}_{F}^{2}}$ for TIs and ${D}_{{\rm{HM}}}({\varepsilon }_{F})=\frac{{m}^{* }}{\pi {\hslash }^{2}}$ for Rashba HM systems. The high electron densities in FM/HM multilayers make it difficult to tune either α_R⁴⁶ or ε_F.

A simplified switching protocol

In general, the optimal switching current exhibits a complex, non-linear modulation of both frequency and amplitude (see Figs. 2 and 5). This raises the question of whether a simpler, more practical switching protocol can be developed – one that is easier to reproduce experimentally while maintaining energy efficiency close to that of the optimal protocol. In this context, we first point out that the optimal switching current maintains an almost constant amplitude in the low damping regime (see Fig. 2). Simultaneously, when the DL torque vanishes and T = T_opt ≳ 10τ₀, the time dependence of the frequency is nearly linear over most of the time domain (see Fig. 5). Motivated by these observations, we focus on a protocol that involves the following down-chirped rotating current:

$${\vec{j}}_{s}(t)=A\left[\cos {\psi }_{s}(t),\sin {\psi }_{s}(t),0\right]$$

(16)

where A is a time-independent amplitude and ${\psi }_{s}(t)={\omega }_{0}\left(t-{t}^{2}/T\right)$, with ω₀ being the initial angular frequency. Its rotation frequency is thus defined as

$$f(t)=\frac{1}{2\pi }\frac{d{\psi }_{s}}{dt}=\frac{{\omega }_{0}}{2\pi }\left(1-\frac{2t}{T}\right).$$

(17)

Fig. 5: Frequency of the optimal switching current.

The calculated frequency of the optimal switching current as a function of time for β = − 1, 0, 1 (blue, green, and red curves, respectively) for α = 0.1 and T = 20τ₀. The dashed black line represents the frequency f(t) of the simplified pulse given by Eq. (17).

Although chirped signals have not yet been applied to field-free magnetization switching via current pulses, they have been successfully utilized in microwave photonics^47,48. These well-established techniques could provide valuable insights for generating current pulses similar to those described by Eq. (16).

The initial frequency was chosen so that the quantity d²ψ_s/dt² roughly coincides with that of the optimal pulse (namely d²ψ_m/dt²) near the energy barrier defined by the anisotropy – i.e., in the vicinity of t = T/2. In particular, we set ${\omega }_{0}=\pi /2\,{\tau }_{0}^{-1}$. Figure 5 illustrates an example of the computed frequency, in units of the resonant frequency ${f}_{r}\equiv {[2\pi {\tau }_{0}(1+{\alpha }^{2})]}^{-1}$, of the optimal pulses for distinct β values and T = 20τ₀, together with that proposed for the simplified pulse. Here, we clearly see that, when β strongly deviates from zero (e.g., β = ±1, shown by the red and blue curves), the optimal frequency becomes more non-linear over the time domain, and no longer aligns with the proposed rotation frequency [Eq. (17)]. Moreover, the cost functional for Eq. (16) reduces to Φ = A²T, which defines a lower bound on the amplitude, ${A}_{m}=\sqrt{{\Phi }_{m}/T}$, determined by the minimum energy cost Φ_m.

To test the magnetization switching using the simplified pulse, we performed direct time integration of the LLG equation (Eq. (4)) including a stochastic term to simulate the thermal noise, and considering $\vec{j}(t)={\vec{j}}_{s}(t)$ (see the Methods section). The temperature was chosen to yield a stability factor of 60¹⁹, defined as the ratio between the energy barrier and thermal energy, which represents a conservative lower threshold for a 10-year data retention time⁴⁹. In practice, MRAM systems typically require a stability factor of around 70 or higher⁴⁹. Additionally, the amplitude of the switching current was set to be close to A_m.

Figure 6 shows the calculated switching probability p_s as a function of β for T = 20τ₀, A = 0.4j₀, and several values of the damping parameter, namely α = {0.01, 0.05, 0.1, 0.3}, compatible with those found in FM/TI heterostructures (see Supplementary Note 5). As can be seen, the small realistic β values for α = 0.01 and α = 0.05 correspond to the plateau region with p_s ≈ 1. The switching probability decreases with α. Still, p_s ≳ 0.8 for α = 0.1. We note that for α = 0.01, using the values given in ref. ⁴², we find p_s ≈ 1 for α = 0.01 and A = 0.4j₀. Moreover, selecting an amplitude A just 10% greater than A_m (i.e., A ≈ 0.346j₀ in this case) results in a switching probability close to 100% near β = 0. This corroborates with the idea that ${\vec{j}}_{s}$ serves as an excellent model for the optimal pulse when β is sufficiently small.

Fig. 6: Magnetization switching probability in the simplified protocol.

The calculated switching probability p_s as a function of β for T = 20τ₀ and selected Gilbert damping values: for A = 0.4j₀ (solid lines) and for different choices of amplitude A (dotted lines). The red star and open black hexagon mark realistic β values for FM/TI systems, as discussed in Supplementary Note 5. Inset: A zoomed-in view of the range p_s ∈ [0, 10⁻²], where the results for α = 0.3 and A = 0.4j₀ become visible.

For the highest Gilbert damping analyzed, α = 0.3, the amplitude has to be increased to at least A = 0.6j₀ to reach p_s ≈ 0.8 – or ~50% larger than the value A_m for that value of α. Nevertheless, switching can be robustly achieved in various realistic setups (specifically considering the typical small α values for FM insulators when compared to FM metals – see Supplementary Note 5), while still ensuring an energy cost that remains close to the minimum value Φ_m. In this sense, we also note that no fine-tuning of the pulse duration is required.

Interestingly, the p_s(β) pattern exhibits a tilt, which is in contrast to the Φ_m(β) curve for which Φ_m(β) = Φ_m(− β) (see Fig. 4). This asymmetry of the switching pattern with respect to β arises from using a non-optimal switching current. This can be explained by analyzing the β-dependence of the polar component of the current-induced torque that drives the switching (see Supplementary Note 4). In particular, it can be shown that the symmetry with respect to β requires the frequency of the switching current to vanish at the top of the energy barrier regardless of the β value, a condition which is not satisfied for switching induced by the chirped current pulse (as demonstrated in Supplementary Fig. 3).

The simplified pulse proposed in Eq. (16) is effective for small β, as observed in certain FM/TI systems. For materials where β deviates strongly from zero, achieving reliable, field-free switching may require alternative pulse designs. In such cases, the pulse in Eq. (16) cannot ensure reliable switching on the timescale of moment oscillations (see Fig. 6). For Dirac-SOT systems with large β, the realization of efficient magnetization switching via down-chirped rotating current requires the β value to be reduced, e.g., via engineering of ε_F and τ. Although chirped pulses can induce slower reversals via the autoresonance mechanism⁵⁰, this approach is likely sensitive to thermal fluctuations, which may disrupt the frequency locking between the oscillator and the excitation.

Discussion

We investigated the energy-efficient switching process in a single macrospin controlled by external currents when subject to the Dirac SOT that is predicted to arise in FM/TI systems²⁵. We used the optimal control theory to obtain the energy-efficiency limits of Dirac SOT-induced magnetization switching in a PMA nanoelement at zero applied magnetic field and derived the optimal time-dependent switching current. We established that the FL component of the Dirac SOT is only responsible for switching and the energy cost is lowest for vanishing DL torque. This represents a fundamental difference to the HM SOT^4,19, arising typically in FM/HM systems, in which the DL torque may compensate for the relaxation and reduce the overall energy cost of the switching.

The obtained minimal switching cost is comparable to that obtained for the HM SOT¹⁹. Results for the respective types of SOTs coincide in the undamped case and the difference between them increases with increasing Gilbert damping. For the damping parameter values expected in the PMA nanoelement on a TI substrate, the energy cost difference is estimated to be less than ≈1% under the assumption of the same model parameters and respective optimal ratio of the torque coefficients for both SOT models. This shows that magnetic systems exhibiting Dirac SOT are not only viable candidates for memory elements, but present several advantages over FM/HM heterostructures, such as: (i) the tunability of the physical parameters, (ii) spin-momentum locking of electron states (which results in a large spin-charge conversion and improved SOT efficiency), and (iii) currents necessary for switching that are one order of magnitude lower, as realized in room temperature experiments^51,52, where the SOT efficiency reflects in a higher ξ parameter, and, thus, in a lower energy cost of switching.

Our analysis naturally has the same limitations as the model developed by Ndiaye et al.²⁵, primarily stemming from the assumption that the TI surface states remain unaffected in the presence of the FM layer (besides the time-reversal symmetry breaking and gap opening at the Diract point), and that transport is strictly two-dimensional, occurring solely on the surface of the TI. When these assumptions are not fully met, the introduction of an FM layer can lead to more complex scenarios. Examples for effects induced in the TI by magnetic impurities or interface with metallic ferromagnets can be found in refs. ^{53,54,55,56,57}, where it is shown that the Dirac cone can be shifted downwards in energy, and the existence of additional metallic bands with Rashba-like character is favored across the Fermi level. Similar conclusions can be found in the case of interfaces with magnetic insulators (see, e.g., ref. ⁵⁸ for a theoretical investigation on MnSe/Bi₂Se₃). Moreover, Mahfouzi et al.⁵⁹ report a non-trivial dependence of the SOT coefficients on the magnetization direction. Another limitation of the present investigation is the presence of surface roughness, which is known to be relevant in topological insulators. On a global scale, this effect can be partially accounted for phenomenologically by adjusting the scattering time parameter τ. On a local scale, surface roughness may introduce additional inhomogeneities in the magnetization, particularly in the vicinity of the interface – an effect that falls beyond the scope of the present macrospin approach. Investigating both the dependence of the SOT coefficients on the magnetization direction and the spatially varying magnetization profiles induced by interface imperfections within the framework of the optimal control theory is a subject for future research.

Finally, we propose a simplified protocol based on a down-chirped rotating current pulse, which can be more accessible to experiments. This protocol was tested through simulations of the stochastic LLG equation, and the results demonstrate its efficiency and robustness across a range of realistic β values. These theoretical predictions motivate experimental validation.

Methods

Magnetization dynamics simulations

The simplified switching protocol is simulated through direct time integration of the Landau-Lifshitz-Gilbert equation:

$$\dot{\vec{s}}=\frac{\gamma }{1+{\alpha }^{2}}\vec{{\mathcal{T}}}+\frac{\alpha \gamma }{1+{\alpha }^{2}}\vec{s}\times \vec{{\mathcal{T}}},$$

(18)

where the torque $\vec{{\mathcal{T}}}$ is defined by the following equation:

$$\vec{{\mathcal{T}}}=\vec{s}\,\times \left[-\left(\vec{b}+{\vec{b}}^{{\rm{fl}}}\right)+\xi \cos \beta \left({\vec{j}}_{s}\times {\hat{e}}_{z}\right)+\xi \sin \beta \,{s}_{z}{\vec{j}}_{s}\right].$$

(19)

Here, ${\vec{b}}^{{\rm{fl}}}$ is a stochastic magnetic field that mimics the interaction with the heat bath. ${\vec{b}}^{{\rm{fl}}}$ is modeled as uncorrelated Gaussian white noise characterized by the following properties:

$$\langle {b}_{k}^{{\rm{fl}}}(t)\rangle =0,$$

(20)

$$\langle {b}_{k}^{{\rm{fl}}}(t){b}_{l}^{{\rm{fl}}}(0)\rangle =2D{\delta }_{kl}\delta (t),$$

(21)

where 〈⋅〉 denotes ensemble averaging, the indices k and l refer to the Cartesian components of ${\vec{b}}^{{\rm{fl}}}$, and the parameter D, which characterizes the amplitude of the stochastic field, reflects the system’s temperature via the fluctuation-dissipation theorem⁶⁰. A semi-implicit algorithm proposed by Mentink et al.⁶¹ is used to integrate Eq. (18), with a time step of 0.02τ₀.

Each simulation consists of three phases: (i) an initial phase with no applied pulse, during which local thermal equilibrium is established; (ii) a measurement phase, which includes thermal fluctuations, during which the simplified current pulse is applied over the time interval T; and (iii) a final phase of thermal equilibration with no applied current. After step (iii), the switching event is considered successful if s_z < −0.5, and the switching probability p_s is defined as¹⁹

$${p}_{s}=\frac{{N}_{s}}{N},$$

(22)

where N_s is the number of successful switching events, and N is the total number of simulations. We choose N = 2000, which ensures that the shape of the resulting p_s curve as a function of β is properly converged.