Probing polarization-tunable sub-terahertz spin pumping in bimodal α-Fe₂O₃/Pt

Abstract

Hematite (α-Fe₂O₃) is an insulating antiferromagnet possessing a room temperature canted phase induced by the super-exchange Dzyaloshinskii-Moriya Interaction (DMI), resulting in enhanced spin pumping and spin transport over uniaxial antiferromagnets. In this work we resonantly excite the quasi-ferromagnetic (acoustic) and purely antiferromagnetic (optical) spin-dynamical modes in bulk and thin-film heterostructures of α-Fe₂O₃/Pt at room temperature, inducing inverse-spin-Hall-voltages up to 255 GHz. Following recent measurements of optical-mode spin-pumping in α-Fe₂O₃, we observe a novel and exotic microwave polarization mapping along with amplified spin-charge conversion in the optical branch and discuss the implications of layer thickness on acoustic and optical spin-modes. The results provide a deeper understanding of spin-wave selection rules for canted antiferromagnets and their potential use in nanoscale terahertz spintronics.

Introduction

Antiferromagnets (AFMs) are promoted as excellent candidates for the next generation of computing and telecommunications due to their diminishing stray fields, and THz frequency magnetization dynamics leading to × 10³ faster switching speeds than in ferromagnets. Moreover, the electrical manipulation of antiferromagnetic dynamics has rapidly progressed in recent years contributing to significant advancements in spintronics^1,2,3. Enhanced spin pumping in canted antiferromagnetic insulators possessing Dzyaloshinskii-Moriya Interactions (DMI) shows promise for increased sensitivity of electrical probing of the antiferromagnetic dynamics in the THz regime⁴. Indeed, in many easy-plane and canted insulating AFMs the high frequency optical mode resonances extend to several THz. In addition, the Néel vector directly contributes to pumped spin currents arising from the optical modes, in contrast to the previously studied acoustic modes which only involve the contribution from the dynamical magnetization^4,5,6,7,8,9. Thus, these systems present a purely antiferromagnetic means of generating THz radiation but with the spin polarization dictated by the direction of the canted magnetization, as opposed to uniaxial antiferromagnets, making them a viable alternative for the next generation of high-frequency oscillators.

The observation of spin-to-charge conversion out of the acoustic resonance modes of α-Fe₂O₃^4,5,6,7,8 and FeBO₃⁹ has established a precedence for canted antiferromagnets as candidates for AFM-based functional devices. Manipulation of and current generation from the high frequency optical modes in canted systems proves challenging due to their zero net rotational magnetization, unlike the net magnetizations characteristic of the acoustic modes or the dynamical net moment along the direction of the Neel vector in uniaxial AFMs. Ultrafast laser pulses have shown to effectively produce THz spin waves in canted AFMs¹⁰, however the underlying process is inherently off-resonant and lacks coherent control of the magnetic order, crucial for the proposed tunable THz resonators. Meanwhile, due to energy scale mismatch between the photons and magnons¹¹, optical excitation methods require very intense THz pulses^12,13,14,15, setting a damage threshold upper limit¹⁶ and, nonetheless, igniting incoherent spin dynamics arising from pulse-induced heating and fast demagnetization effects. Alternatively, spin precessions in insulating AFMs coupled to coherent microwave excitation are highly tunable with losses limited to the dynamical Gilbert damping and interface compensation inherent to the system¹⁷. While this method is typically limited to tens of GHz due to instrumental constraints, progress in solid state THz sources and detectors allows a quasi-optical implementation which can extend excitations into the THz regime^18,19, thus suitable for probing the optical modes.

Alpha-hematite (α-Fe₂O₃) is arguably the most well-studied canted insulating AFM. The presence of both DMI and an ultra-low Gilbert damping creates a diverse magnetic landscape for spintronics exploration. It is a multiferroic material²⁰ with a uniaxial phase below the Morin Transition temperature (T_m~260 K) due to its strong magnetoelastic coupling. In its canted phase, the DMI leads to elliptical resonant precessions of its sublattice magnetizations which enables enhanced spin pumping over easy-axis AFMs^4,17. Additionally, the DMI enhances the amplitude of efficient off-resonant THz transients²¹, making hematite a strong contender for integrated THz devices. In addition, the ultra-low magnetic damping (on the order of 10⁻⁵)^22,23,24,25 allows for tunable spin currents/magnons to propagate up to the micrometer range^26,27, proving its long range spin order to be robust.

Despite extensive and promising studies promoting hematite as a material for THz devices, there remains much to uncover. For instance, its high frequency mode has largely been neglected, with few reports of the resonance behavior available^25,28,29,30. This is due to experimental limitations on high microwave frequency generation alongside the polarization selectivity required to fully explore the optical modes. Recently we have reported spin current excitation in both acoustic and optical modes of hematite, exhibiting highly polarization selective spin pumping (i.e., the creation of spin current in the absence of a bias voltage). The study represents the first experimental evidence of coherent spin currents originating from the pure antiferromagnetic spin dynamical mode in an easy-plane antiferromagnetic material⁶. Therein we show that these modes are highly dependent on the polarization of the microwave magnetic field, which acts as a switch for the Inverse Spin Hall Effect (ISHE). This study follows some controversy in the literature regarding spin pumping from the optical branch of hematite reported by Hattori et al.⁷, where the non-observation of spin pumping from the optical mode was interpreted as a result of a cancelation between diagonal and off-diagonal terms in the spin-mixing conductance matrix. That conclusion has been proven incorrect with the report of coherent spin pumping from the optical mode in a bulk hematite-based heterostructure in our previous work⁶, where we also showed that the spin pumping fails to realize in thin film hematite-based heterostructures, likely explaining the absence of an optical mode signal in the original work by Hattori et al. To shed more light on this controversy, here we further explore the polarization dependence of both modes and compare the resulting rectifications in bulk and thin film samples. Contrary to the expected polarization-dependence patterns of the acoustic mode, our results provide an intricate behavior of the spin pumping signals originated from excitation of the purely antiferromagnetic optical mode, including non-sinusoidal patterns and magnetic field shifts of the corresponding resonance for different (linear to circular) microwave polarizations. The examination of these modes via finely tuned microwave polarization offers a unique experimental probe for the underlying physics related to spin-to-charge conversion in canted antiferromagnets. Simultaneously, understanding the excitation and tunability of high order magnons down to the thin film becomes crucial for the development of practical terahertz oscillators in easy-plane AFMs. We note that no coherent spin pumping has been reported yet from a purely antiferromagnetic mode in thin film antiferromagnetic heterostructures. Determining whether this remains as an experimental challenge or stands a fundamental limitation of thin film antiferromagnets currently remains as a crucial topic for investigation.

Antiferromagnets are characterized by their opposing sublattice magnetizations, whose cancellation leads to a negligible net-magnetization within the lattice. AFMs possess small magnetic anisotropy fields whose energy contributions define how the magnetizations align themselves within lattice. The arrangement of sublattice magnetizations accompanying these fields defines several AFM subclasses. Uniaxial antiferromagnets possess a singular magnetic easy axis, a preferred direction along which the sublattice magnetizations align and prefer to precess during resonance. Examples include MnF₂, Cr₂O₃, and MnO. Easy-plane antiferromagnets, however, possess several degenerate easy axes, defining a preferred plane which the magnetizations will lie within rather than an axis. This is typical of materials with low in-plane magnetic anisotropy, and include, α-Fe₂O₃, NiO, NiF₂, and Sr₂IrO₄. Contrasting to the small anisotropy energies are large exchange fields (a.k.a. exchange-bias, antiferromagnetic exchange, or super-exchange) between the sublattice magnetizations. The exchange field establishes between non-neighboring magnetic ions, mediated through a nonmagnetic ion like Oxygen or Florine. It is the combination of small anisotropy and high exchange that yields the characteristic high-frequency dynamics of AFMs. Another energy contribution in certain AFMs is the Dzyaloshinskii-Moriya Interaction (DMI) or antisymmetric exchange, which adds an additional canting to the magnetic moments. Such AFMs with canted moments are known as canted antiferromagnets.

To predict the resonant frequencies of canted AFMs we seek a dispersion relation, relating the frequency to the externally applied magnetic field. This is traditionally done by minimizing the free energy of the magnetic system characterized by the two sublattice magnetizations. In the two-sublattice model, the system is represented by the two unit-vectors ${{\boldsymbol{m}}}_{{\boldsymbol{1}}}$ and ${{\boldsymbol{m}}}_{{\boldsymbol{2}}}$. For a DMI canted AFM the free energy can be written as⁵:

$$\begin{array}{rcl}\begin{array}{l}\varepsilon ={H}_{E}({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})-{H}_{D}\hat{z}\cdot ({{\boldsymbol{m}}}_{{\bf{1}}}\times {{\boldsymbol{m}}}_{{\bf{2}}})+\frac{{H}_{\perp }}{2}({{\rm{m}}}_{1,{\rm{z}}}^{2}+{{\rm{m}}}_{2,{\rm{z}}}^{2})\\ -\frac{{H}_{\parallel }}{2}({{\rm{m}}}_{1,{\rm{y}}}^{2}+{{\rm{m}}}_{2,{\rm{y}}}^{2})-{\boldsymbol{H}}\cdot ({{\boldsymbol{m}}}_{{\bf{1}}}+{{\boldsymbol{m}}}_{{\bf{2}}})\end{array}\end{array}$$

(1)

Where ${H}_{E}$ is the exchange field, ${H}_{D}$ is the antisymmetric exchange field, ${H}_{\perp }$ is the hard-axis anisotropy, ${H}_{\parallel }$ is the easy-plane anisotropy, and ${\boldsymbol{H}}$ is the externally applied magnetic field. Note that ${\boldsymbol{n}}$ and ${\boldsymbol{m}}$ can be used as the coupled moments in the LLG equations rather than ${{\boldsymbol{m}}}_{{\boldsymbol{1}}}$ and ${{\boldsymbol{m}}}_{{\boldsymbol{2}}}$, where ${\boldsymbol{m}}=\left({{\bf{m}}}_{{\bf{1}}}+{{\bf{m}}}_{{\bf{2}}}\right)/2$ is the normalized spin density (a.k.a. net magnetization) and ${\boldsymbol{n}}=\left({{\boldsymbol{m}}}_{{\boldsymbol{1}}}-{{\boldsymbol{m}}}_{{\boldsymbol{2}}}\right)/2$ is the Néel vector (a.k.a. antiferromagnetic ordering parameter). The derivation of the dispersion in this basis is known as the Sigma model. Following the work of Wang et al., 2021, we simplify the math by writing the free energy in terms of frequencies as⁴:

$$\varepsilon ={\omega }_{E}{{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}}+\frac{{\omega }_{\perp }}{2}\left[{\left(\hat{{\boldsymbol{z}}}\cdot {{\boldsymbol{m}}}_{{\bf{1}}}\right)}^{2}+{\left(\hat{{\boldsymbol{z}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}}\right)}^{2}\right]-\frac{{\omega }_{\parallel }}{2}\left[{\left(\hat{{\boldsymbol{y}}}\cdot {{\boldsymbol{m}}}_{{\bf{1}}}\right)}^{2}+{\left(\hat{{\boldsymbol{y}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}}\right)}^{2}\right]$$

$$-{{\boldsymbol{\omega }}}_{{\boldsymbol{D}}}\hat{{\boldsymbol{z}}}\cdot \left({{\boldsymbol{m}}}_{{\bf{1}}}\times {{\boldsymbol{m}}}_{{\bf{2}}}\right)-{{\boldsymbol{\omega }}}_{{\boldsymbol{H}}}\hat{{\boldsymbol{x}}}\cdot \left({{\boldsymbol{m}}}_{{\bf{1}}}+{{\boldsymbol{m}}}_{{\bf{2}}}\right)$$

(2)

where $\omega =\,\gamma H$ has been used to replace the respective fields, and$\,\frac{\gamma }{2\pi }\,=\,28{MHz}/{Oe}$ is the gyromagnetic ratio. By assuming that all contributions are small compared to the exchange field, the minimized free energy yields a canted equilibrium state in the form:

$$\bar{{\boldsymbol{m}}}\approx \frac{{\omega }_{D}+{\omega }_{H}}{{\omega }_{E}}\hat{{\boldsymbol{x}}}$$

(3)

where $\bar{{\boldsymbol{m}}}$ is a small net magnetization in the canted ground state, and the canting angle is defined by $\phi \approx \frac{{\omega }_{D}+{\omega }_{H}}{2{\omega }_{E}}$. The Landau-Lifshitz-Gilbert Equation describing the motion of a magnetic moment, ${\boldsymbol{M}}$, in a magnetic field is:

$$\frac{d{\boldsymbol{M}}}{{dt}}=-\gamma {\boldsymbol{M}}\times {{\boldsymbol{H}}}_{{\boldsymbol{eff}}}+\alpha {\boldsymbol{M}}\times \frac{d{\boldsymbol{M}}}{{dt}}$$

(4)

where the motion about the effective field, ${{\boldsymbol{H}}}_{{\boldsymbol{eff}}}$, is scaled by the gyromagnetic ratio and the Gilbert damping coefficient $\alpha$, whose contribution is intrinsic to the system. For exciting magnetic resonance, we introduce the microwave magnetic field torque, and arrive at two coupled LLG equations:

$$\dot{{{\boldsymbol{m}}}_{1}}={{\boldsymbol{m}}}_{{\bf{1}}}\times \left[{\omega }_{E}{{\boldsymbol{m}}}_{{\bf{2}}}+{\omega }_{\perp }\hat{{\boldsymbol{z}}}-{\omega }_{\parallel }\hat{{\boldsymbol{y}}}+{\omega }_{D}\hat{{\boldsymbol{z}}}\times {{\boldsymbol{m}}}_{{\bf{2}}}-{\omega }_{H}\hat{{\boldsymbol{x}}}\right]+\alpha {{\boldsymbol{m}}}_{{\bf{1}}}\times \dot{{{\boldsymbol{m}}}_{1}}+\gamma {{\bf{h}}}_{{\bf{rf}}}\times {{\boldsymbol{m}}}_{{\bf{1}}}$$

(5)

$$\dot{{{\boldsymbol{m}}}_{2}}={{\boldsymbol{m}}}_{{\bf{2}}}\times \left[{\omega }_{E}{{\boldsymbol{m}}}_{{\bf{1}}}+{\omega }_{\perp }\hat{{\boldsymbol{z}}}-{\omega }_{\parallel }\hat{{\bf{y}}}-{\omega }_{D}\hat{{\boldsymbol{z}}}\times {{\boldsymbol{m}}}_{{\bf{1}}}-{\omega }_{H}\hat{{\boldsymbol{x}}}\right]+\alpha {{\boldsymbol{m}}}_{{\bf{2}}}\times \dot{{{\boldsymbol{m}}}_{2}}+\gamma {{\boldsymbol{h}}}_{\text{r}{\bf{f}}}\times {{\boldsymbol{m}}}_{{\bf{2}}}$$

(6)

These now define an eigenvalue problem whose solutions have been reported extensively^4,5,31,32,33 and are given by two modes:

$${\omega }_{0}=\sqrt{{\omega }_{H}\left({\omega }_{H}+{\omega }_{D}\right)+2{\omega }_{E}{\omega }_{\parallel }}$$

(7)

$${\omega }_{1}=\sqrt{{\omega }_{D}\left({\omega }_{H}+{\omega }_{D}\right)+2{\omega }_{E}{\omega }_{\perp }}$$

(8)

These dispersions describe the two resonance modes for canted antiferromagnets in the weak ferromagnetic phase, which for hematite exists in ambient conditions. The ${\omega }_{0}$ mode, or the acoustic mode is low frequency and for hematite at low fields resonates around 13 GHz. The ${\omega }_{1}$ mode, or the optical mode, is higher frequency, resonating around 160 GHz at low fields. A more general solution for a field applied along an arbitrary direction is given by Elliston (1968)³¹. For the findings in this text, we will make the small angle approximation, assuming a good alignment of the AFM easy plane with the magnetic field.

In the early days of spintronics it was predicted that externally driving a magnetically ordered system would produce a flow of spin-polarized current without the application of a bias voltage, the effect known as spin-pumping³⁴. This theoretically is analogous to quantum charge pumping³⁵. For the case of an AFM/NM bilayer, the quantum analogy holds as the pumping effect takes place at the interface within the quantum decoherence length scale. The spin current generated in a two-sublattice antiferromagnet has been derived as a result of time-dependent scattering processes³⁶ and more recently the same result has been shown in a static Néel parameter frame³⁷. The pumped spin current is expressed as:

$$\frac{e}{\hslash }{I}_{s}={G}^{r}\left(n\times \dot{n}+m\times \dot{m}\right)-{G}^{i}\dot{m}$$

(9)

where ${G}^{r}$ and ${G}^{i}$ are the real and imaginary components of the interfacial spin mixing conductance, which characterizes the spin momentum reflected from and transmitted through the magnetic boundary and has been calculated by the tight binding model^36,38. The pumped spin current (9) has been widely used to model spin-pumping in both uniaxial and canted AFMs^4,19,39, although there has arisen some debate in the literature over the form of the spin mixing conductance. We will follow Tang and Cheng (2023)⁴⁰ in the expansion of the spin mixing conductance. In its most general form Eq. (9) can be expressed as:

$$\frac{e}{\hslash }{I}_{s}=\left(m,n\right)\times \left(\begin{array}{cc}{G}^{{mm}} & {G}^{{mn}}\\ {G}^{{nm}} & {G}^{{nn}}\end{array}\right)\left(\begin{array}{c}\begin{array}{c}\dot{m}\\ \dot{{\boldsymbol{n}}}\end{array}\end{array}\right)-{G}^{m}\dot{m}$$

(10)

and transforming into the sublattice basis gives:

$$\frac{e}{\hslash }{I}_{s}=\left({{\boldsymbol{m}}}_{{\bf{1}}},{{\boldsymbol{m}}}_{{\bf{2}}}\right)\times \left(\begin{array}{cc}{G}^{11} & {G}^{12}\\ {G}^{21} & {G}^{22}\end{array}\right)\left(\begin{array}{c}\begin{array}{c}\dot{{{\boldsymbol{m}}}_{1}}\end{array}\\ \dot{{{\boldsymbol{m}}}_{2}}\end{array}\right)-{G}^{1}\dot{{{\boldsymbol{m}}}_{1}}-{G}^{2}\dot{{{\boldsymbol{m}}}_{2}}$$

(11)

where ${G}^{11}$ = ${G}^{22}$ = ${G}^{r}/2$ are the intra-sublattice terms and together with ${G}^{1}$ = ${G}^{2}$ = ${G}^{i}/2$ relate the equation back to (9). The cross-sublattice (CS) terms ${G}^{12}$ = ${G}^{21}$ = 0 are traditionally considered non-contributing, however, several recent theoretical works^41,42,43 have proposed that these terms do indeed contribute to the scattering matrix and consequently spin-pumping and the reciprocal STT. The existence of the terms would imply modifications to the strength of the spin-pumping (addressed in Chapter 4 in the hematite case) and allow for spin-pumping in a fully compensated collinear AFM, whose inter-sublattice terms sum to zero. Tang and Cheng (2023) in their study have proven theoretically the absence of the CS contributions in collinear AFMs as well as only higher-order correction for noncollinear systems. In the following sections these concepts will be referred to and we will show the relevance of our results in supporting the traditional picture of the spin-mixing conductance.

At the barrier between a magnetic and a nonmagnetic material, spin and charge currents can be interchanged through phenomena known as the spin Hall effect (SHE) and inverse spin Hall effect (ISHE). When a spin-polarized current flows through a metallic layer, the spins will tend to separate transverse to the direction of current flow according to their polarization. Intrinsically this has been explained as a spin-dependent electron scattering mechanism, where spin momenta determine the scattering direction and an imbalance of polarizations produces a spin accumulation in one direction^44,45. Intrinsically, it has been shown that the topological band structures of spin-polarized electrons in the presence of an electric field will produce the effect⁴⁶. In an M/NM heterostructure the creation of charge current from pure spin current injection occurs when the spin current flows perpendicularly to the magnetic interface and couples to the HM layer through the electron orbitals, otherwise known as spin-orbit coupling (SOC). The coupling strength is dependent on the angular momentum, the fine-splitting, and the atomic number, and goes as $\sim {Z}^{4}$ for the spherical potential of a hydrogen-like atom⁴⁷. Heavier atoms with larger electron orbitals consequentially have better coupling. The efficiency of a material in transforming spin-current to charge current is given by the spin-Hall angle, ${\theta }_{\text{SH}}$, which increases with the coupling strength. Pt is often chosen for its large spin Hall angle (${\theta }_{\text{SH}}$ reported up to 8%⁴⁸) and relatively low cost, however even larger spin Hall angles are predicted for topological insulators due to spin-momentum locking^49,50. The relation between the spin and charge currents is given by:

$${J}_{c}={{\rm{\theta }}}_{\text{SH}}{J}_{s}\times {\rm{\sigma }}$$

(12)

where ${{\boldsymbol{J}}}_{{\boldsymbol{c}}}$ is the charge current density, ${{\boldsymbol{J}}}_{{\boldsymbol{s}}}$ is the spin current density and ${\boldsymbol{\sigma }}$ is the spin polarization. Through the ISHE in this way the polarized spin current from a resonantly pumped AFM can transform into a measurable charge current at an interface with an HM. The exact voltage obtained from such a device based off of a canted AFM is given by Cheng as:

$${V}_{\text{SP}}={\rm{\xi }}\widetilde{{g}_{r}}\frac{L{{\rm{\theta }}}_{\text{SH}}{\rm{\rho }}e}{2{\rm{\pi }}}\frac{{\rm{\lambda }}}{{d}_{N}}\tanh \left(\frac{{d}_{N}}{2{\rm{\lambda }}}\right){h}_{\text{rf}}^{2}$$

(13)

where L is the device length, λ is the spin diffusion length, ρ is the resistivity in the metal layer, and dN is the thickness of the metal layer. Here $\widetilde{{g}_{r}}$ is a separate effective spin mixing conductance term. The ${\rm{\xi }}$ term is related to the spin-susceptibility, which for uniaxial antiferromagnets is straightforward analytically and has been employed in experimental fittings¹⁹. For canted AFMs possessing DMI the analytical method becomes tedious and numerical methods have been chosen instead⁴, however, in other forms the analytical approach has been used in the canted AFM case^5,8. The power supplied by the rf magnetic field is given by:

$${P}_{\text{AC}}=\frac{c}{2}S{{\rm{\mu }}}_{0}\times {\left({h}_{\text{AC}}\right)}^{2}$$

(14)

Where $c$ is the speed of light, ${\mu }_{0}$ is the magnetic permittivity of vacuum, and $S$ is cross sectional area of the AFM. Equations (13) and (14) allow a linear relationship to be drawn between the ISHE voltage and the power supplied by the rf magnetic field. In this way a linear dependence on microwave power provides experimental support for the pure spin-current generation measured via ISHE.

Results

Spin-to-charge conversion through the magnetic landscape of hematite

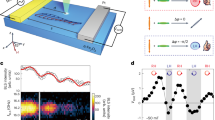
We choose c-plane α-Fe₂O₃ as our sample so that the basal plane (111) lies in the sample plane and the c-axis is perpendicular to the surface (Fig. 1a). The sample sits in a split-bore superconducting magnet, which applies a peak external magnetic field of up to 9 T. The sample circuit is contained within a variable-temperature insert with a 5 K base temperature, although all findings in this work were performed at room temperature. Figure 1b shows our device geometry, which remains the same for bulk (1 mm) and thin film (30 nm) heterostructures (See Methods for fabrication details).

Fig. 1: Polarization tunable antiferromagnetic resonance (AFMR) and inverse spin Hall effect (ISHE) measurement in α-Fe₂O₃/Pt heterostructures.

a Magnetic structure of α-Fe₂O₃. Red and blue arrows indicate oppositely polarized sublattice magnetizations. Green circles represent Iron atoms. Oxygen atoms are omitted for clarity. b Device geometry showing spin-to-charge conversion within α-Fe₂O₃ and schematic illustration of microwave polarization. c Room temperature resonant response (blue line) for 120 GHz microwave excitation and resulting ISHE voltage (orange line). d Field frequency mapping of the acoustic and optical resonance modes for both samples extracted from ref. ⁶. Solid (dashed) black lines are theoretical fits to the bulk (thin-film) signals. Error bars are extracted from the FWHM of peak.

At room temperature, α-Fe₂O₃ is in an easy-plane antiferromagnet state, where ${H}_{D}$ cants the sublattice Fe spins in the basal plane. Due to the canting, would-be linear oscillations of the sublattice moments assume an out-of-plane component leading to elliptical precessions. As the DMI field (${H}_{D}$) increases the precessions becomes increasingly circular, enhancing spin pumping efficiency⁴. Since linearly polarized spin dynamical modes do not generate spin pumping⁵¹, it is this effect of canting which allows the generation of spin currents. Moreover, the canted systems possesses a spin pumping enhancement over uniaxial antiferromagnets, theoretically shown to be a factor of sin³(θ), where θ is the canting angle¹⁷. When the external DC magnetic field is swept in the basal plane ($\vec{H}\,\perp \,\vec{z}$), the DMI allows for these high frequency elliptical magnetization precessions, whereas for $\vec{H}\,\parallel \,\vec{z}$ the DMI is diminished, resulting in a near-DC low-frequency resonance mode⁵². Thus, the former field orientation is chosen for our experiments.

We employ a quasi-optical method for high-frequency spin excitation, enabling sample irradiation with free-space microwaves ranging from 60 GHz to 1.5 THz without using a cavity or a resonator. In this scheme, a series of solid-state multipliers and microwave amplifiers is coupled to corrugated horn antennae creating a gaussian beam. The beam’s polarization state is determined before it is focused into the sample position (See Methods). The THz microwaves can propagate in two geometrical arrangements relative to the applied magnetic field ($\vec{x}$): Faraday ($\vec{k}\parallel \vec{x}$) and Voigt ($\vec{k}\perp \vec{x}$). The polarization state of the microwave (direction of the microwave field ${\vec{h}}_{{ac}}$) is controlled within the zy(xy) plane for the Faraday(Voigt) geometry and is determined by the phase difference, $\phi$, within a Martin-Puplett Interferometer (see ref. ¹⁸ for instrumentation details). The projections of the polarization states onto the sample are shown for both geometries in Fig. 1b. The polarization state can be transformed continuously from linear to right-handed or left-handed circular polarization through elliptically polarized states. See Figure (S4) for the shape of the microwave beam with respect to $\phi$. Here, references to microwave polarization will strictly refer to the direction of the microwave magnetic field ${\vec{h}}_{a{\rm{c}}}$. Both geometries are used to probe the polarization dependence of the resonance modes within the plane visible to the THz beam. The ISHE voltage, V_ISHE, is measured between two parallel gold leads with a lock-in amplifier triggered at a 94 kHz repetition rate, locked to the pulsing frequency of the microwave input. The room-temperature microwave absorption, as measured by the cross-polarized reflected component (S₁₁), and the corresponding V_ISHE for a 120 GHz $\vec{x}$-polarized excitation in the Voigt geometry as measured in a 1 mm thick sample are shown in Fig. 1c.

Figure 1d shows the dispersion for both mode branches as measured by AFMR and ISHE in bulk and thin film samples. Data is extracted from ref. ⁶. EPR absorption peaks and ISHE signals are observed for both acoustic and optical modes in the bulk sample, α-Fe₂O₃(1 mm)/Pt(5 nm). No EPR absorption is possible in the thin film sample, α-Fe₂O₃(30 nm)/Pt(5 nm), and ISHE signals are only observed for the acoustic branch as discussed in ref. ⁶ and below. For the dispersion mapping, all acoustic resonances are induced with $\vec{y}$-polarized microwaves (${\vec{h}}_{{ac}}\parallel \vec{y}$), while the optical resonance is only excited with $\vec{x}$-polarized microwaves (${\vec{h}}_{{ac}}\parallel \vec{x}$). Positive field traces are exclusively used in Fig. 1d. The resonant frequencies for the hematite acoustic and optical modes for an external field applied in the basal plane are given by^31,32:

$${f}_{0}=\left(\frac{{\rm{\gamma }}}{2{\rm{\pi }}}\right)\sqrt{2{H}_{E}{H}_{\Vert }+H\left(H+{H}_{D}\right)},$$

(15)

$${f}_{1}=\left(\frac{{\rm{\gamma }}}{2{\rm{\pi }}}\right)\sqrt{2{H}_{E}{H}_{\perp }+{H}_{D}\left(H+{H}_{D}\right)},$$

(16)

where γ is the gyromagnetic ratio, ${H}_{D}$ is the DMI field, ${H}_{E}$ is the exchange field, ${H}_{\parallel }$(${H}_{\perp }$) is the in-plane (out-of-plane) anisotropy. The details of the curve fittings and linewidth data for both samples are reported in the supplementary information of our previous report⁶. Therein we conclude that increased damping in the thin film along with lowered in-plane anisotropy evidences the intrinsic suppression of the optical mode in the thin film sample.

Recent results have shown that the ISHE generated from the acoustic and optical modes of α-Fe₂O₃ is highly polarization dependent, and that a 90° rotation of the rf-field acts as a switch to selectively excite one mode over the other⁶. This result directly follows directly from the theoretical picture of the orbital motions of the sublattice magnetizations and the resulting net magnetization and Néel order. In resonance, the microwaves coherently drive the sublattice magnetizations in elliptical orbits of opposing chirality. The major or minor axes of the orbits lie along the $\vec{z}$-axis corresponding to the acoustic (ω₀) and optical (ω₁) modes, respectively⁵³.The acoustic (optical) frequency mode is characterized by linear oscillations of the Néel vector (net magnetization) and coherent precessions of the net magnetization (Néel vector)^5,17,32. In other words, in the acoustic (optical) mode the magnetization (Néel vector) elliptically precesses. This exchange in dynamics between the magnetization and Néel vector is directly caused by this exchange of major and minor axes of the sublattice magnetizations in the two modes^6,33.

Pumped spin currents require that angular momentum be transferred from the precessing magnetization to the carrier electron spins⁵¹, i.e. an angular component in the spin dynamics must exist to pump spins into the interface. In the acoustic mode, spin angular momentum is transferred out of the elliptical orbit of $\vec{m}$ when the rf-field drives the orbit under the Lamor condition ${\vec{h}}_{{ac}}\perp {\,\vec{m}}_{0}$. However, for the optical mode, the small vibration of $\vec{m}$ about its equilibrium (${\vec{m}=\vec{m}}_{0}+\hat{x}\,\delta m\cos \omega t$), must be driven, requiring ${\vec{h}}_{{ac}}\parallel {\,\vec{m}}_{0}$. The requirement for spin-angular momentum transfer in this case implies that the coupled optical elliptical orbit of $\vec{n}$ pumps spin, although the resulting spin current polarization is directed along $\vec{m}$. When properly excited, spin currents propagate perpendicular to the Néel ordering parameter and perpendicular to the interface (in the $\vec{z}$-direction fixed by our device geometry) and generate a measurable voltage across the Pt capping layer via the ISHE.

Thus, careful consideration must be given to the system geometries in order to properly excite these polarization selective modes. For the sake of this experiment, it becomes useful to use the projections of magnetic structure as seen by the microwaves to understand how coupling occurs. For the acoustic mode excited in the Voigt geometry, the coupling to the equilibrium ordering parameter is theoretically maximized for y-polarized (180°) ${h}_{{ac}}$, since the Voigt projection of the magnetization precession lies along the $\vec{y}$-axis. While in the Faraday geometry the maximal driving polarization would match the highly elliptical precession of $\vec{m}$ projected in the zy-plane. For the optical mode, the coupling to the equilibrium magnetization is maximized for x-polarized (0, 360°) ${h}_{{ac}}$ in the Voigt geometry. No coupling in the optical mode can occur in the Faraday geometry since the vibration of $\vec{m}$ lies along the Poynting vector, inaccessible to the rf magnetic field.

Spin current polarization dependence in bulk hematite

The relationship between ${V}_{{\rm{ISHE}}}$ and the microwave polarization state for both modes is shown in Fig. 2. A 160 GHz microwave beam is chosen as an ideal frequency in our range for exciting both modes in a single field sweep. The beam propagates in the Voigt geometry so that it is incident to the sample surface and $\vec{k}\,\parallel \,\vec{z}$ (Fig. 1b). We vary the polarization state of the microwaves within a Martin-Puplett interferometer (MPI), with $\phi$ denoting the phase delay which alters the state. Polarization values of 0(180) degrees correspond to $x\left(y\right)$-polarized microwaves and 90(270) degrees corresponds to CW(CCW) circularly polarized microwaves in the xy-plane. Intermediate polarization angles correspond to varying degrees of ellipticity (Fig S4). Traces are taken continuously from −6 T to 6 T in 10° steps of ɸ. At 160 GHz, the optical resonance falls in the −1 to +1 T range, while the acoustic resonance appears at 4.65 T and −4.70 T, where the slight hysteresis is accounted for by the remanence associated with the field ramp direction. The acoustic ${V}_{{\rm{ISHE}}}$ signal follows the traditional field inversion polarity expected from time reversal symmetry for a mode with a well-defined net dynamical magnetic moment, while the optical signal remains positive under field inversion. For 160 GHz, the maximum ISHE signal is 27 nV for the acoustic mode, while a significantly higher ${V}_{{\rm{ISHE}}}$ of 85 nV is obtained from the optical mode. Indeed, higher conversion is seen in the optical mode across our entire frequency range, up to 180 nV for 170 GHz scans.

Fig. 2: Voigt polarization dependence of ISHE for both branches.

a Polarization contour map of ${VISHE}$ at 160 GHz. ɸ denotes the phase delay within one arm of a Martin-Puplett interferometer. High field features correspond to $\omega 0$ and low field features correspond to $\omega 1$. Traces are taken continuously from -6 T to 6 T in 10° steps. Black traces highlight the relative signal size of the features. b, c Theoretical planar projections of the magnetization dynamics of $\omega 0$ (b) and $\omega 1$ (c) from the perspective of the microwave beam. Dashed lines indicate the motion within the ${xy}$ plane. The canting angle of the magnetization and dynamic paths are exaggerated for visual clarity. d, e Polar plots of the signal maximums for the $\omega 0$ (d) and $\omega 1$ (e) modes for both field directions. In (d) blue and red lines are fits to a two-term tilted sine function.

To further understand the polarization dependence of the resonance modes, polar plots of the signal maxima are shown in Fig. 2d, e. The acoustic mode possesses a single lobe centered near 190° while the optical mode exhibits a bifold distribution. The acoustic mode is fitted to a two-term tilted sine function (continuous lines in Fig. 2d). For reference, theoretical planar projections of the magnetization dynamics for each resonance mode are shown in Figs. 2b and 2c from the perspective of the microwave beam, where dashed lines indicate motion within the xy plane. In this projection, the elliptical precessions of $\vec{m}$ in the acoustic mode and $\vec{n}$ in the optical mode appear to be flat vibrations. The same would be true for the orbits of the sublattice magnetizations (not pictured). These diagrams help to illustrate the polarization-dependent microwave coupling to the magnetic order for the Voigt geometry and the magnetization and dynamic paths are exaggerated for visual clarity. For optical resonance, coupling to the equilibrium ordering parameter, ${\vec{n}}_{0}$, occurs for linearly $\vec{x}$-polarized (0, 360°)) ${\vec{h}}_{{ac}}$, thus perpendicular to ${\vec{n}}_{0}$ ($\vec{y}$-axis). For acoustic resonance, coupling to the equilibrium magnetization, ${\vec{m}}_{0}$, occurs for $\vec{y}$-polarized (180°) ${\vec{h}}_{{ac}}$, thus perpendicular to ${\vec{m}}_{0}$ ($\vec{y}$-axis).

We repeated this measurement at various microwave excitation frequencies in both geometries for the bulk sample. Figure 3 shows the polarization dependency for 120 GHz excitation of the acoustic mode in the Faraday geometry. In this measurement geometry, the beam is perpendicular to the sample surface and propagates along the externally applied field ($\vec{k}\,\Vert \,\vec{x}$). We now take a closer look at the signal maximum from ${90}^{\circ }\,-\,{270}^{\circ }$ and increase the averaging to 16 field sweeps. We find that maximum spin transfer into the Pt layer is for neither fully circular nor y-polarized microwaves, but a degree of ellipticity produces the largest component of spin. Figure 3c shows the extracted signal maxima fitted to a two-term tilted sine function to good agreement, and the maximum response is found at $\phi =190{(191)}^{\circ }$ for $\mp \vec{H}$. The process is repeated at 155.5 GHz for both Faraday and Voigt geometries to verify this phase shift and expand the faraday scan to the full polarization range (Figure S2). Figure 3b shows the planar projection of the magnetization dynamics from the perspective of the microwave propagation in the Faraday geometry, where the elliptical precession of ${\vec{m}}_{0}$ is visible. For the acoustic resonance, coupling to ${\vec{m}}_{0}$ may now occur for any ${\vec{h}}_{{ac}}$ in the zy-plane. The maximum response for an ellipticity of $\phi ={190}^{\circ }$ agrees phenomenologically with a resultant vector applied almost entirely along y (${\vec{n}}_{0}$ direction) with a slight rotation towards $\vec{z}$. Again, in the case of the optical resonance for this geometry, the magnetization oscillates along the x-axis (see Figure S3b), so for x-propogating microwaves of any polarization, no coupling to ${\vec{m}}_{0}$ can occur. We thus observe a null result in the Faraday geometry for ${\omega }_{1}$ as expected.

Fig. 3: Faraday polarization dependence of ISHE for the acoustic branch.

a Contour map of the polarization dependence of V_ISHE at 120 GHz in the Faraday geometry. Traces are averaged over 16 field sweeps taken in 3.75° steps. b Theoretical planar projection of the magnetization dynamics of $\omega 0$ from the perspective of the microwave beam. Dashed lines indicate the motion of $m0$ within the ${zy}$ plane. The canting angle of the magnetization is exaggerated for visual clarity. c Polar plot of the signal maximum with respect to the MPI phase delay. Solid lines are fits to a two-term tilted sine function.

Spin Current Polarization Dependence in Thin-Film Hematite

We now show the results of the same experiments in a α-Fe₂O₃(30 nm)/Pt(5 nm) thin film heterostructure to explore how dimensional constraints play a role in the development of these signals. For thin films, standard microwave absorption measurements are not sensitive enough to detect the AFMR, however the ISHE signals originated from spin pumping into the adjacent Pt are expected to be similar than in bulk samples, as the effect originates in the close vicinity of the interface. Figure 4 shows the ISHE results obtained for 130 GHz in the acoustic mode. We vary the polarization in both Voigt and Faraday geometries as before. Polarization contour plots of the observed ISHE signal magnitudes are shown in Fig. 4a, b for the Voigt and Faraday geometries, respectively. Figures 4c, d show the corresponding polar plots and fits to a two-term tilted sine function. Contrary to the bulk sample, we observe less evidence of elliptical dominance in the signal. In the Voigt geometry, only a −3.4° shift is seen in positive field sweeps and the shift is negligible for negative field sweeps. For the Faraday measurements the shifts are slightly larger, however the fits straddle the $\phi ={180}^{\circ }$ midline and as compared to the consistent tilting in the bulk, these can be considered within normal experimental error. While polarization is tested for higher frequencies in the optical branch, no excitations are observed via the ISHE, even in the Voigt geometry when the microwave polarization lies along the $\vec{x}$-axis, fulfilling the resonant requirement. As reported previously, we propose this is due to extrinsic dampening effects related to fact that the small film thickness and/or film inhomogeneities can extinguish higher order resonance modes⁶.

Fig. 4: Polarization dependence of ISHE in thin-film α-Fe₂O₃/Pt.

a, b Polarization contour map of V_ISHE at 130 GHz in the Voigt (a) and Faraday (b) geometries. Traces are averaged over 4 (8) field sweeps for the Voigt (Faraday). c, d Polar plot of the signal maximum with respect to the MPI phase delay for Voigt (c) and Faraday (d) contours. Solid blue and orange lines are fits to a two-term tilted sine function. Dashed lines indicate ${\boldsymbol{\phi }}$ at the maximum amplitude of ${{\boldsymbol{V}}}_{{\boldsymbol{ISHE}}}$.

The power across our frequency range is varied, however we have used the maximum available power for our system in the ISHE experiments. Highest amplitude voltage signals are achieved in the 115–145 GHz range with a nominal power of 300 mW. This power is scaled by a terahertz lens by a factor of ~8, proportional to the spot size area. Assuming no losses in the free space circuit, we calculate for the acoustic mode a maximum sensitivity of 22 nV/W in the 1 mm sample and 13 nV/W in the 30 nm sample (Fig. S1). The conversion efficiency is consistent with the spin-pumping susceptibility of hematite which drastically drops off for magnetic fields above 1T⁴. Higher conversion efficiencies have been measured in lower frequency setups (below 40 GHz) where resonances occur for magnetic fields below this limit^4,8. However, higher conversion efficiencies give a maximum sensitivity of 80 nV/W in the optical mode.

Discussion

Having laid this framework, we can now address the polarization dependencies to determine the origin of these signals. While the picture for coherent spin pumping explains much of the behavior in the acoustic mode, the observed polarization phase shift may be indicative of additional contributions to the ISHE signal than spin pumping alone. We note that in reviewing the literature, some reports of angular dependence are note-worthy. Polarization-angle dependent absorption in hematite²⁵ at high frequency shows similar shifting within the basal plane. In α-Fe₂O₃/Pt and other AFM heterostructures, tilted sine shifting can be clearly seen and is directly associated to the Néel vector orientation^12,54. Perhaps more intriguing still, THz ultrafast excitations reveal that light propagating through hematite gains ellipticity with respect to the magnetic field⁵⁵. In the same study, the measured dynamical response depends on the retardation of the microwave within the lattice and is fully dependent on the THz electric field. The effect results in a sin2θ dependence on polarization angle and may account for this term. It remains unclear at this point the precise reason this shift vanishes for the hematite film. If the shift is a result of lattice strain on the magnetic anisotropy¹² then one would expect the enhanced inhomogeneous broadening in the film could extinguish it. However, if the contribution arises from the THz electric field, a removal of the essential static phase retardation is easily explained by the reduction in sample thickness.

In spin pumping experiments, the competition of multiple unique spintronic effects can make determining the precise origin of signals difficult. Conclusions can be drawn from analyzing the spectral shape and power dependences in our sample in order to isolate the effects. While some effects can be immediately discarded due to the insulating band-structure, c-plane α-Fe₂O₃ has indeed shown in many studies to exhibit a significant anomalous magneto-resistance (AMR)^{56,57,58,59,60}, which results in an asymmetric contribution to the spectral line shape⁶¹. To isolate this dependence, we decompose the spectral line shapes. Figure (S1b, d) shows the spectrally decomposed and total amplitude voltage signals for both modes, scaled to the output power of the THz modules. The asymmetric contribution can be attributed to the AMR induced voltage, proposed to be linked to a finite ferromagnetic ordering in hematite. Alternatively, the Anomalous Hall Effect (AHE) arising from a nonvanishing Berry curvature can contribute an asymmetric signal.

The Spin Seebeck Effect (SSE) is often readily proposed as a contributor to ISHE voltages in the presence of microwaves. A thermal gradient through the sample thickness could emerge at the onset of optical microwaves at the sample surface, creating an incoherent magnon contribution to the pumped voltage. Rapid thermalization and decoherence of pumped spin currents at AFM/NM interfaces has also been proposed⁴. However, this does not overshadow the association of coherent spin currents to their polarization selectivity. Additionally, Figure (S1a) and (S1c) show the ISHE voltages for both modes with respect to the output power of the microwave source for the bulk and thin-film samples, respectively. For both we see a clear linear relationship, a signature of coherent spin pumping^4,19. We can thus immediately rule out thermally pumped magnons by SSE, which scales quadratically with power. Anomalous Hall Effect (AHE) and Planar Hall Effect (PHE) contributions cannot be completely ruled out by power dependence alone⁶¹.

A portion of the large measured V_ISHE signals could arise from long range ferromagnetic ordering brought about by the uncompensated interface of α-Fe₂O₃⁵⁹. For perfect c-plane grown hematite, the lattice structure in the ideal case gives a fully uncompensated surface, and by XRD (Figure S6) we observe that our sample is at least slightly uncompensated. However, such a contribution would be antisymmetric with respect to field direction. The same antisymmetry would be true for Spin-Seebeck and Anomalous Nernst Effect signals. Uniquely, rectification from the optical mode is invariant under field-inversion. This sharp contrast with the acoustic signals calls for further study. Staggered spin currents and PHE signals which are symmetric with field inversion can also be considered.

To understand the behavior of the optical resonance as a function of the polarization phase and magnetic field, we show the relationship between the microwave polarization states and the optical-mode spin responses in Fig. 5. Ellipses correspond to each major grouping of observed resonances. Color gradings are scaled to the maximum signal in the positive field, so that the darkest colors indicate 0-field resonances. We observe a maximum signal of 81 nV with slight elliptical coupling at $\phi ={10}^{\circ }$. This major signal region corresponds to a tight matching to the x-polarized magnetization path. The minor signals develop with opposite handedness, mirrored across the $\phi ={180}^{\circ }$ linear state. With the application of an external field the DMI angle increases. We observe this effect in that higher degrees of ellipticity universally excite the resonance at higher field values up to a saturation point (lightest colored ellipses). The underlying mechanism behind the optical mode development is unclear. Some angular dependence may be drawn from the AMR; however, it is not sufficient to explain the full picture. Similarly, it is not clear why the signal disappears/collapses beyond a given polarization phase. Certainly, the triply degenerate subdomain magnetizations will rotate gradually to align with the external field and will not be fully aligned until the saturation field is reached around 1T⁵⁶. Thus, the low-field state may be an ensemble response with some ellipticity as the sub-domain linearly oscillating magnetizations are excited in and out of phase with each-other by separate components of the microwave beam.

Fig. 5: Visualization of optical-mode ISHE signal strength with respect to polarization degrees.

a Optical spin-to-charge conversion at 160 GHz with respect to polarization degree. b Ellipses map the polarizations associated with the three signal groups and are color coded to the magnetic field of the voltage peak in the positive field direction.

Although the field shifts of the optical resonance in response to microwave polarization are not clearly understood at this time, this is a behavior not observed in uniaxial antiferromagnets, providing a novel knob for controlling the field-frequency response of future spintronic devices based on easy-plane, canted antiferromagnetic systems. Further studies are needed to further probe the complexities of the optical mode, and we leave this point open to interpretation at this time.

Despite the open questions arising from the polarization dependence of the optical mode observed in our experiments, we have provided a comprehensive study of the dynamical spin behavior in bulk hematite in a broad range of frequencies, magnetic fields, microwave polarization degree, and light-matter interaction geometry (i.e., Voigt vs Faraday), which we believe provide useful information for future investigations and potential use of this material in emerging spintronics technologies that may leverage its high frequency response.

Methods

Device fabrication

Bulk α-Fe₂O₃(0001) (MTI) is capped in-situ with a 5 nm Pt layer at 4 mTorr in Ar plasma, at 20 mA with DC off-axis sputtering and base pressure below 1e-7 Torr. The α-Fe₂O₃(0001) film was epitaxially grown on an Al₂O₃(0001) substrate by off-axis sputtering. A 50 W RF power was used and a substrate temperature of 400 °C in 12 mTorr pressure Ar + 5% O₂. The film was capped in-situ with a 5 nm Pt layer grown with DC off-axis sputtering at room temperature in 2 mTorr Ar. Contact pads of Cr(7.5 nm)/Au(50 nm) were deposited by PVD for both samples.

Experimental setup

Microwaves are generated by solid state THz modules (Virginia Diodes Inc.) and amplified via biased waveguide amplifiers (Virginia Diodes Inc.) to a maximum power of 300 mW. The linear T01 microwave then enters a Martin-Pupplett Interferometer (MPI, Thomas Keating Ltd.) where the polarization state is altered. Within the MPI a single polarizing wire grid splits the wave into orthogonal components. A single arm of the split beam is phase delayed by a motorized roof mirror so that the polarization state of the recombination can be varied. The beams are recombined at the splitting grid and focused by parabolic mirrors into the room temperature bore of our magnet fitted with a corrugated wave guide which carries the beam to the cryostat. Before polarization dependent measurements the MPI is carefully calibrated to render a polarization mapping for the given excitation frequency. A 1mm-thick single crystal of alpha-Fe₂O₃/Pt(5) is mounted in the center of a 9 T split coil superconducting magnet (Cryogenic Ltd.) with room temperature bores for the insertion of a variable temperature insert (VTI, Cryogenic Ltd.) and corrugated microwave waveguides. The sample is leveled to our optical bench and the leveled position is verified in ImageJ. The sample is sealed at the focal center of a window-block fitted with THz focusing lenses. Temperature dependent measurements (supplementary information) are performed using a closed loop VTI fitted with a helium cold head compressor.

The high frequency microwave is pulsed with a microwave switch fed by Lock-In amplifier TTL at 93.76 kHz before being multiplied in the solid-state source. The resulting voltage signal at the sample is carried via flexible and rigid coaxial. The signal enters a filtered circuit consisting of a Thorlabs EF502 low-pass filter and a SR560 Pre-amplifier and is finally measured in an SRS830 Lock-In amplifier. The EF502 and SR560 create a 30–100 kHz band pass filter. We filter the circuit in two ways. The signal arrives first to the SRS560 preamplifier equipped with a 30 kHz high pass filter with 12 dB rejection. The signal is amplified by 2000 times before entering a Thorlabs EF502 low pass filter, creating an equivalent bandpass of 30–100 kHz. The Lock-In is pulsed at 93.76 kHz with 24 dB of filtering and a 1 s time constant.

Data analysis

Voltage and absorption data are fit to a linear combination of symmetric and antisymmetric Lorentz functions and the fitting linewidths are taken as the error. In a small number of cases a linear combination of symmetric and antisymmetric Voigt functions is used. Fig. 6 shows the fitting for the 155.5 GHz acoustic mode averaged over 4 field sweeps.

Fig. 6: Lorentzian line fitting of at $V_{ISHE}$ 155.5 GHz for acoustic resonance.

The measured ISHE voltage is averaged over several magnetic field sweeps and fit to a Lorentzian function. Symmetric and antisymmetric portions of the fitting are then extracted.

The line fitting equations are provided here for reference. The symmetric and asymmetric Lorentzian fittings are given by,

$$y=y0+S* \left(\frac{d{H}^{2}}{{\left(x-{H}_{0}\right)}^{2}+d{H}^{2}}\right)+A* \left(\frac{{dH}* \left(x-{H}_{0}\right)}{{\left(x-{H}_{0}\right)}^{2}+d{H}^{2}}\right)$$

(17)

where S and A are the respective amplitudes, H₀ is the resonance peak, and dH is the linewidth. The symmetric and asymmetric Voigt fittings are given by,

$$v={y}_{0}+\frac{A\cdot 2\cdot \mathrm{ln}\left(2\right)\cdot d{H}_{L}}{{{\rm{\pi }}}^{1.5}\cdot d{H}_{G}^{2}}\cdot \int \frac{\exp \left(-{t}^{2}\right)}{{\left(\frac{\sqrt{\mathrm{ln}\left(2\right)}\cdot d{H}_{L}}{d{H}_{G}}\right)}^{2}+{\left(\frac{\sqrt{4\cdot \mathrm{ln}\left(2\right)}\cdot \left(x-{x}_{c}\right)}{d{H}_{G}}-t\right)}^{2}}{dt}$$

(18)

$$y=v+v* \frac{x-{H}_{0}}{{w}_{L}}$$

(19)

where $L$ and $G$ subscripts denote the parts of the Lorentzian and Gaussian fits. Equations (18) and (19) show the sub-form and total form of the fitting function, respectively.