Introduction

Wave non-reciprocity (NR) – the alteration of a wave’s property upon the reversal of its wavevector – is a fascinating phenomenon that is seldom observed in linear time-invariant systems1, with the notable exception of those involving magnetism. The NR of spin-waves (SWs), which can arise from either dipolar interactions2 or Dzyaloshinskii–Moriya interaction (DMI)3, has been long regarded as a physical curiosity, primarily enabling a limited number of novel microwave functionalities, or more recently as a handy tool to determine magnetic properties4. However, recent insight has revealed that NR could be significant enough to confer unidirectionality to the energy flow (or to the information flow) carried by SW ensembles5. Moreover, this non-reciprocal behavior can be transferred to other quasiparticles, for instance by appropriate coupling to elastic waves6,7. This realization has spurred numerous theoretical and experimental investigations of SW NR in extended films and multilayers8,9,10,11,12.

Theoretical investigations were subsequently conducted in laterally confined geometry13,14,15 primarily focusing on materials exhibiting weak non-reciprocity induced by interfacial DMI. It was predicted that the profiles of the confined SWs would be affected by the NR, meaning that the confined eigenmodes could no longer be represented as a superposition of oppositely propagating SWs with equal wavelengths. Experimental works conducted in stripe geometry16 concluded that the frequency asymmetry between counter-propagating spin waves could be even suppressed, suggesting that the confinement may partly restore reciprocity.

These past studies focused on how NR modifies the eigenmode frequencies and the resulting resonance spectra, yet they overlooked the propagative nature of waves and its potential interest. A first category of studies that fully accounted for the propagative nature of the spin waves utilized Brillouin Light Scattering microscopy in extended media, and analyzed the two-dimensional patterns generated either by diffraction from arrays of slits17, or the directional spin wave beams generated by non-uniform transceivers18. The patterns could be pertinently analyzed with arguments based on iso-frequency theory19. A second category of studies devoted to SW propagation utilized electrical propagating spin wave spectroscopy (PSWS20), and involved injecting SWs in wide conduits5, which offered minimal guidance for the waves. The analysis was systematically done using a 1D model21,22 that implicitly assumes that the wavevectors and the group velocity of SWs present in the system are both collinear to the SW conduit. We will demonstrate that this description is inappropriate when applied to materials with significant NR such a synthetic antiferromagnets (SAFs). Even when the conduit is aligned parallel to the reciprocal direction of a non-reciprocal material, the emission can exhibit features that strongly differ from that encountered when using reciprocal materials. These include for instance the generation of bidirectional nodal structures by a one-dimensional transceiver, as well as the radiance of a caustics-like energy beam in a single direction that substantially differs from the conduit length.

Results

Experimental results

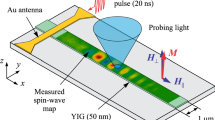
We use CoFeB/Ru/CoFeB synthetic antiferromagnetics (SAF), patterned into stripes meant to channel the spin waves. The stripes have widths wmag = 5 μm [Fig. 1] and are covered by a microwave antenna of width want = 1.8 μm, able to couple to spin waves of wavevectors satisfying \(| {k}_{y}| < {k}_{{\rm{y,max}}}^{{\rm{ant}}}=3\,{\rm{rad}}/\mu\) m. A static field Hx is applied perpendicularly to the stripe. This field orientation induces a situation where the SWs are reciprocal in the direction of the stripe (i.e. y) and non-reciprocal in the transverse direction (i.e. x). We will analyze the magnetization response when powering the antenna to generate an rf field \({\vec{h}}_{{\rm{ant}}}^{{\rm{rf}}}\perp {\vec{H}}_{x}\) meant to excite spin waves under the antenna and to channel them in the stripe. This rf field is expected –and was checked (see Supplementary Fig. S1)– to excite the sole acoustic branch of the spin waves of the SAF.

Fig. 1: Experimental configuration.
figure 1

a Optical image of the device, sketch of the stack and coordinate conventions. The sub-micron vertical gray segments near the left edge of the stripe are resist residues from the fabrication process. Red boxes: regions investigated by BLS microscopy. b Antenna efficiency function versus wavevector. c Direction of the applied field, sketch of the resulting scissors state, and micromagnetic configuration at μ0Hx = 50 mT. Notice the slight non-uniformity of the magnetizations near the edges of the SAF stripe. d Example of an experimental BLS microscopy image obtained for μ0Hx = 50 mT, and a r.f. field oscillating at 4.5 GHz. The image extends 0.8 μm on both sides of the stripe, whose width is 5 μm. The top and bottom BLS images have dimensions of 6.6 μm × 10.2 μm and 6.6 μm × 2.2 μm, respectively.

Full size image

The magnetization response is imaged by Brillouin Light Scattering microscopy (BLS). The pixel size is 200 × 200 nm2 and the optical resolution is estimated to be \(2\pi /{k}_{\max }^{{\rm{BLS}}}\approx 350\) nm, with \({k}_{\max }^{{\rm{BLS}}}=18\,{\rm{rad}}/\mu\) m being the largest wavevector that can be collected by the BLS set-up (see methods).

Images of the magnetization response were recorded for applied fields of 27, 50, 75 and 100 mT, with qualitatively similar conclusions. Apart from some amplitude non-reciprocity, the magnetization profiles are axially symmetric with respect to the antenna, as in the example of Fig. 1d; we shall thus now show only the y > 0 side of the antenna. The profiles of the response can be cast in 3 archetypal categories. The Fig. 2 illustrates these categories for the representative 50 mT case, for which the most uniform modes have frequencies in the range \({f}_{{\rm{ac}}}(\vec{k}=\vec{0})\approx 5.5-6.5\) GHz .

Fig. 2: Experimental BLS images (logarithmic color scale) taken at an applied field of μ0Hx = 50 mT, and ordered according to the frequency of the rf signal supplied by the antenna.
figure 2

The images are grouped in 3 types. a Low frequency patterns with nodes and antinodes in the x direction and intensity maxima at the bottom left corner of the stripe. b Near \({f}_{{\rm{ac}}}(\vec{k}=\vec{0})\): patterns with tilted energy flow, first approximately in the \(\vec{x}+\vec{y}\) direction, then progressively rotating towards \(\vec{y}\) when increasing the frequency. c High frequency patterns, first exhibiting nodes and antinodes in two directions, then solely in the \(\vec{y}\) direction. The sketches indicates that wavevectors and their group velocities that most contribution to the spatial profile of the BLS signal.

Full size image

At low frequencies (top raw in Fig. 2), the driven spin waves exhibit nodes and antinodes aligned in the x direction, i.e. transverse to the SAF stripe. The spacing between the nodes gradually increases from 600 ± 100 nm at 3.65 GHz to approximately the half stripe with at 5.2 GHz. The BLS signal is confined in the 2 μm vicinity of the antenna: the driven SWs do not seem to radiate energy away from the antenna. Noticeably, the BLS amplitude is maximal near the left edge of the antenna, as if the spin waves were emitted from the bottom left corner of the images towards the bottom right corner. Note that this feature –emission seemly from the left corner– would never be measured in electrical measurements like propagating spin wave spectroscopy (PSWS), owing to the experimental limitation of only accessing to the spatial average of the magnetization below an antenna. This directionality towards x > 0 holds strictly at the lowest frequency (3.65 GHz) but some curvature gradually appears when increasing the frequency (see e.g. the 4.65 and 5.2 GHz patterns in Fig. 2).

Approaching the frequency of the uniform acoustic SWs disrupts the pattern of dynamic magnetization [5.45 GHz and subsequent frames in Fig. 2b]: the antinodes are expelled from the stripe, and the pattern rotates as a whole: it seems that the SWs are now emitted by the antenna in a tilted directional manner. The direction of decay of the BLS intensity has become approximately \(\vec{x}+\vec{y}\). Because of this ≈45 degree directional emission, the BLS signal vanishes at a distance of want away from the antenna, exactly when the caustics-like SW beam hits the right edge of the stripe. Energy is indeed radiated away from the antenna but the BLS signal does not decay exponentially along the stripe length. Noticeably, this indicates that the usual way23,24 of deducing SW attenuation length becomes inadequate in the joint presence of non-reciprocity and confinement. A slight further increase of the frequency [6.15 GHz case, Fig. 2b] rotates the decay direction to the (more conventional) \(\vec{y}\) direction, with a long propagation distance comparable to the image size (10.2 μm). In this narrow frequency range the decay direction is the one expected from a channeling by the stripe; however the material non-reciprocity still plays a role and breaks the {x, − x} symmetry: the maximum intensity is not at the midst of the SAF stripe but rather offset by 1 μm to the right.

In the 7–9 GHz range [Fig. 2c], a bidimensional array of nodes and antinodes reappears progressively, with beatings in the two x and y directions, indicating the coexistence of several modes with unequal wavevectors. The overall decay of the BLS signal stays essentially in the y direction, still with a long attenuation length. The density of nodes and antinodes increases with the frequency. Finally at the highest investigated frequencies (9.7 GHz), we recover a behavior resembling the low frequency one, i.e. with an apparent emission from the bottom left corner of the SAF stripe, but with some beating along the y direction.

Physical understanding

Several features of these BLS profiles are quite unusual. They include: (i) the systematic breaking of the {x, − x} symmetry that witnesses the material non-reciprocity and, (ii) the apparent ability of an antenna that generates a field with translational invariance in the x direction to excite magnetization profiles with a surprisingly large number of nodes in this same direction.

In past studies of the SWs in confined geometries, it has often been possible to understand the nature of the modes by using the dispersion relation in the corresponding unbounded films and applying some quantification of the transverse wavevector25 according to specific boundary conditions26. The BLS images could then be understood from overlap integrals of the antenna r.f. field and the profiles of the few allowed modes27.

Dispersion relations

Let us apply the same rational for the SAF stripes with the dispersion relations reported in Fig. 3 and calculated in the dynamical matrix formalism (see methods). The dispersion relation in Fig. 3 recalls that as well-known for SAFs in the scissors state, the acoustic spin waves are reciprocal in the ky direction [inducing ωac(kx, ky) = ωac(kx, − ky)] while being non-reciprocal and unidirectional in the field direction (i.e. for small kx, we have \(\frac{\partial \,{\omega }_{{\rm{ac}}}}{\partial \,{k}_{x}}{| }_{{k}_{y} = 0} > 0\)). For the applied fields considered here, this unidirectional character extends to far above the region \([-{k}_{y,{\rm{ant}}}^{\max },-{k}_{y,{\rm{ant}}}^{\max }]\) that can be addressed by the antenna, except for modes with very large − kx that can anyway not be detected by BLS (Fig. 3).

Fig. 3: Dispersion relations of the acoustic spin waves in an infinitely extended SAF film at a field of μ0Hx = 50 mT.
figure 3

a Dispersion according to the dynamical matrix formalism. The shaded areas are the regions in which the antenna cannot detect spin waves. Sketched dispersion relations at low frequency (b), at \(\vec{k}=\vec{0}\) frequency (c), slightly above (d) and much above (e). The arrows sketch the directions of the group velocities. The arrows are gray when the group velocity points downward from the antenna.

Full size image

Interpretation guidelines

The presence of several to many nodes in the x direction argues for the generation of SWs of wavevectors with arbitrarily large kx components. This requires non-uniformity in the x direction at scales compatible with all these kx’s, hence at lateral scales smaller than \(2\pi /{k}_{\max }^{{\rm{BLS}}}\). These non-uniformities are likely the tiny regions near the stripe edges where the equilibrium magnetization and its demagnetizing fields are non-uniform [see Fig. 1c].

Besides, we can interpret the BLS images by considering only the wavevectors whose group velocity is directed to the upper side (i.e. y > 0) of the antenna, since the other SWs cannot radiate energy into the region under evaluation. Since the driven SWs must have a ky component that can couple to the antenna spectrum [Fig. 1b], the relevant wavevector space to be considered for the qualitative analysis of the BLS images is thus:

$$\left\{\begin{array}{l}\{{k}_{x},{k}_{y}\}\in [-{k}_{{\rm{BLS}}}^{\max },{k}_{{\rm{BLS}}}^{\max }]\times [-{k}_{y,{\rm{ant}}}^{\max },{k}_{y,{\rm{ant}}}^{\max }]\\ {\rm{and}}\,({\vec{\nabla }}_{\vec{k}}\omega ).\vec{y} > 0\end{array}\right.$$
(1)

For each applied frequency ωapplied/(2π), we shall thus analyze the BLS images by considering the corresponding isofrequency contour ωac(kx, ky) = ωapplied after truncation of the spin wave manifold according to Eq. (1). The complicated shape of the isofrequency contours (Fig. 3) provides the second interpretation guideline: the large differences in spatial patterns among the BLS images are likely to result from the mutual orientation of the wavevector, the group velocities (\({\vec{v}}_{g}={\vec{\nabla }}_{\vec{k}}\omega\)), the antenna, and the stripe-shaped SW conduit.

Qualitative understanding of the experimental BLS images from the dispersion relation

At low frequencies (4 GHz), the relevant SWs almost share the same group velocity pointing in the \(\vec{x}\) direction and the same large (\({k}_{x}^{4\,{\rm{GHz}}}\approx -14\,{\rm{rad}}/\mu\) m) value of kx. They only differ by their –comparatively much smaller– ky value. Because of their common vg direction, the amplitude of the signal of every SW present in the system decays in the \(\vec{x}\) direction. This explains why the bottom left corner of the BLS images at low frequency appeared systematically as the brightest spot in experiments (see the top left images in Fig. 2). Note that the SWs are emitted in-phase at every position \({x}_{0}\in [-\frac{{w}_{{\rm{stripe}}}}{2},\frac{{w}_{{\rm{stripe}}}}{2}]\) along the antenna, but each of these SWs has a spatially-dependent phase factor \({e}^{i{k}_{x}^{4{\rm{GHz}}}(x-{x}_{0})}\) and an amplitude decay factor \(\propto {e}^{-((x+w/2)/{L}_{{\rm{att}}})}{\mathcal{H}}(x-{x}_{0})\), where \({\mathcal{H}}\) is the heaviside function and Latt the attenuation length. The phases of these spin waves rotate along the \(\vec{x}\) direction at the common spatial pace \({k}_{x}^{4\,{\rm{GHz}}}\). The interference of all these waves leads to a BLS pattern whose envelope is maximal at the left edge and decays like Latt. Interference of the profiles of these waves is constructive whenever they are emitted at x0 positions spaced by integers of \(\delta x=2\pi /| {k}_{x}^{4\,{\rm{GHz}}}| \approx 450\) nm away from the left edge. The destructive interference will lead to nodes in the BLS images, and antinodes otherwise, in reasonable agreement with the experimental node-to-node spatial periodicity.

At 6.34 GHz (which is the uniform resonance of the acoustic mode in an extended film), the truncated isofrequency contour is line-shaped and it runs along approximately the kx = −ky diagonal direction, as sketched in Fig. 3c. All the SWs that can be excited at this frequency share the same direction of group velocity, pointing approximately in the \(\vec{x}+\vec{y}\). These SWs span over a continuous range of wavevectors from \(\vec{0}\) to \({k}_{\max }^{{\rm{ant}}}(\vec{y}-\vec{x})\). The broadband character of the wavevector spectrum is such that no fine structure is expected in the spatial domain. However, the common group velocity ensures that every generated SW decays in the same \(\vec{x}+\vec{y}\) diagonal direction. This is the reason why a very well defined ≈45° directional pattern was observed experimentally in this frequency range [Fig. 2b].

When slightly increasing the applied frequency to 6.5 GHz, a semi-circular protuberance starts to stick out of the angled part of the isofrequency contour [Fig. 3d]. The SWs whose wavevector belongs to this protuberance have group velocities that lie out of the approximate \(\vec{x}+\vec{y}\) direction and span from \(+\vec{x}\) to \(+\vec{y}\). This growth of the protuberance is expected to weaken the directional character of the BLS image that was originating from the line-shaped ≈ 45°-oriented segment of the isofrequency contour. In experiments, the directionality was indeed progressively lost as increasing the frequency slightly above the frequency of the uniform acoustic spin wave resonance.

At 7.5 GHz [Fig. 3e], the protuberance takes all the relevant wavevector space while distorting to get a trapezoidal shape. The driven SWs have now wavevectors that are broadly distributed, but with two well-defined subgroups of group velocities, heading either along approximately \(\vec{x}+\vec{y}\) like before, or along approximately \(\vec{y}-\vec{x}\). This two-flavor distribution is expected to lead to beating patterns in these two directions as was indeed anticipated from the experimental result. [Fig. 2d]. Note that if we were performing electrical propagating spin wave spectroscopy in such a narrow spin wave conduit, the conventional analysis of PSWS data28 would fail because it requires a 1D flow of a single family of SWs, a condition that is obviously not satisfied here.

Finally at high frequency (10 GHz for instance), we recover a situation that bears some similarity with the low frequency case: the isofrequency contour is almost a vertical line, such that the relevant SWs share a large common wavevector \({k}_{x}^{10\,{\rm{GHz}}}\approx +13\,{\rm{rad}}/\mu\) m and a common group velocity pointing towards x. With the same rational as for the low frequency case, this results in a line of nodes and antinodes of decaying amplitude from the bottom left corner to the bottom right corner of the BLS images. The node-to-node distance is expected to be now \(2\pi /{k}_{x}^{10\,{\rm{GHz}}}=480\) nm, close to the resolution of our images, hence difficult to detect experimentally [Fig. 2e].

Discussion

In partial conclusion, qualitative understanding of the BLS images is possible from the thin-film dispersion relation, at least in situations selected for their simplicity. However it cannot account for the details of the images, notably when the isofrequency contours are very curvy and the node/antinode pattern runs in two different directions. Also, the above analysis relies on plane waves, such that it does not account for demagnetizing effects leading to a difference between an unbounded SAF and a patterned stripe, where the internal field is non-uniform and lower than the applied field. Finally, it misses any possible hybridation between the optical and the acoustic spin waves. It has been indeed shown that there are regions of the parameter space where the two SW branches cross each other [i.e. when ωac(kx, ky, Hx) ≈ ωop(kx, ky, Hx)] thereby hybridizing the optical and acoustic characters29. As a result, SWs with a partial optical character may in principle be weakly driven by the antenna in this region of the parameter space. These deficiencies of the qualitative rational can be resolved by calculating the response from micromagnetics for a quantitative comparison with the experimental results.

The Fig. 4 reports a selection of BLS images predicted by micromagnetics (see Eq. (2) in methods) for our stripe width of 5 μm. Calculations of other stripe widths from 1 to 10 μm are reported in Supplementary Fig. S3. If convolved with the optical resolution of the BLS, the agreement with their experimental counterparts (Fig. 2) is remarkable, but there are several small differences that deserve a discussion.

Fig. 4: Micromagnetic simulations of the BLS images for an infinite lateral resolution (Eq. (2), logarithmic color scale) and after convolution with a Gaussian filter reducing the lateral resolution to 350 nm.
figure 4

a, b Low frequency patterns with nodes and antinodes that alternate in the x direction. c Near \({\omega }_{{\rm{ac}}}(\vec{k}=\vec{0})\): patterns with a tilted flow of energy in the \(\vec{x}+\vec{y}\) direction. d Patterns measured in the intermediate frequencies, exhibiting nodes and antinodes in two directions.

Full size image

In the low frequency case [see Fig. 4a as well as the data for other stripe widths in the Supplementary Figs. S3 and S4], the micromagnetic calculations indicate that, in addition to the line of nodes and antinodes seemingly emitted from the bottom left corner already identified in experiments, another line of nodes and antinodes seems emitted from the bottom right corner. This second line of nodes has a substantially smaller spatial period and could not be resolved in the experiments. However when convolved with the optical resolution of the BLS, this second line of nodes results in a secondary maximum of BLS intensity at the bottom right corner, which was indeed perceived experimentally [Fig. 2a]. This second line of nodes can be understood with the same rational as the first one, by noticing that the isofrequency contours at low frequency have egg shapes and thus cross Eq. (1) twice [Fig. 3a]. For instance the 4 GHz contour extends far in the kx < 0 direction and passes at the point \(\{{k}_{x}^{4{\rm{GHz}}{\prime} },{k}_{y}\}=\{-25,0\}\) rad/μm., where the group velocity points in the \(-\vec{x}\) direction. This wavevector and its group velocity is responsible for the line of antinodes of periodicity \(2\pi /{k}_{x}^{4{\rm{GHz}}^{\prime} }\), decaying leftwards from the bottom right corner of the BLS images.

This pattern of nodes and antinodes progressively expands when increasing the applied frequency. When approaching the frequency of the uniform mode [Fig. 4b] there remains a clear directional pattern with a decay approximately in the \(\vec{x}+\vec{y}\) direction, which reproduces nicely the experiment and the expectations drawn from the dispersion relation. This directional pattern is also predicted for other stripe widths, see Fig. S3. However at 8.4 GHz [Fig. 4c], the micromagnetic simulation fails to reproduce the bidirectional beating pattern observed experimentally and that could be understood from the shape of the protuberance within the dispersion relation. The absence of the modulation in the x direction in the micromagnetics result at 8.4 GHz is probably indicative that the inhomogeneity of the magnetization distribution in the x direction (near the stripe edges) is not correctly modeled and does not allow to populate the second flavor of modes that appears at after the blossoming of the protuberance.

Finally, the evolution of the predicted BLS images for very narrow stripes is worth discussing. The non-reciprocity of the spin waves in the relevant wavevector space (Eq. (1)) is progressively lost when the stripe width gets smaller than the antenna width. For a 1 micron stripe width (see Supplementary Fig. S4), we recover a situation close to the well-known case of a single-layer magnet in the (reciprocal) Damon-Eshbach case, where interference occurs between the uniform mode and the higher order confined spin waves, leading to periodic self-modulation of the amplitude pattern21.

In summary, we have used Brillouin Light Scattering microscopy and micrometer-sized rf antennas to study the confinement and the propagation of the acoustic spin waves in narrow conduits made of synthetic antiferromagnets that exhibit a giant non-reciprocity (NR). One could think that when the SWs are injected in a conduit that is parallel to the reciprocal direction, the NR would not play a major role. The contrary happens: the non-reciprocal nature of the dispersion relation is such that the direction in which a line-shaped antenna radiates SW energy rarely matches with the conduit direction. The most striking consequence of NR is that when below the frequency of uniform acoustic SWs, the SWs driven by the antenna have wavevectors running parallel to the antenna, i.e. perpendicular to the expected guiding direction. This leads to a unique nodal structure of the SW pattern in the vicinity of the antenna, with no possible analogy to reciprocal situations.

Electrical spectroscopy of propagating spin waves has recently become a popular tool for the study of spin waves. It involves measuring the magnetization response, but spatially averaged below a receiving antenna. Since imaging a system’s response is key to understand such a spatially averaged response, our results are essential to interpret PSWS experiments done on non-reciprocal systems and avoid errors. Beyond magnonics, our results can be used to anticipate which modes can be harnessed for the transport of energy/information in conduits when using non-reciprocal waves.

Methods

Devices

We use in-plane magnetized Synthetic AntiFerromagnetic (SAF) films of composition Co40Fe40B20 (17 nm)/Ru (0.7 nm)/Co40Fe40B20 (17 nm) [Fig. 1a]. The SAF film was patterned into stripes of width wmag = 5 μm [Fig. 1b]. We then deposited a s = 150-nm-thick insulation layer of Si3N4 and a single-wire antenna of width want = 1.8 μm and thickness h = 160 nm. A static field Hx is applied in the direction transverse to the stripe. The films, devices and variants thereof were characterized extensively by ferromagnetic resonance 30 and propagating spin wave spectroscopy 5 to deduce the material properties. This include magnetization Ms = 1.35 MA/m, damping α = 0.011, exchange stiffness A = 16 pJ/m, and interlayer coupling J = −1.0 mJ/m2. These values were concluded from the analysis of the 4 lowest frequency spin wave modes of an unpatterned SAF, as measured by VNA-FMR 30.

The experiments shall analyze the magnetization response when feeding the antenna with an rf source. The field of the antenna obeys \({\vec{h}}_{{\rm{ant}}}^{{\rm{rf}}}\perp {\vec{H}}_{x}\) such that it should excite the acoustic spin waves. However it would not excite the optical spin waves if the SAF was an infinitely extended film. We show in the Supplementary Fig. S1 that this also holds in our stripe despite of the lateral confinement. Besides, at the applied fields used in this study, the optical spin waves have frequencies above our investigated frequency interval, as shown in Supplementary Fig. S2. We will thus primarily analyze our experiments by considering the sole acoustic branch of the spin wave manifold.

Brillouin light scattering measurements

Our goal is to understand how the lateral confinement within the SAF stripe affects the SWs and their propagation, for fields applied in the width direction of the stripe. The spectra of the magnetization response and their spatial profiles are measured by Brillouin Light Scattering (BLS). The images in Figs. 1d and 2 are taken in microscopy imaging configuration and in driven mode: the laser spot is scanned across the sample, and the antenna is fed by a monochromatic continuous r.f. source. The pixel size is 200 × 200 nm2 and the optical resolution is estimated to be \(2\pi /{k}_{\max }^{{\rm{BLS}}}\approx 350\) nm, with \({k}_{\max }^{{\rm{BLS}}}=18\,{\rm{rad}}/\mu\) m being the largest wavevector that can be collected by the experimental set-up.

Micromagnetic simulations

Our micromagnetic simulations are done using the mumax3 code at zero temperature31. For each applied field Hx, we start by energy minimization to converge to the ground state, which is a scissors state. The magnetizations are uniform in the central part of the stripe but tend to be more parallel to the edges of the stripe in the regions near the edges of the stripe [see Fig. 1c].

The theoretical dynamical response of the stripe is evaluated by computing the steady state response of the magnetization to the two components \({h}_{y}^{{\rm{rf}}}(y,\forall x)\) and \({h}_{z}^{{\rm{rf}}}(y,\forall x)\) of the antenna field. The spatial profile of the r.f. field is calculated for the real geometry (Eqs. A1-A4 of ref. 22) and a peak field of \({h}_{y}^{{\rm{rf}}}=1\) mT at the SAF surface under the middle of the antenna. The power spectral density of \({h}_{y}^{{\rm{rf}}}({k}_{y})\) in wavevector space is displayed in Fig. 1b. It has a substantial amplitude up to \(| {k}_{y}| < {k}_{{\rm{y,max}}}^{{\rm{ant}}}=3\,{\rm{rad}}/\mu\) m.

We assume that the BLS signal comes essentially32 from the square of the out-of-plane (i.e mz) component of the magnetization in this steady state: we thus construct the expected BLS microscopy images by the following variance:

$${\rm{BLS}}(x,y)={\int}_{\!\!{\rm{period}}}{\left({m}_{z}(x,y,t)-{m}_{z}(x,y,t = 0)\right)}^{2}dt$$
(2)

To account for the finite lateral resolution of BLS microscopy, a Gaussian filter will be applied to expected images.

Theory

The images will be discussed from a thorough examination of the dispersion relations of the spin waves of an unbounded SAF, which we obtained using the formalism of the dynamical matrix33,34 with explicit accounting of the interlayer dipole-dipole interactions using Eqs. 26 and 32 of ref. 35. We describe each of the two layers of the SAF by discretizing it into two slices. The key ingredient for the non-reciprocity is the dipole-dipole interaction between the dynamic magnetizations of each layer of the SAF: the dynamic magnetization associated with a spin wave rotates in space, creating a stray field that is stronger at one side of the layer, this side being defined by the sign of the wavevector (see Fig. 4 of ref. 22). This effectively couples more the two layers for one sign of the wavevector, creating the non-reciprocity. The non-reciprocity scales with the thickness and the cosine of the wavevector direction (Eq. (3) of ref. 36). For each applied field, the calculations are run for a grid of wavevectors {kx, ky} and up to ±40 rad/μm. The two lowest order families of SAF spin waves are calculated: the acoustic (ac) SWs of frequencies ωac, and the optical (op) SWs. A representative example of the dispersion relation of the acoustic SWs is reported in Fig. 3.

As well-known for SAFs in the scissors state (see the part on acoustic SW modes in Table I, in ref. 36), the acoustic spin waves are reciprocal in the ky direction [inducing ωac(kx, ky) = ωac(kx, − ky)] while being non-reciprocal and unidirectional in the field direction (i.e. \(\forall {k}_{x},\frac{\partial \,{\omega }_{{\rm{ac}}}}{\partial \,{k}_{x}}{| }_{{k}_{y} = 0} > 0\)). For the applied fields considered here, this unidirectional character extends to far above the region \([-{k}_{y,{\rm{ant}}}^{\max },-{k}_{y,{\rm{ant}}}^{\max }]\) that can be addressed by the antenna, except for modes with very large − kx that can anyway not be detected by BLS (Fig. 3).