Introduction

Study of two-dimensional (2D) magnetic materials with van der Waals (vdW) structures has garnered significant attention due to their ultra-thin nature and promising applications in novel spintronic devices1. Although the Mermin-Wagner theorem suggested that 2D materials could not sustain magnetic properties at finite temperatures2, recent discoveries have demonstrated the possibility of long-range magnetic order in 2D systems3. Notably, chromium-based monolayers such as \({{{\rm{C{r}}_{2}G{e}_{2}Te}}}_{{{\rm{6}}}}\), CrSiTe3, and CrI3 exhibit magnetocrystalline anisotropy, as confirmed by experimental observations4,5,6. These findings have spurred extensive research into 2D magnetic materials in recent years.

One of the most exciting developments in this field is the emergence of a new class of materials, transition metal dihalides (MX2, where X = Cl, Br, I), which are valued for their semiconductive and magnetic properties7. The CrI2, a member of this class, adopts a trigonal structure similar to CdI2, belonging to the \({\rm{P}}{\bar{3}}{\rm{m}}1\) space group. However, one of the iodine sites becomes slightly elongated to the b-axis direction, caused by the Jahn-Teller effect, and possesses P21/m symmetry. Note that, after distortion, the CrI2 remains centrosymmetric8. In its bulk form, CrI2 exhibits two phases: monoclinic and orthorhombic; these phases were differentiated by the stacking of monolayers that interact weakly via van der Waals interaction9,10. Monolayers of CrI2 can be experimentally isolated through exfoliation techniques11, molecular beam epitaxy12, or annealing of CrI313. Furthermore, a recent study suggests that CrI2 may impose helimagnetism14.

Strain engineering is one of the methods for controlling the physical properties of low-dimensional materials15,16,17. In particular, the lattice constant of a monolayer can be significantly influenced by the substrate on which the material is grown18. It has also been shown that some magnetic materials have tunability of the magnetic moments, anisotropy, ordering, or even skyrmions under external strain19,20,21,22,23. The control of magnetism by strain in van der Waals material has already been shown in several systems such as FePS324, FeCl225, and CrSBr26. The strain can be utilized by using the piezoelectric cell or controlling the substrate mechanically to obtain uniaxial and biaxial strain26,27.

Additionally, it has been reported that monolayer CrI2 exhibits remarkable superelasticity, with a failure strain as high as 39%28. In contrast, its counterpart compound CrI3 can only sustain a pressure of around 2.2 GPa, fracturing at ~6.09% strain29. Given CrI2’s ability to withstand such large strains, it is essential to investigate the effects of strain on its magnetic properties, as CrI2 could potentially serve as a viable alternative to CrI3 for spintronic devices.

In this work, we investigate the monolayer of CrI2 using first-principles calculations. We assess the stability of antiferromagnetic (AFM) and ferromagnetic (FM) configurations and explore how external strain impacts magnetic coupling, where we focus on a strain range from 5% to 5%. Our calculations reveal that tensile strain destabilizes AFM coupling. The mechanism of strain-induced AFM-FM phase transition is clarified as an interplay between the direct magnetic interaction and the superexchange interaction.

Results

Ground states of CrI2 monolayer

We specifically derive the U value from the monolayer structure, which is relevant to our study. On-site Coulomb interaction to the Cr d orbitals was calculated using the linear response method30. We calculate the charge density of the Cr 3d orbital under small perturbations of the spherical potential, both self-consistently and non-self-consistently. This approach results in a U value of 5.6 eV, which is higher than the commonly used range of 3–3.5 eV in some prior studies13,14,28,31, but lower than the values reported in other ones8,32. Our high value of U arises from the stronger electron localization effects inherent in two-dimensional structures compared to the bulk system. Incorporating the U value in our calculations is essential, as it has a significant impact on the ground-state properties of CrI2, such as the lattice constant and band gap33.

We used a rectangular unit cell as Fig. 1a with the lattice constants calculated using the U value from the linear response. Our lattice constants are a = 4.02 Å and b = 7.55 Å, with first NN d1 = 4.02 Å and second NN d2 = 4.28 Å. These results are consistent with the previous experimental and theoretical results13,28,34,35. The lattice constants depend on the chosen U parameter, as shown in the supplemental Table S1. The formation energy of CrI2 freestanding monolayer can be calculated using an equation \({E}_{{{\rm{Form}}}}={E}_{{{{\rm{CrI}}}}_{2}}-{\mu }_{{{\rm{Cr}}}}-2{\mu }_{{{\rm{I}}}}\). Here, we used the A-type AFM bcc of Cr and I2 molecule for calculating the chemical potentials μCr and μI. The calculated formation energy indicates that the CrI2 monolayer is energetically stable, with a value of −4.26 eV/Cr atoms. This value is within the range of calculated formation energies for other monolayer structures such as WSe2, VI2, and MoS2 that have been previously synthesized36,37,38.

Fig. 1: Crystal structure and magnetic configuration.
figure 1

a Rectangular unit cell of CrI2, with dark blue and orange circles representing Cr and I atoms. The green arrow shows the local xyz coordinate, and J1 and J2 denote first and second nearest-neighbor (NN) exchange couplings. The red arrows highlights these interactions. The red and blue dashed ellipses mark the Cr1-I and Cr2-I interactions considered in the COHP calculation. b Magnetic configurations of FM, AFMS, and AFMZ, with light coral and green arrows indicating spin-up and spin-down, respectively. In the AFMS phase, spins align antiparallel along the b-axis, while in the AFMZ phase, spins alternate antiparallel along the a-axis.

Full size image

To compare the ground-state magnetic configurations, a 2 × 1 × 1 supercell was employed. Three magnetic configurations were considered: ferromagnetic (FM), antiferromagnetic-stripe (AFMS), and antiferromagnetic-zigzag (AFMZ), as illustrated in Fig. 1b. In the FM configuration, the spins are aligned parallel for both the first- and second-nearest neighbors (NN). In the AFMS configuration, the Cr chain’s first NN is aligned parallel, while the second NN is antiparallel. For the AFMZ configuration, the first NN are antiparallel to each other. The same supercell dimensions were used for all configurations to ensure consistency and eliminate variations due to different cell sizes.

The magnetic stability of a CrI2 monolayer was analyzed by calculating the energy differences between several magnetic configurations. Using U = 5.6 eV, our results show that the AFMS configuration is the magnetic ground state, aligning with previous calculations for the freestanding CrI2 monolayer8,13,39. We also calculated the energy using various U values as shown in Fig. 2. Different U values affect the relative energy of AFMS or AFMZ states with the FM state. For U = 0, the ΔE < 0 indicates that FM is less stable compared to AFMS and AFMZ states. An increase in U will stabilize the FM energy. For example, U = 3 gives a more stable FM state than the AFMZ state. At U = 7, the FM state is more stable than the AFMS and AFMZ states. The AFMZ state energy is consistently the highest. Therefore, it is preferable for the system to undergo a phase transition between AFMS and FM states.

Fig. 2: The relative energy of AFM with FM as variation of U.
figure 2

The red (blue) bar indicated the relative energy of AFMS (AFMZ), respectively.

Full size image

Strain-induced magnetic properties

Given the instability of the AFMZ configuration, we will compare the energy of strain effects on the FM and AFMS configurations. As shown in Fig. 3, both biaxial and uniaxial strains influence the magnetic coupling energy. The compressive strain strengthens the stability of the AFM state. In contrast, tensile strain destabilizes the AFM state, which can be seen by an increase of ΔE = EAFMS − EFM. Notably, a transition from AFM to FM occurs when tensile strain exceeds 2% under biaxial strain and 4% under uniaxial strain along the a-axis. This strain-driven tunability remains robust across different U parameters, e.g., U = 7 eV (Fig. S3), where the FM state is preferred at zero strain.

Fig. 3: Energy difference between the AFMS and FM configurations under strain calculated with U = 5.6 eV.
figure 3

The light coral background indicates the stable region of the AFM phase, and the light green indicates the FM phase.

Full size image

The magnetocrystalline anisotropy (MCA) energy, denoted as EMCA, is defined as the energy difference between a system with magnetization along an arbitrary axis \(E\left(\theta \right.\) and the system with magnetization along the easy axis E0, expressed as EMCA = E(θ) − E0. The spin-orbit coupling (SOC) is included in the MCA calculation. We confirmed that SOC does not influence the magnetic stability or the robustness of our results, as demonstrated in Fig. S2.

The EMCA strain-dependent behavior is plotted as supplemental Figs. S8 and S9. In the unstrained case (Fig. S8d), the easy-axis magnetization directions are oriented at angles θ = 30∘ and 210∘ relative to the out-of-plane direction of the monolayer on the y-z plane. However, under compressive biaxial strain, the anisotropy energy is reduced and even reorients the easy axis to θ = 150∘ and 330∘ at −3% strain. This reorientation aligns with the elongated Cr-I bond direction.

Conversely, the biaxial tensile strain substantially enhances the MCA energy, increasing up to 1.77 meV at 5% strain, indicating a stabilization of the ferromagnetic order. A similar enhancement is observed under uniaxial strain: the MCA energy rises to 1.6 meV under 5% tensile strain along the a-axis and 0.47 meV under 5% strain along the b-axis (Fig. S6b, d. Interestingly, the easy-axis reorientation observed under compressive strain is absent under −5% uniaxial strain along the a-axis.

Exchange coupling and magnetic interactions

To investigate the exchange interactions of Cr neighbors, we analyze spin-spin interactions using the Heisenberg Hamiltonian:

$$H=-2\mathop{\sum}\limits_{i < j}{J}_{ij}\,{\hat{{{\bf{S}}}}}_{i}\cdot {\hat{{{\bf{S}}}}}_{j},$$
(1)

The Jij represents the symmetric exchange coupling constant between Cr sites. The sign of J determines the nature of the interaction: J > 0 indicates FM coupling, while J < 0 signifies AFM coupling. The \({\hat{{{\bf{S}}}}}_{i}\) and \({\hat{{{\bf{S}}}}}_{j}\) are the spin unit vectors of the i-th and j-th Cr atoms.

We consider the first (J1) and second (J2) NN interactions shown in Fig. 1a. We ignore J3 because this interaction is minor, and the third NN distance is more than 7 Å (see Supplemental Materials S5). The J values are calculated by analyzing the energies of three magnetic configurations described in Fig. 1b. Therefore, their respective energies are expressed as:

$$E=\left\{\begin{array}{ll}-4{J}_{1}-8{J}_{2}\quad &\,{\mbox{(FM)}}\,\\ -4{J}_{1}+8{J}_{2}\quad &\,{\mbox{(AFMS)}}\,\\ 4{J}_{1}\quad &\,{\mbox{(AFMZ)}}\,\end{array}\right.,$$
(2)

Then, the J1 and J2 can be determined and can be plotted under various compressive and tensile strain conditions, as shown in Fig. 4. The results show that J1 > 0 for strain levels between −4% and 5%. This strong FM interaction explains the instability of the AFMZ configuration. We deduce that the AFMZ state could be stabilized by introducing compressive biaxial strain or uniaxial strain along the a-axis as shown by J1 < 0 at −5% strain regime indicated from Fig. 4a. Additionally, J1 exhibits minimal variation under the uniaxial b-strain compared to the biaxial and uniaxial a-strain. It should be noted that the exchange coupling J1 is ferromagnetic in the AFMS state. Although J2 is smaller in magnitude compared to J1, it plays a pivotal role in the magnetic phase transition from the AFM to the FM state under tensile strain, as shown in Fig. 4b. In the strain-free state, J2 promotes AFM interactions. Applying tensile strain causes J2 to shift to FM, as the trend is similar to Fig. 3.

Fig. 4: Magnetic exchange coupling under variation of strain.
figure 4

a The first NN exchange coupling J1 and b the second NN exchange coupling J2 under strain. The light coral indicates the stable region of the AFM phase, and the light green indicates the FM phase.

Full size image

To explain the magnetic phase transition in CrI2, it is essential to consider the origin of its magnetic coupling, which involves two key mechanisms: direct interaction and superexchange interaction. Direct interaction refers to the direct coupling between the d-orbitals of adjacent Cr atoms. This interaction favors AFM ordering due to the overlap of d-orbitals40. The AFM coupling from direct interaction gets stronger for a shorter Cr-Cr distance as the electron hopping increases. This can be seen in Fig. 4a, where the compressive strain of biaxial and along a-axis causes J1 to decrease strongly.

The suppression of the AFM coupling with reduced hopping explains the increasing stability of the FM phase relative to AFMS or AFMZ as U increases, as shown in Fig. 2. As U enhances electron localization in the d-orbitals, it weakens direct d-d hopping interactions between the first NN. Note that U has minimal effect on the relative energy between AFMS and AFMZ because both configurations preserve the antiparallel alignment of the second NN spins. Since electron localization affects their exchange interactions similarly, their relative stability is maintained.

Conversely, the superexchange interaction follows the Goodenough-Kanamori rules41,42 and involves an indirect magnetic interaction mediated through a non-magnetic ion. In CrI2, the superexchange occurs via the d-p-d pathway, where the iodine p-orbitals mediate the coupling between the d-orbitals of Cr atoms. The geometry of the Cr-I-Cr bond is critical to the nature of this interaction. When the bond angle is close to 90∘, superexchange favors FM coupling. Thus, the overall magnetic behavior of CrI2 results from the combined influence of direct interaction (JD) and superexchange (JS) interaction. The relative magnitudes of these terms determine the net magnetic ordering, expressed as J = JD + JS.

Bonding and electronic structure analysis

The competition between AFM and FM interactions is strongly influenced by atomic distances and bond angles, which are modified under strain. Figure 5a illustrates these structural changes, focusing on Cr-Cr distances (d1 and d2) for the first and second NN, which correspond to direct interaction coupling (JD), as well as Cr-I bond distances (db1 and db2) and their respective angles (Θ1) and (Θ2) that connect the Cr-I-Cr pairs corresponding to (JS).

Fig. 5: Structural change under variation of strain.
figure 5

a Structural parameter of CrI2. The distances of the first (d1) and second (d2) NN, as well as Cr-I bond distances (db1 and db2), under b biaxial, c uniaxial-a, and d uniaxial-b strain.

Full size image

The strain has minimal effect on bond angles, causing the angle to fluctuate between 86∘ and 95∘ for Θ1 and 86∘ and 92∘ for Θ2, as shown in the supplemental Fig. S6. As expected, Θ1 is sensitive to strain along the a-axis, while Θ2 responds primarily to strain along the b-axis. Additionally, biaxial strain modulates both angles simultaneously. Nevertheless, these fluctuations remain close to 90∘, ensuring the superexchange interaction is always ferromagnetic based on Goodenough-Kanamori rules. Under biaxial strain (Fig. 5b), the bond lengths d1, d2, and db1 increase or decrease uniformly with minimal deviation of db1. Notably, d1 and d2 increase more rapidly under tensile strain and will significantly reduce the AFM direct interaction.

In contrast, uniaxial strains along the a- and b-axes exhibit distinct behaviors. Under uniaxial tensile strain along the a-axis (Fig. 5c), d1 and db1 increase, while d2 remains unchanged, and db2 decreases. Conversely, tensile strain along the b-axis (Fig. 5d) results in an increase in d2 and db2, accompanied by a decrease in d1. A comparison of db1 and db2 under both uniaxial strains indicates that db2 is more sensitive to strain than db1. We confirmed that db1 is identical for both the top and bottom layers, and likewise for db2, indicating the preservation of inversion symmetry. This confirms the absence of the Dzyaloshinskii-Moriya interaction in both the unstrained and uniaxially strained states.

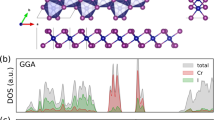
To explore the role of superexchange interaction, we calculated the partial density of states (PDOS) and crystal orbital Hamiltonian population (COHP) for the ground-state FM phase. The unit cell was oriented such that the xyz-axis aligns with the octahedral bonding direction. The COHP analysis was conducted on the Cr-I interaction according to Fig. 1a. The PDOS for CrI2 is presented in Fig. 6a, b, revealing semiconductive behavior with an energy gap of ~1.7 eV, consistent with previous studies on monolayer CrI28,13.

Fig. 6: Electronic structure and bonding interactions in CrI2.
figure 6

The PDOS of FM CrI2 for a Cr-d orbitals and b I-p orbitals. The −COHP for Cr-I interaction is shown for c spin-up and d spin-down.

Full size image

Approximately, the octahedral crystal field created by surrounding ligands splits the d-orbitals of Cr atoms into two groups: eg orbitals (\({d}_{{x}^{2}-{y}^{2}}\) and \({d}_{{z}^{2}}\)) and t2g orbitals (dxy, dxz, and dyz). However, Further energy split occurs within the eg group, where the in-plane \({d}_{{x}^{2}-{y}^{2}}\) orbital lies higher than the out-of-plane \({d}_{{z}^{2}}\) orbital due to Jahn-Teller distortion.

Strong hybridization occurs between the \({d}_{{z}^{2}}\)-pz orbitals and \({d}_{{x}^{2}-{y}^{2}}\)-px/py orbitals. The highest occupied states are dominated by \({d}_{{z}^{2}}\)-pz, and lowest unoccupied states mainly consist of \({d}_{{x}^{2}-{y}^{2}}\)-px/py. The COHP is plotted for up spins and down spins in Fig. 6c, d, respectively. While bonding interactions are located in occupied states, we find that the hybridization \({d}_{{z}^{2}}\)-pz below the proximity of the Fermi level has an antibonding character. This antibonding interaction weakens one of the Cr-I bonds, resulting in the observed Jahn-Teller elongation.

To quantify the bond interaction, integrated −COHP (−ICOHP) were calculated and shown in Fig. 7. The Cr1-I bonding comes from several interactions, but is dominated by Cr1 \({d}_{{x}^{2}-{y}^{2}}^{\downarrow }\)-I \({p}_{x}^{\downarrow }\) and Cr1 \({d}_{{x}^{2}-{y}^{2}}^{\uparrow }\)-I \({p}_{x}^{\uparrow }\) interactions. Additionally, the Cr2 \({d}_{{z}^{2}}^{\downarrow }\)-I \({p}_{z}^{\downarrow }\) interaction is dominant in Cr2-I bonding. Because the Cr1-I (Cr2-I) interaction corresponds to db1(db2) bonds, we conclude that these three interactions greatly contribute to the FM superexchange interaction.

Fig. 7: The orbital resolved −ICOHP for the Cr-I interaction.
figure 7

a spin-up component and b spin-down component. The blue (red) bar indicates the Cr1-I (Cr2-I), respectively.

Full size image

Discussion

Now, let us discuss the mechanism of superexchange interaction. In the standard theory of the Goodenough-Kanamori rule, the superexchange interaction can be described by Anderson’s mechanism43 of hopping and exchange interaction. In this framework, hopping occurs only between non-orthogonal orbitals, while the orthogonality of the exchange integral governs spin interactions. Specifically, FM interaction arises between orthogonal orbitals, whereas antiferromagnetic AFM interaction occurs between non-orthogonal orbitals.

The FM superexchange mechanisms of J1 and J2 are facilitated by virtual tpdσ hopping through σ-bonds, as illustrated in Fig. 8. The J1 FM superexchange involves Cr1 and \({{{\rm{Cr1}}}}^{{\prime} }\) sites, where each Cr atom connects through I px and I py orbitals, respectively. Our −ICOHP calculations (Fig. 7a) reveal a strong interaction between the Cr1 \({d}_{{x}^{2}-{y}^{2}}^{\uparrow }\) orbital and I \({p}_{x}^{\uparrow }\) orbital. By symmetry, an equivalent interaction occurs between \({{{\rm{Cr1}}}}^{{\prime} }\,{d}_{{x}^{2}-{y}^{2}}^{\uparrow }\) and I \({p}_{y}^{\uparrow }\) orbitals, as confirmed in Supplementary Fig. S7. These strong interactions facilitate electron hopping, as shown by the dashed black arrows in Fig. 8a. Then, the remaining half-filled \({p}_{x}^{\downarrow }\) and \({p}_{y}^{\downarrow }\) orbitals interact through ferromagnetic exchange.

Fig. 8: Scheme of superexchange interaction.
figure 8

a J1 and b J2 interactions. The dashed light green/coral arrows indicate virtual spin, the dashed black arrows indicate the hopping path, and the red arrows indicate exchange interaction.

Full size image

The J2 mechanism exhibits more complex behavior. Despite DOS calculations indicating effective hybridization between the Cr2 \({d}_{{z}^{2}}^{\uparrow }\) orbital and I \({p}_{z}^{\uparrow }\) orbital, the transfer of electrons between these orbitals requires higher energy due to the nature of antibonding interaction. Hopping from the I \({p}_{z}^{\uparrow }\) orbital to the Cr2 \({d}_{{z}^{2}}^{\uparrow }\) orbital is prohibited by the Pauli exclusion principle, as the Jahn-Teller effect lowers the energy of the Cr2 \({d}_{{z}^{2}}\) orbital, leaving the \({d}_{{z}^{2}}^{\uparrow }\) state occupied. Conversely, our −ICOHP calculations (Fig. 7b) show a strong bonding interaction between Cr2 \({d}_{{z}^{2}}^{\downarrow }\) and I \({p}_{z}^{\downarrow }\), indicating significant hopping along the Cr2 \({d}_{{z}^{2}}^{\downarrow }\)-I \({p}_{z}^{\downarrow }\) pathway. Unpaired I \({p}_{z}^{\uparrow }\) orbital couples ferromagnetically with the I \({p}_{x}^{\uparrow }\) orbital, as the I \({p}_{x}^{\downarrow }\) electron also hops into the unoccupied Cr1 \({d}_{{x}^{2}-{y}^{2}}^{\downarrow }\) by bonding interaction. These hopping pathways for the J2 superexchange mechanism are illustrated in Fig. 8b. Interestingly, the p↓ electron hopping in J2 interaction fails to maximize the Cr atom’s magnetic moment as it is antiparallel with spins in occupied t2g orbitals, resulting in higher energy compared to the FM interaction in J1 and consequently weakening of the ferromagnetic coupling.

The interactions between orthogonal unpaired p orbital due to hopping yields Hund’s coupling \({J}_{H}^{p}\). The FM superexchange interaction for J1 and J2 can be expressed as44:

$${J}_{{{\rm{FM}}}}=-\frac{{t}_{pdm}^{2}{t}_{pd{m}^{{\prime} }}^{2}}{{\Delta }_{{{\rm{CT}}}}^{2}{(2{\Delta }_{{{\rm{CT}}}}+{U}_{pp})}^{2}}{J}_{{{\rm{H}}}}^{p},$$
(3)

here, the ΔCT is the charge transfer gap that represents the energy required to transfer an electron from the ligand p orbital to the metal d orbital. Meanwhile, Upp denotes the on-site Coulomb-repulsion energy between two holes in the p orbital. The hopping parameter, tpdm, is closely related to the bonding interaction. For J1, the symmetry of the px and py orbitals ensures that \({t}_{pdm}={t}_{pd{m}^{{\prime} }}\).

The Cr-I bond interactions influence the J2 FM interaction. Moreover, tensile strain reduces the FM superexchange, which affects the dependence of magnetic interaction on the fashion of strain application, i.e., biaxial, a-uniaxial, or b-uniaxial. To demonstrate this weakening, we can correlate tpdm with the −ICOHP. As shown in Fig. 9, the interactions between Cr1 \({d}_{{x}^{2}-{y}^{2}}^{\downarrow }\)- I \({p}_{x}^{\downarrow }\) and Cr2 \({d}_{{z}^{2}}^{\downarrow }\)-I \({p}_{z}^{\downarrow }\), which contribute to J2, diminish under tensile strain due to the increased Cr–I bond lengths (db1 and db2).

Fig. 9: The − ICOHP values under strain for the bond interactions related to J2.
figure 9

a Cr1 \({d}_{{x}^{2}-{y}^{2}}\)-I px spin-down, and b Cr2 \({d}_{{z}^{2}}\)-I pz spin-down.

Full size image

Under biaxial tensile strain, despite the FM interaction being weakened, the reduction of the direct AFM interaction is more pronounced, ultimately leading to the AFM–FM phase transition. Meanwhile, tensile strain along the a-axis reduces the Cr1 \({d}_{{x}^{2}-{y}^{2}}^{\downarrow }\)-I \({p}_{x}^{\downarrow }\) interaction, though its strength remains substantial. The enhancement of the Cr2 \({d}_{{z}^{2}}\)-I pz interaction also contributes to the phase transition to the FM state. Conversely, since the Cr2 \({d}_{{z}^{2}}^{\downarrow }\)-I \({p}_{z}^{\downarrow }\) interaction is already weak, applying tensile strain along the b-axis further suppresses it. This results in a more pronounced weakening of FM superexchange compared to a-axis uniaxial strain, making the phase transition more difficult to achieve under b-axis uniaxial tensile strain.

In addition to the fine-tuning of magnetic couplings using strain, we expect the increase of the critical temperature Tc under tensile strain. According to Berezinskii-Kosterlitz-Thouless (BKT) theory, the critical temperature Tc of low-dimensional materials can be estimated as 0.89 J1/kB45, where kB is the Boltzmann constant. With increasing biaxial strain, Tc rises from 37.3 K at 2% strain to 48.9 K at 5% strain. Furthermore, to provide a more accurate description of CrI2’s magnetism under strain, biquadratic interactions should be considered46, especially given their strain-dependent behavior, as demonstrated in CrTe247. The Kitaev interactions may contribute to the magnetic behavior of CrI2. However, the elongation of Cr-I bonds and two-fold coordination in CrI2 might lead to different anisotropic properties compared to other MX2 materials, such as NI248.

In summary, we investigated the magnetic interaction of a CrI2 monolayer under various strain applications. Using a U value of 5.6 eV derived from linear response calculations, we identified the AFMS configuration as the magnetic ground state. Compressive strain enhances the AFM stability, while tensile strain induces a phase transition to the FM ordering, with critical thresholds of 2% for biaxial strain and 4% for uniaxial a-strain. Exchange coupling constants, analyzed using the Heisenberg model, revealed that FM superexchange dominates J1, whereas J2 plays a key role in capturing the AFM-FM phase transition under tensile strain. Further analysis reveals that the FM superexchange interaction strongly correlates with the hybridization of \({d}_{{x}^{2}-{y}^{2}}\)-px/py and \({d}_{{z}^{2}}\)-pz orbitals. Electronic structure calculation and bond distance modulation suggest that a rapid weakening of direct interactions primarily drives the phase transition under tensile strain rather than the enhancement of FM superexchange interaction. Our prediction of the weakening of AFM coupling suggests that a pronounced signal should be observable in magneto-optic measurements, such as reflective magnetic circular dichroism (RMCD) or the magneto-optical Kerr effect (MOKE). Additionally, the magnetic configuration can be directly probed using techniques like neutron scattering or Mössbauer spectroscopy. Our findings highlight the interplay between electronic structure, strain, and magnetic coupling in CrI2, offering valuable insights into the tunability of its magnetic properties for nanospintronic applications.

Methods

Density functional theory calculation

We performed first-principles calculations of CrI2 using density functional theory (DFT) with the projector augmented-wave (PAW) method49 and the PBE exchange-correlation functional50, as implemented in the VASP code51. A vacuum of ~15 Å was used to prevent interlayer interactions. The 520-eV plane-wave cutoff energy and a 0.4 π-Å−1 k-mesh were used for the calculations. Lattice and atomic positions were relaxed until the forces acting on each atom were <0.01 eV/Å. To account for van der Waals interactions, the DFT-D3 functional by Grimme was applied52.To properly describe the strongly correlated system, the DFT + U scheme is introduced53. The U parameter was calculated using the linear response method based on perturbation theory30 using a 3 × 3 × 1 supercell of the monolayer structure (see Supplemental Materials S1).

We applied biaxial and uniaxial strains along the a- and b-axes. Strain is defined as (u − u0)/u0, where u is the strained lattice vector and u0 is the unstrained one. For uniaxial strain, one in-plane lattice vector is strained while the other is allowed to relax. Magnetic stability is assessed by calculating the energy difference at each strain level.

The bonding and antibonding characteristics were analyzed using the crystal orbital Hamilton population (COHP) method (see Supplemental Materials S6), as implemented in the LOBSTER code54,55, where the −COHP > 0 indicates bonding interaction and −COHP < 0 is the antibonding interaction.