Introduction

Ultrafast optical spectroscopy has been extensively used to study the dynamics of a variety of novel phenomena, such as the coherent optical excitation of phonons in solids1,2,3,4, the driving of metastable phase transitions5,6,7,8, and the dynamic control of magnetic materials9,10,11. In particular, the optical control of magnetic order is of great importance to push the bounds of magnetic memory storage12 and spintronic13,14 devices. However, in order to achieve this, a clear understanding of how the charge, spin, and lattice subsystems interact on their intrinsic timescales is of critical importance4,15,16,17. With the recent discovery of van der Waals (vdW) materials hosting intrinsic magnetic order down to the monolayer limit, there has been a new push to explore how ultrafast photoexcitation can be exploited to manipulate their properties at the nanoscale18,19,20. This, in turn, could yield revolutionary advances relevant to nanoscale information storage9,12, spintronic applications21,22,23, and proximal control of complementary nanomaterials24.

In addition to thickness (i.e., layer number), the properties of vdW magnets are highly sensitive to external stimuli25, making them an ideal candidate material from the perspective of dynamically reconfigurable nanoscale magnetic devices. Various studies have shown how their magnetic properties can be altered through pressure, chemical doping, proton irradiation, and photoexcitation26,27,28,29,30,31,32. The latter is particularly interesting because it is a contactless route for high-speed control of magnetic properties. Recently, intense femtosecond pulses have proven successful in driving picosecond de- and re-magnetization4,33, all-optical switching of magnetic states in an atomically thin ferromagnet34, the coherent excitation of GHz magnons35, and revealing the presence of spin-coupled coherent lattice vibrations4. The latter is due to strong coupling between the lattice and spin degrees of freedom, a feature that has proven to be of importance in a variety of layered magnetic materials.

In this work, we explore the electronic, spin, and structural dynamics of the pseudo-vdW ferrimagnet Mn3Si2Te6 driven by femtosecond optical pulses. By applying an augmented two-temperature model (A2TM)36, we are able to extract the electron-electron thermalization time and electron-phonon coupling constant, and simulate the pump-induced incoherent reflectivity dynamics. This reveals unusual temperature dependencies in the decay time associated with slow electronic relaxation, suggestive of spin-mediated relaxation pathways. Moreover, we reveal the presence of strong coherent lattice vibrations whose oscillatory frequency is sensitive to the onset of ferrimagnetic order. We observe a pronounced temperature-dependent stiffening of the phonon below the critical temperature (\({T}_{c}\)) that coincides with the temperature-dependent magnetization. This suggests a significant interplay between structure and magnetism in this material, which has recently been linked to novel emergent phenomena37,38.

Results

Ultrafast dynamics

As shown in Fig. 1a, Mn3Si2Te6 is a self-intercalated layered magnetic material comprising two distinct magnetic sublattices. The first sublattice hosts an Mn site (Mn1), which is within a hexagonal structure, typical of vdW materials. The second sublattice contains another Mn site (Mn2), which fills a third of the octahedral holes within the vdW gap37,39,40. The Mn1 moments lie primarily along the \({ab}\)-axis while the Mn2 moments are aligned in an antiparallel fashion39,41. This magnetic structure gives rise to frustration39, setting the stage for ferrimagnetic order below \({T}_{c}\approx 75\text{K}\)37,42. The unusual magnetic order also gives rise to nodal line degeneracies, which, when lifted with external magnetic fields, reveal the presence of colossal magnetoresistance41 due to helically aligned chiral orbital currents that circulate along the Te–Te edges of the Mn–Te octahedra38. Additionally, this field also drives a concomitant reduction in the \({ab}\)-plane lattice parameter, pointing to the presence of strong spin-lattice coupling. Recently, spontaneous Raman studies have characterized the temperature evolution of various phonon modes in Mn3Si2Te6. Djurdjić et al. found two Raman modes with A1g symmetry that provide evidence of three successive phase transitions (between \(142\,\mathrm{and}\,285\,\text{K}\)) that could arise from competing magnetic states known to exist in the material43. Nevertheless, to date, the manifestation of the strong spin-lattice coupling, alluded to in ref. 37, particularly under dynamic non-equilibrium conditions, has yet to be investigated.

Fig. 1: Crystal structure and ultrafast dynamics of Mn3Si2Te6.
figure 1

a The self-intercalated trigonal structure of Mn3Si2Te6 with its magnetic moments (red arrows) lying within the ab-plane, b \(\Delta R/R\) from 25 to 125 K at a pump fluence of \(1.5\) \(\text{mJ}/{\text{cm}}^{2}\), and c the \(\Delta R/R\) traces with varying pump fluence measured at 300 K. The black lines in both b and c are fits to the data using Eq. 1.

Full size image

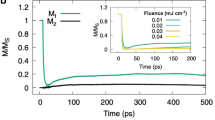
In our study, bulk-like flakes of single-crystal Mn3Si2Te6 were prepared via the self-flux method37,40. The sample was mechanically exfoliated and transferred to an optical cryostat in an argon atmosphere to prevent the formation of TeO2 complexes43. Degenerate ultrafast transient reflectivity measurements were then performed using 1.55 eV, ~60 fs pulses supplied by a regeneratively amplified Ti:sapphire laser system. The photon energy used was higher than the estimated bandgap (<0.5 eV) for this material41,44. Figure 1b shows the differential reflectivity (ΔR/R) as a function of temperature. Two main components are observed, namely a broad time-dependent incoherent background superimposed with pronounced coherent oscillations. The former is due to the nonequilibrium dynamics associated with hot electrons driven by the above bandgap photoexcitation. This can be fit using a biexponential function2,16,45,

$$\frac{\Delta R}{R}=A{e}^{-\frac{t}{{\tau }_{1}}}+B{e}^{-\frac{t}{{\tau }_{2}}}$$
(1)

where the amplitudes (\(A\) and \(B\)) and time constants (\({\tau }_{1}\) and \({\tau }_{2}\)) are treated as free parameters. The black curves in Fig. 1b show the best fits to the temperature-dependent data using a trust-region reflective least squares algorithm, revealing a relatively fast rise followed by a slow relaxation, which is consistent across the entire temperature range. Similar fits were calculated for the pump-fluence-dependent measurements (Fig. 1c), which readily reveal an increase in the magnitude of \(A\) and \(B\) at higher fluences (see Supplementary Fig. 1), consistent with their hot electron origin.

Augmented two-temperature model and incoherent dynamics

To help interpret the incoherent dynamics, we implemented an A2TM approach36 that allows us to capture the dynamics of the two primary subsystems, namely electrons and phonons, that lead to the pump-induced reflectivity modulations. The influence of magnetization dynamics is incorporated by applying a first-order approach for the electron-spin interaction, assuming strong coupling of electronic and magnetic excitations. The A2TM system is defined by the temperatures of the electrons and phonons (\({T}_{{\rm{e}}}\) and \({T}_{{\rm{p}}}\), respectively) and the electronic, lattice, and spin heat capacities (\({C}_{{\rm{e}}}\), \({C}_{{\rm{p}}}\), and \({C}_{{\rm{m}}}\), respectively). The governing equations are

$$\left({C}_{{\rm{e}}}+{C}_{{\rm{m}}}\right)\frac{{{dT}}_{e}}{{dt}}=-{g}_{{\rm{ep}}}\left({T}_{{\rm{e}}}-{T}_{{\rm{p}}}\right)+S\left(t\right)$$
(2)
$${C}_{{\rm{p}}}\frac{{{dT}}_{p}}{{dt}}={g}_{{\rm{ep}}}\left({T}_{{\rm{e}}}-{T}_{{\rm{p}}}\right)$$
(3)

Where \({g}_{{\rm{ep}}}\) is the coupling between the electrons and phonons. The values of \({C}_{{\rm{e}}}\) and \({C}_{{\rm{m}}}\) can be obtained from literature37, while \({C}_{{\rm{p}}}\) can be calculated from the Debye model with the experimentally measured Debye temperature of \({T}_{{\rm{D}}}=159{\rm{K}}\) (see Supplementary Fig. 3)37. Finally, \(S(t)\) is the absorbed laser pulse energy that excites the electronic system. While this can be described by a Gaussian function corresponding to the experimental laser pulse, a more accurate approach involves convoluting this pulse with a memory kernel that models the build-up and depletion of a bath of non-thermal photoexcited electrons45. This leads to

$$S\left(t\right)\to \hat{S}\left(t\right)={\int }_{0}^{t}d{t}^{{\prime} }S\left({t}^{{\prime} }\right)W\left({{t}}-{{{t}}}^{{\prime} }\right)$$
(4)

where \(S\left(t\right)={S}_{0}{e}^{-{t}^{2}/2{\sigma }^{2}}\) and \(W\left(t\right)=1-{e}^{{\left(t/{\tau }_{{\rm{ee}}}\right)}^{2}}\). Here, \({S}_{0}\) is the absorbed pulse energy, \({w}_{t}=2{\left(2\mathrm{ln}2\right)}^{1/2}\sigma\) is the Gaussian laser pulse width, and \({\tau }_{{\rm{ee}}}\) is the electron-electron thermalization time. Using Eqs. (2)–(4) and assuming that the differential reflectivity scales with the electronic temperature, we can fit the experimental data to \({\hat{T}}_{{\rm{e}}}\left(t\right)={c}_{t}\left({T}_{{\rm{e}}}\left(t-{\tau }_{0}\right)-{T}_{0}\right)/{T}_{{\rm{e}},\max }\), where \({c}_{t}\) is a scaling factor to account for the peak height and \({\tau }_{0}\) is used to account for small offsets in the delay time of the experimental data. We note that we neglect any explicit spatial dependence of the pulse excitation and temperature profiles.

Having fixed the heat capacities associated with the explicitly computed subsystems from Eqs. (2) and (3), we are left with a set of five fit parameters to model the experimental data, namely \({\tau }_{{\rm{ee}}}\), \({g}_{{\rm{ep}}}\), \({S}_{0}\), \({c}_{t}\), and \({\tau }_{0}\), where only the first two are essential in capturing the physics of the system. Using these parameters, we can accurately and consistently model the experimentally observed incoherent reflectivity dynamics over the entire range of temperatures explored in our study (see Supplementary Fig. 4). This leads to excellent agreement between the experimental values of \({\tau }_{1}\) and \({\tau }_{2}\) from Eq. (1) (teal dots in Fig. 2b, c) and those from the A2TM (orange dots in Fig. 2b, c). On the basis of our model, we associate \({\tau }_{1}\) primarily with rapid electronic quasi-thermalization, while \({\tau }_{2}\) is the timescale governed predominantly by quasiparticle (e.g., phonon) mediated electronic scattering processes. \({\tau }_{2}\) increases slightly from 125 to 60 K (teal dots in Fig. 2c). This trend reverses below ~60 K, where the scattering becomes faster, reaching a value of ~13 ps at 25 K. This is likely due to the activation of additional scattering channels associated with the long-range magnetic order that sets in below the critical temperature. A likely driver is phonon-mediated spin-flip scattering46, which is known to significantly influence the relaxation dynamics of other vdW magnetic materials, notably CrI34. Additionally, other spin-dependent processes, such as those where the magnon plays an analogous role to that of the phonon (i.e., electron–magnon scattering)47 can also be activated near or below the critical temperature. These two contributions, together, are the likely cause of the slight suppression of \({\tau }_{2}\) at low temperatures.

Fig. 2: Incoherent dynamics and A2TM simulations.
figure 2

a The experimental \(\Delta R/R\) (gray) measured at 25 K with the biexponential fit from Eq. 1 (blue trace) and the A2TM simulation (magenta trace). b The temperature dependence of τ1 (rise time) and c τ2 (decay time), along with the time constants extracted from the A2TM simulation. Error bars in b and c correspond to the 95% confidence bounds of the time constants from the fitting algorithm.

Full size image

Another feature of interest is the slightly non-monotonic temperature dependence of \({\tau }_{2}\). This could be due to a critical slowing down of the spin-mediated electronic scattering processes. Indeed, similar phenomena have been observed in the reflectivity dynamics of, for example, BiFeO3 films48. Additionally, other vdW magnets show analogous effects, with large variations in how much their spin relaxation slows near their phase transitions. These variations are correlated with features in their temperature-dependent heat capacities, \(C\left(T\right)\). For instance, NiPS3 does not have a pronounced \(\lambda\) peak in its \(C(T)\), reflected in a relatively small slowing down of its relaxation dynamics49. In contrast, FePS3 has a more pronounced \(\lambda\) peak in its \(C(T)\), leading to a greater increase in its decay time in the vicinity of its phase transition temperature49,50. For the case of Mn3Si2Te6, this material does have a pronounced \(\lambda\) peak, as demonstrated by prior reports37,51. This would support the presence of critical spin fluctuations in the vicinity of the transition temperature, which would reasonably impact both spin-flip mediated electron-phonon scattering and electron-magnon scattering pathways and, in turn, lead to the observed non-monotonic temperature variation of \({\tau }_{2}\).

Coherent dynamics

We now turn our attention to the coherent oscillatory dynamics. Figure 3a shows the measured residual \(\Delta R/R\) (\({\Delta R}_{\text{res}}/R\)) obtained by subtracting out the electronic background discussed above. Strong cosine-like coherent oscillations are observed at all temperatures with a decay time of \(\sim 3\,\text{ps}\) and an oscillatory frequency of \(\sim 3.52\,\text{THz}\), seen from the Fourier transforms (FTs) of the time-domain data, that softens with increasing pump fluence (see Supplementary Fig. 6). Based on past measurements52, we identify this mode as a symmetric coherent A1 tellurium phonon, driven via a displacive excitation process53,54, that originates from Te segregation on the surface of Mn3Si2Te6. Such segregation is relatively common in Te-containing compounds and is typically associated with accumulated laser-induced heating55,56, though its presence is notable in our experiments given our relatively low pump fluences and laser repetition rate. We also observe a subtle, yet significant, stiffening of this mode at lower temperatures, evidenced by the shift of the FT peak to higher frequencies in Fig. 3(b). To better capture the temperature-dependent variation of the phonon frequency, we fit a damped sine function to the \({\Delta R}_{\mathrm{res}}/R\),

$$\frac{{\Delta R}_{\mathrm{res}}}{R}={A}_{DO}{e}^{-\frac{t}{{\tau }_{DO}}}\sin ({\omega }_{DO}t+{\phi }_{DO})$$
(5)

where \({A}_{\mathrm{DO}}\) is the amplitude, \({\tau }_{\mathrm{DO}}\) is the time constant, \({\omega }_{\mathrm{DO}}\) is the frequency, and \({\phi }_{\mathrm{DO}}\) is the phase shift of the damped oscillator. The black lines in Fig. 3a are the fits to Eq. 5 using a trust-region reflective least squares algorithm. We plot the temperature dependence of \({\omega }_{\mathrm{DO}}\) in Fig. 4 (the temperature dependence of \({A}_{\mathrm{DO}}\) and \({\tau }_{\mathrm{DO}}\) are also shown in the Supplementary Fig. 7). The frequency is relatively constant (~3.53 THz) above \({T}_{\text{c}}\), but increases rapidly from 75 K down to 50 K, before stabilizing to ~3.57 THz at lower temperatures. This temperature dependence is distinct from what would be expected under the assumption of thermally driven lattice contraction57,58. This can be modeled as a temperature-dependent phonon frequency, \(\omega \left(T\right)\), with contributions from both thermal lattice contraction and anharmonicity. This is expressed as58

$$\omega \left(T\right)={\omega }_{o}+{\Delta }_{0}\left(T\right)+\Omega \left(1+2{n}_{{\omega }_{0}/2}\right)$$
(6)

where,

$${\Delta }_{0}\left(T\right)=-{\omega }_{0}\gamma {\int }_{0}^{T}\left[{\alpha }_{\parallel }\left(T{\prime} \right)+2{\alpha }_{\perp }\left(T{\prime} \right)\right]{dT}{\prime}$$
(7)

Here, \({\omega }_{0}\) is the phonon frequency at the low-temperature limit, \(\gamma =1.45\) is the Grüneisen parameter of Mn3Si2Te658,59, \({\alpha }_{\parallel }\) and \({\alpha }_{\perp }\) are the linear thermal expansion coefficients parallel and perpendicular to the \(c\)-axis of the crystal, \(\Omega\) is an anharmonic constant, and \({n}_{\omega }={\left[\exp \left(\hslash \omega /{k}_{{\rm{B}}}T\right)-1\right]}^{-1}\) is the Bose-Einstein factor. \({\alpha }_{\parallel }\left(T\right)\) and \({\alpha }_{\perp }\left(T\right)\) were determined from derivatives of the temperature-dependent \(c\)- and \(a\)-axis lattice parameters, respectively39. This allows us to calculate expected \(\omega \left(T\right)\) curves, which are shown as black lines in Fig. 4 for various values of the free parameters \({\omega }_{0}\) and \(\Omega\). It is immediately evident that the entirety of the sigmoidal shape of \({\omega }_{\text{DO}}(T)\) cannot be reproduced with Eq. (6), implying that thermal lattice contraction and anharmonicity cannot explain the coherent phonon frequency’s temperature dependence, unlike the case of single-crystal tellurium52 and other materials58,60. Indeed, our results stand in stark contrast to another recent study of the ultrafast vibrational dynamics of Mn3Si2Te6, where the A1 tellurium phonon’s temperature dependence was found to follow such conventional behavior61.

Fig. 3: Coherent phonon dynamics.
figure 3

a The experimental \(\Delta R_{\mathrm{res}}/{R}\) at various temperatures above and below \({T}_{c}\) and b the magnitude of their respective Fourier transforms (FTs). The black lines in a are fits calculated from the damped sine function (Eq. 5), and the dotted line in b denotes the high temperature frequency of the phonon mode (\(3.52\,\text{THz}\)).

Full size image
Fig. 4: Phonon frequency and magnetization temperature dependencies.
figure 4

The damped oscillation frequency (blue dots, left y-axis) obtained from Eq. 5, plotted as a function of temperature and the temperature-dependent magnetization (green dots, right y-axis) measured with an applied field of 0.5 T. The black lines are fits from Eq. (6), with \({\omega }_{0}=3.55\) THz and \(\varOmega =-0.01\) (solid), with \({\omega }_{0}=3.578\) THz and \(\varOmega =-0.01\) (dashed), with \({\omega }_{0}=3.63\) THz and \(\varOmega =-0.055\) (dots).

Full size image

We postulate that the unusual temperature dependence of the A1 tellurium phonon is due to the ferrimagnetic ordering of Mn3Si2Te6, which leads to a subtle dynamic renormalization62 of the Te lattice in the segregation region, likely due to a spin-driven proximal interaction with the surrounding Mn3Si2Te6. Indeed, it has previously been shown that the interplay between magnetic exchange interactions and distortions of the structural lattice in vdW magnets can even lead to spin-coupled coherent phonon dynamics4. An overlay of the temperature-dependent magnetization (green dots in Fig. 4), obtained via SQUID measurements, shows the temperature-dependence of the ferrimagnetic order parameter and reveals a relatively close agreement with the experimental \({\omega }_{\text{DO}}(T)\) (given the laser-induced heating of the lattice). This indicates that the temperature dependence of the phonon frequency roughly follows the onset of ferrimagnetic order in the crystal, suggesting a spin-driven component to the temperature-dependent stiffening of the tellurium phonon mode. We note that similar spin-order dependent shifts of thermal phonon frequencies have been observed in other materials63,64,65 through spontaneous Raman scattering.

Discussion

In conclusion, we use ultrafast optical spectroscopy to study electronic and coherent phonon dynamics in the ferrimagnetic crystal Mn3Si2Te6. By using the A2TM, we model the electronic dynamics due to the presence of the strong spin-lattice coupling below 70 K. Most importantly, we identify a tellurium coherent phonon mode that couples strongly to the ferrimagnetic order of Mn3Si2Te6. This phonon’s frequency shift across \({T}_{\text{c}}\) mirrors the temperature-dependent magnetization and most likely originates from an exchange-mediated interaction between the coherent phonon and spins. Additional studies focusing on the spin dynamics could provide greater insight into the relationship between the phonon and spin systems in Mn3Si2Te6. This is of crucial interest in the evolving field of vdW magnetism, as we look to uncover the subtle yet profound connection between lattice structure and spin-driven properties in these materials, which have critical applications in emerging microelectronic devices. Indeed, the intrinsic connection between strain and magnetoresistance in this material suggests a pathway by which the dynamic perturbation of the lattice with light might be a means by which the conductive properties of Mn3Si2Te6 can be harnessed for high-speed reconfigurable devices needed for advanced computing architectures.

Methods

Ultrafast measurements

Time-resolved differential reflectivity measurements were performed using a regeneratively amplified Ti:sapphire laser system with a repetition rate of \(100\,\text{kHz}\). The pump and probe photon energies were \(1.55\,\text{eV}\) with a nominal pulse width of ~60 fs. The laser beam was split into pump and probe arms that were focused onto the sample at near-normal incidence using a 20× apochromatic objective (to ~7 μm diameters) and linearly cross-polarized in order to suppress spurious signals due to pump scattering. The probe fluence was held at \(0.125\,\text{mJ/}{\text{cm}}^{2}\) while the pump fluence was varied with a maximal limit of \(2.5\,\text{mJ/}{\text{cm}}^{2}\) to mitigate sample damage. The pump and probe beams were separately modulated at \({f}_{{\rm{pump}}}=0.7\text{kHz}\) and fprobe = 0.5 kHz\(,\) and the pump-induced changes in the probe reflectivity were measured using phase-sensitive detection at the fpump + fprobe intermodulation frequency.

Augmented two-temperature model

The model was formulated on the basis that there exist dynamical changes in the primary electron, phonon, and spin subsystems on the timescale of picoseconds following the pulse excitation. The essential timescales and the energy-flow between these baths is typically described in temperature models in which the photoexcited electrons relax by scattering with phonons and exciting spin dynamics. We further presume that the reflectivity signal scales, primarily, in the dynamics of the electronic subsystem. This allowed us to employ the rate equation set given in Eqs. (2) and (3), driven by an optical excitation in the form of Eq. (4). Here, it is assumed that electron- and spin-systems are strongly coupled and react as an internally thermalized bath36. The temperature-dependent \({C}_{{\rm{e}}}\), \({C}_{{\rm{p}}}\), and \({C}_{{\rm{m}}}\) were obtained from literature (see Supplementary Fig. 3).

The A2TM was simulated for a single layer of Mn3Si2Te6 with a 5th order Rutta–Kunge-method. The fitting procedure was done by a parameter sweep of the fitting parameters \({\tau }_{{ee}}\), \({g}_{{\rm{ep}}}\), \({c}_{t}\), and \({\tau }_{0}\). The sweep ranges were manually determined through preliminary analysis to lie close to the global minimum under the given restirction of fixed heat capacities of the electronic, phononic, and magnetic subsystems, which constrained the optimization landscape and enabled a unique and well-defined fit. The loss function was defined as the mean square difference of predicted and measured datapoints at any delay time. The fitting procedure was conducted several times with slightly varying the parameter ranges and initial values to ensure convergence to the local minimum within the given parameter range, which coincides with the global minimum.