Enabling multi-resolution droplet-on-demand metal jetting through tailored pulsing

Abstract

Like most additive manufacturing methods, droplet-based molten metal jetting (MMJ) techniques face a fundamental trade-off between printing resolution and speed, which naturally imposes limits on the fabrication of parts. Herein, we present some of these limits and propose a novel method and nozzle design to circumvent them: multi-resolution metal additive manufacturing via magnetohydrodynamic (MHD) droplet-on-demand MMJ. Multi-resolution printing enables high resolution and high deposition by selectively ejecting molten metal droplets of varying size from a single-reservoir nozzle equipped with two orifices. When ejecting droplets from the smaller orifice, fine resolution features can be printed at the expense of deposition rate. Conversely, larger orifices allow coarser features to be printed quickly. The complexity of activating only a single orifice is overcome by carefully tailoring MHD pulses to comply with the characteristic fluid dynamics of each individual orifice. The concept is established using 3D fluid dynamics simulations of a nozzle equipped with two orifices (200 and 500 μm diameter) and validated experimentally with an identical nozzle configuration using an aluminum alloy as the ejection liquid.

Introduction

Droplet on Demand (DOD) Molten Metal Jetting (MMJ) is an emerging metal additive manufacturing (AM) process that uses precise, repeated pressure pulses to eject a sequence of molten metal droplets of a uniform size and velocity to build up a part in three dimensions (3D). In addition to AM of metal parts, MMJ has been shown to work for part repair¹, printed electronics^2,3, extreme ultraviolet light generation for lithography⁴, as well as terahertz light generation for photonics⁵. Lately, work in MMJ has increased rapidly due to its promise to enable a balance between affordable, rapid, and precision metal AM, without the need for expensive feedstocks such as powder nor directed energy sources such as a laser, an arc, or an electron beam^{2,6,7,8,9,10,11,12,13}. Relatively slower metal cooling rates and reduced thermal gradients also imply the potential to make MMJ compatible with many more traditional alloy systems, which is an ongoing challenge in metal AM due to unusual microstructure development and high residual stress^14,15,16. At this time, two commercial MMJ systems are on the market and several research-grade systems are exploring MMJ fundamentals, design, and applications. Despite many opportunities in MMJ, little research has been dedicated to the limits of MMJ printing resolution and printing speed.

With nearly all AM processes, feature resolution of a printed part is limited by the physics of voxel formation and the part construction strategy used during printing^17,18,19. Almost universally, AM is constrained by a strong tradeoff between minimum feature size and printing speed. Thus, parts that require finer features take longer to print, reducing either productivity or the complexity of the printed parts. One solution to this problem is to develop multi-resolution capability in the same process, preferably without any interruption in the printing process. Kang and Mueller recently developed an example of this for extrusion-based AM processes and proposed that a variable resolution AM process can be used to tailor resolution to particular geometric features within a part²⁰.

As an example, Fig. 1 shows a conceptual drawing of a how a gear might be digitally subdivided into features that require high precision, and features that can be printed more coarsely at a faster rate. Using this multi-resolution printing method ensures that the speed of the printing process will not be limited by the smallest feature of the object.

Fig. 1

Examples of how a layer of a 3D printed part may be used to detect features and print using the corresponding multi-resolution mode.

For many 3D printed objects, high resolution is only needed in certain portions of the object such as corners, holes, the perimeter, or joining sites, whereas the bulk of the part can take up most of the printing time and does not require maximum resolution. The challenge for metal 3D printing lies in enabling the ability for in operando resolution switching. Once established, the part building process can be optimized to take advantage of multi-resolution AM which offers dramatic savings in printing time.

For droplet-based metal jetting printing processes, the resolution is highly correlated to the size of the ejected droplet, which for nozzle-based MMJ is dependent on the size of the pre-manufactured orifice and the driving waveform used to pressurize it. In other words, the droplets act as effective “voxels” that influence minimum feature size. Examples of MMJ published in the literature utilize one nozzle with a single orifice, which practically limits the overall resolution of the system to be on the order of the orifice diameter. To change the resolution of the printer, one can either replace the nozzle, which presents difficulties during the printing process, adjust the printing strategy²¹, or use multiple printheads/nozzles in parallel, similar to modern inkjetting printers.

As a pulse-actuated droplet deposition technique, MMJ can be compatible with a multi-resolution process by operating multiple parallel, independent nozzles with different native resolutions: separate reservoirs, separate actuation mechanisms, and separate orifices. However, process control with independent nozzles is difficult, given that instabilities, actuator noise or positional errors in even one nozzle can lead to defect-laden printed parts. Using multiple independent nozzles in droplet-on-demand MMJ increases system cost, complexity, and size. Furthermore, independently actuated nozzles also require high repeatability and reduction of cross-talk, which is a known problem that impacts the quality of inkjetting, a related technology^22,23.

Another way to adjust resolution is to eject droplets smaller than the orifice size. Chen and Basaran were able to overcome the seemingly inherent coupling between orifice size and droplet size for aqueous inkjetting by tuning the waveform of their piezoelectric forcing function, thus exhibiting droplets sized 50% of the orifice²⁴. Poozesh et al. performed a similar study with a pull-push-pull waveform and obtained water droplets 20% of the orifice diameter²⁵. Clearly, waveform control of droplet breakup is a powerful way to adjust resolution. However, it is unknown whether such waveform control can be effectively utilized in single-orifice MMJ systems, because the rheology of liquid metals, and consequently the droplet breakup dynamics, are markedly different than inks^26,27.

In this study, we introduce a novel multi-resolution metal jetting system by integrating waveform control with a single multi-orifice nozzle. This system achieves varying resolutions and proposes high build rates by utilizing orifices of different diameters, which can be selectively activated through tailored drive waveforms of a shared actuation mechanism. Unlike traditional multi-nozzle systems, our approach features a single reservoir and actuation mechanism, simplifying the setup while providing multiple resolution capabilities. The focus of the work is enabling at-will resolution control within a droplet-on-demand metal jetting system, rather than a direct demonstration of multi-resolution metal printing. Printing using multi-resolution control includes great complexities in part building strategy (e.g., droplet location control, varying droplet cooling rates, etc.) beyond the scope of this effort, but the new design and proof-of-concept demonstration in this work will lay the foundation for these challenges to be addressed in the future.

We start by calculating physics-based resolution limitations for a generic droplet-on-demand MMJ process with a single nozzle and orifice, and then introduce multi-resolution molten metal jetting as a method to overcome some of these limits. Specifically, we develop multi-resolution MMJ from a single printhead equipped with two orifices: a 200 μm and a 500 μm diameter orifice. Ejection from the smaller orifice can be used for finer resolution at the expense of deposition rate while a high deposition rate with lower resolution is achieved with the larger orifice. This enables multiple modes of printing: “Fine Mode”, “Coarse Mode” and “Infill Mode”, where the latter refers to ejecting from both orifices at the same time to enable rapid infill of molten metal as suggested in Fig. 1. We first use a numerical simulation approach, composed of three models: (1) a circuit model of the power electronics to simulate the input current for a magnetohydrodynamic (MHD) printhead; (2) a 2D MHD-computational fluid dynamics (CFD) model to simulate the pressure pulse at the nozzle exit and to enable a third, reduced-order simulation; (3) 3D CFD simulations of just the nozzle exit that models the ejection of droplets from each orifice. Model 3 is exercised to establish the multi-resolution MMJ concept. We then experimentally validate the concept using a custom-designed nozzle in a modified MHD-DOD printhead and identify challenges and opportunities with this process.

Discussion and Results

Resolution-deposition tradeoffs of droplet-on-demand MMJ

Droplet-on-demand material jetting processes use the droplet as the effective voxel for determining resolution. Although the spreading, remelting, flow and solidification of the droplet on the substrate complicates the effective resolution of the process, the droplet diameter D_d remains an excellent measure of MMJ resolution. Deposition rates in DOD-MMJ can be calculated by multiplying the jetting frequency f_j (Hz), otherwise known as droplet deposition rate (droplets/s) by the volume of a droplet. In practice, f_j can be adjusted according to the translation velocity of the motion stage to maintain a constant droplet-droplet spacing during printing. This makes the printing speed somewhat limited by the finite time needed to accelerate and decelerate during various movements. For example, when printing lines back and forth using parallel hatching, the motion stage needs to decelerate, which dictates a temporary reduction in the jetting frequency at the end of each line. As a consequence, the average jetting frequency for any given print job depends on the complexity of the part’s travel path in the plane of the printing stage. For the purposes of the calculations presented here, we ignore the accelerations of the motion platform, and establish a framework for a theoretical maximum deposition rate based on the droplet-ejection dynamics at the orifice. Pre-factors that include the practical limitations mentioned above can be added to represent more realistic scenarios, but the inclusion of these complexities will still be bounded by the proceeding derivations.

To estimate the maximum jetting frequency f_j,max for any orifice size and any liquid metal with a high ratio of surface tension effects to viscous effects (most liquid metals), we use the characteristic timescale that dominates surface tension-mediated droplet breakup, namely the capillary time, defined as,

$${t}_{cap}=\sqrt{\frac{\rho {D}^{3}}{8\gamma }}$$

(1)

where ρ and γ are the density and the surface tension of the molten metal, and D is the diameter of the liquid column before ejection. Here, it is assumed to be the diameter of the ejection orifice^28,29. Note that the metal jetting process relies on forced ejection of the droplets rather than gravity-induced dripping, and the low effects of gravity are evidenced by a low droplet Bond number (≪1). Physically, the capillary time describes the characteristic timing of capillary forces during breakup of a liquid column when surface tension dominates viscosity. Based on the Rayleigh-Plateau slender jet approximation, the time-to-breakup t_pinch of any ejection is a multiple of t_cap²⁹,

$${t}_{pinch}=c\cdot {t}_{cap}$$

(2)

Where c is a constant that depends on the nature of the perturbation that leads to droplet breakup and varies depending on the type of actuation (droplet on demand vs continuous breakup). In inkjetting literature, to get stable, single droplet breakup of a pulsed water jet, this is approximately c = 5 to 8^28,29,30, and based on the MHD push-pull waveform discussed in this work, pinch time for metals ranges between c = 2 to 4, taken from simulations of the MHD push-pull MMJ system^26,31. Because tcap depends only on the rheological properties of the metal and the orifice diameter, and c depends on the actuating waveform, tpinch can be used to estimate the maximum theoretical jetting frequency of any metal and any orifice size:

$${f}_{j,\max }=\frac{1}{{t}_{pinch}}=\frac{1}{2{t}_{cap}}=\sqrt{\frac{2\gamma }{\rho {D}^{3}}}$$

(3)

Here, t_pinch = 2t_cap represents the minimal elapsed time between the initial motion of a liquid metal meniscus and the droplet pinch-off for an MHD push-pull waveform of the kind shown in Fig. 3b²⁹. In a previous study, the value c = 2 was determined using CFD-MHD simulations^26,31. Note that a smaller multiple c of the capillary time implies a faster droplet breakup, and thus a higher f_j,max. Molten metals or metalloids with higher surface tension and lower density tend to have lower capillary times, and can be deposited faster (e.g. Li, Al, Ti, Si). In reality, additional time is needed for the droplet to move away from the orifice and for the meniscus oscillations to dampen before the next ejection, so in effect, an ejection frequency based on t_pinch represents the fastest theoretical droplet generation rate, given the constraints set by the physics of droplet breakup.

Assuming that the droplet diameter D_d is identical to the orifice diameter, which is reasonable for a push-pull MMJ waveform, one can construct a relationship between the resolution (D), max ejection frequency (f_j) and the resulting volumetric deposition rate (Q), which is simply the product of the droplet volume (V_d) and f_j:

$$Q={V}_{d}\times {f}_{j}$$

(4)

For a given droplet diameter, the deposition rate increases linearly with jetting frequency until f_j,max, after which droplet formation, ejection, and jetting are unreliable. This maximum jetting frequency establishes a corresponding maximum volumetric deposition rate Q_max:

$${Q}_{\max }={V}_{d}\times {f}_{j,\max }=\frac{1}{6}\pi {D}^{3}\times \frac{1}{{t}_{pinch}}=\sqrt{\frac{{\pi }^{2}\gamma }{18\rho }}{D}^{\frac{3}{2}}$$

(5)

Figure 2 shows a plot of D vs. f_j vs. Q for pure aluminum. The dashed, magenta curve represents a physics-bound resolution-deposition tradeoff for stable, single-orifice ejections. Note that at larger droplet diameters (lower resolution), the max deposition rate is always higher than smaller diameters (higher resolution). For example, with an orifice diameter D = 500 μm, given molten aluminum density and surface tension shown in Table 2, the maximum possible theoretical jetting frequency is f_j,max = 2.4 kHz, which corresponds to a maximum deposition rate of Q_max = 570 cm³/hr. If we increase the resolution (decrease the droplet diameter) to 50 μm, the new maximum jetting frequency is 76.6 kHz, but the deposition rate drastically reduces to 18 cm³/hr. We note that the current state of the art in droplet-on-demand metal jetting cannot achieve frequencies of tens of kilohertz, since it is challenging to eject smaller droplets at high repetition rates. However, the values presented here serve as theoretical limits.

Fig. 2: Resolution-deposition tradeoff plot for droplet-on-demand metal jetting.

Droplet size is assumed to be the same as the orifice size and is shown on the x-axis, droplet jetting frequency based on the theoretical droplet pinch-off time on the y-axis, and the resulting volumetric deposition rate in cm³/hr on the z-axis. a 3D view of the tradeoff plot; b 2D (top-down) view. The magenta curve outlines the max deposition rate based on a the max ejection frequency for a given orifice size for aluminum. Jetting is not feasible beyond the dotted line because droplets do not have enough time to break up.

Assuming the hypothetical gear shown in Fig. 1 is 10 cm wide and 2 cm thick, we can estimate the build time with aluminum using

• 1. Fine Mode (only)

• 2. Coarse Mode (only)

• 3. Dual Mode (Fine+Coarse, no Infill)

• 4. Fine+Coarse+Infill Modes

where appropriate in the object design. For this hypothetical scenario, we assume that Fine Mode represents 200 μm droplet diameter, coarse mode represents 500 μm and infill mode represents a combination of 500 μm and 300 μm droplets. The 300 μm droplet in infill mode is a consequence of dual ejection actuation creating larger-than-orifice droplets as shown later in the results. Based on these assumptions, and the maximum build rates shown in Fig. 2, the times to build the gear are as follows: 77 minutes for Fine mode; 20 min for Coarse mode; 34 min for Dual mode; and 32 min for Fine, Coarse, and Infill modes. Case 4 is pictured in Fig. 1. While the use of Coarse mode is naturally faster than the Fine mode by more than a factor of three for this gear example, there is an inherent resolution limit with this mode. Dual mode reduces the time by over a factor of three with respect to Fine mode while maintaining the same resolution for critical features. Using additional Infill mode in the blue region improves the time over Coarse Mode in that region, but only yields a 2-min reduction in overall build time (Fine+Coarse+Infill). Because this geometry does not have large portions of bulk volume, Infill mode does not exhibit substantial time difference despite the respectable improvement in deposition rates between Coarse and Infill modes (570 cm³/hr vs 673 cm³/hr). For parts that include substantial planar, bulk volume, Infill mode would offer greater time savings over Coarse mode.

By examining the scaling of deposition rate with frequency and resolution, Fig. 2 reveals a nonlinear diminishing deposition rate, owed to the fact that droplet volume scales with D³, and maximum jetting frequency with ${D}^{-\frac{3}{2}}$. Beginning from a maximized jetting frequency for a given droplet diameter, if the diameter of droplets is halved, those higher-resolution droplets need to be ejected at 8 × the original rate to maintain the same deposition rate. A half-sized-droplet jetting frequency that high is impossible due the finite time needed for droplets to pinch off and move away from the meniscus. Note that accelerating the process of droplet breakup past a certain multiple of t_cap usually leads to the formation of satellite droplets, which are unwanted in MMJ. Satellite droplets are analogous to “spatter” in laser powder bed fusion (LPBF) due to their stochastic formation, direction and size.

Similar plots to Fig. 2 can be created for each molten metal, as long as liquid density, surface tension and orifice diameter are known. Comparisons between several molten metals based on known rheological parameters are shown in supplementary Figures 1 and 2. By calculating the appropriate t_pinch value based on the appropriate multiple of t_cap, individual plots can also be created for non-MHD or non push-pull DOD-MMJ techniques. Note that if t_pinch > 2t_cap, the limiting curve in Fig. 2 will be shifted towards the origin, further decreasing the maximum theoretical deposition rate. Given the narrow space in which stable, satellite-free jetting can occur^25,26,27, the limits on deposition rate imposed by orifice diameter strongly drive a need for multi-resolution methodologies.

Selective ejection using pulsed waveform control

The main MMJ parameters that allow selectable and controllable ejection from orifices under the influence of a single push-pull actuation mechanism are:

• 1. diameter of the orifice, D,

• 2. length of the orifice, L,

• 3. pulse duration, t_drive,

• 4. positive actuation or “push” amplitude, p_push,

• 5. negative actuation or “pull” amplitude, p_pull,

• 6. molten metal fluid properties, ρ, γ, η.

with D and L being geometrically fixed parameters, t_drive, p_push, and p_pull being tunable parameters associated with the actuating drive pulse, and η being the dynamic viscosity of the metal. The central challenge of this work is to discover a pulsed waveform with the capacity to independently address each orifice of a two-orifice nozzle with a shared fluid reservoir and single, shared MHD actuation coil. One method to parameterize the pulsed waveform is through the pressure impulse definition, which takes into account both the amplitude and the duration of the pressure waveform³²:

$$M=\int_{0}^{{t}_{drive}}{p}_{push}(t)\,dt$$

(6)

Using this definition, exceeding a critical value of pressure impulse M in an MMJ system will lead to a successful droplet ejection. Since the critical value of M depends on D, L and the fluid properties ρ, γ and η, it will vary with nozzle geometry and the molten metal properties.

The shared reservoir and MHD actuation coil imply that the two orifices experience the same transient pressure profile, so the driving waverform must be tailored to selectively eject from one orifice while preventing an ejection from the other. For the MHD-DOD system used in this study, t_drive and p_push can be varied by controlling the current pulse to the MHD actuation coil (Eq. (7)), while p_pull is a resultant response determined by the electronics that are used to create the current waveform, and cannot be controlled in our MHD-DOD system^25,26.

A single nozzle with multi-resolution capability is assumed to have two orifices with diameters D₁ < D₂ and D₁ sufficiently different from D₂ to enable different droplet sizes. A quiescent orifice (i.e., before ejection) should have a liquid metal meniscus with a shape determined by a balance between the surface tension of the fluid and the hydrostatic pressure of the fluid reservoir. Ejecting a droplet from either orifice amounts to applying a pressure pulse of sufficient amplitude to overcome the surface tension and for a sufficient duration to establish flow of the fluid at the orifice: droplet ejection occurs only after pushing hard enough for long enough, hence exceeding a critical value of M.

We set the inertial timescales for each orifice to be the capillary times of Eq. (1), and those times are differentiated between each orifice by their diameters such that t_cap1 < t_cap2. We define the minimum pressure necessary to achieve a critical M to be p^*. Because the pulsed flow through an orifice is never in a steady-state flow regime, this p^* is not readily derived like t_cap. However, p^* should be at minimum the Laplace pressure for the evolving droplet and likely depends on the L/D ratios of each orifice³³. The Laplace pressure will scale as p_l ~ D⁻¹, so we expect ${p}_{1}^{* } \,>\, {p}_{2}^{* }$. Simply put, the smaller orifice requires a higher pressure for a shorter time to eject a droplet than does the larger orifice. To simplify the proof-of-concept, we hold L₁/D₁ ≈ L₂/D₂ ≊ 1, but note that these ratios could be a source of further selectivity.

To only eject from the smaller orifice (D₁), we let t_drive1 = t_cap1 and find a p_push1 that is large enough to eject a stable droplet (${p}_{push1} \,>\, {p}_{1}^{* }$). These same conditions are experienced by the larger orifice (D₂), but while p_push1 is likely greater than ${p}_{2}^{* }$, t_drive1 < t_cap2, so the pulse duration does not exceed the inertial timescale of the larger orifice. In other words, a droplet is not expected to eject from the larger orifice with this t_drive1 and p_push1 combination, because the pulse does not push long enough.

To eject from the larger orifice (D₂) only, we let t_drive2 = t_cap2 and find a p_push2 that is large enough to eject a stable droplet. Again, these same conditions are experienced by the smaller orifice. For this case, t_drive2 > t_cap1, but p_push2 is lower than ${p}_{1}^{* }$, so the pulse pressure does not exceed the pressure scale for the smaller orifice. A droplet is not expected to eject from the smaller orifice with this t_drive2 and p_push2 combination, because the pulse does not push hard enough.

Finally, to eject from both orifices, another combination of pressure and pulse duration is needed that allows stable ejection from both orifices. This can be achieved by choosing an intermediate drive time t_drive2 < t_drive3 < t_drive1, and an intermediate pressure amplitude p_push1 > p_push3 > p_push2. Here, the combination of pressure and pulse duration exceed the critical values of M for each orifice, achieving effective dual orifice ejection. We point out that the range of values for t_drive3 and p_push3 that result in dual ejections could be quite substantial, with dual ejection potentially encompassing a wider range of impulse parameters than either small or large individual ejections.

Note that there are likely limits to this selectivity effect: orifice geometries with very similar diameters will have similar t_cap values, making it difficult to create differing flow rate profiles inside them. Orifices with very small diameters will require small t_drive values, which may not be possible to attain with actuation techniques that have physical response bandwidth limitations. Similarly, orifice geometries that have vastly different diameters, for example a very small and very large orifice are also unlikely to yield stable ejections out of both orifices due to a lack of overlap in their input-output responses. Varying L/D ratios may offer some benefit by adjusting the resulting orifice flow rates, but a full exploration of the sensitivities to each of the five variables mentioned above is beyond the scope of this study.

CFD modeling of multi resolution MMJ

The t_cap values for D = 500 and 200 μm, with pure aluminum at the melting point correspond to 202 μs and 51 μs, respectively. Based on the similar magnitudes of the temperature dependence of surface tension and density above the melt, t_cap is expected to remain within 1% of these values for at least 200^∘C above the melting temperature. To isolate ejection from the smaller orifice, the pulse duration is set to t_drive = 50 μs and the peak-to-peak amplitude of the push-pull pulse is scaled linearly with a pre-factor until a single droplet ejects. By adjusting the corresponding transient pressure boundary condition on the top of the computational domain (Fig. 8c) and re-simulating the ejection, “Fine Mode” shown in Fig. 4a can be isolated. The corresponding current and pressure pulses used to achieve this are shown in Fig. 3. For this case, the ejected droplet diameter is 189 μm and the droplet velocity is ${v}_{d}^{200}=1.72\,{{\rm{m}}}/{{{\rm{s}}}}$. As the pressure amplitude increases, eventually an ejection will occur from both orifices. In effect, Fine Mode represents the range of pressure amplitudes that only eject from the smaller orifice.

Fig. 3: Simulated magnetohydrodynamic actuation pulses.

a Actuator coil current pulses from Model 1 and b resulting nozzle pressure pulses for each ejection mode using Model 2. Fine mode requires a higher peak pressure pulse than coarse mode to eject from the smaller orifice because of its shorter capillary time.

Next, to isolate ejections from the larger orifice (Coarse Mode), t_drive was set to 250 μs to approximate t_cap for that diameter orifice. This is slightly longer than the ideal 200 μs for the larger orifice (t_drive/t_cap = 1.25), but much longer for the smaller orifice (t_drive/t_cap = 5). The actuation pulse amplitude associated with this 250 μs drive time results in a droplet diameter smaller than the orifice, D_d = 365 μm. Figure 4b shows the transient ejection of pure aluminum using Model 3, serving as an example of Coarse Mode. Note that in this case, a droplet ejects from the smaller orifice, but has low velocity (${v}_{d}^{200}=0.27\,{\rm{m{/}s}}$), so the oscillating meniscus of the smaller orifice re-captures this low-velocity small droplet, leaving only the larger droplet to move away from the nozzle, albeit with a low velocity ${v}_{d}^{500}=0.19\,{\rm{m/s}}$. This low velocity may be improved by adjusting the relative lengths of each orifice and by further increasing the pressure pulse amplitude. As long as the smaller droplet is re-captured, Coarse Mode will continue to function. Since each 3D transient simulation is computationally expensive, fine-tuning the pressure to achieve greater droplet velocity has not been pursued for this study.

Fig. 4: VOF-CFD model results alongside experimental high speed images.

The three panels show ejection of aluminum droplets from: a with t_drive = 50 μs, only the 200 μm orifice (Fine Mode), b with t_drive = 250 μs, the 500 μm orifice (Coarse Mode), and c with t_drive = 200 μs both orifices (Infill Mode).

Finally, to show ejection from both orifices, t_drive is chosen to be intermediate between the two t_drive extremes, namely 200 μs. While there are multiple pressure-t_drive combinations that could lead to dual ejection, for demonstration we show only one of these pairs. As before, the amplitude of the pressure is adjusted until both droplets have enough momentum to travel away from the orifice without satellite ejections, as shown in Fig. 4c. The droplet velocities are 0.85 m/s and 1.37 m/s for the larger and smaller orifice, respectively. The resulting droplet diameters are 261 and 390 μm. All droplet size and velocities are summarized in Table 1.

Table 1 Summary of Model 3 droplet ejection results for each mode and each orifice

It is noteworthy that the Coarse Mode droplet diameter was only 365 μm, even though the orifice diameter was 500 μm. This shows that a properly timed push-pull pulse, with a tailored amplitude can eject droplets with diameters smaller than the orifice, consistent with the work by Chen and Basaran²⁴ and by Poozhesh et al.²⁵, wherein they used pull-push-pull waveforms. As previously stated, further adjusting the pressure waveform and the orifice geometry should allow the user to bring this value closer to D_d = 500 μm.

To extend this approach to other metals and orifice combinations, dimensionless printability windows can be used. In DOD-MMJ, printability windows based on dimensionless quantities are used to draw thresholds for the onset of a droplet ejection and the transition from single droplet to satellite-laden ejections. A range of authors have used the Weber jet number $W{e}_{j}=\frac{\rho {v}_{j}^{2}D}{\gamma }$ to characterize whether a certain orifice jet velocity will lead to an ejection for both inkjetting and metal jetting^26,27. Because We_j incorporates the two most important fluid parameters for molten metals, density and surface tension, as well as orifice diameter, it covers a broad range of molten metal droplet ejection behavior. Here, v_j is the peak jet velocity inside the orifice, prior to droplet breakup. The value of v_j is a consequence of both the applied pressure p_push and the pulse duration t_drive via Equation (8), and thus v_j is directly connected to the threshold pressure p^* for ejecting a droplet.

In previous work, Sukhotskiy et al. have shown that for an MHD push-pull waveform, 10 < We_j < 20 ensures single-droplet ejection with appreciable velocity and without satellites^26,31. Most values in the range 5 < We_j < 10 exhibit either slow droplets or droplets with a negative (backward) velocity. Values well below 5 do not yield ejections. Based on this range, a general approach in selecting orifice ejection for any metal and any orifice combination means ensuring 10 < We_j < 20 (inside the single droplet regime) for the ejecting orifice, and simultaneously We_j < 10 for the non-ejecting or recombining orifice.

For the case of a magnetohydrodynamic DOD metal jetting system like the one used in this study, a combination of We_j and a MHD dimensionless number ${S}_{j}=\frac{\sigma {B}^{2}{D}_{n}^{2}{v}_{j}}{\gamma }$ can be used to screen peak magnetic field values (and consequently peak pressures) a priori, as outlined in²⁶. This number estimates the ratio of the Lorentz force (Equation (7)) and surface tension, providing a link between the forcing mechanism and the resulting jet velocity. Therefore, a combination of t_drive/t_cap ≈ 1, appropriate pressure pulse amplitude to drive We_j into the favorable range, and a carefully selected L/D ratio for each orifice allows this to be extended to other liquid metals and orifice combinations. As mentioned in the previous section, not all orifice combinations permit each mode to be isolated, and having more than two orifices will make selectivity even more difficult.

Experimental demonstration of multi resolution MMJ

Experimental demonstrations of Fine, Coarse and Infill modes are shown in Fig. 4 and in supplementary videos 1 to 3. All three modes of ejection are successfully isolated in the experimental device using the pulse durations and current amplitudes discovered using Models 1–3. In addition, supplementary videos 4 and 5 show repeatable ejection of each orifice, proving that the modes are stable over repeated ejections at a relatively high droplet ejection frequency (f_j = 200 to 300Hz).

Because it was not feasible to measure the pressure or the velocity inside the molten metal directly, transient current pulses and the final droplet velocities are used to compare experimental data to the simulations (Figs. 3-4). Naturally, this introduces some discrepancy, since the MHD coupling between the actuation coil and the molten metal is not ideal in the experimental apparatus. Nevertheless, Fig. 5 shows a comparison between the simulated current pulses in Models 1 and 2, and the current pulses used to obtain the simulated ejections shown in Fig. 4.

Fig. 5

Comparison of the simulated coil current pulses obtained using Model 1 versus experimentally measured pulses for each mode.

Ejection from the 200 μm orifice (Fine Mode) was achieved using t_drive = 50 μs and V = 249 V, which resulted in an experimental current peak of 456 A, and a simulated peak of 465 A. The droplet velocity, measured using high speed video, was ${v}_{d}^{200}=0.85\pm 0.12\,{\rm{m/s}}$, about 50% slower than the simulation. The value was a result of averaging across four measured samples. Note that the experimental velocity is slower than the simulated Fine Mode ejection, which can be partially attributed to differences in L/D, since the experimental nozzle had a longer orifice (270 μm experimental vs 200 μm simulated). In addition, CFD models 2 and 3 are not likely to represent all system dynamics perfectly. A relatively complicated chain of events leads to droplet ejection in the MHD actuation mechanism, and there is currently no efficient method to incorporate all the relevant physics into a single transient model, while maintaining acceptable physics fidelity.

Ejection from the 500 μm orifice (Coarse Mode) was achieved using t_drive = 250 μs and V = 75 V, which resulted in an experimental peak current of 569 A, and a simulated peak of 570 A. The droplet velocity was measured to be ${v}_{d}^{500}=0.63\pm 0.28\,{\rm{m/s}}$. The experimental droplet is faster than the simulated droplet in Coarse mode even considering the uncertainty in the experimentally determined velocity. This time, the experimental nozzle has a shorter orifice length (445 μm experimental vs 500 μm simulated), so this may also be a source of error. Measurements of the smaller droplet velocity before recombination with the meniscus were unreliable, and so were excluded from comparison.

Ejection from both orifices was achieved using t_drive = 200 μs and V = 100 V, which resulted in experimental peak current of 633 A, and a simulated peak of 645 A. The smaller droplet velocity was ${v}_{d}^{200}=0.95\pm 0.23\,{\rm{m/s}}$ and the larger droplet velocity was ${v}_{d}^{500}=1.30\pm 0.25\,{\rm{m/s}}$. As previously mentioned for Fine Mode and Coarse Mode, the ejection velocity is higher than expected from the larger orifice and slower from the smaller orifice.

In summary, we have developed a framework to quantify the natural limitations of resolution and printing speed in a single nozzle-orifice, droplet-on-demand MMJ process and developed a multi-resolution method to alleviate these limitations. We have demonstrated independently controlled ejections in a unique two-orifice, contactless MHD-actuated nozzle via tailored push-pull pulses. By aligning pulse durations with the capillary timescales of each orifice and fine-tuning the push-pull waveform amplitudes, we identified three printing modes that enable multi-resolution metal jetting: Fine Mode, Coarse Mode, and Infill Mode. This method can be implemented with a single actuator-nozzle setup, reducing both cost and complexity. The multi-resolution MMJ droplet ejection method presented herein has been demonstrated for the first time and advanced through simulations and experiments. The concept has not been exhaustively explored, suggesting that there are likely limits to the selectivity of this technique, but also opportunities for optimization through parameters other than pulse durations or amplitudes (e.g., nozzle internal geometry, L/D ratios of the orifices). Further work will need to explore printing strategies with multi-resolution MMJ by addressing multi-resolution-aware droplet deposition sequencing and digital part slicing, droplet-droplet spacing, cooling rates of varying diameter droplets, and printing defects such as porosity at the interface of Fine, Coarse and Infill Mode regions. Furthermore, the simulations and experiments are limited to the MHD-actuated DOD-MMJ printer used in this study, but the technique may be extendable to other DOD-MMJ actuation methods like pneumatic or piezo-driven ejection printheads, as well as other metals, using dimensionless quantities like We_j.

Methods

Numerical Modeling Methods

A 3D computational fluid dynamics (CFD) model is developed using the Volume of Fluid method in Ansys Fluent 2023-R1 to virtually test the multi resolution nozzle and calibrate the pulse duration-amplitude combination needed to isolate the ejections from specific orifices. The modelling approach follows that of Sukhotskiy’s dissertation³¹, with an added Simulation Program with Integrated Circuit Emphasis (SPICE) model to calculate an accurate current waveform used as input to an intermediate 2D axisymmetric MHD model of the MMJ printhead.

Pressure-driven simulations of pure liquid aluminum ejections were performed using 3D free surface CFD analysis in ANSYS Fluent 2023 R1. One transient instance of the simulation represents a single MHD-DOD pulse and the subsequent ejection behavior of pure molten aluminum. Figure 6 shows a summary computational workflow, highlighting the numerical approaches and the corresponding inputs and outputs.

Fig. 6

Diagram of the modelling approach used to simulate droplet ejections from individual orifices.

Initially, Model 3 was exercised repeatedly to study the influence of pressure pulse duration and amplitude on the ejection modes. By calculating reference pressure pulses for each t_drive value using Model 2 and linearly scaling their amplitudes within Model 3, the three ejection modes could be isolated and then replicated in the experiment. Then after the modes were isolated, Model 2 was used to re-calculate accurate pressure waveforms for each pulse duration and amplitude setpoint. Model 3 results are discussed in CFD modeling of multi resolution MMJ. The computational domain in Model 3 used half-plane symmetry as shown in Fig. 8c and represents a small volume of both fluids (metal and argon) near the nozzle exit. This is referred to as Model 3 in this work. The model numerically calculated fluid flow and pressure distribution using the incompressible version of the Navier–Stokes equation, and the free surface movement and metal droplet breakup was represented using the volume of fluid (VOF) method, a popular multiphase flow numerical technique. Further description of the VOF implementation can be found in the ANSYS Fluent Theory Guide³⁴ and in Chapter 3 of Sukhotskiy’s dissertation³¹.

A pressure boundary condition was used to simulate droplet ejections in Model 3. Unlike many simulations of fluid ejections, which impose a velocity boundary condition, a pressure boundary condition is applied at a virtual inlet to emulate the forcing of the MHD actuator. A transient pressure boundary condition is a more useful way of screening input amplitudes, since the resultant velocity distribution in each orifice is not known beforehand. Because Model 3 represents the bottom portion of a larger fluid domain inside the nozzle, the pressure boundary condition is effectively applied inside the molten metal. This is a reasonable assumption given that the pressure at this location varies minimally in the radial direction³¹. The transient pressure pulses used as boundary conditions for Model 3 were calculated using a second CFD model (Model 2), namely, a 2D axisymmetric numerical simulation of the entire MHD-DOD nozzle via COMSOL Multiphysics 6.1, as described in Chapter 2 of Sukhotskiy’s dissertation³¹. Since the MHD model is computationally difficult to rapidly simulate in 3D, Model 3 effectively circumvents this by simulating a sub-domain of the entire MHD-DOD nozzle.

To enable Model 2, a transient Simulation Program with Integrated Circuit Emphasis (SPICE) model (Model 1) was used to calculate the triangular current pulse generated by the Pulsed Power Electronics unit sketched in Fig. 6. Model 1 was built using NI Multisim 14.2. A transient current boundary condition is required as input to the actuation coil in the COMSOL model (Model 2) to generate the magnetic flux density for the MHD-DOD ejection mechanism. The electrical current pulses, resulting pressure pulses, and their corresponding ejection modes are shown in Fig. 3.

Experimental Methods

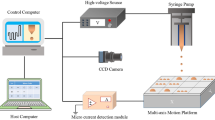
The results of the 3D model were experimentally validated using a Xerox ElemX MHD-DOD system equipped with a custom graphite nozzle tailored to eject an aluminum 4008 alloy. Aluminum 4008 is the standard material for this system and has well-characterized properties (Table 2). The nozzle was customized by fabricating it with two orifice diameters: 200 μm and 500 μm. Both orifices were initially made to have approximately the same length to diameter ratio. The 200 μm side of the nozzle was adjusted to a length of 270 μm using 1200 grit sandpaper. A custom trigger pulse system is used to trigger ejections and sync them with a high speed camera. Figure 7 shows a diagram of the essential experimental systems including the MHD-DOD printhead equipped with a dual orifice nozzle, argon cover gas flow system, laser fill level sensor, wire feeding system, voltage/current pulse generating power electronics unit connected to the actuator coil, high speed camera and a function generator used to trigger the high power pulse and the camera recording.

Table 2 Molten metal rheological properties for pure vs. alloyed aluminum near melting temperature³⁷

Fig. 7: Simplified diagram of the MHD-DOD metal jetting process customized for this study, not to scale.

To eject droplets, the coil creates pressure pulses magnetohydrodynamically inside the molten metal. The coordination of the wire input rate, level sensing, and heating is done by computer numerical control.

The key elements of the ElemX MHD-DOD printhead ^26,31 include : (1) a two-part ejection nozzle consisting of a reservoir where metal melting occurs and an ejection chamber with a submillimeter orifice. The upper portion of the nozzle is made of boron nitride, while the lower is machined from graphite; (2) a solenoid that surrounds the ejection chamber and part of the reservoir, as shown in Fig. 7. (3) A water-based cooling system is used for thermal management of the coil. (4) The coil is pulsed with a high peak current waveform with the help of a coil driver power electronics unit to generate a time-varying magnetic field $\overrightarrow{B}$. Pure argon gas (99.999%) is flowed near the ejection orifice to ensure a semi-inert local environment for the liquid metal droplets during ejection and transit. This setup is summarized in Fig. 7. In these experiments, the reservoir is resistively heated to 830 ^∘C, well above the melting point of the 4008 aluminum alloy.

To eject a droplet, a current pulse like the one in Fig. 5 is applied to the coil which creates a rapidly rising and falling magnetic field inducing a circulating current density inside the molten metal according to Faraday’s law. The circulating current density $\overrightarrow{J}$ couples to the magnetic flux density $\overrightarrow{B}$ and creates a Lorentz body force f_MHD inside the conductive molten metal according to Equation (7),

$$\begin{array}{rcl}{\overrightarrow{f}}_{{{\rm{MHD}}}}&=&\overrightarrow{J}\times \overrightarrow{B}\\ {\overrightarrow{f}}_{{{\rm{MHD}}}}&\propto &\overrightarrow{B}\frac{\partial \overrightarrow{B}}{\partial t}\propto I\frac{\partial I}{\partial t}\end{array}$$

(7)

where I is the current inside the coil. The Lorentz body force propels the liquid metal in the reservoir and leads to a pressure inside the nozzle, which scales according to

$$\begin{array}{rcl}{f}_{{{\rm{MHD,peak}}}}&\propto &{p}_{push}\\ {p}_{push}&\propto &\sigma {\mu }_{0}^{2}\frac{{I}_{peak}^{2}}{{t}_{drive}}\end{array}$$

(8)

where μ₀ is the permittivity of free space. The exact value of p_push depends on the internal geometry of the nozzle. Coil current pulses are assumed to be triangular in form for Equation (8) to hold. Realistic coil current pulses and the corresponding pressure pulses due to the Lorentz force are shown in Fig. 3. Experimental current pulses in Experimental demonstration of multi resolution MMJ were measured using a Rogowski current probe (Model CWT Mini50HF, GMW Associates) after the completion of the experiment at room temperature, with a solid metal charge inside the nozzle.

It is useful to note that the MHD-DOD Lorentz force is a contactless electromagnetic body force, not an inertial-mechanical surface force as is the case in piezoelectric inkjetting. As a result, the forcing mechanism works on the timescales set by the mutual inductance between the actuation coil and the molten metal, allowing for very rapid pressure and flow generation inside the molten metal, a feature that is essential for DOD metal jetting and to the multi-resolution concept presented here. Since there is no contact between the liquid metal and any electrodes, the MHD method is deemed “contactless”. The body force is radially inward during the rising portion of the coil current, and radially outward during the falling portion, corresponding to the “push” and the “pull” portions of the the pressure above the orifice, as shown in Fig. 3.

The lower portion of the nozzle is prepared by milling the shape and the two orifices out of small particle (<1 μm) graphite (POCO EDM-AF5, Entegris). Since at this point, both orifice lengths are 500 μm, the 200 μm side of the nozzle is hand-polished with 1000 grit sandpaper to remove approximately 300 μm of graphite. The final lengths of each orifice, measured with a Mitutoyo micrometer (Model 342-371-30), are 445 and 270 μm for the larger and smaller orifice respectively. The resulting nozzle is shown in Fig. 8b. As discussed in Selective ejection using pulsed waveform control, this is necessary to create favorable flow conditions inside both orifices under application of the same upstream pressure. The orifice diameters correspond to the existing default resolution of the ElemX printer (500 μm) and an estimated practical resolution of LPBF melt pool size (200 μm)³⁵.

Fig. 8: Critical features of the dual resolution nozzle.

Nozzle preparation for the multi orifice jetting experiment is shown via: a an ideal 3D CAD model emulating the manual sanding process used to reduce the length of the 200 μm orifice; b photo of experimental graphite nozzle; c Model 3 computational mesh used to simulate the nozzle.

Experimental ejections of 4008 aluminum ejections were captured using a Photron Nova S12 high speed camera by triggering both the ejection and camera record functions with an external 5V trigger pulse. In the still images of Fig. 4 and in the supplementary videos, the graphite nozzle exit is shown at an angle of 30^∘ from the floor, which is necessary since the nozzle is recessed inside a ceramic chamber that protects it from oxygen reactions. The droplet velocities were extracted from the videos using the open source Tracker 6.0.9 video analysis software³⁶.