Introduction

The advancement and improved performance of smart mobile devices have resulted in an exponential growth of data. Creating efficient indexing and search methods for handling massive information has become paramount in several applications, including image retrieval and e-commerce1,2,3. However, the real-time information feedback requirements and limited computational resources of edge devices pose significant challenges to energy consumption and retrieval speed4,5,6,7. Two key issues need to be addressed. The first involves retrieval strategies. The process of precisely comparing the query vector with every sample vector in the database during retrieval tasks is often inefficient, mainly because vectors in real-world applications are typically high-dimensional and high-precision, leading to high computation complexity. The second issue relates to the conventional von Neumann architecture used by computing systems. In this setup, a large amount of data needs to be transferred frequently between the computing units and memory, resulting in considerable energy consumption and latency.

To overcome these challenges, the hashing technique has gained increasing attention due to its exceptional efficiency in retrieving information from large datasets8,9,10. Unlike an exact search, which typically uses Euclidean or cosine distance as a similarity measure to find the exact nearest neighbor, hashing is an effective approximate nearest neighbor search technique. It finds the approximate nearest neighbor with high probability and uses the Hamming distance as a similarity metric (Fig. 1). The fundamental concept of hashing is to construct a mapping function to index each object into a compact binary code, minimizing the Hamming distances for similar objects and maximizing it for dissimilar ones.

Fig. 1: Schematics of the hash coding.
figure 1

(left) Performing an exact comparison across all items presents a challenge due to the high computational complexity and memory requirements, thereby making the nearest neighbor search impractical for edge devices. (right) Hash coding aims to resolve this issue by mapping high-dimensional, real-valued vectors to low-dimensional binary hash codes. This is achieved by designing suitable hash functions that can preserve the similarity of these vectors in the original space. Subsequently, the similarity can be gauged using the Hamming distance of the binary hash code. This approach results in a high search speed and energy efficiency, albeit with a minor loss in accuracy.

Full size image

Despite the efficacy of the hashing technique in reducing computation demands, the energy consumption associated with data transfer remains a significant concern. One promising solution is to perform the search using the in-memory computing (IMC) paradigm, i.e., in-memory search (IMS), where certain arithmetic operations, such as the calculation of Hamming distance11 and vector-matrix multiplication (VMM)12,13, are carried out by the memory itself, reducing the need for data transfer between the computing unit and memory14,15,16. Content-addressable memory (CAM) is a key search function of IMS and has been employed to store codes generated by hash function17. Given an input search vector, the Hamming distance between the search vector and all the stored vectors is calculated to identify the vector closest to the search vector. Emerging non-volatile memories, such as resistive random-access memory (RRAM)18,19,20, phase-change memory11,21,22, and ferroelectric FET (FeFET)17,23, etc., have been used to create CAMs, pursuing the highly energy-efficient IMS. Besides, hashing approaches that generate the search vectors and stored vectors are a crucial function that needs to be accelerated by the IMC paradigm, especially considering the increasing scale of data. Recently, locality-sensitive hashing (LSH), which explores data-independent hash functions with random projections or permutations24,25,26,27, has been implemented using the IMC paradigm by exploiting the intrinsic stochasticity of RRAM devices19. Learning-based hash method, that is, learning-to-hash (LTH), leverage machine learning techniques to create data-dependent and task-specific hash functions28,29,30,31. Compared to LSH, LTH produces more compact binary codes, leading to improved search performance. However, the experimental validation of an IMS architecture that incorporates LTH with IMC and CAM is still required.

In this work, we proposed an IMS architecture that combines the concepts of LTH and CAM. We validated its performance using a simulation with statistical measurements of the RRAM crossbar array for graph-based recommender system acceleration. The LTH method efficiently encodes user and item features in recommender systems, simplifying similarity calculations and enhances hardware compatibility and storage efficiency. Then the proposed IMS architecture collaborates the LTH with CAM to perform in-memory hashing encoding and Hamming distance calculations. The results demonstrated a level of accuracy comparable to software, while with significantly reduced energy consumption compared to digital systems.

Results

The proposed LTH model for the recommender system

Recommender systems have become integral tools in our everyday digital interactions, providing vital support to various online services such as web searches and e-commerce platforms. These systems are designed to select a group of items from a large database that a user is likely to prefer, based on a specific query. Graph neural networks (GNNs) utilize graph structures to encode information, capitalizing on the relationships between nodes to disseminate and process data32,33,34,35. Recommender systems based on GNNs can effectively model the intricate interplay between users and items, overcoming challenges presented by traditional recommendation methods, such as the cold start issue and problems related to sparsity36. The GNN-based methods denote each entity in the user-item interaction network with a unique, continuous embedding vector, expecting that similar users or items exhibit similar embeddings. Predictions are subsequently made based on the similarity score between these embeddings. However, filting numerous candidates in a continuous embedding space can be computationally expensive and inefficient. This is primarily due to the high-dimensional nature of the vectors and exact search strategy, which can cause a slowdown during the inference process.

In order to improve search accuracy and efficiency, we proposed an LTH model for the GNN-based recommender system. As depicted in Fig. 2a, this recommender system consists of three key components: a filtering layer, a hash layer, and an item embedding table. The filtering layer is responsible for learning latent features, also known as embeddings, which represent users and items based on their past interactions. Assuming \(\Omega\) is the original continuous representation space, the purpose of the hash layer is to establish a similarity-preserving mapping from \(\Omega\) to \(k\)-bit compact binary code: \({\mathcal{F}}:\) \(\Omega \to {\left\{+1,-1\right\}}^{k}\). This nonlinear transformation is learned through a fully-connected layer. Unlike the clear and available label information in classification learning tasks, recommendation tasks typically aim at generating similar vector embeddings for nodes with similar topology. To facilitate this, we design the loss function to draw the codes of observed user-item pair closer together, and push the codes of unobserved user-item pairs further apart. This is achieved by minimizing or maximizing the distance between user-item pairs during the training stage. The obtained item hash codes are stored in the item embedding table, which performs NNS lookup operations to provide a list of candidate items for users.

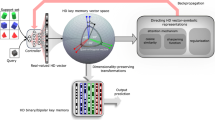
Fig. 2: The proposed RRAM-based LTH model for the recommender system.
figure 2

a The recommendation process of the MovieLens dataset is facilitated through the RRAM-based in-memory search system. During the training process, an LTH method is introduced, which includes a filtering layer to manage user-item interaction data, and a hash layer to generate hash codes for both users and items. The predicted similarity scores between the hash codes of users and items are compared with the ground truth similarity scores to generate a loss. This loss is then backpropagated through the network to update the learnable parameters of both the hash layer and filtering model. In the training stage, the hash layer learns corresponding hash-like representations, which are then converted into bipolar in the inference stage. b During the inference phase, the RRAM-based crossbar array is used to generate the hash codes and support parallel search operations across all items. c The IMS hardware with a 40 nm 256 kb RRAM chip is employed in this process. d The cumulative probability of the LRS and HRS. We sampled 100 devices from the measured results of the test chip. e The switching endurance of the RRAM devices.

Full size image

The hardware implementation of the proposed LTH model is depicted in Fig. 2b. The binary weights of the hash layer and all item hash codes are written into the RRAM-based multiply-and-accumulate (MAC) and CAM crossbar array, respectively. It should be noted that the filtering layer could be various feature extractors and we employ it on digital hardware for convenience. The hash code of the query user is subsequently compared against all previously stored item hash codes in the CAM to calculate the Hamming distance in parallel and identify a set of items that the query user is most likely to prefer. This rapid retrieval system benefits from the low power consumption of the in-memory computing paradigm and the software-comparable retrieval performance of the hardware-friendly LTH method. The hash layer and item embedding table are implemented on the MAC and CAM, respectively. We utilized an RRAM chip accommodating a 512 × 512 one-transistor one-resistor (1T1R) TaOx RRAM crossbar array, as shown in Fig. 2c. The effectiveness of the MAC and CAM functionalities is validated through a hybrid simulation method (see Supplementary Note 1), where both MAC and CAM share the same RRAM array, and their distinct functionalities are achieved through different peripheral circuit designs. Complementary metal-oxide-semiconductor (CMOS)-compatible nanoscale TaN/TaOx/Ta/TiN RRAM devices are fabricated using the backend-of-line (BEOL) process on a 40 nm technology node tape-out (see Methods). The chip is integrated on a printed circuit board with analog-digital conversion circuitry and a Xilinx ZYNQ system-on-chip, constituting a hybrid analog-digital computing platform37. Figure 2d depicts the device-to-device variation at a read voltage of 0.2 V. The low resistance state (LRS) and high resistance state (HRS) follow a Gaussian distribution with a mean of 36.8 kΩ (135.4 kΩ), respectively, and a standard deviation of 3.7 kΩ (16 kΩ), respectively. Figure 2e presents the endurance characterization of the RRAM devices.

RRAM-based MAC crossbar array for hash code generation

We establish the efficacy of the proposed LTH approach by implementing VMM operation and hash layer activation function on the RRAM-based MAC crossbar array by the hybrid simulation method (see Supplementary Note 1). Figure 3a depicts the schemetic of MAC design, complete with peripheral circuit, which includes components such as wordline (WL) driver, bitline (BL) driver, transimpedance amplifiers (TIA), and sense amplifiers (SA). Initially, the weights of the hash layer are obtained through offline training and then mapped onto the RRAM devices. Given that the weights can be either positive or negative, each weight is symbolized by a pair of RRAM devices, as illustrated in Fig. 3b. “−1” is represented by two devices where the top one is in the HRS, and the bottom one is in the LRS. The opposite pattern is used for “+1”.

Fig. 3: The hardware implementation of the hash layer.
figure 3

a Schematic of VMM operations for hash code generation. Here, bipolar weights are stored in the RRAM array as different resistance state combinations, represented by pairs of adjacent RRAM cells. b The truth table of a single RRAM cell is provided for clarity. c The readout resistance map, which represents different MAC situations, is displayed after a 9 × 8 binary weight matrix is stored in the crossbar. d The voltage distributions of corresponding MAC results. The final hash codes can be obtained through a sense amplifier (SA).

Full size image

Regarding the BL input, \({V}_{{{\mathrm{high}}}}\) of 0.7 V represents “1” and \({V}_{{{\mathrm{low}}}}\) of 0.3 V represents “0”. The voltage on sourceline (ScL) is consistently kept at 0.5 V, generating a read voltage of 0.2 V. VMM operations are conducted by simultaneously applying read voltages to the BL and reading the current from ScL. The current flowing through each weight-cell in read operation depends on the combination of BL input voltage and stored data pattern. The sign function required for the hash layer is realized by incorporating an SA for every pair of rows. This setup enables the SA to realize the generation of the hash code by comparing the voltage emanating from the positive and negative rows, thereby considerably simplifying the peripheral circuit design and diminishing energy consumption. Figure 3c shows the conductance distribution of the MAC crossbar array, taking into account device variation. Under the full “+1” input scenario, the voltage difference distributions corresponding to different MAC results, along with the final output, are shown in Fig. 3d. The final output remains largely uninfluenced by device variation, making the design robust and reliable.

RRAM-based CAM crossbar array for Hamming distance calculation

The learned hash codes of items are stored in the RRAM-based CAM crossbar array. When a user query arrives, the RRAM-based CAM array carries out a parallel search operation, based on Hamming distance, across all the item vectors stored within the memory. The similarity search operation is validated on the RRAM-based CAM array. Figure 4a demonstrates the architecture of a CAM cell and the schematic of the CAM crossbar array. In contrast to the MAC cell in Fig. 3a, each bit of the hash code is stored by two adjacent RRAM devices (\({R}_{L}\) and \({R}_{R}\)) in the same match line (ML). Therefore, each row stores the hash code of an item. With this design, the CAM cell operates similarly to an XOR gate, with the output result “0”/“1” (indicating “match”/“mismatch”) corresponding to the low/high voltage in ML. Figure 4b shows the truth table. The data stored is determined by the resistance state of \({R}_{L}\)/\({R}_{R}\), wherein the HRS/LRS represents “1” and LRS/HRS represents “0”. Moreover, the complementary voltage of the searchline (SL) signifies the query data, where VS/0 and 0/VS are defined as “1” and “0”, respectively.

Fig. 4: The hardware implementation of in-memory search.
figure 4

a RRAM-based CAM crossbar array. Each row stores the hash code of an individual item. b The truth table of a single CAM cell. c Schematic of SA, which is used to sense the voltage of the ML and compare it to a reference voltage. This comparison generates a digital output by SA, representing a match or a mismatch result. d The transient simulation of match and 1-bit mismatch. The search operation can be executed promptly. e The ML voltage increases with the number of mismatched bits, which is a result of different voltage division patterns. f The overlap rate with varying code length.

Full size image

Different from the conventional discharge-based CAM, our proposed RRAM crossbar-based CAM quantifies the degree of mismatch with the output voltage of the ML. Initially, each ML undergoes a pre-discharge operation managed by the discharging transistor MN before the ML voltage measurement. Following this, a standard current latch SA is used to measure the ML voltage (\({V}_{{{\mathrm{ML}}}}\)), as shown in Fig. 4c. When a minor difference between \({V}_{{{\mathrm{ML}}}}\) and the reference voltage \(({V}_{{{\mathrm{ref}}}})\), the current flow of the corresponding transistors (M1 and M2) governs the serially linked latch circuit. This is then converted to a significant output voltage, digitally represented at Q/QB. Figure 4d provides the timing diagram for a 1-bit search on CAM. The discharge signal (DCH) initiates pre-discharge operation, reducing the \({V}_{{{\mathrm{ML}}}}\) to the ground level. Subsequently, the query hash code of a user is converted to the complementary voltages on SLs and SLBs. The voltage on ML then escalates based on the level of mismatch with the stored item hash codes. Once the SAE signal is activated, the SA is ready to detect whether the \({V}_{{{\mathrm{ML}}}}\) voltage has surpassed \({V}_{{{\mathrm{ref}}}}\). The correlation between the raised \({V}_{{{\mathrm{ML}}}}\) and the degree of mismatch (also known as the Hamming distance) is linear, as demonstrated in Fig. 4e.

The simulated equivalent values of hash codes stored in the CAM follow a quasi-Gaussian distribution due to the device variation. This may result in indistinguishable outcomes in terms of different Hamming distance. As shown in Fig. 4f, the simulated overlap rate increases with the array size, reaching 0.8 in 256 hash bits. The overlap ratio of two adjacent distributions is defined by the difference between the local minimum and maximum points of the probability density function (PDF). To ensure the retrieval accuracy of our in-memory search system, we select a shorter code length for better robustness. When the code length reaches 32-bit, the impact of device variation is not particularly significant, and various matching states can be easily distinguished. Therefore, we can determine the most matched item stored in the array based on the results of SAs. Notably, by using SAs to bypass analog-to-digital converters (ADCs), peripheral circuitry contributes to only a small fraction of energy consumption.

Discussion

To validate the efficacy of the LTH method, we benchmark it against existing hash-based recommendation models using the widely recognized MovieLens dataset38. Our evaluation metrics are HR@K (HitRate) and NDCG@K (Normalized Discounted Cumulative Gain). The HR metric visually gauges whether the test item appears in the top-k list, while NDCG indicates the hit location by assigning a higher score to the top-ranked hit (see Methods). We refer to the model that does not use the hashing technique, that is, exact search with Euclidean distance metric as the baseline, which represents the maximum potential attainable by the hash function. As shown in Fig. 5a, the LTH method outperforms other similar learning-based hash models, such as the HashGNN30 model and HSGCN39. Furthermore, compared to the LTH method, LSH often falls into suboptimal accuracy. This may be attributed to the fact that LSH uses a random projection to map similar items into the same codes, while LTH uses training data to preserve the original spatial similarity relationship, thereby enhancing the quality of the learned hash code. In addition, LTH improves hardware compatibility by binary computation, making it more suitable for the implementation of an RRAM-based crossbar array.

Fig. 5: Simulation results of RRAM-based LTH on recommendation task.
figure 5

a HR and NDCG score of different methods. b Simulated impact of device-to-device variation on accuracy. c Accuracy with different code lengths without considering any device variation. d Energy consumption of different approaches. The exact compare method denotes approaches that do not implement any hashing technique. The energy calculated under exact compare and LTH methods originates from the implementation using digital hardware.

Full size image

Despite the high parallelism and efficiency of in-memory computing on the RRAM crossbar array, the non-idealities of the device need to be carefully considered. To achieve optimal performance, we first finetune the hyperparameters of the model. Then, we evaluate how these non-ideal device factors affect model performance. The atomic mechanisms of the device resistance switching result in final conductance values being random. The mean of this distribution roughly aligns with the target conductance. We interpret this noise as a natural Gaussian distribution and incorporate it into the computation during the inference process. As shown in Fig. 5b, when the standard deviation of the device noise reaches 10.1% of the mean conductance, it only causes a minor decrease in recommendation accuracy (less than 0.01) on the Movielens dataset.

In the software simulation, without considering any device variation, extending the length of the codes tends to improve retrieval accuracy, primarily due to their ability to offer robust representations of features, as shown in Fig. 5c. Nevertheless, when implemented on hardware devices, longer code length will, in fact, lead to a certain decrease in retrieval accuracy (see Supplementary Note 2). This discrepancy is attributed to the device variation, especially within the parameters of the hash layer as it is integrated into the MAC crossbar. It should be noted that noise from the RRAM-based CAM also impacts retrieval accuracy, especially as code length increases (see Fig. 4f). To mitigate this problem, our algorithm simulation takes into account such noise by probabilistically adjusting the Hamming distance. This adjustment results in less than a 1% drop in accuracy for 32-bit codes, which is relatively insignificant. The recommendation task’s resilience to this impact is likely due to its inherent characteristic, which involves a large number of candidate items where minor rank shifts among them do not significantly alter the outcome. However, the situation is markedly different in cases with a high overlap rate in recommendations coupled with a limited pool of items. Under these conditions, accuracy degradation can be substantial, necessitating further exploration and optimization to maintain high-performance levels. This specific scenario warrants additional attention to devise strategies that can effectively counteract the negative effects of hardware-induced variability on retrieval accuracy.

We evaluate the energy consumption of the RRAM-based LTH method on the MovieLens 1 M dataset. As shown in Fig. 5d, we compare the energy consumption of various approaches when recommending items during a single-user inference. To gain clearer insights into the impact of the hashing technique, we employed the same feature extractor and intentionally excluded the energy consumption of this part from our evaluation. The exact compare method denotes approaches that do not implement any hashing technique in traditional digital systems. In such methods, user and item embeddings are represented as high-precision floating-point numbers, and the similarity between them is estimated using the Euclidean distance metric. In this case, the energy consumption is exclusively due to the similarity computation. The LTH method, on the other hand, incurs energy consumption on both the generation of hash code and the subsequent retrieval of these hash codes, labeled as “others” and “search operation”, respectively in our analysis. Remarkably, the search phase accounts for less than 10.1% of the total energy consumed, benefiting from the straightforward Hamming distance calculation for hash codes, i.e., XOR computation. The hash generation phase represents a more substantial fraction of energy use, because of the necessary multiplication and addition operations. Therefore, the inherent energy efficiency of retrieval strategy that employ hashing techniques avoids complex floating-point operations and enables the LTH method to achieve a 133-fold reduction in energy consumption compared to the exact compare retrieval strategy. Moreover, compared to LTH with digital hardware implementation, the RRAM-based LTH exhibits a 30-fold reduction in energy consumption, benefiting from the in-memory computing paradigm on the RRAM crossbar array as well as simplified peripheral circuit design. Compared to existing state-of-the-art works on non-volatile CAM, our work demonstrates comparable energy efficiency (see Supplementary Table 1). The method and parameters employed for estimating energy consumption are detailed in Methods.

The latency of different implementation methods were evaluated (see Supplementary Note 3). Compared to the exact compare method, the LTH method enhances search speed by reducing vector dimensionality and precision through hashing techniques. However, the current RRAM-based method does not outperform state-of-the-art GPUs for LTH methods, particularly when compared to low-bit GPUs due to the low parallelism of the RRAM array we used. Notably, we only need to store the ItET and the hash layer parameters and perform the search across the ItET (see Methods). The reprogramming is not required since the RRAM array size is sufficient. However, recommendation tasks in real applications often involve large datasets, resulting that the RRAM capacity is insufficient to support inference for a single user. Reprogramming is necessary for each user throughout the recommendation process. Therefore, higher-capacity or higher-endurance RRAM chips are still needed in the future for large-scale recommendation tasks.

In conclusion, we have developed an in-memory search system designed to enhance recommender systems, incorporating a hash layer and CAM, both designed based on RRAM crossbar arrays. The hash layer generates hash codes for users and items through MAC operation, streamlining the search process. The CAM then identifies items that exhibit a high degree of similarity to the user query, regarding as suitable recommendations. Our system supports XNOR operations and avoids traditional high-precision distance metrics, making compatible computations with RRAM devices and simplifying peripheral circuit design by replacing ADCs with comparators. This approach integrates the LTH algorithm with in-memory computing and hash code retrieval via in-memory search, achieving 30-fold energy savings compared to its implementation by traditional digital systems while maintaining accuracy comparable to software methods. These results underscore the potential of our approach as a highly energy-efficient and robust hardware-based solution for recommendation applications.

Methods

The RRAM chip fabrication

The RRAM chip features a crossbar structure, comprising 256 kb RRAM cells arranged in a 512 rows × 512 columns37. Each cell is integrated into a 40 nm standard logic platform, positioned between Metal 4 (M4) and Metal 5 (M5). This includes top electrodes (TEs), a TaOx-based oxide resistive layer, and bottom electrodes (BEs). The TE, made of a 3 nm Ta layer and a 40 nm TiN layer, is deposited sequentially using a sputtering process. The resistive layer is then constructed from 10 nm of TaN and 5 nm of Ta, which is deposited onto the BE via physical vapor deposition. Subsequently, the Ta is oxidized in an oxygen-rich environment to create an 8 nm TaOx dielectric layer. The BE, measuring 60 nm, is patterned using photolithography and etching techniques. It is then filled with TaN using physical vapor deposition and polished using chemical mechanical polishing (CMP). Following the fabrication process, the logic BEOL metal is deposited as per the standard logic process. Cells in the same columns share a TE, and those in the same row share a BE, culminating in the formation of the RRAM array chip. Lastly, the chip undergoes a post-annealing process, which involves heating it to 400 °C for a duration of 30 min.

Recommender system simulation

The MovieLens dataset38, which consists of 1,000,209 anonymized ratings across nearly 3900 movies, is widely used as a benchmark for evaluating recommender systems, These ratings were provided by 6040 MovieLens users. Following the approach used in previous work40, we transformed the rating scores into implicit feedback. Each user-item pair was labeled as either 1 or 0, indicating whether the user had rated the movie or not. The user-item pairs were then randomly divided into two groups: 70% for training and 30% for testing. Within the training set, interactions that were observed are treated as positive instance, while uninteracted pairs are treated as negative instances. In order to avoid the ineffectiveness of hashing technique arising from the imbalanced amount of positive and negative samples in the dataset, we implement a probabilistic sampling method that reflects the respective occurrence rates of the positive and negative instances.

The observed user-item interaction data can be depicted using a bipartite graph, \(G(V,E)\), where V represents the nodes set, comprising users and items, and E represents the edges set. Initially, we randomly initialize the parameter matrix of the user and item embedding tables (ET). The initial embeddings of users or items are derived through lookup operations. These initial embeddings then undergo propagation through L layers, aggregating information from local neighbors. The final layer’s output serves as the representations of users and items, denoted as \({{\boldsymbol{u}}}_{{\boldsymbol{i}}}\).

Given the intermediate representation \({{\boldsymbol{u}}}_{{\boldsymbol{i}}}\) of user or item nodes, we first binarize the \({{\boldsymbol{u}}}_{i}\) using the Sign function:

$${{\boldsymbol{u}}}_{i}^{b}={\mathrm{Sign}}({{\boldsymbol{u}}}_{i})=\left\{\begin{array}{c}+1\,if\,{{\boldsymbol{u}}}_{i}\ge 0,\\ -1\,{\mathrm{otherwise}},\end{array}\right.$$
(1)

The Sign function, however, is not differentiable at zero, and its gradient is undefined, so we utilize the straight-through estimator for back-propagation41. This means that the gradients of \({{\boldsymbol{u}}}_{i}^{b}\) are copied from \({{\boldsymbol{u}}}_{i}\) by a clip function clip(-1,1) in the backward pass. Subsequently, a fully-connected hash layer converts \({{\boldsymbol{u}}}_{{\boldsymbol{i}}}\) into a compact K-bit binary-like hash code, \({{\boldsymbol{h}}}_{{\boldsymbol{i}}}\) as follows:

$${{\boldsymbol{h}}}_{i}=\tanh \left({{\boldsymbol{W}}}^{T}{{\boldsymbol{u}}}_{i}+{\boldsymbol{b}}\right)$$
(2)

where \({\boldsymbol{W}}\) is the binary parameter matrix, b is the bias matrix. To encourage the network to learn binary-like embeddings, we employ tanh() as the activation function during training. Unlike classification learning tasks, where label information is readily available, recommendation tasks aim to generate similar vector embeddings for topologically similar nodes. To achieve this, the loss function is designed to draw the codes of observed user-item pairs closer together and distance the codes of unobserved user-item pairs by minimizing or maximizing the distance between pairs. During the inference process, we set Sign() as the activation function to acquire precisely binary hash codes, and then calculate the Hamming similarity between a user’s hash code and all item hash codes. Items are ranked based on these similarity scores, and the top-k items with the highest scores are recommended.

All algorithm simulations were executed using Python 3.7. The simulations for the circuits used in this work were conducted on Cadence, and the device parameters were obtained from an RRAM in-memory-computing chip.

Similarity and accuracy metrics

For LTH method, we use dot product similarity in the training phase, and use Hamming similarity in the inference phase. These two similarity metrics correspond when the hash code is denoted as \(h\in {\left\{\pm 1\right\}}^{K}\), where K is the length of the hash codes. Hamming similarity is defined as the number of identical bits between two vectors. The dot product similarity score is proportional to Hamming similarity.

$${HD}\left({h}_{u},{h}_{i}\right)=\frac{1}{2}+\frac{1}{2K}{{h}_{u}}^{T}{h}_{i}$$
(3)

For evaluation metrics, we adopted HR@K42 and NDCG@K39. NDCG@K is defined formally as:

$${{\mathrm{NDCG}}}{\rm{@}}K=\frac{{{{\mathrm{DCG}}}}_{K}}{{{{\mathrm{IDCG}}}}_{K}}$$
(4)
$${\mathrm{N}}{{{\mathrm{DCG}}}}_{K}=\mathop{\sum }\limits_{i=1}^{K}\frac{{2}^{{y}_{i}}-1}{{\log }_{2}\left(1+i\right)}$$
(5)

IDCG is the ideal DCG, \({y}_{i}\) indicates whether the i-th item is recommended or not, and we set K = 50 to calculate the average accuracy for all users in the test set.

Energy consumption evaluation

As shown in Table 1, we estimate the energy consumption of LTH for a single-user recommendation task using the in-memory search method proposed above. We evaluate the different components of the recommendation process using the proposed RRAM-based MAC and CAM array with specific peripheral circuits. A detailed analysis of energy estimation can be found in Supplementary Note 4. The hash layer is a fully-connected layer with a dimension of 64 × 32. We need to perform the search operation across the item embedding table (ItET), which has a dimension of 3706 × 32. For the exact compare method and LTH method, the multiplication and addition operations are estimated based on the 45 nm standard CMOS technology43, while the XOR operations are estimated using the 65 nm process44. To ensure a fairer comparison, we scaled the 45 nm process and 65 nm process to 40 nm (see Supplementary Note 5). As for the RRAM-based LTH method, the array operations are carried out by the read operations of device cells on the RRAM chip, and all the simulations were based on a 40 nm process. All the detailed parameters for energy consumption are summarized in Table 2.

Table 1 Energy consumption evaluation of different approaches.
Full size table
Table 2 The detailed experimental parameters used for the evaluation of energy consumption.
Full size table