Introduction

Data centers, which usually house massive racks of graphics processing units (GPUs), consume nearly a third of the world’s computing energy budget1. A large portion of the workload in data centers is occupied by recommendation models, which are mostly based on deep neural networks (DNNs)2. For instance, in 2020, Meta’s data centers allocated 79% of their artificial intelligence (AI) inference cycles exclusively to run pre-trained recommendation models (RMC1, RMC2, RMC3, and others)3. Training the underlying DNNs (before deployment for inference) is also extremely energy inefficient and occupies large portions of data center workloads. As an illustration, training the GPT-3 model, the basis for the popular ChatGPT, costed over US$12 million, accompanying over 500 tons of CO2 equivalent emissions4.

The computer science literature is dominated by applications such as computer vision or natural language processing, and large language models (e.g., ChatGPT). However, recommendation models, which are much smaller than large language models but far more complex, dominate both the expenditures and revenue of many large corporations that make up the consumer electronics industry. Because of limited progress in developing efficient recommendation systems (consisting of models, the hardware, and the training algorithm), the large energy and cost expenses associated with data centers are becoming unsustainable and have begun to impede the growth of the consumer electronics industry4.

Recommendation models utilize both explicit information (e.g., name, address) and implicit behavioral information (e.g., clicks, searches, purchases, views) to deliver individualized and compelling content to users5. Such varied parameters make recommendation models very high in dimensionality (not necessarily large in size) and thus very complex to train. There is thus a crucial need to sustain commercial growth by finding efficient ways to offer recommendation, which requires ways to train complex AI models.

Why is AI training inefficient today? Training of DNNs in data centers is sustained by digital GPUs, the hardware workhorse of AI, and backpropagation, the algorithmic workhorse of AI. This solution has become a bottleneck as the data volumes have grown exponentially over the past decade. GPUs have started hitting the limits of Moore’s law. For instance, in late 2022, Nvidia justified increasing GPU prices disproportionately to the improved computing capabilities, owing to the increased costs, with limited performance gains, associated with going below the 5 nm CMOS technology node6. This issue highlights a bottleneck in the hardware workhorse of AI training, particularly for recommendation models. This hardware inefficiency makes it expensive to run recommendation models in large data centers and makes it prohibitive to implement them in edge devices. Therefore, we need to find an alternative system of models, algorithm and hardware for the next generation of recommendation models.

The last decade has witnessed a keen interest in post-digital hardware aimed at AI applications. Crossbars of two-terminal resistive switching nonvolatile memories (NVMs) are likely the most prominent among them7,8,9. The NVM crossbar is naturally more energy-efficient than general-purpose processors10,11. Unlike the sequential nature of central processing units (CPUs) and semi-sequential GPUs, NVM crossbars enable matrix-vector multiplications (MVMs) in a single clock cycle by exploiting the natural physics of Ohm’s law and Kirchoff’s law12,13,14,15. Owing to their accelerated MVM capabilities, NVM crossbars are researched for applications in image classification16,17,18, solving linear equations19,20, nonpolynomial time (NP) hard optimization10,21,22,23, and time-series forecasting24,25. While NVM crossbars offer the theoretical basis for accelerating DNN training, unlike digital GPUs, NVM crossbars routinely suffer from low precision, high variability, noise, and asymmetric and nonlinear response to programming voltages. As such, the prevailing backpropagation algorithm, which is an analytical and sequential process of training, is suitable for digital GPU environments, but cannot be easily implemented on NVM crossbars4,6,26,27,28,29,30,31,32,33.

Here, we introduce a backpropagation-free AI training algorithm-model framework for recommendation systems co-optimized with NVM hardware. Our model is based on a deep reinforcement learning framework (DRLF) and is inspired by the restless multi-armed bandit (RMAB) problem, which offers an efficient decision-making framework by relentlessly activating each arm (corresponding to each content for recommendations)34,35. The technique uses a network-wide metric, the Whittle index, to balance exploration of arms and exploitation of rewards to the agent seeking to deliver recommendations. Similar models, such as NeurWIN36, have been studied in academia but have not demonstrated commercial viability. For instance, to train a model with only 100 arms, training every arm requires 9,000,000 MVMs. Although GPU-based hardware is efficient to repeated MVM operations, NVM crossbars can further eliminate the data movement bottlenecks and enable energy-efficient one-shot MVM operations through Ohm’s and Kirchoff’s laws in analog domain37,38,39. We implemented our technique on a 12 Mb analog-digital hybrid RRAM crossbar chip14, which was end-to-end foundry manufactured, thus representing both realistic scales and performance (along with limitations) of large-volume manufactured post-CMOS electronics. While the underlying NVM crossbar hardware exhibits the expected limitations of post-CMOS hardware outlined above, our model, along with a local training algorithm, both tolerates and exploits such limitations. For instance, our technique performs well even under limited bit precision in each NVM cell. Also, the randomization of the arms is driven by the natural noise present in the non-digital nature of the hardware. As a result of the benefits above, using performance benchmarking via detailed circuit simulations, we show that the RMAB-inspired DRLF run in-situ on NVM crossbars can outperform CPUs and GPUs by many orders of magnitude in energy efficiency, while offering algorithmic performance that matches backpropagation up to 100 arms.

Results

Overview of the process

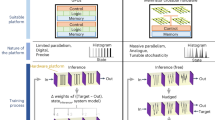
Figure 1 illustrates the schematic of the RMAB-inspired recommendation model, comprising our system with NVM crossbar (agent), user (environment), and various content items (arms) that can be delivered as recommendations via ads. Recommendation models need to carefully avoid user habituation to content caused by information overload. Thus, all ads should not be delivered to the user at the same time. The RMAB-inspired model addresses this issue by selecting a limited number of tunable M contents as ads out of a total of N contents (denoted as (N, M)) to minimize habituation and maximize profit.

Fig. 1: Proof-of-concept restless multi-armed bandit (RMAB)-inspired recommendation system.
figure 1

Users navigate through the main web page to specific category pages, referred to as either the initial state (S0) or current state (S1) utilized to estimate cost (λ) and Whittle index, respectively. Specifically, S (S0 and S1) serves as input to each core in the nonvolatile memory (NVM) crossbar, which cores are programmed to represent the weight values of neural networks for each arm (A~D), in this case, the contents. Based on the initially estimated λ to compute Whittle index, the agent selects the arm with the highest Whittle index at each S1 to maximize the total discounted rewards (TDR) for recommendation.

Full size image

The states, denoted as S0 and S1 (in our example, integers ranging from 1 to 20), are used to estimate the cost (λ) and the Whittle index, respectively. The Whittle index serves as a deterministic metric that guides content selection, driven by system dynamics such as the state-dependent reward (gain for the agent) and the tradeoff between exploration and exploitation in the time domain (for instance, exploration of many contents preceding exploitation of specific profitable contents)40. The states are determined by the behavior of the user (e.g., clicks, visited web pages, scrolling patterns, etc.). For instance, an ad being clicked by a user resets its state (S1 = 1), while the state is incremented as a function of timestep (i.e., the user is clicking other ads) from 1 up to 20.

Our recommendation system includes three phases: training, inference-like, and evaluation. These phases are performed sequentially and repeatedly with iteration variables such as mini batch (b), training episode (e), and timestep (t). Figure 2 illustrates the detailed training phase. For each content, the training phase starts with initializing S0 as an input to the multilayer perceptron (MLP, denoted as a function f) that estimates λ (f(S0)), which has no standard activation function. Another initialized S1 is then passed through the same MLP to produce a Whittle index (f(S1)).

Fig. 2: Algorithm block diagram of activity-difference training of RMAB.
figure 2

The two groups of weight matrices (W and W*) are initialized for forward and backward path, respectively. The randomized states (S0 and S1) are the input to the neural network, generating the cost (f(S0), denoted as λ) and Whittle index (f(S1)), respectively. The discounted net reward at each training episode (e), denoted as G, is used to compute the accumulate reward. After updating the weight update matrices (dW and dW*) through the activity-difference training, the episode dimension e are averaged together, weighted by (G-Gmean) at each e to update final W and W*.

Full size image

At each t, the content is activated if the Whittle index is higher than λ. To determine the optimal action with the environment’s activation cost, we define different objective functions (J(t)), comparing f(S1) and \(\lambda\)36:

$$J(t)=\log \frac{1}{1+\exp \left(-5\left(f\left({S}_{1}\right)-\lambda \right)\right)}(f\left({S}_{1}\right) > \lambda )$$
(1)
$$J(t)=\log \left(1-\frac{1}{1+\exp \left(-5\left(f\left({S}_{1}\right)-\lambda \right)\right)}\right)(f\left({S}_{1}\right)\le \lambda )$$
(2)

The previous software RMAB study used an analytical derivative of J(t) to update the weight values, making the computation costly like the gradient flow in standard backpropagation36. Instead of the analytical update, we alternatively utilize activity-difference training, a numerical algorithmic solution compatible with in-situ training in NVM hardware, which eliminated the need for backpropagation41. Activity-difference training utilizes the two types of outputs collected from all layers in MLP, which are denoted as a free phase (Afree) and a nudged phase (Anudged). Afree refers to the output group of neurons from each layer in MLP (forward path). After generating Afree, the difference between f(S1) and J(t), scaled by a nudge constant (β), serves as a nudging input at the last node (i.e., forcing a signal in the backward direction), which would result in a settled output Anudged. The outer product difference (AfreeAfreeT - AnudgedAnudgedT) is used to update the weight values.

Another metric used for the weight update is the discounted net reward (G), a S1-dependent reward subtracted by λ:

$$G(t)=(R({S}_{1})-\lambda ){0.99}^{t-1}$$
(3)

R(S1) represents the intrinsic reward distribution for each content, defined as:

$$R({S}_{1})={\theta }_{0}\left(1-\exp \left(-{20\theta }_{1}{S}_{1}\right)\right)$$
(4)

where \({\theta }_{0}\) and \({\theta }_{1}\) are the pre-defined parameters differentiating R(S1) of each content (Supplementary Fig. S1). G is accumulated during all t in a mini batch of e and multiplied by the outer product difference. The multiplied term for each e is summed to update the weight matrices for each b36. After completing a single batch—i.e., once all elements in weight update matrices (dW and dW*) are updated—the episode dimension e are averaged together, weighted by (G-Gmean) at each e to update the actual weight matrices (W and W*) of the MLP. The weight values are increased if the corresponding Whittle index exceeds λ, and decreased if it falls below λ.

In the inference-like phase, S1 is initialized again, and MLP estimates f(S1) for each content, which again serves as the Whittle index, as in the training phase. The Whittle indices from each content are used to select contents with higher Whittle indices. In the following evaluation process, R(S1) of the selected content is used to estimate the total discounted reward (TDR), agent’s total gain or revenue.

Neural network and hardware implementation

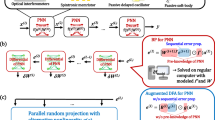
Figure 3a illustrates the neural network model of a three-layered network with 1-16-32-1 MLP mapped onto the NVM crossbar, which indicates the presence of both forward and backward paths. Instead of using bidirectional circuits (e.g., those used in prototypical backpropagation-based training) where information would flow in both directions across forward-path weight matrix (W), another weight matrix (W*) is used for the backward path in the RMAB-inspired network. The two activations of Afree and Anudged includes output set ([u1, u2, u3, u4]), where u1, (u2, u3), and u4, are from input, hidden, and output layer, respectively. The collected Afree and Anudged are in turn used to update the different W and W* matrices in conjunction with the corresponding G.

Fig. 3: Hardware implementation of RMAB within deep reinforcement learning framework (DRLF).
figure 3

a Workflow of three-layered network-based DRLF. As input of the three-layered network, the red and blue arrows indicate the starting points of free and nudged phases, respectively. The gray arrows correspond to the propagation between layers, including matrix-vector multiplication (MVM) and activation function. b Schematic of weight mapping of DRLF NVM crossbar. For backward path, transposed backward matrices are used (W*T). To clarify the hardware implementation, the symbols and lines matched to the features in (a). c One-shot m×n MVM through one-transistor one-resistor (1T1R) array in NVM crossbar. Bit line (BL); source line (SL); word line (WL). d Optical microscopy image of NVM crossbars. Inset: each corelet consists of a 16 × 16 1T1R array and neuron, and one NVM crossbar consists of 256 corelets. e Results of weight mapping of positive weight values to NVM crossbar. A differential pair of conductance matrices is used for signed weight values. f Error histogram of weight mapping.

Full size image

We represent each content’s neural network model using a 106 × 53 NVM crossbar array (53 × 53 for positive weights and another 53 × 53 for negative weights). Each NVM crossbar is physically independent of other NVM crossbars and is accompanied by intrinsic and peripheral circuit noise unique to the specific NVM crossbar, which perturbs the Whittle index output and enhances the training performance. Without using backpropagation, each core can be independently and simultaneously trained in-situ, achieving high efficiency in terms of both time and energy. More detailed electrical operation of NVM crossbar is included in Method section.

Figure 3b illustrates the hardware implementation of the 1-16-32-1 network, representing the target objective within a 53 × 53 RRAM NVM crossbar with bipolar weights for each content14, where the forward and backward paths are implemented using W and W* matrices, respectively. W and the transpose of W* matrices (W*T) are symmetrically mapped into a square (53 × 53) NVM crossbar. Figure 3c depicts the MVM scheme of our hardware’s one-transistor one-resistor (1T1R) array, involving voltage input, current output, and selection of voltage input to bit lines (BLs), sources lines (SLs), and word lines (WLs), respectively. The weight matrices are mapped onto the RRAM conductance, and the 1T1R cell configuration enables both full-array one-shot programming and MVM. Each RRAM crossbar consists of 256 corelets, each containing 16 × 16 1T1R cells (synapses) and one readout circuit serving as a neuron (Fig. 3d). Analogous to the incremental step pulse programming in commercial NAND flash memories42, we employ multiple programming pulses with reduced set and reset voltages (Vset and Vreset) to mitigate the risk of dielectric breakdown but also preserves the intrinsic endurance of the RRAM channel. Controlled by an FPGA board, the gradual write-and-read process for programming the RRAM allows for reliable conductance mapping in the range of 1–30 μS (Fig. 3e, f). The mapping of trained weight matrices and provided in Supplementary Fig. S2. More detailed hardware implementation of RMAB is included in Method section.

Experimental results of four-content scenario

We first experimentally demonstrated in-situ training, inference-like, and evaluation phases by benchmarking a recommendation system for four contents. During the training phase, the estimated λ increases as e increases (Arm A, Fig. 4a). The cost evolution of other arms exhibits a similar trend to that of Arm A (Supplementary Fig. S3). During the training phase, the state-dependent reward distributions (Fig. 4b, based on Eq. (4)) allow the Whittle indices to increase with the increase of λ. When a user is interested in specific content, they are more likely to receive a higher reward when navigating specific categories of the content rather than the main general pages (thereby also enhancing the reward of the agent). Consequently, all reward distributions are expected to exhibit an increasing trend with the increase of S1 irrespective of λ.

Fig. 4: Experimental results of RMAB in four-content scenario.
figure 4

a Evolution of λ with respect to randomly generated S0 (uniformly distribution) and S1 (weighted distribution). b S1-dependent reward distributions of four contents. c Evolution of Whittle indices of four contents. During the in-situ training phase, the Whittle index also increases with the increase in λ, leading to the positive slopes with respect to S1 (in the inference-like phase) to enhance the total discounted reward (TDR). d Selection matrices and e cumulative selections of (4, 1) scenario. The brown and green squares indicate the selected and not-selected arms, respectively. f Selection matrices and g cumulative selections of (4, 2) scenario. The in-situ training phase enables balanced selections among four contents for both (4, 1) and (4, 2) scenarios, enhancing the TDR. h Evolutions of TDR for experiment, model, and software for (4, 1) and (4, 2) scenarios. The model without noise fails to enhance the TDR, indicating that the intrinsic hardware noise is necessary for the successful training of the neural Whittle index network. The experimental result also exhibits a comparable TDR evolution with the software result.

Full size image

Our recommendation system learns these trends during the in-situ training phase. Figure 4c displays the experimental results of inference-like phase after each e during in-situ training phase. The Whittle indices exhibit negative or near-zero slopes with respect to S1 at small e (blue lines), while continuous weight updates result in a positive slope at large e (red lines). This observation indicates that the training phase ensures a monotonically increasing trend, where the Whittle index and reward distribution are positively correlated, a relationship that can further enhance the TDR in the subsequent evaluation phase. Given the balanced reward distributions of the four arms (Fig. 4b), it is essential to evenly select each arm to maximize the TDR. Figure 4d illustrates the results of arm selection in a (4, 1) scenario. At e = 5 (i.e., after going through the first mini-batch update with five episodes) for all t (0–20), only Arm A is selected (brown squares); however, the server fairly selects all contents when e = 250. As shown in Fig. 4e, the sum of all selections for all t at large values of e converges to fair distributions. The (4, 2) scenario exhibits similar trends, suggesting that various scenarios with fair distributions can be handled by the proposed system (Fig. 4f, g). Supplementary Figs. S4 and S5 provide all selection matrices for each mini batch in the (4, 1) and (4, 2) scenarios.

Substantial weight updates occur when f(S1) surpasses f(S0), a constraint that can be stochastically satisfied by the intrinsic noise in the RRAM crossbars. Figure 4h illustrates the evolutions of TDR for (4, 1) and (4, 2) scenarios. The experimental results (solid data points) closely match the simulated model (lines) and demonstrate performance comparable to that of backpropagation-based software results. The hardware noise and 5-bit input precision in the model moderately perturbate f(S1) and enhance the TDR convergence, while simulated higher noise and lower-bit input precision drive excessive perturbation and degrade the convergence (Supplementary Fig. S6). Through the even selection of arms, both sets of results converge to TDR values of 123 and 204 for the (4, 1) and (4, 2) scenarios, respectively. Software training using backpropagation uses an additional logistic function as well as random number generation to determine the arms to be activated, as proposed by Nakhleh et al.36. However, a model without noise, requiring no such mathematical operations, exhibits no increase in TDR. Thus, to increase TDR, intrinsic noise is needed, which is available for free (without incurring additional power) in our RRAM hardware (in the form of time-varying circuit noise, programming errors, etc.). Therefore, the algorithm not only tolerates noisy hardware but also exploits it.

System scalability

The four-content scenario experiment validated the feasibility of our hardware-software co-designed system for in-situ training, inference-like, and evaluation phases. To showcase the system’s scalability and flexibility, we expanded the DRLF parameters with a 10-content scenario in another experimental demonstration. In this scenario, we alternatively employed ex-situ training phase owing to the limited capability of our post-CMOS hardware for simultaneous large-scale MVMs, which can be resolved by employing larger scale post-CMOS to date43,44,45. Figure 5a illustrates the evolution of Whittle indices, showing significantly increased slopes with respect to S1 at e = 1000 compared to e = 100. This increase in e led to a 43% higher maximum Whittle index, reaching 80 × 10−7, compared to the evolution in the four-content scenario. The Whittle indices of a software (backpropagation) case are also provided as a comparison (Supplementary Fig. S7). The corresponding parameters and all reward distributions for the 10 contents are detailed in Supplementary Figs. S1 and S8, respectively.

Fig. 5: Results of scaled RMAB.
figure 5

a Experimental results of Whittle index estimation for 10-content scenario. Similar to the four-content scenario, positive slopes of Whittle indices can be achieved after the training phase. b Bubble plot of selections in (10, 2) scenario at e = 1000. The color and size of the bubble indicate the individual content and the Whittle index, respectively. c Selection evolution of 10 contents. The high e of 1000 enables balanced selections that enhance the TDR. d Improvement of TDR with scaling N and M. The (10, 1), (10, 2), and (10, 4) scenarios are the experimental results, while the (100, 25) scenario is the simulation. e Evolution of TDR with large-scale N. Our system is expected to outperform the backpropagation-based software when N < 100. f Benchmarking performance of various artificial intelligence (AI) accelerators. Although additional cycle parameters in the NVM crossbar, the NVM crossbar outperforms other AI accelerators for energy consumption.

Full size image

Figure 5b displays the selection transitions for all 10 contents at e = 1000 in a (10, 2) scenario. The size of the circles indicates the Whittle indices, which continue to increase when the corresponding content is not selected. However, after the training phase, the server evenly selects 2 contents at every t, maintaining the Whittle indices at comparable values for all 10 contents for all t. The selection matrices for (10, 1) and (10, 2) scenarios are provided in Supplementary Figs. S9, S10. Figure 5c displays the number of selections for each content, with Arm J beginning to be selected at e = 1000. The balanced selection increases TDR, as shown in Fig. 5d. All scenarios exhibit an increase in TDR after the training phase, with the increase improving when scaling both N and M simultaneously, as in the (100, 25) scenario. All scenarios up to (10, 4) were experimentally measured, while the (100, 25) scenario was simulated using our experimentally calibrated model. Further scaling of the number of contents is also provided in Fig. 5e. Up to a 100-content scenario, our system is expected to outperform backpropagation-based software accuracy, suggesting the algorithmic competitiveness of our system as post-CMOS hardware.

Benchmarking and discussion

We also conducted a benchmarking analysis to compare the energy consumption and latency of our system with other systems based on flash memory, CPU, and GPU (Fig. 5f). For the flash memory system, we assumed a similar architecture as NVM crossbars (to perform MVMs), along with a model and algorithms identical to the ones used here. For the CPU and GPU systems, we employed backpropagation-based training. The energy consumption analysis includes both training and inference-like phases, while latency is defined as the time taken for the TDR to reach 120 in a (4, 1) scenario. Despite our energy-based system incorporating an additional 10 cycles for each free and nudged phase, it outperforms the CPU-based system by over three orders of magnitude and the GPU-based system by nearly two orders of magnitude in energy consumption. Our system achieves the second-lowest latency among the compared platforms, following the GPU-based system. However, our system’s latency is over two orders of magnitude lower than that of the CPU-based system. While flash memory represents another AI accelerator paradigm that excels in fast and efficient inference, its high programming voltage poses a disadvantage in the training phase, resulting in a higher latency compared to both our system and the GPU-based system. Detailed calculations are provided in Supplementary Note 1 and Supplementary Figs. S11, S12.

Future work could explore the in-situ training of a group of contents simultaneously sharing their λ and Whittle indices. Another future direction involves the full hardware implementation of recommendation systems in DRLF using complementary metal-oxide-semiconductor (CMOS)-based spiking circuits. The evaluation phase can be executed via CMOS spiking circuits capable of leaky-integrate-and-fire operations and winner-takes-all selections46,47,48, interpreting the accumulation of Whittle indices and selecting the contents with the highest accumulated Whittle index, respectively. Volatile two-terminal memories, serving as artificial neurons, can further enhance functionality by introducing temporal dynamics. Potential candidates for such neurons include Mott switches and diffusive neurons22,49,50,51. The temporal discount factor and the time-dependent response can be interpreted in a diffusive-memory-based reservoir computing framework25,51,52,53,54, which incorporates randomly distributed reservoir nodes for higher-dimensional embedding of S0 and S1 into λ and Whittle index vectors for each t, respectively. The potential hardware implementation of the entire training phase across thousands of contents, along with inference-like and evaluation phase potentially deployed in local or edge devices.

Discussion

Conventional recommendation systems—namely Meta’s Deep learning recommendation model (DLRM)55 and Google’s Wide & Deep56—focus on learning static mappings from existing commercial recommendation datasets such as Criteo57 or Avazu57,58. These datasets typically assume static user-item interactions and features, whereas our system specifically targets non-stationary reward processes that can learn dynamic policies over evolving system states. As edge intelligence, our system exhibits approximately ~163× inference energy advantage over the conventional recommendation systems that use digital platforms such as GPU and TPU. Detailed comparisons are provided in Supplementary Note 2 and Supplementary Fig. S13.

The multi-armed bandit (MAB) approach for recommendation systems is still in its early stages, with many improvements expected in the future. For example, in terms of the size of problems, Nakhleh et al.36 and Chapelle et al.59 tackled 100-arm problems, Zhao et al.60 had 48-arm problems. However, the action space grows exponentially with the number of arms. Therefore, a one-to-one matching between the number of arms in MAB studies (e.g., 10–100 arms) and the number of total items in real-world applications (>10,000 items) is not feasible in the near future. Rather, hand-engineered (or human-labored manually performed) classification depending on the sub-category, or neural network-based preprocessing together with the MAB problem solving is plausible55.

Solving more generalized RMAB problems is not merely limited to recommendation systems but also applies to a wide range of real-world problems with the exploration-exploitation dilemma. Examples include deadline scheduling for electric vehicle charging stations61, wireless communications62, and maternal and child health care60,63. Our energy-efficient neural network training for inferring the Whittle index can also help these problems of the wide spectrum with the exploration-exploitation dilemma in continuously changing (restless) environments.

We have demonstrated a recommendation system that consists of a model, hardware and operating (training and inference) algorithms that are co-designed with one another. The algorithm-hardware combination not only tolerates the noise from RRAM hardware (that most past efforts have tried to minimize via expensive engineering approaches) but also exploits it to perform better. Our system performs better than any prevailing or upcoming hardware solutions (based on flash memory, CPUs or GPUs) in terms of energy efficiency, and is also comparable with backpropagation-based software training in terms of algorithmic accuracy at edge scales (~100 contents). Our solution offers clear advantages at edge-friendly scales, a domain that has not been sufficiently addressed. While the scalability of different components of our system (algorithm, model, and/or hardware) to server-relevant scales remains to be evaluated, we opine that server-relevant sizes will likely be dominated by GPU-like digital hardware for the foreseeable future, while edge solutions like ours will start occupying the edge market within the next few years.

Methods

Operation of NVM crossbars

We utilized large-scale TiN/TaOx/HfOx/TiN RRAM crossbars with n-type CMOS selectors fabricated through a standard 130-nm foundry process14. The system comprised 48 cores, with each NVM crossbar featuring a 256 × 256 1T1R array (256 corelets). Control of the cores was achieved using an XEM6310-LX150 FPGA (Opal Kelly) with a custom-designed PCB. For the set and reset operations, Vset and Vreset ranged from 1.2 V to 3.3 V and −2.5 V to −3.3 V, respectively, with a pulse width of 1 μs. RRAM conductances spanned from 1 μS to 30 μS, with a tolerance of 1 μS. A 5-bit precision was employed for all MVM with an unsigned input configuration. The reference voltage (VREF) was set at 0.9 V, and the calibrated positive and negative bit line voltages (VBL) with respect to VREF were 0.69 V and −0.595 V, respectively.

Hardware implementation of RMAB

We benchmarked the evaluation phase and generation of reward distributions and S0 and S1 in the software implementation of RMAB (NeurWIN)36. To ensure the voltage scale with our hardware implementation, we scaled down the ranges of S0 and S1 to [0.05, 1]. The weight matrices (W and W*) were initialized by a normal distribution with mean (μ = 0) and standard deviation (σ = 0.1), followed by the weight conversion process from the 1T1R compact model23. The learning rate (α) and β were 0.002 and 0.01, respectively. The three-layer network incorporates 1-16-32-1 MLP with 3 bias columns for each differential weight matrix, thus a total 106 × 53 RRAM array was used for each content. Between the layers in the network, the rectifying linear unit function was used as an activation function. Both forward and backward propagation during the training and inference phases operated with 10 cycles, which outputs of each layer in MLP were than multiplied by a factor of 450.

The total numbers of timesteps used in four-content and 10-content scenarios are 20 and 100, respectively. The simulated noise for the model was a normal distribution with μ = 0 and σ = 0.35. For the comparison between our system and the backpropagation-based software in Fig. 3h, the same DRLF parameters were used for both systems such as α, t, e, and b. To demonstrate the scalability of our system, the Whittle indices and reward distributions for more than 10 contents were duplicated from the experimental results of the 10 contents.