Directional sound propagation in acoustic artificial structures

Abstract

Wave manipulation involves harnessing and tailoring wave properties to meet specific requirements, driving advancements across a wide range of scientific, industrial, and technological fields. A critical aspect of wave manipulation is directivity control, which has broad applications in areas such as underwater communication, non-invasive medical diagnosis, and targeted audio delivery. This review introduces various methods for achieving directional sound propagation, including both conventional techniques and emerging approaches based on acoustic artificial structures. It highlights how these methods, particularly those utilizing engineered artificial materials, control acoustic wave behavior to enable directional sound emission and transmission, with illustrative examples demonstrating their principles and practical applications. Finally, the review addresses the challenges of achieving broadband, low-frequency, and adaptive control of acoustic waves, while outlining potential future research directions in directional sound manipulation.

Introduction

Light can scatter in all directions, as with the light emission from a light bulb, or it can propagate in a highly directed manner as seen in laser beams. Can sound present similar behavior? The answer is unequivocal. Sound, carried by acoustic waves, traditionally perceived as propagating in a dispersive, omnidirectional, and three-dimensional manner, can also be confined within a localized area, demonstrating high directivity. As illustrated in Fig. 1(a), since the sound is focused in a specific direction, unintended listeners are not affected by the transmitted sound. The directional sound can transmit waves in a narrow acoustic beam, enhancing detection resolution, signal-noise-ratio, and focusing energy in a specific direction. It has garnered significant interest due to its potential applications in areas such as underwater communication, non-invasive medical imaging, remote sensing, and targeted audio delivery systems^1,2,3,4,5.

Fig. 1: Acoustic wave propagation.

a Schematic representation of omnidirectional versus directional sound propagation. b Frequency spectra of acoustic waves. c Comparison of ideal acoustic monopolar point source and plane wave source.

Acoustics encompasses the study of mechanical waves in gases, liquids, and solids, including vibrations, audible sound, ultrasound, and infrasound. The frequency range of acoustic wave applications spans from infrasound at a few Hz to THz frequencies associated with heat (Fig. 1(b)). Audible sound, ranging from 20 Hz to 20 kHz, is prevalent in everyday applications such as human hearing, speech communication, general-purpose loudspeakers, microphones, and architectural acoustics. Ultrasound, which encompasses frequencies beyond the audible range and can reach several gigahertz, is employed in various applications requiring high precision, such as medical imaging, non-destructive testing, sonar systems, and animal communication. This review focuses on various approaches based on artificial structures for achieving directional propagation of acoustic waves across both audible and ultrasonic frequency ranges.

Considering the inherent nature of acoustic waves, wave manipulation is essential for achieving controlled directional sound propagation. By leveraging techniques such as wavefront shaping, phase alteration, or the introduction of local resonance, the characteristics of acoustic wave propagation can be tailored on demand^6,7,8. This customization enables precise control over acoustic wave directionality, leading to advanced functionalities such as high-resolution imaging, directed sound delivery, and enhanced signal transmission.

Directional sound propagation can be achieved through either an emitter or a transmitter. In free space, the directivity of common emitters, i.e., conventional sound sources, is primarily governed by the emitting area, the structure of the emitting surface, and the frequency of the acoustic waves. Considering the ratio between the size of the sound source and the wavelength of the emitted acoustic wave, higher frequencies tend to be more directional, and lower frequencies tend to be more omnidirectional. For a given frequency, the directivity pattern of any wave source is dictated by the aperture function according to the Huygens-Fresnel principle. Specifically, an ideal monopolar point source radiates sound equally in all directions, whereas an ideal plane source emits sound in a single direction without spreading, as Fig. 1(c) illustrates. In practice, sound sources typically exhibit behavior that lies between these two extremes. The progress in directional sound emitter has seen advancements in techniques such as parametric loudspeakers and phased array systems, which enable the projection of acoustic waves in a specific direction, effectively minimizing sound spillover to surrounding areas^9,10,11.

On the other hand, directional sound transmitters are designed to transmit acoustic signals along a specific path with minimal interference from environmental noise, thereby enhancing the performance of targeted sound delivery and improving the transmission effectivity. Acoustic artificial structures, which are engineered materials or systems with precisely designed geometric configurations at subwavelength scales, offer flexible control over acoustic waves. Recent advancements in these structures, including phononic crystals, acoustic metamaterials, acoustic metasurfaces, and acoustic topological insulators, etc., have demonstrated their exceptional ability to manipulate and fine-tune the properties of acoustic waves, such as reflection, transmission, absorption, dispersion, and directivity^{12,13,14,15,16}. By shaping wave behavior both within and around the structure, acoustic artificial structures serve as highly effective tools for achieving directional acoustic propagation^17,18,19,20.

In this review, we present various approaches to achieving directional sound propagation, with a particular focus on methods that utilize acoustic artificial structures. Following the introduction, we first discuss conventional approaches for creating directional sound emitters in free space and outline the commonly used criteria for evaluating directivity. Next, we examine approaches for engineering the directivity of acoustic waves with artificial structures. The review concludes with a summary and an outlook on potential future developments in the field of directional sound. For each approach discussed, we provide illustrative examples to elucidate the underlying principles and enhance understanding. Rather than serving as an exhaustive overview of all research in this field, this review aims to offer valuable insights into the principles and techniques of directional sound control.

Directional sound propagation with excitation source modulation

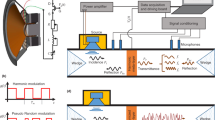
Acoustic sources that are smaller than the operating wavelength typically generate non-directional radiation patterns, dispersing sound energy across a broad angular range. Conventional methods to enhance the directivity of acoustic wave propagation in free space have predominantly focused on modifying the acoustic source itself to create a more directional emitter. Currently, three widely adopted approaches are employed to achieve directional sound propagation in free space: sound domes, acoustic phased arrays, and acoustic parametric arrays. The main features of these approaches will be introduced in the following.

Topology optimization of horn drivers and acoustic parabolic reflectors is an effective design method for enhancing sound projection and directivity, and has been widely applied to improve speaker performance^21,22. A sound dome utilizes either a parabolic speaker or advanced beamforming techniques to concentrate audible energy within a confined space. This design ensures that only individuals directly beneath or within the dome’s projection hear the sound, significantly reducing sound leakage to adjacent areas. As illustrated in Fig. 2(a), the sound dome operates with a small emitter positioned at the focal point of a large parabolic structure made from sound-reflective material. Acoustic waves passing through the focal point are reflected by the parabolic surface, aligning parallel to its axis and reaching the structure’s mouth in phase. This configuration effectively transforms the dome into a flat emitter, with an effective diameter corresponding to that of the structure. The underlying principles of sound dome technology have practical applications in sound insulation for environments such as museums, libraries, and exhibition spaces, and can also be employed in the design of loudspeakers for directional sound emission. Commercially available sound domes are capable of achieving up to 14 dB of sound isolation within the designated listening area, which corresponds to the dome’s diameter, and they support a frequency response range of 150 Hz to 20 kHz²³. However, the relatively large wavelengths associated with audio frequencies often result in sound domes reaching physical sizes in the meter scale, which can limit their practicality in certain scenarios. In addition to acoustic horns, advanced loudspeakers featuring dome-shaped diaphragms or microdome arrays can be specifically designed for uniform sound radiation within the 2 kHz to 20 kHz frequency range^24,25,26. Compared to traditional cone speakers, dome speakers offer several advantages, including wider sound dispersion, lower distortion, and improved high-frequency response. However, these designs are generally more complex to manufacture and less effective in controlling low-frequency sound.

Fig. 2: Conceptual illustration of directional sound emitters.

The principles of (a) sound dome, (b) acoustic phased array, and (c) acoustic parametric array.

Following the introduction of the sound dome, which relies on geometric acoustics, acoustic phased arrays represent a widely used method for achieving directional sound emission through local phase modulation. Phased array technology, initially developed for radar systems, has been adapted for acoustics, allowing precise control of sound propagation through transducer arrays. Acoustic phased arrays steer and focus sound beams by selectively adjusting the phase angles of multiple sound emitters, as illustrated in Fig. 2(b). By introducing phase differences among the array elements, constructive interference enhances the intensity of the main lobe in the desired direction, while destructive interference suppresses acoustic waves in other directions. This technique allows for precise beam steering and efficient sidelobe mitigation across from tens of Hz to several MHz. Acoustic phased arrays are advantageous in applications requiring precise beamforming and real-time steering of acoustic waves, such as acoustic imaging, sonar systems, and particle manipulation. In these contexts, the ability to dynamically adjust the directionality and focus of the sound beam across a broad frequency range is essential^{27,28,29,30,31}. However, this approach requires multiple sound sources, each paired with individual electronic circuits to control phase and amplitude, leading to increased manufacturing and operational costs as well as system complexity. Furthermore, the performance of acoustic phased arrays is constrained by their physical size and transducer spacing. Specifically, effective control at lower frequencies necessitates larger array structures, while maintaining the required λ/2 spacing at higher frequencies—particularly in the ultrasonic range—presents significant challenges. Additionally, phased arrays may suffer from grating lobes at certain frequencies, especially at higher frequencies, further limiting their effectiveness.

Acoustic parametric arrays address the limitations associated with size by utilizing nonlinear acoustic effects to achieve highly directional sound propagation, particularly at lower frequencies. A directional sound system based on acoustic parametric arrays allows audible sound signals to be carried on an ultrasonic wave^32,33,34,35. As illustrated in Fig. 2(c), when a high-powered ultrasound source is amplitude-modulated with an audio signal, the nonlinear effect of air during transmission causes the modulated signal to undergo self-demodulation. The resulting acoustic wave inherits the radiation pattern of the ultrasonic carrier, thereby offering significantly enhanced directionality compared to a conventional speaker of similar size operating at audible frequencies. The underlying principle involves superimposing two waveforms, generating two new waveforms where one with a frequency equal to the sum of the originals and another with a frequency equal to their difference. When the original waveforms are ultrasonic and the frequency difference lies within the audible range, the difference frequency is perceived as sound and the other three frequencies get attenuated. By leveraging the inherently high directivity of ultrasonic waves, this technique enables highly directional propagation of audio sound with minimal side lobes, while maintaining a compact system size by transmitting at higher frequencies. Acoustic parametric arrays are particularly effective in scenarios requiring highly directional sound emission at low frequencies, without the need for large transducer arrays. Common applications include public address systems, museum displays, and long-distance communication, where focused sound beams with minimal interference are essential. Although acoustic parametric arrays enable directional transmission of low-frequency sound, this comes at the cost of energy efficiency due to the significant power loss inherent in the process, necessitating the use of high-intensity ultrasonic waves. For typical configurations, the conversion efficiency from ultrasound to audible sound is generally below 0.15%³⁶. Despite these challenges, advances in parametric array technology have led to more precise sound transmission in complex environments, substantially improving the performance and accuracy of acoustic technologies.

While various approaches can achieve directional sound propagation, evaluating and comparing their directivity performance is essential to determining their effectiveness. Directivity control is a fundamental consideration for acoustic wave emitters and transmitters. The directivity of an acoustic source describes how sound intensity or sound pressure level varies with angle around the source at a given frequency, measured in a free-field environment at a fixed distance. The directivity characteristics of loudspeakers, periodic transducer arrays, and even randomly distributed transducers can be determined through theoretical derivation³⁷, as well as through numerical simulations or experimental mapping. For more complex acoustic sources, computational tools such as the boundary element method and finite element method, in conjunction with experimental measurements, are frequently utilized to model the acoustic field and obtain accurate directivity patterns.

Leveraging the principles of ray tracing, both parabolic reflectors and sound domes manipulate sound waves through curved surfaces, with their curvature determining how sound is redirected. Sound domes disperse sound over a wider area, creating collimation, and finding applications in targeted audio systems, immersive sound environments, and acoustic beamforming. In contrast, parabolic reflectors typically converge sound at the focus, amplifying sound and enhancing directionality. The relationship between amplification performance and factors such as geometry, acoustic wavelength, and frequency have been studied and documented in prior research^39,40,41. Essentially, a sound dome can be considered a reversed application of a parabolic reflector. The functions of parabolic reflectors and sound domes can be integrated by utilizing both forward and reverse reflections to enhance directional intensity.

Figure 3(a-c) presents an acoustic double-parabolic-reflector waveguide designed for increased ultrasound emission intensity²¹. Figure 3(a,b) illustrates schematic diagrams of a conventional waveguide with a piezoelectric element and a double-parabolic-reflector acoustic waveguide with a piezoelectric element ring, respectively. In the parabolic reflecting design, two parabolic reflectors share a common focal point. The first parabolic reflector increases the contact area between the piezoelectric element and the waveguide while focusing the ultrasound. The concentrated ultrasound is then reflected by the second parabolic reflector, converting it into a planar wavefront with higher energy density. Notably, the second reflector functions as a sound dome, collimating the wave propagation. Figure 3(c) compares the acoustic pressure in the waveguides with diameter φ = 1 mm at 1.4046 MHz, demonstrating the waveguide’s effectiveness in generating high-intensity ultrasound. In addition to the contribution of the large-size piezoelectric element ring, the enhancement results from plane-wavefront ultrasound optimized through double parabolic reflections. The vibration amplitude of the incident plane-wavefront ultrasound is enhanced approximately 20 times as it propagates through the thin waveguide within the 1–2 MHz range.

Fig. 3: Directional sound propagation with excitation source modulation.

a-c Double parabolic reflectors acoustic waveguides for high-power medical ultrasound: a Schematic diagram of a conventional waveguide with a piezoelectric element. b Schematic diagram of the proposed parabolic-focusing waveguide with piezoelectric element ring. c Transmitted ultrasound comparison for two waveguides. Adapted from ref. ²¹., Copyright © 2019, Kang Chen et al. d-f Frequency-selective directional beam in acoustic phased arrays: d Space-time-periodic phased array with a dynamically changing phase gradient. e Acoustic fields for a 1010 Hz plane wave incident from five specific angles. f Directivity patterns for different listening channels. Adapted from ref. ³⁸., Copyright © 2020, Revant Adlakha et al. g-i Directional acoustic waves generated by a horned parametric acoustic loudspeaker (PAL). g Schematic diagram of a horned PAL with a typical piezoelectric transducer array. h Directivity spectrum of the horned PAL with flare constants $\delta =7$. i Sound beam directivity of the horned PAL at 5000 Hz. Adapted with permission from ref. ³⁴., Copyright © 2019, ASME International.

The directional characteristics of acoustic emitters are most intuitively represented by directivity patterns, typically displayed in the form of polar plots or Cartesian coordinates. Figure 3(d-f) illustrates a controllable acoustic phased array with space-time-periodic phase variation, capable of generating distinct radiation patterns with high directivity, where both the emission direction and operating frequency can be flexibly modulated³⁸. Figure 3(d) shows an acoustic phased array with a dynamically varying phase gradient. Figure 3(e) presents the simulated acoustic fields and corresponding dominant frequencies obtained from time-domain finite element simulations, depicting an acoustic wave at 1010 Hz transmitted from five distinct incident angles. Figure 3(f) illustrates the directivity patterns for various listening channels, demonstrating the sensitivity of the phased array to incident waves as a function of the incident angle. Figure 3(g-i) demonstrates the directional acoustic radiation generated by a horned parametric acoustic loudspeaker (PAL)³⁴. The schematic diagram of the horn PAL is depicted in Fig. 3(g). The sound beam directivity, with a modulation parameter $\delta =7$ (where $\delta$ represents the flare constant related to the cross-sectional area of the exponential horn) and a frequency of 5000 Hz, is shown in Fig. 3(h,i), respectively, theoretically showcasing the high directivity of the flared horn-assisted directional emitter.

Various formats, as illustrated in Fig. 3(e,f) and Fig. 3(h,i), can be utilized to extract directionality information from the sound pressure level distribution. Indeed, the directivity index and beamwidth can serve as two critical parameters for further evaluating the directivity of acoustic emitters and transmitters. The directivity index quantifies the concentration of sound energy in a specific direction compared to an ideal omnidirectional source. It is calculated as the ratio of the acoustic intensity in the primary direction to the average intensity over an imaginary sphere surrounding the source and is expressed in decibels (dB)⁴². Beamwidth refers to the angular width (in degrees) of the main lobe of the directivity pattern, typically measured at the points where the sound pressure level decreases by 3 dB from the peak value^43,44. It should be noted that in the near-field region, sound pressure and intensity can vary in a complex manner, with acoustic waves exhibiting a non-uniform distribution that may not yet form a clear directivity pattern, depending on specific cases. The threshold between the acoustic near field and far field is generally defined by the Rayleigh distance ${r}_{0}$, which depends on the size of the sound source and the wavelength of the emitted sound. The Rayleigh distance is given by the formula ${r}_{0}={D}^{2}/\lambda$, where $D$ is the largest dimension of the sound source and $\lambda$ is the wavelength. However, with the increasing diversity of sound emitters, particularly those based on artificial structures, the criteria for distinguishing between near-field and far-field may need to be adjusted for specific situations.

While sound domes, acoustic phased arrays, and acoustic parametric arrays effectively achieve directional sound propagation, they often rely on wavelength-scale structures or require high-power inputs. The advent of acoustic artificial structures, however, provides enhanced flexibility in manipulating acoustic waves, allowing for on-demand control of sound directionality with more compact designs. This capability makes them particularly advantageous for applications demanding lightweight or miniaturized devices. Furthermore, most of artificial structures exhibit scalability, allowing them to function across a broad range of frequencies, from low audio frequencies to extreme high frequencies, even extending into the thermal range.

Directional sound propagation with artificial structure modulation

Acoustic artificial structures offer capabilities for sound manipulation that are challenging to achieve with conventional materials. These structures can take various forms, including periodic, quasiperiodic, or even disordered distributions. While they adhere to fundamental acoustic principles, their engineered designs enable precise control of sound through mechanisms such as periodicity, localized resonances, sub-wavelength manipulation, and tailored anisotropy. These mechanisms, which are either absent or difficult to realize in conventional materials, make acoustic artificial structures powerful tools for advanced sound manipulation. In recent years, significant advancements in acoustic artificial structures—including phononic crystals, metamaterials, metasurfaces, and metalenses—have led to the observation of intriguing phenomena such as negative refraction, super-resolution imaging, acoustic cloaking, and topological transport, both theoretically and experimentally^{8,45,46,47,48}. These peculiar phenomena hold significant potential for the specialized manipulation of acoustic energy, with the aim of addressing specific practical applications in advanced audio devices, soundproofing, and energy harvesting. The following sections introduce the most widely recognized types of acoustic artificial structures. It is important to note that there is no strict classification for these structures, and the categorization presented in this review represents one particular perspective, serving as an organizational framework to enhance readability and comprehension.

Phononic crystal

Phononic crystals (PnCs), composed of a periodic array of artificial scatterers, create a structured potential landscape for acoustic waves. The distinctive wave behavior in these structures primarily arises from interaction among unit cells, typically sized at approximately half the operating wavelength. The overall acoustic response is significantly influenced by long-range interactions and spatial dispersion effects. Due to their periodic arrangement, PnCs manipulate the band structures of acoustic or elastic waves through mechanisms such as Bragg scattering, local resonance, and inertial amplification^16,49,50. These mechanisms give rise to a wide range of unique and anomalous wave propagation behaviors across spectral, wavevector, and phase spaces, leading to phenomena such as wave localization⁵¹, waveguiding⁵², self-collimation⁵³, negative or zero refraction^54,55, total reflection⁵⁶, and phase reconstruction⁵⁷.

The periodicity of phononic crystals enables the description of wave solutions through Bloch functions, resulting in the formation of quantized energy levels that manifest as bands. The band diagram illustrates the allowed and forbidden frequencies, which create band gaps as a function of wavevector in various directions within the crystal’s Brillouin zone. Introducing defects or impurities into a phononic crystal—by locally modifying the geometric or material properties of one or more unit cells—gives rise to localized modes within the bandgap. This leads to wave localization at the defect sites, while acoustic waves propagating away from these defects experience rapid decay, thereby facilitating selective wave propagation at specific frequencies.

Phononic crystals leverage coupling effects between a series of defect cavities, which exhibit strong wave localization and low group velocity. These characteristics render PnCs particularly advantageous for designing tailored wave paths and functional acoustic devices such as waveguides, microcavities, and frequency dividers, all of which facilitate directional sound propagation⁵⁸. Figure 4(a) illustrates a PnC cavity resonance device featuring a line array defect introduced into a perfect PnC. The band structures of the line-defect doped PnC, shown in Fig. 4(b), reveal a defect band within the bandgap, presenting a propagating acoustic solution at the cavity resonance frequency. The surrounding perfect PnC, characterized by an effective refractive index ${n}_{{eff}}$, serves as a reflector, thereby enhancing the performance of directional acoustic sensing. Figure 4(c) presents the acoustic directivity of the doped line-defect PnC at the cavity resonance frequency for various incident angles. The beamwidth of the main lobe, defined by the angular width at the half-power points, is approximately 20°. Figure 4(d) depicts the acoustic directivity as a function of the incident angle ${\theta }_{i}$, reflection coefficients r of the periodic arrays, and effective refractive index ${n}_{{eff}}$. The analysis highlights that the reflection coefficient of the PnC structure primarily governs the system’s response, playing a pivotal role in determining the quality factor Q of the central acoustic cavity. However, defect-based phononic waveguide suffers the limitation of narrow bandwidth with a given structure, high sensitivity to fabrication defects, and low power transmission.

Fig. 4: Directional sound propagation with phononic crystals.

a-d Enhanced directional acoustic sensing with PnC cavity resonance: a Schematic illustration of the PnC cavity resonance device. b Band structures of the doped line-defect PnC. c Acoustic directivity of the doped line-defect PnC at the cavity resonance frequency. d Acoustic directivity as a function of the incident angle ${\theta }_{i}$, the reflection coefficients of periodic arrays r, and effective refractive index ${n}_{{eff}}$. Adapted with permission from ref ⁵⁸., Copyright © 2018, AIP Publishing. e-h Self-collimating acoustic beams in a 2D sonic crystal: e Band structure of the sonic crystal. f Equifrequency contours in the first Brillouin zone of the sonic crystal. g Simulation of the collimated acoustic beam propagation in the sonic crystal. h Acoustic beam splitting with diagonal line defects in the sonic crystal. Adapted with permission from ref ⁵⁹., Copyright © 2015, AIP Publishing.

To achieve directional wave propagation in phononic crystals, in addition to utilizing cavity structures for resonant states, one can also exploit the high density of states at the band edge. This phenomenon is typically characterized by a flatter band near the edge frequency, which enhances the localization and directionality of acoustic waves^60,61.

Compared to phononic waveguides, self-collimated beams with minimal diffraction present distinct advantages for directional propagation by eliminating the need for precisely engineered structural defects. Self-collimation allows for waveguiding in phononic crystals without predefined waveguide structures, as illustrated in Fig. 4(e-h)⁵⁹. In a square lattice of 2D sonic crystals composed of epoxy resin rods immersed in water, the band structure and equifrequency contours in the first Brillouin zone are shown in Fig. 4(e,f). At a normalized frequency $f=0.578{C}_{w}/a$ (where ${C}_{w}$ represents the sound speed in water and a is the lattice constant) located at the first band, the equifrequency contours along the ${\rm{\Gamma }}{\rm{M}}$ direction are flat, as indicated by the red arrow in Fig. 4(f). Consequently, acoustic waves at this frequency are expected to self-collimate along the ${\rm{\Gamma }}{\rm{M}}$ direction without diffraction. The simulation result in Fig. 4(g) demonstrates that after propagating through several periods, the incident monochromatic beam continues along the ${\rm{\Gamma }}{\rm{M}}$ direction with minimal diffraction, thereby illustrating the self-collimation effect with high directionality. To extend the applications of collimated waves, a defect-based approach can be integrated with the self-collimation effect to achieve acoustic beam splitting. As shown in Fig. 4(h), in a sonic crystal with a diagonal line defect, the incident beam is split into transmission and reflection beams with nearly equal power and a phase difference of π/2. In fact, beam self-splitting can also be achieved through defect-free methods by exploiting the shape of equifrequency contours^62,63. However, the directional emission remains strongly dependent on the specific frequency at which the equifrequency contour is flat, thereby constraining the operational bandwidth and limiting the ability to achieve broader directional control.

A gradient phononic crystal is a specialized type of phononic crystal comprising multiple layers with gradually varying constitutive parameters, including filling factors, inclusion geometry, and material properties. This gradual variation enables precise acoustic wave engineering, supporting functionalities such as focusing with a hyperbolic secant profile function⁶⁶, collimation through equifrequency contours⁶⁷, and waveguiding via the rainbow effect⁶⁸. The flexible design of gradient PnC offers a wide range of possibilities for achieving diverse functionalities. Furthermore, gradient PnCs can effectively manage waves across a broad spectrum, making them suitable for applications that require handling both low- and high-frequency acoustic waves. Figure 5 illustrates the wavefront shaping capabilities of gradient PnCs. Figure 5(a,b) showcases a partitioned gradient-index phononic crystal (pGRIN-PnC) designed as a collimator to convert a cylindrical wave source into a plane wave⁶⁴. Figure 5(a) presents the manufactured pGRIN-PnC system along with the gradient distribution of radii across its layers. The simulation and experimental results depicted in Fig. 5(b) demonstrate in-phase outgoing waves at 50 kHz, confirming the successful formation of collimated wavefronts and directional propagation.

Fig. 5: Directional sound propagation with phononic crystals.

a, b Partitioned gradient-index phononic crystals (pGRIN-PnC) for wave collimation: a Manufactured system with a gradient distribution of the inclusion radii. b Simulation and experimental results of the pGRIN-PnC collimator with in-phase wavefronts at 50 kHz in the monitoring area. Adapted with permission from ref. ⁶⁴., Copyright © 2020, Jaeyub Hyun et al. c, d Bending of the one-way self-collimated acoustic beams with circulating fluids in circulating-fluid sonic crystals (CFSCs). c Equifrequency contours at $f=0.758{c}_{0}/a$ in air and CFSCs with varying angular velocities of the circulating fluids. d Sound distribution in the CFSCs with an incident angle of +13°, where the angular velocity of the circulating fluids is gradient-distributed. Adapted with permission from ref. ⁶⁵., Copyright © 2017, IOP Publishing.

With the integration of multiple wave manipulation techniques, the performance of acoustic devices can be enhanced by leveraging the strengths of various methods, leading to improved control over the wave propagation path, directionality, and intensity. For instance, gradient PnCs can be combined with the self-collimation effect to facilitate one-way dynamic directional propagation along predefined pathways.

By introducing circulating fluids around rigid rods, circulating-fluid sonic crystals (CFSCs) break both parity and time-reversal symmetries due to the asymmetric crystal lattice and the motion of the circulating fluids⁶⁵. Figure 5(c) illustrates the equifrequency contours at $f=0.758\,{c}_{0}/a$ for various angular velocities of the circulating fluids: 80 rad/s (clockwise), 0 rad/s, and −80 rad/s (anticlockwise). The equifrequency contours exhibit shifts in the positive or negative y-direction with an offset when the fluids rotate clockwise or anticlockwise, respectively. Figure 5(d) presents the acoustic field distribution in the CFSCs with an incident angle of +13°. The top 13 layers of circulating fluids maintain an angular velocity of 80 rad/s, decreasing by 4 rad/s per layer. This gradient distribution of angular velocities induces a gradual bending of self-collimated acoustic beams, resulting in an acoustic one-way mirage effect. These self-collimated one-way acoustic waves, characterized by designable trajectories, offer promising applications in acoustic communication systems and devices such as isolators, modulators, and transducers. Yet, beam steering and focusing in gradient PnCs are highly dependent on the gradient design, which poses challenges in achieving sharp directionality and dynamic control. Furthermore, precise modulation of acoustic waves demands meticulous control over spatial material properties, complicating fabrication processes and increasing sensitivity to defects. It is important to note that conventional PnCs, including gradient PnCs, typically require lattice spacings comparable to the wavelength, imposing a fundamental limitation on the directional radiation of acoustic waves from finite-sized sources. As a result, achieving precise control over acoustic radiation patterns with subwavelength micro-devices remains a challenging yet promising area of research.

Acoustic metamaterial

Acoustic metamaterials exhibit “on-demand” effective properties, functioning as continuous media with unconventional characteristics that are unbounded by the limitations of natural materials. These metamaterials are typically composed of structures where the interaction with acoustic waves is governed primarily by the internal behavior of individual unit cells, referred to as meta-atoms. To ensure that the response of the meta-atom predominates, its size is generally much smaller than the acoustic wavelength with which it interacts. This subwavelength feature enables the metamaterial to behave as a continuous medium, with its response remaining invariant to changes in shape or boundaries. Consequently, the overall material behavior is determined by the local properties of the meta-atoms, allowing bulk properties to be effectively predicted through simulations or measurements of small samples.

Various approaches based on metamaterials are available for achieving directional propagation of acoustic waves. For example, inhomogeneous metamaterials utilizing conformal transformation and homogeneous metamaterials with zero-reflection indices are designed to facilitate directive emission. Topological acoustics provide topologically protected states that ensure defect-immune directional wave propagation. Additionally, other artificial structures including acoustic metasurfaces, anisotropic metamaterials, Willis effect-based materials, pentamode materials, Mie resonant-based structures, and quasicrystals, can also enhance sound directivity. While these structures and their corresponding mechanisms exemplify current strategies of acoustic metamaterial, the discipline is actively evolving, with new techniques continually emerging to achieve precise directional sound propagation.

Zero refractive index materials enable sound propagating without phase variation, facilitating minimal distortion and efficient transmission to the target area. By engineering the refractive index to be zero at specific frequencies, these materials can focus acoustic waves beyond the diffraction limit and guide sound along unconventional paths, presenting significant potential for wavefront shaping and dispersion control^69,71,72. Figure 6(a-d) illustrates the directional emission in a zero refractive index metamaterial⁶⁹. A Dirac-like cone is shown at the center of the Brillouin zone (Fig. 6(a)). At the Dirac point, where the two bands converge, both the effective mass density and the inverse of the bulk modulus simultaneously approach zero. This gapless band structure facilitates high transmission, enabled by the finite acoustic impedance. Figure 6(b) presents the pressure field radiated by a point source operating at the Dirac point frequency (18.7 kHz) within the metamaterial. The uniform phase along the metamaterial’s edge results in the collimation of the cylindrical wavefront into a plane wave. In contrast, Fig. 6(c) displays the pressure field in an empty waveguide, illustrating a typical cylindrical wave pattern. Figure 6(d) highlights the directivity of the collimated plane wave produced by this double-zero refractive index metamaterial. The blue circles and red curve represent the directivities corresponding to the pressure field radiations with and without the metamaterial, respectively, while the black curve indicates the calculated directivity of an ideal line source with dimensions identical to those of the metamaterial. The amplitude of the collimated plane wave is confined within an angle of 11° ± 1°, approaching the theoretical limit of 10.6° for a line source of comparable size, thereby demonstrating the capability of strong directional emission control provided by the acoustic zero refraction index metamaterial. Furthermore, prior studies have indicated that acoustic wave collimation can also be achieved with high directivity performance in anisotropic zero-index media⁷³. Similar to phononic waveguiding, acoustic zero-refraction index materials are typically effective only within a narrow frequency range, which limits their versatility in broadband applications. Additionally, their performance is highly sensitive to material imperfections^74,75, as defects may induce unwanted scattering or loss of directional control.

Fig. 6: Directional sound propagation with acoustic metamaterials.

a-d Directional emission in a zero refractive index metamaterial: a Three-dimensional dispersion surfaces near Dirac-like cone. Measured pressure fields radiated by acoustic point source embedded (b) in the zero refractive index metamaterial and (c) in the empty waveguide. d Directivity of collimated plane wave. The blue circles and red curves represent pressure field radiations from (b) and (c), respectively. Adapted with permission from ref. ⁶⁹., Copyright © 2017, Marc Dubois et al. e-h Bioinspired conformal transformation acoustics for acoustic collimation: e Sound-speed distribution in the artificial forehead. f Schematic illustration of the bioinspired artificial model assembly. g Normalized sound intensity distribution of the artificial model at 30 kHz. h Directional pattern of the artificial model. Adapted with permission from ref. ⁷⁰., Copyright © 2020, American Physical Society.

Inspired by transformation optics, transformation acoustics provides a theoretical framework that applies the principle of coordinate transformations to manipulate acoustic wave propagation in a highly controlled manner. The materials designed for transformation acoustics are typically inhomogeneous and anisotropic, with properties engineered to vary spatially. This allows for highly customizable manipulation of acoustic waves, with applications spanning acoustic imaging, stealth technology, and noise reduction^76,77,78,79. A bioinspired metamaterial based on acoustic conformal transformation has been developed to enable acoustic steering and collimation, emulating the sound-manipulation capabilities found in whale morphology⁷⁰. This metamaterial mimics the acoustic properties of a whale’s forehead, with sound speed estimated via the Laplacian equation. Figure 6(e) shows the sound speed distribution achieved through conformal mapping. To realize this distribution and assess its effectiveness in controlling underwater acoustic beams, the structure of the metamaterial was engineered by varying radii from 2.64 mm to 4.17 mm, which increased the filling fraction of the hexagonal lattice along the y-axis (Fig. 6(f)). This variation led to an effective sound speed increase from 1483 m/s to 2577 m/s. Figure 6(g) illustrates the simulation results at 30 kHz, while Fig. 6(h) presents the directivity pattern measured at a distance of 1 meter, demonstrating the successful conversion of the omnidirectional source into a directional beam. The model achieved upward and downward beam steering with main lobe angles of +6.8° and −5.8°, respectively. Furthermore, these acoustic models exhibit broadband performance over a frequency range of 30 to 60 kHz. Despite its significant potential, transformation acoustics faces challenges in material fabrication and the complexity involved in achieving the precise anisotropy and inhomogeneity required for desired effects⁷⁶, which limits its range of application scenarios.

Additionally, Membrane- and plate-type acoustic metamaterials, a key area of metamaterial research, are lightweight and geometrically simple with the capability for active tuning of their effective density. These materials can achieve negative effective density and/or bulk modulus over a broad frequency range, making them highly effective for low-frequency sound attenuation and high transmission loss^80,81,82,83. Although their potential for wave directivity control is relatively underdeveloped, integrating them with metasurfaces offers promising solutions for lightweight, compact wavefront manipulation^84,85.

Topological acoustics

In the past decade, topological metamaterials have garnered significant attention for their ability to exhibit topologically protected interface, edge, or surface states. Inspired by topological phases in condensed matter physics, particularly in electronic systems, topological acoustics focuses on designing materials and structures where acoustic waves exhibit robust and unidirectional propagation in phononic systems, immune to backscattering and disorders. The robustness and versatility of acoustic topological systems hold great promise for breakthroughs in applications such as acoustic waveguiding, sound isolation, acoustic imaging and sensing. These systems enable customized wave propagation, facilitating directional emission and high transmission in 1D, 2D, and 3D configurations^{86,89,90,91,92,93,94}.

The acoustic analog of the Su-Schrieffer-Heeger (SSH) model has gained considerable attention in recent years. In contrast to nonradiable topological interface state designs based on the single SSH model, the proposed double SSH waveguide supports radiative modes⁸⁶. This waveguide features a pair of degenerate points away from the Brillouin zone boundary, as depicted in the upper panel of Fig. 7(a). A leaky-wave waveguide is engineered to enhance directional acoustic radiation, improving the radiation resistance and efficiency of a point source, with the radiation direction determined by the momentum of the degenerate points. Figure 7(b) shows the state distributions in waveguides with and without distinct topological phases, revealing two interface states within the bandgap around 3000 Hz for the waveguide with different topological phases. As demonstrated in Fig. 7(c), although the interface states are aligned along the x-direction, most acoustic waves leak through the upper wall slits, resulting in highly directional radiation in two lateral directions. Experimental results indicate that this design achieves over a tenfold enhancement in directional acoustic radiation energy, highlighting the potential of the 1D topological design for developing extremely compact devices with highly directional acoustic emission.

Fig. 7: Topological acoustics-based directional sound propagation.

a-c Compact topological waveguide for enhanced acoustic directional radiation: a Upper panel: schematic illustration of the Su-Schrieffer-Heeger (SSH) chain, its corresponding band structure, and the nonradiable topological interface state. Lower panel: schematic illustration of double SSH chain, its corresponding band structure, and the radiable topological interface state. b State distributions of the waveguides with and without distinct topological phases. c Pressure field distributions of the two radiable interface modes from leaky-wave waveguides with 16 cells. Adapted with permission from ref. ⁸⁶., Copyright © 2022, AIP Publishing. d-g Directional acoustic antennas based on valley-Hall topological insulators: d Dispersion relation of the ribbon-shaped 2D structure. e Superdirectional sound radiation by out-coupling of valley-polarized edge states from the topological acoustic antenna. f Simulated and measured far-field pattern with normalized energy emerging from the negative-type interface at 8.66 kHz. g Experimentally detected spectral relation between acoustical energy and the directional angle within the entire topological band gap. Adapted with permission from ref. ⁸⁷., Copyright © 2018, John Wiley and Sons. h-k Topological surface states in a gyroid acoustic crystal: h Geometry of gyroid acoustic crystals. i Bulk dispersion along the high symmetry lines of the 3D Brillouin zone. j Dispersion of surface states in the surface Brillouin zone. The equifrequency contour at 16.5 kHz acts as a demonstration of open surface arcs. k Experimental measured acoustic field distribution at 18.4 kHz. Adapted with permission from ref. ⁸⁸., Copyright © 2022, Yuning Guo et al.

Acoustic topological insulators, the acoustic analogs of electronic topological insulators, are typically categorized based on the underlying physical mechanisms that give rise to their topological properties^94,95,96. These categories include Chern insulator^97,98, Floquet topological insulator^99,100, analogs of quantum Hall effect^101,102,103, quantum spin Hall effect^104,105 and quantum valley effect^87,106, and higher-order topological insulator^107,108. Each classification is characterized by distinct topological mechanisms, providing unique methods for on-demand control of sound propagation.

As a demonstration, acoustic topological valley transport has been introduced to achieve beamforming, enabling highly directional sound radiation and reception^87,109. Figure 7(d-g) demonstrates the design of a superdirectional topological acoustic antenna for audible sound based on the acoustic valley Hall effect⁸⁷. The antenna consists of isotropic rigid rods arranged in a Kagome lattice, where varying the distance between rod centers and unit cell centers induces distinct topological phases through the contraction and expansion of the unit cells. Figure 7(d) illustrates the dispersion relations for a ribbon-shaped supercell with a zigzag interface, categorized as either positive-type or negative-type based on the refraction angle of the emitted beams. The red dashed line represents helical edge states within the bulk bandgap for the negative-type interface, while the blue solid line corresponds to those for the positive-type interface. These states exhibit opposite group velocities, reflecting distinct topological properties. Superdirectional sound radiation has been achieved by coupling valley-polarized edge states from the topological acoustic antenna. As shown in Fig. 7(e), acoustic waves traveling along the negative-type interface from left to right are projected from the high-symmetry K valley, resulting in directional radiation that aligns with the characteristics of equifrequency contours. Figure 7(f,g) displays the far-field radiation patterns obtained from both numerical simulations and experimental measurements. The half-power beamwidth of the main lobe is 9.72° for the topological acoustic antenna with the negative-type interface and 9.54° for the positive-type interface. Notably, the antenna operates throughout the entire frequency range of the topological bandgap spanning from 8.30 to 9.31 kHz. The collimated out-coupling of valley-polarized edge states effectively focuses sound toward a designated target area.

In parallel with advances in gapped phases of topological insulators, significant interest has emerged in the exploration of topological semimetals with gapless phases. Classical analogs of these semimetals are extensively studied in photonic and phononic systems. These semimetals are distinguished by their band structures, which feature multifold band degeneracy points such as Weyl and Dirac points, along with other contact patterns such as nodal lines and nodal rings^{110,111,112,113,114}. Unlike topological insulators, these structures do not require a band gap and can give rise to Fermi arcs associated with topologically protected surface states.

Figure 7(h-k) illustrates a 3D gyroid acoustic crystal that hosts multifold topological degenerate points, supporting robust topological surface states⁸⁸. Figure 7(h) highlights the geometry and distinctive features of the gyroid surface, a triply periodic minimal surface with body-centered cubic symmetry, characterized by its left-handed and right-handed helices. Figure 7(i) presents the dispersion along the high-symmetry lines of the 3D Brillouin zone, revealing a fourfold degenerate band crossing at the high-symmetry point P and a threefold degenerate band crossing at Γ. These nodal points are identified as a spin-1 Weyl point and a charge-2 Dirac point, with their topological properties protected by nonsymmorphic symmetry. The upper panel of Fig. 7(j) illustrates the dispersion of surface modes across the entire surface Brillouin zone in the projected ${k}_{x}{k}_{y}$ plane. Four sheets of surface states surrounding the degenerate point span a broad frequency range with a relative bandwidth ${\rm{\Delta }}\omega /\omega$ of approximately 45%, connecting to chiral topological states confined to the surfaces. The bottom panel provides an example of open arcs at a frequency of 16.5 kHz, demonstrating their chiral nature, where only a single pair of arcs exists on one surface, leading to highly directional propagation along that surface. Figure 7(k) displays experimentally measured acoustic fields at 18.4 kHz, showing that the acoustic energy is well confined to the surfaces of the 3D bulk material, with waves propagating directionally along specific paths. This is facilitated by the small curvature of the surface arcs across a wide range of wavevectors, highlighting the strong beam-steering capabilities of 3D acoustic topological materials.

Acoustic topological systems are inherently robust against defects and disorder, making them highly reliable for practical applications. These systems support interface, edge, and surface states that allow sound to travel along material boundaries or predefined paths, enabling precise control over sound propagation and enhanced wave manipulation. However, the complex designs of these materials can pose fabrication challenges and are often sensitive to geometric parameters, requiring precise engineering to achieve optimal performance. While topological acoustics offers exciting opportunities for directional sound manipulation, addressing challenges related to material complexity and operational conditions is crucial for fully realizing its practical potential.

Acoustic metasurface

Acoustic metamaterials often rely on bulky 3D structures for wave manipulation, limiting their applicability for lightweight or compact applications. Acoustic metasurfaces, 2D structures based on the principles of generalized Snell’s law, offer a more efficient solution for controlling phase, amplitude, and direction of acoustic waves. By precisely arranging subwavelength elements, metasurface can manipulate wave reflection, refraction, absorption, and transmission, while reducing material usage and system complexity. Typically designed with Helmholtz resonators^115,116,117, resonant membranes^84,118,119, and coiling-up space structures^120,121,122, acoustic metasurface enables precise wave steering and focusing through spatial phase gradients. These structures provide miniaturized materials and devices with advanced functionalities, making them particularly effective for addressing the challenge of controlling long-wavelength sound in air and water with thin, lightweight solutions. Due to their exceptional wavefront shaping capabilities, acoustic metasurfaces are ideal for achieving directional acoustic emission^{7,123,124,125}.

Figure 8(a-d) present an acoustic passive metascreen featuring a resonator-based design that provides high transmission, complete phase control, and deep subwavelength spatial resolution, enabling both beam steering and bending¹²⁶. Figure 8(a) shows an experimentally fabricated metasurface sample comprising eight elementary units with phase shifts ranging from 0 to 2π in increments of π/4. Each elementary unit consists of a straight pipe and four acoustic Helmholtz resonators. Figure 8(b,c) illustrates the theoretical acoustic field and directivity patterns of the redirected beams generated by a 150-element metascreen. With a stair-step phase profile, the metascreen successfully steers the beam at a designed angle of 38° relative to the incident direction at the Fabry-Perot resonant frequency. The polar directivity graph, measured ten wavelengths from the screen’s center, contrasts the redirected beams at the resonant frequency (solid curve) with those at two cutoff frequencies (dot-dashed curves), demonstrating effective directional emission. Beyond beam steering, the metascreen is capable to reshape the acoustic field of a point source into a self-bending beam, as illustrated in Fig. 8(d), which extends its beam control capabilities beyond the paraxial approximation.

Fig. 8: Directional sound propagation with acoustic metasurfaces.

a-d Metascreen-based acoustic phased array: a Each element of the passive screen consists of a straight pipe and four Helmholtz resonators as the photograph of the experimental sample shows. b Theoretical demonstration of metascreen-modulated acoustic field redirecting a normally incident acoustic beam to an angle of 38° at the Fabry-Perot resonant frequency ${f}_{0}$. c Directivity pattern of the redirected beams measured at a distance of ten wavelengths from the screen’s center at ${f}_{0}$. d Illustration of sound energy penetrating the screen, resulting in self-bending beam. Adapted with permission from ref. ¹²⁶., Copyright © 2015, American Physical Society. e-h Wavefront modulation with an acoustic metasurface based on labyrinthine structures: e Photograph of the designed prototype where the unit cells with varying intricate modulations. f Six types of unit cells and their corresponding phase changes. g Radiation patterns for incident angles of 5°, 20°, and 35°. h Acoustic field modulation by the acoustic metasurface at 45°. Adapted with permission from ref. ¹²⁷., Copyright © 2014, Springer Nature. i-l Dispersionless manipulation of reflected acoustic wavefront by a subwavelength corrugated surface: i Illustration of the dispersionless phase front. j Schematic illustration of subwavelength corrugated surface, featuring grooves with subwavelength width. k Numerical and experimental scattered acoustic field with extraordinary reflection subwavelength corrugated surface at 7.277 kHz. l Directionality obtained from the theoretical analysis and the simulation of phased array theory at 7.277 kHz. Adapted with permission from ref. ¹²⁸., Copyright © 2015, Springer Nature.

As a widely used design for wavefront modulation, coiled-up configuration offers high energy throughput, a broad complex modulation range, and non-resonant dispersion. An acoustic transmissive metasurface with labyrinthine structures is present in Fig. 8(e-h), showcasing features such as wave mode conversion, extraordinary beam steering, and negative refraction through higher-order diffraction¹²⁷. Figure 8(e) displays fabricated tapered labyrinthine unit cells with varying complex modulations, highlighting intricate modulations across the planar metasurface. The unit cells, with a uniform thickness of approximately 0.25 ~ 0.35 times the acoustic wavelength, can achieve a complete 2π phase change range using double layers in the transmissive case. Figure 8(f) shows the phase change of six distinct unit cell types over the frequency range of interest. A transmissive metasurface consists of a set of unit cells with π/6 phase change between adjacent ones. A linear transducer array generates a plane wave in front of the metasurface, while a microphone sweeps the measuring area behind the metasurface to record the transmitted wavefronts. When the incident angle ${\theta }_{i}$ approaches a critical angle ${\theta }_{c}$ which is determined by generalized Snell’s law incorporating a nonlocal term, the transmitted wave will bend towards the surface and become evanescent on the transmitted side. Figure 8(g) presents the measured (dots) and simulated (solid lines) transmitted field patterns for incident angles of 5° (${ < \theta }_{c}$), 20° (around ${\theta }_{c}$), and 35° (${ > \theta }_{c}$), confirming the emergence of extraordinary beam steering effect related to the passing off orders found in diffractive grating anomalies. Figure 8(h) demonstrates directional propagation and negative refraction enabled by the transmissive metasurface in the region of extraordinary beam steering, showcasing its capability of wavefront modulation from the subwavelength thin interface.

In addition to resonator-based metasurfaces and coil-up space metasurfaces, various other types of metasurfaces have been explored for advanced acoustic manipulation in a directional propagation manner. Figure 8(i-l) introduces the concept of dispersionless wavefront manipulation, presenting a general scheme for designing reflective metasurfaces that overcome bandwidth limitations¹²⁸. Figure 8(i,j) illustrate a schematic representation of a dispersionless subwavelength corrugated surface, characterized by a phase front where $d\phi /{dx}$ is proportional to ${k}_{0}$. This corrugated surface features grooves with subwavelength widths, filled with an acoustically rigid medium (shown in blue), while the surrounding medium is air. The groove depth varies as a function of $x$, denoted as $y=h(x)$, allowing for spatially varying phase shifts between incident and reflected waves. Figure 8(k) presents the numerical and experimental scattered acoustic field at 7.277 kHz, showcasing extraordinary reflections at $\theta =45$° without sidelobes, thereby highlighting the surface’s capacity to achieve highly directional wave propagation. The subwavelength width of the grooves enables the abnormal reflected wave to be interpreted as new acoustic radiation generated by a line of secondary sources, with phase delays modulated by the groove depths of the subwavelength corrugated surface. Figure 8(l) illustrates the directivity patterns derived from theoretical analysis and simulations using phased array theory, further corroborating the emergence of highly directional reflection. This property of ultra-broadband extraordinary reflection suggests that the proposed reflective structure could be integrated with waveguide designs to enable unconventional wave steering effects.

According to Huygens’ principle, all wave fields can be constructed by superimposing the wavefronts of elementary waves, regardless of the modulation approach. For example, both acoustic phased arrays and metasurfaces enable beamforming through precise phase control, offering flexible design possibilities with customizable geometries to achieve specific acoustic effects. The choice between these methods depends on the specific application scenario. Phased arrays allow dynamic and reconfigurable beam steering, making them ideal for applications such as sonar, medical ultrasound, and directional audio systems, where real-time control is crucial. However, they typically require large apertures and numerous transducers, demanding complex synchronization of electronically controlled elements, which increases cost and design complexity. In contrast, acoustic metasurfaces, which can be viewed as a passive phased array, present several advantages including subwavelength manipulation with highly compactness, lightweight design, cost-effectiveness, and enhanced functionality. This makes them particularly promising for applications that require miniaturized and highly efficient wave manipulation, such as sound barriers, acoustic cloaking, and wearable or portable acoustic devices. Despite these benefits, metasurfaces face challenges with narrow bandwidth and functional dispersion. To broaden the frequency range, gradient elements with distinct internal resonances could be integrated¹²⁹, though this approach would increase geometric complexity potentially compromising the compactness that makes metasurfaces desirable.

Other types of acoustic artificial structures

Beyond the commonly used artificial structures discussed above, various alternative designs and mechanisms offer effective solutions for directional sound emission and transmission. These innovative methods enhance flexibility and creativity in acoustic wave manipulation, broadening the scope of potential applications in this field.

In addition to the geometric design of the unit cell in acoustic artificial structures, the orientation of the unit cell can also serve as an additional degree of freedom to facilitate directional wave manipulation. Acoustic anisotropic metamaterials exhibit direction-dependent properties in the manipulation of acoustic waves. Their inherent anisotropy, which can arise from geometric design or material composition, provides high directional selectivity, enabling efficient sound propagation in one direction while attenuating or suppressing it in another. Directional acoustic emission can be enhanced in acoustic anisotropic metamaterials by leveraging resonance or gradient impedance effects^130,134. Figure 9(a) illustrates a periodically distributed anisotropic metamaterial array, consisting of a straight channel and four symmetrical side branch cavities. The simulated distributions of the normalized sound pressure fields at 3540 Hz, shown in Fig. 9(b,c), demonstrate distinct behaviors along the x- and y-directions. In the x-direction, the acoustic wave experiences significant attenuation as it traverses the metamaterial array, resulting in a pronounced decrease in sound pressure amplitude on the right side. In contrast, the acoustic wave propagates with minimal attenuation in the y-direction, indicated by the nearly equal normalized sound pressure amplitudes on both sides of the array. With a monopole source positioned at the center of the array, the metamaterial exhibits broadband directional acoustic emission enhancement along the y-axis. Through optimizing the array’s parameters, enhanced acoustic emission is achieved across a frequency range of 3335 to 4625 Hz. Experimental validation supports these simulations, revealing that at a distance of 35 cm from the source, the sound pressure level in the y-direction is increased by an average of 4 dB, while the sound pressure level in the x-direction is reduced by an average of 12 dB¹³⁰. However, since the performance of anisotropic metamaterial is highly sensitive to the angle of incidence, minor deviations from the design parameters can significantly impact directional behavior, thereby reducing the effectiveness of sound manipulation.

Fig. 9: Directional sound propagation with other types of acoustic artificial structures.

a-c Directional emission through acoustic anisotropic metamaterials: a Schematic illustration of the anisotropic metamaterial, featuring a unit composed of a straight channel and four symmetrical side branch cavities. Simulated distributions of the pressure fields in (b) x-direction and (c) y-direction of the metamaterial array at 3540 Hz with an incident plane wave. Adapted with permission from ref. ¹³⁰., Copyright © 2022, Elsevier. d, e Interfacial wave between acoustic media with Willis coupling: d Detailed view of the designed 2D slab waveguide with C-shaped Helmholtz resonators. The red dotted line indicates the interface of two different acoustic Willis materials, and θ represents the orientation angle of the Helmholtz resonator. e Simulated and experimental acoustic fields of the slab waveguide with two Willis materials oriented at angles of (left panel) −135° and 45°, and (right panel) 45° and −135°, respectively. Adapted with permission from ref. ¹³¹., Copyright © 2022, Elsevier. f-h Bioinspired directional emission via hybrid metamaterials: f Physics-based porpoise model. g Acoustic beam formations of the model with air component V at 30 kHz. h Acoustic beam formation of physics-based porpoise model with I, II, III, IV, and V at 30 kHz. Adapted with permission from ref. ¹³²., Copyright © 2019, Erqian Dong et al. i-k Directional acoustic emission in a Penrose quasi-crystal structure: i Geometry of a Penrose quasicrystal realized with 86 rods. j Distribution of the acoustic pressure outside the circular Penrose quasi-crystal with 86 rods at 459.5 kHz. k Experimental mapping of the directivity pattern of the water-immersed quasi-crystal with the non-directional source positioned at the center. Adapted with permission from ref. ¹³³., Copyright © 2019, Elsevier.

Analogous to the electromagnetic bianisotropy effect, acoustic Willis materials exhibit nonreciprocal interactions between a materials’ monopole and dipole responses, enabling unconventional coupling between pressure and velocity, as well as between momentum and strain. This coupling breaks the traditional separation between these two acoustic responses, facilitating the simultaneous manipulation of sound pressure and velocity fields in ways that are typically unattainable with conventional materials. The Willis coupling effect can be achieved using deep subwavelength structures, providing a more compact and lightweight solution for directional sound applications and enabling phenomena such as asymmetric sound transmission¹³⁵, high-efficiency sound insulation¹³⁶, and directional sound emission with improved performance at low frequencies¹³⁷. Figure 9(d) illustrates a two-dimensional slab waveguide featuring C-shaped Helmholtz resonators, with an interface at the center formed by two distinct Willis materials, as indicated by the red dotted line. The orientation angle θ of the resonant cavities is adjustable, allowing for the investigation of Willis coupling effects on interfacial waves. Figure 9(e) shows the simulated and experimental acoustic fields of the slab waveguide at 4950 Hz, with two Willis materials oriented at angles of (left panel) −135° and 45°, and (right panel) 45° and −135°, respectively. These results align with the theoretical predictions, demonstrating the emergence of an interfacial mode when the Helmholtz resonator slits on either side are aligned in a back-to-back configuration, satisfying the conditions for interfacial wave existence. Conversely, the interfacial wave vanishes when the slits of Helmholtz resonators on both sides are face-to-face as the conditions for interfacial mode are not met. The presence of the interfacial wave critically depends on the relative alignment of the Willis coupling vectors between the two materials, offering a flexible approach for directional waveguiding¹³¹. Additionally, introducing airflow also enables asymmetric sound radiation phenomena such as extreme nonreciprocal Willis response¹³⁸ and odd-symmetric Willis coupling¹³⁹. Willis coupling offers innovative strategies for directional sound transport, while challenges related to energy losses and sensitivity to design parameters warrant careful consideration.

Anisotropic and Willis materials focus on specific geometrical designs or mechanisms, meanwhile hybrid metamaterials are gaining prominence in acoustic wave manipulation, owing to their ability to integrate multiple physical mechanisms or combine components with distinct functions, thereby providing enhanced control over acoustic waves. By leveraging the strengths of various acoustic parts, these engineered materials offer a versatile platform for advanced sound control, enabling functionalities that would otherwise be challenging or unattainable^140,141,142. A physical model for directional acoustic emission has been developed to bridge the gap between the biosonar capabilities of porpoises and artificial metamaterials¹³². This hybrid metamaterial system, comprising multiple composite structures, exhibits improved directivity and increased main lobe energy across a broad bandwidth, as validated by both numerical simulations and experimental results. Figure 9(f) illustrates the bioinspired composite assembly, which approximates the complex morphology and sound speed distribution characteristic of a porpoise. Figure 9(g,h) presents the acoustic fields generated by the hybrid structures within this porpoise-inspired model. In the configuration utilizing only the air component V, the left air cavity functions as a curved boundary, reflecting the acoustic wave forward. However, the fully realized directional acoustic field emerges only when all components—including the air cavity, hybrid metamaterials, and the skull—work together. The measured main lobe energy in the porpoise-inspired model is approximately 6.5 dB higher than the case in the absence of the model across a broad bandwidth. The case demonstrates that natural structures can inspire the design of artificial media for directional wave control. Despite these advantages, the integration of multiple components or mechanisms in hybrid metamaterials often increases fabrication complexity and costs. The precise modulation of material properties and structural arrangements required can further limit scalability and pose significant production challenges.

While most artificial structures are designed with periodic or gradient-distributed patterns, structures exhibiting quasi-periodic translational order can also demonstrate unique functionalities. Quasicrystals, with their aperiodic structures characterized by long-range order, produce distinctive wave propagation behaviors, such as unusual diffraction patterns and the ability to create highly localized or tailored propagation paths^143,144,145. The work introduces a directional acoustic emitter based on Penrose quasi-crystal structures¹³³. Figure 9(i) illustrates the geometry of a Penrose quasi-crystal consisting of 86 rods embedded in a fluid. The far-field acoustic pressure distribution surrounding the circular Penrose quasi-crystal, depicted in Fig. 9(j), reveals pronounced directional emission along specific orientations at 459.5 kHz. The experimental directivity pattern, mapped in Fig. 9(k), further confirms this directional emission behavior. Quasicrystals often exhibit broad or multifrequency bandgaps, enabling them to control acoustic waves across a wide range of frequencies, thus offering greater versatility than periodic structures that typically operate within narrower frequency bands. However, the aperiodic nature of quasicrystals complicates the prediction and control of precise wave propagation paths. Additionally, the complexity involved in the design, fabrication, and optimization of these intricate structures may pose significant challenges for their widespread application in practical acoustic systems.

Pentamode materials, distinguished by their ability to demonstrate five independent modes of elastic deformation, represent another promising approach to material design in acoustics and wave manipulation. Their anisotropic behavior allows mechanical properties to vary with the direction of applied stress, enabling for tailored acoustic responses based on the material’s orientation and facilitating directional control of acoustic waves^149,150,151. A pentamode material has been proposed for developing an underwater emitter with directional emission capabilities¹⁴⁶. This design provides significant flexibility, allowing precise control over the direction of emitted acoustic waves. Theoretical simulations confirm the emitter’s ability to achieve directional transmission, as illustrated in Fig. 10(a). The corresponding directivity pattern, shown in Fig. 10(b), features two prominent peaks in pressure amplitude at angles of 60° and 240°, with values reaching 0.344 Pa—approximately 3.4 times higher than the pressure measured in the absence of the emitter’s shell (0.078 Pa). To realize this design, an aluminum honeycomb lattice structure was utilized as a practical approximation of a pentamode material, as depicted in Fig. 10(c). The lattice was statically homogenized to ensure that the pentamode behavior is maintained across a broad frequency range. Simulations of the acoustic field at 4.5 kHz, also shown in Fig. 10(d), effectively demonstrate the latticed structure’s capability to achieve directional emissions with high precision. While pentamode materials offer significant advantages in directional sound manipulation, challenges related to fabrication and sensitivity to design parameters remain. Addressing these challenges is crucial for practically implementing pentamode materials in advanced acoustic applications.

Fig. 10: Directional sound propagation with other types of acoustic artificial structures.

a-d Underwater directional acoustic emitter based on pentamode material: a Emission radiation modulated by the shell constructed from pentamode material at 10.5 kHz. b Corresponding directivity pattern illustrating acoustic emission characteristics. c Detailed schematic of a practical pentamode material featuring a honeycomb lattice structure. d Simulated acoustic pressure field at 4.5 kHz, accompanied by a close-up view of the honeycomb lattice configuration. Adapted with permission from ref. ¹⁴⁶., Copyright © 2023, Binghao Zhao et al. e-h Tunable directional subwavelength acoustic antenna based on Mie resonance: e Schematic illustration of the Mie-resonator-based antenna, with an acoustic point source positioned adjacent to a sub-wavelength maze-like Mie resonant unit. f Simulated field distribution of sound intensity in the xy-plane for the antenna at the resonance frequency of 1755 Hz. g Corresponding directivity pattern based on simulated and measured far-field field. h Field distributions of sound intensity in the xy-plane at resonance frequency of 1755 Hz for the array antenna. Adapted with permission from ref. ¹⁴⁷., Copyright © 2018, Jin Zhang et al. i-m Directional wave energy amplification in non-Hermitian odd plates: i The piezoelectric-patch-based feed-forward control allows the coupling between the sensed x-directional bending deformation (${B}_{x}$) and the actuated shear deformations (${Q}_{x}$ and /or ${Q}_{y}$) in different directions. j Equifrequency contours as functions of the real part of wave number with odd parameters tuning. k Equifrequency controls as functions of the corresponding imaginary part of wave number. l Corresponding simulation for directional flexural wave propagation. m Simulation of interfacial flexural wave waves propagating along the interface between two odd plates with the odd parameters of opposite signs. Adapted with permission from ref. ¹⁴⁸., Copyright © 2023, Elsevier.

In addition to mechanisms such as topological protection, pentamode design, and Willis coupling, alternative mechanisms like Mie scattering also provide promising avenues for achieving directional sound manipulation. Mie scattering refers to the phenomenon of scattering electromagnetic or acoustic waves by particles whose dimensions are comparable to the wavelength of the waves. This scattering mechanism enables flexible design, as specific geometric configurations can be engineered to achieve tailored scattering patterns, providing considerable versatility in acoustic applications. The inherently directional nature of Mie scattering often results in highly directional sound emission with reduced side lobe levels, thereby enhancing the signal-to-noise ratio and overall system performance. Additionally, its broad frequency response makes Mie scattering-based structures particularly well-suited for broadband applications, such as communication systems.

The work presents a Mie-resonance-based acoustic antenna designed to significantly enhance both the emissivity of radiated power and the directivity of the radiation pattern^147,152. Figure 10(e) provides a schematic illustration of the Mie-resonator-based antenna, where a monopole source is positioned adjacent to a sub-wavelength maze-like Mie resonant unit. This labyrinthine structure forces acoustic waves to propagate through folded channels rather than along a direct path, effectively increasing the path length and yielding a high relative refractive index. The acoustic intensity field distributions generated by the antenna at a resonance frequency of 1755 Hz are depicted in Fig. 10(f), where the Mie resonator operates in dipole mode, exhibiting forward unidirectional radiation. Figure 10(g) presents the directivity pattern of the simulated and experimentally measured far-field sound radiation, where the unidirectional radiation in the 0° direction exhibits acoustic intensity 7.81 times greater than that of the monopole source, with a half-power beamwidth of 68°. The intensity difference between the main lobe and the side lobes is approximately 5.3 times. Moreover, the coupling between the Mie resonator and the sound source, as well as the coupling between adjacent resonators, impacts the radiation pattern. Figure 10(h) presents the intensity distribution in the xy-plane at resonance for the array antenna, illustrating an increase in the amplitude of the main lobe and suppression of the side lobes, which enhances directivity. The intensity difference between the main lobe and the side lobes reaches approximately 22.3 times, while the half-power beamwidth narrows from 68° to 48°, indicating a more concentrated radiated power. However, the efficiency of Mie scattering is contingent on particle dimensions being comparable to the wavelength, which constrains its applicability in compact systems, particularly at lower frequencies. Furthermore, its performance is highly dependent on material properties, such as density and elasticity, posing challenges in identifying materials that achieve optimal scattering over a broad frequency range.

The acoustic artificial structures discussed above are passive designs, which effectively demonstrate wave manipulation capabilities for static applications. These passive designs rely solely on material properties and geometric configurations, making them robust, energy-efficient, and cost-effective with long-term stability. However, their dispersive nature limits their anomalous characteristics to narrow frequency bands, restricting adaptability, functionality, and real-time modulation. In contrast, embedding active elements within acoustic artificial structures allows for flexibly controlled manipulation of acoustic waves by tuning their original¹⁵³ or effective properties^154,155, enabling diverse phenomena such as nonreciprocal transmission¹⁵⁶, real time modulation¹⁵⁷, and multi-functionality¹⁵⁸. Although more complex and costly, active systems can enhance the performance of artificial structures by offering dynamic tunability, greater functionality, and broader application potential.

Active metamaterials break spatiotemporal symmetries and violate reciprocity relations and conservation laws, making them open-loop systems suitable for exploring non-Hermitian phenomena. These non-conservative systems, which involve energy loss and/or gain modulation, feature complex eigenvalues that give rise to unique topological effects, such as acoustic radiation phenomena^159,160 and non-Hermitian skin effect^{161,162,163,164}. As non-Hermitian systems, active materials can accommodate antisymmetric (odd) components of the static elastic modulus tensor, leading to a loss of symmetry known as odd elasticity. An active odd plate is created by integrating piezoelectric sensors and actuators with a feed-forward circuit system, forming an open, non-Hermitian system¹⁴⁸. The feed-forward control based on piezoelectric patches couples the sensed x-directional bending deformation (${B}_{x}$) and the actuated shear deformations (${Q}_{x}$ and/or ${Q}_{y}$) in different directions, as illustrated in Fig. 10(i). The active lattice plate can be homogenized as an effective odd plate with four independently adjustable odd parameters. In such plates, harmonic flexural waves exhibit complex wave vectors, where the imaginary part governs wave amplification or attenuation along the propagation direction. Altering the odd parameters enables precise control of these flexural wave amplification behaviors. As an example, Fig. 10(j,k) shows equifrequency contours of the wave vector’s real and imaginary parts for dimensionless frequencies ${\rm{\Omega }}=0.03,0.06,0.09$, with one nonzero odd parameter (${\mathop{P}\limits^{\bar{} }}_{{xx}}=1.96$) while the other three being zero (${\mathop{P}\limits^{\bar{} }}_{{yy}}={\mathop{P}\limits^{\bar{} }}_{{xy}}={\mathop{P}\limits^{\bar{} }}_{{yx}}=0$). The real part indicates isotropic flexural wave propagation, while the imaginary part exhibits directional-dependent attenuation and amplification zones. The numerical result in Fig. 10l confirms these amplification-attenuation behaviors and exhibits directional wave propagation. Additionally, Stoneley-like flexural interfacial waves arise along the interface between two adjacent odd plates with opposite-sign odd parameters, as shown in Fig. 10m. These interfacial waves rely on cross-coupling between bending and shear deformations and can exist at any frequency, unlike those in topological structures. This feature facilitates the design of novel waveguides and advances the understanding of 2D non-Hermitian elastic systems.

This review highlights several mainstream approaches to achieving directional sound propagation while also recognizing a flourish of alternative techniques with notable effectiveness. These include designs such as leveraging multiple scattering theory^43,165, nonreciprocal transitions via spatiotemporal modulation^166,167, acoustic vortex with orbital angular momentum¹⁶⁸, utilization of nondiffractive beams including Airy or Bessel beams^{169,170,171,172,173,174}, and integration of resonator-based sensors with deep learning^175,176, offering diverse strategies for directional sound control.

Overview and discussion

This section begins with a structured taxonomy of the primary methods of directional wave manipulation, followed by a discussion on the current state of directional sound propagation and its prospects. Each approach offers distinct advantages, from conventional directional audio systems to advanced acoustic communication and imaging. Source modulation-based methods—such as sound domes, acoustic phased arrays, and acoustic parametric arrays—adjust the properties of the sound emitter itself to achieve directional propagation with diverse working principles. To be specific, sound domes rely on geometric acoustics to confine sound within a specific space. They operate across a broad frequency range but require large structures, as acoustic wavelengths are typically much smaller than the characteristic dimensions of boundaries they interact with. Acoustic phased arrays use wave interference to steer and focus sound beams by adjusting phase variations across multiple transducers. This enables precise beamforming and real-time control, making them ideal for applications such as acoustic imaging, medical ultrasound, sonar, and particle manipulation. Yet their implementation requires a complex system with higher costs. Acoustic parametric arrays, on the other hand, utilize nonlinear acoustic effects to generate directional sound from ultrasonic carriers. This approach effectively achieves highly directional low-frequency sound emission without requiring large transducer arrays, while suffers from low energy efficiency due to power loss during the conversion of ultrasonic waves to audible sound.

Artificial structure modulation-based approaches manipulate acoustic waves through engineered materials and structures, enabling applications such as wave guiding, sound isolation, and compact wavefront control. Phononic crystals, which consist of periodic or gradient arrays with unit cells typically around half the operating wavelength, control wave propagation through long-range interactions and spatial dispersion, facilitating wave localization and filtering. Governed primarily by the internal behavior of individual unit cells, acoustic metamaterials allow subwavelength meta-atoms and inhomogeneous configuration, and offer customizable functions such as stealth, super-resolution imaging, and directional emission with compact and flexible designs. As a subset of acoustic metamaterials, acoustic metasurfaces, are two-dimensional structures that use subwavelength elements to control phase, enabling efficient beam steering and absorption. They are particularly useful for miniaturized applications like sound barriers, acoustic cloaking, and wearable devices. However, those artificial structures generally operate within narrow frequency ranges with a specific design and are sensitive to material imperfections. Topological acoustics help address these limitations by enabling robust, unidirectional wave propagation resistant to backscattering and defects, making them ideal for resilient signal routing. However, they often require precise geometric design and delicate tuning.

Beyond these primary strategies, various alternative methods exploit unique physical effects or integrate multiple mechanisms to achieve directional sound. Anisotropic and hybrid metamaterials leverage direction-dependent properties or integrated components to achieve directional sensing and acoustic filtering. Designs based on Willis coupling and Mie resonance offer compact solutions for wave rectification and advanced signal processing, though they face challenges related to energy losses. Quasicrystals and pentamode materials are aperiodic yet ordered structures whose properties arise from their geometry or material orientation, allowing for controlled directional sound emission through unique diffraction effects. Non-Hermitian acoustic systems leverage gain and loss mechanisms to achieve non-reciprocal wave behavior and asymmetric mode conversion, enhancing signal transmission and directional amplification. Finally, active control systems integrate dynamic elements to manipulate sound properties in real time, allowing for adaptable and tunable acoustic solutions. Many artificial structure-based approaches can transition from passive to active designs, enhancing their versatility for smart acoustic systems and adaptive noise control.

Directional sound propagation remains a critical research area with significant technological and industrial implications. While conventional methods such as acoustic phased arrays and parametric arrays are effective, they face challenges related to physical size, frequency bandwidth, and power efficiency. Acoustic artificial structures—such as phononic crystals, acoustic metamaterials, and metasurfaces—provide flexible control over acoustic waves, enabling compact, high-precision sound directionality across a wide frequency range. The review highlights the growing significance of acoustic artificial structures in facilitating controlled directional sound emission and transmission, with promising applications across various industries.

Nevertheless, the gap remains between fundamental research of artificial structures and their practical deployment, making it essential to bridge this divide to advance the field further. Challenges such as fabrication complexity, limited tunability, narrow operational bandwidth, and energy losses require further development for a given structure. Substantial efforts have been made to address these issues. For instance, active control systems with dynamic tuning capabilities allow real-time adjustments to accommodate varying environmental conditions and operational requirements, providing flexible and interactive solutions for sound control in acoustic artificial structures^177,178,179. Moreover, artificial intelligence-assisted directional sound propagation utilizes machine learning, neural networks, and data-driven techniques to enhance the precision, adaptability, and efficiency of sound control systems. By optimizing the performance of acoustic artificial structures like acoustic metamaterials, artificial intelligence enables more effective manipulation of acoustic waves by predicting and compensating for potential interferences, which improves the operational bandwidth of directional sound propagation while reducing energy consumption and physical size^{175,180,181,182,183}. Recent advancements in additive manufacturing have further improved the feasibility of fabricating complex structures, making acoustic artificial structures more viable for real-world applications^184,185.

However, the practical implementation of these artificial structures introduces additional complexities that are often not encountered in theoretical models. Certain effects require careful consideration in acoustics for effective directional wave manipulation. For instance, thermoviscous losses, which vary with frequency, are particularly relevant in acoustic systems with narrow channels. When acoustic waves propagate through subwavelength channels, the presence of velocity gradients, viscous friction between the medium particles, and thermal conduction effects lead to energy dissipation, significantly impairing performance. Additionally, acoustic-structure interaction arises when acoustic waves interact with non-rigid boundaries or the walls of artificial structures. Proper impedance matching between the structure and the background medium is essential for developing practical, efficient, and versatile sound control solutions. Acoustic artificial structures enable customizable, on-demand functionalities, while these capabilities require further quantitative validation to achieve a level of maturity and practical usability. A specific topic worthy of mention is low-frequency sound control, which is crucial for applications such as underwater communication, noise control, and structural health monitoring^186,187,188. This area warrants greater attention due to its capacity to propagate over long distances and penetrate barriers. Efficiently manipulating these long wavelengths while minimizing bulky structures and reducing energy consumption requires the development of new modulation mechanisms and innovative design strategies.

Currently, the field of acoustic wave manipulation continues to evolve rapidly, driven by interdisciplinary research and the increasing demand for 3D precise and efficient sound control across diverse applications. This evolution is particularly evident in smart technologies, where high-quality directional sound plays a pivotal role. For example, by integrating more sophisticated algorithms and advanced sensor designs involving metastructures^189,190,191, acoustic holography can serve as a versatile and precise tool for visualizing acoustic fields, holding the potential to revolutionize immersive experiences in virtual and augmented reality by creating highly realistic and spatially accurate sound environments^192,193,194. Efficient real-time adaptive beamforming has the potential to revolutionize applications in telecommunications, surveillance, and noise control by enabling dynamical steering of acoustic waves, thereby improving signal quality and minimizing interference^195,196. These advancements are further enhanced by cross-disciplinary innovations, where acoustic control technologies are integrated with other wave-based systems in areas such as medical diagnostics, environmental sensing, and quantum information processing. Such integration is opening new avenues for generalized acoustic research and paving the way for cutting-edge practical applications.