Learning from one and only one shot

Abstract

Humans can generalize from only a few examples and from little pretraining on similar tasks. Yet, machine learning (ML) typically requires large data to learn or pre-learn to transfer. Motivated by nativism and artificial general intelligence, we directly model human-innate priors in abstract visual tasks such as character and doodle recognition. This yields a white-box model that learns general-appearance similarity by mimicking how humans naturally “distort” an object at first sight. Using just nearest-neighbor classification on this cognitively-inspired similarity space, we achieve human-level recognition with only 1–10 examples per class and no pretraining. This differs from few-shot learning using massive pretraining. In the only-few-shot regime of MNIST, EMNIST, Omniglot, and QuickDraw benchmarks, we outperform both modern neural networks and classical ML. For unsupervised learning, by learning the non-Euclidean, general-appearance similarity space in a k-means style, we achieve multifarious visual realizations of abstract concepts by generating human-intuitive archetypes as cluster centroids.

Introduction

Modern machine learning (ML) has made remarkable progress, but this is accompanied by increasing model complexity, with hundreds of neural layers (e.g., ResNet-152) and millions to trillions of parameters (e.g., ViT: 86-632M, GPT-4: 1T). This results in a huge appetite for data and resources, making data curation hard and energy costs irresponsibly high, which particularly challenges domains like low-resource languages or rapidly-evolving pandemics. The increased model complexity further leads to inscrutability and nonintuitiveness, making the model hard both for users to control and for developers to tune (e.g., hyperparameters, architecture). As such, there is a need for ML models that are prior- and data-efficient¹, that are human-like², and that exhibit human-interpretable behaviors³.

Regarding data-efficiency or learning from very few data in particular, few-shot learning (FSL)^4,5,6 via transfer learning^7,8,9 has succeeded in some data-scarce scenarios, but requires “relevance” between the transferring source and target¹⁰. However, knowing such relevance in advance and understanding what is transferred are often black arts. This is especially the case in new, understudied domains, with a risk of unwanted negative transfers^7,11. There has also been a shift from “big transfer”¹² to “small transfer”¹³, introducing a need for reduced pretraining. We push this reduction to the limit—no pretraining at all. As such, we introduce the term only-few-shot, to differentiate it from standard few-shot learning that uses pretraining.

These engineering challenges are intertwined with a scientific puzzle: how do humans learn so much from so little¹⁴? Given one instance, humans abstract from it, e.g., conceive of further equivalent instances, and from a nativist perspective, many of humans’ abstraction abilities are innate¹⁵. Nativism holds that certain human cognitive abilities are innate rather than learned from a blank slate. Babies can tell things apart based on general appearance—how things look in general—knowing they may be translated, rotated, scaled, or deformed. Sloutsky et al.¹⁶ further showed humans’ early induction is mainly based on appearance similarity rather than kind information. Babies can easily see similarity between a written digit “1” and a crutch before knowing what they are. This view of categorization after appearance similarity yields our focus on learning such a similarity, after which simple ML models such as k-NN or k-means can be used to maintain interpretability—people can understand both how a prediction is made, e.g., via “nearest neighbors”, and in what sense they are “neighbors”.

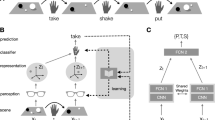
We present a theoretically sound, white-box model that mimics how humans learn and generalize from only a few examples. By “white-box” we mean that not only the model output but also the full modeling process is interpretable, i.e., the model is transparent. More specifically, we devise a distortable canvas to computationally realize the nativist intuition about humans’ innate perception. The idea is to view every image being smoothly painted on an elastic (e.g., rubber) canvas that can be distorted in many ways (Fig. 1a). Due to elasticity/viscosity, larger distortions expend more energy, so intuitively, two images have a similar appearance if one can transform into the other with little energy. This yields our mathematical formulation of general-appearance similarity based on minimal canvas distortion (${{\mathcal{D}}}_{V}$) and color distortion (${{\mathcal{D}}}_{C}$).

Fig. 1: Demonstration of a distortable canvas.

a transformations, b flows, and c distortions.

We address three main technical challenges in learning this similarity. First, we parameterize and efficiently handle all transformations (including those without a formula) instead of handpicking special ones by domain knowledge (like scale, translation, and rotation invariances commonly used in classical computer vision). Second, we introduce an abstracted multi-level gradient descent (AMGD) method to mimic humans’ hierarchical abstraction ability and lift the curse of local minima during optimization. Third, we make gradient descent, and hence the full optimization process, interpretable by eliciting the full transformation flow (Fig. 1b) instead of just the final transformation (Fig. 1c). These flows produce insights that either match our intuition (“Yes, that is what I would naturally do to transform 7 into 1.”) or unveil new perspectives (“I did not realize this other way of transforming 7 into 1. Now I see it and it makes sense to me.”). It is this interpretability at the level of the learning process that makes the learning model transparent, or white-box.

Our distortable canvas advances upon other transformation-based models using morphing^17,18, elastic matching¹⁹, optimal transport²⁰, group theory^21,22,23, invariances²⁴, or equivariances²⁵. The main difference is that we do not handpick or restrict the type of transformation, but instead, learn the transformation in the same pass as we learn similarity. Our AMGD shares similar ideas with annealed gradient descent²⁶ but with multi-level abstractions applied directly to the GD parameter space rather than the data set. Compared to data augmentation²⁷, we introduce transformations into the model rather than the data, which can be viewed as infinite data augmentation with perfect learning.

We achieved success on abstract visual tasks such as character and doodle recognition. On image classification benchmarks including MNIST²⁸, EMNIST²⁹, as well as the more challenging Omniglot² and QuickDraw³⁰ datasets, simply running the nearest-neighbor method on our learned similarity space outperformed both contemporary neural networks and classical ML in the tiny-data or single-datum regime. To name a few highlights: with no pretraining, our model reached 80% MNIST accuracy using only the first training image per class (reached 90% using only the first four) and achieved near-human performance on Omniglot and QuickDraw one-shot learning tasks. In unsupervised learning, simply integrating k-means into our model captured human-level visual abstractions, which generated human-intuitive archetypes as cluster centroids (e.g., different ways of writing “7” or doodling a giraffe).

The idea of running a nearest-neighbor classifier in our learned similarity space parallels exemplar-based classification in the feature space learned from large vision models (e.g., deep nearest centroids), promoting simplicity, transparency, explainability, as well as insight into the latent data structure³¹. The key difference is that our work centers on metric learning (rather than classification) and targets the tiny-data regime. It is again worth noting that our results are achieved in the only-one-shot (or only-few-shot) setting with absolutely no extra data (labeled or unlabeled) for pretraining and no data augmentation. For instance, one might mistakenly think that the one-shot MNIST result of 90.9% reported by Mocanu and Mocanu³² rivals what we achieve, but it is a best-of-five-type performance metric rather than standard test accuracy. The closest setting to only-one-shot can be found in their paper’s Fig. 1—particularly the left end of the curve corresponding to using zero unlabeled data—which shows about 45% (without data augmentation) and 60% (with data augmentation) standard test accuracy, both far below our only-one-shot result (80%).

Results

Using ${{\mathcal{D}}}_{C}$- or ${{\mathcal{D}}}_{V}$-distance in the nearest-neighbor method yields our ${{\mathcal{D}}}_{C}$- or ${{\mathcal{D}}}_{V}$-nearest-neighbor classifier. The transparency of the distortable canvas and the simplicity of nearest-neighbors makes the whole metric-learning and classification process human intuitive and interpretable. We demonstrate classification performances on hand-drawn characters/doodles from four benchmarks. These include the MNIST (digits) and EMNIST (letters) datasets restricted to the tiny-data regime, as well as the Omniglot (scripts) and the QuickDraw (doodles) one-shot learning challenges.

MNIST only-few-shot classification

The original benchmark has 60k images for training and 10k for testing, spanning 10 classes. To evaluate how a model performs in the tiny data regime, we train the model on the first N images per class from the original training set, test it on the full test set, and record test accuracy for N = 1, 2, 3, …. We compare our model to both contemporary neural networks and classical ML models, including TextCaps³³ that has state-of-the-art performance in the small-data regime, SVM, nearest-neighbor, etc. Classical ML is included to show that success in the tiny-data regime does not mean using simple models. For stochastic models, we record mean and standard deviation from 5 independent runs. TextCaps only runs when N≥4 and sometimes returns a random guess (10%), so we record trimmed mean and standard deviation from 11 runs (where we trim the best two and worst four). We also report results from the literature that ran MNIST in a similar tiny-data setting, including FSL that uses extra data for pretraining (whereas all our other comparison models do not). These results are from the same training-testing sizes but not the same data sets, and hence are considered indirect comparisons. We present all results in Fig. 2a.

Fig. 2: MNIST and EMNIST only-few-shot classification.

a shows sample images from MNIST, and b shows those from EMNIST. The first 1–20 training images per class and the full test set are used. For each classifier, we plot test accuracy versus training size N, as well as the smallest N needed to reach an accuracy threshold (90% for MNIST and 75% for EMNIST due to increased difficulty). Our model outperforms all other comparison models for all N, requiring the least amount of training data to achieve strong performance.

EMNIST-letters only-few-shot classification

The original benchmark has 4.8k training images per class and 0.8k test images per class, spanning 26 classes of case-insensitive English letters. We keep the same experimental setting as in MNIST (except for TextCaps being more stable now: we do 7 independent runs for each N and trim the best and the worst). Results are shown in Fig. 2b. EMNIST-letters is harder, not only with more classes but also more intrinsic ambiguities (e.g., l and I, likewise h and n, can be written very similarly; while r and R look different despite their semantic similarity). So, all models perform significantly worse than in MNIST. The intrinsic ambiguity, as well as more labeling errors, narrows our superiority over other models as training size increases. This is especially true for the state-of-the-art TextCaps model, catching up quickly in Fig. 2b.

Being sensitive to ambiguities and outliers, however, is not a result from our distortable canvas model. It is due to the nearest-neighbor inference. To improve, we might consider integrating our model with more robust classifiers, e.g., k-nearest-neighbor (k-NN) with proper voting. However, k-NN is not very effective in the tiny-data regime, not only because the training size can be as small as k but also there is little room to hold out a validation set for selecting k. An adaptive k-NN may be desired, with k remaining 1 in the tiny-data regime and becoming tunable when training size increases to a level that affords a held-out validation set. A related issue due to lacking validation data is in picking a proper model configuration. One may expect better results from any comparison model in Fig. 2 by trying new configurations which however can be a black art. For TextCaps, we used its original implementation and configuration; for the rest, we used scikit-learn implementations with default configurations (except for tweaks like neural-network size and regularization for the tiny-data setting). By contrast, our distortable canvas has little to tune, other than the $(\hat{G},{\rho }_{c})$-solution path in AMGD. In general, the more gradual the path is, the better. We picked $(\hat{G},{\rho }_{c})$ based on runtime and image size (28 × 28 here) only.

Omniglot one-shot classification

The Omniglot dataset contains handwritten characters from 50 different alphabets, which include historical, present, and artificial scripts (e.g., Hebrew, Korean, “Futurama”) and are far more complex than MNIST digits and EMNIST letters. The characters are stored as both images and stroke movements. Unlike MNIST/EMNIST that come with large training data, Omniglot was designed for human-level concept learning from small data. Its one-shot classification task was benchmarked to evaluate how humans and machines can learn from a single example. This benchmark contains 20 independent runs of 20-way within-alphabet classifications. The (2k − 1)th and (2k)th runs for k = 1, …, 10 use the same set of 20 characters from a single alphabet. Each run uses 40 images: one training and one test image per character. The unit task here is for each test image, to predict the character class it belongs to (one of 20), based on the 20 training images. In total, there are 400 independent unit tasks across all 20 runs. Figure 3a shows a unit task (in red) and the first two runs, covering 1 alphabet, 20 characters, and 80 distinct images.

Fig. 3: Omniglot one-shot classification.

a shows the first two runs out of 20 total runs: the red outline marks one of 400 unit tasks, each consisting of 1 test and 20 training images. b displays the error-rate leaderboard: unlike all other comparison models, ours requires no background set for pretraining and achieves near-human performance.

The Omniglot benchmark adopts the standard FSL setting, where a background set is also provided for pretraining. The original background set contained 964 character classes from 30 alphabets; later, a reduced background set was proposed to make the classification task more challenging. We dispense with any background set and any stroke information when running our ${{\mathcal{D}}}_{C}$-nearest-neighbor. In each unit task, we predict the test image based on one and only that training image per character, and we read all images from raw pixels. Shown in Fig. 3b, our model (with a 6.75% error rate) approaches human performance (4.5%), and despite not using the background set or stroke information, outperforms all models in the Omniglot leaderboard¹³ but BPL—specifically designed for Omniglot by making additional use of both the background set and the stroke information.

QuickDraw only-one-shot classification

Beyond handwritten characters, we experiment with recognizing human doodles in the only-one-shot setting. Unlike writing systems designed for people to follow certain ways of writing, there is no “correct” way of doodling a particular object or concept in mind—everyone has their own picture of Hamlet and hurricanes. Further, unlike photos, doodles are often unfaithful visual reproductions of an object’s outlook: many doodles only capture core features abstractly. These attributes make doodle recognition a fundamentally much harder task, even for humans. In this experiment, we use Google’s QuickDraw dataset containing 345 categories of human doodles. QuickDraw data are visually much more abstract and difficult than other datasets of human sketches such as Sketchy^34,35.

Mimicking the Omniglot setup, we randomly divide all categories into 23 runs (15 categories per run). In each run, we randomly sample two doodle images from each category—one for training and one for testing—forming a training and a test set, each containing precisely one image per category. The unit task here is for each test image, to predict the doodle category it belongs to (one of 15), based on just the 15 training images. Every unit task is an independent one-shot 15-way classification problem, meaning the fact that every test image is from a distinct category is not leveraged. In total, there are 345 unit tasks across all runs. Figure 4a illustrates the training and test images in one run and a unit task (in red). All models in this experiment read images directly from raw pixels, without using stroke-movement information. Unlike Omniglot that adopts the standard FSL setting, all models here have no access to any pretraining set and hence reside in the only-one-shot setting.

Fig. 4: QuickDraw only-one-shot doodle classification.

a shows one sample run that illustrates the training images, test images, and a unit task marked in red. b shows test accuracies from various models, including ours and human performance. Accuracy is reported as a percentage, with error bars indicating the mean and the standard deviation across five independent runs. Error bars are omitted for deterministic models. c displays inter-rater agreement, measured by Fleiss’ kappa, between our model and human performances. It shows that our model not only achieves near-human accuracy but also makes similar mistakes. Human results are from five healthy subjects, H₁–H₅, aged 20 to 29.

Shown in Fig. 4b, our model (with a 34.2% accuracy) approaches human performance (39.7 ± 4.6%) and significantly outperforms all other models. Due to the only-one-shot setting, there is no extra room for a validation split normally used for configuration/hyperparameter tuning. All comparison models in Fig. 4b use their standard implementation in sklearn or keras, e.g., the convolution neural network (CNN) and the vision transformer (ViT) are from keras’ code examples with proven test performance in the standard MNIST and CIFAR-100 benchmark. Our model is the same ${{\mathcal{D}}}_{C}$-nearest-neighbor used in the previous MNIST/EMNIST experiments. In Fig. 4c, we see fair agreement (quantified by Fleiss’ kappa in 0.21–0.4) among humans as well as a similar level of agreement between our model and each human. This indicates that our model performs not just at an accuracy level near humans, but also has fair agreement with humans on the mistakes it makes.

Notably, unlike computational models, human participants in this experiment are not really in the only-one-shot setting. Unlike babies faced with the doodles for the first time, participants might have unconsciously (or inevitably) used extra knowledge even though they were instructed to try not to. For example, when a subject looked at the last test image in Fig. 4a, (s)he might have first inferred that “this is a crab or spider” and then attempted to find a “crab or spider” among the training images. Knowledge of concepts like that of “a spider” puts experienced humans at an advantage in this experiment.

Beyond classification, our distortable canvas enables k-means-style clustering in a general-appearance similarity space that is non-Euclidean and human-intuitive. As in k-means, we try different values of k, and for each k, we try multiple random starts and record the best within-cluster sum of distances (WCSD). We use the elbow method to pick good k-values. Figure 5a shows the WCSD-versus-k curve obtained by running our clustering method on a set of 16 images of “7”s from MNIST. The curve indicates k = 2 or 3 as a potential elbow point. The resulting two clusters of “7”s agree with human intuition regarding two general ways of writing “7”, depending on whether there is an extra stroke. The resulting three clusters further divide the cluster of “simpler 7s” based on the angle of the transverse stroke. Figure 5b shows four clusters of giraffe doodles and their centroids learned from the first 16 giraffes in Google’s QuickDraw. We see a clear separation of outline sketches, focused views of the neck, and two different pose orientations.

Fig. 5: Archetype generation through k-means-style clustering in our learned general-appearance similarity space.

a shows archetypes of “7”s, corresponding to common human writing styles. b shows archetypes of giraffe doodles, reflecting major drawing styles in the dataset. c shows comparisons to Euclidean k-means and DBSCAN, which fail to generate reasonable archetypes.

Compared to Euclidean k-means and DBSCAN (Fig. 5c), our model yields clusters that are more intuitive to humans. More importantly, standard clustering algorithms are not well-suited for archetype generation, e.g., DBSCAN lacks a built-in notion of centroids, while k-means computes centroids by averaging raw images—essentially just overlaying images within a cluster. In contrast, both examples in Fig. 5 show that the cluster centroids learned from our model can be effectively viewed as archetypes of the input images (e.g., different ways of writing “7” or doodling a giraffe). These human-intuitive archetype generations demonstrate our model’s ability in effective visual abstractions (a strong contender in Pictionary) and further imply their value in education.

Discussion

This paper designs a white-box model to learn from few and only those few examples—in particular one and only one example—requiring no extra data for pretraining. Based on nativism, our distortable canvas effectively models human intuition about general appearance and learns transformation-based similarity akin to how humans naturally “distort” objects for comparison. This notion of similarity is formalized in our proposed optimization problem, which minimizes canvas and color distortions to transform one object into another with minimal distortion. To remedy vanishing gradients and solve the optimization efficiently, we mimic human abstraction ability by chaining anchor lattices and image blurs into a solution path. This yields our AMGD method capable of optimizing at multiple levels of abstraction. Our model outputs not only transformations but also transformation flows that mimic efficient human thought processes. We demonstrate success in benchmarks focused on abstract visual tasks such as character and doodle recognition. By simply using 1-NN, we achieve state-of-the-art results in the only-few-shot regime on MNIST/EMNIST and achieve near-human performance in Omniglot and QuickDraw only-one-shot learning. Our model also enables k-means-style clustering to capture human-level visual abstractions in human-intuitive archetype generations.

This paper represents a first step towards a general framework aimed at both learning and performing like humans across diverse applications. Although our distortable canvas can mathematically represent arbitrary images, its current learning efficacy remains limited in several key respects. We discuss two major limitations—(1) restriction to abstract images and (2) bias toward nearest neighbors—each of which is elaborated on in the paragraphs below, along with potential directions for generalization.

Regarding the first limitation, consider two general types of images: abstract images (like those of symbols and doodles) and real-world images (like those in CIFAR10/100³⁶). This paper focuses on the former type. To handle real-world images in the future, it may be more efficient to first model cognitive simplification and then apply our current distortion model. Humans have remarkable visual abstraction ability to classify real-world images by first converting them into abstract icons or e (picture)+moji (character)s (e.g., the emoji of a face, the outline of a mountain, the shape of a lake) and then comparing these simplifications³⁷. Notably, the structure of objects found in natural scenes often match that of letters and symbols throughout human history³⁸. Following this, an efficient way to apply our method to real-world images is to follow this pipeline—preprocessing them first into “emojis” and then comparing “emojis” with distortion. Stylized or abstract images, such as giraffe doodles and hieroglyphics, are those that can be treated as “emojis” already. There are baselines to attempt first, e.g., smart edge detectors³⁹, but the human visual system does more than edge detection. In future work, we aim for a complete theory of icon or “emoji” creation mimicking human capacity in order to deal with real-world images, 3D objects, and more.

Regarding the second limitation, the nearest-neighbor method is known to be biased towards its chosen neighbors and hence sensitive to noise, errors, outliers, and ambiguities in the training data. Accordingly, although our model demonstrates dominant classification performance in the tiny-data regime of the presented benchmarks, its dominance diminishes when training size increases. This suggests thinking beyond k-NN. One future direction is to jointly design our distortable canvas model with a new, human-like classifier that introduces human-style learning into the classification process. The goal is to achieve state-of-the-art results across all training sizes, which is not merely about swapping existing classifiers in and out.

Exploring multimodal problems such as visual question answering (including from recognizing text in images) is also an important future direction⁴⁰.

In order to create data- and energy-efficient ML prepared to face novel challenges that necessarily involve data-sparsity like growing children, artificial general intelligence (AGI) must replace experience with reason. Inspired by this goal, AGI cannot simply rely on black-box models, but must maintain interpretability by thinking in the human way, where we learn functions from small training sets to drive cognitive simulations of similarity. Figure 6 summarizes the pipeline for generalizing our current distortable canvas model to more general similarity simulations that reveal more insights about human-level visual abstractions. These insights can in turn advance our understanding about various aspects of human cognition and facilitate learning and communication⁴¹.

Fig. 6

Generalization to real-world images requires two key future directions (highlighted in the blue boxes): developing an “emoji” generation algorithm to preprocess real-world images into their abstract counterparts, and integrating classifiers beyond k-NN to improve robustness against noise.

Methods

We introduce a distortable canvas model, where any image can be thought of as smoothly painted on an elastic (rubber-like) canvas that can be flexibly bent, stretched, and deformed—just like how we naturally “distort” an image in our minds.

Formally, we define a smooth image by a piecewise differentiable ${\mathcal{M}}:{{\mathbb{R}}}^{2}\to {{\mathbb{R}}}_{+}$, where ${{\mathbb{R}}}^{2}$ denotes an infinite canvas and ${{\mathbb{R}}}_{+}$ denotes color (grayscale in this paper). We define a canvas transformation by $\alpha :{{\mathbb{R}}}^{2}\to {{\mathbb{R}}}^{2}$, which reshapes the underlying canvas of a smooth image. We also define a color transformation by $\chi :{{\mathbb{R}}}_{+}\to {{\mathbb{R}}}_{+}$, which repaints the color of a smooth image. We simplify color transformation and only use it to adjust image contrast via affine χ(c) := ac + b. In contrast, we do not restrict canvas transformation to any pre-specified types such as translation, rotation, or scaling, but instead allow all possible transformations. Given ${\mathcal{M}},\alpha ,\chi$, the composition $\chi \circ {\mathcal{M}}\circ \alpha$ denotes the transformed image of ${\mathcal{M}}$ by transformations α, χ.

To mimic human intuition about general-appearance similarity, we introduce canvas distortion ${{\mathcal{D}}}_{V}(\alpha )$ for any canvas transformation α and color distortion ${{\mathcal{D}}}_{C}({\mathcal{M}},{{\mathcal{M}}}^{{\prime} })$ between two smooth images ${\mathcal{M}},{{\mathcal{M}}}^{{\prime} }$. Our idea is to search for a transformation that mimics what humans naturally do to transform one image into another. That is, a low-distorted α which makes little difference in color between ${\mathcal{M}}$ and the transformed ${{\mathcal{M}}}^{{\prime} }$. More precisely, we want to minimize both ${{\mathcal{D}}}_{V}(\alpha )$ and ${{\mathcal{D}}}_{C}({\mathcal{M}},\,\chi \circ {{\mathcal{M}}}^{{\prime} }\circ \alpha )$. This yields two dual variants of our desired general-appearance distance:

• ${{\mathcal{D}}}_{C}$-distance: minimizes the color distortion ${{\mathcal{D}}}_{C}$ while controlling the canvas distortion ${{\mathcal{D}}}_{V}$

• ${{\mathcal{D}}}_{V}$-distance: minimizes the canvas distortion ${{\mathcal{D}}}_{V}$ while controlling the color distortion ${{\mathcal{D}}}_{C}$.

We detail the implementation of our distortable canvas model as a computational framework below.

Digital and smoothed images

An m × n digital image is a discrete ${\mathsf{M}}:[m]\times [n]\to [0,1]$, where [k] := {0, 1, …, k − 1} for any $k\in {\mathbb{Z}}$. We call [m] × [n] the canvas grid and any z ∈ [m] × [n] a grid point. For any m × n digital image ${\mathsf{M}}$, we smooth it to ${\mathcal{M}}$ via a sum of kernels:

$${\mathcal{M}}(x):=\sum _{z\in [m]\times [n]}{\mathsf{M}}(z)\cdot \kappa (\rho (z,x))\quad \,{\rm{for}}\, {\rm{any}}\,\,x\in {{\mathbb{R}}}^{2},$$

(1)

where a kernel $\kappa :{{\mathbb{R}}}_{+}\to {{\mathbb{R}}}_{+}$ is a decaying function (e.g., linear, polynomial, Gaussian decay) and ρ is a metric on ${{\mathbb{R}}}^{2}$ (e.g., ℓ₁, ℓ₂, ℓ_∞). In this paper, we use linear decay and ℓ_∞, i.e., $\kappa (\rho (z,x))=1-\frac{1}{{\rho }_{c}}\parallel z-x{\parallel }_{\infty }$ if ∥z − x∥_∞ < ρ_c (for some cutoff radius ρ_c > 0) and κ(ρ(z, x)) = 0 otherwise. Note: ${\mathcal{M}}$ is defined everywhere on ${{\mathbb{R}}}^{2}$. This differs from Gaussian blurring as we do not discretize kernels. It is key to use the smoothed image as input, which allows computing gradients analytically. As such, we always smooth any digital image first and then only manipulate the smoothed image.

Arbitrary canvas transformations

We consider all 2D transformations (including those without a formula), but how do we represent them in a computer? With respect to the standard grid [m] × [n], we use the transformed grid α([m] × [n]) to represent α digitally. Thus, any canvas transformation α is digitally represented by ($\mathop{=}\limits^{d}$) a matrix ${\boldsymbol{\alpha }}\in {{\mathbb{R}}}^{(mn)\times 2}$ whose ith row is the 2D coordinate of the transformed ith grid point. We use the lexicographical order of a 2D grid, e.g., with respect to [2] × [3], the identify transformation ${\rm{id}}\mathop{=}\limits^{d}{\bf{id}}=[[0,0],[0,1],[0,2],[1,0],[1,1],[1,2]]$. Any transformed image ${\mathcal{M}}\circ \alpha \mathop{=}\limits^{d}{\mathcal{M}}({\boldsymbol{\alpha }}):=(\,{\mathcal{M}}({{\boldsymbol{\alpha }}}_{0}),\,\ldots ,\,{\mathcal{M}}({{\boldsymbol{\alpha }}}_{(mn-1)}))\in {{\mathbb{R}}}^{(mn)}$, i.e., a (vectorized) digital image sampled from ${\mathcal{M}}$ at the transformed grid α.

Color and canvas distortions

The color distortion ${{\mathcal{D}}}_{C}$ measures the color discrepancy between ${\mathcal{M}}({\bf{id}})$ and ${{\mathcal{M}}}^{{\prime} }({\boldsymbol{\alpha }})$ up to an affine color transformation χ. The canvas distortion ${{\mathcal{D}}}_{V}$ measures the distortion between the original grid id and the transformed grid α. Formally,

$${{\mathcal{D}}}_{C}({\mathcal{M}},\,\chi \circ {{\mathcal{M}}}^{{\prime} }\circ \alpha )\mathop{=}\limits^{d}{{\mathcal{D}}}_{C}(\,{\mathcal{M}}({\bf{id}}),\,\chi ({{\mathcal{M}}}^{{\prime} }({\boldsymbol{\alpha }}))):=\parallel a{{\mathcal{M}}}^{{\prime} }({\boldsymbol{\alpha }})+b-{\mathcal{M}}({\bf{id}}){\parallel }_{2}^{2},$$

(2)

$$\begin{array}{ll}{{\mathcal{D}}}_{V}(\alpha )\mathop{=}\limits^{d}{{\mathcal{D}}}_{V}({\bf{id}},{\boldsymbol{\alpha }}):=\mathop{\max }\limits_{\{\{i,j\},\{{i}^{{\prime} },{j}^{{\prime} }\}\}\in {B}_{E}}\left\vert {\Delta }_{\{i,j\}}^{{\boldsymbol{\alpha }}}-{\Delta }_{\{{i}^{{\prime} },{j}^{{\prime} }\}}^{{\boldsymbol{\alpha }}}\right\vert ,\\\qquad\qquad\qquad\qquad\qquad{\rm where}\;\;{\Delta }_{\{i,j\}}^{{\boldsymbol{\alpha }}}:=\log \frac{\parallel {{\boldsymbol{\alpha }}}_{i}-{{\boldsymbol{\alpha }}}_{j}{\parallel }_{2}}{\parallel {{\bf{id}}}_{i}-{{\bf{id}}}_{j}{\parallel }_{2}}.\end{array}$$

(3)

Here, B_E comprises all pairs of neighboring edges in a canvas lattice (introduced below). Eq. (3) is derived from the mathematical definition of distortion of a function by discretizing it across the canvas lattice. This formula measures how far an arbitrary transformation is from being conformal, which is flexible for local isometries and scaling. Given a canvas grid [m] × [n], its corresponding canvas lattice is an undirected graph L = (V, E), with the set of vertices V = [m] × [n] and the set of edges obtained by connecting neighboring vertices in the ℓ_∞ sense: E = {{i, j}∣∥v_i − v_j∥_∞ = 1for v_i, v_j ∈ V}. We say two edges are neighbors if they form a 45^∘ angle (Fig. 7).

Fig. 7: Illustration of a canvas grid and its corresponding lattice.

Local distortions caused by a transformation α are computed at each pair of neighboring edges; one such pair is highlighted in red.

General-appearance distance via distortion minimization

To minimize color and canvas distortions (2) and (3), we consider two dual views: minimizing ${{\mathcal{D}}}_{C}$ among low-distorted αs or minimizing ${{\mathcal{D}}}_{V}$ among best-matching αs. We write the two views as the following two constrained optimization problems, together with their respective unconstrained equivalents: with ϵ → 0₊ and μ → 0₊,

$$\mathop{\min.}\limits_{\alpha ,\chi }\,\,{{\mathcal{D}}}_{C}({\mathcal{M}},\,\chi \circ {{\mathcal{M}}}^{{\prime} }\circ \alpha )\quad \,{\text{s}}.{\text{t.}}\,\,{{\mathcal{D}}}_{V}(\alpha )\le \epsilon \ \iff \ \mathop{\min.}\limits_{\alpha ,\chi }\,\,{{\mathcal{D}}}_{V}(\alpha )+\mu {{\mathcal{D}}}_{C}({\mathcal{M}},\,\chi \circ {{\mathcal{M}}}^{{\prime} }\circ \alpha ),$$

(4)

$$\mathop{\min.}\limits_{\alpha ,\chi }\,\,{{\mathcal{D}}}_{V}(\alpha )\quad \,\text{s.t.}\,\,{{\mathcal{D}}}_{C}({\mathcal{M}},\,\chi \circ {{\mathcal{M}}}^{{\prime} }\circ \alpha )\le \epsilon \ \iff \ \mathop{\min.}\limits_{\alpha ,\chi }\,\,{{\mathcal{D}}}_{C}({\mathcal{M}},\,\chi \circ {{\mathcal{M}}}^{{\prime} }\circ \alpha )+\mu {{\mathcal{D}}}_{V}(\alpha ).$$

(5)

We let the optima ${{\mathcal{D}}}_{C}^{\star }$ for (4) and ${{\mathcal{D}}}_{V}^{\star }$ for (5) denote two versions of our general-appearance distance that mimics human innate intuition. We call them ${{\mathcal{D}}}_{C}$-distance and ${{\mathcal{D}}}_{V}$-distance, respectively.

Transformation flow

Besides the final optimal solution, we apply the minimal-distortion principle throughout the entire optimization process⁴², i.e., we aim to keep canvas/color distortions small at every optimization step. Gradient descent (or projected gradient descent for constrained minimization) naturally fits this goal, since it always follows the steepest descent direction. The iterative gradient steps not only give us an optimal transformation α^⋆ as an end result but also a transformation flow id = α⁽⁰⁾ → α⁽¹⁾ → ⋯ → α^⋆. The resulting sequence of transformed images ${{\mathcal{M}}}^{{\prime} }={{\mathcal{M}}}^{{\prime} }\circ {\alpha }^{(0)}\to {{\mathcal{M}}}^{{\prime} }\circ {\alpha }^{(1)}\to \cdots \to {{\mathcal{M}}}^{{\prime} }\circ {\alpha }^{\star }\approx {\mathcal{M}}$ (we omit χ for simplicity) makes up an animation (Fig. 1), which simulates human intuition on smoothly transforming ${{\mathcal{M}}}^{{\prime} }$ to ${\mathcal{M}}$. For example, our mind does not treat translations as sudden jumps from one location to another, but instead tends to auto-complete a translation path that is continuous and desirably short.

In summary, our model outputs the optimal transformation α^⋆, its associated distance ${{\mathcal{D}}}_{C}^{\star }$ or ${{\mathcal{D}}}_{V}^{\star }$, and the corresponding transformation flow α⁽⁰⁾ → ⋯ → α^⋆ leading to the optimal solution. This achieves our goal of making both the transformation and the transformation process human-like and interpretable, thus rendering the entire model white-box.

However, ordinary (projected) gradient descent on (4) or (5) has a problem: the curse of local minima. Our solution is to lift gradient descent to multiple levels of abstraction via multiscale canvas lattices and color blurring, mimicking human abstraction capabilities that are extremely flexible in multiscale optimization. We name this technique the abstracted multi-level gradient descent (AMGD), controlled by an anchor-grid system $\hat{G}$ and a blurring parameter ρ_c. AMGD outputs a $(\hat{G},{\rho }_{c})$-solution path that forms the backbone of a desired transformation flow. We detail AMGD in the sequal.

The canvas distortion ${{\mathcal{D}}}_{V}$ is invariant under a variety of transformations (e.g., ${{\mathcal{D}}}_{V}(\alpha )=0$ for any conformal α), which nicely mimics humans’ flexible transformation options. But this also implies numerous local/global minima and other critical points where the gradient is 0. How much the color distortion ${{\mathcal{D}}}_{C}$ fluctuates as a function of α depends on the images ${\mathcal{M}},{{\mathcal{M}}}^{{\prime} }$. But in most cases, ${{\mathcal{D}}}_{C}$ also has many local/global minima, the majority of which represent unwanted “short cuts”—unnatural transformations that make ${{\mathcal{D}}}_{C}\to 0$ but would break the rubber canvas or create holes in it. The curse of vanishing gradients can freeze gradient descent. To unfreeze it, we lift gradient descent to higher levels, once again mimicking humans’ abstraction power, as our internal optimization system is quite flexible in pursuing “gradient-descent” moves at multiple levels of abstraction. We design two abstraction techniques: a chain of anchor lattices to make hierarchical abstractions of canvas transformations and a chain of color blurring to make hierarchical abstractions of image painting.

Anchor grids and lattices

An anchor grid and its corresponding anchor lattice offer a simpler parameterization (i.e., an abstraction) of canvas transformations. Without such an abstraction, any transformed [m] × [n] grid ${\boldsymbol{\alpha }}\in {{\mathbb{R}}}^{(mn)\times 2}$ consists of 2mn free parameters. So, the optimization problems (4) and (5) are 2mn + 2 dimensional, which is not only computationally inefficient for large images but also has too much room for vanishing gradient. We use a simpler α-parameterization that regularizes transformation, lowers distortion, and agrees with our intuition on rubber transformations.

Formally, an anchor system $(G,\hat{G})=(M\times N,\hat{M}\times \hat{N})$ uses two layers of grids: an underlying grid G and an anchor grid $\hat{G}$ atop, satisfying $\hat{M}\subseteq M,\hat{N}\subseteq N$, and $G\subseteq {\rm{ConvexHull}}(\hat{G})$. Figure 8a shows one example, where G = [5] × [6] = {0, …, 4} × {0, …, 5} and $\hat{G}=\{0,2,4\}\times \{0,2,5\}$. Under an anchor system, we can uniquely represent any grid point g ∈ G via four anchors ${A}_{g},{B}_{g},{C}_{g},{D}_{g}\in \hat{G}$ via proportional interpolation, or more precisely, the following double convex combination

$$g=(1-{\lambda }_{g})(1-{\nu }_{g}){A}_{g}+(1-{\lambda }_{g}){\nu }_{g}{B}_{g}+{\lambda }_{g}(1-{\nu }_{g}){C}_{g}+{\lambda }_{g}{\nu }_{g}{D}_{g}.$$

(6)

Here, A_gB_gD_gC_g can be uniquely selected as the smallest rectangle in $\hat{G}$’s lattice containing g; the two weight parameters λ_g, ν_g are computed based on relative position, e.g., as in Fig. 8a. The relation between grid points and anchors can be summarized by a weight matrix $W\in {{\mathbb{R}}}^{| G| \times | \hat{G}| }$. Its ith row stores weights for the ith grid point (say g in (6)) and contains at most four non-zero entries (i.e., coefficients in (6)) located at the columns corresponding to A_g, B_g, C_g, D_g, respectively.

Fig. 8: Core AMGD components.

a anchor system, b its transformation, and c a configuration of $(\hat{G},{\rho }_{c})$-solution path consisting of a chain of anchor grids/lattices and a chain of blurring.

Given an anchor system $(G,\hat{G})$, any canvas transformation $\alpha \mathop{=}\limits^{d}{\boldsymbol{\alpha }}\in {{\mathbb{R}}}^{| G| \times 2}$ under G and $\mathop{=}\limits^{d}\hat{{\boldsymbol{\alpha }}}\in {{\mathbb{R}}}^{| \hat{G}| \times 2}$ under $\hat{G}$. $\hat{{\boldsymbol{\alpha }}}$ is a submatrix of α, which induces an equivalence relation on the set of all canvas transformations: α, β are equivalent iff $\hat{{\boldsymbol{\alpha }}}=\hat{{\boldsymbol{\beta }}}$, and $\hat{{\boldsymbol{\alpha }}}$ abstracts the equivalence class $\{{\boldsymbol{\beta }}| \hat{{\boldsymbol{\beta }}}=\hat{{\boldsymbol{\alpha }}}\}$. Based on the maximum entropy principle⁴³, a reasonable selection of a representative of this equivalence class is $W\hat{{\boldsymbol{\alpha }}}$, because $W\hat{{\boldsymbol{\alpha }}}\in \{{\boldsymbol{\beta }}| \hat{{\boldsymbol{\beta }}}=\hat{{\boldsymbol{\alpha }}}\}$ and evenly distributes the transformed grid points. Figure 8b illustrates this type of even distribution, which agrees with human intuition on how a rubber surface would naturally react when transforming forces are applied at anchors.

Using an anchor system in optimization problems (4) and (5) adds very little to computing distortions and gradients: we reuse the computation with ${\boldsymbol{\alpha }}=W\hat{{\boldsymbol{\alpha }}}$ and perform only one additional chain-rule step $\partial {\boldsymbol{\alpha }}/\partial \hat{{\boldsymbol{\alpha }}}=W$. By doing so, however, the number of optimization variables in (4) or (5) reduces from ∣G∣ + 2 to $| \hat{G}| +2$ (e.g., if G = [28] × [28] and $\hat{G}=\{0,27\}\times \{0,27\}$, the number reduces from 1570 to 10). It is important to note that using a simpler anchor grid is not the same as downsampling. If it were, one would plug in $\alpha \leftarrow \hat{{\boldsymbol{\alpha }}}$, but we plug in $\alpha \leftarrow W\hat{{\boldsymbol{\alpha }}}$. In our case, image colors are still sampled from the underlying grid rather than downsampled from the anchor grid. So, using our anchor system is not information lossy while still benefiting from reduced optimization size. Running gradient descent (w.r.t. anchors) in abstracted optimization spaces effectively bypasses critical points.

Blurring

Another view to lifting gradient descent to a high-level, abstracted optimization space, is to blur the image. Intuitively, blurring ignores low-level fluctuation, similar to how humans naturally abstract an image. Blurring helps remedy vanishing gradients and is done in our image smoothing process. The cutoff radius ρ_c in κ in (1) controls the blurring extent: larger ρ_c means more blurred.

Algorithm 1

Traverse the anchor-lattice chain and the blurring chain in a solution path.

Abstracted multi-level gradient descent

Mixing the two abstraction techniques yields our AMGD technique proceeding from higher- to lower-level abstractions. Given an anchor grid $\hat{G}$ and a cutoff radius ρ_c, we denote the corresponding (4) and (5) by $DC(\hat{G},{\rho }_{c})$ and $DV(\hat{G},{\rho }_{c})$, respectively. For either, we solve for a $(\hat{G},{\rho }_{c})$-solution path, from coarser $\hat{G}$ and larger ρ_c to finer $\hat{G}$ and smaller ρ_c. Let ${\hat{G}}_{k}$ be a k × k evenly distributed anchor grid and ${\hat{L}}_{k}$ be its corresponding lattice. Figure 8c shows a chain of anchor lattices ${\mathcal{L}}={\{{\hat{L}}_{{3}^{i}+1}\}}_{i = 0,1,2,\ldots }$ and a chain of cutoff radii ${\mathcal{R}}={\{{\eta }^{j}{\rho }_{{c}_{0}}\}}_{j = 0,1,2,\ldots }$. The pseudocode in Algorithm 1 shows an example of traversing the two chains in a solution path. The procedure starts from the coarsest lattice and traverses the blurring chain first (from the most blurred to the least blurred image) and then, with the clearest image fixed, traverse the lattice chain (from coarsest to finest). It is easy initially to align two blurred blobs via small canvas adjustments, implying a small number of iterations to converge to ${{\mathcal{D}}}_{C}\approx {{\mathcal{D}}}_{V}\approx 0$. As we proceed along the solution path, the images restore more detail but the finer ${\hat{L}}_{k}$ helps manage that detail. In a solution path, an earlier solution is used to warm start the subsequent solve step, which further alleviates the curse of vanishing gradients. Notably, even the starting ${\hat{L}}_{2}$ comprising only four corner anchors parameterizes a large family of transformations containing all affine transformations. Finer anchor grids/lattices express more flexible transformations (including local, global, piecewise affine, and more), approaching human-level flexibility.

Interpretability makes our model configuration intuitive, avoiding the black art of hyperparameter tuning in many ML methods. Consider a 28 × 28 image as an example. Both the anchor lattice list and the cutoff radius list can be set as geometric sequences, with their granularity flexibly controlled by the sequence length. For the anchor lattices, we start from the smallest possible grid, i.e., 2 × 2, and gradually refine it to the full grid 28 × 28. The cutoff radii can be configured intuitively because they have a physical meaning, e.g., a radius of 4 defines the extent of blurring, where each pixel blurs into a 4-pixel radius neighborhood, forming a 9 × 9 blob, or superpixel. This represents considerable blurring for a 28 × 28 image, which is easy to visualize. The stopping criterion for gradient descent can be controlled by the color distortion threshold ϵ, which has a physical meaning too, e.g., a distortion of 1 can correspond to flipping a pixel from black (0) to white (1). Thus, setting ϵ = 5 represents a small color-distortion tolerance for a 28 × 28 grayscale image.

The number of parameters in our model scales linearly with the size of the input image, implying linear memory requirements. As a comparison, ViT scales linearly with number of tokens, which itself depends not only on image size but also patch size and architecture details such as embedding dimension and number of layers. Our runtime depends on the number of gradient-descent steps, which is small for visually similar images and large for dissimilar ones. For the two examples in Fig. 1c, transforming “1” to “7” to compute their distance took 65 gradient-descent steps and 235 ms on a MacBook Pro (M1 Max), whereas transforming “6” to “7” took 196 steps and 452 ms.

We next detail k-means-style clustering in our general-appearance similarity space. As in other non-Euclidean metric learning settings⁴⁴, it is unrealistic to run k-means on explicitly computed distances. Learning a distance in our model requires solving an optimization problem, which is much more expensive than computing Euclidean distances. Further, computing a centroid in a non-Euclidean space requires solving another optimization problem (minimizing the sum of within-cluster distances), which is much more expensive than an arithmetic mean. What is more challenging is that the two optimizations are nested, yielding an optimization problem of optimization problems.

To address these challenges, we generalize our idea of a transformation flow between two images into multi-flows among multiple images. Under this generalization, we do not explicitly compute pairwise distances, meaning we do not solve the inner optimizations first. Instead, we solve the inner and outer optimizations at the same time, where we flatten the nested optimizations into a single one.

More specifically, to group N smooth images ${{\mathcal{M}}}_{1},\ldots ,{{\mathcal{M}}}_{N}$ into K clusters, we solve the following optimization problem:

$$\mathop{{\rm{minimize}}}\limits_{\begin{array}{c}{\alpha }_{1},\ldots ,{\alpha }_{N}\\ {\overline{\alpha }}_{1},\ldots ,{\overline{\alpha }}_{K}\\ {C}_{1},\ldots ,{C}_{K}\end{array}}\,\,\mathop{\sum }\limits_{k=1}^{K}\sum _{i\in {C}_{k}}{{\mathcal{D}}}_{C}({\overline{{\mathcal{M}}}}_{k}\circ {\overline{\alpha }}_{k},\,{{\mathcal{M}}}_{i}\circ {\alpha }_{i})\quad \,{\rm{subject}}\, {\rm{to}}\,\,\mathop{\sum }\limits_{i=1}^{N}{{\mathcal{D}}}_{V}({\alpha }_{i})\le \epsilon ,$$

(7)

where C_k denotes the kth cluster, ${\overline{{\mathcal{M}}}}_{k}\circ {\overline{\alpha }}_{k}$ denotes the kth centroid, and ${{\mathcal{M}}}_{i}\circ {\alpha }_{i}$ denotes the ith transformed image flowing to its corresponding centroid together with all other N − 1 transformed images. One can check that (7) is an extension of (4) where we omitted χ for simplicity. Solving (7) is similar to k-means via alternating refinement:

• the assignment step assigns each transformed image ${{\mathcal{M}}}_{i}\circ {\alpha }_{i}$ to ${C}_{{k}^{\star }}$ according to

  $${k}^{\star }=\mathop{{\rm{arg}}\,{\rm{min}}}\limits_{k=1,\ldots ,K}{{\mathcal{D}}}_{C}({\overline{{\mathcal{M}}}}_{k}\circ {\overline{\alpha }}_{k},\,{{\mathcal{M}}}_{i}\circ {\alpha }_{i});$$

• the update step solves (7) for one gradient-descent step given the C_ks.

Upon convergence, we obtain ${C}_{1}^{\star },\ldots ,{C}_{K}^{\star }$ as clusters and ${\overline{{\mathcal{M}}}}_{1}\circ {\overline{\alpha }}_{1},\ldots ,{\overline{{\mathcal{M}}}}_{K}\circ {\overline{\alpha }}_{K}$ as centroids.