Introduction

Human body temperature is a critical health indicator, even a slight change in it can mean a vital change in organ functions1,2. The maintenance of a constant body temperature mainly relies on the automatic regulation of metabolic rates. However, prolonged exposure to high environmental temperatures and strenuous activities can overwhelm the body’s natural thermoregulation, notably impact both physiological and psychological aspects3. Individuals such as athletes, soldiers, and workers encounter significant health risks in high-temperature environments4. Furthermore, in tropical climates, it becomes a ubiquitous problem even without engaging severe activities5. Recently, there has been a growing interest in personal cooling garments. Compared with traditional centralized air conditioning system, personal cooling garments not only reduce the energy loss, but also can adapt to various outdoor working environments6,7,8,9. Current personal cooling garments are typically categorized into passive cooling garments and active cooling garments. Passive cooling garments employ the fabric as the emitter, allowing heat to be conducted from the human body to the fabric. Although this type of garment is lightweight and energy efficient. Its cooling capacity is mostly limited ( < 5 °C), and it can only be applied in open outdoor environments10,11,12. Active cooling refers to achieving cooling effects through the utilization of external power input. In comparison to passive cooling, it can deliver significantly enhanced cooling performance. However, current active cooling garments require auxiliary equipment such as fans, pumps, and compressors, resulting in a large volume and heavy weight13,14,15,16,17,18.

The thermoelectric cooler emerges as a promising candidate for the next generation of personal cooling garments. As a solid-state heat pump, it is light in weight and portable to carry, with readily adjustable cooling power to meet varying demand in different situations19,20,21,22,23,24,25,26. Recently, several wearable coolers with thermoelectric units have entered the commercial market, such as Wristify TE bracelet and Flowtherm TE vest. However, the continuous operation of most TECs relies on an external heat sink to dissipate heat from their hot side, compromising the lightweight and portable advantages of them. Additionally, the cooling effect is not satisfactory27,28,29,30,31. The limitation lies in the intrinsic dimensionless figure of merit of TE semiconductor, ZT, which is defined as:

$${ZT}=\frac{{S}^{2}}{\rho {\kappa }_{\text{s}}}T$$
(1)

where S, \(\rho\), \({\kappa }_{\text{s}}\), and \(T\) are the Seebeck coefficient, electrical resistivity, thermal conductivity, and temperature of TE semiconductor, respectively. It was introduced to simplify the equation of COP, which is defined as the ratio between cooling power and input electrical power32. Maximum COP and the corresponding optimal current can be simplified as:

$${{\rm{COP}}}_{\max }=\frac{{T}_{\text{c}}}{{T}_{\text{h}}-{T}_{\text{c}}}\times \left(\frac{\sqrt{1+Z{T}_{\text{m}}}-{T}_{\text{h}}/{T}_{\text{c}}}{\sqrt{1+Z{T}_{\text{m}}}+1}\right)$$
(2)
$${I}_{\text{opt}}=\frac{S\left({T}_{\text{h}}-{T}_{\text{c}}\right)}{R\left(\sqrt{1+Z{T}_{\text{m}}}-1\right)}$$
(3)

where \({T}_{\text{c}}\) and \({T}_{\text{h}}\) denote the temperature of the cold side and the hot side of TEC. \({T}_{\text{m}}\) is the average temperature which is defined as: \({T}_{\text{m}}=\left({T}_{\text{h}}+{T}_{\text{c}}\right)/2\). \(R\) is the electrical resistance. Since then, enhancing ZT has been the ultimate goal in most related studies to improve the performance of thermoelectric devices. The limited advancement in ZT poses a constraint on the cooling capabilities of thermoelectric devices32,33. As a result, even with the optimized structure design, the maximum cooling capability is constrained to approximately 10 °C without the assistance of an external heat sink34.

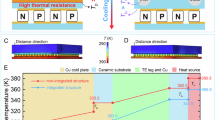
Research suggests that enhanced cooling performance is anticipated with an extended TE pillar35. However, the drawback lies in the considerable reduction of wearability and mechanical stability due to the excessive length34. Figure 1a shows the heat transfer and solid mechanics model in COMSOL with varying lengths of TE. The results indicate that a TEC with a longer length achieves a lower temperature at the cold side, attributed to the reduced thermal conductance impeding backflow from the hot side to the cold side. Considering structural integrity and user comfort metrics, the wearability can be measured by the indicator of bending capability of TEC devices. Therefore, the normalized bending stiffness is calculated based on the applied force and corresponding deformation, revealing a noticeable increase (Fig. 1b). The reason is that although the substrate used in wearable TECs is flexible, the overall bending capability of the device is constrained by the mechanical stiffness of the thermoelectric pillars and their interfaces with the electrodes.

Fig. 1: Thermal and mechanical analysis of TEC with varying pillar lengths.
figure 1

a Schematic of heat transfer and solid mechanics simulation. b Thermal conductance and normalized bending stiffness of TEC with various TE pillar heights. c Schematic of TEC with 3D structural TE pillars.

Full size image

In this work, we proposed a novel approach to enhance the cooling performance of TECs without compromising their wearability by introducing 3D structural TE pillars. Previous studies have shown that leg geometry plays a critical role in thermoelectric performance enhancement. Complex geometries—such as asymmetrical, semi-cylindrical, honeycomb, and hourglass shapes—have been successfully realized using advanced fabrication techniques like 3D printing, demonstrating improved temperature gradients and reduced interfacial resistance36,37,38,39. However, 3D configurations like zig-zag and helical structures, which offer extended effective lengths within a compact form factor, have not yet been investigated. Here, we introduce such designs and systematically evaluate their cooling performance and mechanical flexibility through numerical simulations, in comparison with conventional straight pillars of varying lengths. The helix structure, with effective length 17.66 and 23.53 mm, demonstrated a remarkable ~30 °C cooling effect by evacuating air inside the TECs, two times as efficient as the straight TEC with the same height. Effective thermal conductance analysis revealed that the superior performance is attributed to the lower thermal conductance of the TE pillar with a longer effective length and the mixed thermal circuit consisting of the pillar and air, resulting in a substantial enhancement with inner air removal. Additionally, the COP was significantly improved, leading to higher power efficiency. The proposed system can significantly improve the cooling capability of wearable TECs, expanding their potential applications in more demanding application scenarios such as hot weather, vigorous exercise (sports, fast walking etc.). Furthermore, our research points out the fact that the performance of thermoelectric devices can be further enhanced without improving the intrinsic ZT value. By altering the geometric structure, we can break through the limitations imposed by traditional theories, opening new pathways for optimizing thermoelectric efficiency.

Results

Heat flux at the cold side of a TEC unit is determined as:

$$Q=-{SI}{T}_{\text{c}}+\frac{1}{2}{I}^{2}\rho \frac{{L}_{\text{s}}}{{A}_{\text{s}}}+{\kappa }_{\text{s}}\frac{{A}_{\text{s}}}{{L}_{\text{s}}}({T}_{\text{h}}-{T}_{\text{c}})+{\kappa }_{\text{a}}\frac{{A}_{\text{a}}}{{L}_{\text{a}}}({T}_{\text{h}}-{T}_{\text{c}})+\varepsilon \sigma {A}_{\text{sub}}({{T}_{\text{h}}}^{4}-{{T}_{\text{c}}}^{4})$$
(4)

where I is the current applied. \({L}_{\text{s}}\), and \({L}_{\text{a}}\) represent the length of TE pillar and air. \({A}_{\text{s}}\), \({A}_{\text{a}}\), and \({A}_{{\rm{sub}}}\) represent the cross-sectional area of TE pillar, air, and substrate, respectively. \(\varepsilon\), and \(\sigma\) denote the emissivity of substrate and Stefan–Boltzmann constant. The first and second term of the equation depict the cooling and heating power resulting from Peltier effect and Joule heating, respectively. The remaining three terms signify the backflow from the hot side to the cold side through the TE pillar, air, and radiation, with the last two terms typically exerting less influence. Here, we do not consider the natural convection inside the TEC because in this enclosed space, conduction dominates as \({GrPr}\approx 390 < 1700\). Detailed thermodynamic calculation can be found in Methods.

It is perceived that both Joule heating and the backflow from the hot to cold surfaces hinder the cooling performance of TEC, emphasizing the preference for smaller electrical resistance (small \({L}_{\text{s}}\), large \({A}_{\text{s}}\)) and thermal conductance (large \({L}_{\text{s}}\), small \({A}_{\text{s}}\)). However, in most TEC operating scenarios, a heat sink (fin, fan, or cooling water) is employed on the hot side to prevent the expansion of temperature difference between the cold side and the hot side. Consequently, heat conduction through the pillar is insignificant. Therefore, commercial TECs typically feature a short length and a large cross-sectional area, which minimizes Joule heating, as shown in Fig. 2a. However, lightweight and portability are essential for wearable devices, it is rational to infer that slender TE pillar is preferred in the absence of heat sink. To validate this hypothesis, we conducted heat transfer simulation on one TEC unit with varying current inputs. As shown in Fig. 2b, a heat flux (Qin) of 87 W/m2 is applied to the cold side of TEC to mimic the metabolic rate from human skin, while the hot side is subjected to natural convection (h = 15 W/m2-K) and radiation (ε = 0.8). The cooling effect is evaluated by ΔT, which is define as the temperature difference at the cold side between the state without current input and the state with a certain applied current. The simulation results are shown in Fig. 2c, all the cooling effects follow a quadratic relationship, increasing initially with the rise in current and then decreasing, consistent to Eq. (3). The peak value increases with a longer pillar length, while the optimum current becomes smaller, attributed to stronger Joule heating. We chose the peak value of each curve with maximum cooling for further analysis. The gray curve in Fig. 2d shows that the growth rate of maximum cooling becomes progressively smaller with a longer pillar length, eventually reaching saturation at around 26 °C for lengths exceeding 20 mm.

Fig. 2: Structural and condition analysis of straight TECs.
figure 2

a Schematic of structural design principles and operating conditions for commercial TEC. b Schematic of structural design principles and various heat flux for wearable TEC. c The current input dependent cooling effect of straight TEC with varying pillar lengths. d The maximum cooling effect of straight TEC with varying pillar lengths under condition 1 (κgap = κair, ε = 0.8), condition 2 (κgap = 0, ε = 0.8), and condition 3 (κgap = κair, ε = 0). The inset is the thermal circuits of the three conditions.

Full size image

As demonstrated in Eq. (4), the backflow consists of three parts in parallel: Thermal conduction through the TE pillar, thermal conduction through air, and radiation between the two substrates. To explore their influence on the cooling performance, similar simulations were conducted with removing air conduction (condition 2: κgap = 0, ε = 0.8) and radiation (condition 3: κgap = κair, ε = 0) separately. As shown in Fig. 2d, Both conditions exhibit a similar trend to condition 1 (κgap = κair, ε = 0.8), initially increasing and then gradually saturating. Due to the reduction in backflow, their cooling effects are notably improved compared to condition 1 (κgap = κair, ε = 0.8). Condition 2 (κgap = 0, ε = 0.8) shows a relatively consistent enhancement, with the temperature difference increasing from approximately 3 °C to 5 °C as the length increases. In contrast, the improvement in condition 3 (κgap = κair, ε = 0) varies more significantly with length, starting from 0 °C and rising to about 8 °C. This can be attributed to the fact that the conductance of air changes linearly with length, while the heat flux from radiation is proportional to the difference in the fourth power of temperature. As the length increases, the total thermal conductance decreases, leading to a larger temperature difference between the hot and cold sides, thereby amplifying the impact of radiation. However, practical limitations arise as the wearability and mechanical stability of TEC deteriorate with longer pillar lengths, preventing the realization of superior performance with long length (Fig. 1a, b).

To address the tradeoff between wearability and cooling performance, as shown in Fig. 3a–e, we proposed 3D structural TE pillars with zigzag shape and helix shape, offering a longer effective length (8.49 mm for zigzag shape, 11.38 mm for helix 1, 17.66 mm for helix 2, 23.53 mm for helix 3) while maintaining the same height (6 mm) and the cross-sectional area (1 mm2) as the straight pillar. Here, the effective lengths of TE pillars with zigzag shape and helix shape are not actively selected values but calculated based on the same total height and the predefined shapes shown in Fig. 3a–e. For helix shapes shown in Fig. 3c–e, the cross section is round with a radius r = 0.564 mm determined from the fixed area of 1 mm2. In this way, the thermal conductance can be effectively decreased due to the longer path of heat flow inside the pillars. To evaluate the performance of these structures, we conducted simulations to explore both wearability and cooling effects. Figure 3f depicts the boundary conditions of the mechanical simulation. To replicate a realistic bending scenario of TEC, the bottom right edge was fixed, while the bottom left edge was constrained vertically but left free horizontally. An upward force was uniformly applied to the middle of the TEC. Figure 3g illustrates the displacement of the upper edge of the TEC in the vertical direction along the edge. As the height of the straight pillar increases from 6 mm to 10 mm and then to 20 mm, the convexity of the curves decreases, indicating a reduced bending capability with greater length. For the 3D structural pillars, the curves for the helix structures display a comparable convexity to the straight pillar with a 6 mm length, whereas the zigzag shape shows a convexity similar to the straight pillar with a 20 mm length. The displacement and stress distributions of the entire TEC structures are shown in Figs. S1 and S2. The stress distributions are consistent across all structures, with maximum stress accumulation occurring at the contact areas between the pillars and electrodes. These results demonstrate that 3D structural pillar designs can effectively maintain the wearability of straight TEC of equivalent height when properly designed. The simulation results of cooling effect in three conditions are presented in Fig. 3h–j. In all conditions, the optimal current decreases with increasing length, which is expected because the pillar’s electrical resistance rises with length, making Joule heating more significant. However, the cooling performance results are counterintuitive. Under condition 1 (κgap = κair, ε = 0.8), The cooling efficiency of the zigzag-shaped pillar is comparable to that of the straight pillar, while the helix-shaped pillar exhibits inferior cooling performance. Moreover, the cooling effectiveness of the helix-shaped pillar further deteriorates as the length increases. The trend under condition 3 (κgap = κair, ε = 0) closely resembles that under condition 1 (κgap = κair, ε = 0.8) with slight enhancement. In contrast, the cooling effect under condition 2 (κgap = 0, ε = 0.8) generally experiences significant enhancement, particularly for pillars with longer effective length, implying that a majority of heat is conducted through air.

Fig. 3: Structural designs and cooling performance of TECs with 3D TE pillars.
figure 3

a–e Schematic of TEC with different structures. The dash lines in the (a, b) represent path of heat flow inside the pillars. a Straight shape with length 6 mm. b Zigzag shape with effective length 8.49 mm. c Helix 1 shape with effective length 11.38 mm. d Helix 2 shape with effective length 17.66 mm. e Helix 3 shape with effective length 23.53 mm. f Schematic of mechanical simulation of TEC. g Displacement of TEC in the vertical direction along the up edge. h–j The cooling effect of the five structures with varying current input under (h) condition 1 (κgap = κair, ε = 0.8), i condition 2 (κgap = 0, ε = 0.8), j condition 3 (κgap = κair, ε = 0).

Full size image

Figure 4a extracts the maximum cooling achieved in each scenario with respect to the effective length of pillars. The solid points represent the data under natural convection. The improvement in the five shapes, with radiation removed, remains nearly constant, whereas the enhancement, with air removal, becomes more significant with longer effective length. The maximum cooling effect of helix 2 and helix 3 shape can reach as high as 30 °C with air removed. We also conducted simulations in a forced convection environment (h = 25 W/m2-K) to explore the cooling effect of our TECs in scenarios such as running and working outdoors, represented by hollow points in Fig. 4a. The trend is similar to that under natural convection, with a slight improvement in cooling effect (2–5 °C). This improvement is due to the reduced temperature rise at the hot side resulting from the larger convective heat transfer coefficient. The detailed cooling effect of the five structures with varying current input under forced convection is shown in Fig. S3.

Fig. 4: Cooling performance and thermal conductance analysis of TECs with 3D TE pillars.
figure 4

a The maximum cooling of TECs with varying effective lengths under three conditions. The solid points represent the data under natural convection, the hollow points represent the data under forced convection. b The effective thermal conductance of TE pillar, air, and radiation of the five structures.

Full size image

To elucidate the results, we calculated the effective thermal conductance of the three components (i.e., TE pillar, air, and radiation). It is worth mentioning that the heat flux from radiation is not linear to the temperature difference between the hot side and the cold side, instead, it is proportional to the fourth power difference of temperatures (Eq. 4). Here we use effective thermal conductance of radiation for a direct comparison with the conductance of pillar and air. In order to minimize errors to the greatest extent possible, we constructed the same geometry models as the simulation aforementioned under three conditions: only TE pillar; TE pillar and air; TE pillar and radiation. We applied a heat flux (\(Q\)) to ensure that the temperatures on both sides are precisely the same as those when the maximum cooling is obtained at the corresponding condition. The effective thermal conductance \({G}_{{\rm{p}}{\rm{illar}}}\), \({G}_{{\rm{p}}{\rm{illar}}}+{G}_{{\rm{g}}{\rm{ap}}}\), and \({G}_{{\rm{p}}{\rm{illar}}}+{G}_{{\rm{rad}}}\) can be obtained by the following equation:

$$G=Q/\left({T}_{\text{h}}-{T}_{\text{c}}\right)$$
(5)

The three types of effective conductance for these five structures are depicted in Fig. 4b. The thermal conductance of the pillar decreases from approximately 0.25 mW/K to about 0.08 mW/K as the effective length increases, due to the linear increase in thermal resistance. In contrast, the effective thermal conductance of radiation remains almost constant at around 0.05 mW/K. This small value of radiation conductance suggests that the temperature differences between the hot and cold ends are not significant in all cases. In contrast, the thermal conductance of air exhibits a noticeable increase with longer length. The reason is that, compared to the purely parallel thermal circuit in a straight pillar structure, the 3D structural pillars involve multi-dimensional heat conduction with both series and parallel pathways, thus the influence of air removal is different. As a result, the effective thermal conductance of air varies across different structures, and this variation becomes more pronounced with increasing complexity of the shapes of TE pillars. It is noteworthy that the proportion of air conductance experiences a significant rise with longer length. In the straight structure, it accounts for 34.9% of pillar conductance, while in helix 3 structure, the proportion reaches 375.7%. This analysis effectively explains the phenomenon that removing air has a larger enhancement in structures with longer effective length, while the contribution of radiation remains almost constant.

We also demonstrated the COP of 3D structural TE pillars, which was determined using:

$$\text{COP}=\frac{{Q}_{\text{in}}{A}_{{\rm{sub}}}}{W}=\frac{{Q}_{\text{in}}{A}_{{\rm{sub}}}}{{UI}}$$
(6)

where W, and I are the input electrical power and current, U is the voltage cross the TE pillar. The simulation results are shown in Fig. 5. We used the COP of straight pillar in condition 1 (κgap = κair, ε = 0.8) as a reference and compare with the COP of the five structures in condition 2 (κgap = 0, ε = 0.8) as air removal results in the best performance. Fig. S4 shows the detailed COP of the five structures in three conditions. Figure 5a illustrates the COP of TECs as a function of cooling temperature. The graph displays a characteristic concave shape to the right, indicating that each cooling temperature corresponds to two COP values. This arises from the parabolic relationship between cooling temperature and input current. In our analysis, we focus on the upper branch of this curve, corresponding to lower current values, as it yields higher COPs. The gray line represents the baseline condition (straight pillars under condition 1: κgap = κair, ε = 0.8). In contrast, the red lines depict the five structures under condition 2 (κgap = 0, ε = 0.8). It is shown from the comparison that all red lines show improved cooling performance relative to the gray baseline. This improvement aligns well with previous findings. Furthermore, when comparing COP values at the same cooling temperatures, it is clear that the COP increases with the effective length. In other words, higher effective lengths result in greater COPs for the same cooling temperature.

Fig. 5: COP performance of TECs with 3D TE pillars.
figure 5

a The COP of TECs with varying cooling performance. The emissivity is 0.8 in this simulation. b The COP of TECs with varying effective lengths. The solid points represent the COP at a cooling performance of 7 °C34, the hollow points represent the COP at a cooling performance of 14.7 °C. c Summary of COP and corresponding cooling effects from the literature34,40,41,42,43,44,45,46.

Full size image

To quantify the improvement in performance, we selected two specific temperatures: 7 °C and 14.7 °C. The 7 °C temperature corresponds to the cooling performance of similar TECs reported in the literature34, while 14.7 °C represents the maximum value of the gray curve, as shown by the dashed lines in Fig. 5a. We identified the intersection points of these dashed lines with the curves. Figure 5b presents the corresponding COP values as a function of effective length. The results clearly demonstrate that for both selected temperatures, the COP increases with effective length. Specifically, at 7 °C, the COP of helix 3 in condition 2 (κgap = 0, ε = 0.8) improves from approximately 3.2 to about 10.2 compared to straight pillars in condition 1 (κgap = κair, ε = 0.8). At 14.7 °C, the COP increases from around 0.2 to 1.7. Figure 5c summarizes the COP and cooling performance of TECs from the literature. Notably, the curve of helix 3 is positioned above and to the right of these points, indicating superior cooling performance and higher COP values. These results suggest that our 3D structured semiconductor pillar design not only achieves enhanced cooling performance, which is unattainable with conventional straight pillars, but also exhibits better energy efficiency and reduced power consumption. Such improvements underline the significant advantages of implementing 3D structural designs in semiconductor pillars for superior TEC efficiency and performance. We also performed COP simulation under forced convection, which is shown in Fig. S5.

We demonstrated the power generation capability from human skin using our 3D structural TE pillars. To accurately simulate real skin and reflect true power generation performance, we maintained the hot side temperature of the thermoelectric generators (TEGs) at a constant 35.2 °C in this simulation. As shown in Fig. 6a, natural convection and radiation were applied to the cold side of the TEG, similar to the TEC simulation. Due to the Seebeck effect, the temperature difference between the two ends of the TE pillar generates a voltage as:

$$U=S\left({T}_{\text{h}}-{T}_{\text{c}}\right)$$
(7)
Fig. 6: Power generation performance of TEGs with 3D TE pillars.
figure 6

a Schematic of wearable TEGs. b The output current and power density of TEGs with respect to generated voltage. c Open circuit voltage and maximum power density of TEGs with respect to effective length.

Full size image

By adjusting the external resistance, the output current, voltage, and power density change accordingly. Figure 6b depicts power generation performance for the straight pillar under condition 1 (κgap = κair, ε = 0.8) and five different pillar types under condition 2 (κgap = 0, ε = 0.8). Comprehensive simulation results for all structures and conditions are presented in Fig. S6. As shown in Fig. 6b, the output current is linear to output voltage, and according to the power output equation:

$$P={U}^{2}\frac{{R}_{\text{ext}}}{{{A}_{\text{sub}}\left(R+{R}_{\text{ext}}\right)}^{2}}$$
(8)

where \(P\), \(U\), and \({R}_{\text{ext}}\) are the output power, output voltage, and external resistance, respectively. The power and voltage exhibit a quadratic relationship, where the maximum power density occurs when the internal electrical resistance \(R\) is equal to the external resistance \({R}_{\text{ext}}\).

We extracted the open circuit voltage and maximum power density of each case. as shown in Fig. 6c, removing air improves both parameters to some extent. For straight TE pillars, the open circuit voltage increased from 1.19 mV to 1.30 mV, while the maximum power density rose from 25.0 to 30.6 μW/cm². Additionally, the open circuit voltage increases with the effective length, reaching 1.9 mV for helix 3. This is due to the higher thermal resistance associated with a longer effective length, which increases the temperature difference between the two sides. However, the maximum power density, which is the most critical metric for TEGs, decreases with increasing effective length, with helix 3 only achieving 20.8 μW/cm². This indicates that the design principles for TECs and TEGs are fundamentally different.

Discussion

In summary, we have developed a 3D structural TE pillar that exhibits excellent wearability and achieves high cooling performance of up to ~30 °C through the removal of inner air. Our observations indicate that the cooling performance of a straight TEC improves with increased length until saturates at around 20 mm, which is not practical due to the poor wearability. Notably, relying solely on 3D structural pillars does not effectively enhance the cooling effect. The removal of radiation consistently enhances cooling across different effective lengths, while the benefits of air removal become more pronounced with longer effective lengths. Thermal conductance analysis reveals that the effective thermal conductance of radiation remains relatively constant across different structures, whereas that of air increases with longer effective lengths. The proportion of air conductance to the overall conductance rises from ~22% for a straight pillar with a length of 6 mm to ~52% for the helix 3 structure with an effective length of 23.53 mm, which is due to the reduced thermal conductance of TE pillar with longer length and the mixed thermal circuit consisting of TE pillar and air. Our study unveils a novel design for TECs, showcasing promising cooling performance and power efficiency. The 3D structured TE pillars overcome the limitations of traditional theories based on straight TE pillars, where cooling performance is constrained by the intrinsic ZT value.

Although this work is based on numerical simulations, the proposed designs provide clear predictive insight into the thermal and mechanical benefits of 3D thermoelectric structures. With ongoing advancements in advanced manufacturing—such as 3D printing—the realization of these complex geometries may become feasible in the near future, opening the door to experimental verification and practical implementation. Additionally, future research should also focus on enhancing the environmental adaptability of wearable TECs by developing novel materials and designs that can withstand real-world challenges such as humidity fluctuations, sweat accumulation and mechanical strain.

Methods

Thermoelectric material properties used in simulation

In this study, the thermoelectric simulations were based on a widely used commercial thermoelectric material—bismuth telluride (Bi₂Te₃). The material properties used in our COMSOL simulations are listed in Table 1.

Table 1 Thermoelectric material properties
Full size table

Thermodynamic calculation in enclosed space

The thermodynamic properties of air at room temperature are listed in Table 2.

Table 2 Thermodynamic properties of air at room temperature
Full size table

Prandtl number \(\Pr\) is calculated as:

$$\Pr =\frac{\nu }{\alpha }=\frac{\mu {c}_{\text{p}}}{\kappa }\approx 0.7$$
(9)

where \(\nu\), \(\alpha\), \(\mu\), \({c}_{\text{p}}\), and \(\kappa\) are kinematic viscosity, thermal diffusivity, dynamic viscosity, specific heat at constant pressure, and thermal conductivity, respectively.

Grashof number \({Gr}\) is calculated as:

$${Gr}=\frac{g{\alpha }_{\nu }\left({T}_{\text{h}}-{T}_{\text{c}}\right){\delta }^{3}}{{\nu }^{2}}$$
(10)

where \(g\) is the gravitational acceleration, \({\alpha }_{\nu }\) is the thermal expansion coefficient, which for air is approximately \(1/{T}_{\text{m}}\), \({T}_{\text{m}}\approx 300\,\text{K}\). \(\delta\) represents the characteristic length, in this case, it is the distance between the two substrates, \(\delta =5\,\text{mm}\). \({Gr}\approx 550\).

In the case, \({GrPr}\approx 390 < 1700\), conduction dominates compared to convection.

Nusselt number \({Nu}\) is calculated as:

$${Nu}=\frac{{\kappa }_{\text{e}}}{\kappa }$$
(11)

where \(\kappa\), and \({\kappa }_{\text{e}}\) depict the thermal conductivity and effective thermal conductivity of air. In the cause \({GrPr} < 1700\), \({\kappa }_{\text{e}}\approx \kappa\), \({Nu}\approx 1\).

Galileo Number \({Ga}\) is calculated as:

$${Ga}=\frac{g{\delta }^{3}}{{\nu }^{2}}\approx 5440$$
(12)