Introduction

On September 14, 2015, the first gravitational-wave (GW) event was detected by the ground-based Laser Interferometer Gravitational-wave Observatory (LIGO)1. More recently, several pulsar timing arrays (PTAs) have reported intriguing evidence of the Hellings-Downs correlation from GW signals in the nanohertz band, including the North American Nanohertz Observatory for Gravitational waves (NANOGrav)2,3, the European PTA (EPTA) along with the Indian PTA (InPTA)4,5,6, the Parkes PTA (PPTA)7,8, and the Chinese PTA (CPTA)9. Additionally, numerous other GW observatories are currently under investigation. These include next-generation (XG) ground-based detectors such as the Einstein Telescope (ET)10,11 and the Cosmic Explorer (CE)12, as well as space-borne detectors such as LISA13, Taiji14, TianQin15,16, and DECIGO17.

Recently, the new Moon-based detectors, such as the lunar gravitational-wave antenna (LGWA)18,19, have gained increasing attention. When GWs pass by the Moon, it will vibrate, behaving like a giant antenna. The LGWA aims to deploy an array of inertial sensors in the Moon’s permanently shadowed regions to monitor its response. Given the exceptionally quiet and thermally stable environment of the permanently shadowed regions on the Moon, the LGWA is expected to observe GWs in the frequency range from 1 millihertz (mHz) to several hertz (Hz), with the optimal sensitivity in the decihertz band. It will bridge the gap between space-borne detectors with their optimal sensitivity at the mHz band, like LISA, Taiji, and TianQin, and ground-based detectors like CE and ET with their optimal sensitivity at the audio band. Meanwhile, a parallel design of a Moon-based detector was proposed by Li et al.20 to make use of the Chinese lunar exploration project, and it becomes a good supplement to other projects.

On the other hand, the intermediate-mass black holes (IMBHs) with masses between 102M⊙ and 105M⊙ are theoretically believed to play a crucial role in understanding the evolution of black holes and dynamics of stellar systems21. The existence of IMBHs is indicated by electromagnetic observations in globular clusters, ultraluminous X-ray sources, and dwarf galaxies22. With equipment of ground-based, space-borne, and Moon-based GW detectors, the binary systems of IMBHs can be observed through GW experiments. Due to the wide mass range of IMBHs, the inspiral, merger, and ringdown phases of their binary coalescence can be observed across the mHz to audio bands23. Recent studies have explored the detectability of IMBHs across different frequency bands: in the mHz range with LISA24,25,26,27, in the decihertz range with DECIGO28, and in the audio band with current27,29,30,31 and XG25,32,33 ground-based GW detectors. Given that the Moon-based GW detectors have the optimal sensitivity in the decihertz band, the IMBHs also become a potentially key science target of those projects18,19,20.

In this work, we focus on the detectability of IMBH binaries with quasi-circular orbits and aligned spins with the LGWA. Following the approach by Reali et al.33, we perform a parameter scan with straightforward priors to generate the masses and redshifts of IMBH binaries. We then calculate the distribution of signal-to-noise ratios (SNRs) with different masses and redshifts for IMBH binaries. Using the Fisher information matrix (FIM) method, we calculate the relative parameter inference errors for some key parameters, such as the primary mass and redshift. We also calculate the localization capability of LGWA on IMBH binaries.

This paper is arranged as follows. In the “Results” section, we present our findings on the detectability of IMBH binaries by LGWA. We conclude and discuss the results in the “Discussion” section. In the “Methods” section, we introduce the methodology and settings adopted in this work, including the parameter priors of IMBH binaries, the GW waveform template, the LGWA configuration, and a brief introduction of the FIM method. Throughout the paper, we adopt natural units G = c = 1.

Results

Horizon redshift

With the definition of SNR shown in Eq. (9), the characteristic strains for a GW event hc, and the characteristic noise hn can be defined as34,

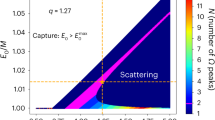
$$\begin{array}{rcl}{h}_{c}&=&2f| h| ,\\ {h}_{n}&=&\sqrt{f{S}_{n}}.\end{array}$$
(1)

In the left panel of Fig. 1, we plot the characteristic strains for five representative events of IMBH binaries and the characteristic sensitivities of the LGWA, ET, LISA, Taiji, and TianQin. These events are put at z = 0.5 with five different primary masses \({m}_{1}\in \left\{50,1000,5000,10000,50000\right\}\,{{\rm{M}}}_{\odot }\). Additionally, the mass ratio is fixed to q = 2, and the four free angle parameters are fixed to α = π/4, \(\cos \delta =1/2\), ψ = π/4, and \(\cos \iota =1\). As we can see, there exists a low-frequency cutoff for lighter binaries, which is determined by the assumed maximum observation time of 10 years. The sinusoidal fluctuation at the low-frequency band actually arises from the orbital motion of the Moon around our Earth, as well as the motion of the Earth–Moon system around the Sun. With the primary mass increasing, the amplitude of the GW signal increases, while the chirp frequency decreases. The chirp signals from IMBH binaries with a primary mass ≳ 5 × 104 M⊙ will fall into the sensitivity range (mHz) of space-borne detectors such as LISA, Taiji, and TianQin, while chirp signals from those with a primary mass ≲ 103 M⊙ will fall into the sensitivity range of the ET. Meanwhile, chirp signals from IMBH binaries with a primary mass between 103 M⊙ and 5 × 104 M⊙ will fall into the sensitivity range of the LGWA. For example, the SNRs of an IMBH binary with a primary mass of m1 = 7500 M⊙ and mass ratio q = 2 are shown in Table 1 for detections by LISA, LGWA, and ET at different redshifts. The LGWA demonstrates better detectability with larger SNRs than LISA, while ET fails to detect these signals. Thus, the unique deci-hertz sensitive frequency range plays a crucial role in detecting IMBH binaries with LGWA. In the right panel of Fig. 1, we plot the horizon redshift for IMBH binaries with the mass ratio between 1 and 10. The four angles are also fixed as in the left panel. The detection threshold is chosen as SNR = 10. We can clearly see that the binaries with primary mass m1 ∈ [103, 104] M⊙ have the best performance, which can be detected with a horizon redshift of \(z \sim {\mathcal{O}}(10)\). These results are consistent with Ajith et al.19.

Fig. 1: Noise, strain, and redshift horizon.
figure 1

a The characteristic strain hc for five representative events with different primary masses. The characteristic noise strains of the LGWA18,19, ET10, LISA53, Taiji14, and TianQin15 are also presented. All events are fixed at z = 0.5 with a mass ratio q = 2. b The horizon redshift with a detection threshold SNR = 10. The region with mass ratio q < 1 is shaded for the requirement of m1 ≥ m2, while the one with q > 10 is shaded for the applicability of the waveform model. For both panels, the four free angles in Table 2 are fixed to α = π/4, \(\cos \delta =1/2\), ψ = π/4, and \(\cos \iota =1\). Packages GWFish36 and astropy54 are used to produce the figure.

Full size image
Table 1 SNRs of an IMBH binary with a primary mass of m1 = 7500 M⊙ and mass ratio q = 2 are shown for detections by LISA, LGWA, and ET at different redshifts
Full size table

SNR distributions

We calculate the angle-averaged SNR for IMBHs at \(z\in \left\{0.05,0.1,0.5,1,5,10\right\}\). The results are shown in Fig. 2. For each point in the figure, we generate 1000 events with the corresponding m1, m2, and z values, while the four free angle parameters α, \(\cos \delta\), ψ, and \(\cos \iota\) are randomly drawn from the uniform priors in Table 2. The angle-averaged SNR is obtained by taking the average of the results from 1000 events. We find that all events can be detected at z ≲ 0.5. However, at redshift z ≳ 1, the binaries with primary mass m1 ∈ [102, 103] M⊙ and m1 ∈ [104, 105] M⊙ show less detection efficiency. The angle-averaged SNRs fall below 10 for binaries at z = 10. It is interesting to note that for nearby binaries (i.e., z ≲ 0.5), the binaries with m1 ∈ [104, 105] M⊙ show better performance. For example, at z = 0.05 or z = 0.1, binaries with m1 ∈ [104, 105] M⊙ can be detected with angle-averaged SNR \(> {\mathcal{O}}(1{0}^{3})\), while for distant systems (i.e., z ≳ 5), binaries with m1 ~ [103, 104] M⊙ show better performance. This phenomenon arises due to the sensitivity profile of LGWA in the decihertz band. In Fig. 3, we plot the evolution of SNR with luminosity distance for each of the above five representative events in Fig. 1. The pink line denotes the binary system with m1 = 50,000 M⊙, while the light orange line denotes the system with m1 = 5000 M⊙. As the luminosity distance increases, the LGWA becomes sensitive first to heavier systems and then to lighter systems. The turning point happens around DL ~ 104 Mpc, which corresponds to z ~ 1.5 in the ΛCDM cosmology model. The SNR evolution for systems with other primary masses is also consistent with the results shown in Fig. 2. It is worth noting that the variation in detection sensitivity with source-frame mass and redshift can be mitigated by converting m1 in Fig. 2 to detector-frame mass. For instance, in the cases of z = 5 and z = 10, the detector-frame mass will be magnified by approximately \(\sim {\mathcal{O}}(10)\), whereas other cases remain almost unaffected.

Fig. 2: Each subfigure shows the angle-averaged SNR for binaries fixed at different redshifts.
figure 2

For each point, we take an average of 1000 events, which are sampled with priors shown in Table 2. The blank region with no points in the lower subfigures represents the binary systems with angle-averaged SNR < 10. Packages GWFish36 and astropy54 are used to produce the figure.

Full size image
Table 2 Parameter priors of IMBH binaries
Full size table
Fig. 3: The evolution of SNR with respect to luminosity distance.
figure 3

These five events have the same parameters as in Fig. 1 with the corresponding color. Packages GWFish36 and astropy54 are used to produce the figure.

Full size image

Detectability on primary mass, redshift, and sky localization

We estimate the relative errors for m1, z, and the 90% sky localization uncertainty of IMBH binaries with the LGWA. In Fig. 4, we show the angle-averaged relative errors of the primary mass Δm1/m1 at different redshifts. For nearby binaries (i.e., z ≲ 0.5), the primary mass can be measured with an accuracy better than 0.1%. For binaries at z = 1, the primary mass can be measured with an uncertainty less than 1% for most cases. However, for distant binaries (i.e., z ≳ 5), the primary mass can only be measured with lower accuracy, typically worse than 10% across most detectable regions. Figure 5 shows results for the angle-averaged relative error of the redshift, Δz/(1 + z). For binaries at z ≲ 0.1, the redshift can be constrained with relative errors ≲ 10%. For binaries at z = 0.05, the redshift can be constrained better than 1%. However, for binaries at z ≳ 0.5, the redshift is constrained worse than 10% for all detectable regions. In Fig. 6, we plot the angle-averaged 90% sky localization uncertainty35,36 for IMBH binaries at different redshifts. For binaries at z ≲ 0.1, those with m1 ∈ [104, 105] M⊙ can be localized within \({\mathcal{O}}(10)\,{{\rm{deg}}}^{2}\), while binaries with m1 ∈ [103, 104] M⊙ can be localized within around \({\mathcal{O}}(1{0}^{2})\,{{\rm{deg}}}^{2}\). However, for binaries at z > 0.5, all events show poor localization precision.

Fig. 4: Same as Fig. 2, but for the angle-averaged relative error of the primary mass, Δm1/m1.
figure 4

Packages GWFish36 and astropy54 are used to produce the figure.

Full size image
Fig. 5: Same as Fig. 2, but for the angle-averaged relative error of the redshift, Δz/(1 + z).
figure 5

Packages GWFish36 and astropy54 are used to produce the figure.

Full size image
Fig. 6: Same as Fig. 2, but for the angle-averaged 90% sky localization errors at different redshifts, \(z\in \left\{0.05,0.1,0.5,1\right\}\).
figure 6

Packages GWFish36 and astropy54 are used to produce the figure.

Full size image

Discussion

We explored the detectability of IMBH binaries with the LGWA. Due to its unique shape of the sensitivity curve at decihertz band, the LGWA is more sensitive to distant binaries (i.e., z ≳ 5) with m1 ∈ [103, 104] M⊙, while preferring nearby binaries (i.e., z ≲ 0.5) with m1 ∈ [104, 105]M⊙. The primary mass can be measured with accuracy better than 0.1% for binaries at z ≲ 0.5, and the redshift can be constrained within 10% for binaries at z ≲ 0.1. Meanwhile, binaries with m1 ∈ [104, 105] M⊙ can be localized within \({\mathcal{O}}(10)\,{{\rm{deg}}}^{2}\) at z ≲ 0.1. As the LGWA fills the unexplored GW frequency band between space-borne detectors (i.e., LISA, Taiji, and TianQin) and ground-based detectors (i.e., CE and ET), it shows the unique advantage for detecting IMBH binaries. The observations of the inspiral and merger phases of IMBH binaries can offer us more insights into the formation and evolution of black holes, especially bridging the gap between stellar-mass and supermassive black holes37. Additionally, it will help us to disentangle the effects between the accretion history and the merger dynamics of black holes38,39.

Several recent studies40,41,42 showed that the power spectrum density (PSD) of the LGWA should be updated when carefully considering the lunar response to GWs. We show the updated PSD with the same approach as in Yan et al.40 in the left panel of Fig. 7, but modify it a little bit using a new sensitivity curve of the LGWA seismometer (we choose the black dotted line as the sensitivity of a single detector, from Fig. 2b in ref. 19). The updated PSD matches marginally well with the original one in the frequency region lower than 10 mHz but becomes two orders of magnitude worse around decihertz. This variation is primarily because Yan et al.40 used the Dyson-type force density, rather than the tidal force density, to calculate the lunar response to GWs. In the right panel of Fig. 7, we show the horizon redshift of IMBH binaries for the updated LGWA PSD. Because of the change of sensitivity in the decihertz band, the IMBH binaries can now only be detected up to \(z \sim {\mathcal{O}}(1)\). Finally, more details, including a more precise calculation of the lunar response with the near-surface fine structure of the Moon, need to be considered for future exploration of the science cases with the LGWA.

Fig. 7: Noise, strain, and redshift horizon, with LGWA update40.
figure 7

a The characteristic noise hn for LGWA and LGWA update. b The horizon redshift same as Fig. 1, but here for LGWA update40. Packages GWFish36 and astropy54 are used to produce the figure.

Full size image

Methods

Priors for the population of IMBH binaries

It is more realistic to consider all relevant parameters for GWs from IMBH binaries, including orbital eccentricity and spin precession. However, recent studies43,44 have found that these two factors have slight impact on the parameter estimation results in this work, specifically on the source-frame masses, redshift, and sky localization. For example, no strong degeneracy was found between spins perpendicular to the orbital momentum and the parameters estimated for IMBH binaries in this work43. No significant degeneracy between spins and eccentricity was observed, particularly in the case of low eccentricity (e < 0.2)44. As a simplification, the aligned-spin, quasi-circular assumption is commonly adopted when modeling stellar-mass black hole binaries to reduce computational complexity45,46. Thus, the IMBH binaries are assumed to have aligned spins and quasi-circular orbits in our work. The GW signals from them are described with 11 free parameters,

$${\boldsymbol{\theta }}=\left\{{m}_{1},\,{m}_{2},\,{\chi }_{1z},\,{\chi }_{2z},\,{D}_{L},\,\alpha ,\,\delta ,\,\psi ,\,\iota ,\,{\phi }_{c},\,{t}_{c}\right\},$$
(2)

where m1 and m2 are source-frame binary masses of the two components, χ1z and χ2z are their dimensionless spin components which parallel with the orbital angular momentum, DL is the luminosity distance of the source, α and δ are the right ascension and declination angles, respectively, ι and ψ are the inclination angle the polarization angle, respectively, and ϕc and tc are the coalescence phase and time, respectively.

Given the debated astrophysical star formation rate and merger rate for IMBHs, we follow Reali et al.33 to adopt sample parameter priors of IMBHs that span the parameter space. As shown in Table 2, the source-frame primary mass is sampled logarithmically uniform from m1 ∈ [102, 105] M⊙, while the secondary mass is sampled logarithmically uniform from m2 ∈ [10 M⊙, m1]. Meanwhile, the mass ratio q = m1/m2 ∈ [1, 10] is further imposed in this work to guarantee the accuracy of the waveform model33,47. We consider IMBH binaries which are fixed at six representative redshifts, \(z\in \left\{0.05,0.1,0.5,1,5,10\right\}\), to cover both nearby and distant cases. The luminosity distance DL is then obtained using the ΛCDM cosmology model. The four angles α, \(\cos \delta\), ψ, and \(\cos \iota\), follow the uniform distributions \({\mathcal{U}}[0,2\pi )\), \({\mathcal{U}}[-1,1]\), \({\mathcal{U}}[0,\pi ]\), and \({\mathcal{U}}[-1,1]\), respectively. The priors for the coalescence phase, coalescence time, and two aligned spins are fixed to zero for all cases.

Waveform model and detectors

The detected GW strain is described as48,

$$h={h}_{+}{\overleftrightarrow{e}}_{+}:\overleftrightarrow{d}+{h}_{\times }{\overleftrightarrow{e}}_{\times }:\overleftrightarrow{d},$$
(3)

where h+ and h× are the ‘+’ and ‘ × ’ polarization components of the GW, respectively, \({\overleftrightarrow{e}}_{+}\) and \({\overleftrightarrow{e}}_{\times }\) are the corresponding polarization tensors, respectively, and \(\overleftrightarrow{d}\) is the response tensor of the detector.

Unlike current ground-based “L” shape laser interferometer type detectors like LIGO, Virgo, and KAGRA, the detection principle of LGWA has significant differences18,19,49. When a GW passes the Moon, its surface displacements can be measured by several seismometers of the LGWA. With the long-wavelength approximation, the response tensor of a seismometer is written as36,

$$\overleftrightarrow{d}={\vec{e}}_{n}\otimes {\vec{e}}_{1},$$
(4)

where \({\vec{e}}_{n}\) is the direction of the surface normal vector at the seismometer, and \({\vec{e}}_{1}\) is the direction of displacement measured by the seismometer. For a more realistic situation, the complete result of the response tensor is somewhat more complicated, including different contributions of radial and horizontal vibrations50. Thus, Eq. (4) can be regarded as a simplified case in which the radial response function is just two times of the horizontal response function, as shown in Eq. (7) in ref. 50.

We use the IMRPhenomXHM waveform template47 to generate h+ and h×. Additionally, we employ the GWFish package36 to calculate the GW strain projected onto the seismometer. Note that GWFish also takes into consideration the orbital motion of the Moon around the Earth, as well as the motion of the Earth–Moon system around the Sun during the detection period. We focus on the GW frequency band ranging from 10−3 Hz to 4 Hz. Additionally, 20,000 points are evenly spaced on a logarithmic scale for each signal. Furthermore, we utilize the default LGWA detector in GWFish, which consists of an array of four stations deployed in the Moon’s permanently shadowed regions. Each station is equipped with two horizontal Lunar inertial GW sensors, which measure the two orthogonal surface displacements18,19,49. The mission duration of the LGWA is expected to be 10 years. Thus, GW signals with time durations longer than 10 years are truncated at a low-frequency end via36,

$$t(f)={t}_{c}-\frac{5}{256{{\mathcal{M}}}_{c}^{5/3}}{(\pi f)}^{-8/3},$$
(5)

where \({{\mathcal{M}}}_{c}\) is the chirp mass.

Fisher information matrix

Under the linear-signal approximation and assuming Gaussian and stationary noise, the posterior distribution of GW parameters becomes51,52,

$$p({\boldsymbol{\theta }}) \sim {{\rm{e}}}^{-\frac{1}{2}{\Gamma }_{ij}\Delta {\theta }_{i}\Delta {\theta }_{j}},$$
(6)

where Γij is the FIM and can be calculated as,

$${\Gamma }_{ij}\equiv \left\langle {\partial }_{{\theta }_{i}}h({\boldsymbol{\theta }};f),{\partial }_{{\theta }_{j}}h({\boldsymbol{\theta }};f)\right\rangle .$$
(7)

Note that the inner product for two quantities A(θ; f) and B(θ; f) is defined as,

$$\langle A,B\rangle =2\mathop{\int}\nolimits_{0}^{\infty }{\rm{d}}f\frac{A({\boldsymbol{\theta }};f){B}^{* }({\boldsymbol{\theta }};f)+{A}^{* }({\boldsymbol{\theta }};f)B({\boldsymbol{\theta }};f)}{{S}_{n}(f)},$$
(8)

where Sn(f) is the one-sided PSD of the detector. The matched-filtering SNR for a GW event is calculated as,

$${\rm{SNR}}=\sqrt{\langle h,h\rangle }.$$
(9)

We also use the GWFish package for FIM calculations.