Introduction

Gravitation, or gravity, is a natural phenomenon that a body attracts another one with a force proportional to their masses. Due to the gravity of Earth, a body on Earth can possess weight and fall to the ground with an increasing speed when dropped. If air resistance is neglected, the corresponding acceleration g0 is the same for all objects no matter what are their compositions and masses1. This effect was first discovered by Galileo Galilei in the late 16th century and becomes the starting point of modern physics.

Gravitation is also responsible for complex phenomena including the motions of celestial bodies and the formation of water waves in seas. Under the restoring force provided by gravity, water waves propagate on the surface of water and their velocities depend on both the gravitational acceleration g0 and water depth2. Such mechanical waves can interact with a host of periodic structures such as rippled bottoms3,4,5,6,7,8,9,10, floating disk arrays11 and vertical cylinder arrays12,13,14,15,16,17. Recently, inspired by the research of metamaterials18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34, a concept of effective liquid was proposed to describe the interaction of water waves with periodic structures35,36. This concept states that for wavelengths much longer than the period, the water with a periodic structure can be viewed as a homogeneous liquid characterized by an effective depth he and effective gravitational acceleration ge35,36. Interestingly, it was theoretically found that the effective gravity can be different from the one on the Earth (ge ≠ g0) in some cases35,36. For example, an increased gravity (ge > g0) is found in water pierced by a cylinder array35, resulting in a new type of water wave refraction16,17. For water with a resonator array, the effective gravity can even be negative (ge < 0) near resonant frequency, so that water waves cannot propagate through the resonator array36. These results promise a new mechanism to control the propagation of water waves, which have applications in wave energy conversion and coastal protection37,38,39,40,41. However, the exotic effects, especially the negative gravity, have not yet been observed in experiments and remain mathematical curiosities which are difficult to understand.

Here we report on experimental observation of the negative effective gravity for water waves through an array of resonators of bottom-mounted split tubes. A displacement averaging method is proposed to obtain and understand the effective gravity. Based on simulations and measurements, it is found that when negative gravity occurs, the averaged displacement of water surface in a unit cell of the array has a phase difference of π to that along the boundary of the unit cell. In contrast, the phase difference is zero for positive gravity.

Results

Sample constructions and the effective medium theory

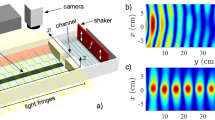
The system under study is a channel of water pierced by a periodic array of vertical bottom-mounted split tubes (Figs. 1a and 1b). The width of the channel w equals to the periodicity a of 12 mm. The water depth h0 is 8 mm. Each split tube has an outer radius r1 of 4 mm, inner radius r2 of 3 mm and slit width Δ of 1 mm and supports a resonant mode for water waves. Here, water waves outside the tube cause the water in the slit to oscillate in and out, resulting in the vibration of the water surface in the tube36. Such a Helmholtz mode has a resonant wavenumber and loss γk, where is the effective neck length of the Helmholtz resonator [see Supplementary information for details]. From the wavenumber k, the angular frequency of water waves can further be obtained by the dispersion of , where the reduced water depth with h being the water depth. We note that the dispersion is valid for both water and effective liquid, when subscripts 0 and e are added under the variables of g, h, u and k, respectively.

Figure 1
figure 1

Water waves propagating through a resonator array and the corresponding effective medium description.

(a) Side view and (b) top view of four resonators of vertical bottom-mounted split tubes placed in a channel of water. The split tubes are made of copper and have outer radius r1 = 4 mm, inner radius r2 = 3 mm, slit width Δ = 1 mm, height of 15 mm and spacing a = 12 mm. The water depth h0 = 8 mm and channel width w = 12 mm. (c) Side view and (d) top view of a homogeneous liquid (orange part) with an effective gravitational acceleration ge and effective depth he. For water waves with long wavelengths, the water with a resonator array shown in Fig. 1a can be replaced by the effective liquid shown in Fig. 1c.

Full size image

For water with a split tube array, the corresponding effective liquid (Figs. 1c and 1d) possesses an effective gravitational acceleration36

and effective reduced depth of , where the filling ratio of split tubes . Hence, our sample has a positive effective reduced depth (, Fig. 2a) and frequency-dependent effective gravitational acceleration (Fig. 2b). For frequencies ranging from 4.1 Hz to 4.85 Hz (called resonant gap), the effective gravity becomes negative (ge < 0) so that surface waves cannot propagate through the split tube array.

Figure 2
figure 2

Observation of the negative effective gravity in water waves.

(a) Effective reduced depth ue, (b) effective gravitational acceleration ge and (c) transmission as a function of frequency for water with a resonator array as shown in Fig. 1. The solid lines, dashed curves and red squares are obtained from effective medium theory, simulations and experiments, respectively. Due to negative gravity (yellow part in Fig. 2b), a transmission dip is observed at 4.4 Hz in Fig. 2c. (d–e) The same as (a–c) but for four bottom-mounted cylinders with radius of 4 mm.

Full size image

Verification of the negative effective gravity from transmission measurements

To experimentally verify the existence of negative gravity, we measured the transmission spectrum for impinging of water waves on the split tube array (Methods), as shown the squares in Fig. 2c. Due to the negative gravity, a transmission dip was observed at 4.4 Hz. The experimental results agree well with the calculated ones based on the effective parameters (solid line in Fig. 2c). We note that the measured transmission data are lower than the theoretical values in the passing bands (with frequencies lower than 4 Hz or between 5 Hz and 6 Hz) because of the propagation loss, imperfect reflection and surface tension effect at tube walls. Although the surface tension influences slightly the dispersion of water waves here (Methods), it has effects on the water surface near the walls and may increase the propagation loss.

For comparison, a control experiment was also carried out with a control sample where the split tubes were replaced by rigid cylinders of the same outer radius. According to our previous theory35, water with the cylinder array has the same effective depth (Fig. 2d), but different effective gravitational acceleration (, Fig. 2e), compared with the parameters for a split tube array. Hence, water waves with long wavelengths can propagate through the cylinder array and the above transmission dip induced by negative gravity is not observed here (Fig. 2f). This control experiment confirmed that the negative gravity is induced by local resonance rather than the lattice periodicity.

A new displacement averaging method to obtain the effective gravity

Although the effect of negative gravity has been verified by the transmission experiments, it remains mysterious since it cannot be understood by simple averaging of gravity over area. Here, borrowing the idea from electromagnetic metamaterials, we derive a new displacement averaging formula to obtain and understand the effective gravitational acceleration (see Supplementary information for derivations):

Here, is the averaged vertical displacement of water surface along the boundary of a unit cell, representing the boundary excitation. is the averaged displacement over the area of the unit cell, namely the averaged response. The averaged displacements can be further expressed as and with η1 and η2 being the averaged displacements inside and outside the split tube, respectively. Using a simple hydrodynamics model, it can be proved (see Supplementary information for derivations) that

Thus, Eq. (1) can be alternatively derived.

Understanding the negative effective gravity by water-wave simulations

From Eq. (2), we can see that for positive gravity, the averaged response in a unit cell has the same phase with the boundary excitation. However, the phase difference becomes π when negative gravity occurs. To confirm the picture of negative gravity, we performed numerical simulations (Methods) for above water wave experiments. The calculated transmission spectra (dashed lines in Figs. 2c and 2f) agree well with experiments and theory, showing the correctness of simulations. Meanwhile, the profiles of displacement of water surface and ratios of response to excitation were obtained for different frequencies (Figs. 3a–3d). It can be seen that for a given excitation, the amplitude of response reaches a maximum at resonant frequency (Fig. 3c). In a frequency range above the resonant frequency, the response has a phase difference of π compared with the excitation (Fig. 3d), resulting in a negative gravity (Fig. 3e). By fitting the simulated data of by the above model, a radiation loss of is obtained for the split tube resonators. Due to such intrinsic loss, an imaginary part is also found in the effective gravity (Fig. 3f).

Figure 3
figure 3

Understanding of the negative effective gravity by simulated mode profiles.

(a) Amplitude and (b) phase profiles of the vertical displacement of water surface η in the leftmost unit cell in Fig. 1b. The left and right panels are for 2.5 Hz (positive gravity) and 4.4 Hz (negative gravity), respectively. (c) Amplitude and (d) phase of ηa/ηb as a function of frequency. ηa and ηb are the averaged η over the area and along the boundary of the unit cell, respectively. The red squares are simulation results and the black curves are theoretical fits. (e) Real and (f) imaginary parts of ge/g0 deduced from the results in Figs. 3c and 3d.

Full size image

Understanding the negative effective gravity by displacement measurements

In corroboration of the simulations, we measured experimentally the surface displacements for two points inside and outside a split tube (Methods). The surface displacement inside tube η1 is found to have the highest amplitude, about 7 time of the value η2 outside tube, at the center frequency of resonant gap (Fig. 4a). Below the resonant frequency of about 4.1 Hz, the surface displacement inside tube has almost the same phase with that outside tube (Fig. 4b). However, above the resonant frequency, the displacements inside and outside tube have different phases and the phase difference increases to π above 5 Hz. The experimental data can be fitted by Eq. (3), showing a higher loss () than the ideal case. Due to this loss, the effective gravitational acceleration is not too negative in the real part (Fig. 4c) and has simultaneously an imaginary part (Fig. 4d). As a result, a small amount of transmission (0.2%) has been measured at the dip frequency in Fig. 2c.

Figure 4
figure 4

Understanding of the negative effective gravity by measured surface displacements.

(a) Amplitude and (b) phase of η1/η2 as a function of frequency. η1 and η2 are the vertical displacements of water surface for the two points as shown in the inset of Fig. 4b. The red squares are experimental data and the blue curves are theoretical fits. (c) Real and (d) imaginary parts of ge/g0 deduced from the results in Figs. 4a and 4b.

Full size image

Discussion

By now the negative effective gravity has been observed experimentally and understood by a displacement averaging method. This method can also be applied to understand the increased effective gravity35 for water with a cylinder array. For a unit cell with a cylinder, the averaged response () is smaller than the boundary excitation ( with η2 being the averaged displacement outside cylinder) so that the increased gravity () can be alternatively obtained.

Due to the negative effective gravity, a low-frequency resonant gap is formed in water waves. Similar resonant gaps also exist for sound waves in metamaterials composed of acoustic Helmholtz resonators, which is interpreted by a negative effective modulus. In the gap with negative modulus, an interesting negative group velocity was found for sounds: for a sound pulse incident on a thin slab of the metamaterial, the peak of transmitted pulse has been detected before the peak of incident pulse enters into the slab29. We note that such a “superluminal” phenomenon32,42 may also been observed in our water-wave system if a wave source of pulse is applied in the water-wave experiment.

Although the negative effective gravity is observed in water with split tubes, it could be achieved by other kinds of resonators. Various resonators such as heaving buoys and underwater pendulums37,38,39,40, have been invented and applied to extract ocean wave energy38 and resonator arrays have been regarded as a key part of future wave power plants41. Our work indicates that when those resonators are arranged in an array, negative gravity or negative depth could be achieved, giving rise to low-frequency stopping bands of water waves. As a result, long wavelength water waves, even including tsunamis, may be blocked by a narrow array of resonators. In addition, if negative gravity and depth are achieved simultaneously, water waves can propagate in a slow and negative velocity through resonator arrays, which may enhance the efficiency of wave energy extraction.

Methods

Experimental set-up

Water is contained in a vessel that is made of Aluminum in four sides and of transparent glass in the bottom. The vessel has a length of 1.4 m and inner width of 12 mm, two vertical long sides and two slanted short sides (where the slopes have a length of 170 mm and height of 10 mm, which can eliminate the reflection of water waves). The vessel is placed horizontally so that the water depth is constant in the middle part of the vessel. The split tubes are made of copper and placed vertically and firmly in the middle of the vessel.

An air tube with oscillating pressure was used to generate harmonic water surface waves with frequency ranging from 2 Hz to 10 Hz. To generate ideal gravity surface waves in this frequency range, a liquid (CFC-113) with low viscosity and low surface tension was applied to replace water. We note that the wave source and liquid have been adopted in our previous experiments7,14,17.

A number of parallel light beams (with diameter of ~1 mm) were applied to measure simultaneously the vertical vibration of a few points on the water surface. Here, the light beams went vertically downward, then passed through the water surface and glass bottom and finally projected to a screen under the vessel. When surface waves are generated in the water, the light spots on the screen can oscillate and the oscillations linearly depend on the vibrations of certain points on the water surface.

A digital camera (Panasonic DMC-FX100) was used record the oscillations of light spots on the screen (with 30 frames/second, 600 × 480 pixels/frame and 20 second for each frequency; see Supplementary Movies S1 and S2). Using the software QuickTime, each recorded movie can be converted into a series of pictures with bmp format. The positions of light spots are then obtained for each picture by using a MATLAB program. Here, the center of a light spot is calculated by a light-intensity-weighted average method so that the accuracy of light spot center can be smaller than 1/200 of a pixel in the digital picture. At last, a Fortran program is used to do Fourier transform for the oscillations of light spots. Using this method, we can obtain at the same time the amplitudes and phases for many points on the water surface, such as the results shown in Figs. 4a and 4b.

Assume only plane waves are generated in the channel of water, namely . By measuring the vibrations of three equally-spaced points along the channel ( and ), we can obtain the complex amplitudes of leftward and rightward waves (A and B) and the wavenumber k0. Using this method, we can obtain the complex amplitudes of incident (Ai) and transmitted (At) waves as well as the transmission () as shown in the squares in Figs. 2c and 2d.

Calculations based on effective parameters

Consider incidence of a harmonic plane wave on the step as shown in Fig. 1c. The water depth and gravitational acceleration are (g0, h0) in the left (x < 0) and right (x > L) regions and (ge, he) in the middle region (0 < x < L). The vertical displacement of water surface can be expressed as: in the left region, in the middle region, in the right region. Using the continuities of η and flow u∇η at the two steps (x = 0 and x = L), we have , , , , A3 + B3 = A4 and . Hence, we can obtain the transmission , such as the solid lines in Fig. 2c.

Simulations for real structures

For harmonic water waves in the structures shown in Fig. 1a, the vertical displacement of water surface satisfies a two-dimensional Helmholtz equation, , which is subjected to a no-flow condition at the surfaces of vertical walls and split tubes with being the surface normal. The left and right sides of the channel are perfect absorbing boundaries. Hence, we can apply the finite-difference time-domain method or finite-element method to calculate the transmission (dashed lines in Fig. 2c) and mode profiles (Fig. 3).