Abstract
A promising method for tomography and step height measurement is proposed, which combines the high sensitivity of the frequency-shifted feedback laser and the axial positioning ability of confocal microscopy. By demodulating the feedback-induced intensity modulation signals, the obtained amplitude and phase information are used to respectively determine the coarse and fine measurement of the samples. Imaging the micro devices and biological samples by the demodulated amplitude, this approach is proved to be able to achieve the cross-sectional image in highly scattered mediums. And then the successful height measurement of nano-step on a glass-substrate grating by combination of both amplitude and phase information indicates its axial high resolution (better than 2 nm) in a non-ambiguous range of about ten microns.
Similar content being viewed by others
Introduction
Optical feedback occurs when a portion of laser output is coupled back into the laser resonator. It was firstly found by King and Steward1 to induce intensity modulation in laser output. This modulation period corresponded to a λ/2 optical displacement of an external feedback reflector. It was also recognized that the intensity modulation depth was comparable to that in conventional interferometer. Therefore, optical feedback effect is also called self-mixing interference. In early days, the self-mixing interferometry, which utilized the steady-state intensity of gas lasers modified by external optical feedback, achieved the measurement of distance1, velocity2, displacement3, etc. However, for gas laser, due to its inherent nature of class-A laser, the sensitivity and dynamical response to external optical feedback is largely limited by photon lifetime of laser cavity. Thus, in such applications, it is necessary to use a cooperative mirror to reflect enough light to construct interference occurring inside laser resonator. But clearly, it is not suitable for the applications of non-cooperative measurement. The challenge is to increase the sensitivity of the laser to external feedback to overcome this defect.
One solution is then to use laser dynamics in class-B laser which are more sensitive to optical feedback than steady state changes in class-A laser. For the first time in 1979, Otsuka4,5 reported a remarkable response of a thin-slice LiNdP4O12 (LNP) laser to Doppler-shifted optical feedback originating from a rotating ground-glass plate. By using the classical rate equations, it is concluded that the sensitivity of such a thin-slice laser to external optical feedback is proportional to the fluorescence-to-photon lifetime ratio τ/τp, where τ and τp are, respectively, the fluorescence and photon lifetimes. For typical solid-state or semiconductor lasers, values of this ratio are of the order of 103. While for a thin-slice solid-state laser, the value is as high as 106 independently of the laser output power6, which makes such lasers a promising solution for non-cooperative targets measurement. Benefiting from this unique nature of thin-slice solid-state laser, the feedback interferometry based on this type of lasers has attracted considerable attention in various kinds of metrology7, including velocimetry8, vibrometry9, flowmetry10, particle sizing11, biological sensing12, displacement sensing13 and optical imaging14,15, in which the thin-slice solid-state laser acts as a high-efficiency mixer oscillator and a shot-noise limited quantum detector.
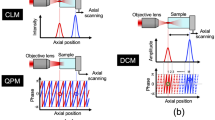
Optical method is reputed to be high resolution, contact-free and noninvasive. Thus, a lot of attention has been paid to optical techniques in noninvasive imaging of biological tissues, such as scanning confocal microscopy16, diffusion photon density-wave propagation17, spectral fluorescence imaging18,19, photoacoustic tomography20,21. Especially, in recent years, optical coherence tomography (OCT)22,23,24 has made a great progress in resolution, penetration depth and scanning speed and thereby has been widely used in the cross-sectional imaging of retina and teeth. However, due to the rapid decrease of the backscattering intensity when the depth increases, these methods are usually confined to measurements of a few millimeters in biological samples. More recently the self-mixing confocal surface imaging of a French coin in milk was demonstrated by Lacot15, in which the de-focus effect on the intensity modulation amplitude and the resonant enhancement of the intensity modulation amplitude by tuning the frequency shift toward the relaxation oscillation frequency25 were introduced. Additionally, Otsuka26 performed the transmission-type of self-mixing optical CT in highly scattering medium by using the ultrahigh sensitivity of thin-slice solid-state laser to external feedback. In this report, we introduce a potential tomography technique, i.e., laser feedback (self-mixing interference) confocal tomography, which combines the ultrahigh sensitivity of class-B laser to optical feedback and axial positioning (tomography) ability of confocal microscopy. Due to the ultrahigh sensitivity of thin-slice solid-state lasers to external frequency-shifted feedback, it is possible for laser feedback confocal tomography to reach a greater depth than OCT. A series of experiments, including imaging a micro-electro-mechanical system (MEMS) device and a biological sample containing pins inserted, are carried out to initially perform its potential in the tomography of highly scattered or diffused medium.
Optical surface profilometry (especially nano-step height measurement) has the advantages of contact-free and high axial resolution. Commercial optical instruments are now widely available and are based on various principles such as confocal microscopy16, mirau phase scanning interferometry27 and white-light interferometry28, etc. Although phase scanning interferometry offers the highest resolution, its measurement range is limited in a non-ambiguous range of only half wavelength. Confocal or white light vertical scanning technologies have a large axial working range, but require other gauges to provide a standard. In addition, as a self-aligned highly-sensitive measurement technique, self-mixing confocal imaging based on He-Ne laser is also proposed to get the surface profile of microfabricated structures29, in which it is necessary to use a piezoelectric transducer to maintain a constant distance between the laser and sample. And then, the piezoelectric transducer's displacement is used to reconstruct the surface profile. However, the nonlinearity and hysteresis of the piezoelectric transducer reduces drastically the accuracy of this scheme. In this report, the laser confocal feedback technology is induced to realize both the relatively large axial working range (10 μm) and high axial resolution (better than 2 nm) in surface profilometry, in which a quasi-common-path technique is used to compensate the environmental disturbance to achieve axial high resolution. Furthermore, due to its inherent ultrahigh sensitivity of thin-slice solid-state laser, it is especially suitable for the surface profilometry measurement of low reflective samples.
Results
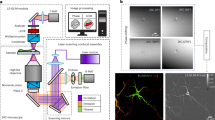
The experimental setup is schematically illustrated in Fig. 1. A Nd:YAG crystal plate (ϕ5 mm × 1 mm) is employed to form a plane-parallel Fabry-Perot cavity. With coating on both surfaces, this Nd:YAG thin-slice forms a laser resonator. The left surface is coated to be antireflective at the pump wavelength of 808 nm (T > 95%) and highly reflective (R > 99.9%) at the lasing wavelength of 1064 nm; the right surface is coated to be 1% transmissive at the lasing wavelength. A fibre-coupled single-mode laser diode (not shown in Fig. 1) with a narrow linewidth (<0.1 nm) served as pump source, whose output was focused on the Nd:YAG crystal using a GRIN lens. The lasing threshold is Pth = 24 mW and the slope efficiency is ~37%. The microchip Nd:YAG laser outputs approximately 29 mW. Given the attenuation of all components in optical path, the final power impinges on measured targets is 2–3 mW. The power fluctuation of the microchip Nd:YAG laser in 3 hours is tested as 1.26%. During the entire experiments, this microchip Nd:YAG laser works in linearly polarized TEM00 transverse mode and single longitudinal mode.
Schematic of experimental setup.
ML: microchip solid-state Nd:YAG laser; BS1–3: beam splitter; L1–3: lens; PH: pinhole; AOM1,2: acousto-optic modulators; RF1,2: rf signal generators; Mr: reference mirror; BE, beam expander; PD: photoreceiver; Lock-in1–3: Lock-in amplifier; OB, objective; SA, sample; ST: two dimensional movement stage; PC: computer.
Laser output is divided into two parts. One part is reflected by BS1 to be detected by PD for signal demodulation. The other part passes through a pinhole to form a point source of light in confocal system. After that, the collimated laser beam (frequency ω) passes through the AOM1 (driven at 70 MHz), whose output contains 0-order (frequency ω, denoted by blue line) and -1-order (frequency ω-70 MHz, denoted by red line) diffracted beams. The distance between the two AOMs is kept short enough to ensure that both the outputs from AOM1 pass through the aperture of AOM2 (driven at 70 + Ω MHz). Simultaneously, the incident angle of the laser beam at AOM2 is carefully adjusted to ensure the generation of a +1-order diffracted beam. Then, after AOM2, two of the resulting beams, whose frequencies respectively are ω and ω + Ω, are selected as the beams of reference (denoted by blue line) and measurement (denoted by red line). The -1-order diffracted beams of AOM1 and the +1-order diffracted beams of AOM2 are combined to obtain the differential effect. That is why it is called differential frequency-shifting. The beam (ω + Ω) serves as measurement beam, which is expanded and focused onto the sample's surface or inner. The reflected light by the sample then returns back to laser resonator along its incoming path, constructing the feedback measurement arm. Due to the twice frequency shifting in a roundtrip, the feedback measurement beam is frequency shifted by 2Ω compared with that inside the laser cavity. And then, it produces a 2Ω-frequency intensity modulation Im(2Ω). The reference beam ω (denoted by blue line) is reflected by Mr back to laser resonator along or parallel to the path of the measurement beam (as illustrated in Fig. 1), constructing the feedback reference arm. Because of only once frequency shifting in a return trip, the feedback reference beam is frequency shifted by Ω compared with that inside the laser cavity. And then, it produces a Ω-frequency intensity modulation Ir(Ω). As to the measurement arm and reference arm, their optical paths between the laser and AOM2 are nearly the same. Thus, the environmental disturbances these two arms subjected are considered to be also the same. Consequently, the phase change in reference arm can be used to compensate that in measurement arm to remove the dead path error between the laser and AOMs. That is the principle of quasi-common-path interferometer reported by Wan from our group in 200713. In this report, this principle is also introduced in nano-step height measurement to achieve high axial accuracy at nanometer level.
An objective with a working distance of 20.4 mm and NA = 0.42 is located on a stage to realize a large scanning in vertical direction. The two-dimensional stage ST can move in the X-Y plane to achieve cross-sectional imaging.
In the tomography, the reference mirror Mr is removed. Therefore, only the intensity modulation Im(2Ω) can be obtained from the photodetector PD, as illustrated in Fig. 1. By demodulating the Im(2Ω), only the amplitude information (A) can be gained, while the phase information (ϕm) is interrupted due to the discontinuous interface of the sample's inner structure. And then, this amplitude (A) is used to represent the internal structure in measured samples such as MEMS devices or biological tissues. Once the amplitude (A) of the intensity modulation is detected, it means a distinctive internal structure exists in the samples.
While, in nano-step height measurement of sample's surface, the reference mirror Mr is added. Thus, both the intensity modulations Im(2Ω) and Ir(Ω) can be got from the photodetector PD, as illustrated in Fig. 1. By demodulating Im(2Ω), not only the amplitude (A) but also the phase (ϕm) can be obtained. After that, these two parameters are combined together to determine the micro-nano structure of the samples' surface. At the same time, the phase information (ϕr) from Ir(Ω) is used to compensate the ϕm to achieve high accuracy in phase measurement and thereby results in the high axial accuracy with nanometer resolution.
Resolution tests for laser confocal feedback system
The resolution of the laser confocal feedback system is a key parameter to judge the performance of the tested samples. For confocal system, it contains two indexes as vertical and lateral resolutions. The similar method with the traditional confocal system is adopted here to test the resolution for laser confocal feedback system.
The vertical resolution can be evaluated by scanning the defocus response curve and measuring its full width at half maximum (FWHM). In this experiment, a glass is adopted as the sample, whose axial position indicates the defocus of its surface, as illustrated in Fig. 2(a). The pinholes with different diameters of 10 μm, 20 μm, 50 μm, 100 μm are used to observe its influence on defocus response curve. In Fig. 2(a), the FWHM of defocus response curve is about 13 μm. It presents a surprising same value for different diameters of pinhole, which should change with the diameter of the pinhole in traditional confocal system. It is caused by the laser confocal feedback, in which the feedback light should return back to laser resonator to modulate laser intensity. From this point of view, in laser confocal feedback system, the microchip Nd:YAG laser is not only the light source but also the coherent detector who captures and amplifies the feedback signals. Consequently, the laser's beam waist with diameter of about 200 μm served as virtual pinholes for both the light source and detector. It is essentially different from the case in traditional confocal system. Thus, theoretically, there is no need to place a pinhole in Fig. 1. In actual practice, a pinhole is still used to filter the scattered light from defocus plane especially in the imaging of strongly scattered or diffused medium.
The theoretical lateral resolution of the system can be given by Δx = 0.61λ/ NA. It is calculated as 1.1 μm by substituting the parameters above. To determine the practical lateral resolution of the system, we test it by using a standard grating (made by MikroMasch corporation, the period is 3 μm and the step height is 493 nm). The step profile can be clearly distinguished as shown in Fig. 2(b) and then the lateral resolution can be obtained to about 1 μm by the image analysis of the step.
NA. It is calculated as 1.1 μm by substituting the parameters above. To determine the practical lateral resolution of the system, we test it by using a standard grating (made by MikroMasch corporation, the period is 3 μm and the step height is 493 nm). The step profile can be clearly distinguished as shown in Fig. 2(b) and then the lateral resolution can be obtained to about 1 μm by the image analysis of the step.
Defocus response curves for different material surfaces
Several types of material surfaces, such as rough aluminum, glass and yogurt, are used as the sample to test the capability of the laser confocal feedback system. All the interfaces between the sample and the air are clearly detected as shown in Fig. 3, which definitely indicates that the system fits for the measurement of all types of material surface, e.g. weak reflective one, or highly scattered one.
Vertical-sectional imaging for MEMS devices
A microfluidic device made of polydimethylsiloxane (PDMS, a kind of high molecular organic silicon compound and widely used in the microfluidic device) is measured by laser confocal feedback system. It is a single layer bonding device, in which there is a fluid channel obtained by soft lithography. The specific structure is illustrated in Fig. 4(a). In the experiment, a longitudinal sectional view in the channel is selected, with a vertical scan depth of 3 mm and a horizontal scanning range of 4 mm. The result obtained is shown in Fig. 4(b). The vertical-sectional image of the sample clearly reflects its structure, from which the height of the fluid passage can be measured as 75 μm.
Inspecting foreign body in biological sample
To fully demonstrate the high sensitivity of the microchip laser to weak diffused feedback signals, a biological sample (onion) with a pin inserted parallel to the X-Y plane is scanned to get its cross-sectional image.
Firstly, we scan the onion sample in the Z-Y plane to get its vertical-sectional image to determine the longitudinal position of the pin in the onion. It is found the pin locates 0.5 mm beneath the onion surface. Then, the probing laser beam is focused on the plane located 0.5 mm below the onion's surface. The two-dimensional stage is moved point by point in the X-Y plane to get the cross-sectional image of the pin in the onion.
The result is displayed in Fig. 5. The section of the pin's tip immerged into the onion is selected to obtain its 2D cross-sectional image in the X-Y plane. As illustrated in Fig. 5, the tapered cross-sectional image denoted by the double dot dash lines clearly indicates the profile of the pin's tip. What's more, it is also found that the pin with immerged length of about 1 mm locates at y = 2.8 mm paralleling to the X-axis. Thus, the position of the pins in the onions can be confirmed as followed: the pin locates 0.5 mm beneath the surface of the onion and at y = 2.8 mm parallel to X-axis. Another experiment not displayed here shows the penetration depth in the onion can reach 2.5 mm.
Nano-step height measurement
A glass-substrate grating is tested by laser confocal feedback system. Different from the two tests above, both the amplitude (A) and phase (ϕm) information of the laser intensity modulation Im(2Ω) are utilized to determine respectively the integral and fractional number of the half laser wavelengths contained in the height variation of the grating surface.
In nano-step height measurement, the laser confocal feedback system combines coarse-resolution measurement using the intensity modulation amplitude and fine-resolution measurement using the phase information to realize the non-ambiguous high-resolution profile measurement of micro-nano structure within about ten microns range. When measuring the height difference Δh of two lateral positions (e.g. steps) on the sample surface, it obtains the integral number n of λ/2 contained in Δh based on the amplitude (A) variation of laser intensity and the fractional number s of λ/2 using the phase measurement. Finally the height difference is computed as followed,

where  is a calibrated coefficient to take into consideration the influence of the high NA of the objective, whose value is carefully calibrated to be 0.93.
is a calibrated coefficient to take into consideration the influence of the high NA of the objective, whose value is carefully calibrated to be 0.93.
Firstly, the defocus response curve is vertically scanned as shown in Fig. 6(a), where the working linear slope region is indicated by dashed ellipse. Its corresponding variation of axial position is about 10 μm. During the test, the defocus amount (z) of the sample is located in this region, whose linear slope can be used to analyze the integral number of the half laser wavelengths. According to Fig. 6(a), the half-wavelength defocus variation (z) corresponds to the amplitude (A) variation of 0.2 V in the laser intensity.
Then, a lateral line-scan is carried out on the grating surface, with the phase and amplitude of the laser intensity modulation Im(2Ω) demodulated simultaneously, shown in Fig. 6(b). Due to the mount adjustment limitation of the current setup, the grating surface is not strictly normal to the probing laser beam, resulting in the slopes in Fig. 6(b). Because the measured glass-substrate grating is an obsolete testing sample from a grating etch department, not a well fabricated one, the results obtained in Fig. 6 (b) are not so good as that in Fig. 2(b). Nevertheless, the upper and lower planes of the steps etched on the glass substrate can still be clearly distinguished and be gained by least-square linear fitting as shown in Fig. 6(b). As shown in Fig. 6(b), the upper and lower planes of the steps are denoted by the two parallel lines in both amplitude and phase curve. Thus, the amplitude (A) variation represented by the spacing between these two lines is slightly greater than 0.2 V, revealing that the steps' height contains one half wavelength (i.e., the integral number is one). With the same process, the height represented by the phase (ϕf = ϕm − ϕr) variation is measured to be 110 nm. At last, the step height is calculated to be 597 nm by using the Eq. (1). The same step height is measured by AFM and the result is 590 nm, which agrees well with our result. Therefore, the measurement proves the capability of laser confocal feedback system to conduct high-resolution profile measurement within a range of about ten microns.
In this part of experiments, to remove the environmental disturbance, a reference mirror Mr in Fig. 1 is used to generate laser intensity modulation Ir(Ω), from which the environmental disturbance (represented by ϕr) can be recovered to compensate the phase information (ϕm) of the measurement beam. Based on this multiplexing principle12, the compensated phase measurement stability (ϕf = ϕm − ϕr) for determining the fractional number s of λ/2 can be largely improved to nanometer scale in common environments, which promises the high accuracy for this approach in nano-step height measurement of mirco-nano structure.
To accurately obtain the amplitude (A) and phase (ϕm) variation of laser intensity modulation, we use a lock-in amplifier (Zurich Instruments, HF2LI) to realize heterodyne measurement of these parameters. The accuracy of phase measurement is about 0.1°, which corresponds to the resolution of 0.3 nm height variation. Taking the environment into account and with the compensation of the reference arm, the effective resolution is about 2 nm in the step height measurement of glass-substrate grating.
Discussion
For an ideal confocal system with infinitesimal point detector and pinhole, the detected intensity can be written as13


where z is the de-focus of the sample surface, sinα is the NA of the objective, λ is the laser wavelength, u is the normalized defocus of the sample surface. According to Eqs.(2) and (3), when the normalized defocus u increases, the detected laser intensity I decreases sharply, which indicates good axial resolution, i.e., the ability of axial tomography.
While, for a practical confocal system with detector and pinhole of finite size, the detected intensity is13

in which Kr is normalized constant, the ρ, ν2 are normalized radial coordinates in pupil and object planes, respectively, νd is the radius of the pinhole.
It has been proven that under weak optical feedback strength, the feedback light induced laser intensity modulation ΔI can be expressed as8,12

in which Is is the free running laser intensity, κ is the effective feedback level, G(2Ω) is the frequency dependent amplification term related to the microchip laser dynamics9,10, ϕ = 4πL/λ is the phase of the feedback light and ϕs is a fixed phase shift.
For laser confocal feedback system, the combination of the Eqs.(4) and (5) can be expressed as

It's obvious from Eq. (6) that through simultaneous demodulation of laser intensity modulation by lock-in amplifier, we can get the amplitude (A = I(u(z)) = I(z)) and the phase (ϕ =  ) information.
) information.
The amplitude A (or I(z)) is the defocus response curve of the laser feedback confocal system, which is used to discriminate the reflective interface in the inner of the samples, such as MEMS device measurement, biological tissue inspection, etc. It utilizes the positioning ability of confocal system to achieve the tomography in the inner of samples. The system's vertical resolution depends on the defocus response curve. The narrower the FWHM of the curve is, the higher the resolution can be, as well as the ability of the tomography. Its typical value ranges from 1 μm to several tens of microns.
However, for surface profilometry, it is far from accurate. In the surface measurement of micro-nano structure, it should reach nanometer accuracy. Apart from the amplitude A, the phase information ϕ can be used to discriminate the defocus amount z with very high resolution at nanometer scale, i.e. the fractional number s of λ/2 can be accurately determined. But then the non-ambiguous range of profilometry measurement will still be λ/2, which greatly limits the applications. While the amplitude information A is directly related to the defocus amount z. The amplitude A(z) gradually decreases as the target surface deviates from the focus plane. As shown in Fig. 7, within the slope region MN of the curve, the amplitude A(z) keeps an approximately linear relationship with z. Therefore, the absolute position of the target surface can be determined within this region based on A measurement. Although it is hard for us to get the z with high resolution by measurement of A, it's easy to discriminate z variation of λ/2 based on the A information, i.e., we can judge the integral number n of λ/2 by amplitude A measurement. Finally, through the combination of the amplitude A and phase ϕ measurement (also seen Eq. 1), the surface profilometry measurement of nanometer resolution and a range of about ten microns can be achieved.
Another advantage of this approach is the high sensitivity to the weak signal scattered or diffused by the samples. Comparing the Eq. (6) with Eq. (2), an extra gain factor G(2Ω) is induced by the laser feedback, whose value ranges from 104 to 106. In traditional laser confocal system, the detectable intensity signal decreases sharply with the increase of the penetration depth, which limits its imaging depth. Benefiting from this large gain factor as large as 104 to 106, the undetectable intensity signals for traditional confocal system will be easily sensed in this approach. Consequently, it promises the application in the imaging of highly scattered or diffused medium, such as biological tissue, MEMS devices and also in contact-free surface profilometry for low reflective samples, such as glass-substrate grating (no coating).
In conclusion, the laser confocal feedback technology is realized by the combination of laser frequency shifted feedback and confocal microscopy. This approach thus has the advantages of various technologies, including high sensitivity of microchip laser feedback, the tomography and absolute positioning ability of the confocal microscopy and the high-resolution and stability of heterodyne phase measurement. The MEMS device and biological samples containing pin inserted are scanned to obtain their cross-sectional images, which proves its ability of tomography and high sensitivity in the imaging of highly scattered medium. The accurate measurement of micro features on glass-substrate grating presents its high resolution and absolute positioning in a non-ambiguous range of about ten microns.
Methods
Optical frequency shifted feedback
A pair of acousto-optic modulators (the driving frequencies are 70 MHz and 70 ± Ω MHz, respectively) is used in this approach, whose different diffraction beams are utilized to generate the probing feedback beam with frequency shifting 2Ω and reference feedback beam with frequency shifting Ω, respectively. The typical value of 2Ω is selected to be approximately 1 MHz, which is close to the relaxation oscillation frequency (1.2 MHz) of the laser. Thus, the gain factor G(2Ω) is obtained to be as large as 105. By this amplification, it is easy for this approach to detect the extremely weak signals scattered or diffused by the sample and thereby to get a large penetration depth in samples. Furthermore, the probing and reference feedback beams induce the intensity modulation at 2Ω-frequency and Ω-frequency, respectively. By demodulating these modulation signals, we obtain the phase variation of these beams, which respectively represents the surface information of the sample and environmental disturbance. The subtraction between these two phase variations accurately reflects the micro-nano structure of the sample surface with high resolution at nanometer scale.
Laser confocal feedback
The laser confocal microscopy is induced to achieve the ability of tomography. Together with the laser feedback, it generates the approach of laser confocal feedback, in which the beam waist of the laser serves as virtual pinholes for both the point light source and the point detector. And thereby the microchip Nd:YAG laser is used as the corresponding point light source and point detector.
Combination of the integral and fractional numbers of half laser wavelength
In the measurement of surface profilometry, the amplitude (A) and phase information (ϕ) obtained from the lock-in amplifier are used to respectively determine the integral and fractional number of the half laser wavelengths contained in the height variation of the sample surface. The combination of them achieves accurate measurement of the surface profilometry with high resolution in a non-ambiguous range of about ten microns.
Data acquisition and analysis
The data were acquired with an acquisition card from National Instruments Inc. (NI, USA). The Labview software program developed by NI was used to analyse the data.
References
King, P. G. R. Metrology with an optical master. New Sci. 17, 180–182 (1963).
Rudd, M. J. A laser Doppler velocimeter employing the laser as a mixer oscillator. J. Phys. E. 1, 723–726 (1968).
James, A. S., Ulrich, W. R. & Chrimsian, P. B. Lasers with optical feedback as displacement sensors. Opt. Eng. 34, 2802–2810 (1995).
Otsuka, K. Laser-Fluctuation measurements in a bath of strong gaussian noise. Appl. Phys. 18, 415–419 (1979).
Otsuka, K. Effects of external perturbations on LiNdP4O12 lasers. IEEE J. Q. E. QE-15, 655–663 (1979).
Otsuka, K. Highly sensitive measurement of doppler-shift with a microchip solid-state laser. Jpn. J. Appl. Phys. 31, L1546–L1548 (1992).
Otsuka, K. Self-mixing thin-slice solid-state laser metrology. Sensors 11, 2195–2245 (2011).
Kawai, R., Asakawa, Y. & Otsuka, K. Ultrahigh-sensitivity self-mixing laser Doppler velocimetry with laser-diode-pumped microchip LiNdP4O12 lasers. IEEE. Photonic. Tech. Lett. 11, 706–708 (1999).
Otsuka, K., Abe, K. & Ko, J. Y. Real-time nanometer vibration measurement with a self-mixing microchip solid-state laser. Opt. Lett. 27, 1339–1341 (2002).
Sudo, S., Miyasaka, Y., Nemoto, K., Kamikariya, K. & Otsuka, K. Detection of small particles in fluid flow using a self-mixing laser. Opt. Exp. 15, 8135–8145 (2007).
Sudo, S., Miyasaka, Y. & Otsuka, K. Quick and easy measurement of particle size of Brownian particles and plankton in water using a self-mixing laser. Opt. Exp. 14, 1044–1054 (2006).
Tan, Y. D., Zhang, S. L., Xu, C. X. & Zhao, S. J. Inspecting and locating foreign body in biological sample by laser confocal feedback technology. Appl. Phys. Lett. 103, 101909 (2013).
Wan, X. J., Li, D. & Zhang, S. L. Quasi-common-path laser feedback interferometry based on frequency shifting and multiplexing. Opt. Lett. 32, 367–369 (2007).
Xu, C. X., Tan, Y. D., Zhang, S. L. & Zhao, S. J. The structure measurement of micro-electro-mechanical system devices by the optical feedback tomography technology. Appl. Phys. Lett. 102, 221902 (2013).
Lacot, E., Day, R. & Stoecke, F. Laser optical feedback tomography. Opt. Lett. 24, 744–746 (1999).
Wilson, T. Confocal Microscopy. 1–64 (Academic Press, London, 1990).
Wanitz, H. & Rinneberg, H. Imaging in turbid media by photon density waves: spatial resolution and scaling relations. Appl. Opt. 36(1), 64–74 (1997).
Denk, W., Strickler, J. & Webb, W. Tow-photon laser scanning fluorescence microscopy. Science 248, 73–76 (1990).
Bewersdorf, J., Pick, R. & Hell, S. Multifocal multiphoton microscopy. Opt. Lett. 23, 655–657 (1998).
Wang, L. H. V. & Hu, S. Photoacoustic tomography: in vivo imaging from organelles to organs., Science 335, 1458–1462 (2012).
Xiang, L. Z., Wang, B., Ji, L. J. & Jiang, H. B. 4-D photoacoustic tomography. Sci. Rep. 3, 1113 (2013).
Huang, D. et al. Optical coherence tomography. Science 254, 1178–1181 (1991).
Gambichler, T., Jaedicke, V. & Terras, S. Optical coherence tomography in dermatology: technical and clinical aspects. Arch. Dermatol. Res. 303, 457–473 (2011).
Li, S. G., Xu, Z. G., Yoon, S. F. & Fang, Z. P. Feasibility study on bonding quality inspection of microfluidic devices by optical coherence tomography. J. Biomed. Opt. 16, 066011 (2011).
Lacot, E., Day, R. & Stoecke, F. Coherent laser detection by frequency-shifted optical feedback. Phys. Rev. A 64, 043815 (2001).
Sekine, T., Shimizu, K. & Otsuka, K. Applying the Self-Mixing Effect of a Microchip Laser to Optical CT. Proc. SPIE 4630, 41–47 (2002).
Schmit, J. & Hariharan, P. Improved polarization Mirau interference microscope. Opt. Eng. 46, 077007 (2007).
Lehmann, P. Systematic effects in coherence peak and phase evaluation of signals obtained with a vertical scanning white-light Mirau interferometer. Proc. SPIE 6188, 618811 (2006).
Bearden, A., O'Neill, M. P., Osborne, L. C. & Wong, T. L. Imaging and vibrational analysis with laser-feedback interferometry. Opt. Lett. 18, 238–240 (1993).
Acknowledgements
This work was financially supported by National Natural Science Foundation of China (Grant No. 50805084), Tsinghua University Initiative Scientific Research Program (2012Z02166) and Special-funded Program on National Key Scientific Instruments and Equipment Development of China (2011YQ04013603).
Author information
Authors and Affiliations
Contributions
Y.T. designed the experiments, developed the concept, constructed up the optical hardware, carried out the experiments of imaging biological samples and wrote this manuscript. S.Z. designed the experiments, developed the concept and supervised the entire project. C.X. implemented the experiments of MEMS devices test. W.W. carried out the grating test.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Tan, Y., Wang, W., Xu, C. et al. Laser confocal feedback tomography and nano-step height measurement. Sci Rep 3, 2971 (2013). https://doi.org/10.1038/srep02971
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02971
This article is cited by
-
In-process monitoring of atmospheric pressure plasma jet etching using a confocal laser displacement sensor
Microsystem Technologies (2023)
-
All-digital 3-dimensional profilometry of nano-scaled surfaces with spatial light modulators
Applied Physics B (2021)
-
High-accuracy self-mixing interferometer based on multiple reflections using a simple external reflecting mirror
Optoelectronics Letters (2018)
-
Measurement of the emission spectrum of a semiconductor laser using laser-feedback interferometry
Scientific Reports (2017)
-
Non-invasive human extremely weak pulse wave measurement based on a high-precision laser self-mixing interferometer
Optoelectronics Letters (2017)