Introduction

Quantum theory and the relativistic no-signalling principle both give ways of controlling information, in the sense that someone who creates information somewhere in space-time can rely on strict limits both on how much information another party can extract and on where they can obtain it. While standard quantum cryptography (e.g.1,2,3,4,5,6) uses only the properties of quantum information, an increasingly long list of applications illustrate the added cryptographic power of the relativistic no-signalling principle, either alone (e.g.7,8,9,10), or when combined with quantum information (e.g.11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37).

A new relativistic quantum cryptographic technique was recently introduced, inspired by the no-summoning theorem35, in which one agency (Alice or A) sends a quantum state, supplied by and known to another agency (Bob or B) but unknown to A, at light speed c in one of a number of possible directions. We use the term agency here to stress that Alice and Bob are not single isolated individuals: they have representatives (who we assume are all loyal and act according to the instructions of their agency) distributed at various points in space-time. The task is securely implemented if the chosen direction is concealed from B until A chooses to return the state. This gives, inter alia, a provably unconditionally secure protocol for bit commitment36 and a way of transferring data at a location unknown to the transferrer37.

Another class of applications arises in scenarios where the unknown state is a quantum authentication token supplied either by B or by a third party C. A may wish to use this token, by transferring it to B, at a space-time location Qi that she chooses, without giving B advance notice of her choice. For example, the token here might be a quantum password authenticating access to a site, or quantum money used to execute a trade.

In their simplest forms, all these applications require A to propagate the quantum state securely from one point P to one of a number of points Q1, …, Qn in its causal future, in such a way that B cannot obtain any advance information about A's choice of Qi. We first discuss ways of implementing this task of secure unknown state transmission to a hidden location.

Next we consider an extended task where A also wants to allow B to verify that the state was sent to the chosen Qi, at or after the point Qi. If the state was indeed securely transmitted, this can in principle be achieved by returning it to B at Qi, where B can measure the returned state and test whether it is the state he originally provided. As we will see, if the state originally supplied is a pure qudit known to B, Alice's probability of passing this test at two distinct specified sites is O(d−1), where d is the dimension of the Hilbert space. We can thus ensure both that A's transmission is secure against B until the state is returned and that B can be near-certain of which point Qi was chosen after the state is returned.

However, secure (or even insecure) quantum transmission from P to the Qi may not always be possible for A. Even in a future world in which reliable long-range quantum transmission technology exists, one can easily imagine scenarios in which A (a user of the infrastructure who has relatively few resources) does not have such technology, while B (an infrastructure provider with large resources) does. We describe here strategies for such scenarios, in which A and B exchange classical and quantum information so as to have the same cryptographic effect – i.e., A chooses one of the Qi, a choice that B can verify at or after the relevant Qi but not earlier – without A necessarily actually transmitting any unknown states to any of the Qi. We also describe a variation which achieves this result even when neither party has reliable long-range quantum transmission.

Furthermore, real life implementations must also allow for losses and errors. Here we show that relativistic quantum cryptography can be made secure even in the presence of moderate levels of losses and/or errors.

The results presented here show that there is considerable flexibility in the implementation of relativistic quantum cryptographic protocols. This makes the prospect of experimental implementation of such protocols much more realistic, thereby bringing them closer to practical applications.

We suppose throughout that B does in fact carry out the optimal verification measurements on states returned to him. The reason for assuming this is to define a quantifiable measure of security against A. In practice, B may actually verify only some, or none, of the returned states in any given run, depending on the ultimate application.

Results

Secure unknown state transmission to a hidden location

Theoretically, the standard assumptions for mistrustful cryptography give a way to justify assuming that A can securely transmit an unknown state from P to any Qi of her choice in the causal future of P, without B learning the choice of Qi in advance. The reason is that we must, in any case, assume that A has a “secure laboratory” – some region shielded from B in which A can carry out any classical or quantum operation securely. If we take A's laboratory to include linear channels between P and Qj for each j, her quantum transmissions along these channels are, by definition, secure.

In practice, however, it may not always be so easy to justify this security assumption. Keeping a long quantum channel physically secure against all eavesdropping is problematic. Indeed, even insecure high fidelity terrestrial quantum transmission over more than 100 km or so is currently difficult. A further practical problem is that one would ideally like no constraint on the Qi except that they lie in the causal future of P: in particular one would like to be able to implement the task when the Qi are (nearly) lightlike separated from P. However, the presently most advanced quantum communication technology involves sending light pulses along standard fibre optic cables. These have relatively high refractive index, so that the transmission speeds are typically only about . Sending light pulses through air or free space is an alternative and allows transmissions at speeds close to c, but keeping such transmissions secure over long ranges may be harder still.

(Perhaps photonic crystal fibres may in the future offer another way of sending light pulses at speeds close to c: even if so, the problem of secure long range transmission remains.).

Here we propose ways around these problems, in the form of implementations that do not require long physically secure quantum channels, or in some cases even long range quantum communication.

To simplify the discussion, we start with the idealized assumptions that all local classical and quantum operations in the protocol can be implemented perfectly and instantaneously and that all classical and quantum signals can be sent at in vacuo light speed. We discuss errors, losses and delays later. We also start with the assumption that both parties can verify that any qudit involved in the protocol really is a qudit, i.e. that it is completely characterised as a quantum state in a prescribed d dimensional Hilbert space and carries no hidden information in other degrees of freedom. While this assumption is quite standard in the quantum cryptographic literature, it is obviously questionable. We discuss later how it can be guaranteed.

Secure quantum channels

We are interested in three types of secure quantum channel:

S1. Physically secure quantum transmission channels As already noted, it is standard (and necessary: without such an assumption, cryptography is effectively pointless), in considering cryptography involving mistrustful parties, to assume that each party has at least one secure “laboratory” – a region of space (or, more generally, space-time) within which they can carry out any operations they wish with an assumed guarantee of privacy. In particular, the parties can transmit quantum states securely within their laboratory. One theoretically legitimate way of ensuring that a party has a secure quantum channel between space-time points P and Q is thus simply to assume that their laboratory contains a timelike or lightlike path between the points.

S2. Quantum teleportation between secure sites If A has predistributed a maximally entangled d-dimensional state between secure sites P and Q, she can teleport an unknown qudit |ψ〉P from P to Q by carrying out a generalized Bell measurement on the two qudits at P, transmitting the outcome i (which ranges from 1 to d2) classically over a public channel to Q and applying an appropriate unitary Ui to the qudit at Q. The outcome i carries no information about |ψ〉P: all outcomes are equiprobable. Thus, |ψ〉P is securely transmitted to Q, even though the classical channel is public.

Note also that if A has predistributed maximally entangled d-dimensional states between P and Qj, for a range of j, she can choose which Qj to teleport the qudit to. If she broadcasts the classical teleportation data, not only is |ψ〉P securely transmitted to Qj, but the identity of Qj is kept secret from B, unless and until A chooses to reveal it, for instance by returning |ψ〉 to B there.

S3. Transmitting randomised quantum states Another way of securely transmitting |ψ〉P is first to apply a randomly chosen teleportation unitary at P, creating the state Ui |ψ〉P, then to send this state over a (not necessarily secure) quantum channel, while separately sending the classical data i over a secure classical channel along (essentially) the same path. The state |ψ〉 is then regenerated by applying at the end of the path. The quantum transmission carries no information about |ψ〉, since

By assumption, the classical data i are sent securely and so also give B no information about |ψ〉.

Hence, if A wants to send |ψ〉 from P to a site Qj and keep the identity of Qj secret, she need simply generate appropriate dummy transmissions from P to Qk, for each k ≠ j. One way of doing this is to send randomly chosen qudits from P to each Qk (k ≠ j) while securely broadcasting the classical data i from P to all the sites Qk (including Qj).

In each case, A uses a secure classical channel to tell her agents at each Qk whether they have received the real state or a dummy. The secure classical channels we consider here and below could, for instance, be created by previously distributed secret keys that allow encryption of classical information followed by public broadcasting.

In theory, any of the secure channels 1–3 could be used for long distance relativistic quantum cryptographic protocols. Presumably technology will ultimately make long range quantum channels of types 2 and 3 practical and reliable. However, at present, we do not have reliable practical teleportation, nor reliable long-term quantum state storage for teleportation with predistributed entanglement and the necessary quantum transmissions for type 3 channels become increasingly challenging as the channel length (in the lab rest frame) increases. Ensuring that a quantum transmission channel of type 1 is physically secure is also challenging: it requires resources that scale at least linearly with length and may simply not be practical or possible over long distances in many scenarios. For example, a party may be able to set up secure labs at well separated locations on Earth and/or satellites, but have no way of keeping secure any nearly linear quantum channel path between them: all such paths may go through regions controlled by or open to others.

Extending a secure quantum channel classically

We propose the following technique to get around these obstacles. Suppose that Alice controls some (perhaps small) region around the space-time point P from which she wishes to send an unknown qudit to one of the space-time points Qj (j = 1, …, N) at (or near) speed c. Define the space-time points such that P, and Qj are collinear and is on the boundary of the region she controls around P. In practice, we imagine will generally be much closer to P than to Qj. Instead of sending a quantum state |ψ〉 securely from P to Qj and returning it to Bob there, Alice sends |ψ〉 securely from P to , applies a random teleportation unitary Ui somewhere en route and returns the state Ui |ψ〉 to Bob at . She transmits the classical data i securely from (or wherever it was generated) to her lab at Qj and gives it to Bob (only) there. (See Figure 1.)

Figure 1
figure 1

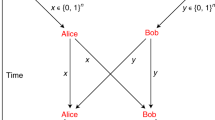
Illustration, in 1 + 1 dimensions (not to scale), of how quantum channels can be securely extended classically.

Alice controls a laboratory including on its border the points P, and and disjoint laboratories including on their borders the points Q1 and Q2 respectively, where and are lightlike lines. Bob may control the rest of space-time. Alice receives the unknown state |ψ〉 from Bob at P and transmits it securely to (where she chooses i = 1 or 2). There she randomizes it and returns the randomized state to Bob. The classical data describing how the state was randomized are transmitted along a secure classical channel and returned to Bob at Qi. Alice transmits dummy quantum and classical information and returns them to Bob at the corresponding points on the opposite wing.

Full size image

Precisely how and where the unitary Ui is applied depends on the type of quantum channel Alice uses between P and . In the cases of quantum teleportation, the teleportation measurement generates i (which Alice sends securely from P rather than to Qj) and the state Ui |ψ〉 is created at by the teleportation. In the case of randomised quantum state transmission, Alice generates the randomised state Ui |ψ〉 at P, transmits it to and returns it there to Bob and again sends i securely from P to Qj. If the channel from P to is physically secure, Alice need not generate i and randomise |ψ〉 until , although again she can do both at P if she wishes.

In each case, to ensure that Bob does not learn the choice of Qj prematurely, Alice generates random dummy qudits that are returned to Bob at (for all k ≠ j). She also either sends random dummy classical transmissions towards each Qk from (for k ≠ j) or, if her classical data were already generated at P, broadcasts the classical data securely to all the Qk. Finally, via secure classical channels, she tells each of her agents at Qk whether “their” state is real or a dummy.

Security of classically extended quantum state transmission

In their original form, the various relativistic cryptographic schemes we consider are secure against Alice essentially because the no-cloning38,39 and no-summoning35 theorems imply that she cannot generate copies of the unknown state |ψ〉 at more than one point Qj, provided the Qj are spacelike separated. Moreover, if P is lightlike separated from each Qj, then her actions at P essentially determine at which of the Qj she will be able to generate |ψ〉. More generally36, they determine her optimal probabilities pj of producing states that give Bob a positive outcome for a projective measurement onto |ψ〉 〈ψ| at Qj and for a fixed number of sites these satisfy .

Perhaps counterintuitively, the same security argument also holds for the classically extended versions of the scheme described here. The reasoning is simple. When Bob receives the state Ui |ψ〉 at , he could transmit it at light speed from to Qj and, upon receiving the classical information provided by Alice at Qj, apply the inverse unitary . This procedure produces at each site Qj a quantum state. Compared to the situation where Alice has physically secure quantum transmission channels from P to the Qj (case S1), this procedure is more restricted for Alice and hence offers her less cheating strategies. Therefore the bounds that apply in case S1 also apply for the present protocol and in particular the optimal probabilities of these states passing Bob's tests must satisfy .

These classically extended schemes are also clearly secure against Bob, since he possesses no information correlated with |ψ〉 until he can combine both Ui |ψ〉 and i, i.e. until the point Qj where the state is returned.

Other schemes and resource tradeoffs

In these classically extended schemes, Alice needs to be able to receive an unknown state, randomize it and transmit it a short distance securely at light speed along her chosen path, return it to Bob and transmit the classical randomization data at light speed securely over a long distance. Short range secure transmission of a quantum state is, clearly, easier than long range transmission. Reliable long range secure transmission of classical data can be easily achieved, using pre-shared one-time pads (or, if the range is within the limits of current technology, quantum key distribution). These schemes thus appear practically advantageous for Alice.

Note, however, that for many cryptographic applications Bob must be able to verify that the points at which the state is returned are space-like separated. For example, this is necessary in the bit commitment schemes of Ref. 36, which require Alice to be forced to choose Qj (and hence ) at or before the point P. (To be precise, Alice is required to choose a probability distribution over j, since she can commit to a superposition of bits.) Any other cryptographic application that requires Alice to be prevented from deciding the value of j at a point in the future of P similarly requires the to be space-like separated: if they are not, she can sequentially send the quantum state between non-space-like separated and decide en route at which site she will return the state. The need for space-like separated poses its own practical challenges, requiring more precise timings and shorter transfer delays, as the separations grow shorter.

Note also that, instead of receiving the quantum state |ψ〉 at Qj and measuring it there, Bob now receives separately Ui |ψ〉 at and i at Qj. He has more than one option, depending on the available technology and on how quickly (where in spacetime) he needs to verify the unveiled commitment. For example:

B1. Bob can transmit Ui |ψ〉 from to Qj, apply at Qj and check there that the resulting state is indeed |ψ〉. This requires Bob rather than Alice to have a long range quantum channel, an advantage in the scenarios we envisage in which Bob's technology is better. A further advantage is that Bob's long range channel need not necessarily be secure. Alice would gain no cheating advantage, compared to the original version of the scheme with long-range quantum transmissions, by being able to tamper with this state en route – in the original scheme, she controls the state throughout the path from P to Qj.

B2. Bob can store Ui |ψ〉 at the space coordinate of , transmit i there from Qj, apply there and check that the resulting state is |ψ〉. This requires Bob to have quantum state storage. It also delays his verification of the state, which is a disadvantage in some contexts. For example, if the state is used as an authentication token, Bob cannot immediately verify Alice's authentication at Qj. However, it would be advantageous in a possible scenario in which reliable local quantum state storage turns out to be easier than reliable long range quantum transmission.

These two options have one very clear advantage in the near-ideal case where Alice and Bob's errors and losses can be made small through error correction or advanced technology. In this case the quantum information encoded in the unknown state remains essentially intact. Bob can thus make use of the token as he wishes. For example, he could return the token to Alice if, at the relevant point Qj, she decides she wishes not to use it, but to propagate it to another site in the causal future of Qj. Alternatively, he could pass it on to a third party for storage or testing.

Errors, losses and delays

In realistic implementations of protocols using any of the secure channels S1–S3, A and B's channels and devices will introduce some errors, their channels will suffer losses and Bob's detectors will also cause losses as well as detection errors. We now show that, in principle, provided the levels of losses and errors are not too great, they can be securely countered by redundant implementations of the protocol.

The idea here is that, instead of providing A with one random qudit at P, B provides her with N independently chosen random qudits in short time sequence (so they all arrive close in time to the spacetime point P). A is supposed to send all of them to (points correspondingly close in space-time to) her chosen site Qj and return them to B there. B accepts the site as chosen provided that he receives and verifies a sufficient fraction of the qudits.

This protocol is more robust than the original protocol because Bob will not abort even if a small fraction of the particles are lost or corrupted by noise. We show below that this protocol can tolerate losses of up to () of the particles. For definiteness we consider only the case where A tries to pass Bob's statistical tests at two distinct sites, Q1 and Q2. The argument generalizes simply to the multi-site case using the fidelity bound40,41,42,43 on symmetric 1 → n approximate cloning.

Recall first the situation when Alice is provided with a single qudit. She returns to Bob at sites Q1 and Q2 the states ρ1 and ρ2 respectively. The probabilities of passing Bob's test at the two sites are

They obey36

Now suppose Alice is given the N independent random qudits |ψ1〉, …, |ψN〉 and carries out a collective operation producing outputs ρi1 and ρi2 for |ψi〉, which are returned to Bob for testing at the respective sites. A complication in analysing this situation is that Alice can act collectively on all N qudits, which in principle might increase her cheating probability compared to strategies involving only individual qudit operations. We now show this is not the case.

We suppose that Bob tests all N pairs of returned qudits in succession at sites Q1 and Q2. Denote by N1 ≤ N and N2 ≤ N the number of qudits that pass Bob's test at sites Q1 and Q2 respectively. Bob accepts at site Qi if . Let be the probability that Bob accepts at site Qi. We show that the sum of the probabilities of acceptance at both sites is bounded by

which is the analog of eq. (3) and establishes security against Alice.

We note that security against Bob is as before, since he does not have access to any information until Alice provides him with the reveal information.

The proof of eq. (4) is carried out in two steps. The first step essentially shows that collective operations do not help Alice. We prove the following. Suppose that Bob's tests on ρi1 and ρi2 for 1 ≤ i ≤ k − 1 produce some results. Then, conditional on these results, the fidelities pk1 and pk2 on the k-th pair of returned qudits must satisfy

To see this, suppose that there were some collective operation O for which, conditioned on some set D of results for 1 ≤ i ≤ k − 1, Alice could violate this bound. She could then proceed as follows: (i) create a random set of qudits |ψi〉 for 1 ≤ i ≤ k − 1 together with a maximally entangled state of two qudits; (ii) apply the operation O on the |ψi〉 together with one of the entangled qudits; (iii) test the first (k − 1) outputs; (iiia) if she does not obtain distribution D of the results, return to (i) generating a new set of qudits. (iiib) if she obtains distribution D, apply a teleportation protocol using |ψk〉 and the other entangled qudit, use the teleportation measurement result to define a teleportation unitary U in the standard way, then apply U to the two outputs corresponding to |ψN〉 and return these rotated outputs to Bob for testing.

The probabilities of Bob's test outcomes after step (iiib) are independent on whether the teleportation was carried out before or after the cloning operation and so must violate (5). But this is a contradiction, since Alice now has a generally applicable protocol for violating the universal bound (5) for cloning a single unknown state.

The second step uses large deviation results for martingales and in particular the Azuma-Hoeffding inequality50,51,52 to prove eq. (4). This more technical step is given at the end of the paper.

Note that security for redundant protocols always requires a total error and loss rate, for Alice's operations, of less than . If the allowed total rate is greater than 1/2, a technologically advanced Alice whose devices have no losses or errors could cheat by sending 1/2 the states to each of Q1 and Q2 and later choosing the site at which she will return the correct states to Bob. This choice may depend on information that may have become available at both Q1 and Q2, allowing her actions at the two sites to be coordinated. For example, it could depend on some event that will happen either at Q1 or Q2 but not both and that Alice cannot predict in advance. (See Ref. 44 for a formal general discussion of security based on an oracle input model. An independent discussion of another proposed security model can be found in Ref. 45.).

On the other hand, the above argument shows that for sufficiently large N a loss rate lower than suffices. Even the weaker of these bounds – total error and loss rate less than – appears practically challenging with current technology.

Delays are another practical issue: realistically, A and B's state exchanges and quantum operations will not be instantaneous and their channels will transmit quantum states at speeds slower than c. As noted elsewhere35, such delays affect the details of B's security guarantee – he is no longer guaranteed that A was effectively committed to a choice Qj (or probability distribution of choices) precisely at the point P, for example. (As with all technologically unrestricted quantum protocols46,47, Alice can create a quantum superposition of commitments – in this case at, or in the non-ideal case near, P. Nonetheless, her optimal probabilities for successful unveiling are constrained by Eq. 5.) However, so long as they are small compared with the spacelike separations of the Qj, B is still guaranteed that A was effectively committed to a choice (or probability distribution of choices) of site Qj in advance, at a point relatively close to P.

Note also that, for secure implementations of variations B1 and B2 to be possible, Alice needs to receive and return N states in times short compared to the short separations between P and the sites .

Long-range implementations when neither party has long distance state transmission or state storage

Redundant implementations also allow security even where neither party has reliable long distance state transmission or state storage. For example:

B3. Suppose again that the unknown state is replaced by N independent states, generated by Bob. Alice receives these N labelled independent random states |ψk〉 in quick succession at (approximately) the same point P and is required to return the ordered set of states to Bob at and the ordered set of numbers {ik} to Bob at Qj. Bob can then test her claimed choice of Qj statistically by carrying out suitable randomly chosen measurements on the states and comparing the results to the list {ik} at any point where he can combine both sets of data: in particular he can do so at Qj.

For example, one simple test strategy is for Bob to take N = M d2 for and to make random guesses of the value of each ik, carry out measurements at to test whether the returned state is (for each k) and later compare these results to the values ik, focussing on the ≈ M cases where he guessed correctly (i.e. ). The probability that Bob guesses correctly at least (say) times is 1 − η(M), where η(M) → 0 as M → ∞. M is chosen so that is suitably large for the security argument above to apply given the level of errors and losses encountered, while η(M) is suitably small.

This variation still requires a total error and loss rate lower than 1/2 and so still appears practically challenging with current technology. However, as it requires neither quantum state storage nor long range quantum transmission from either party, it may be implemented in practice sooner than B1 or B2, as it requires only states of small dimension d to be created and manipulated, with no more advanced quantum technology needed by either party.

Note again, though, that for a secure implementation to be possible Alice needs to receive and return N states in times short compared to the short separations between P and the sites . Also, the quantum information encoded in the states is effectively destroyed by Bob's measurements, so this variation of the protocol cannot generally be combined with applications in which some quantum states supplied by Bob are subsequently used for another purpose.

Side channels and related security issues

As noted above, a quite general potential concern in quantum cryptography is that an adversary may exploit physical degrees of freedom other than those prescribed by the protocol. For example, in the protocols considered here, Bob is supposed to provide a randomly chosen qudit, which might for instance be supposed to be encoded in photon polarizations. He could, however, use a side channel and surreptitiously encode extra information in other degrees of freedom, such as position/momentum, energy/time, or number/phase. If Alice then sends the photons along physically insecure channels, she is in principle vulnerable, even if the polarization degree of freedom is appropriately randomized. If Bob can carry out a nondestructive measurement of the other degree of freedom, he can identify the channel carrying the photons he supplied, without detection.

A (theoretically) simple way for Alice to counter this was first noted by Lo and Chau48 in considering an analogous security problem in quantum key distribution. Alice can prepare her own maximally entangled pairs of qudits, in separate secure (but closely adjacent) labs in the neighbourhood of P. She teleports the relevant information encoded in each (purported) qudit supplied by Bob from the first lab to the second and uses the resulting teleported states in the remainder of the protocol. Since she prepared the relevant qudits herself, she can ensure that they carry no information other than that prescribed by the protocol.

To employ this strategy, Alice clearly must be able to teleport states at least over short distances. She may thus simply use the version of the protocol described above, in which teleportation is used as a short secure channel. If so, of course, she needs only teleport any given qudit supplied by Bob once (from P to ). This already guarantees the qudit carries no extra information and so there is no need for a separate initial teleportation in the neighbourhood of P.

Another possible way of dealing with this issue could be to design device independent protocols for the tasks discussed here. Device-independent protocols have been proposed for QKD18,19,20,21,22,23,24,25,26,27,28,29, quantum randomness expansion30,31,32 and bit commitment and coin tossing33, among other tasks. Many of these protocols have been shown to be vulnerable to attacks when devices are reused49, although possible defences have also been identified49. The ultimate scope of device-independent quantum cryptography remains an intriguing open question. It therefore would be interesting to explore whether device- independent protocols can be adapted to the relativistic cryptographic setting considered here.

Discussion

Each of the strategies discussed here has theoretical and practical advantages in some plausible potential future scenario. The teleportation-based strategies are particularly simple and elegant; strategies involving transmitting randomised states require no pre-distributed entanglement or joint operations on states; strategies involving physically secure quantum channels require no operations on quantum states.

We have also discussed schemes involving multiple states transmitted over classically extended quantum channels. These need only states of small dimension to be created and manipulated and need only short range secure quantum communication. While even these schemes still pose experimental challenges, they seem to us interesting candidates for practically implementing the unconditionally secure bit commitment protocol of Ref. 36 and other relativistic quantum cryptographic tasks over long ranges.

Note that, in the case of bit commitment, there are also other relativistic protocols available9,34, which rely on different principles. Which of these is most suited to practical implementation will depend on the precise application, as well as on the evolution of technology. Each has advantages that may be compelling in some scenarios. In particular, the protocol of Ref. 36 has the advantage that a bit can be committed at a point P and then persuasively unveiled at a single point Q lightlike separated from P, without waiting for data gathered at other spacelike separated points in order to verify the unveiling. It also has an efficiency advantage in networks where multiple lightlike transmission directions are possible: log N bits can be committed by transmitting an unknown qudit in a direction chosen from N possibilities.

In summary, we hope the schemes outlined here will encourage further theoretical and experimental investigation of the extent to which relativistic quantum cryptographic tasks can be securely and reliably implemented with current or forseeable technology. From a broader theoretical perspective, our discussion also illustrates an intriguing application of teleportation to cryptography, somewhat different from those previously considered. It was realised from the outset that teleportation has the beautiful cryptographic features that it enables A to communicate quantum information to B securely and to do so even when A does not know B's location. We see here another cryptographic feature of teleportation, relying on the fact that A can securely teleport a state, known to B but not to A, to a location, known to A but not to B. When light speed delays are negligible, this is not very significant, since A can teleport between any sites effectively instantaneously. In relativistic cryptography, though, it means that A can be constrained – she must choose one destination from a spacelike separated set – and yet conceal information (her choice of destination) from B. Our protocols also illustrate that, in quantum relativistic cryptography, the principle underlying teleportation – that classical and quantum communications can advantageously be separated and recombined at different locations – has much wider applications.

Methods

Proof details

We complete here the proof of eq. (4).

Suppose that Bob makes his measurements on the states in succession in some order. Denote by Dik the random variable which equals 1 (respectively 0) if Bob's test at site i on returned qudit k succeeds (respectively fails). Alice passes Bob's test at site i if where the security parameter . Let . To establish security with respect to a dishonest Alice, we need to bound .

Denote by . In section it was shown that A conditioning on the measurement results on returned pairs of qudits 1 ≤ i ≤ k − 1 cannot increase above her success probability of passing Bob's test on the k-th returned pair of qudits. From this it follows that Zk is a supermartingale50. That is |Zk| < ∞ and E(Zk|Wj) ≤ Zj for all k > j, where Wj is the set of all measurement outcomes up to and including round j. The martingale increments are bounded in absolute value by . Hence we can apply the Azuma-Hoeffding inequality50,51,52 to get (for any )

We now use this result to bound . We have

QED.