Introduction

Perovskite manganites RE1−xAExMnO3, where RE is the rare-earth element and AE the divalent alkaline-earth element, have attracted considerable attention due to the presence of multiple competing phases with essentially distinct physical properties but proximate free energies1,2. The delicate balance among the diverse phases can be easily tilted through “weak” external or internal perturbations and thus dramatic variation of the physical properties can be achieved. One of the typical examples is the magnetic field driven charge-order (CO) to ferromagnetic (FM) phase transition, which is accompanied by an insulator-metal transition and tremendous reduction in resistivity-the colossal magnetoresistance (CMR)3,4,5.

The CO-FM phase transition is crucial for understanding the competition among various exchange interactions not only in CMR manganites but also in other magnetic transition metal oxides and indeed attractive for potential applications due to the concurrent huge change in resistivity. For manganites, most of earlier investigations were focusing on hole-doped or half-doped CO systems (x ≤ 0.5) and the phase boundary between the CO and FM phases in these materials was well figured out2,6. According to the phase diagram of Pr1−xCaxMnO3, the critical field of the CO-FM transition increases dramatically with increasing x from 0.3 to 0.56, suggesting a distinct enhancement of the CO-state-stability due to the reduction of eg electron density. This relation is reasonably well understood since higher eg electron density always favors the double exchange FM interaction which competes with the charge-ordering. In this sense, more stable CO state in electron-doped region x > 0.5 in the phase diagram would be expected upon further decreasing the eg electron density.

In fact, the CO-FM phase transition in electron-doped CO manganites (x > 0.5) was less studied, while it is currently receiving more and more interests since the electron doping is remarkably asymmetric from the hole doping in terms of electronic structure, magnetism and transport behaviors1,7,8,9,10,11. In Sm1−xCaxMnO3 (0.5 < x ≤ 0.85)12, the CO melting magnetic field was revealed to decrease monotonously with increasing x, while the eg electron density decreases simultaneously. Recently, although the CO state is very robust in La1−xCaxMnO3 (0.5 < x ≤ 0.87)13,14, exceptional CO breaking and ferromagnetism upon size reduction (down to nano-scale) or impurity doping was broadly reported15,16,17,18,19,20. Moreover, photo-induced CO melting was observed in La0.42Ca0.58MnO3 and the threshold fluence for melting the CO phase was revealed to be significantly lower than that for hole-doped La1/4Pr3/8Ca3/8MnO321,22, which seems inconsistent with the fact that an electron-doped material has a much more stable CO state13,23. These works revealed interesting CO suppression and FM generation in the impurity-doped or nano-scaled CO manganites La1−xCaxMnO3 (0.5 < x ≤ 0.87), while the CO and FM phase boundary in these materials is not revealed until now.

On the other hand, the magnetic field induced CO melting process for phase separated (PS) state24, in which the CO and FM phases coexist and compete with each other, was found to be very different from that of the pure CO state in half-doped CO manganites6. It originates from an additional elastic energy arising at the CO and FM domain walls in the PS manganite, which prefers to block the magnetic field driven CO-FM phase transition. Following this line, it would be of interest to investigate the magnetic response of the CO phase within a PS state or spin-glass (SG) like state caused by the competition among diverse exchange interactions25. The consideration is that the possible magnetic field induced CO melting in these states would be further challenged by the spin freezing, in addition to the elastic energy at the CO/FM domain walls and free energy barriers between CO and FM phases.

In present work, La0.4Ca0.6MnO3 is selected as the prototype CO manganite to study the CO-FM phase transition since it has nearly the highest CO phase transition temperature (T) TCO~260 K1. The roughly pre-estimated CO melting field in La0.4Ca0.6MnO3 should be higher than 20 T, supported by the fact that the value in La0.5Ca0.5MnO3 is already as high as H = 20 T26 and the CO state becomes even more stable upon increasing the Ca2+ content to 0.613,14. In this sense, pulsed high magnetic field (up to 55 T) is used to make the present investigation feasible. Besides the pulsed high magnetic field, Cr3+-doping is utilized simultaneously to study the CO-FM phase transition in La0.4Ca0.6MnO3. The consideration for choosing Cr3+ as the doping species is threefold. First, the Cr3+ charge valence was confirmed to be stable in doped CO manganites27, which would simplify the underlying physics. Second, Cr3+-doping was revealed to be effective in mediating the CO suppression and FM promotion in CO manganites, because it allows lattice defect and magnetic coupling with Mn simultaneously28,29,30, which would weaken the CO state in La0.4Ca0.6MnO3 and thus facilitate our investigation. Third, various ground states, such as pure CO state, PS state and SG-like state, are expected through Cr3+-doping based on the aforementioned reasons, providing an opportunity to systematically investigate the evolution of the CO-FM phase transition as the ground state varies from the pure CO state to the SG one. Our results reveal significant CO suppression and FM tendency upon the Cr3+-doping at Mn-site in La0.4Ca0.6MnO3. Three different states, including the CO state, the PS state and the SG-like state are identified. High magnetic field study reveals an interesting CO-FM phase transition and the three states show distinct responses to the high magnetic field.

Results

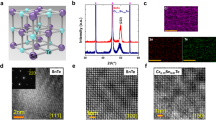
In Fig. 1(a), we present the measured X-ray diffraction (XRD) θ-2θ patterns at room temperature for all samples. Pure orthorhombic crystalline structure with space group Pnma can be identified for all samples. The diffraction peak positions are identical for all samples, indicating no evident change in lattice parameters upon the Cr3+-doping. This is consistent with the similar ionic radius between Cr3+ and Mn3+31. Furthermore, we show in Fig. 1(b)–(m) the elemental mappings using the energy-dispersive X-ray spectrometer (EDS), which suggests the homogeneous distributions of La, Ca, Mn, Cr and O. To investigate the Cr3+-doping induced modulation on physical properties, we subsequently measured the magnetization of the samples under various conditions.

Figure 1
figure 1

(a) X-Ray diffraction θ-2θ spectra at room temperature for a series of samples La0.4Ca0.6(Mn1-yCry)O3 (0 ≤ y ≤ 0.2). High angle annular dark field scanning transmission electron microscopy for samples (b): y = 0.1 and (h): y = 0.2 and corresponding elemental mappings by using energy dispersive X-ray spectrometer of La, Ca, Mn, Cr and O for samples (c) – (g): y = 0.1 and (i) – (m): y = 0.2.

Full size image

As we expect, the CO and antiferromagnetic (AFM) phase transitions for the sample with y = 0 (La0.4Ca0.6MnO3) arise at TCO = 260 K and TN = 143 K, respectively, shown in Fig. 2(a). Both phase transitions well match the data in literature1, indicating good quality of our samples. Upon the Cr3+-doping, the M(T) curves present clear downward shift in both TCO and TN, implying strong suppression of the CO/AFM state. With y > 0.06, the CO phase transition becomes ambiguous, but the broad magnetic upturn around 275 K (indicated by green arrows in Fig. 2) related to the initiation of the CO phase can still be observed. This feature suggests a crossover from long range CO phase to short range one happening at y ~ 0.06. For the sample with y = 0.2, both TN and TCO disappear but instead, a cusp-like peak arises at Tf ~ 68 K in the ZFC case and subsequently large bifurcation emerges between the FC and ZFC curves. These features are typical characteristics of a SG state25 and hence lead us to argue a possible SG-like transition occurring at Tf ~ 68 K in the sample with y = 0.2. Additionally, the weak but sharp peak at TB ~ 40 K in the ZFC case for the doped samples with 0.02 ≤ y ≤ 0.15 is probably due to thermal blocking of finite AFM clusters considering their small magnetization (M ~ 10−1 emu/g). Actually, a similar phenomenon was reported in modestly doped CO manganite Pr0.5Ca0.5(Mn0.975Al0.025)O3 and was confirmed to be induced by the thermal blocking of nanoscale AFM clusters32.

Figure 2
figure 2

Temperature profiles of magnetization at H = 100 Oe for all samples.

The green arrow indicates the initiation of charge-ordering phase.

Full size image

To confirm the possible SG-like state in the sample with y = 0.2, ac magnetic susceptibility was performed and shown in Fig. 3(a). Significant downright frequency dispersion of the peaked χ′-T relation is identified, which characterizes the dynamic response of spins in the SG state. Here we use the critical slowing-down power law, assuming a true equilibrium phase transition with a divergence of relaxation time near the freezing point, to analyze spin dynamics of the SG state. We found a good scaling relation between ε = (Tf/Tg-1) and τ shown in Fig. 3(b), where Tf is the peak temperature measured at frequency f, Tg is the transition temperature in the low frequency limit and τ is the observation time. According to the fitting with critical power law τ/τ0 = (Tf/Tg-1)−zv33,34, we obtained the critical exponents zv = 4.4, Tg = 76.9 K (consistent with Tf at low frequency) and τ0 ~ 3.4 × 10−9 s. The long spin flipping time τ0 (≫single spin flipping time 10−13 s) and relative small critical exponent zv suggest a cluster SG state in the sample y = 0.233,34, in which the Cr3+-doping induced FM clusters are randomly oriented.

Figure 3
figure 3

(a) Measured ac susceptibility χ′ as a function of T at f = 1, 10, 100 and 1k Hz for sample y = 0.2. The inset shows data in full measuring temperature range, in which the ferromagnetic phase transition is TC ~ 89 K well matching the value of dc measurement. The difference in Tf obtained from the ac and dc data is due to the different measuring magnetic field. (b) dynamical scaling of the observation time τ with the reduced temperature ε = (Tf/Tg-1).

Full size image

The H dependence of M measured at T = 4 K for all samples is shown in Fig. 4, which is useful to get more details on the phase evolution with the Cr3+-doping. Evidently, very thin M(H) hysteresis and small M can be seen for the samples with y ≤ 0.06, confirming the robust long range CO/AFM state. For y > 0.06, the magnetic hysteresis becomes striking and M increases dramatically with y, which solidly suggests the emergence of a FM phase in the CO/AFM matrix. The remnant and maximum magnetization (Mr and Mm at H = 5 T) were derived from the M(H) curves and plotted as a function of y in Fig. 5(a). Distinct increase of Mr and Mm ensues around y = 0.06, which marks the onset of FM phase and coincides with the crossover from long range CO phase to short range one evidenced by the M(T) data. This fact indicates the essential role of the short range charge ordering in mediating the competition between FM and CO phases. Based on the M(T) and M(H) data, a T-y phase diagram is summarized in Fig. 5(b), in which the state evolution with y can be clearly seen. For 0 ≤ y ≤ 0.06, the long range CO/AFM ground state is robust, while the uniform decrease in both TCO and TN signals the Cr3+-doping induced suppression of the CO/AFM phase. By the further increase of y from 0.06 to 0.15, the PS state arises, in which the short range CO/AFM orders and the FM phase coexist and compete with each other. As y reaches up to 0.2, a SG-like state arises due to the competition between FM and AFM interactions. In addition, the Mm ~ 0.65 μB/f.u. at y = 0.15 is ~19% of the expected moment M ~ 3.4 μB/f.u. in La0.4Ca0.6MnO3, which is close to the percolation threshold value as predicted theoretically in the 3D percolation model35. Therefore, it would be interesting to explore a possible CMR effect in the highly doped samples. However, insulating transport behaviors (shown in Fig. 6), even with applied magnetic field as high as H = 10 T, are revealed for samples with y = 0.1, 0.15 and 0.2, pointing towards strong localization of electrons. Additional isothermal magneto-resistance data are plotted in Fig. 6(e). Clearly, just one to two orders of magnitude decrease in the resistivity can be seen as H = 16 T, suggesting the robust insulating state of the samples. In fact, we will see below that the critical field for inducing CO-FM phase transition is much higher than 10 T, which means that the applied magnetic field during the magneto-transport measurements is not high enough to generate a FM metallic state. Intriguingly, a positive MR can be seen in the sample with y = 0.2, which is probably due to the tunneling effect across insulating regions sandwiched by metallic phase36. The transport behavior of the samples well follow the variable range hopping (VRH) model: ρ = ρ0exp[(T0/T)1/4], where ρ0 is the pre-factor and T0 is the characteristic temperature37. It is consistent with the scenario of dominant CO-AFM state and strong localization of electrons in the samples.

Figure 4
figure 4

Measured magnetization as a function of magnetic field at T = 4 K for all samples.

Magnetization curves, except for the y = 0 data, are shifted upward (0.2 μB/f.u. in each shift) for clarity.

Full size image
Figure 5
figure 5

(a) Remnant magnetization Mr (left axis) and maximum magnetization Mm at H = 5 T (right axis) as a function of doping content y. Solid circles and squares are the data from Cr3+-doping samples, while open circles and squares are the data from Fe3+-doping samples. The shadow region around y = 0.06 indicates the crossover from long range charge-order phase to a short range one due to the Cr3+-doping. (b) Summarized T-y phase diagram, in which (L)CO means long range charge-order phase and (S)CO means short range charge-order phase.

Full size image
Figure 6
figure 6

Temperature profiles of resistivity at various applied magnetic fields for samples (a) y = 0.1; (b) y = 0.15; (c) y = 0.2. (d) Fitting of zero field resistivity ρ as a function of T−1/4 using the variable range hopping model for the three samples. (e) Resistivity as a function of magnetic field for the three samples measured at T = 45 K.

Full size image

The experimental results presented above indeed suggest three different states upon the Cr3+-doping: the long range CO/AFM state, the PS state with coexisting short range CO/AFM and FM phases and the SG-like state due to the competition between FM and AFM interactions. This provides an ideal avenue to systematically study the magnetic field driven CO-FM phase transitions between diverse ground states. The measured magnetization using pulsed high magnetic field at T = 4.2 K is shown in Fig. 7. Sharp CO-FM phase transitions and remarkable hysteresis in M(H) curves are observed and particularly clear in the low Cr3+-doping leves. The saturated magnetization is derived to be in the range of 3.1 to 3.3 μB/f.u. for y ≤ 0.1 and even smaller value appears in the samples with y = 0.15 and y = 0.2. The saturated moment of all the samples is lower than the expected value of 3.4 μB/f.u. for Mn cation. Considering the very high sweeping rate of the pulsed magnetic field (~103 T/second), a small part of the moments probably can't be well aligned by the field, thus inducing the relatively low saturated moment1,2. This effect becomes more striking when the spin-glass state is involved, such as the case in the sample with y = 0.2. Considering the very robust CO state for the samples, spin tilting would happen in the resultant FM phase, which may be one of the reasons for the slightly smaller saturated magnetization of the FM state. An H-y phase diagram obtained from the high magnetic field data is shown in Fig. 7(b), where the critical fields (Hc) of the CO-FM phase transition are estimated from derivative of magnetization dM/dH (the inset of Fig. 7(b)).

Figure 7
figure 7

(a) Magnetization as a function magnetic field measured at T = 4.2 K. Magnetization curves, except for the y = 0 data, are shifted upward for clarity. For samples 0.02 ≤ y ≤ 0.1, each curve is shifted 0.6 μB/f.u., while the curve of y = 0.15 is shifted 0.9 μB/f.u. and the curve of y = 0.2 is shifted 1.2 μB/f.u. (b) H-y Phase diagram, in which the solid squares and circles stand for the critical fields obtained from the up and down sweep of H, respectively. The hatched area represents the magnetic field hysteresis region accompanied by the first-order nature of the charge-order to ferromagnetic transition. The inset in (b) presents the derivative of magnetization dM/dH of sample y = 0, in which the critical fields of charge-order to ferromagnetic phase transition are indicated by red arrows.

Full size image

Indeed, different evolving paths of Hc with y can be observed. For 0 ≤ y ≤ 0.06 where the samples are in the CO/AFM ground state, Hc decreases rapidly with y corresponding to the dramatic decrease in TCO. This can be easily understood by the competition between the Zeeman energy by external magnetic field and energy barrier between the CO and FM phases. Because of the Cr3+-doping, the long range CO state is broken into short range orders, resulting in a smaller energy barrier between the CO and FM phases. In this sense, concurrent decreases of Hc and TCO are reasonably expected upon increasing y. For 0.06 ≤ y ≤ 0.15, where the samples have the PS ground state, the H(y) curve becomes gentle and only slight variation in Hc can be seen. Based on the low magnetic field data, the FM phase emerges around y = 0.06 and its volume fraction shows distinct enhancement with further increasing of y, suggesting the continuous reduction of the CO and FM phase energy barrier. On the other side, as a consequence of the FM phase emergence, elastic energy related to the elastic strain arises at the interface of the CO and FM domain wall due to the different lattices of both phases, which tends to compete with the Zeeman energy and block the magnetic field driven CO-FM phase transition24. Therefore, slight variation in Hc is evidenced, although the CO phase is largely suppressed within the doping range of 0.06 ≤ y ≤ 0.15. In the sample with y = 0.2, the competition between FM and AFM interactions drives the SG-like state below Tf. Such spin freezing is a cooperative phenomenon and would further compete with the Zeeman energy besides the elastic energy and the barrier between the CO and FM phases. It is thus no magnetic field driven CO-FM phase transition and magnetic saturation can be observed in the sample with y = 0.2. Additionally, from the high field phase diagram, the Zeeman energy (E1) driving the CO-FM phase transition can be derived to be of few meV. On the other hand, the free energy (E2) of the CO state can be estimated from the TCO, which is about tens of meV. Therefore, the energy of spin-charge coupling can be extrapolated to be E = E2-E1 ~ 10–100 meV in these materials, which is responsible for the coexistence of AFM and CO phases in manganites. Here, we would like to mention that the sweeping rate of pulsed high magnetic field used in the present work is about five orders of magnitude higher than the quasi-static case and thus it is not yet clear what variation is to be expected in these pulsed high magnetic field experiments with respect to those quasi-static field ones, which surely deserves further investigations.

Discussion

The mechanism of the Cr3+-doping induced ferromagnetism can be discussed as the following. Generally, three straightforward effects can be induced by the Cr3+-doping: i) disorder effect due to the lattice defects, which always frustrate the long range CO phase, ii) antiferromagnetic coupling between the Cr3+ and Mn cations38, iii) substitution of Cr3+ for Mn3+ reduces the local eg charge density, which stabilizes the AFM superexchange interaction. It is clear that the third factor has a negative contribution to the FM generation and therefore we just need to consider the first two ones. The disorder effect is inevitable for the Mn-site doping and plays an important role in the FM tendency in half-doped CO manganites. However, it was revealed that the disorder effect can not induce ferromagnetism although the CO/AFM state was dramatically suppressed in La0.4Ca0.6MnO339. Hence, it is likely that the Cr-Mn AFM coupling is decisive for the FM phase promotion. In La0.4Ca0.6MnO3, the AFM state is dominated by the CE-type order, which means a stacking of zigzag FM chains with inter-chain AFM coupling1. Based on this picture, one may expect that the Cr3+ can be introduced into one zigzag chain without impacting the spin direction of the neighboring zigzag chains due to the Cr-Mn AFM interaction. On the contrary, within the Cr3+-doped zigzag chain, the Mn moments will be reversed to maintain the Cr-Mn AFM interaction and inner-chain Mn-Mn FM coupling simultaneously, which gives rise to microscale FM clusters surrounding the Cr3+27,29. However, such spin reversal would be vigorously competed by the inter-chain Mn-Mn AFM interaction and thus the FM clusters can only appear in case of largely weaken inter-chain AFM interaction, corresponding to the distinct enhancement of FM volume fraction of 0.06 ≤ y ≤ 0.15 in the present work. In fact, submicrometric FM metallic clusters were reported in Cr3+-doped Nd1/2Ca1/2MnO3, supporting such kind of mechanism30.

Furthermore, we also measured the M(H) curves of Fe3+-doped La0.4Ca0.6MnO3 to make a comparison with the Cr3+-doping effect and the derived Mr and Mm are plotted in Fig. 5(a) (black open circles and squares). No FM phase can be detected in the Fe3+-doping samples, although Fe3+ is closely analogous to Cr3+, such as the same trivalence, close ionic radius to Mn3+ and AFM coupling with Mn cations. Therefore, besides the AFM interaction of Cr-Mn, additional ingredient should be taken into account to understand the Cr3+-doping induced CO suppression and FM promotion. We note that both of Fe3+ and Cr3+ are not Jahn-Teller (JT) active cations, which indicates an enhancement in local electron hopping strength due to the reduced JT effect by Fe3+/Cr3+ doping. However, different from the empty eg state of Cr3+ (d3), the 3d states of Fe3+ (d5) with the same spin polarization are occupied (in accordance with the 1st Hund's rule) and the hopping electron should reverse its spin, which is energetically unfavorable and thus leading to block the double exchange process28. Therefore, both the AFM interaction of Cr-Mn and the empty eg state of Cr3+ are proposed to be responsible for the CO suppression and FM generation in Cr3+-doped La0.4Ca0.6MnO3.

In conclusion, the phase diagrams in both T-y and H-y planes were determined through extensive magnetic measurements in La0.4Ca0.6 (Mn1-yCry)O3 (0 ≤ y ≤ 0.2). Upon Cr3+-doping, the ground state was transformed from a robust long range CO/AFM one (0 ≤ y ≤ 0.06) to a phase separated one (0.06 < y ≤ 0.15) and eventually to a SG-like one (y = 0.2). Interestingly, high magnetic field induced CO-FM phase transition was observed in samples exhibiting long range CO/AFM state or PS state, while distinct evolving paths of the critical field with y were identified as the ground state was changed. Separately, in the sample with y = 0.2, no CO-FM phase transition and magnetic saturation can be observed, which consisted with its SG-like state. The origin of the Cr3+-doping induced CO suppression and FM generation in La0.4Ca0.6MnO3 was discussed in terms of the antiferromagnetic coupling of Cr-Mn and local enhancement of electron hopping strength due to reduced JT effect by Cr3+.

Methods

A series of samples La0.4Ca0.6(Mn1−yCry)O3 (0 ≤ y ≤ 0.2) were synthesized using standard solid state reaction in air. Stoichiometric amounts of high purity La2O3, CaCO3, MnCO3 and Cr2O3 were used as reagents and well ground and the mixture was calcined at temperatures ranging from 1100°C to 1300°C for several times. Finally, the obtained black powder was pressed into pellets and calcined at 1400°C for 24 hours in air. The crystalline structures of samples were investigated using X-ray diffraction with Cu Kα radiation at room temperature. High Angle Annular Dark Field (HAADF) Scanning Transmission Electron Microscopy (STEM) and elemental mappings by using energy dispersive X-ray spectrometer (EDS) were carried out in the FEI-TITAN 80-300 microscope. Extensive measurements on the magnetic property were performed by using a Quantum Design superconducting quantum interfering device (SQUID). The measuring magnetic fields for dc and ac magnetic measurements were 100 Oe and 3.5 Oe, respectively. Electric transport measurements were performed using a standard four-probe method under various magnetic fields on a physical properties measurement system (PPMS).

Pulsed high magnetic field measurements for magnetization were performed at T = 4.2 K by means of a standard inductive method employing a couple of coaxial pickup coils. The pulsed magnetic field up to ~55 T with a duration time of ~50 ms was generated by using a nondestructive long-pulse magnet energized by a 1 MJ capacitor bank, which is installed at the Huazhong University of Science and Technology, China.