Introduction

The resolution of conventional imaging systems is fundamentally limited to the diffraction limit1 because evanescent waves, which carry subwavelength information, decay exponentially during propagation in free space. Serving as a powerful impetus to semiconductor fabrication, biological studies, material science and medicine development, the unconventional imaging techniques that can break the diffraction limit have attracted considerable interest in recent years. In addition to the near-field scanning optical microscope2,3 and stimulated emission depletion microscope4, perfect lens5 and hyperlens6 perform the function to recover subwavelength details of objects to be imaged. By folding electromagnetic space, a perfect lens can achieve unlimited resolution in theory and has been demonstrated with left-handed metamaterials composed of artificial “atoms” in experiments7,8,9,10,11,12,13,14. A hyperlens is made of anisotropic media with a hyperbolic k surface, in which evanescent waves can be converted to propagating ones. The best realized resolution of all fabricated hyperlenses so far is about one out of tens in terms of wavelength15,16,17,18,19. To refresh this record further has practical demand but is widely acknowledged to be challenging.

Different from perfect lens and hyperlens, canalization regimes20,21,22,23,24,25,26, which do not involve left-handed materials and amplification of evanescent waves, can realize subwavelength imaging as well. This strategy is based on the eigenmode analysis of photonic crystals. The media for subwavelength imaging are constructed by metallic rod array, whose effective parameters are defined with a nonlocal effective medium model27,28,29,30,31. Several proofs of concept have been experimentally demonstrated in microwave regimes32,33,34,35 and exhibit potential applications in near-field microscopy and in medical imaging from microwave frequencies to infrared frequencies36.

Recently, singular media37,38 have shown potential ability in realizing deep subwavelength imaging. Singular media have the property that some components of the permittivity or permeability tensors are infinite or almost zero and therefore have already been taken into consideration of various potential electromagnetic applications, e.g. waveguide39, optical isolation40, metamaterials with ultrahigh refractive index41,42,43, superlens44 and subwavelength channeling applications45,46,47.

In this Letter, with the use of transformation optics48,49,50,51 and singular media, we report a practical meta-lens design methodology to realize ultra-high resolution in terms of wavelength for transverse magnetic (TM) polarized waves. The alternate metallic and dielectric layers, which form effective permittivity with extremely high anisotropy and can be treated as a kind of singular media, are adopted in our design and fabrication. The meta-lens is demonstrated experimentally over a broad frequency band from 1.5–10 GHz with the resolution varying from 1/117 to 1/17 wavelength.

Results

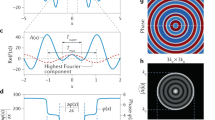
The scheme of a TM cylindrical meta-lens is shown in Fig. 1(a). Two point sources are located closely at the inner boundary of the lens with subwavelength distance. For a specific material, the dispersion relation of electromagnetic waves can be written as in cylindrical coordinates, where kρ and kϕ are wave vectors along the ρ and ϕ directions, εϕ and ερ are the permittivities along the ϕ and ρ directions, μz is the permeability along z direction and ω is the angular frequency of incident waves. The k surface for free space exhibits a circular shape (blue curve in Fig. 1(b)) and the energy flow of electromagnetic waves will spread out during propagation because of diffraction and loss of evanescent waves with tangential wave vector kϕ> k0. The medium with hyperbolic dispersion, which is adopted in hyperlens design, keeps the large tangential wave vector coefficient kϕ propagating without being evanescent.

Figure 1
figure 1

(a) A two-dimensional scheme of an unconventional lens for TM waves. (b) The k surfaces for an isotropic medium (circle in blue) and a singular medium (parallel lines in red). (c) The corresponding virtual space of materials in (b). In isotropic materials, energy flow will spread out in all the directions. After squeezing the original virtual space (the regime in blue) in the azimuthal direction, can only propagate in the transformed tube-like space (the regime in red) without spreading out. (d) The metamaterial with infinite anisotropy is made of metal-air structure with the period pϕ and the thickness of metal dm.

Full size image

Because hyperbolic dispersion metamaterials always involve negative value of constitutive parameters, hyperlens achieved with these hyperbolic dispersion metamaterials can only work in a narrow frequency band. However, without hyperbolic dispersion metamaterials, we can still design a meta-lens to achieve the goal of subwavelength resolution. To overcome the energy spreading associated with the diffraction in free space, squeezing the whole space in the ϕ direction is a practicable transformation procedure, i.e. and z′ = z, where N is the squeezing constant. From the transformation optics, it is known that the permittivity coefficient along the radial direction becomes infinite as N tends to infinite. Therefore, the medium in the transformed space has the property of singular media. As is a finite value and , the dispersion relation for an electromagnetic wave with electric field perpendicular to z axis becomes (parallel lines in red, Fig. 1(b)), which implies that the Poynting vector of incident wave is always along the ρ direction and the propagation velocity is controlled by the permittivity and permeability μz. The energy is confined in the transformed space and cannot spread out as the space transforms from free space to an extremely thin tube-like space. Thus, the information carried by the tangential waves can be preserved and the diffraction limit can be overcome. The corresponding changes in virtual space between isotropic medium (e.g. air) and suppressed medium with infinite anisotropy are plotted in Fig. 1(c). Therefore, a practical high-resolution meta-lens in terms of wavelength can be realized by a singular medium, but without hyperbolic dispersion relation.

As shown schematically in Fig. 1(d), metamaterial realized by alternate metallic and air layers with subwavelength period pϕ is a potential choice to achieve extremely high anisotropy. With the effective medium theory, the perpendicular and parallel coefficients of the effective permittivity can be calculated as and , where F = dm/pϕ is the filling factor of the metal, εm is the permittivity of metal and εair is the permittivity of air. For the case of microwave regime, infinite permittivity of metal εm and finite filling factor F introduces a singular medium property (i.e. and ). For the case of higher frequency or optical regime, the permittivity of metal is not an infinite value due to the dispersion, but the permittivity ratio between the absolute value of metal and air still tends to a large value, especially in the infrared spectrum. Therefore, alternate metal-air layers can exhibit approximately singular medium property in optical regime as they exhibit in microwave regime. In such a medium, the wave can only propagate along the ρ direction and no energy can be spread out.

As an example, we simulate TM polarized electromagnetic waves with the frequency of 100 THz incident onto the homogeneous medium with high anisotropy (|Re(εy/εx)| > 40, Fig. 2(a) and the effective medium constructed with gold-air layered structure (the filling factor of gold is 0.1, Fig. 2(b)), respectively. The simulated result is obtained with the use of the commercial software Comsol Multiphysics. The permittivity of gold is given by and for bulk gold, the plasma frequency ωp = 2π × 2.175 × 1015 s−1 and the collision frequency ωc = 2π × 6.5 × 1012 s−152. The incidence angle is 30 degree. Two media in Fig. 2(a) and 2(b) have the same constitutive parameters based on the effective medium theory. From the results, one can see the field distributions are identical in these two cases, indicating the layered metal-air structure can be well characterized as a homogeneous singular medium. Following the Drude model, |Re(εgold)| will drop to a finite value from infinity as the frequency increases, especially when the frequency tends to the plasma frequency of gold. At this condition, the layered gold-air structure cannot exhibit the highly anisotropic property of finite ε⊥ and infinite ε||. This will introduce the loss of evanescent waves and therefore deteriorate the performance of hyperlens. However, this structure can still perform as a singular medium in a broad frequency band from microwave to Terahertz regimes as long as it meets the effective medium theory.

Figure 2
figure 2

Electromagnetic wave with the frequency of 100 THz propagate through (a) the homogeneous medium with high anisotropy (|Re(εy/εx)| > 40) and (b) the effective medium with the same effective parameters constructed with gold-air layered structure.

The permittivity of gold is given by and for bulk gold, the parameters are ωp = 2π × 2.175 × 1015s−1 and ωc = 2π × 6.5 × 1012s−1. The incidence angle is 30 degree and the filling factor of gold is 0.1.

Full size image

Fig. 3 shows the schematic of microwave meta-lens we realized. In order to simplify the fabrication, we separate the semicircle of the meta-lens into 18 tubes by 0.03 mm-thick Cleanwrap® aluminum foils and therefore the azimuthal periodicity of the tube is 10 degree. The metal-air structures are fixed by two pieces of synthetic glasses, whose radius of inner semicircle and of outer semicircle are r = 1.5 mm and R = 500 mm respectively. The height of the meta-lens in z direction is h = 200 mm. Two slits, with the width of 0.3 mm and height of 200 mm on a horn antenna covered by an aluminum foil, are used as two separated point sources in the experiment. The distance between two slits is 1.7 mm. In the experiment, a composite source, which is subwavelength, is connected to the meta-lens with contact terminals. According to the calculation above, the effective permittivities close to the inner semicircle are εϕ = ε⊥ = 1.1 and ερ = ε||→∞, which match the requirement of meta-lens.

Figure 3
figure 3

The effective 3D scheme of our practical meta-lens for microwave.

The inner and outer radius are r = 1.5 mm and R = 500 mm respectively. The height of meta-lens in z direction is h = 200 mm and the azimuthal periodicity of the tube divided by 0.03 mm-thick Cleanwrap® aluminum foils is 10 degree.

Full size image

Both simulations and experiments are carried out in microwave regime to verify our idea. For the case of free space (Fig. 4(a)), the field distribution of two point sources with the distance 1.7 mm is identical to the one of a single point source because the distance between two point sources is far less than half of free space wavelength at 1.5 GHz. However, for the case of sources with our meta-lens, the TM waves excited by the same pair of point sources can be efficiently separated (Fig. 4(b)). In the experiment, the distance between the receiver and the center is 0.6 m. The scanning angle ϕ varies from 0 to 180 degree. The experimental results at 1.5 GHz agree well with simulated results (Fig. 4(c)). Moreover, in order to verify the broadband property of our meta-lens design, we measured the field at different frequencies. Fig. 4(d–f) are the experimental results at 10 GHz, from which one can see that the two points can also be efficiently separated in the imaging plane, indicating that our meta-lens can overcome the diffraction limit from 1.5 GHz to 10 GHz with the resolution varying from 1/117 to 1/17 wavelength.

Figure 4
figure 4

The results at 1.5 GHz are enclosed in the top panel (a–c) while the results at 10 GHz are enclosed in the bottom panel (d–f): the simulated field distributions (a, d) for the case without meta-lens and (b, e) for the case with meta-lens and (c, f) the image intensity normalized by the input intensity.

In the experiment, the distance between the receiver and the center is 0.6 m.

Full size image

Discussion

There are two limitations relating to the bandwidth and resolution of our design. The first one is the effective medium theory (EMT), which can be used only when the periodicity of the layered structure has to be much smaller than the wavelength of interest (e.g. smaller than 1/5 wavelength). In our design, the periodicity of the layered Al-foam structure is 0.26 mm, which corresponds to 1/5 wavelength of 230 GHz. The other one is the diffraction limit, which means that the distance between the two imaging point at the outer boundary should be larger than 1/2 wavelength. In the design, this distance is 500 mm, which corresponds to 1/2 wavelength of 0.3 GHz. Therefore we estimate that the bandwidth limitation of our design is 0.3-230 GHz.

One may question that the squeezing constant must be a definite number for a real practical sample. As a result, the radial component of permittivity cannot be infinite in experiment. However, even with a definite squeezing number, the effective radial permittivity still tends to infinite, as the permittivity of metal is infinitely large at microwave regime. Hence, a definite squeezing constant would not deteriorate the subwavelength imaging performance in our practical design. For higher frequency, e.g. optical regime, a definite squeezing parameter will deteriorate the imaging performance because it is difficult to find a kind of material whose permittivity tends to infinite, but a medium with highly anisotropic permittivity can be still achieved for subwavelength imaging with the use of layered structure in Fig. 2.

In conclusion, we introduce a meta-lens design methodology with deep subwavelength resolution combining transformation optics and singular media. We implement this concept and demonstrate a practical broadband meta-lens in microwave regime. The meta-lens is made of alternate metallic and air layers, which can be treated as a singular medium. The advantages of this design include ultra-high-resolution (up to λ/100 resolution at 1.5 GHz in the experiment) and broadband performance from 1.5–10 GHz with the resolution varying from 1/117 to 1/17 wavelength. Our work provides an alternative way for future practical implementation of subwavelength imaging devices.