Introduction

Magnesium oxide (MgO) films with a highly effective spin filtering effect and a large bandgap1,2,3,4 have been used as tunnel barriers to obtain a huge tunnel magnetoresistance (TMR) ratio at room temperature (RT) in magnetic tunnel junctions (MTJs). Such MTJs include fully epitaxial Fe/MgO/Fe, polycrystalline CoFe/MgO/CoFe and amorphous CoFeB/MgO/CoFeB junctions5,6,7,8,9. The great success of MgO barriers is owing to a giant TMR ratio at RT of up to 600% in CoFeB/MgO/CoFeB junctions9, of 330% in Heusler alloy-based MTJs such as Co2FeAl films with a high degree of spin polarization10 and of 120% in CoFeB-based MTJs with perpendicular magnetocrystalline anisotropy11. Furthermore, the anomalous Hall effect was significantly enhanced in Co/Pt multilayers sandwiched by MgO layers12.

While the spin filtering property of MgO is desirable in a MTJ, its large bandgap is usually not because it causes a high value of the product of resistance and junction area (RA). Since the conduction of electrons is perpendicular to the film, the junction resistance scales as the inverse of its in-plane area and the material is characterised by its RA product. To achieve good signal to noise ratio in applications it is essential to reduce the RA value, which is determined predominantly by the barrier bandgap. With this in mind, wurtzite zinc oxide (ZnO) with a band gap of 3.4 eV appears advantageous with respect to rocksalt MgO with a bandgap of 7.8 eV19,20,21. ZnO also has a large piezoelectric coefficient, transparency in the visible wavelength range and a great potential for applications in optoelectronic devices13,14. ZnO films have also been used as the tunnel barrier in MTJs with electrodes of Co-doped ZnO dilute magnetic semiconductors (DMS)15,16,17,18. However, the fundamental properties of ZnO films, including its bandgap, Curie temperature and conductivity, limit the TMR ratio at RT. For example, we recently reported a TMR ratio of 86% at 5 K in fully epitaxial ZnCoO/ZnMgO/ZnCoO junctions18, where Mg-doped ZnO layer with a wurtzite structure is used as the barrier. Therefore, a potential approach is to combine MgO with ZnO, such as Zn-doped MgO or Mg-doped ZnO, in order to tailor the bandgap and crystal structure.

Doping has previously been used to modify the bandgap of MgZnO22. Starting with wurtzite ZnO, Mg was added to increase the bandgap. However, the wurtzite structure remained unchanged, which has been shown to have a detrimental effect on spin filtering18. In contrast, the rocksalt structure provides a good filtering effect to improve the TMR ratio. Therefore, a more promising approach for device application is to reduce the bandgap of rocksalt MgO which allows effective manipulation of RA. It is desirable to start by doping into MgO. Some initial work has been carried out, such as our theoretical calculations of doping Zn, Al, Ca, Ta and Cu into the MgO lattice23.

In this work, Zn-doped MgO layers are used as tunnel barriers in fully epitaxial Fe/Mg1−xZnxO/Fe (x ≤ 0.3) MTJs grown by molecular beam epitaxy (MBE). It is shown that the RA value can be greatly decreased, while simultaneously preserving a high TMR ratio. First-principles calculation is used to determine the band structure of Zn-doped MgO. The bandgap can be precisely tuned and the spin filtering effect due to Bloch states with Δ1 symmetry is maintained. Our research addresses one of key issues of tunnel junctions, both for fundamental physics and for spintronic devices. It is important to point out that MgZnO films with a tailored bandgap will find wider applications in semiconductor devices, such as tunable solar-blind responsivity of photodetectors based on cubic MgZnO films24.

Results

Theoretical calculations

All calculations are performed using the local spin density approximation (LSDA) of the density functional theory (DFT) implemented in the layer-Korringa-Kohn-Rostoker (layer-KKR) code25 as exactly the same manner as the calculations of the complex band structure for pure bulk MgO and tunneling conductance of Fe/MgO/Fe junctions in Ref. 1. Doping of Zn and oxygen vacancies are modeled as random substitutional impurities with a uniform concentration within the coherent-potential approximation (KKR-CPA)26 whose effective medium preserves the undoped unit cell and the translational symmetry. The lattice constants of Zn-doped Mg1−xZnxO layer are 2.866 Å within the plane (rotated 45° to match the iron lattice) which equals to that of the bcc iron and is close to times of pure MgO lattice constant and 2.21 Å perpendicular to the plane, which is the measured value in the Fe/MgO/Fe junction5. The lattice constants are not varied with Zn doping for calculation, which is verified by transmission electron microscopy (TEM) measurements shown later on. The complex band structure of Zn-doped Mg1−xZnxO bulk crystal along the (001) direction is calculated for x = 0 up to x = 0.3. The bandgap is extracted from the complex band structure for each doping level. The interface structure between Fe and Mg1−xZnxO is assumed to be the same as the Fe/MgO interface in Ref. 1. Tunneling conductance is calculated for each doping level and for oxygen vacancy levels of 0, 0.5% and 1%, respectively, for both parallel (P) and antiparallel (AP) alignments of the ferromagnetic electrodes.

From the calculations, the spin filtering effect due to Δ1 states is maintained although the complex band structure changes with Zn-doping. Figure 1 shows typical complex band structure for x = 0 and 0.3, respectively, indicating that the spin filtering effect is preserved even in the case of x = 0.3. The spin filtering effect due to Δ1 states is critical for achieving a high TMR ratio in MTJs. Furthermore, Zn-doping leads to an upward shift of the conduction band due to larger number of Zn valence electrons, resulting in a decrease of the bandgap. The bandgap as a function of Zn-doping x in Figure 2(a) shows a gradual decrease with doping, making it more applicable in spintronic devices, e.g., the tunable bandgap will affect the TMR ratio and RA value. We note that the experimentally obtained bandgap for single crystal MgO is 7.8 eV19, but the value obtained by DFT calculations is 4.2 eV, which is systematically lower20. The difference in absolute values does not play a role for the following discussion, as it is concerned with a continuous increase of the Zn doping. Figure 2(b, c) shows the barrier height at the bottom and top interfaces across the barrier (denoted by φ1,2) in the P and AP configurations obtained by fitting I – V curves based on asymmetric interface model, respectively. The model and the I – V fitting will be discussed in detail later on and in the Supplementary Information.

Figure 1
figure 1

Calculated band structure of Mg1−xZnxO film.

(a) x = 0 and (b) x = 0.3, respectively.

Full size image
Figure 2
figure 2

Calculated bandgap and barrier height of Mg1−xZnxO as a function of Zn doping x.

(a) calculated results, (b,c) the barrier height at bottom/top interfaces (φ1,2) in parallel and antiparallel configuration obtained by fitting I – V curves, respectively. The solid lines are guide for the eyes only.

Full size image

Based on the theoretical results, it is reasonable to conclude that the bandgap of MgZnO films can be well tailored, whereby the rocksalt structure with a spin filtering effect is maintained for lower doping. Therefore, it is critical to find suitable systems to prove this calculation. In this work, a nanometre thick MgZnO layer is incorporated as a tunnel barrier in MTJs. Due to the complicated interfacial structures between metal oxides (such as MgZnO barrier) and metals (such as ferromagnetic electrodes), it is a great challenge to fabricate tunnel junctions based on nanometre thick MgZnO barrier, while maintaining the rocksalt structure together with a good spin filtering effect.

Sample preparation and characterisation

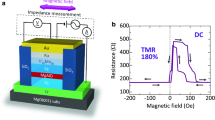
Epitaxial multilayers with a core structure of Fe(25)/Mg1−xZnxO(3)/Fe(10)/IrMn(10) (thicknesses in nm) were grown on single crystal MgO(001) substrates by molecular beam epitaxy (MBE). The Zn-doped Mg1−xZnxO barriers were grown by co-evaporation of MgO and Zn. The structure of each layer during deposition is monitored by in situ reflection high energy diffraction (RHEED) shown in Supplementary Figure S1, presented and discussed in the Supplementary Information. Tunnel junctions were fabricated from size of 2 × 4 to 5 × 10 μm2 using ultra-violet optical lithography together with Ar ion etching. The magnetotransport properties of the MTJs were measured by a physical properties measurement system using a standard four-point probe technique.

In order to identify Zn in the MgO layer, X-ray photoelectron spectroscopy (XPS) technique is used, which has been proven to be a very useful tool for the element identification and interface characterisation27. For XPS measurements (Thermo Scientific ESCALAB 250), the barrier is much thicker (~8 nm) than that in MTJs for transport measurements (~3 nm) in order to distinguish the signals of top Fe layer from those of bottom Fe layer. Furthermore, a thinner top Fe layer (~3 nm) is used without IrMn antiferromagnetic layer. Figure 3(a–d) shows typical high resolution XPS spectra for the Fe(25)/Mg0.7Zn0.3O(8)/Fe(3) (in nm) sample: Fe 2p, Mg 1s, Zn 2p and O 1s, respectively. For Fe 2p at the MgZnO/Fe top interface (TI) shown in Figure 3(a), two sharp intense peaks located at 707.0 eV and 720.0 eV for Fe 2p3/2 and Fe 2p1/2, respectively, indicate metallic Fe. No significant signal of the Fe 2p is detected in the MgZnO barrier. At the Fe/MgZnO bottom interface (BI), weak peaks from bottom Fe layer are observed. With respect to Zn 2p at TI shown in Figure 3(c), a low intensity peak is detected. In the barrier, a typical Zn signal is detected with a sharp intense peak located at 1021.5 eV, in good agreement with previous reports28,29. Therefore, we conclude that Zn is successfully incorporated into the MgO lattice, forming single crystal Mg1−xZnxO barrier with rocksalt structure. The discussion about Mg 1s and O 1s spectra is the same as that in epitaxial Fe/MgO/Fe MTJs27.

Figure 3
figure 3

High resolution XPS spectra for a sample with x = 0.3 of Fe(25)/Mg1−xZnxO(8)/Fe(3) (in nm).

(a) for Fe 2p, (b) for Mg 1s, (c) for Zn 2p and (d) for O 1s, respectively.

Full size image

The structure and composition of tunnel junctions with Zn-doped MgO barriers was characterised by transmission electron microscopy (TEM) using a JEOL JEM-2100F. The TEM sample was prepared from an MTJ device using a focused ion beam (FEI Strata Dual Beam FIB operated at 30 and 5 keV). Figure 4 presents a typical high-resolution TEM (HRTEM, phase contrast) micrograph showing an overview of a junction with Mg0.8Zn0.2O as barrier. The barrier thickness is approximately 3 nm as planned for the MBE growth. Despite the high content of Zn as expected from the growth conditions, the crystalline quality of the barrier does not appear degraded compared to epitaxial, rocksalt NaCl-type MgO based MTJs30. Rocksalt-type MgO and bcc-Fe are known to grow epitaxially despite an approximately 3.8% lattice mismatch. We find that the epitaxial relation remains as in the case of Fe/MgO/Fe: Fe[010](001)//Mg0.8Zn0.2O[110](001)//Fe[010](001), which is demonstrated by comparing the power spectra of HRTEM micrographs from the barrier-Fe electrode region and the MgO substrate-Fe electrode region. The addition of Zn to MgO is expected to increase the lattice parameter of cubic MgO by approximately 0.01 Å as reported for Mg1−xZnxO films, 250–400 nm thick31. Using these HRTEM results, we measured the lattice parameter of the MgO substrate and the Zn-doped MgO barrier to be 4.22 ± 0.01 Å, which means that this approach can not detect the incorporation of Zn. The compressive strain in the Zn-doped MgO barrier is relieved by misfit dislocations (not shown here) as previously reported for Fe/MgO based MTJs30.

Figure 4
figure 4

Cross-sectional HRTEM image of a tunnel junction.

Insets: power spectra of the regions denoted by the red rectangles. The zone axes are [1–10] and [010] for MgO and Fe, respectively.

Full size image

The presence of Zn in the barrier was also confirmed by energy-dispersive X-ray spectroscopy (EDS). The distribution of Zn within the barrier is uniform with no apparent segregation or significant interface intermixing according to both Z-contrast high angle annular dark-field scanning TEM and elemental mapping by energy filtered TEM (Mg K, O K, Fe L core-loss edges). The amount of Zn in the barrier was estimated by EDS. Experimental K-factors were determined by measuring MgO and ZnO single crystal samples of comparable thickness and collection conditions. Due to the thickness of the barrier, the X-ray photon count statistics is low therefore limiting the quantitative analysis. Nevertheless, even when accounting for statistical errors the Zn composition was found to be lower than expected according to the nominal composition, Mg0.8Zn0.2O.

Based on the microstructural analysis from RHEED, XPS and HRTEM, the epitaxial structure of Fe/MgZnO/Fe can be well maintained up to x ≤ 0.3. Furthermore, the uniform distribution of Zn in the barrier was confirmed, in good agreement with our theoretical calculations with a random substitution. We now present and discuss the spin-dependent transport properties of Fe/MgZnO/Fe MTJs.

Spin-dependent tunneling

The magnetotransport properties of Fe/Mg1−xZnxO/Fe MTJs were investigated at RT (300 K) and low temperatures. Typical RA values as a function of magnetic fields (RA – H curves) at 10 K and 300 K for junctions with various Zn doping concentrations are shown in Figure 5, where x for (a–d) is 0, 0.075, 0.15 and 0.3, respectively. The red open dots and blue open squares stand for 10 K and 300 K, respectively. With respect to temperature dependence of the TMR ratio and RAP,AP value for P and AP configuration, typical results are summarised in Supplementary Figure S3 with a discussion in the Supplementary Information. These results show that the TMR ratio decreases with increasing Zn doping concentration x. For example, the TMR ratio is more than 172% at 300 K for junctions with x = 0 and decreases to about 15% at 300 K with x = 0.3. Furthermore, RA value in parallel configuration (RAP) shows a stronger temperature dependence with increasing x, as seen from Figure 5(c, d). Note that a break in the axis is used in Figure 5(d) for a clearer comparison. The temperature dependence for samples with various x is presented in Supplementary Figure S2, where RAP for x = 0 and x = 0.075 shown in Supplementary Figure S2(a, b) is nearly temperature independent, but RAP for x = 0.15 and x = 0.3 shown in Supplementary Figure S2(c, d) decreases greatly with decreasing temperature.

Figure 5
figure 5

Plots of the RA product as a function of magnetic fields at 10 K and 300 K with various Zn doping x.

(a–d) for x = 0, 0.075, 0.15, 0.3, respectively.

Full size image

In order to have a better understanding on the effect of Zn doping on the spin-dependent transport, the TMR ratio and RA value at 10 K and at 300 K as a function of Zn-doping x are shown in Figure 6, where the values of RA in the parallel and antiparallel configurations (RAP, RAAP) are shown by the right axis and the TMR ratio is shown by the left axis. Both values of RAAP at 300 K and 10 K decreases with increasing Zn-doping x, with a faster decrease rate around x = 0.1. The value of RAP at both 300 K and 10 K exhibit a gradual decrease with x, but much slower than that of RAAP. The TMR ratio both at 300 K and 10 K decreases with x increasing from 0 to 0.075. Importantly, we find that the TMR ratio decreases slowly with increasing Zn fraction, while maintaining a high value, e.g. above 100% for samples with x ~ 0.15. Fortunately, in the range of x = 0.075 and 0.15, the values of RAP,AP show an marked decrease with increasing x. With further increasing x to 0.3, the values of both RAP,AP and the TMR ratio decrease significantly. Therefore, from Figure 6 we observe that the doping range x from 0.075 to 0.15 is applicable in order to achieve a significant decrease in the RA value, but still retain a high TMR ratio, as is the goal for novel industrial applications. For this research, the barrier thickness was chosen as 3 nm, because we required high quality MgZnO barriers, namely reduction of defects and pinholes. Consequently, the values of RAP,AP can be further reduced by decreasing the barrier thickness, down to 1 nm for instance.

Figure 6
figure 6

Plots of RAP,AP (left axis) and TMR ratio (right axis) as a function of x.

(a) at 300 K and (b) at 10 K. The solid lines are a guide for the eyes only.

Full size image

The transport properties including the TMR ratio, the RA value and the temperature dependence prove that a thin Zn-doped MgZnO layer can be successfully epitaxially grown for a tunnel barrier in MTJs. As predicted by first-principles calculation, the bandgap of these ultrathin MgZnO barriers is tunable, whereby the rocksalt structure is kept in order to achieve spin filtering effect due to Δ1 states.

Discussion

The barrier height in tunnel junctions is also an important aspect related to tunable bandgap. In general, the barrier height can be estimated using the Simmons formula32,33. However, the Simmons formula is inadequate for MTJs for two reasons. First, even in its full form without the assumption of low or intermediate bias voltage, it neglects the higher order 1/d terms thus is only suitable for relatively thick barrier layers (d > 10 nm), where d is barrier thickness. Most MTJs have barrier thickness close to 1 nm. Second, the standard Simmons formula32 was derived for symmetric barriers. The asymmetric generalisation33 was based on an expansion of a small difference between barrier heights on two sides of the tunnel barrier. Neither formula can fit the MTJs where the I – V behaviour between parallel and antiparallel configurations exhibits great difference because the interfacial structures across the barrier are asymmetric. This asymmetry in MgO-based MTJs was confirmed by the surface X-ray diffraction, XPS and the inelastic electron tunneling spectroscopy (IETs) with the support of the first-principles calculation27,34,35.

Therefore, we develop a model for an asymmetric tunnel junction. The derivation is given in the Supplementary Information. The current density J of such a junction is expressed as,

where D contains the barrier asymmetry

and

where the barrier heights of bottom and top interface are denoted by φ1,2, respectively and their average value is defined as . with m* being the effective mass of the tunneling electrons and the bias voltage and barrier thickness are V and d, respectively. If we take d in nanometres, φ1,2 in electron Volts and V in Volts, then S = 10.25 eV−1/2nm−1 and e/2πh = 6.2 × 108 eV−1nm2 and the resulting current density J is in the unit of A/cm2.

Typical results of fitting I – V curves using Eq. (1) of the above model were presented in Supplementary Figure S4 for x = 0 and 0.15, respectively. Figure 2(b, c) shows the barrier heights at the bottom and top interfaces across the barrier (denoted by φ1,2) in the parallel and antiparallel configuration, respectively. It can be seen that with increasing x, the value of φ shows a gradual decrease. For the parallel configuration shown in Figure 2(b), the values for bottom and top interfaces across the barrier are similar. However, the difference between φ1 and φ2 is much larger for the antiparallel configuration shown in Figure 2(c). This observation proves the asymmetry between bottom and top interfaces, in agreement with previous results27,34,35. The barrier height deceases gradually with increasing x, another proof of the tunable bandgap of Zn-doped MgO layer.

The dynamic conductance dI/dV is a unique tool to study spin-dependent tunneling34,36. Here the dynamic conductance has been measured at 30.79 Hz with an ac modulation voltage of 4 mV using a standard lock-in method. Figure 7(a–d) shows typical data for x = 0, 0.075, 0.15 and 0.3, respectively. The dynamic conductance in parallel state for x = 0 and 0.075 shown in Figure 7(a, b) exhibits a bias voltage independent behaviour, indicating a high quality barrier with spin filtering effect. However, the dynamic conductance both in P and AP states for x = 0.3 shown in Figure 7(d) has a strong dependence on the bias voltage, indicating a weak spin filtering effect similar to the amorphous AlOx barrier34. This result demonstrates another aspect showing that Zn-doping into an MgO barrier can tailor the spin-dependent tunneling across the barrier.

Figure 7
figure 7

Dynamic conductance dI/dV for P and AP configurations with varying x at 4.2 K.

(a–d) for x = 0, 0.075, 0.15 and 0.3, respectively.

Full size image

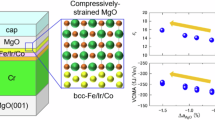
For spintronic devices, V1/2 is defined as the value of voltage at which the TMR ratio is half of that at zero bias. This parameter is critical for MTJs because the devices work at a certain bias voltage. Bias voltage dependence of normalised TMR ratio with various Zn-doping x was presented in Supplementary Figure S3. Figure 8 shows the values of , and V1/2 as a function of Zn-doping x at 10 K, where and for positive and negative voltage where the TMR ratio decreases to 50%. The value of V1/2 is the average of and . It can be seen that the value of does not change significantly with doping, together with a small peak around x = 0.1. However, the value of shows an obvious decrease with doping. Therefore, the value of V1/2 shows a slight decrease. It is interesting to find that the value of V1/2 with x = 0.1 drops only 10% compared with that of x = 0. This drop will not affect the working performance for devices if other parameters can be optimised, such as the TMR ratio and RA value. From the values of and , it can be seen that the difference decreases with further increasing x. The asymmetry of dynamic conductance and values between positive and negative bias comes from the different interfacial structures27,34.

Figure 8
figure 8

Value of , and V1/2 as a function of x at 10 K.

The solid lines are guide for the eyes only.

Full size image

Based on above results and discussion, we confirm that the spin filtering effect due to Δ1 can be maintained under Zn-doping from the band structure of MgZnO shown in Figure 1, even for x = 0.3, which guarantees a high TMR ratio shown in Figure 6. The bandgap shown in Figure 2 decreases with increasing x, leading to a decrease of RAP,AP shown in Figure 6. Actually, the spin-dependent tunneling across the barrier which determines the values of RAP,AP and the TMR ratio, is very complicated. For example, the interfacial structures such as oxygen vacancies and dislocations, together with defects and vacancies in the barrier, play a great influence on tunneling behaviour23,27,34.

The first-principles Layer-Korringa-Kohn-Rostoker (LKKR) approach1 is used to calculate the conductance in Fe/Mg1−xZnxO/Fe tunnel junctions, where Zn doping x ≤ 0.3 in order to keep the rocksalt structure. Figure 9 presents the calculated results of parallel and antiparallel resistance (RP,AP) as a function of Zn doping, where the data without any oxygen vacancies (OVs), with 0.5% OVs and 1% OVs are shown in Figure 9(a–c), respectively. For a simplified case, the oxygen vacancies are assumed to be uniformly distributed in the barrier. For Zn-doped MgO barrier without any OVs shown in Figure 9(a), RAP shows a monotonic decrease with increasing x, whereas RP is almost independent on Zn-doping. For 1% OVs in the barrier shown in Figure 9(c), RAP shows a sharp decrease with very lowe x (x < 0.075) and it doest not change greatly with further increasing x. In this case, RP is nearly independent on Zn-doping. With respect to 0.5% OVs shown in Figure 9(b), RAP decreases greatly with Zn-doping (x < 0.05), but shows a slight increase with further increasing x up to 0.1, leading to a peak around x = 0.1. Finally, RAP shows a slowly monotonic decrease with further increasing x up to 0.3. In the case of 0.5% OVs, RP shows a delicately decrease at lower x and it is almost independent on further increasing x. Based on the comparison between theoretical results shown in Figure 9 and experimental data shown in Figure 6, we conclude that the case with 0.5% OVs is more close to the situation of Zn-doped MgZnO barrier. The oxygen vacancies in the barrier can be well controlled by the pressure and the ratio of argon and oxygen in the sputtering systems and by the oxygen plasma in the MBE system.

Figure 9
figure 9

Influence of the oxygen vacancies on the resistance.

Calculated RP,AP as a function of Zn doping x. (a) without OVs, (b) for 0.5% OVs and (c) for 1% OVs, respectively. The solid line is a guide for the eyes only.

Full size image

Our experimental data with the support of first-principles calculation clearly shows that light Zn-doping is a applicable method to tune the bandgap of MgZnO barrier, where the spin filtering effect with rocksalt structure can be maintained, leading to a greatly decreased RA value but with a high TMR ratio. Optimal Zn-doping is achieved in the range of 0.075 to 0.15, where the TMR ratio of about 120% at RT (250% at 10 K) can be kept and RAP,AP value can be greatly reduced (about 50%). It is necessary to emphasise that the tunable bandgap of Zn-doped MgZnO with rocksalt structure can be applicable not only in spintronic devices such as tunnel junctions here, but also in the semiconducting devices such as photodetectors. Furthermore, the idea can be applied to the other case of ZnO films, where the light doping of Mg into ZnO lattice to tune the bandgap of ZnMgO while keeping a wurtzite structure. The tunable bandgap of Mg-doped ZnMgO with wurtzite structure should have wider applications in semiconductor.

In summary, we have demonstrated an effective method to tune the bandgap in MgO tunnel barriers by incorporating Zn into the MgO lattice while maintaining its rocksalt crystal structure. A nanometre thick MgZnO layer with a tunable bandgap is successfully fabricated as a barrier in epitaxial Fe/Mg1−xZnxO/Fe magnetic tunnel junctions. First-principles calculation in the local density approximation has been used to determine the bandgap in MgZnO barriers, in excellent agreement with our experimental results. Through materials optimisation, a high TMR ratio (such as 120% at 300 K) and greatly reduced RAP,AP values (50% decrease) could be realised, which presents a major breakthrough for magnetic device applications. This work opens up a new method to control the bandgap of films that will have great impacts not only on spintronic applications but also on semiconducting devices.