Introduction

Many of the micro-scale mechanical systems such as micro-electro-mechanical systems (MEMS) have been developed in recent years. Rapid improvements in the manufacturing process of silicon chips enabled such trends. The demand for producing highly integrated functions in ever smaller dimensions significantly increases, which we can see obviously in present-day industrial products. Although the current techniques based on the photolithography, which are often used in manufacturing integrated circuits, enable us to produce layered structures that work as MEMS, in order to realize highly functional systems, precise manipulation and assembly of micro-parts into a fully three dimensional structure is recognized to be still indispensable. Additionally, the techniques of micro-manipulation and assembly could be helpful to investigate scientific phenomena in micro/nano world. For instance, the development of intelligent materials that can play roles as photonic band devices was reported1. As described in the article1, the micro-manipulation technique includes three processes: picking a micro-object from a substrate, carrying and then placing it to an arbitrary point. By the repetition of these processes, a three dimensional structure can be constructed. In such processes, the use of gripper mechanism is effective down to the millimeter scale. In the micrometer (or even smaller) scale, however, it is not effective anymore to execute these processes by the gripper mechanism because the adhesional force that causes the micro-object to unexpectedly adhere to one of the gripper fingers becomes much greater than the gravitational force due to the scale effect. Therefore, it becomes difficult to achieve high precision and repeatability by the gripper mechanism in micro-manipulation2.

In order to realize the technique of micro-manipulation with high precision and repeatability, a mechanical technique of micro-manipulation by a single probe was suggested3,4. This technique considers the change of mechanical interaction versus the force variation from the probe-tip. Because the probe-object or object-substrate interface could be selectively broken with the use of the technique, picking-up and placing objects can be more repeatable and precisely controlled. In parallel, it is critical to understand the contact mechanics of an elastic particle in adhesional contact with a substrate. For example, the Johnson-Kendall-Roberts (JKR) model5 of elastic contact under a compressive load has found tremendous applications in micromanipulation6 (including adhesional contact of biological cells7).

Although the rolling-resistance of a micro-object was mentioned in the literature3,4, a quantitative understanding is still missing and, consequently, the high repeatability required during micro-manipulation cannot be achieved. Recently, some researchers have tried to evaluate the order of magnitude of the rolling-resistance via their theoretical and/or experimental approaches8,9,10,11,12. For example, Soltani and Ahmadi8 theoretically discussed the rolling of a spherical and a cylindrical object in terms of geometry and rotational moment around a certain axis, but did not provide a reasonable criterion for the critical point of rolling. Dominik and Tielens12, for the first time as far as we know, explicitly mentioned the existence of rolling resistance beyond which an irreversible rolling of an object occurs and analytically calculated the relation between the moment opposing the attempt to roll and angular displacement; however, they did not clarify which factors determine the critical status from not-rolling to rolling. She et al.11 reported the relation of the adhesion hysteresis and rolling contact mechanics via theoretical and experimental approaches using polymer materials in terms of crack propagation along the edges of the contact interface; still they did not reveal the transition mechanism from quasi-static status to dynamic status (mentioned as “instability”). Peri and Cetinkaya10 and Ding et al.9 experimentally demonstrated the existence of a critical rolling resistance of a microsphere. For interpreting the experimental results, they adopted Dominik and Tielens’ theory which did not explain the dominant factors of the critical condition. Barquins et al.13, She et al.11 and Greenwood et al.14 established a linear elastic fracture mechanics (LEFM) based asymptotic method to study the functional dependences for the problem of rolling; nevertheless, in these earlier studies, explicit expressions for the critical conditions of initial rolling were not fully developed. To date, a model sufficiently convincing and theoretically consistent for explaining the critical status of the rolling behavior in micro-scale is not yet available.

To solve nonlinear contact mechanics problems where exact closed-form solutions are rather difficult to obtain, it has been proven practically very useful to derive approximate closed-form dimensionless functions from parametric computational simulations15,16. Therefore, in this study, we calculate rolling resistances of micro-cylinders for a few kinds of materials in terms of the total energy and extract the normalized dimensionless functions in order to understand the rolling behavior of a micro-object in adhesional contact. To simplify the problem, we assume an isotropic and elastic cylindrical micro-object in adhesional contact with a rigid surface. The plane strain condition is assumed. Once an external moment is applied, we can calculate the total energy of this system consisting of the following three terms: the elastic energy stored in the deformed micro-cylinder, the interface energy within the contact area and the mechanical potential energy that depends on the external moment. Then we adopt the finite element method (FEM) to compute the elastic energy. The total energy is obtained as the function of contact area. We identify the equilibrium state of the system by finding the local minimum value of the total energy. We determine the rolling resistance for various conditions by obtaining the critical external moment at which the micro-cylinder makes the transition from equilibrium static state to non-equilibrium rolling state. The normalized dimensionless functions of rolling resistance can be deduced by plotting numerical solutions for various parameters in logarithmic scales. In addition, extending the asymptotic LEFM approach developed in the literature11,13,14, explicit critical rolling resistant conditions can be obtained. Direct comparison and cross-validation are given between the asymptotic LEFM based analytical solutions and the full-field FEM/dimensional analysis based results.

Results

Theoretical considerations

Figure 1 shows the schematic illustration of the rolling process of an elastic micro-cylinder, which we consider in this study. Assuming no strain in the z direction, the adhesional contact between the substrate and the micro-cylinder is treated as a plane strain problem. The rolling process is taken to be quasi-static. Figure 1(a) shows the initial state that is the adhesional contact between the substrate and the micro-cylinder with neither moment nor force applied. As shown in Fig. 1(a), R represents the radius of the micro-cylinder and binitial represents the initial width of the contact area without any applied moment or force. According to the theory proposed by Kalker17 and Barquins13, binital is given by

Figure 1
figure 1

Cross-sectional schematic illustration of the rolling process of an elastic micro-cylinder adhered to a rigid substrate.

(a) The initial state and (b) propagation of the contact width under an external moment M.

Full size image

where Δγ is the work of adhesion of the interface between the cylinder and the substrate, ν is the Poisson’s ratio, E is the Young’s modulus and is the reduced modulus. The substrate is taken to be a rigid flat surface and the micro-cylinder to be linearly elastic and isotropic. We assume no friction between the substrate and the micro-cylinder.

Figure 1(b) shows the loaded state, when an external moment M is applied to the center of the cylindrical micro-object. Consequently, the width of the adhesional contact area between the substrate and the cylindrical micro-object reduces and varies from binitial to b. As shown in Fig. 1(b), Δb is the variation in the width of the contact area from binitial to b. Therefore, Δb can be given as

Since the positive direction of b is defined as the incremental direction of b, Δb is negative. The change in the width of the contact area represents the propagation of the adhesional contact surface between the substrate and the cylindrical micro-object. When Utotal is defined as the total energy of this system with a given M, Utotal varies with b. In other words, Utotal can be computed once M and b are both defined.

The rolling resistance of the micro-cylinder, Mroll, is defined as the external moment that enables the cylindrical micro-object to start rolling. As illustrated in Fig. 2(a), if the external moment M is smaller than Mroll, the micro-cylinder is in equilibrium with the given external moment M and adheres to the substrate stably. In Fig. 2(a), bmin and θ represent the width of the contact area and the deformed angle in the equilibrium state respectively. In this case, among all possible elasticity solutions with a contact width b, bmin minimizes Utotal, as shown in Fig. 3(a). In other words, if the adhesional contact surface propagates quasi-statically along the interface between the micro-cylinder and the substrate, the contact width b reaches its minimum, bmin, at the equilibrium state. However, if the given moment M is greater than Mroll, bmin does not exist and the micro-cylinder begins to roll as illustrated in Figs 2(b) and 3(b). In summary, the state of the micro-cylinder with M applied depends on the balance between Utotal and b with M given. The total energy of this system, Utotal, is given as,

Figure 2
figure 2

Cross-sectional schematic illustration of the energy state of the cylindrical micro-object under an applied moment M.

(a) The equilibrium state and (b) the state when the cylindrical micro-object begins to roll.

Full size image
Figure 3
figure 3

Schematic illustration of the relation between total energy Utotal, and contact width b under an external moment M.

(a) The equilibrium state and (b) the state when the cylindrical micro-object begins to roll.

Full size image

where Uelastic is the elastic energy that is stored in the cylindrical micro-object, Uinterface is the interfacial energy that is stored in the interface between the substrate and the micro-cylinder and Umechanical is the potential energy that is defined with the external moment M. Uinterface and Umechanical are given by the following equations respectively:

where t is the thickness, i.e., the length of the cylindrical micro-object in the z direction (see Fig. 4).

Figure 4
figure 4

Isometric schematic illustration of the model of the micro-cylinder for calculating total energy Utotal, rotational angle θ and contact width b for an external moment M given.

Full size image

In order to calculate the total energy Utotal, the rotation angle θ and the contact width b for a given external moment M, systematic simulations were conducted using FEM simulations. In order to obtain the elastic energy Uelastic with a contact width b, the constraint condition is given to the contact interface and the external moment M is applied to the axis of the micro-cylinder. As a result, the stress is distributed along the interface due to the adhesional force as illustrated in Fig. 4 by the broken line. The right-hand-side edge (trailing edge) of the contact area behaves similarly as the crack front where the resultant stress is singular. The left-hand-edge (leading edge) however behaves differently, where no stress singularity exists and essentially zero stress is found along the leading edge. This means no new interface is formed due to the external moment M as long as the quasi-static loading and JKR potential for interface are assumed. The value of Utotal is numerically obtained as a function of b. While the stress states on both edges are carefully monitored in the FEM simulations, it is noted that the criterion of reaching the critical conditions for incipient (initial) rolling is governed by the total energy Utotal (see also Fig. 3) instead of the stress state (or stress singularity) on the edges.

We used the commercially available FEM package ABAQUS Standard (SIMULIA, Providence, RI, USA) for numerical simulations. As an example, the elastic energies of the micro-cylinder with different values of contact width b were calculated with respect to various external moments given. In the first example studied, the radius and thickness of the micro-cylinder are both 1 [μm]. The cylinder material assumed in the model is polystyrene, where Young’s modulus E = 3.8 [GPa] and Poisson’s ratio ν = 0.34 and the work of adhesion between the cylinder and the substrate is taken as Δγ = 0.1 [N/m]3. Figure 5(a) shows the relation between total energy Utotal and contact width b for an external moment M = 0.07 [10−12 Nm] given. As shown in Fig. 5(a), Utotal reaches the local minimum value for b = 0.104 [μm]. Therefore, at M = 0.07 [10−12 Nm], the micro-cylinder is in equilibrium with the external moment for b = 0.104 [μm].

Figure 5
figure 5

Relation between total energy Utotal and contact width b.

(a)The equilibrium state for M = 0.07 [10−12 Nm] and (b) the state when the micro-cylinder begins to roll for M = 0.1 [10−12 Nm].

Full size image

Figure 5(b) shows the relation between total energy Utotal and contact width b for an external moment M = 0.1 [10−12 Nm] given. As demonstrated in Fig. 5(b) and discussed earlier with Fig. 3(b), the local minimum point does not exist anymore. Therefore, at M = 0.1 [10−12 Nm], the micro-cylinder can not be in equilibrium with the external moment any more and has to roll. In the case of M = 0.105 and 0.11 [10−12 Nm], no minimum Utotal can be found. Figure 6 shows the relation between the reduction of the contact length, |Δb| and the corresponding external moment M. The critical value of the rolling moment, Mroll, is approximately 0.1 [10−12 Nm]. The error of Mroll ranges within ±5% of the estimated value 0.1 [10−12 Nm], because the equilibrium state can be definitely confirmed with M = 0.095 [10−12 Nm], but not with M = 0.105 [10−12 Nm] anymore. Although the static rolling resistance between a pair of friction-free solid surfaces seems to be zero in the macro scale, such rolling resistance has a certain finite value in micro scale due to adhesional effect. The critical rolling conditions can be determined by evaluating the balance of the total energy, Utotal, which is influenced by both the external moment and the adhesional effect between the substrate and the micro-cylinder.

Figure 6
figure 6

Relation between the external moment, M and the reduction of the contact length, |Δb|, equilibrated with the corresponding external moment.

The point for M = 0.1 [10−12 Nm] is the critical point of M = Mroll. Beyond and at this point, no bmin is found and no equilibrium is possible. See text for more details.

Full size image

General dimensionless functions for micro-cylinder adhesional rolling

For various radii R of a polystyrene micro-cylinder (E = 3.8 [GPa], ν = 0.34) and interfacial works of adhesion Δγ, we calculated the rolling resistance per unit length, [10−6 Nm/m], the corresponding width of contact area at the beginning of rolling, broll and the rotational angle at the beginning of rolling, θroll, where the errors are all kept within ±5% in each case. Figure 7 shows the relation between and R for Δγ = 0.01, 0.1 and 1.0 [N/m]. Each solid line is obtained by fitting a line to the plotted data with the least-square method. The results clearly show that is proportional to the radius R for each Δγ.

Figure 7
figure 7

Rolling resistance per unit length at the beginning of rolling, [10−6 Nm/m].

(Material: polystyrene, E = 3.8 [GPa], ν = 0.34).

Full size image

Figure 8 shows the relation between broll and R for Δγ = 0.01, 0.1 and 1.0 [N/m]. The data shows that broll is nearly proportional to R1/3 for each Δγ.

Figure 8
figure 8

Width of contact area at the beginning of rolling, broll [μm].

(Material: polystyrene, E = 3.8 [GPa], ν = 0.34).

Full size image

Figure 9 shows the relation between θroll and R for Δγ = 0.01, 0.1 and 1.0 [N/m]. The data shows that θroll is nearly proportional to R−1/3 for each Δγ.

Figure 9
figure 9

Rotational angle at the beginning of rolling, θroll [rad].

(Material: polystyrene, E = 3.8 [GPa], ν = 0.34).

Full size image

Furthermore, to investigate the dependency of Young’s modulus for the normalized formulas, we also calculated , broll and θroll, for various radii R and Δγ = 0.1[N/m] for Au, as shown in Figs 10, 11 and 12, respectively.

Figure 10
figure 10

Rolling resistance per unit length at the beginning of rolling, [10−6 Nm/m].

(Work of Adhesion: Δγ = 0.1 [N/m]).

Full size image
Figure 11
figure 11

Width of contact area at the beginning of rolling, broll [μm].

(Work of Adhesion: Δγ = 0.1 [N/m]).

Full size image
Figure 12
figure 12

Rotational angle at the beginning of rolling θroll [rad].

(Work of Adhesion: Δγ = 0.1 [N/m]).

Full size image

The calculation results surprisingly shows that the value of is independent of Young’s modulus although values of broll and θroll do depend on Young’s modulus.

The general expressions of , broll and θroll can be written in terms of R, Δγ and E*:

Using the ∏-theorem in dimensional analysis, we obtain the general dimensionless functions:

where ∏M, ∏b and ∏θ, are normalized dimensionless functions. To extract approximate explicit functional forms of ∏M, ∏b and ∏θ, FEM simulation results are plotted in logarithmic scales as shown in Fig. 13. We have confirmed that /R2E*, broll/R and θroll are linearly related to Δγ/RE* in logarithmic scales, which can be easily fitted with the functional form c (Δγ/RE*)n (c and n: are constants). By using least-square method, we can now extract the constants, c and n, for each dimensionless function at the maximum coefficient of determination (Rdet) as follows:

Figure 13
figure 13

Relations between normalized and dimensionless values ((a) Mroll/R2E*, (b) broll/R and (c) θroll) and the normalized variable, Δγ/RE*, plotted in logarithmic scales.

Full size image

We have found out that the power indices of Δγ/RE* for Mroll/R2E*, broll/R and θroll in Eqs (8a), (8b) and (8c) are very close to 1, 1/3 and 1/3, respectively. We thus re-write Eq. (8) using the following functions with best fitting:

with all the coefficients of determination fairly close to 1. This is similar to Kalker’s earlier work17 where binitial/R was found to be proportional to the 1/3 power of Δγ/RE* for the pull-off problem. These equations are formulas of rolling resistance in the normalized and dimensionless form for a cylindrical elastic object per unit length in adhesional contact.

Within the explored parameter space in this study, we obtain

Surprisingly, the rolling resistance is determined only by ‘work of adhesion times cylindrical radius’ and independent of Young’s modulus (E*). According to Kalker’s theory17, the pull-off force Fpull-off per unit length to detach a cylindrical object from the plate should be (3/2)(πΔγ2RE*/2)1/3, while the value of apull-off, one half of bpull-off, should be (2ΔγR2/πE*)1/3. Thus we have Fpull-off apull-off = (3/2)ΔγR, also independent of Young’s modulus.

From the results of dimensional analysis, the solution of the rolling problem only depends on one single dimensionless variable, Δγ/RE*. The parametric study covered the variable range for Δγ/RE* across 3 orders of magnitude, i.e., from 1.05 × 10−7 to 1.16 × 10−4. Within this range, the normalized dimensionless functions we extracted provide us with a quantitative understanding about the rolling-resistance of a micro-cylinder.

An asymptotic linear elastic fracture mechanics solution

In this section, we compare the full-field FEM results with an asymptotic solution based on the linear elastic fracture mechanics (LEFM) approach.

As illustrated in Fig. 14 and following the asymptotic LEFM approach described in the literature11,13, the stress distribution on the interface can be analytically estimated as:

Figure 14
figure 14

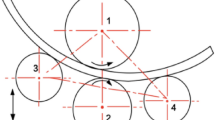
Schematic of a cylinder rolling on a flat plate counterclockwise.

Here, the cylinder is deformable and the flat plate is rigid. Adapted from ref. 11.

Full size image

where wh is the Hertzian, non-adhesive half width for a contact under the same vertical load, P* and the center of the roller is r = −d. Note that w in Fig. 14 and the following discussion corresponds to b/2 denoted in earlier sections. Consequently, the moment per unit micro-cylinder length M* can be evaluated by integrating the stress distribution as:

The corresponding stress intensity factors at r = ±w are

and the energy release rates at r = ±w are

The net change in energy release rate between r = +w and r = −w can now be given as

With Eq. (12) and Eq. (15) and setting ΔG = Δγ at the incipient rolling we have

For the case with P* = 0 in Fig. 14, we obtain , which is the same as we obtained earlier using full-field FEM analysis in Eqs (9a) and (10). In this case, the critical moment of initial rolling identified using the asymptotic LEFM approach agrees well with that obtained through FEM simulations.

For incipient (initial) rolling, the stress at the leading edge (r = −w) will be finite, i.e. Kr=−w = 0, then we have

at the point of initial rolling. The change in mode I plane strain energy release rate in Eq. (15) can be rewritten as

Note that when P* = 0 in Fig. 14, we have wh = 0 and thus w = 2d after applying Eq. (17). Since the contact width b = 2w by definition, manipulating Eq. (18) gives

and thus at the initial rolling,

This again agrees well with 2.727, the coefficient we obtained in Eq. (9b) using FEM simulations. We can see an excellent agreement in contact width at the initial rolling. And at this point, d in Fig. 14 is now

We further evaluate the initial rolling angle. For the definition of the rotational angle θ = d/R, the rolling angle can be obtained as

wheredroll = d′roll + doffset; d′rollis the displacement given by Eq. (20) resulted from with the contact width broll and doffset is the offset displacement due to the changing of contact width from binitial to broll assuming the leading edge does not move. doffset can be calculated from Eqs (1) and (19) as:

As a result, we obtain the rolling angle as the sum of two terms:

This result again agrees well with the full-field FEM solution given by Eq. (9c).

Discussion and Concluding Remarks

As an example for a first order comparison with our results, Peri and Cetinkaya10 experimentally evaluated the value of rolling resistance moment of a micro-sphere. They described the value as Mroll = 6π Δγ ξ r whereMrollis the critical rolling resistance moment, Δγ is the work of adhesion, ξ is the shift displacement in oscillation, r is the radius of the sphere. In the experiment of a polystyrene latex micro-sphere (with 21.4 μm in radius) on silicon, ξ was 29.96 nm, the contact radius of the micro-sphere and the silicon substrate a was 231 nm and contact area was 0.168 [μm2]; consequently Mroll would be Mroll = 6πΔγ (29.96 [nm]) (21.4 [μm]) ≈ 12Δγ × 10−12 [Nm] (Δγ in [N/m]). Using the present theory for a micro-cylinder, we have which corresponds to Mroll = Δγ R a if we count only the contribution within a length a in the micro-cylinder. Therefore for a polystyrene latex micro-cylinder (with 21.4 μm in radius) on silicon, we have Mroll = Δγ (21.4 [μm])(231 [nm]) ≈ 5Δγ × 10−12 [Nm] (Δγ in [N/m]). Note that the reduced modulus E* = 3.04 GPa for this case and the estimated contact radius at incipient rolling is and the contact area is broll × a = 416 [nm] × 231 [nm] = 0.096 [μm2], which is comparable to the contact area for the micro-sphere. The predicted critical rolling moments are found to be on the same order of magnitude for a micro-cylinder and a micro-sphere, when the contact areas for these two cases are similar.

In summary, we obtained closed-form expressions describing the critical rolling resistance of an isotropically-elastic cylindrical micro-object in adhesional contact with a rigid surface in normalized and dimensionless forms. In order to systematically evaluate the critical conditions of the rolling resistance, we established the procedure using finite element method, taking into account the full field stress, strain and strain energy distribution. By considering the energy balance of the system, we confirmed the existence of the contact area that provides the equilibrium state of the model. We calculated the rolling resistance with different cylinder radii, works of adhesion and Young’s moduli in adhesional contact with a frictionless rigid surface and numerically established the critical conditions of rolling resistance in closed-form dimensionless functions. The critical rolling moment was found to be determined only by work of adhesion times cylindrical radius and independent of Young’s modulus, while the initial rolling contact area and initial rolling angle still depend on Young’s modulus. In addition, building upon a linear elastic fracture mechanics based approach, exact asymptotic analytical solutions were obtained for the critical rolling moment, initial contact area and initial rolling angle; these asymptotic solutions compare very well with the full-field finite element results. In future work, we will study the rolling resistance for other geometries and analyze the influence of the friction parallel to the substrate on the rolling resistance.

Additional Information

How to cite this article: Saito, S. et al. Rolling behavior of a micro-cylinder in adhesional contact. Sci. Rep. 6, 34063; doi: 10.1038/srep34063 (2016).