Introduction

In quantum mechanics a quantum system is associated with a separable complex Hilbert space H. A quantum state ρ is a density operator, that is, which is positive and has trace 1, where and denote the von Neumann algebras of all bounded linear operators and the space of all trace-class operators with , respectively. Let us denote by the set of all states in the quantum system associated with H. A state ρ is called a pure state if ρ2 = ρ; otherwise, ρ is called a mixed state.

Consider two quantum systems associated with Hilbert spaces H and K respectively. Recall that a quantum channel between these two systems is a trace-preserving completely positive linear map from into . It is known1,2,3,4 that every channel has an operator-sum representation

where 1 ≤ N ≤ ∞ and is a sequence of bounded linear operators from H into K with . Eks are called the operation elements or Kraus operators of the quantum channel Φ. The representation of Φ in Eq. (1) is not unique. If both H and K are finite-dimensional, it is well known that N ≤ dim H dim K < ∞ and the sequences and of operation elements of any two representations of Φ are connected by a unitary matrix, such that , . This fact is so-called the unitary freedom in the operator-sum representation for quantum channels. However, unitary freedom is no longer valid for infinite-dimensional systems5. In fact, what we have is so-called the bi-contractive freedom, which asserts that, if a channel has two operator-sum representations , then there exist contractive matrices Ω = (ωij) and Γ = (γji) such that for each i and for each j. The converse is also true. Particularly, if Ω = (ωij) is an isometry so that for each i, then holds for any X.

Let R and Q be two quantum systems described by Hilbert spaces HR and HQ, respectively. Suppose that the joint system RQ is prepared in a pure entangled state and the initial state of system Q is . The system R is dynamically isolated and has a zero internal Hamiltonian, while the system Q undergoes some evolution that possibly involves interaction with the environment E. The final state of RQ is possibly mixed and is described by the density operator ρRQ′. Thus, if the dynamical evolution that Q is subjected to is described by ΦQ, then the final state is and the entanglement fidelity is refs 6, 7, 8, 9

The value of Fe is independent of the choice of purification of ρQ. In fact, it was shown5,7,10,11 that for any with dim H ≤ ∞ and any quantum channel Φ with operation elements {Ei}, we have .

For finite-dimensional systems there is another quantity concerning channels and states that is intrinsic to subsystem Q. This quantity is called the entropy exchange. For a given state ρQ and a given channel ΦQ in a finite-dimensional system Q, recall that the entropy exchange Se is defined by refs 1, 6 and 12, 13, 14

where and is a purification of ρQ. It was shown1,6 that the entropy exchange Se is independent of the choice of purification of the state ρQ. It was also shown1 that the entropy exchange Se has another explicit formulation

where with the sequence of the Kraus operators of an operator-sum representation of ΦQ and the minimum is taken over all operator-sum representations of ΦQ.

It is clear that Eq. (3) can be naturally generalized to infinite-dimensional case to give a definition of the entropy exchange for channels and states in infinite-dimensional systems. In continuous variable systems, Chen and Qiu15 studied the coherent information Ie = S(ρQ) − Se of the thermal radiation signal ρQ transmitted over the thermal radiation noise channel, one of the most essential quantum Gaussian channels, and derived an analytical expression for computation of the value of it. However, as the von Neumann entropy S(ρ) of a non-Gaussian state in an infinite-dimensional system may be +∞16, we may have Se = +∞. In this paper we consider general states and channels and show that the definition Eq. (3) does not depend on the choice of the purification of the state either, and Eq. (4) is still true for infinite-dimensional systems.

For finite-dimensional systems, it is known6 that the entropy exchange is larger than or equal to the change of the entropy, that is,

where ρQ′ = ΦQ(ρQ). The second purpose of the present paper is to compare the entropy exchange with the change of the entropy and to check whether or not the inequality (5) is still valid in infinite-dimensional systems. We show that, for infinite-dimensional case, what we can have are the following three inequalities: , and . Thus, if both S(ρQ) and S(ρQ′) are finite, we still have . To prove the above inequalities, we need the subadditivity and the triangle inequality of von Neumann entropies for infinite-dimensional quantum systems. These two inequalities were established in a more general frame of von Neumann algebras for normal states with finite entropy17. However, for the convenience of readers, we present some elementary proofs including the case of infinite von Neumann entropy here by establishing the generalized Klein’s inequality for infinite-dimensional case. We also give some examples which illustrates that the entropy exchange is different from the change of entropy.

Entropy exchange for infinite-dimensional systems

In this section, we mainly give some properties of the entropy exchange for infinite-dimensional systems. In fact, the results in this section hold for both finite- and infinite-dimensional cases.

Recall that a linear operator U from a Hilbert space into another is called an isometry if ; a coisometry if . Obviously, if the spaces are finite-dimensional with the same dimension, isometries and coisometries are unitary operators.

Lemma 1. Suppose |ϕ〉 and |ψ〉 are two pure states of an infinite-dimensional composite system with subsystems R and Q. If they have identical Schmidt coefficients, then there are isometries or coisometries U on system R and V on system Q such that .

Proof. By the assumption, |ϕ〉 and |ψ〉 have respectively the Schmidt decompositions and , where and are two orthonormal sets for system R, and are two orthonormal sets for system Q, λi > 0 with . Extend to an orthonormal basis , and to an orthonormal basis {|i′R〉, |j′R〉} of the system R. In the same way, extend {|iQ〉} to an orthonormal basis {|iQ〉, |lQ〉}, and {|i′Q〉} to an orthonormal basis {|i′Q〉, |l′Q〉} of the system Q. Denote the cardinal number of a set by . Let , , and . Clearly, we have 9 possible cases.

Case 1. d1 = d2 and d3 = d4. Let unitary operators U on system R and V on system Q be defined respectively by U|iR〉 = |i′R〉 for 1 ≤ i ≤ N and U|jR〉 = |j′R〉 for 1 ≤ j ≤ d1 = d2; V|iQ〉 = |i′Q〉 for 1 ≤ i ≤ N and V|lQ〉 = |l′Q〉 for 1 ≤ l ≤ d3 = d4. Then .

Case 2. d1 = d2 and d3 < d4. Let U be defined as in Case 1 and V be defined by V|iQ〉 = |i′Q〉 for 1 ≤ i ≤ N and V|lQ〉 = |l′Q〉 for 1 ≤ l ≤ d3 < d4. Then U is a unitary operator on system R and V is an isometry V on system Q satisfying .

Case 3. d1 = d2 and d3 > d4. Define U on system R as in Case 1 and define V on system Q by V|iQ〉 = |i′Q〉 for 1 ≤ i ≤ N, and V|lQ〉 = |l′Q〉 for 1 ≤ l ≤ d4 and V|lQ〉 = 0 for d4 < l ≤ d3. Then U is unitary and V is coisometric so that .

In a similar way, it is obvious to see that

Case 4. d1 < d2 and d3 = d4. There is an isometry U on system R and a unitary V on system Q such that .

Case 5. d1 < d2 and d3 < d4. There are isometries U on system R and V on system Q such that .

Case 6. d1 < d2 and d3 > d4. There is an isometry U on system R and a coisometry V on system Q such that .

Case 7. d1 > d2 and d3 = d4. There is a coisometry U on system R and a unitary V on system Q such that .

Case 8. d1 > d2 and d3 < d4. There is a coisometry U on system R and an isometry V on system Q such that .

Case 9. d1 > d2 and d3 > d4, there are coisometries U on system R and V on system Q such that . ◽

Lemma 2. If and are purifications of a state ρQ to a composite system RQ, then there exists an isometry VR on system R such that either or .

Proof. Let be the spectral decomposition of ρQ with λi ≥ λi+1. Since both and are purifications of ρQ, their Schmidt decompositions have the form and , where and are two orthonormal sets for system R. Hence and have identical Schmidt coefficients. Making use of lemma 1, there is an isometry or a coisometry UR on system R such that . If UR is already an isometry, we have done. If UR is a coisometry, by the proof of Lemma 1 we see that there is an isometry VR such that and .◽

Lemma 3. Assume that and are two purifications of a state ρQ to a composite system RQ, and each is subjected to the same evolution superoperator with the resulting states respectively and , i.e., and . Then there exists an isometry VR on system R such that either or .

Proof. By lemma 2, there exists an isometry transformation VR acting on system R such that either  or . Without loss of generality, assume that . Let be an operator-sum representation of ΦQ. Then

Similarly, if holds, then we have

◽

Lemma 4. If A is a bounded self-adjoint operator on a complex Hilbert space and f is a continuous function on σ(A), the spectrum of A, then, for any isometric operator V, we have .

Proof. As A is a bounded self-adjoint operator, is a bounded closed set. Because f is a continuous function on σ(A), we can apply the Weierstrass theorem to find a sequence of polynomials {Pn} such that Pn → f uniformly on σ(A). Write . It is clear that since V is an isometric operator. Let n→∞, we see that .

The following result reveals that, for infinite-dimensional systems, similar to the entanglement fidelity5, the value of entropy exchange is also independent of the choice of purifications of the initial state.

Theorem 5. The entropy exchange of a channel ΦQ and a state ρQ is independent of the choice of purifications of the state ρQ.

Proof. Let and be two purifications of the state ρQ in composite system RQ, and denote and . By the definition Eq. (3), we have to show that

By lemma 3, there is an isometry VR so that the resulting states and satisfy either or . Without loss of generality, suppose . Note that f(x) = x log x is a continuous function on . Then, by lemma 4,

as desired.◽

In the sequel, analogue to Eq. (4) for finite-dimensional systems, we derive an explicit expression for Se in terms of ρQ and ΦQ for infinite-dimensional systems.

To do this, we need some more lemmas.

Lemma 6. Let with . For any and , we have and .

Proof. Fix an orthonormal basis {|i〉} of HB. Then B can be written in a matrix B = (bij), and and ρ can be written in operator matrices and ρ = (ρij), respectively. Thus we have , and then

Similarly, we can drive that

Lemma 7. Let with . Then, for any and , we have

Proof. By lemma 6 and with the same symbols as in the proof of lemma 6, we have

◽

Let ΦQ be a channel from system Q into system Q′. Suppose (M ≤ ∞) is an operator-sum representation for the channel ΦQ. If ρQ is a state of system Q and is a purification of ρQ into composite system RQ, then, for any μ, let . Thus the resulting state ρRQ′ can be written in

Therefore is a pure state ensemble for ρRQ′. Let us adjoin a system E with Hilbert space HE, where dim HE = M. Then, for any orthonormal basis , the state is a purification of ρRQ′. With these symbols, we have

Lemma 8. Let . Then we have Se = S(ρE).

Proof. Since the state is a pure state, the reduced states and have the same von Neumann entropy. Therefore, by the definition of the exchange entropy, we get .◽

Furthermore, let us write down the density operator ρE in matrix form. Clearly,

with . By lemmas 6 and 7, we see that

Let W be the density operator with components . Then, by lemma 8, Se = S(W). Now, let with Pμ = Wμμ. Thus is a probabilities which is given by the state W from a complete measurement using the basis that yields the matrix elements Wμν. Therefore we have as measurements increasing the entropy.

Now, we are at a position to give an explicit formula for the entropy exchange based upon the operator-sum representation for quantum channel ΦQ and the initial state ρQ for an infinite-dimensional system.

Theorem 9. Let be a state with dim HQ ≤ ∞ and a channel. Then the entropy exchange

◽where is a sequence of Kraus operators of an operator-sum representation of ΦQ, that is, , and the minimum is taken over all operator-sum representations of ΦQ.

Proof. For given state ρQ and quantum channel ΦQ, if {Aμ} is the sequence of Kraus operators of an operator-sum representation of ΦQ, then by lemma 8 and the discussion previous theorem 9, , where, , for some orthonormal basis {|μE〉} for the environment system E. Hence we have . In the sequel we show that for some suitable choice of operator-sum representation of ΦQ. In fact, for a given sequence {Aμ} of Kraus operators for an operator-sum representation of ΦQ, s are the matrix elements of ρE in the orthonormal basis {|μE〉}. Let W be the associated matrix with entries , that is, W is the matrix of ρE in an appropriate basis; then Se = S(W). Since W is a matrix representation of the environmental density operator, it may be diagonalized by a unitary matrix U = (uμν), i.e., , where is a diagonal matrix. Letting |μ′E〉 = U|μE〉, we have ρE = W0 in the basis {|μ′E〉}. Thus . Now let ; then, due to the theorem 2.1 in the paper5, {Bν} is a sequence of Kraus operators for an operator-sum representation of the quantum channel ΦQ, i.e. . Moreover, with obviously . So we have

where and the minimum is taken over all operator-sum representations of ΦQ.◽

Comparison with entropy change

The entropy exchange Se simply characterizes the information exchange between the system Q and the external world during the evolution given by ΦQ. It is interesting to explore the relationship between the entropy exchange and the entropy change during the same evolution. Such a question was studied for finite-dimensional systems and the inequality (5) was established6. However, the inequality (5) does not always valid in infinite-dimensional case. To solve the question for infinite-dimensional systems, we need the subadditivity and the triangle inequality of von Neumann entropies for infinite-dimensional systems which was established in the textbook17 for normal states with finite entropy in a more general frame of von Neumann algebras. However, we have to deal with the states with infinite entropy. Here we present somewhat elementary proofs for these two inequalities by generalizing the generalized Klein’s inequality from finite-dimensional systems to the infinite-dimensional systems and clarify when the inequalities are still valid for states with infinite entropy.

Let be a function. The following lemma 10 and 11 are obvious18.

Lemma 10. If f is a convex (concave) function, then f is continuous.

Lemma 11. If f is a convex (concave) function, then f(y) − f(x) ≥ (≤)(y − x) f′(x).

Lemma 12. Suppose f is a convex (concave) function and A is a bounded self-adjoint operator on a Hilbert space H with . If is an unit vector, then .

Proof. By lemma 10, f is continuous. Let be the spectral decomposition of the self-adjoint operator A. Assume that f is convex. For any unit vector , denote by μ the probability measure defined by for any Borel set Δ. With {Δk} any finite Borel partition of σ(A) and , we have

Similarly, if f is concave, then one gets

◽

Lemma 13. Suppose f is a convex (concave) function. If A, B are two positive operators acting on a Hilbert space H and A is of trace-class, then

Proof. As A is a positive operator of trace-class, by spectral theorem, there exists an orthnormal basis of H and nonnegative numbers λi such that . If f is convex, then by lemma 12 and lemma 11 we have

Similarly, if f is concave, then

◽

In finite-dimensional case, the following result is valid and is called the generalized Klein’s inequality. We generalize it to infinite-dimensional case.

Lemma 14. (Generalized Klein’s inequality) Let A, B be two positive operators of trace-class on a Hilbert space H. If , then

Proof. Take f so that f(x) = −x log x for x > 0 and f(0) = 0. Then f(x) is a concave function with and for x > 0. By lemma 13, we have◽

Since TrA log A < ∞, we get , as desired.

Making use of this result, we see that the relative entropy is also non-negative for the infinite-dimensional quantum systems whenever S(σ) < ∞.

Corollary 15. For any two density operators ρ, , if Tr(σ log σ) < ∞, then

Proof. Since ρ, σ are two density operators, Tr ρ = Tr σ = 1. Substituting these in the inequality (24), we have .◽

Next, we apply the corollary 15 to prove the subadditivity inequality (27) and the triangle inequalities (29) and (30) for Von Neumann entropy.

Lemma 16. Let be a state with . Then

where ρA = TrBρAB and ρB = TrAρAB.

Proof. Let ρ = ρAB and . Then, . Note that

If S(σ) < ∞, corollary 15 and the above equations imply . If S(σ) = ∞, then S(ρA) + S(ρB) = ∞, and obviously S(ρAB) ≤ S(ρA) + S(ρB) holds.◽

In finite-dimensional case, the inequalities holds for any bipartite states and is called the triangle inequality. In infinite-dimensional case, this inequality may be not valid except the case when both S(ρA), S(ρB) are finite. What we can have is the triangle inequalities of the following kind.

Lemma 17. Let with . Then

and

where , and .

Proof. To prove the inequality (29), we introduce a system C which purifies the system AB. Let be a purification of ρAB; then

and

Applying the subadditivity, that is, lemma 16, we have

Since is a pure state, S(ρAB) = S(ρC) and S(ρAC) = S(ρB). Hence the previous inequality is the same as .

By symmetry between the systems A and B one sees that is also true.◽

Now, we relate the entropy exchange to change in the entropy of the system Q for infinite-dimensional quantum systems.

Theorem 18. For any evolution ΦQ and initial state ρQ in an infinite-dimensional system Q, with ρQ′ = ΦQ(ρQ), the following inequalities are true.

and

Proof. The evolution ΦQ in fact is due to a unitary evolution of a larger system that includes an environment E with a pure initial state |0E〉 and the joint initial state . Obviously, we have S(ρQE) = S(ρQ). Since the joint system QE evolves unitarily, say , one sees that and the entropy of the joint state remains unchanged. Thus we have . Let be a purification of ρQ to a larger system RQ; then . This means that is a purification of ρRQ′. Let . Then by the lemma 8, the entropy exchange Se = S(ρE). Using the inequality (27), one gets , which gives . Applying the inequality (30), we obtain , which entails . The inequality (29) implies that , which establishes .◽

By theorem 18 we known that is always true. And, if both S(ρQ), S(ρQ′) are finite, then, as in finite-dimensional case, we have , which means that the entropy exchange is not less than the change in entropy of the system Q. In general, the entropy exchange is different from the change in entropy of the system Q, that is, holds for some channels and states.

Examples

The following is an example for finite-dimensional case.

Example 1. Let with dim HQ = 2. The bit flip channel ΦQ flips the state of a qubit from |0〉 to |1〉 with probability 1 − p. It has operation elements

After some calculation, , thus .

On the other hand, note that is a purifications of ρQ to a composite system RQ, where dim HR = 2. Thus

Obviously, the nonzero eigenvalues of ρRQ′ are p and 1 − p, and thus, . Hence we have whenever 0 < p < 1.

Next we give an example for infinite-dimensional case.

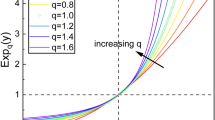
Example 2. Consider the thermal radiation signal ρQ on a Gaussian system Q, which has Glauber’s P representation . Here N is the average number of photons of ρQ, |α〉 is the coherent state and is an eigenstate of the annihilation operator a for each complex number α. Let ΦQ be the thermal radiation noise channel, , where is the displacement operator, and Nn is the average photon number of the output state if the input is the vacuum. If the input state ρQ is a thermal noise signal with its average photon number Ns, then the output state ρQ′ will be a thermal noise signal with its average photon number Ns + Nn19. We know that the entropy of any Gaussian state ρ is finite and is formulated by S(ρ) = g(N), where g(x) = (x + 1) ln(x + 1) − x ln x is a monotonically increasing convex function and N is the average number of photons of the Gaussian state ρ. Thus, we can get . Now, we introduce a reference system R, initially, the joint system RQ is prepared in a pure entangled states with , i.e., the pure state is a purification of the state ρQ. The system R is dynamically isolated and has a zero internal Hamiltonian, while the system Q undergoes an internal with above thermal noise channel ΦQ. The final state of RQ is described by the state ρRQ′. Then the entropy exchange Se = S(ρRQ′) = g(N1) + g(N2), where , , , 15 and u is the positive root of the equation .

  1. 1

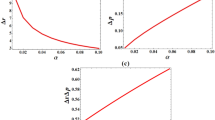
    If Ns = 0, i.e., the input state ρQ = |0〉 〈0|, then we can easily derive . On the other hand, as vs = 0 and u = 1, we see that N1 = 0, and Se = g(N1) + g(N2) = g(Nn). Thus it follows that in this case.

  2. 2

    If , we can set Ns = 1 and Nn = 1. Then, and . In this case we can derive and . Then it is easily checked that and . Hence we have whenever ρQ.

Discussion

The notion of entropy exchange can be introduced in infinite-dimensional quantum systems with the same form as that in finite-dimensional systems if we allow it may take infinity value. Thus, for a state ρQ and a channel ΦQ in an infinite-dimensional system Q, the entropy exchange Se is defined as Se = S(ρRQ′), where and is a purification of ρQ in a larger system RQ. This quantity does not depend on the choice of purifications of the state ρQ and characterizes the information exchange between the system Q and the external world during the evolution given by ΦQ. An explicit expression for Se in terms of ρQ and ΦQ is established, which asserts that , where with the sequence of Kraus operators in an operator-sum representation of ΦQ, and the minimum is taken over all operator-sum representations of ΦQ. In general, the entropy exchange is not equal to the change in entropy of the system Q, where ρQ′ = ΦQ(ρQ). But we have , and . Thus, if S(ρQ), S(ρQ′) are both finite, then . We also give some examples which illustrates that the entropy exchange is different from the change of entropy. In general the entropy exchange is larger than the change of entropy.

Additional Information

How to cite this article: Duan, Z. and Hou, J. Entropy exchange for infinite-dimensional systems. Sci. Rep. 7, 41692; doi: 10.1038/srep41692 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.